УСТРОЙСТВО ДЛЯ УСПОКОЕНИЯ КОЛЕБАНИЙ УПРУГОГО ЭЛЕМЕНТА ПЕРЕМЕННОЙ ЖЕСТКОСТИ Российский патент 2002 года по МПК G05D19/02 F16F15/00 

Изобретение относится к области демпфирования колебаний упругих элементов объектов, может быть использовано при проектировании и создании перспективных систем управления объектами нежесткой конструкции и является усовершенствованием изобретения по авторскому свидетельству 1500990 [1].

Целью изобретения является повышение быстродействия устройства.

На фиг.1 представлена функциональная схема предлагаемого устройства, на фиг. 2 - структурная схема блока преобразования координат, на фиг.3 - то же, нормирующего блока, на фиг.4 - то же, блока расчета параметров, на фиг.5 - то же, блока оценки частоты, на фиг.6 - то же, блока формирования параметра глубины управления, на фиг.7 - то же, блока управления жесткостью упругого элемента, на фиг.8 - фазовая траектория движения упругого элемента.

Устройство для успокоения колебаний упругого элемента переменной жесткости содержит (фиг. 1): объект 1 управления с присоединенным упругим элементом, датчик 2 отклонения упругого элемента, дифференцирующий блок 3, блок 4 оценки частоты, блок 5 формирования параметра глубины управления, блок 6 управления жесткостью упругого элемента, регулятор 7 жесткости, генератор 8 тактовых импульсов, ключ 9, компаратор 10, блок 11 преобразования координат, нормирующий блок 12 и блок 13 расчета параметров. Первый, второй и третий источники постоянного напряжения на схеме не показаны.

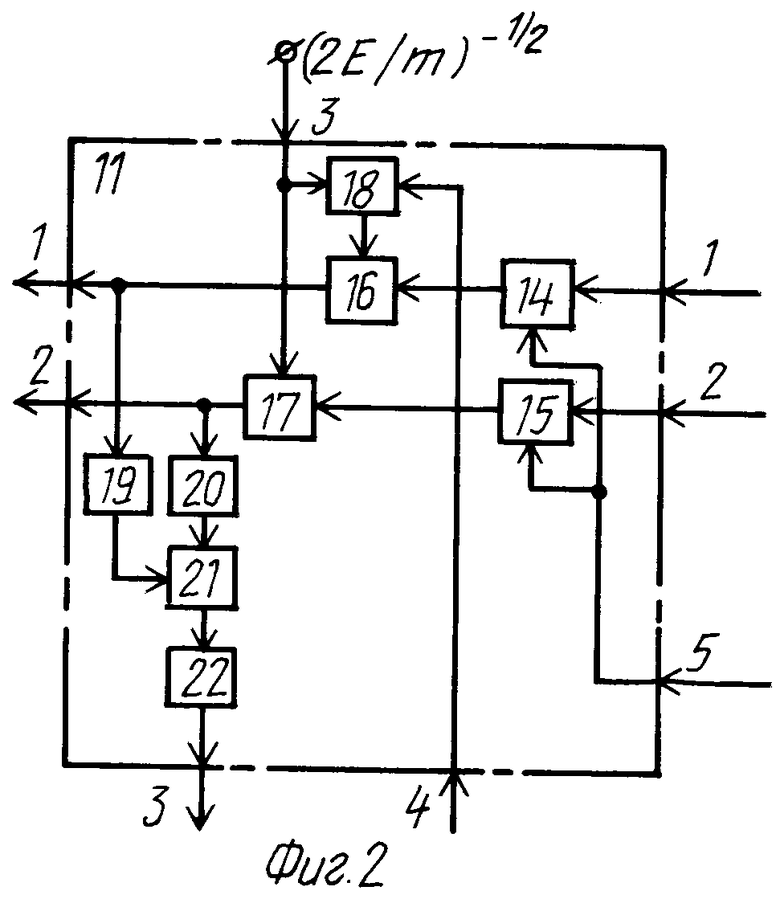
Блок 11 преобразования координат (фиг.2) содержит первый и второй ключи 14 и 15, первый 16, второй 17 и третий 18 блоки умножения, первый и второй квадраторы 19 и 20, сумматор 21, нелинейный элемент 22, выполняющий функцию извлечения квадратного корня.

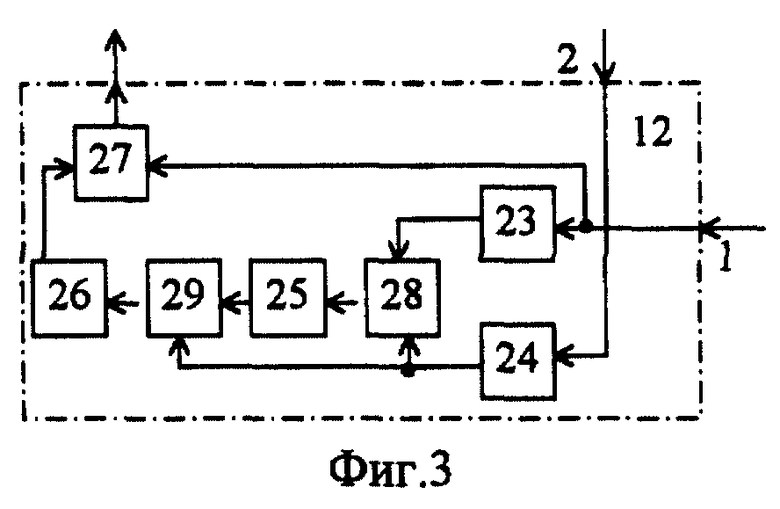
Нормирующий блок 12 (фиг.3) содержит первый 23, второй 24, третий 25 и четвертый 26 нелинейные элементы, первый и второй делители 27 и 28, блок 29 умножения, причем нелинейные элементы 23 и 24 служат для формирования функции натурального логарифма от входных сигналов, нелинейный элемент 25 осуществляет выделение целой части от входного сигнала, а нелинейный элемент 26 обеспечивает реализацию экспоненциальной функции.

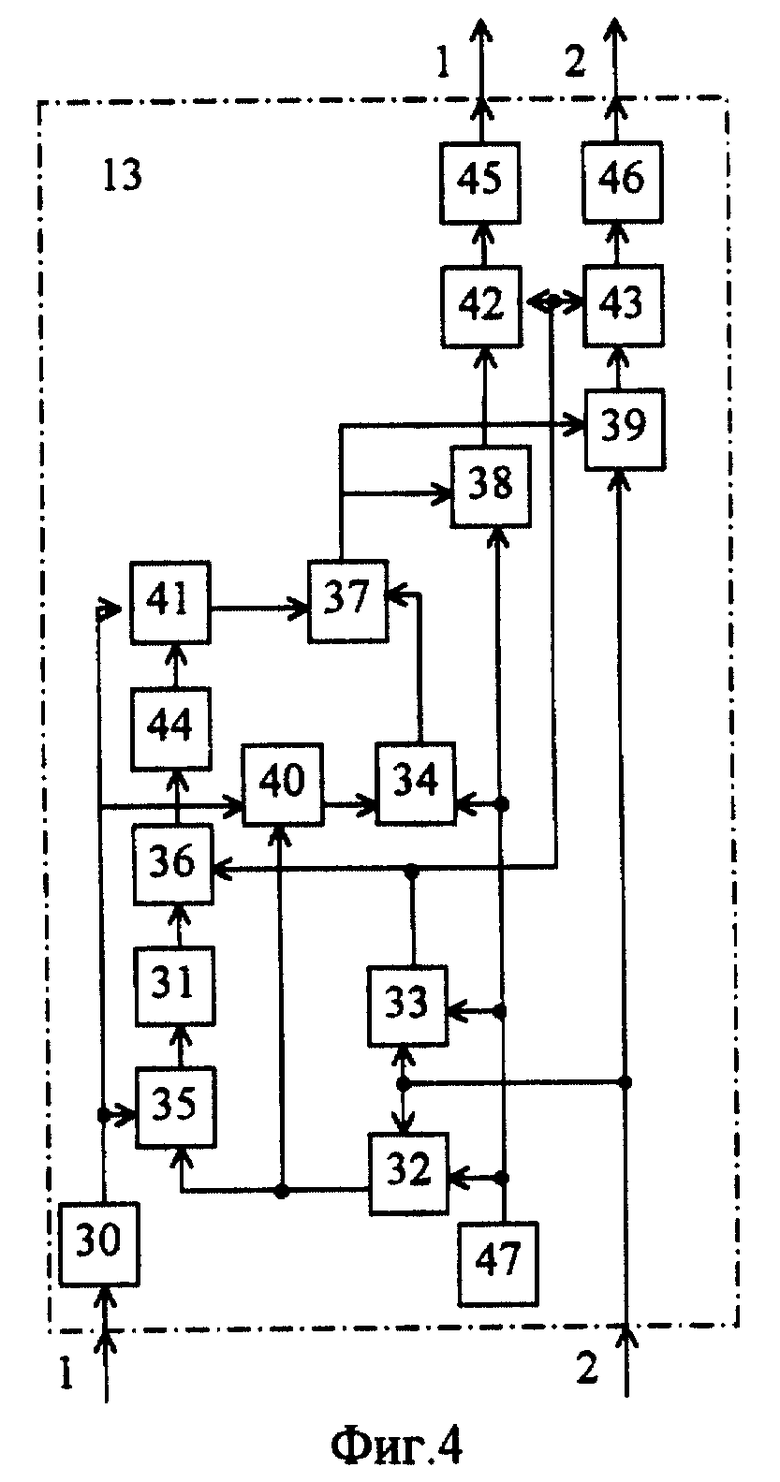
Блок 13 расчета параметров (фиг. 4) содержит первый 30 и второй 31 квадраторы, первый-восьмой сумматоры 32-39, первый-четвертый делители 40-43, первый 44, второй 45 и третий 46 нелинейные элементы - формирователи квадратного корня, источник 47 единичного постоянного напряжения.

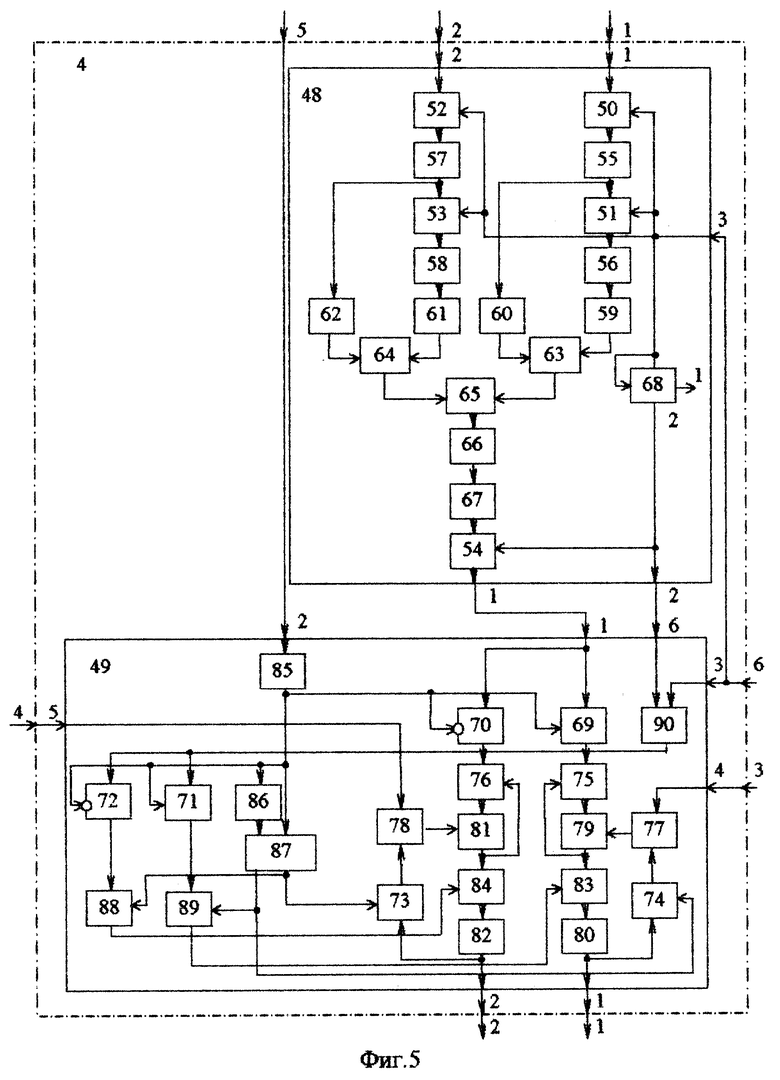
Блок 4 оценки частоты (фиг.5) содержит блок 48 формирования оценки и блок 49 осреднения.

Блок 48 формирования оценки содержит пять ключей 50 54, четыре запоминающих элемента 55-58, четыре квадратора 59-62, два сумматора 63 и 64, делитель 65, формирователь 66 модуля, нелинейный элемент 67, двухразрядный сдвиговый регистр 68.

Блок 49 осреднения содержит шесть ключей 69-74, четыре сумматора 75-78, четыре запоминающих элемента 79-82, два делителя 83 и 84, элемент 85 задержки, инвертор 86, триггер 87, два счетчика 88 и 89, элемент И 90.

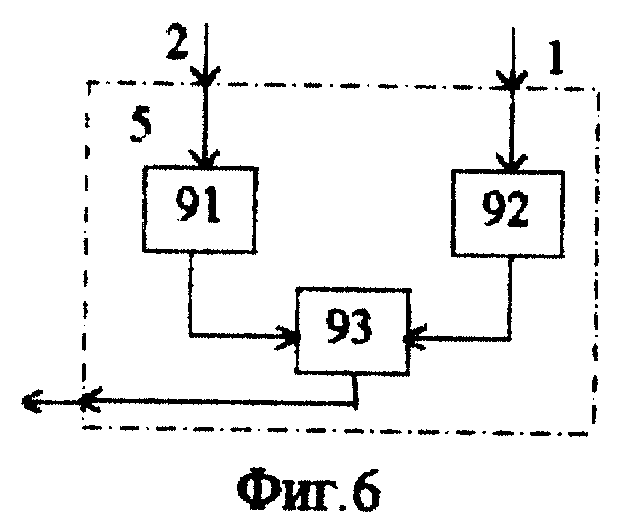
Блок 5 формирования параметра глубины управления (фиг.6) содержит два квадратора 91-92, делитель 93.

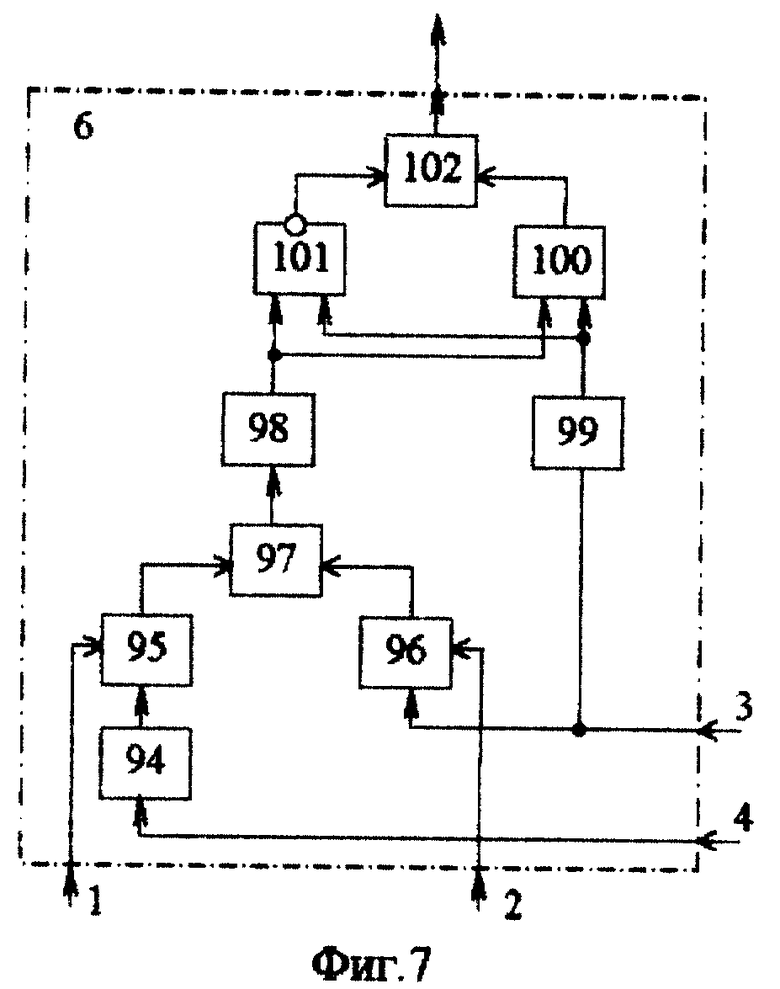
Блок 6 управления жесткостью упругого элемент (фиг.7) содержит инвертор 94, два делителя 95 и 96 напряжения, сумматор 97, два релейных элемента 98 и 99, элемент И 100, элемент ИЛИ-НЕ 101, элемент ИЛИ 102.

В основу изобретения положено следующее.

Динамика объекта управления в режиме свободных колебаний, в предположении малости его собственной диссипации, описывается системой дифференциальных уравнений второго порядка: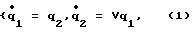

где q₁, q₂ - обобщенные фазовые координаты осциллятора;
V∈[V_min, V_max] - управляющий параметр, характеризующий жесткостные свойства упругого элемента (УЭ),
V_min = ω2min

; V_max = ω2max; ω_max и ω_min - максимальное и минимальное значения собственной частоты колебаний осциллятора из диапазона возможных изменений.

Известна формулировка задачи t-оптимального подавления колебаний упругого элемента за счет изменения его жесткости и в виде [1,2]: требуется найти закон изменения параметра V, обеспечивающий перевод объекта (1) из начального состояния {q₁(t₀)=q₁₀, q₂(t₀)=q₂₀} в конечное состояние {q_1k(t_k)=0, q_2k(t_k)=0} и при этом доставляющий минимум показателю качества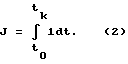

Однако следует отметить, что с технической точки зрения целесообразно обеспечить перевод УЭ в некоторую достаточно малую окрестность начала координат, в которой энергия остаточных колебаний не превышает заданный максимально допустимый уровень E. В этой связи возможна другая постановка задачи t-оптимального гашения колебаний осциллятора. Пусть в номинальном режиме функционирования жесткость УЭ устанавливается максимальной (ω = ω_max). Тогда полную механическую энергию колебаний осциллятора в начальный момент времени t₀ оценим соотношением E₀ = 0,5m(ω2max

q210+q220)>E_*, где m - инерционный параметр УЭ.

Требуется найти закон изменения параметра V, который обеспечивает перевод объекта (1) в конечное состояние {q₁(t_k)=q_1k, q₂(t_k)=q_2k}, удовлетворяющее ограничению
E_k = 0,5m(ω2max

q21k+q22k)<E_*, (3)
и доставляет при этом минимум функционалу (2).

В дальнейшем без ограничения общности положим t₀=0. Заменим ограничение (3) равенством Е_k=Е_*. Отметим, что если в управляемом процессе обеспечивается невозрастание энергии колебаний УЭ, то проведенная замена не приводит к суживанию множества искомых решений поставленной задачи.

Введем обозначения: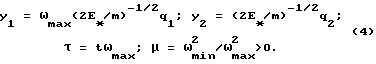

В новых координатах система (1) преобразуется к виду:
y'₁=y₂, y'₂=-uy₂, (5)
где 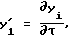i= 1,2; u = ω²/ω2max

; и ∈[μ;1] - ограниченный управляющий параметр, и рассматриваемая задача t-оптимального управления жесткостью осциллятора формулируется следующим образом.

Требуется найти управление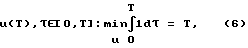

переводящее систему (5) из состояния {y₁(0), y₂(0)}: y₁ ²(0)+y₂ ²(0)>1 в состояние
{y₁(T),y₂(T)}∈Φ(T):y21

(T)+y22(T)-1 = 0. (7)
Задача (5)-(7) является классической задачей оптимального управления и может быть решена с использованием принципа максимума Л.С. Понтрягина [3].

Введем в рассмотрение гамильтониан
H = -1+ψ₁y₂-uψ₂y₁, (8)
где ψ₁,ψ₂ - сопряженные переменные, удовлетворяющие каноническим уравнениям: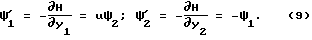

В соответствии с принципом максимума оптимальное управление u₀, являющееся решением задачи (5)-(7), удовлетворяет условию 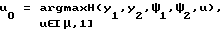из которого устанавливается его структура: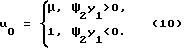

Несложно показать, что в рассматриваемой задаче не существует вырожденных управлений, не заданных структурой (10). Данное обстоятельство позволяет доопределить функцию u₀ в точках, где ψ₂у₁=0, из условий ее непрерывности справа (слева). Следовательно, допустимо принять, что оптимальное управление u₀ является кусочно-постоянной функцией и на каждом интервале постоянства может принимать значения либо u₀=1, либо u₀=μ.

На каждом интервале постоянства управления u₀ решение систем (5) и (9) имеют вид: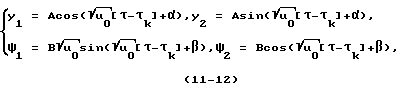

где τ∈[0,τ_k], τ_k - конец интервала; А, В, α,β - постоянные на интервале амплитуды и фазы колебаний - решений соответственно прямой и сопряженной систем, причем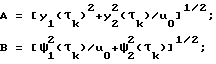


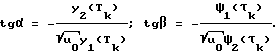
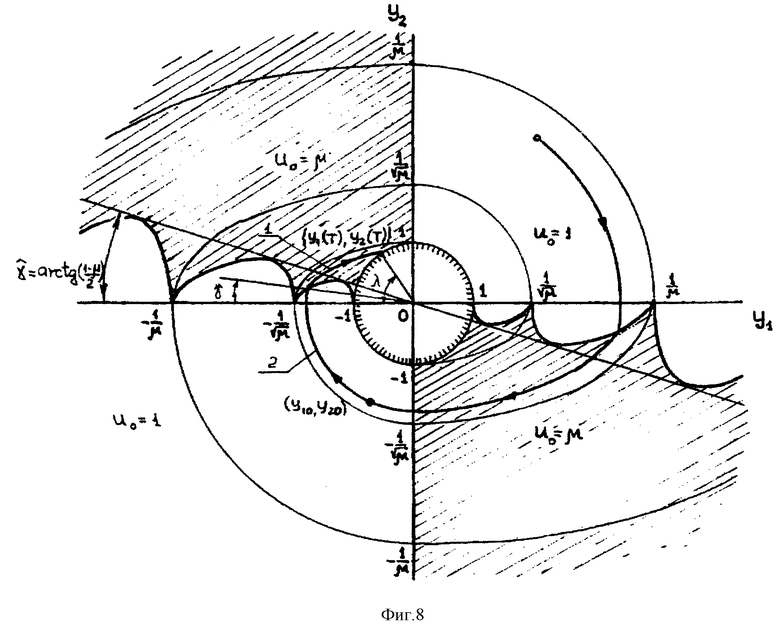
В дальнейшем удобно воспользоваться построениями на фазовой плоскости (y₁, y₂), на которой множество конечных состояний Ф(Т), определенное соотношением (7), представляет единичную окружность. Из (11) получим уравнение фазовой траектории осциллятора в этой плоскости
y₁ ²+y₂ ²/u₀=A². (13)
Отсюда непосредственно следует, что при u₀= 1 фазовая траектория УЭ представляет собой окружность с центром в начале координат, а при u₀=μ>0 - эллипс, получаемый из соответствующей окружности сжатием по оси Оy₂ с коэффициентом 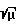. Движение фазовой точки по указанным траекториям осуществляется по часовой стрелке.

Учитывая данные обстоятельства, а также принимая во внимание непрерывность фазовых траекторий УЭ, заключаем, что окончание управляемого процесса (приход фазовой точки на финальное множество Ф(Т)) может иметь место лишь при u₀= μ, причем только во втором или четвертом квадрантах фазовой плоскости. В свете вышесказанного, в соответствии с оптимальной логикой (10), переключение с минимальной жесткости на максимальную должно осуществляться на оси y₁=0, а обратный переход - в точках фазовой плоскости, удовлетворяющих условию ψ₂=0.

Исследуем случай, когда достаточно одного переключения управления дня перевода фазовой точки на множество Ф(Т), при этом для определенности будем полагать, что финальная точка лежит в четвертом квадранте фазовой плоскости (фиг.8).

Пусть в начальный момент времени упругая система находится в одной из точек дуги окружности 2 и характеризуется начальной амплитудой ρ₁(y210

+y220)^1/2. Согласно логике (10), в некоторый момент τ_* в точке фазовой траектории {y₁(τ_*), y₂(τ_*)}, характеризующейся фазовым углом γ = -arctg[y₂(τ_*)/y₁(τ_*)], должно произойти переключение с режима u₀=1 на режим u₀=μ. Очевидно, что для сокращения времени процесса γ∈[0,π/2 После переключения управления система движется по эллиптическому участку 1 и в конечный момент Т приходит в точку {y₁(T), y₂(T)}∈Φ(T), характеризующуюся фазовым углом λ∈(0,π/2. Связь между γ и λ может быть получена из (13) в применении к эллиптическому участку траектории:
y21(τ_*)+y22(τ_*)/μ = y21(T)+y22(T)/μ.
Отсюда с использованием соотношений
y₁(τ_*) = -ρ₁cosγ; y₂(τ_*) = ρ₁sinγ;
y₁(T) = -cosλ; y₂(T) = sinλ
имеем
sin²λ = {ρ21[μ+(1-μ)sin²γ]-μ}/(1-μ). (14)
Определим время процесса. Затраты на движение по дуге 2 окружности составляют
τ₁ = |arctg(y₂₀/y₁₀)|+γ.
Для определения временных затрат на движение по эллиптическому участку 1 целесообразно осуществить переход на фазовую плоскость 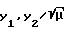На этой плоскости траектория участка 1 представляется дугой окружности, движение по которой (см. (11)), осуществляется с постоянной угловой скоростью, равной 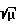Вычислим углы γ′ и λ′, соответствующие углам γ и λ на новой плоскости.

Имеем

или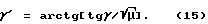

Аналогичным образом получим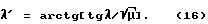

Следовательно, время движения по эллиптическому участку 1 составит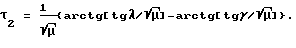

Таким образом, суммарное время процесса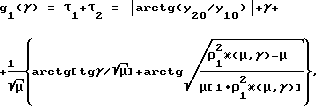

где учтена связь (14) и введено обозначение κ(μ,γ) = μ+(1-μ)sin²γ.
Смысл оптимизации управления сводится к нахождению угла γ^*:

Исследования функции g₁(γ^*) на экстремум показывает, что ее точка минимума должна удовлетворять условию
tgγ^*/{[ρ21

κ(μ,γ^*)-μ][1-ρ21κ(μ,γ^*)]}^1/2-1 = 0 (17)
при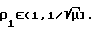
Соотношение (17) может быть преобразовано к виду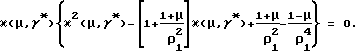

Учитывая, что при допустимых значениях параметров μ и γ^* κ(μ,γ^*)≠0, находим интересующий нас корень приведенного выше квадратного уравнения: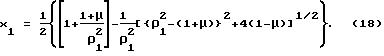

Используя (18), получим выражение для оптимального угла γ^*:
γ^* = arcsin{[κ₁-μ]/(1-μ)}^1/2. (19)
Отношения (18) и (19) свидетельствуют о том, что в случае одного переключения управления оптимальный угол логики γ^* зависит не только от параметра μ глубины управления жесткостью, но также от начальной амплитуды процесса. Данный результат существенно отличается от полученного в работе [2] и положенного в дальнейшем в основу изобретения [1].

Получение аналитических зависимостей для параметра γ^* в случае нескольких переключении управления в течение процесса представляет существенные трудности. В этой связи предлагается воспользоваться свойством подобия рассматриваемой системы, суть которого состоит в том, что для любого из диапазонов начальных амплитуд 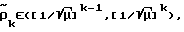где k - натуральное число, можно сформулировать задачу о t-оптимальном приведении осциллятора на границу диапазона - окружность радиуса 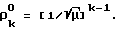Эта задача преобразованием координат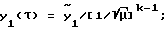

.

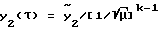сводится к постановке (5)-(7), решение которой известно. Следовательно, для каждого из вышеуказанных диапазонов начальных амплитуд соотношения (18)-(19) сохраняют свой вид при условии, что в этих соотношениях принято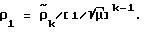

На фиг. 8 на фазовой плоскости (у₁, у₂) для значения параметра μ=const качественно показан вид линии переключения управления. На интервале начальных амплитуд 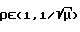она построена с использованием соотношений (18) и (19), а для диапазона начальных амплитуд 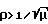- с использованием свойства подобия.

Предлагаемое устройство функционирует следующим образом. После воздействия внешнего возмущающего момента упругий элемент начинает колебаться с максимальной частотой ω_max, поскольку в состоянии покоя жесткость упругого элемента максимальна (из условия снижения амплитуды колебаний, возникающих от действия внешнего возмущающего импульса). Датчик 2 отклонения начинает выдавать текущее значение величины обобщенной координаты q₁ отклонения упругого элемента, которое поступает на вход дифференцирующего блока 3, первый вход блока 4 оценки частоты и первый вход блока 11 преобразования координат. Текущее значение обобщенной скорости q₂ упругого элемента, выдается с выхода дифференцирующего блока 3 на второй вход блока 4 оценки частоты и второй вход блока 11 преобразования координат. Сигналы с первого и второго входов блока 11 преобразования координат поступают на информационные входы ключей 14 и 15 соответственно, которые открываются импульсами с генератора 8 тактовых импульсов, благодаря чему осуществляется общая синхронизация процессов в блоке 11 преобразования координат с процессами в остальной части системы. Поэтому в начале каждого (i+1)-го такта генератора тактовых импульсов на втором выходе блока 4 оценки частоты уже сформирована оценка текущего значения ω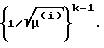(i)max

максимальной частоты упругого элемента, которая поступает на четвертый вход блока 11 преобразования координат, а оттуда - на вход блока 18 умножения. На выходе блока 18 умножения формируется сигнал (2E_*/m)^-1/2ω(i)max причем информация о коэффициенте передачи блока 18 умножения поступает на его второй вход с третьего входа блока 11 преобразования координат. Аналогичный сигнал поступает и на второй вход блока 17 умножения. На выходах блоков 16 и 17 умножения формируется соответственно ω(i)max(E_*/m)^-1/2q₁ и (E_*/m)^-1/2q₂, что соответствует преобразованию на основе формул (4). Полученная информация выдается на первом и втором выходах блока 11 преобразования координат, которым в известном устройстве соответствуют выходы с датчика 2 отклонения и дифференцирующего блока 3. Одновременно эта же информация используется для того, чтобы с помощью квадраторов 19 и 20, сумматора 21 и нелинейного элемента 22 сформировать сигнал ρ = [y21+y22]^1/2 о величине текущей амплитуды колебаний упругого элемента, который с выхода нелинейного элемента 22 поступает на третий выход блока 11 преобразования координат, а оттуда - на вход компаратора 10, где сравнивается с единицей. Если ρ≤1, то сигнал с компаратора 10 закрывает ключ 9, и возможность управления жесткостью упругого элемента блокируется: фиксируется максимальная жесткость упругой системы. В противном случае, когда ρ>1 (см. (7)), ключ 9 открывается и сигнал с выхода блока 6 управления жесткостью упругого элемента начинает изменять состояние регулятора 7 жесткости (а через него и частоту упругого элемента) в соответствии с оптимальной логикой. Информация о текущей амплитуде ρ колебаний упругого элемента с третьего выхода блока 11 преобразования координат поступает также на первый вход нормирующего блока 12, а текущее значение μ⁽ⁱ⁾ параметра глубины управления, сформированное на выходе блока 5, подается на второй вход нормирующего блока 12. Сигналы с первого и второго входов нормирующего блока 12 поступают соответственно на входы нелинейных элементов 23 и 24, на выходе которых формируются соответственно сигналы Inρ и 0,5 Inμ⁽ⁱ⁾ На выходе делителя 28 формируется 2lnρ/lnμ⁽ⁱ⁾, на выходе нелинейного элемента 25 - сигнал [2lnρ/lnμ⁽ⁱ⁾] = k-1 где k∈N, k≥1, [•] - целая часть числа; на выходе блока 29 умножения формируется сигнал - 0,5 (k-l)lnμ⁽ⁱ⁾, который нелинейным элементом 26 преобразуется в На выходе делителя 27 в полном соответствии с формулой (20) формируется сигнал 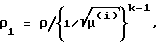который образует выход нормирующего блока 12.

Информация с выхода нормирующего блока 12 поступает на первый вход блока 13 расчета параметров, на второй вход которого приходит сигнал μ⁽ⁱ⁾ сформированный на выходе блока 5. Отметим, что совокупность элементов 30-37, 40, 41, 44 и 47 используется для формирования значения функции κ₁ по соотношению (18), а элементы 38, 39,42,43,45,46 и 47 - для формирования значений cosγ^* и -sinγ^* по соотношениям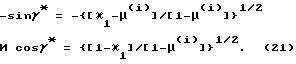

На выходах сумматоров 32 и 33 формируются соответственно сигналы (1+μ⁽ⁱ⁾) и (1-μ⁽ⁱ⁾) на выходе сумматора 35 - сигнал {ρ21

-(1+μ⁽ⁱ⁾)}, на выходе сумматора 36 - сигнал {ρ21-(1+μ⁽ⁱ⁾)}²+4(1-μ⁽ⁱ⁾) на выходе делителя 41 формируется -1/ρ21[ρ21-(1+μ⁽ⁱ⁾)}²+4(1-μ⁽ⁱ⁾)]^1/2, на выходе сумматора 34 - сигнал (1+μ)/ρ21+1, а на выходе сумматора 37 - сигнал κ₁ образованный по формуле (18). Далее на выходах сумматоров 38 и 39 формируются соответственно 1-κ₁ и κ₁-μ⁽ⁱ⁾, а на выходах нелинейных элементов 45 и 46 - соответственно cosγ^* и -sinγ^* согласно формулам (21).

Полученная информация выдается на первом и втором выходах блока 13 расчета параметров, которым в устройстве-прототипе отвечает информация, поступающая соответственно на первый и второй входы блока 6 управления жесткостью упругого элемента.

В остальном функционирование предлагаемого устройства аналогично известному.

Положительный эффект - сокращение длительности переходных процессов в предлагаемом устройстве достигается за счет осуществления непрерывной коррекции параметров линии переключения управления в зависимости от текущей величины амплитуды колебаний в соответствии с оптимальной логикой.

Таким образом, отличительные признаки предлагаемого устройства способствуют достижению поставленной цели.

Источники информации
1. А.с. СССР 1500990, кл.⁴ G 05 В 11/01, 1987 (прототип).

2. Мануйлов Ю.С. Синтез оптимального управления жесткостью упругих динамических объектов // Приборостроение, 1986, т. XXIX, 11, с. 27-31.

3. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Г.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. - М.: Наука, 1969, 384 с.

Изобретение относится к демпфированию колебаний упругих элементов конструкции объектов, может быть преимущественно использовано при проектировании и создании перспективных систем управления объектами ограниченной жесткости. Технический результат заключается в повышении быстродействия устройства. Устройство содержит объект управления с присоединенным упругим элементом, датчик отклонения упругого элемента, дифференцирующий блок, блок оценки частоты, блок формирования параметров глубины управления, блок управления жесткостью упругого элемента, регулятор жесткости, генератор тактовых импульсов, ключ, компаратор, блок преобразования координат, нормирующий блок, блок расчета параметров. 3 з.п.ф-лы, 8 ил.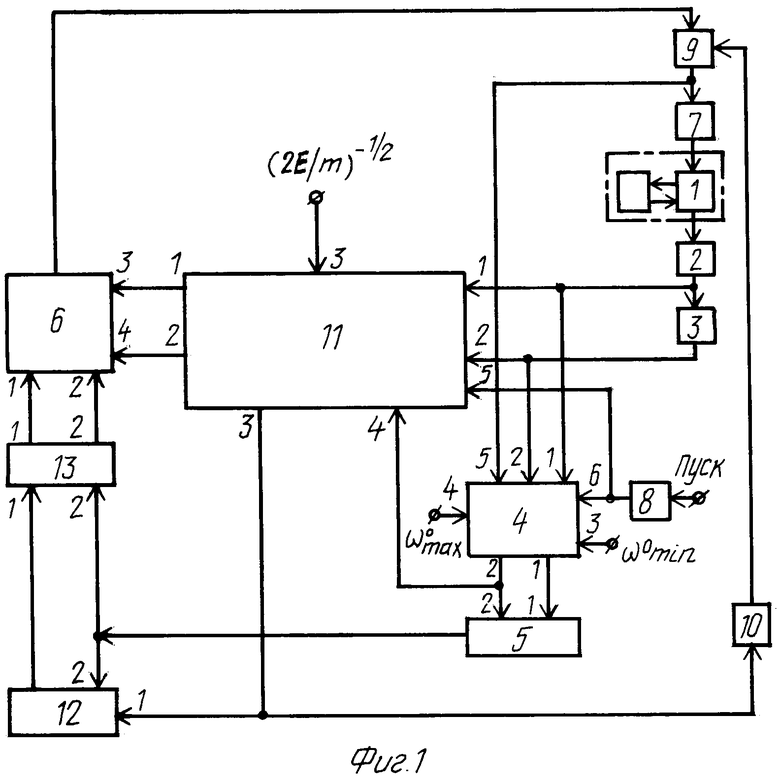

1. Устройство для успокоения колебаний упругого элемента переменной жесткости, содержащее блок управления жесткостью упругого элемента, объект управления с присоединенным упругим элементом переменной жесткости, к выходу которого подключен датчик отклонения упругого элемента, а ко входу - регулятор жесткости упругого элемента, выход датчика отклонения упругого элемента соединен с входом дифференцирующего блока и первым входом блока оценки частоты, второй, третий, четвертый, пятый и шестой входы которого подключены соответственно к выходу дифференцирующего блока, к первому и второму источникам постоянного напряжения, к входу регулятора жесткости упругого элемента и выходу генератора тактовых импульсов, первый и второй выходы блока оценки частоты соединены соответственно с первым и вторым входами блока формирования параметра глубины управления, отличающееся тем, что оно дополнительно снабжено ключом, компаратором, нормирующим блоком, блоком расчета параметров, третьим источником постоянного напряжения и блоком преобразования координат, первый, второй, третий, четвертый и пятый входы которого связаны соответственно с выходами датчика отклонения упругого элемента, дифференцирующего блока, третьего источника постоянного напряжения, вторым выходом блока оценки частоты и выходом генератора тактовых импульсов, первый и второй выходы блока преобразования координат соединены соответственно с третьим и четвертым входами блока управления жесткостью упругого элемента, а третий выход - с первым входом нормирующего блока и через компаратор - с управляющим входом ключа, выход нормирующего блока подключен к первому входу блока расчета параметров, первый и второй выходы блока расчета параметров соединены соответственно с первым и вторым входами блока управления жесткостью упругого элемента, выход которого через ключ связан с входом регулятора жесткости упругого элемента, выход блока формирования параметра глубины управления подключен ко вторым входам нормирующего блока и блока расчета параметров. 2. Устройство по п. 1, отличающееся тем, что блок преобразования координат содержит первый и второй ключи, первый, второй и третий блоки умножения, первый и второй квадраторы, сумматор и нелинейный элемент, выполняющий функцию извлечения квадратного корня, причем первый и второй входы блока преобразования координат соединены соответственно с информационными входами первого и второго ключей, выходы которых подключены соответственно к входам первого и второго блоков умножения, третий вход блока преобразования координат связан с входом третьего блока умножения и вторым входом второго блока умножения, выход которого соединен со вторым выходом блока преобразования координат и через последовательно соединенные второй квадратор, сумматор и нелинейный элемент - с третьим выходом блока преобразования координат, четвертый вход которого подключен ко второму входу третьего блока умножения, выход третьего блока умножения связан со вторым входом первого блока умножения, выход которого соединен с первым выходом блока преобразования координат и через первый квадратор - со вторым входом сумматора, пятый вход блока преобразования координат подключен к управляющим входам первого и второго ключей. 3. Устройство по п. 1, отличающееся тем, что нормирующий блок содержит первый и второй нелинейные элементы - формирователи натуральных логарифмов от входных сигналов, третий нелинейный элемент - формирователь целой части, четвертый нелинейный элемент, реализующий экспоненциальную функцию, первый и второй делители и блок умножения, причем первый вход номирующего блока соединен с входом первого делителя и через последовательно соединенные первый нелинейный элемент, второй делитель, третий нелинейный элемент, блок умножения, четвертый нелинейный элемент - со вторым входом первого делителя, выход которого подключен к выходу нормирующего блока, второй вход нормирующего блока через второй нелинейный элемент соединен со вторыми входами второго делителя и блока умножения. 4. Устройство по п. 1, отличающееся тем, что блок расчета параметров содержит первый и второй квадраторы, первый - восьмой сумматоры, первый - четвертый делители, первый, второй и третий нелинейные элементы - формирователи квадратного корня, источник единичного постоянного напряжения, причем первый вход блока расчета параметров через последовательно соединенные первый квадратор, четвертый сумматор, второй квадратор, пятый сумматор, первый нелинейный элемент, второй делитель, шестой сумматор, седьмой сумматор, третий делитель и второй нелинейный элемент соединен с первым выходом блока расчета параметров, выход первого квадратора связан со вторым входом второго делителя и через последовательно соединенные первый делитель и третий сумматор - со вторым входом шестого сумматора, выход источника единичного постоянного напряжения подключен к входу второго сумматора и вторым входам третьего и седьмого сумматоров, а также через первый сумматор - ко вторым входам четвертого сумматора и первого делителя, второй вход блока расчета параметров подключен ко вторым входам первого и второго сумматоров, а также через последовательно соединенные восьмой сумматор, четвертый делитель и третий нелинейный элемент связан со вторым выходом блока расчета параметров, выход второго сумматора соединен со вторыми входами пятого сумматора, третьего и четвертого делителей, а второй вход восьмого сумматора подключен к выходу шестого сумматора.