Изобретение относится к области демпфирования колебаний упругих элементов конструкции объектов и может быть преимущественно использовано при проектировании и создании перспективных систем управления объектами нежесткой конструкции.
Известно устройство [1] (аналог), предназначенное для гашения колебаний упругого элемента с малым коэффициентом пассивного демпфирования. Однако, это устройство недостаточно эффективно при успокоении колебаний упругих элементов конструкций с постоянной в течение процесса достаточно высокой пассивной диссипацией энергии. Целесообразнее в этих случаях использовать устройство [2] (прототип). Вместе с тем, весьма часто в упругой системе в течение управляемого процесса синхронно с изменениями жесткости происходят значительные изменения диссипативного параметра. Как правило, это явление обусловлено особенностями исполнительных органов системы управления. В частности, демпферы - регуляторы жесткости [3], построенные на использовании способности магнито-реологической суспензии (МРС) изменять свои свойства под действием электромагнитного поля [4] , согласованно с релейным изменением жесткости привносят в систему дополнительную диссипацию, зависящую от режима их работы.
В таких условиях устройство [2] не может обеспечить достаточного быстродействия. Целью изобретения является повышение быстродействия устройства.
На фиг.1 представлена функциональная схема предлагаемого устройства, на фиг. 2 - структурная схема блока выбора коэффициента диссипации, на фиг.3 - то же, блока расчета параметра глубины управления, на фиг.4 - то же, функционального блока, на фиг.5 - то же, блока расчета параметров, на фиг.6 - то же, блока оценки частоты, на фиг.7 - то же, блока управления, на фиг.8 - то же, блока преобразования координат, на фиг.9 - фазовая траектория упругого элемента на характерном полупериоде колебаний.
Устройство для успокоения колебаний упругого элемента переменной жесткости (фиг. 1) содержит: объект 1 управления с присоединенным упругим элементом, датчик 2 отклонения упругого элемента, дифференцирующий блок 3, блок 4 оценки частоты, блок 5 коррекции частоты, блок 6 управления, регулятор 7 жесткости, генератор 8 тактовых импульсов, блок 9 преобразования координат, блок 10 выбора коэффициента диссипации, блок 11 умножения.
Блок 5 коррекции частоты содержит блок 12 расчета параметра глубины управления, функциональный блок 13, блок 14 расчета параметров.
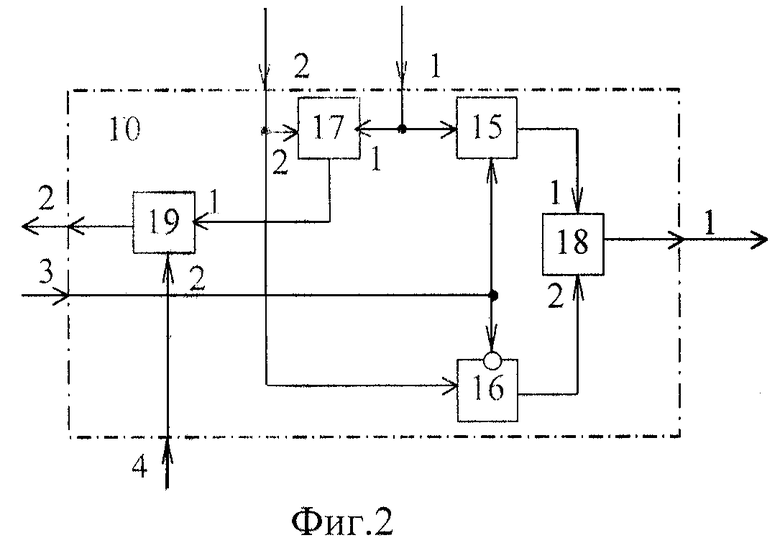
Блок 10 выбора коэффициента диссипации (фиг.2) содержит: первый и второй ключи 15 и 16, первый и второй сумматоры 17 и 18, делитель 19.
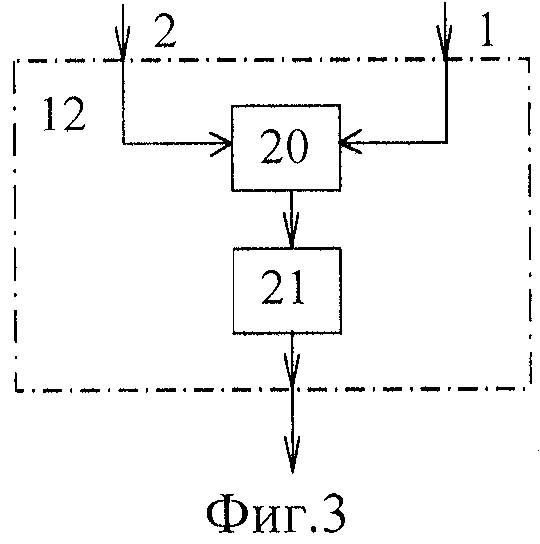
Блок 12 расчета параметра глубины управления (фиг.3) содержит: делитель 20 и квадратор 21.
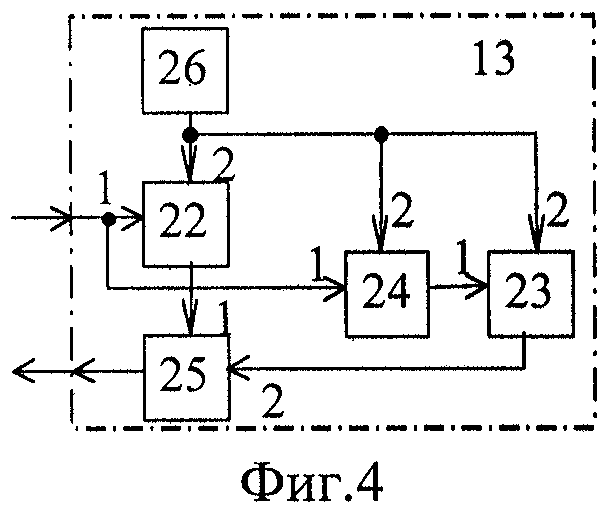
Функциональный блок 13 (фиг.4) содержит: первый и второй сумматоры 22 и 23, блок умножения 24, делитель 25, источник постоянного напряжения 26.
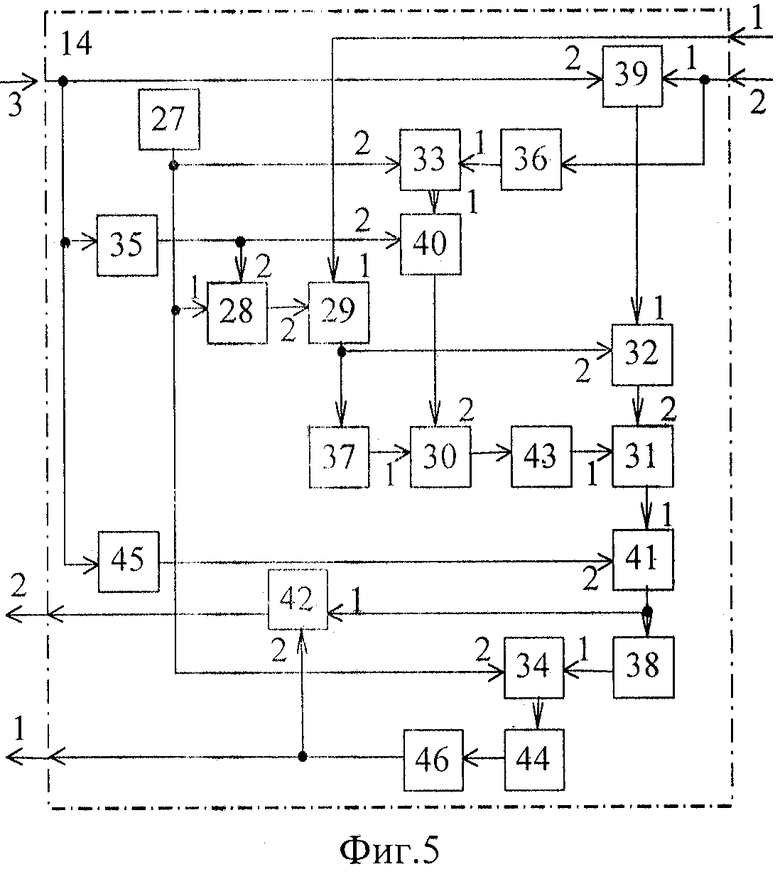
Блок 14 расчета параметров (фиг.5) содержит: источник постоянного напряжения 27, первый-седьмой сумматоры 28-34, первый-четвертый квадраторы 35-38, первый-четвертый блоки умножения 39-42, первый и второй вычислители квадратного корня 43 и 44, первый и второй вычислители обратной величины 45 и 46.
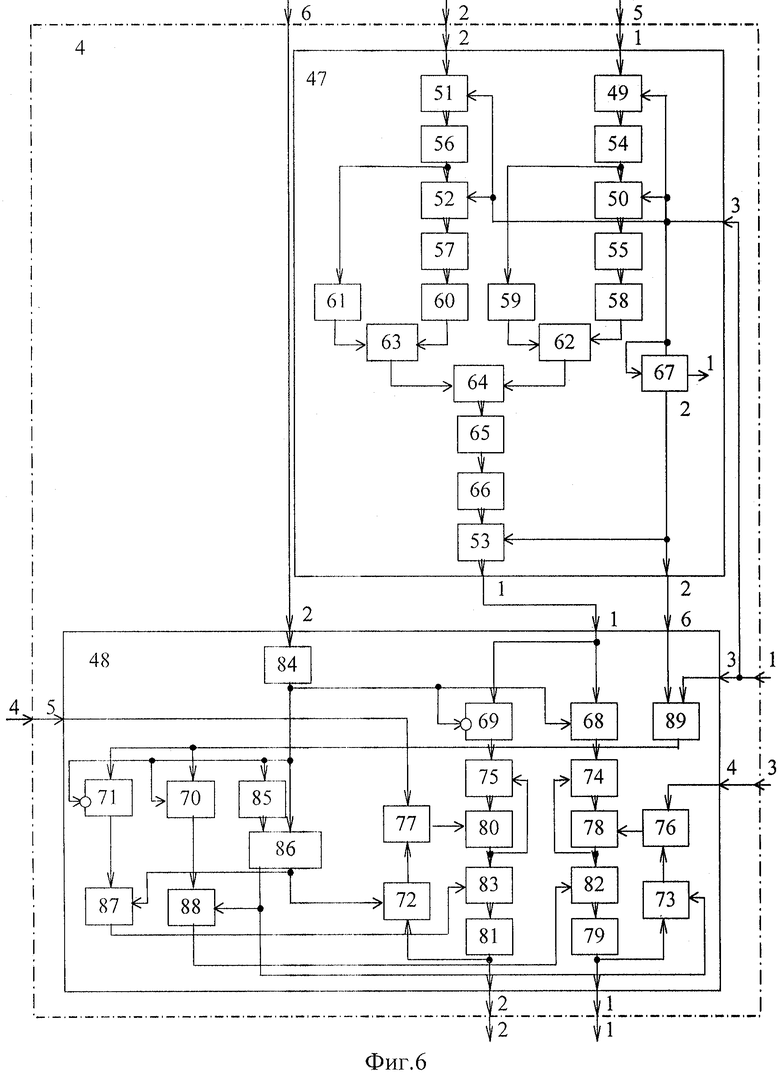
Блок 4 оценки частоты (фиг.6) содержит блок 47 формирования оценки и блок 48 осреднения.
Блок 47 формирования оценки содержит пять ключей 49-53, четыре запоминающих элемента 54-57, четыре квадратора 58-61, два сумматора 62 и 63, делитель 64, формирователь 65 модуля, нелинейный элемент 66, двухразрядный сдвиговый регистр 67.
Блок 48 осреднения содержит шесть ключей 68-73, четыре сумматора 74-77, четыре запоминающих элемента 78-81, два делителя 82 и 83, элемент 84 задержки, инвертор 85, триггер 86, два счетчика 87 и 88, элемент И 89.
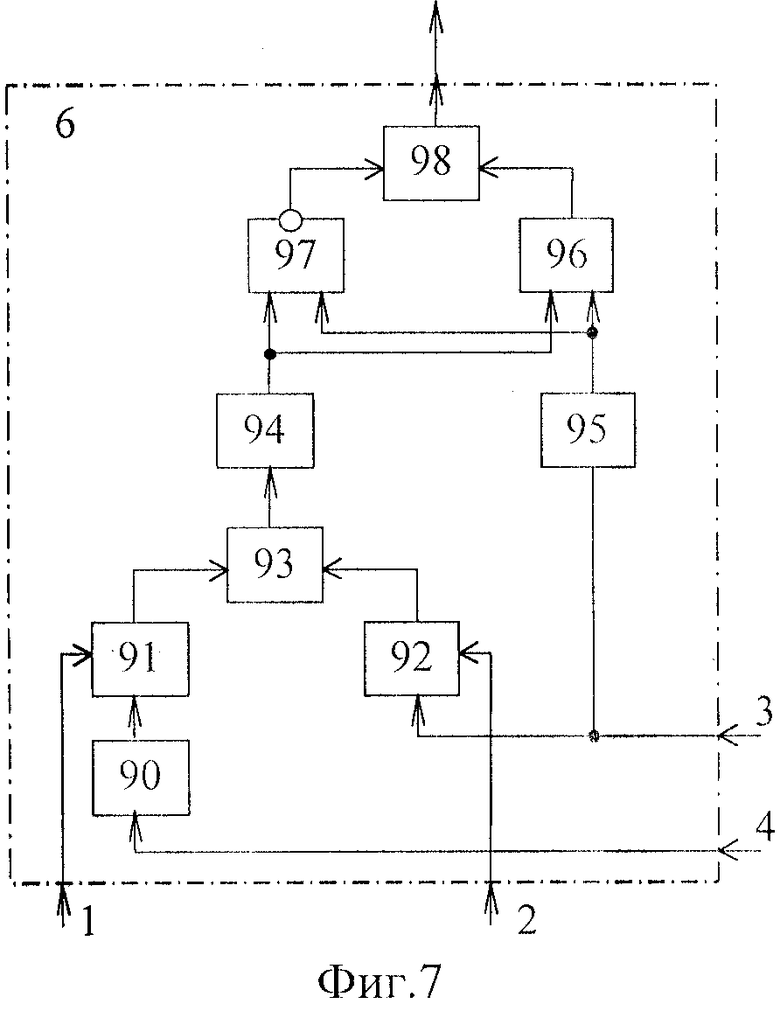
Блок 6 управления (фиг.7) содержит инвертор 90, два делителя 91 и 92 напряжения, сумматор 93, два релейных элемента 94 и 95, элемент И 96, элемент ИЛИ-НЕ 97, элемент ИЛИ 98.
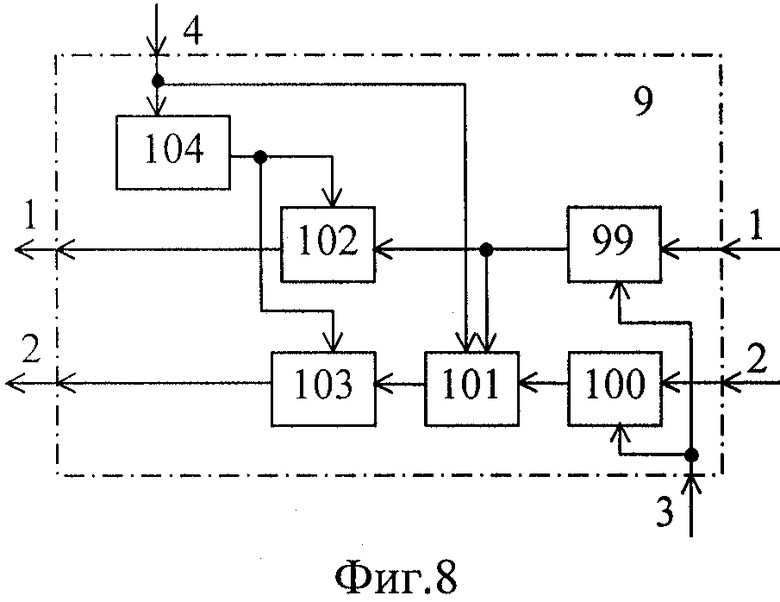
Блок 9 преобразования координат (фиг.8) содержит два ключа 99 и 100, сумматор 101, два блока умножения 102 и 103, генератор 104 экспоненциального напряжения.
В основу изобретения положено следующее.
Динамика упругого элемента (УЭ) с пассивным демпфированием описывается системой дифференциальных уравнений второго порядка: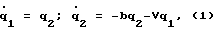
где qi, 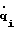 , i=1,2 - фазовые координаты и скорости; V∈[ω
, i=1,2 - фазовые координаты и скорости; V∈[ω
Построение строго оптимального управления жесткостью в задаче гашения колебаний системы (1) представляет значительные трудности. Вместе с тем, принимая во внимание синхронность и зависимость изменений диссипативного параметра системы от ее жесткости, целесообразно этот эффект считать сопутствующим. Такой подход позволяет в основу решения положить синтез субоптимального управления жесткостью по методике, изложенной в [2] для систем с постоянным демпфированием с коррекцией на нестационарность коэффициента диссипации. При этом используется структура и основные свойства оптимального управления, но достигается инвариантность субоптимального решения от начальных и терминальных условий процесса, что существенно упрощает его техническую реализацию.
Исходя из вышесказанного, далее считаем, что искомое управление жесткостью является кусочно-постоянным и может принимать значения либо V = ω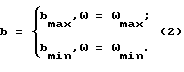
Данные обстоятельства позволяют путем проведения преобразования координат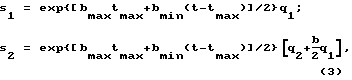
где t≥0, 0≤tmax≤t - соответственно текущее и суммарное время движения упругой системы с максимальной жесткостью, свести (1) к системе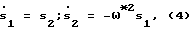
описывающей динамику свободного осциллятора без пассивного демпфирования. Здесь ω* = [ω2-b2/4]1/2 (соответственно ω
Далее целесообразно провести дополнительное преобразование
y1 = ω
и нормировать систему (4):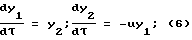
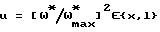 - управляющий параметр;
- управляющий параметр; 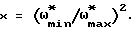
На каждом участке постоянства управляющего параметра решение системы (6) имеет вид: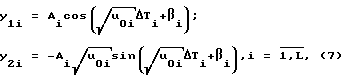
где ΔTi = τi-τki,τi∈[0,τki],τki>0 - интервал постоянства; L - число интервалов; Аi>0 и βi - постоянные на интервале амплитуды и фазы колебаний, причем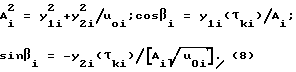
Первое уравнение (8) есть уравнение i-го участка траектории осциллятора на фазовой плоскости (y1, y2). Отсюда непосредственно следует, что при u0i= 1 фазовая траектория на i-м участке представляет собой дугу окружности с центром в начале координат и радиусом, равным амплитуде Аi, а при u0i=х - дугу эллипса, получаемого сжатием дуги соответствующей окружности по оси OY2 с коэффициентом 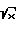 . Фазовая точка движется по часовой стрелке.
. Фазовая точка движется по часовой стрелке.
Необходимо иметь в виду, что с релейным согласно (2) изменением коэффициента диссипации b преобразования координат (3) теряют свою непрерывность. Это, в свою очередь, в общем случае приводит к разрывам фазовых траекторий в точках переключения управления на плоскости (у1, y2). Однако такие разрывы вполне допустимы, так как указанные координаты являются вспомогательными и не имеют непосредственного физического смысла. Тем не менее исследование удобно проводить именно на этой плоскости, поскольку она предоставляет неоспоримое преимущество: формальное разделение эффектов, обусловленных влиянием управления жесткостью и действием пассивного демпфирования на каждом из участков постоянства параметров упругой системы. Чтобы рассчитать параметры разрывов траекторий на плоскости (y1, y2) при переключениях управления, будем постоянно привязываться к непрерывному по фазовым координатам процессу, рассматриваемому на плоскости {q1, q2).
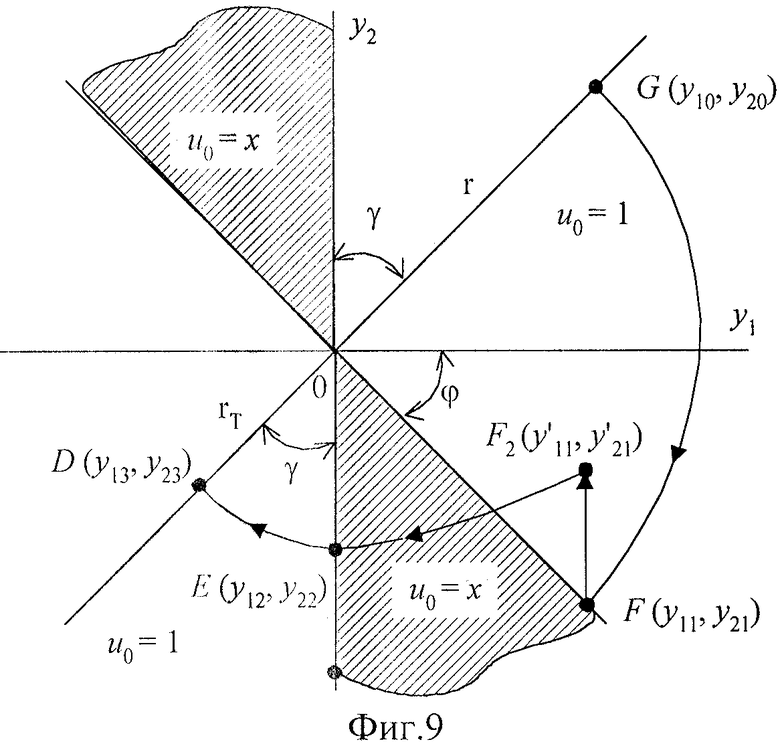
В соответствии с развиваемым подходом, фазовая траектория на характерном полупериоде колебаний аналогично случаю b = const [2] разбивается на три участка (фиг. 9). Пусть для определенности в начальный момент УЭ находится в точке G(y10, y20) 1-го квадранта фазовой плоскости {y1, y2). Как нетрудно убедиться, такой выбор начальной точки не является принципиальным для дальнейших рассуждений. Для координат конечной точки F первого участка движения по дуге окружности с максимальной жесткостью можем записать: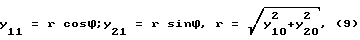
где ϕ - угол субоптимальной логики на плоскости (у1, у2).
Длительность этого участка составит
τ1 = π/2-ϕ-γ,ϕ∈(-π/2,π/2)γ∈(0,π). (10)
Согласно преобразованиям (3),(5) точке F на фазовой плоскости (q1, q2) соответствует точка F1 с координатами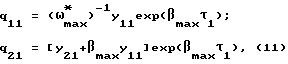
где βmax = -bmax/(2ω
При переключении управления на минимальную жесткость из-за разрывности преобразований (3) точка F на плоскости (у1, у2) отображается в точку Fz, координаты которой определяются из условий непрерывности фазовой траектории в точке F1 на плоскости (q1, q2):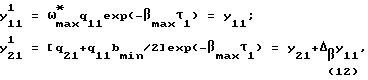
где 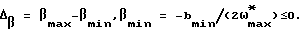
Дальнейшее движение с минимальной жесткостью, осуществляемое вплоть до пересечения оси OY2, удобнее рассматривать в плоскости 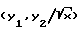 , где фазовая траектория представляется дугой окружности, по которой фазовая точка перемещается с постоянной угловой скоростью
, где фазовая траектория представляется дугой окружности, по которой фазовая точка перемещается с постоянной угловой скоростью 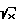 . На новой плоскости начальный фазовый угол ϕ1 участка траектории удовлетворяет соотношению
. На новой плоскости начальный фазовый угол ϕ1 участка траектории удовлетворяет соотношению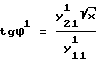 ,
,
откуда с использованием (12) найдем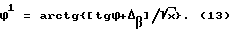
Поскольку конечный фазовый угол равен -π/2, то длительность рассматриваемого интервала движения с минимальной жесткостью определится следующим образом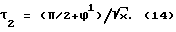
Координаты конечной точки Е этого участка на плоскости (y1, y2) вычисляются из условий ее принадлежности оси ОY2 и эллипсу y1 2+y2 2/x= (y11 1)2+(y21 1)2/x:
y12 = 0;y
Согласно преобразованиям (3), (5) точке Е на фазовой плоскости {q1, q2) соответствует точка E1 с координатами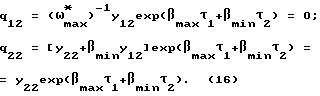
Из условий непрерывности траектории в точке Е1 следует непрерывность траектории и в точке Е (отсутствие скачка при переключении на максимальную жесткость).
Дальнейшее движение вплоть до окончания характерного полупериода колебаний осуществляется с максимальной жесткостью по дуге окружности в течение времени
τ3 = γ. (17)
Для квадрата амплитуды колебаний в конечной точке D можем записать r2 т = у2 13 + у2 23 = у2 12 + у2 22, откуда с использованием (9) и (15) получим выражение для коэффициента изменения квадрата амплитуды за полупериод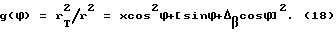
Длительность характерного полупериода на основе (10), (14) и (17) представляется в виде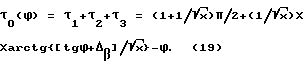
Используя (18) и (19), получим для коэффициента затухания амплитуды колебаний, вносимого в систему за счет согласованных синхронных регулярных переключений ее жесткости и диссипации и усредненного на целом числе базовых интервалов - характерных полупериодов, следующее выражение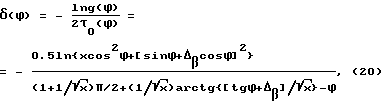
при фиксированных х и Δβ/ зависящее только от ϕ.
Таким образом, можно поставить задачу параметрической оптимизации: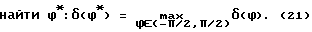
При определении области допустимых значений параметра ϕ здесь учтены симметрия субоптимальной логики относительно начала координат и невозможность переключения на минимальную жесткость на оси OY2.
При этом закон управления в координатном базисе (у1, у2) может быть представлен в виде: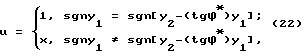
Подробное решение задачи (20)-(21) дано в [5]. Здесь лишь отметим, что аналитическое исследование функции δ(ϕ) из (20) на экстремум показало, что она достигает максимума в точке ϕ*, удовлетворяющей условию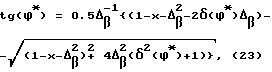
Для случая Δβ=0 соотношение (23) преобразуются к виду
tg(ϕ*) = -δ(ϕ*).
Связь (23) является трансцендентным уравнением, решение которого осуществлялось численным способом с помощью ПЭВМ. Результаты расчетов подтверждают тезис о том, что для повышения диссипативных свойств упругой системы параметр х целесообразно выбирать минимально возможным, т.е. обеспечивать максимально широкий диапазон регулирования жесткости. Также установлено, что зависимость δ*(x)|Δp=0 хорошо аппроксимируется соотношением
δ*(x) = (1-x)/[π(1.3+0.7x)],x∈[0.01,0.99]. (25)
Проведенные оценки степени близости аналитической зависимости (25) к численному решению уравнения (24) показали, что погрешность приближения не превышает 5%. Кроме того, оказалось, что полученная с использованием (25) и (23) аппроксимациониая зависимость субоптимального угла логики ϕ* от х
при допустимых значениях параметра Δβ отклоняется от численного решения задачи (20), (21) не более чем на 10%.
Предлагаемое устройство функционирует следующим образом. После воздействия внешнего возмущающего момента упругий элемент начинает колебаться с максимальной частотой ω
Датчик 2 отклонения начинает выдавать текущее значение величины обобщенной координаты отклонения упругого элемента, которое поступает на вход дифференцирующего блока 3 и первый вход блока 9 преобразования координат. Текущее значение скорости обобщенной координаты отклонения упругого элемента выдается с выхода дифференцирующего блока 3 на второй вход блока 9 преобразования координат.
При этом на выходе блока 6 управления сформирован сигнал u = 0, который через третий вход блока 10 выбора коэффициента диссипации поступает на управляющие входы ключей 15 и 16, открывает ключ 16 и закрывает ключ 15. Через ключ 16 и сумматор 18 на первом выходе блока 10 выбора коэффициента диссипации формируется сигнал b=bmax, который поступает на четвертый вход блока 9 преобразования координат.
В случае переключения жесткости упругого элемента с максимальной на минимальную, на выходе блока 6 управления формируется сигнал u= 1, который открывает ключ 15 и закрывает ключ 16. В результате на первом выходе блока 10 выбора коэффициента диссипации формируется сигнал b=bmin. Таким образом, блок 10 выбора коэффициента диссипации реализует кусочно-постоянную функцию (2) изменения параметра b упругой системы синхронно с управляемым изменением ее частоты.
Импульсы с генератора 8 тактовых импульсов обеспечивают общую синхронизацию процессов в блоке 9 преобразования координат с процессами в остальной части системы. На первом и втором выходах блока 9 преобразования координат с каждым тактовым импульсом формируется соответственно сигналы 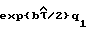 и
и 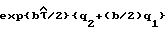 , что соответствует дискретному преобразованию на основе формул (3) (здесь
, что соответствует дискретному преобразованию на основе формул (3) (здесь  - период следования импульсов с генератора 8 тактовых импульсов, параметр b изменяется согласно (2)).
- период следования импульсов с генератора 8 тактовых импульсов, параметр b изменяется согласно (2)).
С использованием этой информации в блоке 4 оценки частоты на каждом такте генератора 8 тактовых импульсов сформируются оценки максимальной ω
cosϕ* = [tg2ϕ*+1]-1/2;
sinϕ* = tgϕ*cosϕ*,
tgϕ* определяется по соотношению (23). При этом элементы 27-33, 35-37, 39-41, 43 и 45 блока 14 расчета параметров применяются для формирования на выходе блока умножения 41 сигнала tgϕ* по формуле (23); элементы 27, 34, 38, 44, 46 - для расчета cosϕ*, а блок умножения 42 - для формирования sinϕ*. Полученным сигналам cosϕ* и sinϕ* соответствуют сигналы 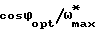 и sinϕopt в устройстве - прототипе.
и sinϕopt в устройстве - прототипе.
В остальном функционирование предлагаемого устройства полностью аналогично известному.
Источники информации
1. Авторское свидетельство СССР 1500990, кл. 4 G 05 B 11/01, 1987 (аналог).
2. Авторское свидетельство СССР 1587465, кл. 4 G 05 B 11/01, 1988 (прототип).
3. Авторское свидетельство СССР 1827465, кл.3 F 16 F 6/00, 1991.
4. Шульман З. П., Кордонский В.И. Магнитореологический эффект. -Минск: Наука и техника, 1982. - 184 с.
5. Шалымов С.В. Оптимальное гашение колебаний простых упругих систем с управляемой жесткостью. - МО РФ, 2001.-101 с.
Изобретение относится к демпфированию колебаний упругих элементов конструкции объектов. Технический результат заключается в повышении быстродействия устройства. Устройство содержит объект управления с присоединенным упругим элементом, датчик отклонения упругого элемента, дифференцирующий блок, блок оценки частоты, блок коррекции частоты, блок управления, регулятор жесткости, генератор тактовых импульсов, блок преобразования координат, блок выбора коэффициента диссипации, блок умножения. 5 з.п. ф-лы, 9 ил.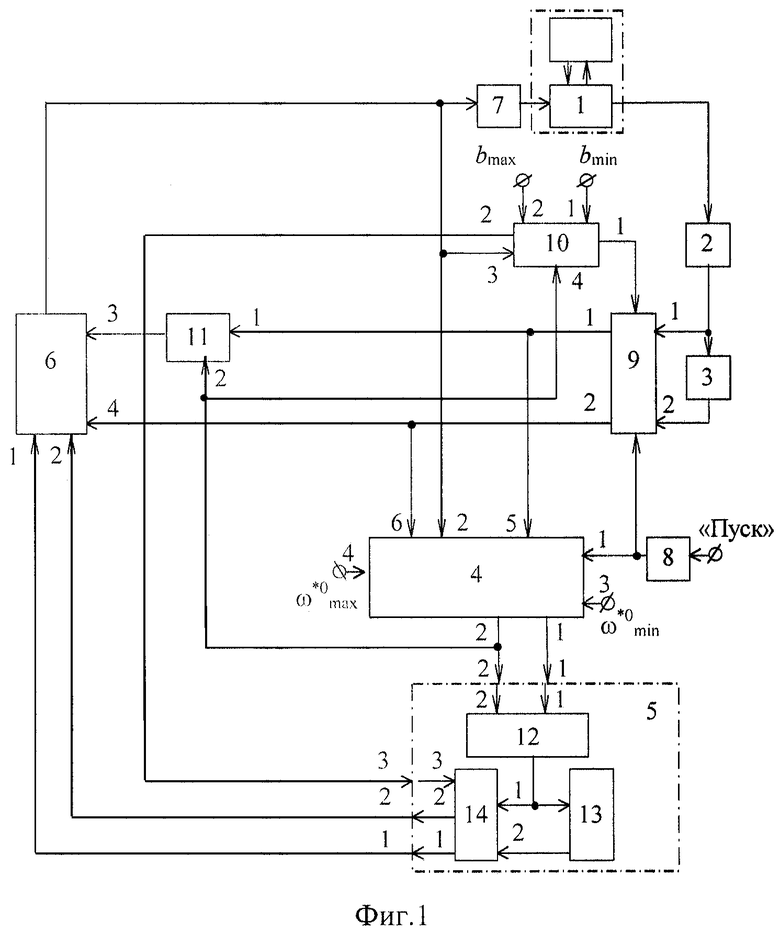
| Устройство для успокоения колебаний упругого элемента переменной жесткости | 1988 |
|
SU1587465A1 |
| Устройство для успокоения колебаний упругого элемента переменной жесткости | 1987 |
|
SU1500990A2 |
| Демпфер | 1991 |
|
SU1827465A1 |
| Устройство для успокоения колебаний упругого элемента переменной жесткости | 1983 |
|
SU1129585A1 |
| US 4633982 А, 06.01.1987. | |||
Авторы
Даты
2002-10-27—Публикация
2001-06-29—Подача