Изобретение относится к металлическим подкрановым конструкциям преимущественно с тяжелым интенсивным режимом (8К, 7К) работы.
Известна металлическая подкрановая конструкция, содержащая двутавровую подкрановую балку с рельсом над стенкой и горизонтальную тормозную балку. Балки соединены между собой и представляют тонкостенный несимметричный стержень незамкнутого профиля подверженный косому изгибу от сил, действующих вертикально - Р и горизонтально - T, причем для режима работы кранов 8К, 7К горизонтальные силы по действующим нормам [1, с. 6] достигают до 10% от вертикальных.
Т=0,1Р
Одновременно на подкрановую балку через рельс передаются крутящие воздействием Мкр, так как силы Р и T действуют с эксцентриситетом [2, с. 48].
Примем известную подкрановую конструкцию за аналог [3, с. 187, рис. 10.9], [4, с. 377, рис. 15.11].
Изготавливают аналог следующим образом: подкрановую балку выполняют из сварного двутавра, двутавры сваривают в специальных станах с использованием автоматической сварки. Тормозную балку изготавливают также посредством сварки листов.
Недостаток аналога - пониженная несущая способность несимметричного сечения, так как его главные оси направлены под углом к плоскости действия максимального изгибающего момента и поэтому прочностные свойства используются нерационально [5, с. 483...485].
Технический результат изобретения - снижение материалоемкости подкрановой конструкции.
Он достигнут трансформированием на прокатном стане вертикального профиля сечения двутавра в наклонный. Этим обеспечена благоприятная ориентация главных осей сечения всей конструкции и снижение расхода материала. То есть плоскость действия максимального изгибающего момента Мmax совмещена с плоскостью максимального момента инерции Jmax сечения.
Несимметричная подкрановая конструкция содержит двутавр с наклонной стенкой и параллельными полками и горизонтальную тормозную балку. Тормозная же балка состоит из тормозного листа и внешнего пояса.
Центробежный момент инерции наклонного двутавра зависит от угла наклона стенки к вертикали и не равен нулю.
Несимметричную подкрановую конструкцию изготавливают следующим способом. Прокатывают в прокатном стане наклонный двутавр, деформируя его профиль и перераспределяя площадь сечения между стенкой и поясами в пропорции 0,5... 0,75 на стенку и 0,5...0,25 на пояса, одновременно наклоняя стенку по отношению к вертикали под острым углом Θ, отсчитываемым в сторону тормозной балки.
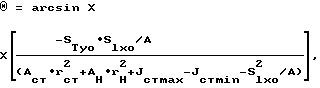
где STyo = AT•ΔT+ABH•ΔBH - статический момент сечения тормозной балки относительно оси y0, проходящей через центр О0 (фиг.1);
SIxo= Aн•rн+Acт•rcт - статический момент сечения вертикального двутавра относительно оси x0, проходящей через центр О0;
А - площадь всего сечения;
Ат - площадь сечения тормозного листа;
ΔT(rT) - плечо тормозного листа;
Авн - площадь внешнего пояса тормозной балки;
ΔBH - плечо внешнего пояса;
Аcт - площадь стенки балки;
rcт - плечо стенки балки;
АВ - площадь сечения верхнего пояса подкрановой балки;
Ан - площадь сечения нижнего пояса;
rн - плечо нижнего пояса;
Jcтmax - максимальный момент инерции стенки до ее поворота;
Jcтmin - минимальный момент инерции стенки до ее поворота;
А=AT+АВН+Aв+Аcт+АН - площадь сечения всей конструкции.
Плечи, измеряются от полюса О0 до центра тяжести соответствующего элемента в радиальном направлении. Наклонный двутавр соединяют с тормозной балкой.
Координаты центра тяжести О несимметричной подкрановой конструкции по отношению к центру тяжести верхнего пояса двутавра О0 определяют следующим образом:
по вертикали относительно оси х0:
cy = [(AH•rH+Acт•rcт)cosΘ]/A (2)
по горизонтали относительно оси у0:
Δx = [AT•rT+ABH•ΔВН+(AH•rH+Acт•rcт)sinΘ]/A (3)
Тормозную балку и наклонный двутавр соединяют вместе, образуя единую несимметричную подкрановую конструкцию. Центробежный момент инерции этой конструкции относительно главных осей: горизонтальной Х и вертикальной Y равен нулю (Jxy= 0). Главные же оси проходят через центр тяжести сечения. Несимметричное сечение конструкции в целом и наклонной двутавровой балки обладают равными по величине, но противоположными по знаку центробежными моментами инерции относительно центра О сечения конструкции.
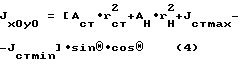
Учитывая, что 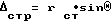 и ΔH = rH•sinΘ, из формулы (4) получена формула (1), определяющая, каким образом должен быть деформирован в прокатном стане двутавр и наклонена его стенка, чтобы главные оси X и Y, проходящие через центр тяжести подкрановой конструкции приняли соответственно горизонтальную и вертикальную ориентацию.
и ΔH = rH•sinΘ, из формулы (4) получена формула (1), определяющая, каким образом должен быть деформирован в прокатном стане двутавр и наклонена его стенка, чтобы главные оси X и Y, проходящие через центр тяжести подкрановой конструкции приняли соответственно горизонтальную и вертикальную ориентацию.
Изготовлять конструкцию можно следующим образом: организуется прокат наклонных двутавровых балок с определенным углом наклона стенки по отношению к вертикали (например, Θ=10o), а затем из (5) находится статический момент тормозной балки, обеспечивающий равенство центробежного момента инерции нулю (JXY = 0).
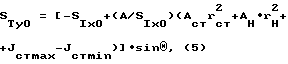
Затем, имея статический момент тормозной балки Sту0, определяем ширину горизонтального тормозного листа
bГ = {SтуО-0,5[АВН(bB+tВН)+АГ•(bВ+tВН)+АТ•bВ]}/[АВН+0,5АГ] (6)
Для нахождения моментов инерции законструированного сечения используем формулу (4) и найдем центробежный момент инерции конструкции относительно главных осей Х и Y
JXY = Jx0y0-A•ΔX•CY (8)
Эту формулу будем использовать для проверки правильности вычислений. При правильном вычислении JXY будет равен нулю.
Несимметричная конструкция, образованная из тормозной балки и наклонной двутавровой балки, имеет горизонтальную и вертикальную ориентацию главных осей Х и Y. В аналоге главные оси Х и Y занимают произвольное положение, отличное от горизонтали и вертикали, так как применен обычный двутавр, поэтому в нашем случае при его изгибе напряжения в крайних точках на 20-25% меньше.
Моменты инерции и моменты сопротивления несимметричного сечения определяем обычным образом [5].
Первоначально для упрощения вычислений находят моменты инерции относительно осей x0uу0, проходящих через центр тяжести верхнего пояса наклонного двутавра.
Тогда моменты инерции Jx0 и Jу0 будут равны
ось х0: Jx0 = ΣJxсoб+(Acт•r
ось у0: 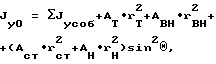
где суммы собственных моментов инерции элементов двутавра и тормозной балки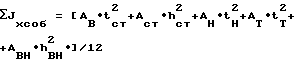

первые три слагаемых учитывают двутавр, остальные тормозную балку. Затем, используя координаты центра тяжести подкрановой конструкции, определяем главные моменты инерции
JX = Jx0-ΣA•C
Моменты сопротивления крайних точек находим обычным образом:
Wx=Jx/у; Wy=Jy/x, (11)
где х и у - координаты соответствующих точек.
Сопоставление несимметричной подкрановой конструкции, образованной из тормозной балки и наклонного двутавра с аналогом [3, 4], показывает его существенные отличия. В аналоге с обычной двутавровой балкой главные оси Х и Y занимают произвольное положение, отличное от горизонтали и вертикали, поэтому при изгибе сечения напряжения в точках, наиболее удаленных от его центра тяжести, возрастают, т.к. расстояние до них приходится измерять по радиусу.
В нашем случае конструкция содержит наклонный двутавр, поэтому оси X и Y занимают соответственно горизонтальную и вертикальную ориентацию и происходит значительное снижение напряжения в наиболее напряженных точках, т.е. прочностные свойства сечения значительно увеличиваются.
На чертеже показано сечение подкрановой конструкции 1, состоящей из наклонного двутавра 2 и тормозной балки 3. Наклонный двутавр 2 содержит верхний пояс а, наклонную стенку b и нижний пояс с. Тормозная балка 3 содержит внешний пояс d и тормозной лист е. Наклонный двутавр 2 и тормозная балка 3 соединены друг с другом в единое целое.
Несимметричную подкрановую конструкцию изготавливают следующим образом: наклонный двутавр 2 прокатывают в прокатном стане, деформируя его сечение и перераспределяя площадь между стенкой b и поясами а и с в пропорции 0,5... 0,75 на стенку, 0,5...0,25 на пояса. При прокате наклоняют стенку к вертикали под острым углом Θ(1).
Моменты инерции и моменты сопротивления несимметричного сечения определяем обычным образом [5].
Первоначально для упрощения вычислений находим моменты инерции относительно осей х0 и у0 (9), проходящих через центр тяжести верхнего пояса наклонного двутавра 2, а затем, используя координаты центра тяжести подкрановой конструкции, определяем главные моменты инерции (10).
Моменты сопротивления находим обычным образом:
Экономический эффект от разработанного способа изготовления подкрановой конструкции возник из-за согласования плоскости, действия изгибающего момента и плоскости в которой момент инерции при изгибе достигает максимума.
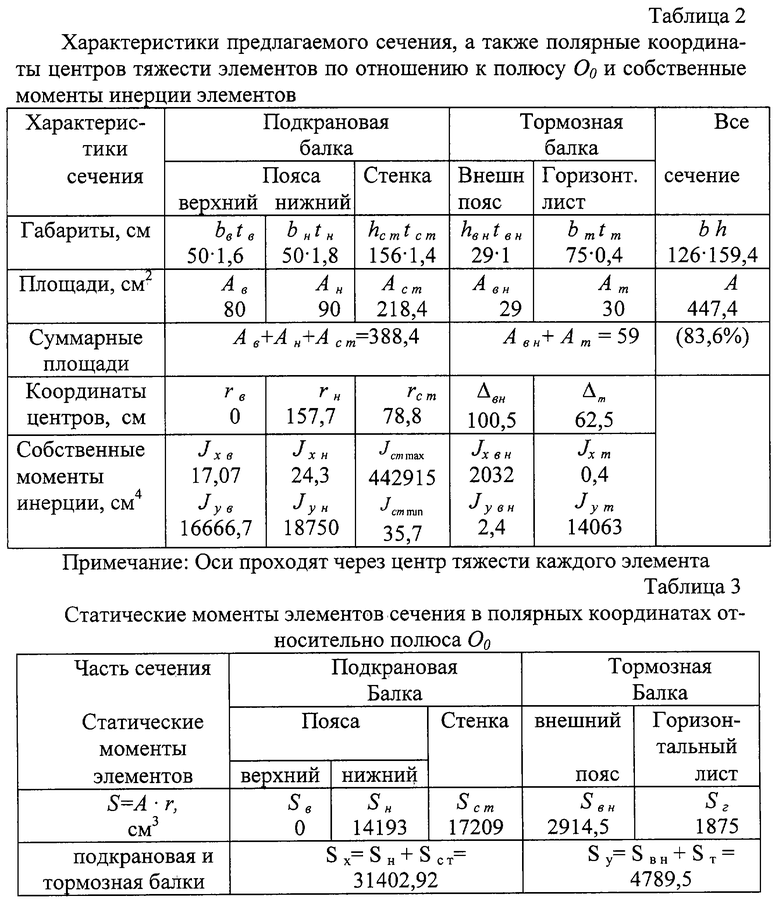
Изготовим по предлагаемому способу наклонный двутавр, а затем и несимметричную в сечении подкрановую конструкцию. За аналог примем конструкцию, рассчитанную в учебнике профессора К.К.Муханова [6, с.254, рис.VI, 44]. Характеристики аналога приведены в табл. 1. В табл.2 - характеристики предлагаемого сечения, уменьшенного на 16,4%. . В табл.3 - статические моменты элементов.
Изготовление производим в следующей последовательности.
1. По формуле (1) определяем угол наклона Θ стенки
Θ = arc sin[4789,5•31402,9/447,4]/
[218,4•78,82+90•157,72+442915-35,7-31402,92/447,4]=10,56736o
Принимаем Θ=10o и прокатываем наклонный двутавр.
2. Уточняем статический момент тормозной балки при Θ=10o.
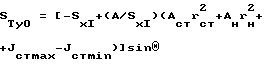
SТу0= [-31402,9+(447,4/31402,9)(218.4•78,82+90•157,72+442915,2-5,7)] sin 10o
STу0=4535,03 cм3
Далее уточняем ширину горизонтального тормозного листа
bг = {SуT-0,5[Aвн(bв + tвн)+Aгbв]}/[Aвн + 0,5Aг
bг = [4535,033-0,5•(29-51+30•50)]/[29+0,5•30]=69,22 см
Δг = 0,5(bв+bг) = 0,5(50+69,22) = 59,61 см;
При этой ширине горизонтального листа тормозная балка обеспечивает заданную величину статического момента S=4535,03. Отрезаем от горизонтального листа полосу шириной 75-69,22=5,78 см (t=0,4 см) и привариваем ее к листу снизу посередине ширины его в качестве продольного ребра жесткости. При этом площадь всего сечения остается неизменной (A=447,4 см2).
Уточняем расстояния до центров тяжести:
Δт = 0,5(bв+bт) = 0,5(50+69,22) = 59,61 см;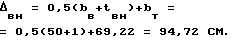
3. Находим координаты центра тяжести сечения всей конструкции по горизонтали: ΔX = [STy0+SIx0sinΘ]/A
по вертикали: Cy = SIx0cosΘ/A,
Су=31402,92 cos 10o/447,4 = 69,123 см
4. Находим центробежный момент инерции относительно полюса О0
Jx0у0 = 0,5 (218,4•78,82+90•157,72+442915,2-35,7)sin 20o=690411,65 см4
5. Находим главный центробежный момент сечения Jyf относительно его центра тяжести О
JXY=690411,65-447,4•22,3247•69,123=0,13
Погрешность 0,13•100/690411,65=0,000019
Убедились, что наклонный двутавр запроектирован правильно.
8. По формулам вычисляем сначала моменты инерции всего сечения относительно осей х0у0
Jx0 = ΣJxсoб+(Acт•r
Jx0=431634,9+(218,4•78,82+90•157,72)cos210o=3917628,8 см4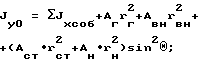
Jу0=60787,7+30•59,612+ 29•94,722+(218,4•78,82+90•157,72)sin210o
Jу0=538040,6 см4
9. Главные моменты инерции
Jx=Jx-А•Су 2=3917628,8-447,4•69,1232=1779956,5 см4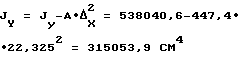
10. Проверяем нормальные напряжения при изгибе в вертикальной плоскости относительно ocи X(h=156•cosl0o+1,6+1,8=157см): на верхнем краю сечения
Jx=1779956,5 см4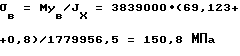
на нижнем краю сечения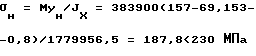
при изгибе относительно оси у слева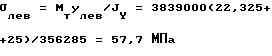
Проверка прочности при косом изгибе
σв+σлев = 150,8+57,7 = 208,5<RY = 230 МПa
Прочность обеспечена со значительным запасом, несмотря на то, что материалоемкость снижена на 16,4% по сравнению с аналогом.
Экономический эффект от разработанного способа изготовления подкрановой конструкции достигает 16-25% и возникает из-за согласования плоскости действия изгибающего момента с плоскостью главного момента инерции при изгибе.
СПИСОК ЛИТЕРАТУРЫ
1.СНиП 2.01.07 - Нагрузки и воздействия./Госстрой СССР-М.: ЦИТП Госстроя СССР, 1987, 36 с.
2. СНиП II-23-81* Стальные конструкции./Госстрой СССР-М.: ЦИТП Госстроя СССР, 1988, - 96 с.
3. Металлические конструкции./ Под ред. Н.П.Мельникова-М.: Стройиздат, 1980-776 с. (Справочник проектировщика).
4. Металлические конструкции. Общий курс: Учебник для вузов./ Е.И.Беленя и др.: под общей ред. Е.И.Беленя - М., Стойиздат, 1986, - 560 с.
5. Беляев Н.М. Сопротивление материалов. - М., Физматлит, 1956, 856 с.
6. Муханов К. К. Металлические конструкции. Учебник для вузов. М., Стройиздат, 1978-572 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕСИММЕТРИЧНАЯ ПОДКРАНОВАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2196720C2 |
| ПОДКРАНОВАЯ КОНСТРУКЦИЯ НЕЖДАНОВЫХ | 1998 |
|
RU2196098C2 |
| МЕТАЛЛИЧЕСКАЯ ПОДКРАНОВАЯ БАЛКА | 1998 |
|
RU2154599C2 |
| РЕЛЬСОБАЛОЧНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2191154C2 |
| БАЛКА | 2002 |
|
RU2232125C2 |
| МЕТАЛЛИЧЕСКАЯ ПОДКРАНОВАЯ КОНСТРУКЦИЯ | 1998 |
|
RU2196097C2 |
| ПОДКРАНОВАЯ ТРАНСПОРТНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2192383C2 |
| ТРЕХГЛАВЫЙ АРОЧНЫЙ РЕЛЬС | 1999 |
|
RU2207316C2 |
| РЕЛЬСОБАЛОЧНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2192381C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ПРОЕКТНОГО ПОЛОЖЕНИЯ ОСЕВШЕЙ КОЛОННЫ КАРКАСА | 2000 |
|
RU2188278C2 |

Изобретение относится к подкрановым конструкциям. Способ изготовления несимметричной в сечении подкрановой конструкции (1), содержащей подкрановую двутавровую балку с наклонной по отношению к вертикали под острым углом стенкой и параллельными друг другу поясами и тормозную балку (3) с внешним поясом и тормозным листом, соединяющим внешний пояс с подкрановой двутавровой балкой, заключается в том, что формируют сечение профиля двутавровой балки на прокатном стане и при прокатывании профиля деформируют сечение, перераспределяя площадь между стенкой и поясами в пропорции 0,5-0,75 на стенку, 0,5-0,25 на пояса, а острый угол θ наклона стенки по отношению к вертикали определяют по расчетной формуле с учетом статических моментов тормозной балки, вертикального двутавра и максимального момента инерции стенки до и после ее поворота. Заявленное изобретение снижает металлоемкость. 1 ил., 3 табл.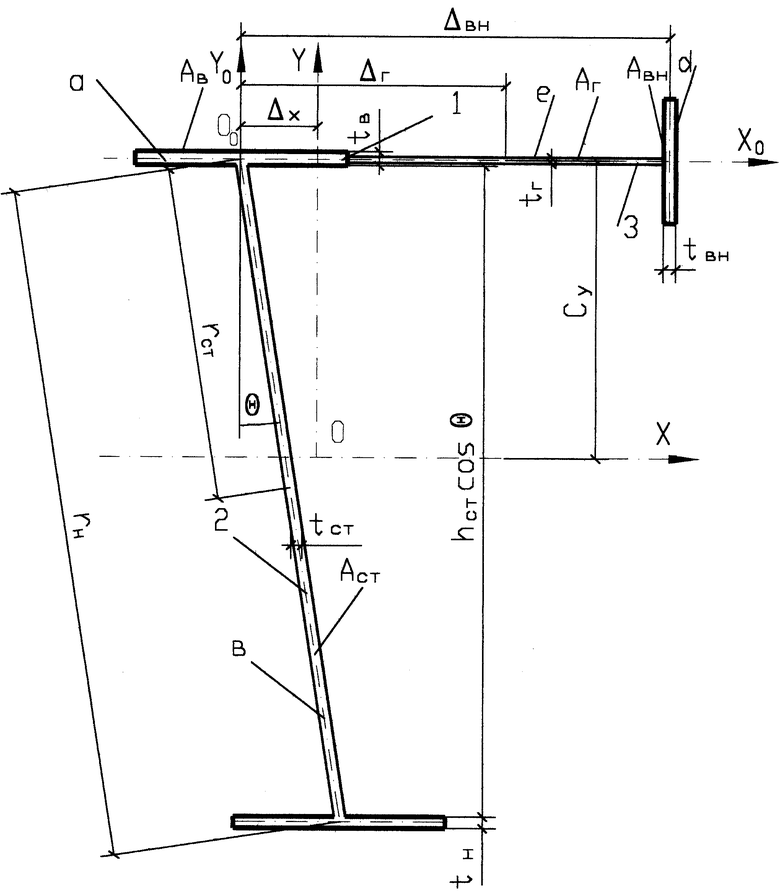
Способ изготовления несимметричной в сечении подкрановой конструкции, содержащей подкрановую двутавровую балку с наклонной по отношению к вертикали под острым углом стенкой и параллельными друг другу поясами и тормозную балку с внешним поясом и тормозным листом, соединяющим внешний пояс с подкрановой двутавровой балкой, заключающийся в том, что формируют сечение профиля двутавровой балки на прокатном стане, отличающийся тем, что при прокатывании профиля на прокатном стане деформируют сечение, перераспределяя площадь между стенкой и поясами в пропорции 0,5 - 0,75 на стенку, 0,5 - 0,25 на пояса, а острый угол θ наклона стенки по отношению к вертикали, определяют по формуле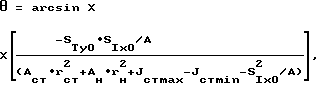
где STy0 = AT•ΔT+Aвн•Δвн - статический момент тормозной балки относительно оси yо, проходящей через центр тяжести верхнего пояса наклонного двутавра;
SIх0= Aн•rн+Aст•rст - статический момент вертикального двутавра относительно оси xо, проходящей через центр тяжести верхнего пояса наклонного двутавра;
А - площадь всего сечения;
АТ - площадь сечения тормозного листа;
ΔT - плечо тормозного листа;
Авн - площадь внешнего пояса тормозной балки;
Δвн - плечо внешнего пояса;
Аст - площадь стенки балки;
rст - плечо стенки балки;
Ан - площадь нижнего пояса;
rн - плечо нижнего пояса;
Jстmax - максимальный момент инерции стенки до ее поворота относительно осей, проходящих через центр тяжести стенки;
Jстmin - минимальный момент инерции стенки до ее поворота относительно осей, проходящих через центр тяжести стенки; тормозную балку соединяют с наклонным двутавром так, чтобы между тормозным листом и стенкой наклонного двутавра образовался острый угол, равный 90o - θ.
| RU 95107457 А1, 20.02.1997 | |||
| СПОСОБ УСИЛЕНИЯ ПОДКРАНОВОГО ПУТИ | 1994 |
|
RU2114045C1 |
| ВНУТРИМАТОЧНОЕ ПРОТИВОЗАЧАТОЧНОЕ УСТРОЙСТВО | 1992 |
|
RU2070007C1 |
| СПОСОБ ЛАЗЕРХИРУРГИЧЕСКОГО ЛЕЧЕНИЯ ОЧАГОВОГО ХОРИОРЕТИНИТА | 2011 |
|
RU2455968C1 |
Авторы
Даты
2003-01-10—Публикация
1998-01-15—Подача