Изобретение относится к металлическим подкрановым конструкциям, преимущественно в цехах черной и цветной металлургии с интенсивным тяжелым режимом работы (8К, 7К).
Известна несимметричная подкрановая конструкция, состоящая из двутавровой подкрановой ориентированной вертикально и горизонтальной тормозной балок. Балки соединены между собой и представляют тонкостенный несимметричный стержень незамкнутого профиля, подверженный косому изгибу от сил, действующих вертикально - Р и горизонтально - T, причем горизонтальные силы по действующим нормам [1, с.6] достигают до 10% от вертикальных (8К, 7К).
Т=0,1Р
Одновременно на подкрановую балку через рельс передаются крутящие воздействия Мкр, так как силы Р и Т действуют с эксцентриситетом [2, с. 48], [3, с. 187, рис. 10.9], [4, с. 377, рис. 15.11].
За аналог примем патентный документ RU 98112777 A, 10.04.2000, в котором описана металлическая подкрановая конструкция, содержащая подкрановую балку с трубчатым верхним поясом, соединенную с горизонтальной тормозной балкой.
Недостаток аналога - пониженная несущая способность несимметричного сечения, так как его главные оси направлены под углом к плоскости действия максимального изгибающего момента и поэтому прочностные свойства используются нерационально [5, с. 483-494].
Техническая задача изобретения - снижение материалоемкости и придание подкрановой конструкции амортизирующей способности.
Задача решена тем, что верхний пояс подкрановой балки выполнен из трубы, а ее стенка ориентирована по радиусу из центра трубы и наклонена под острым углом θ к вертикали.

где статические моменты элементов тормозной балки относительно второстепенной оси y из полюса О0:
Sуг = AгΔг - горизонтального тормозного листа;
Sувн = AвнΔвн - внешнего пояса тормозной балки;
SуТ = AгΔг+AвнΔвн - всей тормозной балки относительно второстепенной оси y;
Sx⊥ - статический момент вертикально ориентированной балки относительно второстепенной оси x при θ=0.
Sст=Астrст - стенки вертикального двутавра;
площади сечений элементов подкрановой конструкции:
Аг - горизонтального листа тормозной балки;
Авн - внешнего пояса тормозной балки;
A0 - трубы;
Ан - нижнего пояса;
Аст - стенки балки;
А=Ат+Авн+A0+Аст+Aн - площадь всего сечения подкрановой конструкции;
моменты инерции: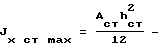 максимальный момент инерции стенки до поворота,
максимальный момент инерции стенки до поворота, минимальный момент инерции стенки до поворота;
минимальный момент инерции стенки до поворота;
плечи, измеренные от полюса О0 до центра тяжести соответствующего элемента в радиальном направлении:
Δг - горизонтального тормозного листа;
Δвн - внешнего пояса;
rн - нижнего пояса;
rст - стенки балки.
θ - угол между осью Х и нормалью к стенке, отсчитываемый в сторону тормозной балки.
Наклоном стенки подкрановой конструкции обеспечена благоприятная ориентация главных осей Х и У сечения и уменьшение материалоемкости, то есть плоскость действия максимального изгибающего момента Мmax совмещена с плоскостью максимального момента инерции Jmax сечения.
Сечение несимметричной подкрановой конструкции содержит трубчатый верхний пояс, наклонную стенку, горизонтальный нижний пояс и горизонтальную тормозную балку, включающую в себя тормозной лист и внешний пояс.
Центробежный момент инерции сечения JXY зависит от распределения материала по сечению и угла наклона θ стенки к вертикали.
Координаты центра тяжести О несимметричной подкрановой конструкции по отношению к центру тяжести трубчатого пояса О0 определяют следующим образом:
по вертикали относительно оси х0.
Cy = Sx⊥cosθ/A, (2)
где Sx⊥ = (Aнrн+Aстrст)cosθ - статический момент нижнего пояса и наклонной стенки;
по горизонтали относительно второстепенной оси y:
Δx=Sy/A, (3)
где Sу - статический момент всего сечения, который складывается из статического момента тормозной балки SyT.
SyT = AгΔг+AвнΔвн
и статического момента наклонной балки Sy⊥ относительно оси y
Sy⊥ = (Aнrн+Aстrст)sinθ.
Статический момент всего сечения
SY = AгΔг+AвнΔвн+(Aнrн+Aстrст)sinθ.
Тормозную и подкрановую балки соединяют вместе, образуя единую конструкцию. Центробежный момент инерции ее относительно главных осей: горизонтальной X и вертикальной Y, проходящих через центр тяжести сечения, равен нулю (JXY=0), так как несимметричное сечение в целом и наклонная стенка обладают равными по величине, но противоположными по знаку центробежными моментами инерции относительно центра О всего сечения.

где rстsinθ, rстcosθ, rнsinθ, rнcosθ - проекции радиусов на оси X, Y соответственно.
Тогда центробежный момент инерции Jxy будет равен
Из формулы (4) получена формула (1), определяющая, каким образом должна быть наклонена стенка, чтобы главные оси Х и Y, проходящие через центр тяжести подкрановой конструкции, приняли соответственно горизонтальную и вертикальную ориентацию.
Конструкцию изготавливаем следующим образом. Точно определяем угол наклона стенки по отношению к вертикали по формуле (1), округляем угол до целого, а затем из формулы (5) находим статический момент тормозной балки, обеспечивающий равенство центробежного момента инерции сечения нулю (Jxy=0).
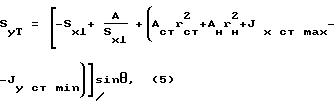
где Sx⊥ - статический момент вертикально ориентированной конструкции относительно оси x при θ = 0.
Затем, имея статический момент тормозной балки SyT, определяем ширину горизонтального тормозного листа
bг={SyT-0,5[Aвн(d+tвн)+Aгd]}/[Aвн+0,5 Aг]. (6)
Для нахождения моментов инерции предлагаемого сечения используем формулу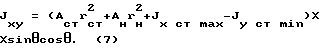
Далее найдем центробежный момент инерции относительно главных осей Х и Y:
JXY=Jxy-AΔXCY. (8)
Эту формулу будем использовать для проверки правильности вычислений. При правильном вычислении JXY будет равен нулю. Разработанная несимметричная конструкция, образованная из трубы, наклонной стенки, нижнего пояса и тормозной балки, имеет горизонтальную и вертикальную ориентацию главных осей Х и Y, поэтому в нашем случае при изгибе сечения напряжения в крайних точках на 20-25% меньше.
Моменты инерции и моменты сопротивления несимметричного сечения определяем обычным образом [5].
Первоначально для упрощения вычислений находим моменты инерции относительно второстепенных осей x и y, проходящих через центр тяжести трубы (при θ=0).
Тогда моменты инерции Jx и Jy будут равны:
относительно оси x
Jx=ΣJxсоб + Aстrст 2 + Aнrн 2
относительно оси y
Jy = ΣJyсоб + AгΔ
где суммы собственных моментов инерции элементов подкрановой балки
ΣJxсоб=J0+[Aстhст 2+Анtн 2+Aгtг 2+Aвнhвн 2]/12;
ΣJyсоб=J0+[Aстtст 2+Aнbн 2+Aгbг 2+Aвнtвн 2]/12;
первые три слагаемых учитывают подкрановую балку, остальные - тормозную балку.
Моменты инерции всего сечения с наклонной стенкой относительно вспомогательных осей x и y при θ ≠ 0
относительно оси x
Jxθ = ΣJxсобθ+[Aстr
относительно оси y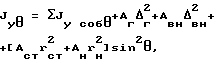
причем при вычислении собственных моментов инерции необходимо учитывать угол поворота θ стенки, то есть
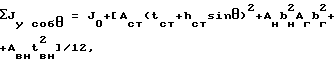
Затем, используя координаты центра тяжести подкрановой конструкции, определяем главные моменты инерции
Моменты сопротивления крайних точек находим обычным образом
WX=JX/y; WY=JY/x, (11)
где x и y координаты соответствующих точек.
Сопоставление разработанной конструкции с аналогом [3, 4] показывает ее существенные отличия. В прототипе главные оси Х и Y занимают произвольное положение, отличное от горизонтали и вертикали, поэтому при изгибе сечения напряжения в точках, наиболее удаленных от его центра тяжести возрастают, т. к. расстояние до них приходится измерять по радиусу.
В нашем же случае оси Х и Y занимают соответственно горизонтальную и вертикальную ориентацию, что приводит к значительному снижению материалоемкости (22,2%, см. пример).
На фиг.1 показано сечение подкрановой конструкции, состоящей из подкрановой 1 и тормозной 2 балок; на фиг.2 - фасад. Подкрановая балка содержит трубу a, наклонную стенку b и нижний пояс с. Тормозная балка 2 содержит внешний пояс d и тормозной лист e и соединена с подкрановой.
Разработанную конструкцию изготавливаем следующим образом.
Моменты инерции и моменты сопротивления определяем обычным образом [5]. Для упрощения вычислений находим моменты инерции относительно второстепенных осей x и y (9), проходящих через центр тяжести трубы, а затем, используя координаты центра тяжести всей подкрановой конструкции, определяем характеристики сечения и изготавливаем конструкцию с полученными характеристиками.
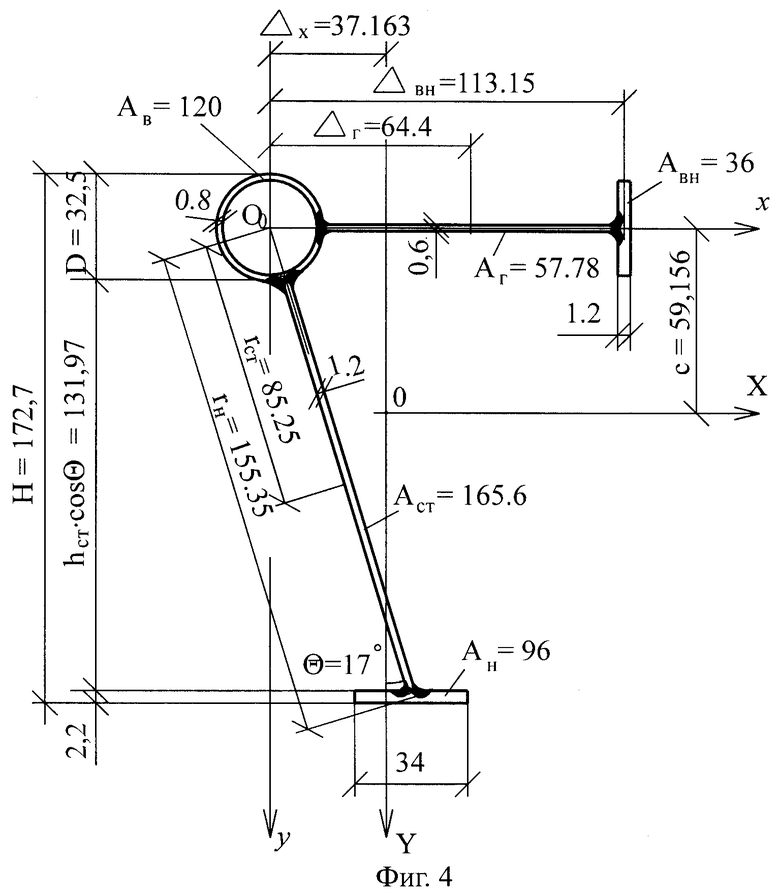
Пример конкретного выполнения (фиг.3 и 4).
Сравним разработанную конструкцию с аналогом, рассчитанным в учебнике профессора К.К.Муханова (6, с. 254, рис. VI, 44).
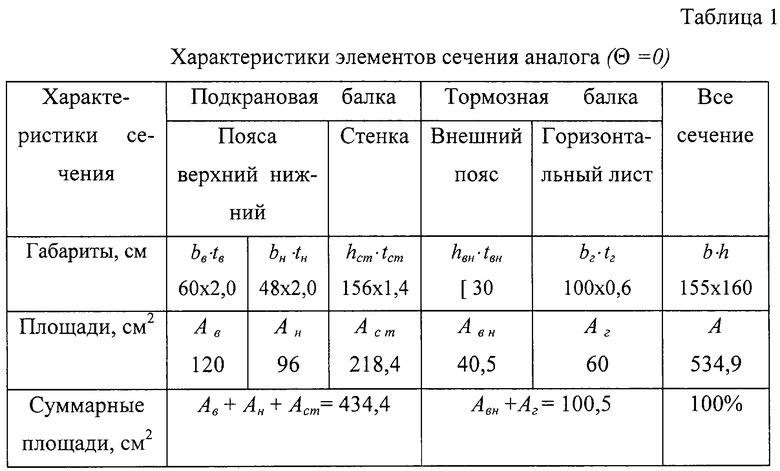
Характеристики его приведены в табл. 1. В этой же таблице приведены размеры, площади и статические моменты элементов сечения разработанной конструкции относительно осей x и y, уменьшенного на 22,2% по сравнению с аналогом.
Для перехода от обычной двутавровой подкрановой конструкции к разработанной необходимо уменьшить площади поперечных сечений нижнего пояса на 20-25%, стенки на 30-35%. Сечение верхнего пояса нужно уменьшить на 30-35% и заменить трубой.
Изготовление производим в определенной последовательности:
1. Определяем моменты инерции стенки балки до поворота ее. Собственные моменты инерции стенки подкрановой балки до поворота (θ=0)
Jстmax=Aстhст 2/12=165,6•1382/12=262807,2 см4;
Jстmmin=Астtст 2/12=165,6•1,22/12=19,872 см4.
2. Определяем статические моменты S подкрановой балки 1, то есть при θ=0 из полюса О0 (см. табл. 2).
3. По формуле (1) определяем угол наклона θ стенки наклонной подкрановой балки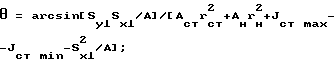
θ =arcsin[8181,6•25737,6/416,07]/[165,6•
•85,252+74,8•155,352+262807,2-19,872-
-25737,62/416,07] = 17,54o.
Принимаем θ=17o.
В табл.2 приведены статические моменты элементов разработанного сечения в полярных координатах относительно полюса O0.
По ормуле (5) уточняем статический момент тормозной балки 2 при θ=17o.


По формуле (6) уточняем ширину горизонтального тормозного листа
bг=(SyT-0,5[Aвн(d+tвн)+Aгd])/[Aвн+0,5Aг];
bг=[7937,59-0,5•(36•(32,5+1,2)+60•
•32,5)]/[36+0,5•60]=96,3 см;
Δг=0,5(d+bг=0,5(32,5+96,3)=64,4 см.
При этой ширине горизонтального листа тормозная балка обеспечивает заданную величину статического момента SyT=7937,59. Отрезаем от горизонтального листа полосу шириной 100-96,3=3,7 см (t=0,4 см) и привариваем ее к листу снизу посередине ширины его в качестве продольного ребра жесткости. При этом площадь всего сечения остается неизменной (A=416,07 см2).
Уточняем расстояния до центров тяжести элементов тормозной балки
Δвн=0,5(d+tвн)+bг=0,5(32,5+1,2)+96,3=113,15 см.
5. Находим координаты центра тяжести сечения (фиг.1) всей наклонной конструкции
по горизонтали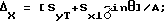
ΔX =[7937,59+25737,6 sin17o]/416,07=37,16 см;
по вертикали
Cy = Sx⊥cosθ/A;
Сy=25737,6 cos17o/416,07=59,16 см.
6. Находим центробежный момент инерции относительно полюса О0
Jxy=0,5 (Астrст 2+Анrн 2+Jстmах-Jстmin)sin2θ;
Jxy=0,5(165,6•85,252+74,8•155,352+
+262807,2-19,87)sin 2•17o=914697,4 см4
7. Находим главный центробежный момент сечения JXY относительно полюса О:
JXY=Jxy-АΔxСy
JXY=914697-416,07•37,1632•59,1557=0
Убедились, что наклонный двутавр запроектирован правильно.
8. Определяем собственные моменты инерции элементов сечения
- ее стенки, после поворота на 17o
Jстmах=0,5(JX+JY)+0,5(JX-JY)cos 2θ;
Jcтmах=0,5(262807,2+19,87)+0,5(262807,2-
-19,87)cos 2•17o=240344 см4;
Jcтmin=0,5(JX+JY)-0,5(JX-JY)cos 2θ;
Jстmin=0,5(262807,2+19,87)-0,5(262807,2-
-19,87)cos 2•17o=22483,3 см4;
- внешнего пояса (30 х1,2) тормозной балки
Jxвн=Aвнhвн 2/12=36•302/12=2700 см4;
Jyвн=Aвнtвн 2/12=36•1,22/12=4,32 см4;
- горизонтального тормозного листа
Jxг=60•0,62/12=1,8 см4;
Jyг=60•96,32/12=46368,5 см4.
Тогда сумма собственных моментов инерции всего сечения будет равна
ΣJхсоб=Jхв+Jхн+Jстmах+Jхвн+Jхг;
ΣJxсоб=10013,9+30,17+240344+2700+1,8=253090 см4;
ΣJyсоб=Jyв+Jyн+Jстmin+Jyвн+Jyг;
ΣJycoб=10013,9+7205,73+22483,3+4,32+46368,5=86075,7 см4.
В табл. 3 приведены характеристики элементов разработанного сечения, а также полярные координаты центров тяжести элементов по отношению к полюсу O0 в центре трубы и собственные моменты инерции элементов.
9. По формулам вычисляем сначала моменты инерции всего сечения относительно осей x, y
Jx = ΣJxсоб+(Aстr
Jx=253090+(165,6•85,252+74,8•155,352)cos217o=3004605,4 см4;
Jy = ΣJYсоб+AгΔ
Jy= 86075,7+60•64,42+36•113,152+(165,6•85,252+74,8•155,352)sin217o; Jy=1053010,1 см4.
10. Главные моменты инерции:
JX=Jx-ACy 2=3004605-416,07•59,15572=1548607 см4;
JY=Jy-AΔ
10. Проверяем нормальные напряжения при изгибе в вертикальной плоскости относительно главной оси Х (h=138 cos17o+2,2+32,5=166,67 см):
на верхнем краю сечения в точке А
σвх =Мyв/JX=3839000(59,1557+32,5/2)/
/1548607=186,93 МПа<230 МПа;
на нижнем краю сечения
σнx =М(h-С-d/2)/JX=3839000(166,67-
-59,15-32,5/2)/1548607=226,2<230МПа;
напряжения при изгибе в вертикальной плоскости на отметке центра трубы
σox =MCy/JX=3839000•59,1557/
/1548607=146,65 МПа;
напряжения при изгибе в горизонтальной плоскости в точке А
σAy = MтΔx/JY=383900•37,1632/
/478372,7=29,82 МПа;
напряжения при изгибе в горизонтальной плоскости в точке С
σCy =Mт(Δx+d/2)/Jy=383900•(37,1632+
+32,5/2)/478372,7=42,86 МПа;
Проверка прочности при косом изгибе в точке С
σcx+σcy =146,647+42,86=189,51 МПа<Ry=230 МПа.
Проверка прочности при косом изгибе в точке А
σвх+σAy =186,931+29,82=216,75 МПа<Ry=230 МПа.
Таким образом, предлагаемый способ изготовления несимметричной подкрановой конструкции позволяет снизить материалоемкость ее на 22,2 %.
Экономический эффект от разработанного способа изготовления подкрановой конструкции достигает 20-25% и возникает из-за согласования плоскости действия изгибающего момента и плоскости, в которой момент инерции при изгибе.
Литература
1.СНиП 2.01.07-85 Нагрузки и воздействия./Госстрой СССР М.: ЦИТП Госстроя СССР, 1987, 36 с.
2. СНиП II-23=81 *Стальные конструкции./Госстрой СССР М.: ЦИТП Госстроя СССР, 1988, 96 с.
3. Металлические конструкции./ Под ред. Н.П.Мельникова. М.: Стройиздат, 1980. - 776 с. (Справочник проектировщика.)
4. Металлические конструкции. Общий курс: Учебник для вузов. Е.И.Беленя и др.: под общей ред. Е.И.Беленя. М.: Стройиздат, 1986. - 560 с.
5. Беляев Н.М. Сопротивление материалов. - М.: Физматлит, 1956. - 856с.
6. Муханов К. К. Металлические конструкции. Учебник для вузов. М.: Стройиздат, 1978. - 572 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗГОТОВЛЕНИЯ НЕСИММЕТРИЧНОЙ В СЕЧЕНИИ ПОДКРАНОВОЙ КОНСТРУКЦИИ | 1998 |
|
RU2196100C2 |
| ТРЕХГЛАВЫЙ АРОЧНЫЙ РЕЛЬС | 1999 |
|
RU2207316C2 |
| РЕЛЬСОБАЛОЧНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2191154C2 |
| РЕЛЬСОБАЛОЧНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2240275C2 |
| МЕТАЛЛИЧЕСКАЯ ПОДКРАНОВАЯ БАЛКА | 1998 |
|
RU2154599C2 |
| ПОДКРАНОВАЯ КОНСТРУКЦИЯ НЕЖДАНОВЫХ | 1998 |
|
RU2196098C2 |
| БАЛКА | 2002 |
|
RU2232125C2 |
| РЕЛЬСОБАЛОЧНАЯ КОНСТРУКЦИЯ | 2000 |
|
RU2192381C2 |
| ПРОКАТНАЯ БАЛКА | 2001 |
|
RU2227069C2 |
| ПОДКРАНОВО-ПОДСТРОПИЛЬНАЯ БАЛКА | 2002 |
|
RU2235674C2 |




Изобретение относится к металлическим конструкциям черной и цветной металлургии и связано преимущественно с тяжелым режимом работы кранов. Несимметричная в сечении металлическая подкрановая конструкция содержит двутавровую подкрановую балку, соединенную с горизонтальной тормозной балкой. Двутавровая подкрановая балка содержит верхний пояс, выполненный из трубы, наклонную стенку и нижний пояс. Стенка подкрановой балки ориентирована по радиусу из центра трубы и наклонена под острым углом к вертикали. Тормозная балка содержит внешний пояс и тормозной лист. Технический результат изобретения - снижение материалоемкости и придание подкрановой конструкции амортизирующей способности. 4 ил., 3 табл.
Несимметричная в сечении металлическая подкрановая конструкция, содержащая подкрановую балку с трубчатым верхним поясом, соединенную с горизонтальной тормозной балкой, отличающаяся тем, что стенка подкрановой балки ориентирована по радиусу из центра трубы и наклонена под острым углом к вертикали.
| RU 98112777 А, 10.04.2000 | |||
| Справочник проектировщика | |||
| Металлические конструкции./Под ред | |||
| Н.П | |||
| Мельникова | |||
| - М.: Стройиздат, 1980, с | |||
| Индукционная катушка | 1920 |
|
SU187A1 |
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Рельсовый путь | 1990 |
|
SU1745804A1 |
| УСТРОЙСТВО для УЛАВЛИВАНИЯ ЛЕНТЫ ЛЕНТОЧНОГОКОНВЕЙЕРА | 0 |
|
SU194615A1 |
| СПОСОБ ПОЛУЧЕНИЯ ЧАЙНОЙ ФУНКЦИОНАЛЬНОЙ ПИЩЕВОЙ КОМПОЗИЦИИ ПРОФИЛАКТИЧЕСКОГО НАЗНАЧЕНИЯ | 2022 |
|
RU2806578C1 |
Авторы
Даты
2003-01-20—Публикация
2000-07-03—Подача