Изобретение относится к энергетике, в частности к способам преобразования энергии.
Под термином "тепловая поточная машина" подразумевается система или устройство, в котором специально организованный газовый поток осуществляет некоторый полезный эффект (преобразование части энергии газового потока в другие виды энергии). Эти машины представлены широким классом газовых машин, в котором в явном виде технической работы не совершается, - это вихревые устройства различного предназначения, химические газовые реакторы, эжекторы, плазмотроны, смесители, акустические газовые устройства и т.д.
Например, в вихревых трубах происходит сепарация газового потока на холодную (на оси трубы) и горячую (на периферии) составляющие [1]. В данном случае полезным эффектом является охлаждение или нагревание внешних тел за счет сепарации газового потока.
Другим примером полезного эффекта в описанных тепловых машинах могут служить газовые акустические устройства, в которых происходит целенаправленное преобразование части энергии газового потока в энергию акустических колебаний среды.
Общим свойством указанного класса тепловых машин является тот факт, что их эффективность тем выше, чем выше степень преобразования энергии газового потока в потенциальную энергию давления.
Известен способ преобразования энергии в тепловой поточной машине (тепловом насосе) путем подведения мощности газового потока на входе в машину и тепловой мощности к машине (см. RU 2083932 C1, F 25 В 30/00, 10/07/1997). В известном способе определяют максимальный коэффициент преобразования применительно к переносу тепла с более низкого уровня на более высокий уровень.
Недостатком известного способа является невозможность его применения к области задач без переноса тепла.
Технический результат, на достижение которого направлено настоящее изобретение, заключается в создании способа с максимальным коэффициентом преобразования в тепловой поточной машине.
Данный технический результат достигается тем, что в способе преобразования энергии в тепловой поточной машине путем подведения мощности газового потока рабочего тела на входе в машину и тепловой мощности к машине, определения статических температур на входе и на выходе из сопла определяют удельную тепловую мощность, подведенную к машине, а максимальный коэффициент преобразования энергии определяют по формуле:

где К - отношение теплоемкостей,  ,
,
Ср - теплоемкость рабочего тела при постоянном давлении;
Сv - теплоемкость рабочего тела при постоянном объеме;
η Карно - термический к.п.д. цикла Карно,  ;
;
ТК - статическая температура на выходе из сопла;
T1 - статическая температура на входе сопла;
 - удельная тепловая мощность, подведенная к машине.
- удельная тепловая мощность, подведенная к машине.
На фиг.1 представлена принципиальная схема тепловой поточной машины.
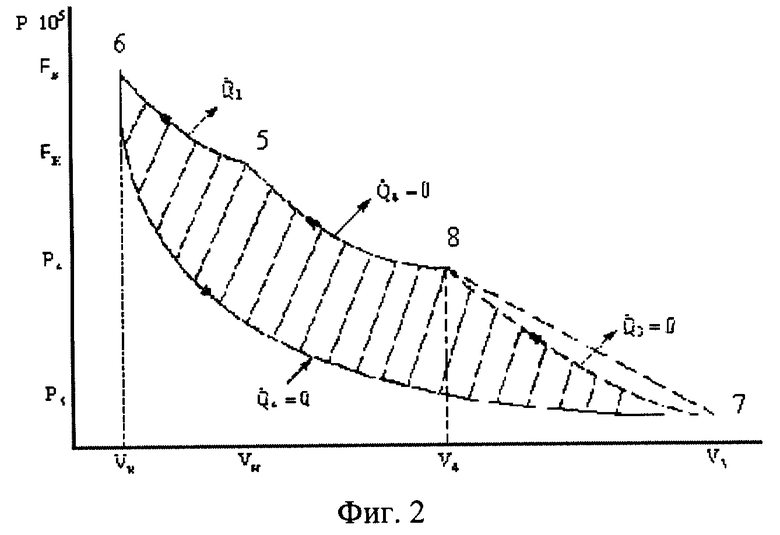
На фиг.2 показан предельный цикл холостого хода тепловой поточной машины.
На фиг.3 показан график изменений максимального коэффициента преобразования энергии в зависимости от коэффициента скорости потока на входе в рабочую камеру.
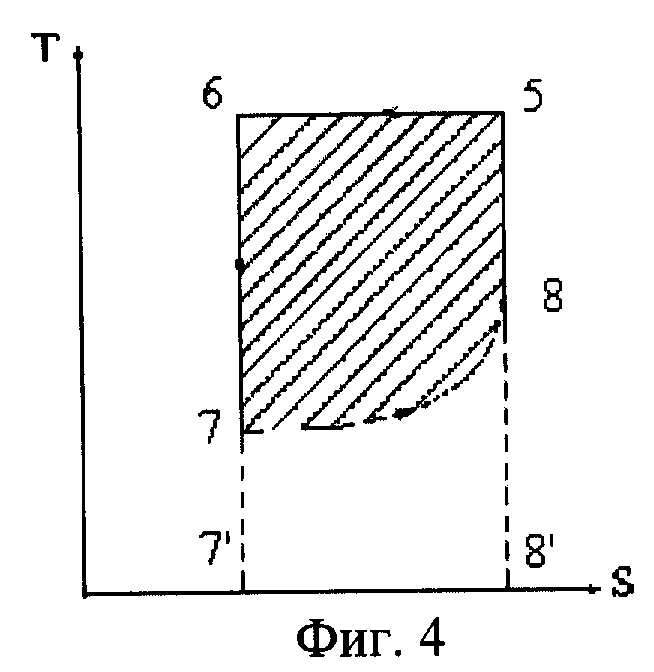
На фиг.4 показан предельный цикл тепловой поточной машины в T-S координатах.
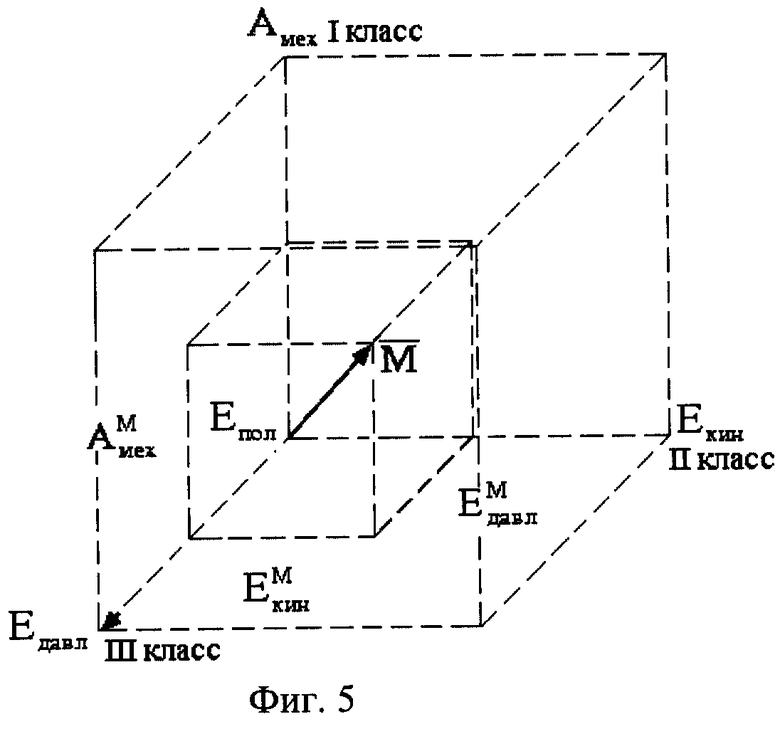
На фиг.5 показана принципиальная схема пространства тепловых машин.
Тепловая поточная машина (фиг.1) включает компрессор 1, сопло 2, рабочую камеру 3 и диффузор 4 с бесконечно большим расширением, давления на входе и на выходе из компрессора соответствуют Рн, Рк. Как отмечено выше, рассматриваемый класс машин имеет тем большую эффективность, чем выше степень утилизации кинетической энергии Екин в энергию давления Едавл. Для идеальной тепловой машины указанного класса максимальная степень утилизации кинетической энергии достигается при бесконечном уширении диффузора Sдиф (ρ) ∞, а значит скорость на выходе из диффузора стремится к нулю (v2(ρ)0) при постоянном расходе (G=const).
Способ преобразования энергии в тепловой поточной машине осуществляется следующим образом.
Компрессор 1 сжимает рабочее тело, осуществляя таким образом подвод мощности на входе в машину. Тепловая мощность подводится к рабочей камере 3. Определяют статические температуры на входе и на выходе из сопла, определяют удельную тепловую мощность, подведенную к машине.
Коэффициент эффективности преобразования энергии в тепловой поточной машине - это отношение максимально возможной доли преобразованной энергии газового потока и подведенных извне источников энергии к полной энергии, подведенной к машине при заданных параметрах в тепловой машине и окружающей среде при нулевой технической работе (Lтех=0), - определяют по теореме Волова, где Р1, ρ 1, v1, Р2, ρ 2, v2 - давление, плотность и скорость на входе в рабочую камеру и выходе из диффузора соответственно;
Сv, Ср, Т ,
, 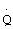 - теплоемкости при постоянном объеме и давлении, температура торможения на входе в рабочую камеру, расход и подведенная в рабочую камеру тепловая мощность соответственно;
- теплоемкости при постоянном объеме и давлении, температура торможения на входе в рабочую камеру, расход и подведенная в рабочую камеру тепловая мощность соответственно;
ТК, T1 - статическая температура на входе и выходе из сопла (С) соответственно;
 - мощность газового потока на входе в машину,
- мощность газового потока на входе в машину, 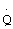 - подведенная мощность (тепловая, электрическая и т.д.) к тепловой машине;
- подведенная мощность (тепловая, электрическая и т.д.) к тепловой машине;
 - механическая мощность на выходе из тепловой машины.
- механическая мощность на выходе из тепловой машины.
В случае отсутствия технической работы (Lтех=0) и разности геометрических высот входа и выхода g(z2-z1)=0 уравнение теплового баланса имеет вид
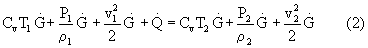
В рассматриваемом случае (Lтех=0) Δ U=Δ N, где Δ U=Сv(Т2-Т1) - изменение внутренней энергии потока в единицу времени.
- изменение внутренней энергии потока в единицу времени.
Изменение мощности газового потока и подведенной извне тепловой мощности на входе и выходе равно:

Отнесем изменение Δ N в поточной тепловой машине к полной тепловой мощности на входе и определим предел этого выражения при стремлении к нулю выходной скорости v2(ρ)0.
Используя соотношение (2), получим следующее выражение:

В результате обезразмеривания, учета уравнения энергии и элементарных преобразований окончательно получаем:

Газодинамический к.п.д. цикла Карно для теплоизолированного сопла определяется по формуле:

где 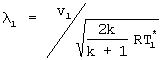 - коэффициент скорости потока на входе в рабочую камеру; статическая температура после компрессора ТК равна полной температуре на входе в сопло ТК=Т
- коэффициент скорости потока на входе в рабочую камеру; статическая температура после компрессора ТК равна полной температуре на входе в сопло ТК=Т
Следовательно, формулу (5) можно переписать в следующем виде:

Максимальный коэффициент эффективности преобразования энергии в поточной тепловой машине равен:

В формуле (8) индекс (G>0) означает, что расход через тепловую машину не равен нулю.
Выражение (7) представляет собой максимально возможное значение относительной доли мощности потока и подведенной тепловой мощности, потерянной и (или) утилизированной в поточной тепловой машине.
Вследствие того, что скорость отходящих газов отлична от нуля и всегда имеются потери, η G>0 поточной тепловой машины будет меньше предельного значения (7):
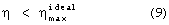
Таким образом получена мажорантная оценка коэффициента эффективности преобразования энергии в тепловой поточной машине при Lтex=0.
Следует отметить, что тепловые машины указанного класса имеют открытый рабочий цикл. Однако использование графического изображения закрытого рабочего цикла так же, как для воздушно-реактивных двигателей, реактивных двигателей (цикл Брайтона), допустимо.
Идеальный цикл тепловой поточной машины (цикл Волова), представленный на фиг.2, состоит из одной изотермы 5-6, двух идеальных адиабат 6-7 и 7-8 и одной ударной адиабаты Гюгонио 8-5. На фигуре  - отведение, подведение теплоты к машине. Следует отметить, что при сверхзвуковом режиме течения (λ 1>1) всегда имеет место скачок уплотнения, так как режим течения в сопле является нерасчетным [2].
- отведение, подведение теплоты к машине. Следует отметить, что при сверхзвуковом режиме течения (λ 1>1) всегда имеет место скачок уплотнения, так как режим течения в сопле является нерасчетным [2].
Потерянная ( ) или утилизированная мощность (η G>0) в тепловой машине указанного класса не может превысить максимальную возможную величину (
) или утилизированная мощность (η G>0) в тепловой машине указанного класса не может превысить максимальную возможную величину ( или
или  ).
).
Заштрихованная площадь 5-6-7-8-5, отнесенная к общей площади по кривой 6-5-8-7, представляет собой относительную долю потерянной  или утилизированной η G>0 мощности.
или утилизированной η G>0 мощности.

Как утверждает теорема, данная величина не может превысить соответствующее максимальное значение, определяемое по формуле (1)

Следует отметить, что в координатах P-V в общем случае траектория ударной адиабаты Гюгонио не определена, а имеются только начальные (Р3, V3) и конечные (Р4, V4) значения траектории. Для случая слабых ударных волн в работе [3] получено решение задачи о кривизне траектории адиабаты Гюгонио  . Однако экстраполяция данного результата в области сильных ударных волн не аргументирована.
. Однако экстраполяция данного результата в области сильных ударных волн не аргументирована.
Второе начало термодинамики и теорема о минимуме производства энтропии И.Пригожина [4] не позволяет определить форму кривой 7-8 без допущения о локальном равновесии в зоне скачка уплотнения. Производная по времени от производства энтропии будет отрицательной:
 , где
, где 
Таким образом, устойчивость термодинамического процесса выполняется при варьировании формы кривой в широком диапазоне.
Для выяснения формы кривой на участке 7-8 используется значение  для случая
для случая 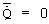 :
:

Площадь цикла по формуле (10) численно определялась для Δ  при варьировании давления на выходе из машины (РН) и фиксированном значении РК=Р
при варьировании давления на выходе из машины (РН) и фиксированном значении РК=Р
В первом приближении на участке 7-8 использовалась линейная зависимость между Р и V.
В этом случае площадь под кривой 7-8 определяется как площадь трапеции:

На фиг.3 показано, что формула (1) удовлетворяется в диапазоне до РН=0,05· 105 Па, т.е. до скоростей на входе в камеру λ 1=2,307.
При дальнейшем понижении давления на выходе из диффузора РН<0,05  становится больше, чем η max, что запрещается теоремой.
становится больше, чем η max, что запрещается теоремой.
Теорема будет удовлетворена при выполнении условия

т.е. траектория 7-8 должна быть вогнута (фиг.2).
Таким образом, теорема позволяет определить форму траектории условного процесса на участке ударной адиабаты в P-V координатах.
Теорема И.Пригожина [4] (формула (4)) в данном случае выполняется автоматически:
 , где
, где 
где S - термодинамическая энтропия; Сv - удельная теплоемкость газа при постоянном объеме; Р3, V3, Р, V - давление и удельный объем перед скачком и после него на участке 3-4; S3 - значение энтропии потока перед скачком при V=V3 и Р=Р3.
На фиг.4 холостой цикл тепловой машины представлен в T-S-координатах. Так как цикл замкнут, то согласно определению энтропии (16), несмотря на участок с необратимыми потерями (скачок уплотнения 7-8), суммарное изменение энтропии равно нулю. Следовательно, учитывая, что на участках адиабатического расширения 6-7 и сжатия 8-5 по определению изменение энтропии равно нулю, повышение энтропии на участке скачка уплотнения 7-8 в точности равно понижению энтропии на участке изотермического сжатия в компрессоре 5-6.

В отличие от цикла Карно, где движение возможно в прямом и обратном направлениях, в данном цикле движение возможно только в одном направлении, т.е. цикл является необратимым при суммарном изменении энтропии, равном нулю.
При этом указанный цикл в отличие от цикла Карно, где прямой цикл соответствует циклу двигателя, а обратный - холодильной машине, может работать в одном и том же направлении как холодильная машина (например, вихревые трубы) и в ином качестве (например, газовые эжекторы).
Эффективность энергетических установок рассматриваемого класса тепловых машин может быть определена индикатором качества поточного процесса I, равного отношению полезной утилизированной доли энергии к максимально возможной доле энергии, которая может быть утилизирована в данном устройстве:

где Eпол - полезная утилизированная энергия.
Полная эффективность указанного класса машин определяется следующим образом:

Например, для проточного газового лазера с электрической накачкой полная эффективность (или к.п.д.) запишется так:

где  η обсл. - это эффективность газового тракта, эффективность обслуживающего лазера; η эо, η кв - это электрооптическое и квантовое к.п.д. газового лазера.
η обсл. - это эффективность газового тракта, эффективность обслуживающего лазера; η эо, η кв - это электрооптическое и квантовое к.п.д. газового лазера.
Так, для СО2-лазера η кв≈0,4, а для СО-лазера η кв~0,8 соответственно, т.е. полное к.п.д. лазерной установки даже в идеальном случае (η эо=η обсл=1) не может превысить для СО2 и СО-лазеров соответственно величин:
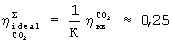 и
и  .
.
В таблице 1 представлена классификация тепловых машин, характеризующаяся направлением преобразования полной энергии, подведенной к тепловой машине.

На фиг.5 представлена графическая иллюстрация таблицы. Видно, что классы тепловых машин (I, II, III) можно изобразить в виде куба со сторонами Епол-Амех-Eпол-Eкин, Eпол-Eдавл.
Весь объем пространства куба представляет собой все многообразие комбинированных схем указанных классов тепловых машин. Вектор 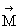 определяет энергетические характеристики некоторой тепловой машины М.
определяет энергетические характеристики некоторой тепловой машины М.
Изобретение позволяет обеспечить оптимальные условия осуществления цикла в тепловой поточной машине и может применяться как при создании конкретных тепловых поточных машин, так и при их эксплуатации.
Литература
1. Меркулов А.П. Вихревой эффект и его применение в технике. М.: Машиностроение, 1969. -187 с.
2. Абрамович Г.Н. Прикладная газовая динамика. М.: Наука, 1991. - 687 с.
3. Ландау Л.Д., Лифшиц М.Е. Гидродинамика. М.: Наука, 1983. - 871 с.
4. Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуации. М.: Мир, 1973. - 279 с.

Изобретение относится к энергетике, в частности к способам преобразования энергии. Способ преобразования энергии в тепловой поточной машине осуществляют путем подведения мощности газового потока на входе в машину и тепловой мощности к машине, определяют среднестатические температуры на входе и на выходе из сопла, определяют удельную тепловую мощность, подведенную к машине, а максимальный коэффициент преобразования энергии определяют по формуле:  где К - отношение теплоемкостей,
где К - отношение теплоемкостей,  ; Ср - теплоемкость рабочего тела при постоянном давлении; Сv - теплоемкость рабочего тела при постоянном объеме; ηКарно - термический к.п.д. цикла Карно,
; Ср - теплоемкость рабочего тела при постоянном давлении; Сv - теплоемкость рабочего тела при постоянном объеме; ηКарно - термический к.п.д. цикла Карно,  ; ТК - статическая температура на выходе из сопла; Т1 - статическая температура на входе сопла;
; ТК - статическая температура на выходе из сопла; Т1 - статическая температура на входе сопла;  - удельная тепловая мощность, подведенная к машине. Изобретение позволяет обеспечить оптимальные условия осуществления цикла в тепловой поточной машине. 5 ил., 1 табл.
- удельная тепловая мощность, подведенная к машине. Изобретение позволяет обеспечить оптимальные условия осуществления цикла в тепловой поточной машине. 5 ил., 1 табл.

Способ преобразования энергии в тепловой поточной машине путем подведения мощности газового потока рабочего тела на входе в машину и тепловой мощности к машине, определения среднестатических температур на входе и на выходе из сопла, отличающийся тем, что определяют удельную тепловую мощность, подведенную к машине, а максимальный коэффициент преобразования энергии определяют по формуле

где К - отношение теплоемкостей, 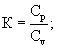
Ср - теплоемкость рабочего тела при постоянном давлении;
Сv - теплоемкость рабочего тела при постоянном объеме;
ηКарно - термический к.п.д. цикла Карно, 
ТК - статическая температура на выходе из сопла;
T1 - статическая температура на входе сопла;
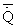 - удельная тепловая мощность, подведенная к машине.
- удельная тепловая мощность, подведенная к машине.
| СПОСОБ ДОСТИЖЕНИЯ МАКСИМАЛЬНОГО ОТОПИТЕЛЬНОГО КОЭФФИЦИЕНТА ТЕПЛОВЫХ НАСОСОВ И УСТАНОВКА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2083932C1 |
| ПОТОЧНЫЙ ДВИГАТЕЛЬ | 1996 |
|
RU2127828C1 |
| ТЕПЛОВОЙ НАСОС | 1999 |
|
RU2152567C1 |
| Устройство для охлаждения проволоки | 1988 |
|
SU1534064A1 |
| US 3861147 А, 21.01.1975 | |||
| US 6076354 А, 20.06.2000. | |||
Авторы
Даты
2004-10-27—Публикация
2002-12-25—Подача