Изобретение относится к области цифровой измерительной техники, где одной из типичных задач является задача определения среднего значения некоторого сигнала, когда используемый цифровой фильтр должен выделить постоянную составляющую сигнала и подавить все помехи, присутствующие в сигнале в виде флуктуации /1/, С.127. Рекомендуется использовать изобретение в составе средств цифровой обработки электроизмерительных сигналов в качестве способа быстрого взвешенного усреднения выборок при построении цифровых измерительных приборов на базе сигнальных микропроцессоров с ограниченным объемом памяти и вычислительными возможностями.
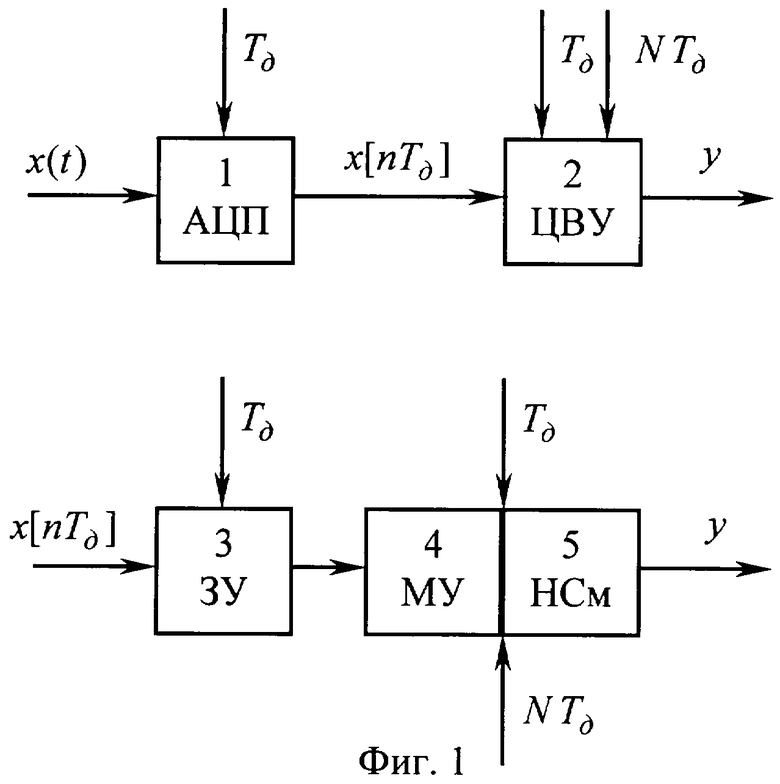
В источнике /1/ - Гутников В.С. Фильтрация измерительных сигналов. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1990, с.160-163 приводится способ КИХ-фильтрации прототипа, реализуемый на базе цифрового вычислительного устройства (ЦВУ) и просматриваемый в структурной схеме на фиг.1. Аналого-цифровой преобразователь (АЦП) 1 вырабатывает коды, пропорциональные мгновенным значениям входного сигнала x(t) с шагом во времени, равным периоду дискретизации КИХ-фильтра 7д, с. Физическая природа входного сигнала может быть любой, поэтому единицы его измерения опущены. Далее эти коды обрабатываются в ЦВУ 2, в качестве которого может выступать любой микропроцессорный элемент, где воспроизводится алгоритм работы цифрового КИХ-фильтра - вычисление взвешенной суммы последовательных значений кода. Указанный алгоритм воспроизводится по структурной схема, представленной блоками 3, 4 и 5. Здесь выборка АЦП, сохраняемая в запоминающем устройстве (ЗУ) 3, поступает на масштабирующее устройство (МУ) 4 и далее на накапливающий сумматор (НСм) 5. Начальная установка МУ и НСм производится с циклом N Тд. При этом в масштабирующем устройстве устанавливается коэффициент передачи а0, а сумматор сбрасывается на нуль. Приходящий после этого выходной сигнал ЗУ запоминается в сумматоре с коэффициентом а0. Далее в МУ устанавливается масштабный коэффициент a1, и в очередном такте 7д сигнал с ЗУ с весом a1 добавляется к сигналу, запомненному раннее в НСм. Всего в накапливающий сумматор поступают N дискретных значений входного сигнала, умноженных на весовые коэффициенты. Полученная таким путем взвешенная сумма есть выходной сигнал КИХ-фильтра. Затем снова производится начальная установка узлов фильтра, и начинается формирование нового выходного сигнала. Таким образом, на формирование одного значения выходного сигнала затрачивается время N Тд, а само значение определяется в соответствии с алгоритмом дискретной фильтрации, приведенном в прототипе на странице 162 и записанном ниже для одного цикла N Тд:
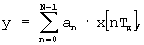
где у - результат взвешенной суммы выборок АЦП;
an - весовое окно;
х[nТд] - выборка АЦП в текущий момент квантованного времени;
nТд - квантованное время, с;
n - номер отсчета квантованного времени (безразмерное время);
Тд - период дискретизации, с;
N - общее число выборок, используемых для взвешенного суммирования (память КИХ-фильтра).
Если в качестве весового окна выступает одно из распространенных усредняющих окон: Дирихле, Бартлетта, Хэмминга, Парзена или Гаусса, /1/, С.130-135, то описанная схема реализует усредняющий КИХ-фильтр /1/, С.127, осуществляющий взвешенное усреднение выборок входного сигнала.
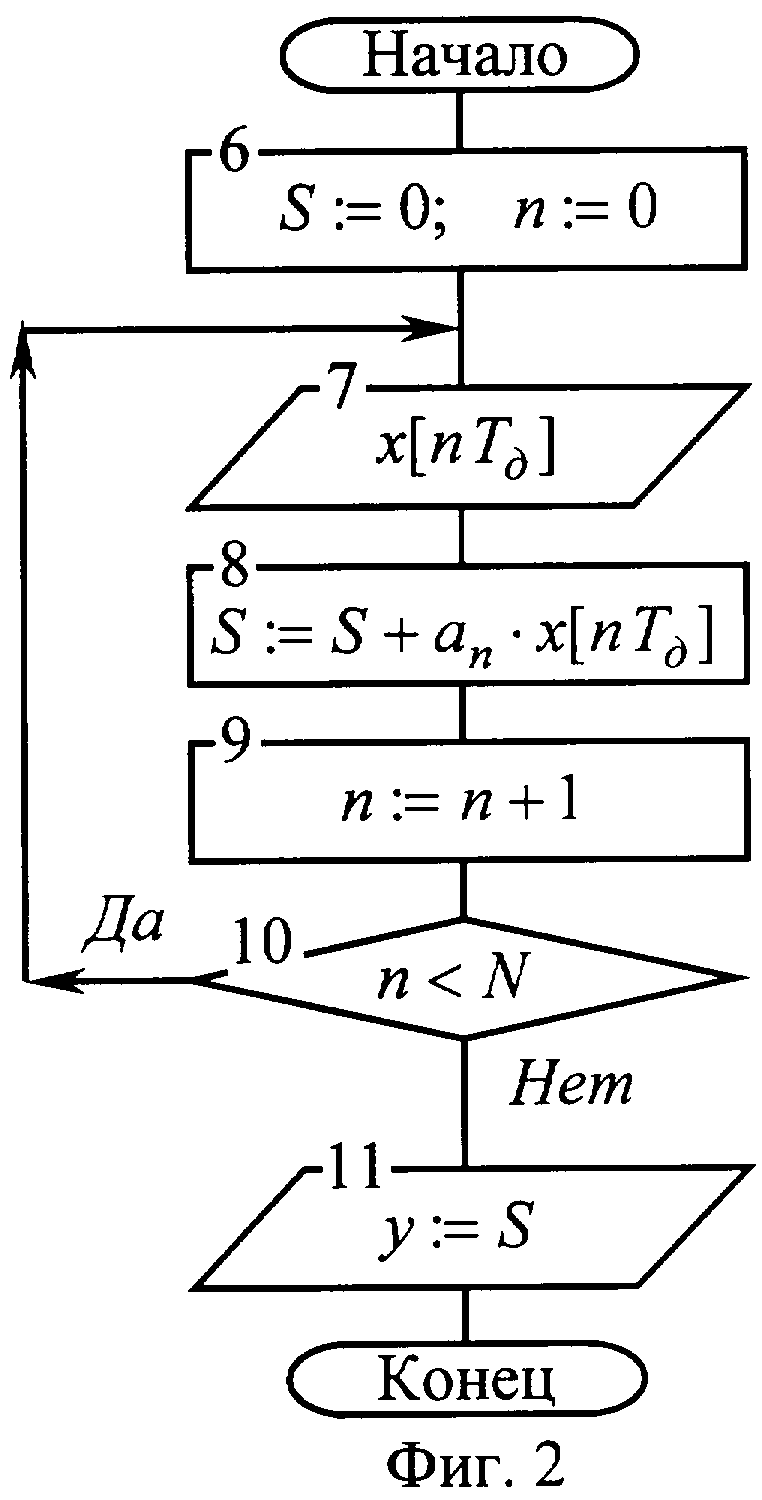
При использовании в качестве ЦВУ процессора алгоритм (1) интерпретируется нами как способ усредняющей КИХ-фильтрации, то есть способ обработки выборок входного сигнала, получаемых с помощью АЦП с шагом во времени, равным периоду дискретизации, и последовательно суммируемых процессором с весами an для получения результата взвешенного усреднения у. Схема реализации указанного способа с помощью процессора приводится на фиг.2. Усредняющее окно аn предварительно сохранено в процессоре в виде массива индексируемого счетчиком квантованного времени n. Перед началом цикла усредняющей КИХ-фильтрации в блоке 6 обнуляются накопитель взвешенной суммы S и счетчик квантованного времени n. Далее в блоке 7 осуществляется получение кода выборки АЦП, который затем с весом а0 добавляется к накопителю суммы S в блоке 8. Потом в блоке 9 счетчик квантованного времени инкрементируется, после чего в блоке 10 его значение проверяется на момент завершения цикла усредняющей КИХ-фильтрации. Вначале блок 10 отрабатывает по ветви "Да", и процесс накопления взвешенной суммы вновь переходит к блоку 7, где получается новое значение кода АЦП, которое затем добавляется к накопителю суммы с весом a1, так как на данный момент n уже равен единице. Процесс накопления взвешенной суммы продолжается циклически до момента, пока блок 10 не идентифицирует равенство n числу N. Это событие соответствует завершению цикла усредняющий КИХ-фильтрации, когда квантованное время принимает значение NТд, а накопитель суммы содержит результат взвешенного усреднения всех выборок в объеме N. В этом случае блок 10 отрабатывает по ветви "Нет" для формирования выходного сигнала усредняющего КИХ-фильтра в блоке 11, значение которого принимается равным S.
Описанный способ усредняющей КИХ-фильтрации, реализуемый на основе процессора, полностью эквивалентен алгоритму работы КИХ-фильтра прототипа и имеет следующие недостатки:
- усредняющее окно должно быть предварительно запомнено в памяти процессора тем большего объема, чем больше точность представления весовых множителей окна и чем больше число выборок используется для взвешенного усреднения. Наличие элемента памяти большого объема может существенно увеличить стоимость аппаратной реализации способа;
- нахождение взвешенной суммы по формуле (1) требует выполнения умножений каждой выборки АЦП на весовой множитель an. Далеко не все современные процессоры имеют аппаратный умножитель с разрядностью, удовлетворяющей требуемой разрядности представления окна. Программное же умножение носит "медленный" характер и нуждается в относительно больших вычислительных затратах. Поэтому реализация формулы (1) либо ограничивает снизу время цикла усредняющей КИХ-фильтрации NTд, особенно при большом числе выборок N, а значит, и сужает область применения способа, либо требует использования высокопроизводительных и, соответственно, дорогостоящих процессоров.
Технический результат, достигаемый предлагаемым изобретением, заключается в исключении недостатков прототипа. При этом заявляемый способ быстрой усредняющей КИХ-фильтрации на основе процессора:
- исключает использование памяти процессора для хранения усредняющего окна, что существенно снижает стоимость аппаратной реализации способа, особенно при большом объеме выборок, обрабатываемых для взвешенного усреднения;
- исключает использование операций умножения выборок АЦП на весовые множители, что существенно снижает вычислительные затраты способа и, как следствие, уменьшает время цикла усредняющей КИХ-фильтрации, без использования дорогих и высокопроизводительных процессоров.
Технический результат достигается за счет использования в качестве усредняющего КИХ-фильтра фильтра среднего высшего порядка, реализуемого "быстрым" способом на одних операциях суммирования, исключая запоминание усредняющего окна, и имеющего дискретную передаточную функцию следующего вида:
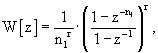
где W[z] - передаточная функция фильтра среднего высшего порядка;
z - оператор 7-преобразования;
n1 - память фильтра среднего первого порядка;
r - порядок фильтра.
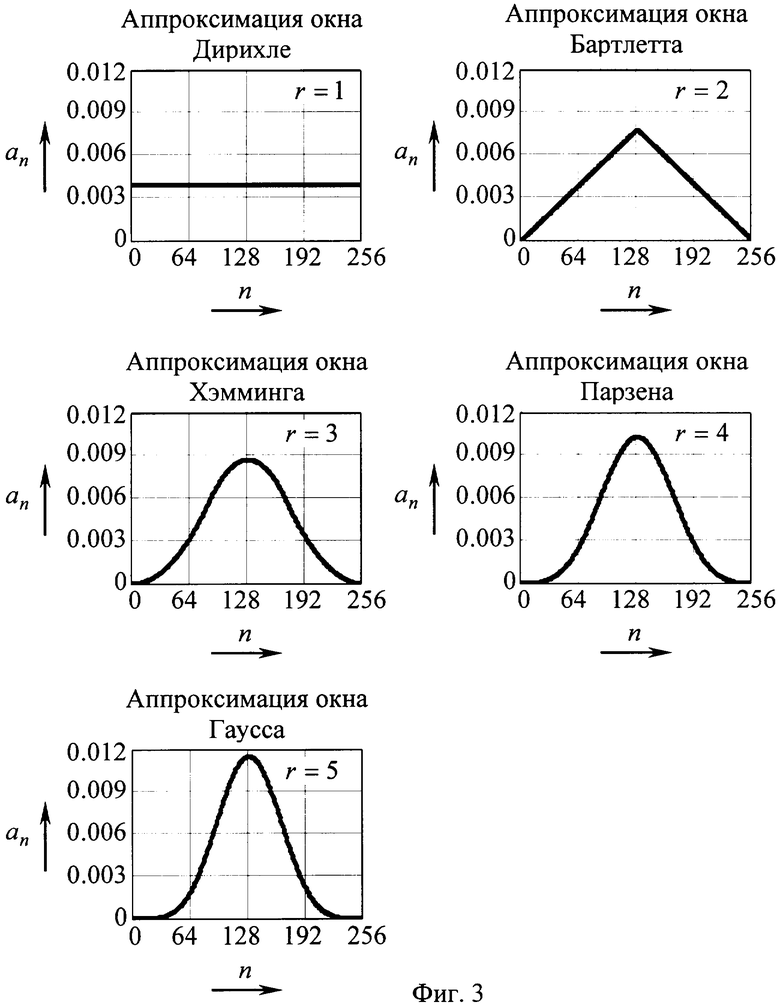
Данный фильтр, будучи фильтром нижних частот, играет роль звена взвешенного усреднения и обладает уникальным свойством - его импульсная характеристика, в зависимости от выбора порядка фильтра r, аппроксимирует несколько типов распространенных усредняющих окон, обеспечивающих высокое подавление переменных флуктуации входного сигнала /1/, С.130-135, /2/, С.287-297. К этим окнам относятся окна: Дирихле, Бартлетта, Хэмминга, Парзена и Гаусса. На фиг.3 приводится семейство указанных окон, полученных путем вычисления импульсной характеристики фильтра среднего высшего порядка через обратное дискретное преобразование Фурье /1/, С.56, /3/, С.45
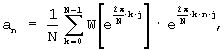
где k - безразмерная линейная частота;
j - мнимая единица;
N - память фильтра среднего высшего порядка (длительность окна), связанная с параметрами фильтра следующим соотношением:
N=r· (n1-1)+1,
где N, r, n1 - целые числа.
N выбрано равным 256. При первом порядке (r=1) импульсная характеристика фильтра среднего аппроксимирует окно Дирихле (естественное окно), при втором - окно Бартлетта, при третьем - окно Хэмминга, при четвертом - Парзена и при пятом - окно Гаусса.
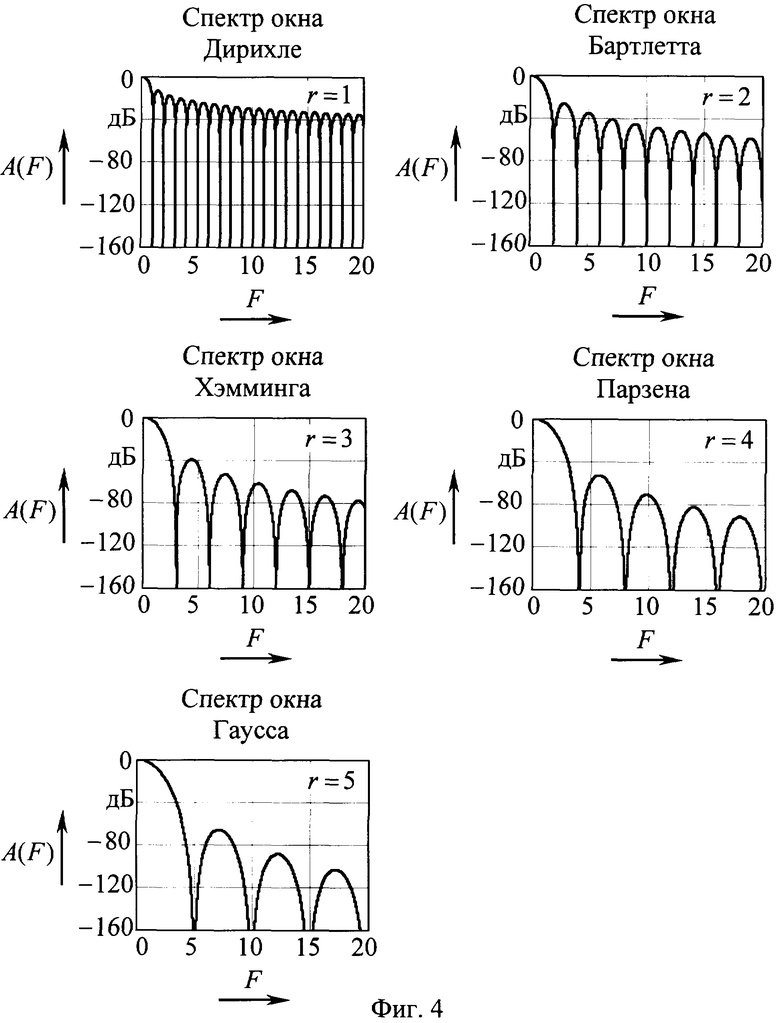
Спектры соответствующих окон представлены на фиг.4 и вычислены посредством формулы
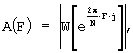
где A(F) - спектр импульсной характеристики фильтра среднего высшего порядка;
F - приведенная частота, равная произведению линейной частоты в герцах на длительность окна в секундах /1/, С.128.
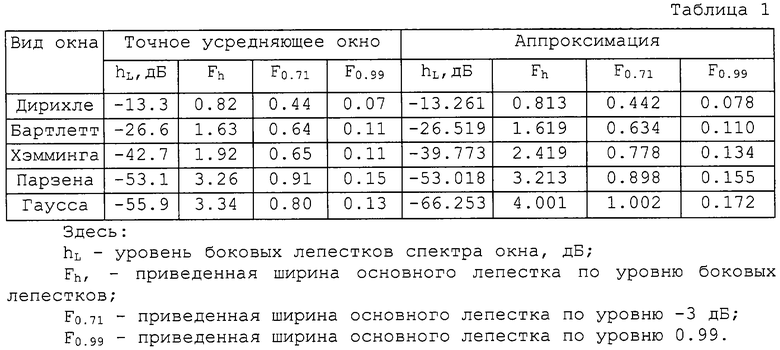
Из фиг.4 следует, что рассматриваемый фильтр среднего пропускает постоянную составляющую входного сигнала без искажений, а переменные флуктуации подавляет тем сильнее, чем больше частота флуктуации. Это свидетельствует об эквивалентности фильтра среднего высшего порядка усредняющей КИХ-фильтрации. В целях анализа аппроксимирующих свойств фильтра среднего ниже приводится таблица 1, где сведены параметры точных усредняющих окон, взятые на странице 130 прототипа, и параметры их аппроксимаций, вычисленные по спектрам на фиг.4.
Из таблицы 1 видно, что фильтры среднего первого, второго и четвертого порядков очень точно аппроксимируют, соответственно, окна Дирихле, Бартлетта и Парзена. Фильтры среднего третьего и пятого порядков, несмотря на то что вид их импульсных характеристик близок к окнам Хэмминга и Гаусса, имеют некоторую ошибку аппроксимации, сохраняя при этом свойства усредняющего КИХ-фильтра. Из таблицы 1 также следует, что с увеличением порядка фильтра среднего параметр hL, уменьшается, а Fh, увеличивается. Это показывает, что подбором порядка, в зависимости от конкретных задач усредняющей КИХ-фильтрации, можно разрешать компромисс между шириной полосы пропускания фильтра (Fh) и подавлением флуктуации за ее пределами (hL).
Способ быстрой усредняющей КИХ-фильтрации на основе процессора базируется на том, что передаточная функция фильтра среднего высшего порядка реализуема без хранения усредняющего окна и использования операций умножения. Для вывода данного способа рассмотрим следующее.
Учитывая, что z-образы выходного и входного сигнала фильтра связаны через передаточную функцию соотношением
y[z]=W[z]· x[z],
где y[z] - z-образ выходного сигнала фильтра;
x[z] - z-образ входного сигнала фильтра,
и раскладывая числитель передаточной функции в бином Ньютона /4/, получим
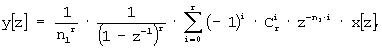
где С
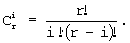
Далее. Дробь 1/(1-z-1) есть не что иное, как передаточная функция дискретного сумматора. Тогда дробь 1/(1-z-1)r в выражении (7) есть передаточная функция многократного сумматора кратности r, образуемого из последовательного соединения сумматоров в количестве r штук, когда на вход последующего сумматора подается выход предыдущего. Кроме того, выражение z-m1.i есть передаточная функция звена чистого запаздывания на т1-i тактов квантованного времени, которое в зависимости (7) показывает, как разнесены во времени значения выходного сигнала многократного сумматора, используемые для формирования выходного сигнала всего фильтра. На основании сказанного, переходя от z-образов в выражении (7) к оригиналам, получим
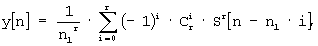
где Sr[n] -многократная сумма выборок входного сигнала х[п] на n-том отсчете квантованного времени;
r - кратность многократной суммы, равная порядку фильтра среднего.
Поскольку длительность импульсной характеристики фильтра среднего составляет N отсчетов квантованного времени, процесс взвешенного усреднения выборок входного сигнала может закончиться только при n, равном N-1. Тогда, подставляя в выражение (9) вместо n величину N-1, с учетом зависимости (4), найдем
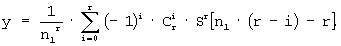
Заметим, что при i, равном r, аргумент многократной суммы становится отрицательным.
В этом случае ее значение можно считать нулевым и выкинуть из рассмотрения:
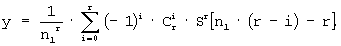
Делая подстановку (i=r-i) и учитывая свойства сочетаний (С
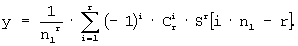
Полученное выражение есть алгоритм способа быстрой усредняющей КИХ-фильтрации на основе процессора. Из него следует, что процесс взвешенного усреднения входного сигнала заключается в накоплении многократной суммы выборок по мере их поступления от АЦП, значение которой фиксируется исключительно для r отсчетов времени с номерами: n1-r, 2n1-r, 3n1-r, и так далее до r• n1-r. Затем, для формирования окончательного результата усреднения, осуществляется однократное суммирование зафиксированных сумм с соответствующими весами: (-1)r-1·C
Таким образом, в заявляемом способе усредняющей КИХ-фильтрации обработка выборок в темпе их появления построена только на операциях суммирования и сравнения для определения моментов времени фиксации сумм. Кроме того, усредняющее окно, аппроксимируемое фильтром среднего, явно не присутствует в алгоритме (12), что исключает использования памяти процессора для его хранения. Выигрыш в вычислительной сложности по сравнению с прототипом, за счет исключения операций умножения выборок входного сигнала на усредняющее окно, будет детально рассмотрен в разделе сведений, подтверждающих возможность осуществления изобретения.
Перечень фигур
Фиг.1 - Структурная схема КИХ-фильтра прототипа на базе цифрового вычислительного устройства.
Фиг.2 - Схема реализации способа усредняющей КИХ-фильтрации прототипа с помощью процессора.
Фиг.3 - Семейство усредняющих окон, аппроксимируемых фильтром среднего высшего порядка.
Фиг.4 - Спектры усредняющих окон, аппроксимируемых фильтром среднего высшего порядка.
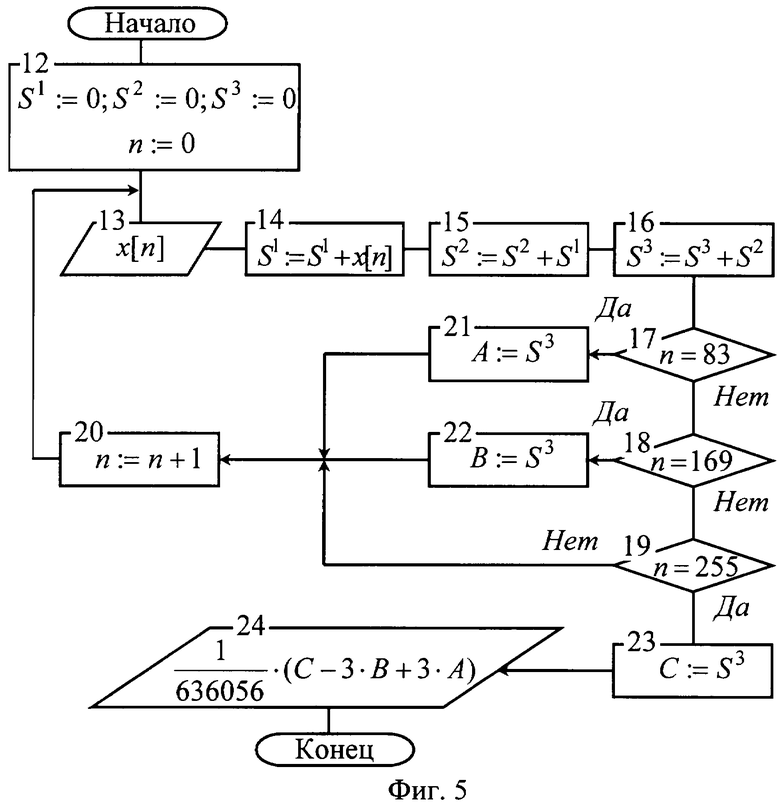
Фиг.5 - Схема реализации способа быстрой усредняющей КИХ-фильтрации на основе процессора.
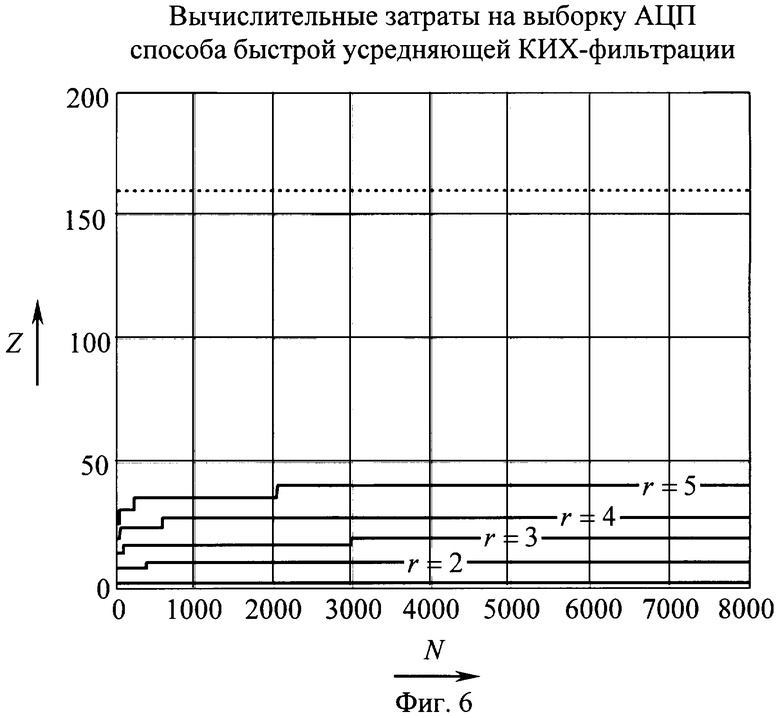
Фиг.6 - Вычислительные затраты способа быстрой усредняющей КИХ-фильтрации на основе процессора.
Заявляемый способ быстрой усредняющей КИХ-фильтрации на основе процессора осуществим при использовании микропроцессорных элементов: сигнальных микропроцессоров, микроконтроллеров со встроенным АЦП или имеющих возможность ввода двоичного кода от внешнего АЦП. В качестве примера указанных микропроцессорных элементов могут рассматриваться следующие микросхемы зарубежных производителей, используемые в России /5/:
- микроконтроллер 68НС705В32 семейства НС05 фирмы Motorola, имеющий 8-разрядное многоканальное АЦП, объем постоянной памяти в размере 32 Кбайт и работающий на тактовой частоте 2 МГц;
- микроконтроллер M430P325I семейства MSP430 фирмы Texas Instruments, имеющий 14-разрядное или 12-разрядное многоканальное АЦП, объем постоянной памяти в размере 16 Кбайт и работающий на тактовой частоте до 3 МГц;
- микроконтроллер ADuC812 семейства MicroConverter™ фирмы Analog Devices, имеющий 12-разрядное многоканальное АЦП, работающий на тактовой частоте 12 МГц и позволяющий адресовать до 16 Мбайт памяти данных и 64 Кбайт памяти программ;
- микроконтроллер Z86C84 семейства Z8 фирмы Zilog, имеющий 8-разрядное многоканальное АЦП, объем постоянной памяти в размере 4 Кбайт и работающий на тактовой частоте 16 МГц;
- новый микроконтроллер AT Mega603L семейства AVR фирмы ATMEL, имеющий 10-разрядное многоканальное АЦП, объем постоянной памяти в размере 64 Кбайт, оперативной памяти в размере 4 Кбайт и работающий на тактовой частоте 4 МГц.
Все указанные микроконтроллеры имеют развитую систему внутренних таймеров, позволяющую управлять периодом дискретизации встроенных АЦП.
На микроконтроллер отводится роль программного осуществления способа быстрой усредняющей КИХ-фильтрации в соответствии с алгоритмом (12). Последовательное получение выборок входного сигнала с помощью встроенного АЦП синхронизируется внутренним таймером микроконтроллера, задающим период дискретизации Тд. Все вычислительные операции, приходящиеся на одну выборку АЦП, должны вложится по времени в интервал периода дискретизации, который существенно меньше для заявляемого способа усредняющей КИХ-фильтрации по сравнению с прототипом. В целях детализации рассмотрим пример осуществления способа быстрой усредняющей КИХ-фильтрации для фильтра среднего 3-го порядка, аппроксимирующего окно Хэмминга (фиг.3).
Пусть длительность импульсной характеристики фильтра составляет 256 отсчета квантованного времени, когда номера отсчетов n могут изменяться от 0 до 255. На основании выражения (4) легко установить, что параметр n1 должен иметь значение 86. Только в этом случае N=3• (86-1)+1=256. Подставляя числовые значения в (12), с учетом сочетаний (8) получим алгоритм способа быстрой усредняющей КИХ-фильтрации
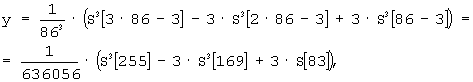
где S3[n] - троекратная сумма выборок входного сигнала на n-том отсчете квантованного времени.
Как видно, фиксация сумм требуется для n с номерами 83, 169 и 255.
На фиг.5 представлена схема осуществления алгоритма (13) на основе процессора.
1) Перед началом цикла усредняющей КИХ-фильтрации в блоке 12 обнуляются: накопитель суммы S1, накопитель двукратной суммы S2, накопитель троекратной суммы S3, а также счетчик квантованного времени n;
2) Далее в блоке 13 осуществляется получение текущей выборки АЦП с последующим наращиванием суммы, двукратной суммы и троекратной суммы в блоках 14, 15 и 16 соответственно;
3) После наращивания троекратной суммы следует система проверок, состоящая из блоков 17, 18, 19, которая в начале полностью отрабатывает по ветвям "Нет", и цикл усредняющей КИХ-фильграции переходит к блоку 20;
4) В блоке 20 инкрементируется счетчик квантованного времени n, после чего все повторяется, начиная со второго пункта - происходит непрерывное получение выборок АЦП и накопление троекратной суммы;
5) Процесс накопления троекратной суммы осуществляется до тех пор, пока блок 17 не идентифицирует момент равенства счетчика n числу 83. Этот случай соответствует событию, когда троекратная сумма приняла значение S3[83]. Поэтому блок 17 отрабатывает по ветви "Да" для сохранения ее значения в фиксаторе А в блоке 21;
6) Далее процесс накопления троекратной суммы продолжается до момента равенства n числу 169, что сопровождается отработкой по ветви "Да" блока 18. В этом случае троекратная сумма имеет значение S3[169], которое сохраняется в фиксаторе В в блоке 22;
7) После этого процесс накопления троекратной суммы вновь продолжается до тех пор, пока блок 19 не идентифицирует момент равенства счетчика n числу 255. Этот случай соответствует завершению цикла усредняющей КИХ-фильтрации, когда квантованное время принимает значение N Тд, а троекратная сумма становится равной S3[255];
8) После завершения цикла усредняющей КИХ-фильтрации и сохранения последнего значения троекратной суммы в фиксаторе С в блоке 23 остается однократно вычислить результат взвешенного усреднения, используя содержимое фиксаторов, что и осуществляется в соответствии с формулой (13) в блоке 24.
Таким образом, в заявляемом способе быстрой усредняющей КИХ-фильтрации на основе процессора обработка выборок входного сигнала в темпе их появления построена только на операциях суммирования и сравнения. Кроме того, усредняющее окно, аппроксимируемое фильтром среднего, явно не присутствует в алгоритме способа, что исключает использования элементов памяти для его хранения. Выигрыш в вычислительной сложности по сравнению с прототипом за счет исключения операций умножения выборок входного сигнала на усредняющее окно рассмотрим детальнее.
Вычислительные затраты, приходящиеся на каждую выборку входного сигнала, определяются блоками 14, 15, 16, 17, 18. Блок проверки момента достижения конца цикла КИХ-фильтрации 19 и блок инкремента счетчика квантованного времени 20 в рассмотрение не входят, так как присутствуют и в алгоритме обработки выборок АЦП прототипа.
Пусть разрядность выборки АЦП составляет 16 бит (знаковых). Для того чтобы не было переполнения многократных сумм при 256 суммированиях, в рассматриваемом алгоритме сумма должна иметь разрядность не менее 24 бита, двукратная сумма - не менее 31 бита и троекратная - не менее 37 бит. При использовании процессора с 16-разрядной арифметикой указанные суммы вычисляются соответственно за 2, 2 и 3 операции суммирования. Таким образом, с учетом того что операции сравнения в блоках 17 и 18 обычно эквивалентны по затратам трем, четырем операциям суммирования, получается, что вычислительные затраты алгоритма на фиг.5 составляют 16 эквивалентных суммирований на каждую выборку АЦП.
В прототипе требуется осуществлять умножение каждой выборки на весовой множитель, разрядность которого обычно не ниже разрядности АЦП. Программное умножение 16-разрядной выборки на 16-разрядный весовой множитель требует, как минимум, шестнадцать 32-разрядных сдвигов и суммировании, каждые из которых эквивалентны двум операциям суммирования. Кроме того, в цикле сдвигов и суммировании требуется осуществлять, как минимум, две операции сравнения для идентификации состояния очередного бита множителя и проверки конца цикла, каждая из которых также эквивалента трем суммированиям. Из этого следует, что вычислительные затраты на программное умножение составляют около 160 эквивалентных суммировании на каждую выборку АЦП, что на порядок больше, нежели в алгоритме на фиг.5.
На фиг.6 представлены результаты численных экспериментов на ЭВМ по определению вычислительных затрат способа быстрой усредняющей КИХ-фильтрации на основе процессора для различных порядков фильтра среднего. Видно, что число эквивалентных суммирований Z, приходящихся на одну выборку АЦП, не столько зависит от объема обрабатываемых выборок N, сколько от порядка фильтра среднего r. На практике для обеспечения высокого подавления переменных флуктуации входного сигнала, пятого порядка фильтра (окно Гаусса) более чем достаточно, при этом объем вычислительных затрат остается существенно ниже, чем в прототипе, для которого на фиг.5 он показан пунктиром.
Источники информации
1. Гутников В.С. Фильтрация измерительных сигналов. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1990. - 192 с.: ил. (прототип).
2. Макс Ж. Методы и техника обработки сигналов при физических измерениях: В 2-х томах. Пер. с франц. - М.: Мир, 1983. - Т.1, С.287-297.
3. Арутюнов П.А. Теория и применение алгоритмических измерений. - М.: Энергоатомиздат, 1990. - С.45.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М., 1967. - С.163-164.
5. Современные микроконтроллеры: Архитектура, средства проектирования, примеры применения, ресурсы сети Интернет. © "Телесистемы". Под ред. Коршуна И.В.; Составление, пер. с англ. и литературная обработка Горбунова Б.Б. - М.: Издательство "Аким", 1998. - 272 с., ил.
Изобретение относится к области цифровой измерительной техники, где одной из типичных задач является задача определения среднего значения некоторого сигнала, когда используемый цифровой фильтр должен выделить постоянную составляющую сигнала и подавить все помехи, присутствующие в сигнале в виде флуктуации. Технический результат, достигаемый предлагаемым изобретением, заключается в снижении стоимости аппаратной реализации способа и в уменьшении времени цикла усредняющей КИХ-фильтрации.Способ основан на обработке выборок в темпе их появления только с помощью операций суммирования и сравнения для определения моментов времени фиксации сумм. 1 табл., 6 ил.
Способ быстрой усредняющей КИХ-фильтрации на основе процессора, заключающийся в том, что с помощью аналого-цифрового преобразователя получают выборки входного сигнала, которые подвергают взвешенному усреднению, последовательно во времени, с помощью процессора, отличающийся тем, что накапливают многократную сумму выборок входного сигнала, значение которой фиксируют для r моментов квантованного времени с номерами n1 - r , 2n1-r, 3n1 - r, и так далее до r • n1 - r , где r - кратность накапливаемой суммы, n1 - целый параметр, связанный с общим объёмом суммируемых выборок N соотношением:
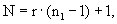
затем зафиксированные значения многократной суммы однократно суммируют с целыми весами в соответствии с формулой:
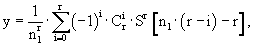
где у - результат взвешенного усреднения выборок аналого-цифрового преобразователя;
Sr[i·n1-r] - зафиксированные значения многократной суммы кратности r;
С
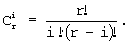
| ГУТНИКОВ В.С | |||
| Фильтрация измерительных сигналов | |||
| - Л.: Энергоатомиздат, Ленинградское отделение, 1990, с.160-163 | |||
| ФИЛЬТРУЮЩИЙ СОПРОЦЕССОР | 1997 |
|
RU2178949C2 |
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
| Способ термообработки высокопрочных холоднокатаных листов | 1983 |
|
SU1168615A1 |
Авторы
Даты
2004-12-20—Публикация
2002-04-29—Подача