Изобретение относится к измерительной технике и может быть использовано для определения пористости труднопроницаемых материалов.
Известен способ определения пористости материалов, заключающийся в ламинарной фильтрации газа через заключенный в обечайку из газонепроницаемого материала образец, создании гармонических колебаний давления газа определенной частоты и амплитуды в замкнутом пространстве перед образцом и измерения колебаний давления газа в замкнутом пространстве после образца (А.С. №1679287, кл. G 01 N 15/02, 1991 г.).
Данный способ определения активной пористости обладает невысокой точностью, так как оценивает только численное значение активной пористости материалов без определения радиуса активных пор и оценки извилистости пор и потерь давления на входе и выходе, а неучтенные радиусы активных пор, извилистость пор и потери давления на входе и выходе приводят к увеличению погрешности измерения активной пористости.
Наиболее близким к предлагаемому изобретению является способ определения активной пористости материалов (Патент №2180743, кл. G 01 N 15/02, 2002 г.), включающий ламинарную фильтрацию газа через заключенный в обечайку из газонепроницаемого материала образец из замкнутого пространства перед образцом в замкнутое пространство после него путем создания в замкнутом пространстве перед образцом гармонических колебаний давления газа изменяющейся частоты и определенной амплитуды и измерение амплитуды колебаний давления газа в замкнутом пространстве после образца. Измеряют изменение амплитуды давления газа в замкнутом пространстве до и после образца, вычисляют разность амплитуд и определяют три значения частоты из условия равенства разности амплитуд, определяя активную пористость материалов, эквивалентный радиус пор и коэффициент, учитывающий извилистость пор и потери давления на входе в образец и выходе из него в результате совместного решения на ЭВМ трех уравнений:
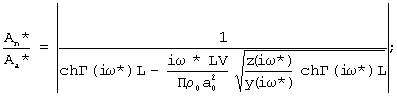
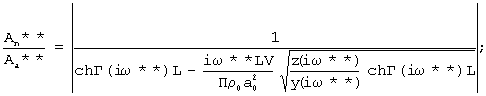
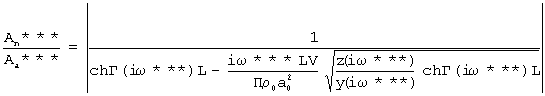 ,
,
где 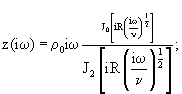
у(iω )=-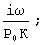
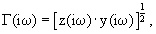 L=β Lм
L=β Lм
где ω *, ω **, ω *** соответственно три значения частоты, при которых обеспечивается одинаковое значение Аа-Аn=Δ Р (или 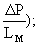
Аа - амплитуда колебаний давления в замкнутом пространстве перед образцом;
Аn - амплитуда колебаний давления в замкнутом пространстве после образца;
Δ Р - перепад давлений на образце;
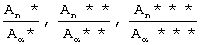 - соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω *, ω **, ω ***;
- соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω *, ω **, ω ***;
β - коэффициент, учитывающий извилистость пор и потери давления на входе и выходе из образца;
Lм- толщина исследуемого материала;
R - эквивалентный радиус пор;
П - значение активной пористости;
ρ 0 - плотность газа в установившемся состоянии;
i - комплексное число;
К - коэффициент адиабаты;
υ - коэффициент кинематической вязкости;
J0, J2 - функции Бесселя;
ch(iω ), sh(iω ) -эллиптический синус и косинус;
V - газовый объем пространства после образца;
а0 - скорость звука.
Данный способ определения активной пористости обладает ограниченными технологическими возможностями, так как оценивает численное значение активной пористости материалов, без учета температуры, что допустимо при определении активной пористости легкопроницаемых материалов (фильтровальных сеток и прессованных сукон), так как проницаемость изделий из этих материалов довольно высока, сопротивление фильтрации газа через материал невелико, невелика разность давлений на торцах образца, которые изменяются в диапазоне 100... 150 Па, поэтому изменением температуры в процессе фильтрации можно пренебречь. При большом же сопротивлении при фильтрации газа может изменяться температура, а перепад давления может составлять до 1 МПа и более. В этом случае, воздух будет вести себя уже не как идеальный газ, а как реальный. Таким образом, этот способ не позволяет определять активную пористость труднопроницаемых материалов (металлокерамика, керамика).
Задачей, решаемой изобретением, является расширение технологических возможностей способа путем обеспечения возможности определения активной пористости труднопроницаемых материалов.
Это достигается тем, что в способе, заключающемся в ламинарной фильтрации газа через заключенный в обечайку из газонепроницаемого материала образец из замкнутого пространства перед образцом в замкнутое пространство после него, путем создания в замкнутом пространстве перед образцом гармонических колебаний давления газа с изменяющейся частотой и определенной амплитудой, измеряют амплитуду колебаний давления газа в замкнутом пространстве до и после образца, вычисляют разность амплитуд, определяют три значения частоты из условия равенства разности амплитуд, одновременно с измерением амплитуды давления измеряют температуру газа до и после образца, определяя активную пористость материалов в результате совместного решения на ЭВМ трех уравнений
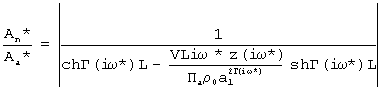 ;
;
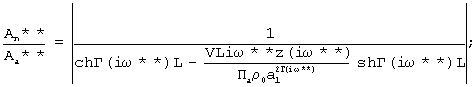 ;
;
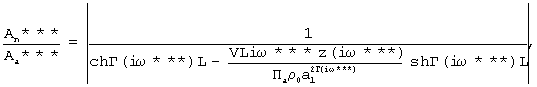
где
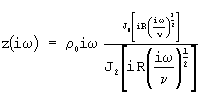 ;
;
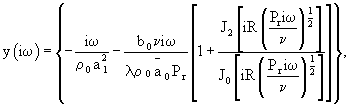
Г2(iω )=z(iω )y(iω ).
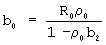
 ,
, 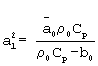 ,
,  , L=β Lм
, L=β Lм
где  ω *, ω **, ω *** соответственно три значения частоты, при которых обеспечивается одинаковое значение Аα -Аn=Δ Р (или
ω *, ω **, ω *** соответственно три значения частоты, при которых обеспечивается одинаковое значение Аα -Аn=Δ Р (или 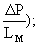
Аа, Аn - амплитуда колебаний давления в замкнутом пространстве перед и после образца;
Δ Р - перепад давлений на образце;
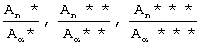 - соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω *, ω **, ω ***;
- соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω *, ω **, ω ***;
ρ 0, Т0 - соответственно плотность и температура газа в установившемся состоянии;
i - комплексное число;
R - эквивалентный радиус пор;
Рr - число Прандтля;
υ - коэффициент кинематической вязкости;
J0, J2 - функции Бесселя;
λ - коэффициент теплопроводности;
ch(iω ), sh(iω ) -эллиптический синус и косинус;
Ср - удельная теплоемкость при постоянном давлении;
R0 - газовая постоянная;
а2, b2 - заданные const;
Lм - толщина исследуемого материала;
β - коэффициент, учитывающий извилистость пор и потери давления на входе и выходе образца;
V - газовый объем пространства после образца;
Пα - значение активной пористости материала.
Введение измерения температуры с помощью датчиков температуры в рабочей и измерительной камерах позволяет расширить технологические возможности способа, что подтверждается следующим.
В системе цилиндрических координат х, r, θ , при допущении осевой симметрии рабочей и измерительной камер и расположенной между ними обечайки, необходимой для размещения в ней образца (при условии, что образец имеет поры в виде капилляров, длина которых намного превышает диаметр), математическая модель перетекания газа по этим порам может быть представлена следующими уравнениями:
- уравнение Навье-Стокса:
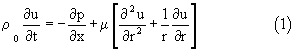
- уравнение неразрывности:
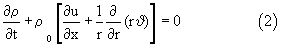
- уравнение сохранения энергии:
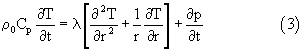
- уравнение Ван-дер-Ваальса:
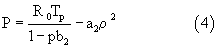
Уравнение адиабаты, используемое в прототипе, описывает состояние идеального газа и применяется при определении активной пористости легкопроницаемых материалов. При фильтрации газа через труднопроницаемый материал газ будет вести себя не как идеальный, а как реальный и возникнет необходимость учитывать температуру газа. В качестве уравнения состояния реального газа предлагается использовать уравнение Ван-дер-Ваальса.
Линеаризируем уравнение (4). Будем иметь
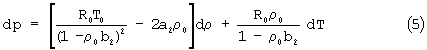
где р - давление;
Т - температура;
u - осевая составляющая скорости течения;
ϑ - радиальная составляющая скорости течения;
ρ - плотность;
λ - коэффициент теплопроводности;
μ - коэффициент динамической вязкости;
х, r, - цилиндрические координаты;
t - время;
Ср - удельная теплоемкость при постоянном давлении;
R0 - газовая постоянная;
ρ 0, Т0 - значения ρ , Т при установившемся режиме;
а2, b2 - заданные const.
При а2=b2=0 получаем уравнение состояния Менделеева-Клапейрона идеального термодинамического газа:
Р=R0Tρ
Проведем ряд преобразований, с помощью которых исключим ρ из (2) и (5). Будем иметь:
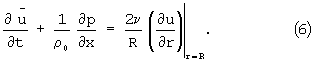
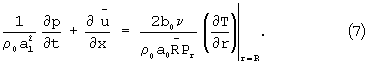

где 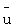 - среднее значение осевой составляющей скорости в поперечном сечении капилляра образца,
- среднее значение осевой составляющей скорости в поперечном сечении капилляра образца,
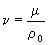 - коэффициент кинематической вязкости,
- коэффициент кинематической вязкости,
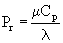 - число Прандтля,
- число Прандтля,
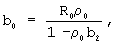
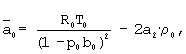
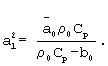
К системе (1, 3, 6, 7) добавим граничные условия, которые получаются при следующих допущениях.
1) Давление во входном сечении равняется давлению Ра, а давление на выходе канала равняется давлению Рn.
2) Изменение давления в рабочей камере происходит только в результате изменения массы рабочего газа, содержащегося в камере.
Итак, граничные условия
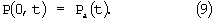
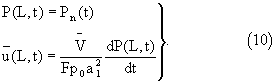
где F - площадь поперечного сечения образца.
Применим к системе (1), (3), (6), (7) преобразование Лапласа по переменной t, тогда получим систему уравнений
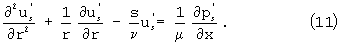
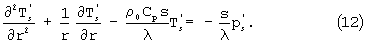
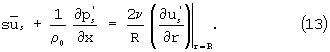
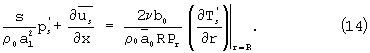
где 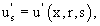

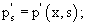
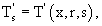

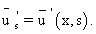
Первые два уравнения - обыкновенные линейные неоднородные дифференциальные уравнения.
При их решении общее решение уравнения есть сумма общего решения соответствующего однородного и частного решения данного неоднородного уравнения. Соответствующее однородное уравнение как для (11), так и для (12) есть уравнение Бесселя. Учитывая его, а также определяя частное решение, входящее в правую часть, мы получили общие решения первых двух уравнений
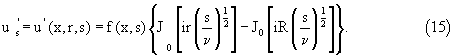
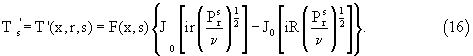
где J0 - функция Бесселя, f(x,s), F(x,s) - произвольные функции, причем
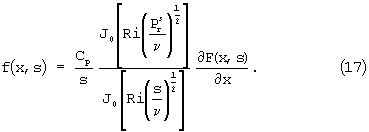

Прежде чем решать третье и четвертое уравнение системы, т.е. (13), (14), мы исключили из них производные 
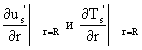 используя найденные решения (15) и (16).
используя найденные решения (15) и (16).
После ряда преобразований получим:
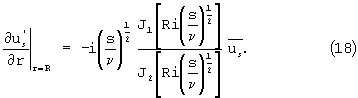
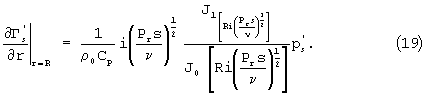
Подставляя (18) и (19) в (13) и (14) преобразуем третье и четвертое уравнения, которые примут вид
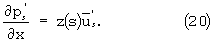
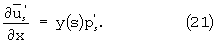
где
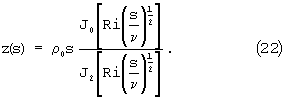
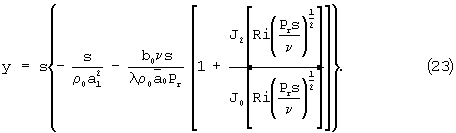

Исключая из (20) и (21) поочередно 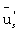 и
и 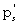
 получили уравнения
получили уравнения

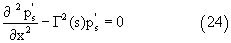
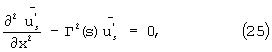

где
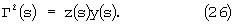
Решая уравнение (24), (25) методом Эйлера получим:
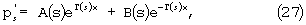
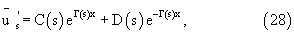
где
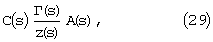 ,
,
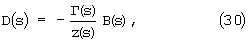
а А(s) и В(s) пока неизвестные функции.
Итак, решением системы (11), (12), (13) и (14) являются функции (15), (16), (27), (28), куда входят неизвестные функции F(x,s), A(s), B(s).
Для определения А(s) и В(s) используем условия (9) и (10). После применения к ним преобразования Лапласа они примут вид:
при х=0 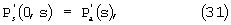
при х=0 
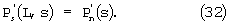
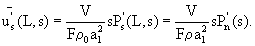
Подставляя (27), (28), (29) и (30) и (31) и (32) получим:
А(s)+В(s)=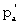 (s),
(s),
А(s)еГ(s)L+В(s)e-Г(s)L=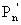 (s),
(s),
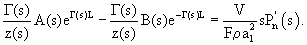
Имеем три уравнения с двумя неизвестными А(s) и В(s). 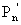 (t) можно считать известным, т.к. это давление в измерительной камере, которое можно измерить.
(t) можно считать известным, т.к. это давление в измерительной камере, которое можно измерить.
Из первого уравнения выразим В(s) через А(s). Из второго и третьего уравнений найдем А(s), и, наконец, подставив А(s) и В(s) во второе уравнение выразим давление в измерительной камере 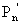 (s) через внешнее давление
(s) через внешнее давление 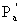 (s).
(s).
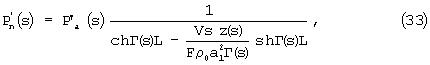
где
chГ(s)L=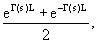 shГ(s)L=
shГ(s)L=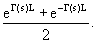
Далее предполагая, что изменение давления в рабочей камере происходит по гармоническому закону, осуществляем замену переменной s на iω .
В результате получаем
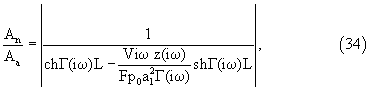
где
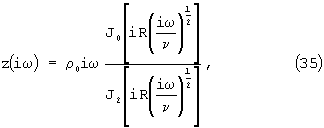
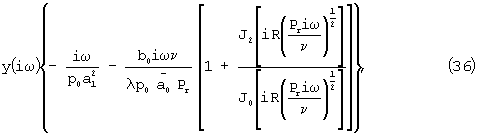
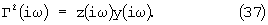
Если в ячейке плотно установить пористое тело с порами в виде ориентированных вдоль оси х цилиндрических капилляров, то с учетом того, что FL=Па, (где F - суммарная площадь поперечных сечений капилляров, L - длина капилляров, Па - активная пористость исследуемого материала) уравнение (34) преобразуется к виду
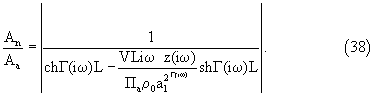
Реальная активная пористость в изделиях из пористых материалов в большинстве своем очень далека от идеальных, вытянутых вдоль оси х капилляров различного диаметра. Реальные поры имеют неодинаковую по всей длине поперечную площадь, направление поровых каналов меняется в процессе фильтрации и не совпадает с направлением фильтрации.
При фильтрации газа через пористую среду, будут наблюдаться потоки газа, которые можно привести к рассмотренной нами физической модели (вытянутым вдоль оси Х цилиндрическим капиллярам различного диаметра) через коэффициент поровой извилистости аизв. При этом L в уравнении (38) будет равна
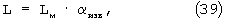
где Lм - толщина пористого материала в направлении фильтрации.
Кроме того, рассмотренная физико-математическая модель не учитывает входные и выходные потери давления газа в пористой среде, которые определяются по уравнениям Вейсбаха

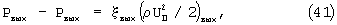
где ξ вх и ξ вых - коэффициент входных и выходных потерь;
Рвх - давление газа до входа в пористое тело;
Рвых - давление газа за пористым телом;
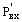 и
и 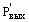 - соответственно давление газа на входном и выходном сечении пор;
- соответственно давление газа на входном и выходном сечении пор;
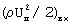 и
и 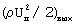 - скоростной напор во входном и выходном сечении пор.
- скоростной напор во входном и выходном сечении пор.
Так как использование уравнений (40, 41) приведет к нелинейности дифференциальных уравнений, предложим более простой способ учета входных и выходных сопротивлений.
Он заключается в искусственном увеличении длины входных и выходных участков пористого тела в направлении фильтрации до тех пор, пока не выровняются относительные (отнесенные к единице длины) потери давления на входных, выходных и внутренних участках пористого материала. С учетом этого длина капилляров L в уравнении (38) будет равна
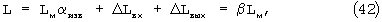
где Δ Lвх и Δ Lвых - величина искусственного удлинения входных и выходных участков пористого тела; β - суммарный коэффициент удлинения, учитывающий как извилистость пор, так и потери давления газа на входных и выходных участках.
Таким образом, введение в исходные зависимости уравнения Ван-дер-Ваальса позволило определить активную пористость, эквивалентный радиус пор, коэффициент извилистости пор труднопроницаемых материалов, что позволило расширить технологические возможности способа.
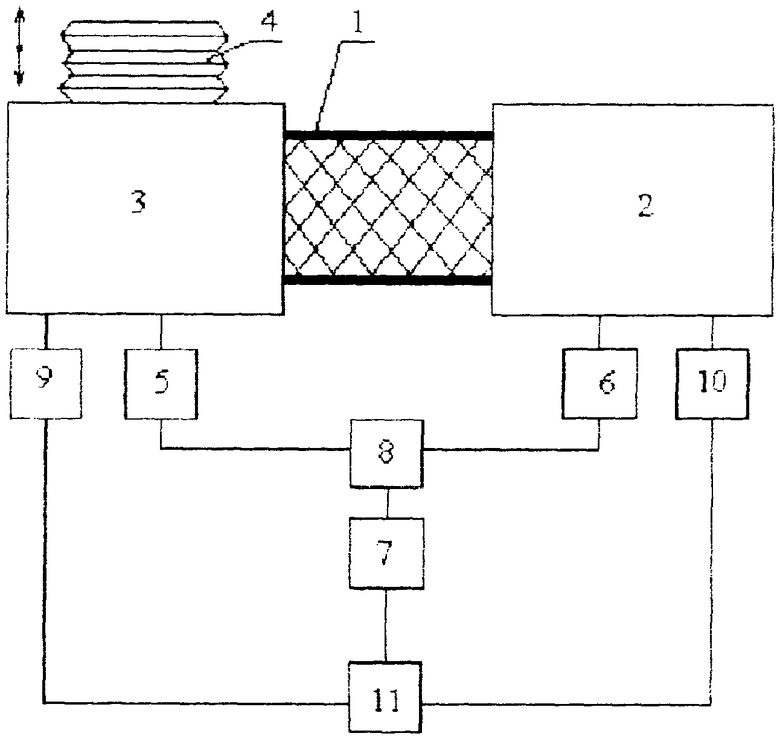
На чертеже приведена схема устройства для реализации предлагаемого способа.
Устройство состоит из цилиндрической выполненной из газонепроницаемого материала обечайки 1, в которую плотно установливают цилиндрический пористый образец таким образом, что длина образца равна длине обечайки 1. Один открытый конец обечайки 1 соединен, например, с помощью резьбового соединения и уплотнителя (условно не показаны) с измерительной камерой 2, а другой с рабочей камерой 3, являющейся генератором гармонических колебаний. Для возбуждения колебаний в камеру 3 вмонтирован сильфон 4. В стенках камер 2 и 3 установлены датчики давления 5 и 6, выходы которых соединены с входом ЭВМ 7 через электронное согласующее устройство 8, и датчики температуры 9 и 10, выходы которых соединены с входом ЭВМ 7 через электронное согласующее устройство 11. При возникновении разницы температур в камерах автоматизированно включается система нагрева (условно не показана) для поддержания одинаковой температуры.
Для определения активной пористости материалов в камере 3 сильфоном 4 создают колебания газа. В результате фильтрации газа на образце возникает давление Δ Р=Аа-Аn. Меняя частоту колебаний давления газа и фиксируя разницу амплитуд, определяют три значения частоты, ω *, ω **, ω ***, при которых перепад давления на образце постоянен Δ Р=Аа-Аn=const. Значения частот ω *, ω **, ω *** и отношения амплитуд Аn*/Аa*, Аn**/Аa**, Аn***/Аa*** подаются на ЭВМ 7.
Данные о номинальном объеме измерительной камеры Vn, температуре Т, площади F образца, разделяющего камеры, газовой постоянной R0, коэффициенте кинематической вязкости ν , плотности газа ρ , толщине образца L, удельной темплоемкости газа Ср, введены в ЭВМ заранее. Поэтому ЭВМ 7 осуществляет определение активной пористости материалов, эквивалентного радиуса пор и коэффициента, учитывающего извилистость пор и потери давления на входе в образец и выходе из него из совместного решения трех уравнений.
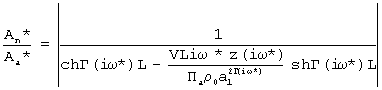 ;
;
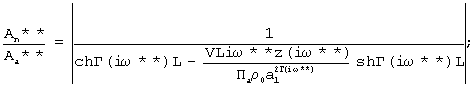 ;
;
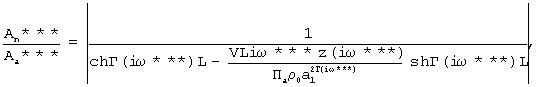
Пример: осуществляли измерение активной пористости материалов, эквивалентного радиуса пор и коэффициента, учитывающего извилистость пор сложной керамической системы (бетон). Образец выполнен в виде цилиндра диаметром 30 мм и толщиной 15 мм. Расход компонента связки, Кс 300 кг на 1 м3 раствора. Отношение затворителя к компоненту связки З/Кс=0,63. ЭВМ 7 зафиксировал значения частот ω *=2,49 Гц, ω **=4,11 Гц, ω ***=8,56 Гц и отношение амплитуд Аn*/Аa*=0,109, Аn**/Аa**=0,081, Аn***/Аa***=0,058 и выдал значение Па=11,5311%. R=13,9875 мкм, β =5,1124.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ АКТИВНОЙ ПОРИСТОСТИ МАТЕРИАЛОВ | 1999 |
|
RU2180743C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОРИСТОСТИ МАТЕРИАЛОВ | 2003 |
|
RU2235308C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОНИЦАЕМОСТИ И ПОРИСТОСТИ МАТЕРИАЛОВ | 2003 |
|
RU2247358C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОРИСТОСТИ МАТЕРИАЛОВ | 2006 |
|
RU2305828C1 |
| АЭРОДИНАМИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ПОВЕРХНОСТИ ТВЕРДОЙ ФАЗЫ, УДЕЛЬНОЙ ПОВЕРХНОСТИ КОНДЕНСИРОВАННОЙ ФАЗЫ, КОЭФФИЦИЕНТА ВЛАГОПРОВОДНОСТИ, ПОТЕНЦИАЛА ВЛАГИ ДЛЯ ОДНОРОДНЫХ ПОРИСТЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2000 |
|
RU2230308C2 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| Способ изучения характеристик пористых материалов | 1975 |
|
SU646231A1 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| Способ определения пористости материалов | 1989 |
|
SU1679287A1 |
| Способ определения эффективной проницаемости пористых коллекторов нефти и газа | 1983 |
|
SU1163210A1 |
Изобретение относится к измерительной технике и может быть использовано для определения пористости труднопроницаемых материалов. Сущность: способ включает ламинарную фильтрацию газа через образец из замкнутого герметичного пространства до образца в замкнутое герметичное пространство после образца. В замкнутом герметичном пространстве перед образцом создают гармонические колебания газа с изменяющейся частотой и определенной амплитудой, измеряют изменения амплитуды давления газа перед образцом и после образца, температуру газа перед и после образца вычисляют разность амплитуд и определяют три значения частоты из условия равенства разности амплитуд. Активную пористость определяют путем совместного решения на ЭВМ трех уравнений фильтрации газа. Технический результат изобретения заключается в обеспечении возможности определения активной пористости труднопроницаемых материалов. 1 ил.
Способ определения активной пористости материалов, включающий ламинарную фильтрацию газа через заключенный в обечайку из газонепроницаемого материала образец из замкнутого пространства перед образцом в замкнутое пространство после него путем создания в замкнутом пространстве перед образцом гармонических колебаний давления газа с изменяющейся частотой и определенной амплитудой и измерение амплитуды колебаний давления газа в замкнутом пространстве до и после образца, вычисляют разность амплитуд, определяют три значения частоты из условия равенства разности амплитуд, отличающийся тем, что одновременно с измерением амплитуды давления измеряют температуру газа в замкнутом пространстве до и после образца, а активную пористость материалов, эквивалентный радиус пор и коэффициент, учитывающий извилистость пор и потери давления на входе в образец и выходе из него, определяют в результате совместного решения на ЭВМ трех уравнений фильтрации газа:
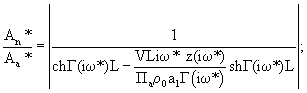
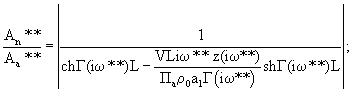
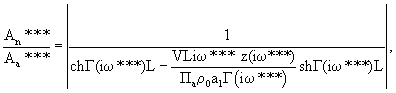
где 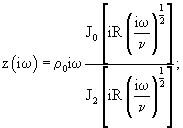
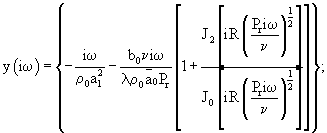
Г2(iω)=z(iω)y(iω);
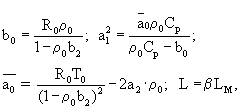
где ω*, ω**, ω*** - соответственно три значения частоты, при которых обеспечивается одинаковое значение Аа-Аn=ΔР 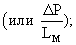
Аа, Аn - амплитуда колебаний давления в замкнутом пространстве перед и после образца;
ΔР - перепад давлений на образце;
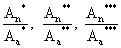 - соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***;
- соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***;
ρ0, Т0 - соответственно плотность и температура газа в установившемся состоянии;
i - комплексное число;
R - эквивалентный радиус пор;
Рr - число Прандтля;
ν - коэффициент кинематической вязкости;
J0, J2 - функции Бесселя;
λ - коэффициент теплопроводности;
ch(iω), sh(iω) - эллиптические косинус и синус;
Ср - удельная теплоемкость при постоянном давлении;
R0 - газовая постоянная;
а2, b2 -заданные const;
Lм - толщина исследуемого материала;
β - коэффициент, учитывающий извилистость пор и потери давления на входе и выходе образца;
V - газовый объем пространства после образца;
Па - значение активной пористости материала.
| СПОСОБ ОПРЕДЕЛЕНИЯ АКТИВНОЙ ПОРИСТОСТИ МАТЕРИАЛОВ | 1999 |
|
RU2180743C2 |
| Способ определения пористости материалов | 1989 |
|
SU1679287A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ПРОНИЦАЕМЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2017135C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МИНИМАЛЬНЫХ ДИАМЕТРОВ ПОР ОБРАЗЦА | 1999 |
|
RU2186364C2 |
Авторы
Даты
2005-01-20—Публикация
2003-05-26—Подача