Изобретение относится к измерительной технике и может быть использовано для определения пористости различных материалов.
Известен способ определения пористости материалов, заключающийся в помещении исследуемого тела в измерительную емкость, соединении измерительной емкости с калиброванной емкостью избыточного давления, перепуске газа из калиброванной емкости в измерительную и измерении давлений в емкостях до и после перепуска (А.С. 1368720 кл. G 01 N 15/08, 1988 г.).
Данный способ обладает низкой точностью определения активной пористости, так как в момент перепуска газа из калиброванной емкости в измерительную газ в основном адсорбирует на исследуемом образце, а не проникает по активным порам внутрь.
Наиболее близким к предлагаемому изобретению является способ определения пористости материалов, включающий ламинарную фильтрацию газа через заключенный в обечайку из газонепроницаемого материала образец, создании гармонических колебаний газа определенной частоты и амплитуды в замкнутом пространстве перед образцом и измерения колебаний давления газа в замкнутом пространстве после образца (А.С. 1679287 кл. G 01 N 15/02, 1991 г.).
Данный способ определения активной пористости обладает незначительными функциональными возможностями, так как оценивает только численное значение активной пористости материалов, без определения радиуса активных пор и оценки извилистости пор и потерь давления на входе и выходе. Необходимо отметить, что неучтение радиуса активных пор, извилистости и потерь давления на входе и выходе приводит к увеличению погрешности измерения активной пористости.
Целью настоящего изобретения является повышение точности измерения активной пористости материалов путем обеспечения возможности определения радиуса активных пор, извилистости пор и потерь давления на входе и выходе.
Поставленная цель достигается тем, что в известном способе, включающем ламинарную фильтрацию газа через заключенный в обечайку из газонепроницаемого материала образец из замкнутого пространства перед образцом в замкнутое пространство после него, путем создания в замкнутом пространстве перед образцом гармонических колебаний давления газа определенной частоты и амплитуды, и измерения амплитуды колебаний газа в замкнутом пространстве после образца, гармонические колебания давления газа в замкнутом пространстве перед образцом осуществляют с изменяющейся частотой, измеряют изменение амплитуды давления газа в замкнутом пространстве перед образцом и после образца, вычисляют разность амплитуд и определяют три значения частоты из условия равенства разности амплитуд, определяя активную пористость материалов в результате совместного решения на ЭВМ трех уравнений: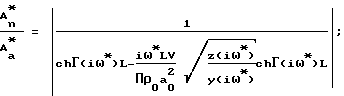
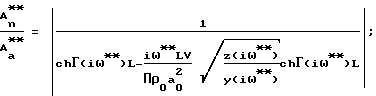
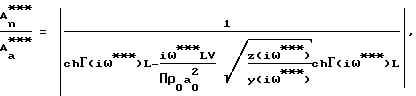
где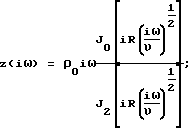
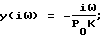
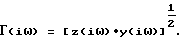
ω*, ω**, ω*** - соответственно три значения частоты, при которых обеспечивается одинаковое значение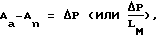
где Аа - амплитуда колебаний давления в замкнутом пространстве перед образцом;
An - после образца;
ΔP - перепад давлений на образце;
Lм - толщина исследуемого материала;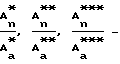 соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***.
соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***.
ρ0 - плотность газа в установившемся состоянии;
i - комплексное число;
R - эквивалентный радиус пор;
Р0 - давление в установившемся состоянии;
К - коэффициент адиабаты;
υ - коэффициент кинематической вязкости;
J0, J2 - функции Бесселя;
ch(iω), sh(iω) - эллиптические синусы и косинусы;
L = βLм, где Lм - толщина исследуемого материала;
β - коэффициент, учитывающий извилистость пор и потери давления на входе и выходе образца;
V - газовый объем пространства после образца;
П - значение активной пористости материала;
а0 - скорость звука.
В системе цилиндрических координат х, r, θ, при допущении осевой симметрии емкостей 4 и 3 и обечайки 1 (при условии, что образец 2 имеет поры в виде капилляров, длина которых намного превышает диаметр) математическая модель перетекания газа по этим порам может быть представлена следующими уравнениями:
- уравнение Навье-Стокса или уравнение, вытекающее из закона сохранения количества движения: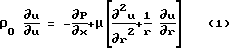
- уравнение неразрывности или уравнение, вытекающее из закона сохранения массы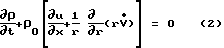
- уравнение адиабаты:
PVK=const (3)
Линеаризируем уравнение (3). Будем иметь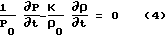
где ρ - плотность газа;
Р - давление газа;
u - осевая составляющая скорости течения газа; радиальная составляющая скорости течения газа;
радиальная составляющая скорости течения газа;
μ - коэффициент динамической вязкости;
r - текущий радиус капилляра;
К - показатель адиабаты.
Решив совместно уравнения 2 и 4, исключим плотность ρ и, умножив полученное выражение на r, выразим 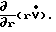
Будем иметь: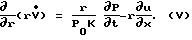 (5)
(5)
Проинтегрировав последнее от 0 до R по r при условии, что 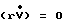 при r=0 и r=R, а также
при r=0 и r=R, а также 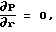 получим:
получим: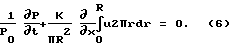
Аналогично проинтегрируем уравнение 1. Используя условие ∂u/∂r/r=0 = 0 и предварительно умножив на r, будем иметь: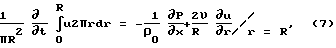
где 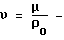 коэффициент кинематической вязкости.
коэффициент кинематической вязкости.
Введем обозначение: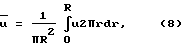
где 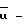 среднее значение осевой составляющей скорости в поперечном сечении капилляра образца 2.
среднее значение осевой составляющей скорости в поперечном сечении капилляра образца 2.
В результате уравнения 6 и 7 преобразуются к виду: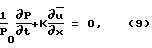
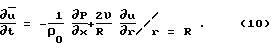
Два последних уравнения совместно с (1) представляют собой систему, к которой применим преобразование Лапласа.
Из уравнения (1) будем иметь: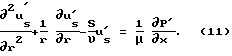
Последнее уравнение представляет собой обыкновенное линейное неоднородное дифференциальное уравнение, решением которого будет уравнение вида: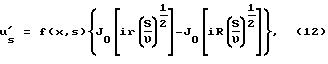
где J0 - функция Бесселя, f(х,s) - неизвестная функция.
Применим преобразование Лапласа к уравнениям 9 и 10. Получим: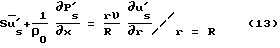
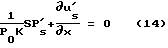
Исключим из (13) производную 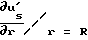
Будем иметь: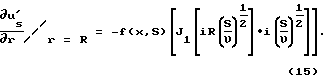
Определим неизвестную f(x,S)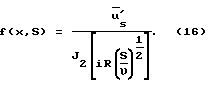
Поставив полученное выражение в (15), будем иметь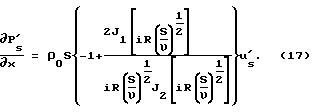
А из уравнения 14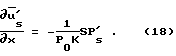
Примем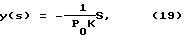
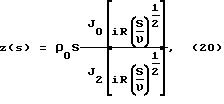
Г2(S)=z(S)•y(S).
С учетом этого из уравнений (17) и (18) получим следующее соотношение между давлением в емкости 4 и в емкости 3: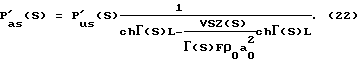
Так как давление в емкости 4 является гармоническим незатухающим, то согласно теории управления возможна замена S на iω.
С учетом этого будем иметь: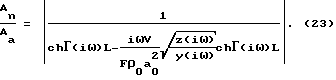
Произведение F•L=П - активная пористость образца. Отсюда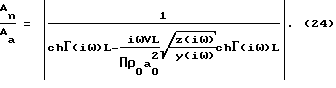
Если пористое тело 2 имеет множество ориентированных вдоль оси Х цилиндрических капилляров различного диаметра, то R - эквивалентный диаметр капилляров.
Реальные открытые поры материалов в большинстве своем очень далеки от идеальных, вытянутых вдоль оси Х капилляров различного диаметра. Тем не менее, при фильтрации газа через реальную пористую среду, как и через идеальную, будут наблюдаться трубки тока, которые можно привести с рассмотренной нами физической модели (вытянутым вдоль оси Х цилиндрическим капиллярам различного диаметра) через коэффициент извилистости αизв. Необходимо также учитывать входные и выходные потери газа на входе и выходе из пористого тела. Если эти потери учитывать традиционным методом через уравнения Вейсбаха, то это приведет к нелинейности уравнений. Чтобы избежать этого, применим также широко известный способ учета входных и выходных сопротивлений, заключающийся в искусственном увеличении длины входных и выходных участков пористого тела в направлении фильтрации. С учетом этого длина L в уравнении 24 будет равна
L = LмαизвΔLвх+ΔLвых = βLм, (25)
где Lм - толщина исследуемого материала;
αизв- коэффициент, учитывающий извилистость пор;
ΔLвх - искусственное удлинение участка пористого тела для того, чтобы учесть потери на входе;
ΔLвых - искусственное удлинение участка пористого тела для того, чтобы учесть потери на выходе;
β - суммарный коэффициент удлинения, учитывающий извилистость пор и потери на входных и выходных участках.
Таким образом расчетное уравнение (24) содержит три неизвестные величины: активную пористость П, эквивалентный радиус пор R и коэффициент β, учитывающий извилистость пор и потери давления на входе и выходе.
Вследствие этого при определении П, β и R необходимо совместно решить три уравнения 24 при различных ω и Аа/An.
Так как потери давления на входе и выходе образца согласно уравнениям Вейсбаха пропорциональны квадрату скорости фильтрации газа в порах образца, а скорость фильтрации для одних и тех же образцов пропорциональна перепаду давления на образце и обратно пропорциональна толщине образца Lм, в трех уравнениях 24 отношение амплитуд Аа/An должны соответствовать тем значениям ω и Lм, при которых отношение перепада давления на образце к толщине образца постоянно (ΔP/Lм = const, или при постоянной ΔP = const).
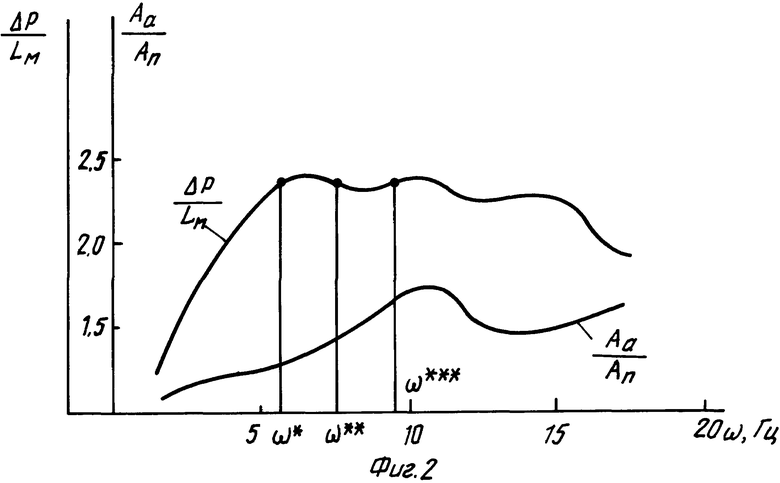
На фиг.2 представлены характерные осциллограммы измерения Аа/An и ΔP/Lм в зависимости от частоты ω при Lм=const.
Характер изменения ΔP/Lм позволяет, как это видно из графика, найти три значения частоты ω*, ω**, ω***, при которых ΔP/Lм = const. Извилистость кривой ΔP/Lм = f(ω) объясняется наличием функций Бесселя и эллиптических синусов и косинусов в уравнении 24. Поэтому при любых материалах и любых Lм всегда можно найти три значения частоты ω, при которых ΔP/Lм = const и ΔP = const.. Так как Lм в процессе измерения остается неизменной, то для упрощения находим три значения частоты ω при ΔP = Aa-An =const.
На фиг. 1 приведена схема устройства для реализации предлагаемого способа.
Устройство состоит из цилиндрической, выполненной из газонепроницаемого материала обечайки 1, в которую плотно установлен цилиндрический пористый образец 2 таким образом, что длина образца 2 равна длине обечайки 1. Один открытый конец обечайки 1 соединен, например, с помощью резьбового соединения и уплотнителя (условно не показаны) с калиброванной емкостью 3, а другой с емкостью 4, являющейся генератором гармонических колебаний. Для возбуждения колебаний в емкость 4 вмонтирован, например, сильфон 5. В стенках емкостей 4 и 3 установлены датчики 6 и 7, выходы которых соединены с входом ЭВМ 9 через электронное согласующее устройство 8.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ АКТИВНОЙ ПОРИСТОСТИ МАТЕРИАЛОВ | 2003 |
|
RU2244915C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МИНИМАЛЬНЫХ ДИАМЕТРОВ ПОР ОБРАЗЦА | 1999 |
|
RU2186364C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОРИСТОСТИ МАТЕРИАЛОВ | 1999 |
|
RU2186365C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЛИНЕЙНОЙ СКОРОСТИ | 1999 |
|
RU2186398C2 |
| СПОСОБ НАЖИВЛЕНИЯ И СБОРКИ ДЕТАЛЕЙ, СОПРЯГАЕМЫХ ПО ЦИЛИНДРИЧЕСКИМ ПОВЕРХНОСТЯМ С ГАРАНТИРОВАННЫМ ЗАЗОРОМ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2207944C2 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ ИЛИ ТОКА СИНУСОИДАЛЬНОЙ ФОРМЫ | 1997 |
|
RU2153679C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОНИЦАЕМОСТИ И ПОРИСТОСТИ МАТЕРИАЛОВ | 2003 |
|
RU2247358C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОРИСТОСТИ МАТЕРИАЛОВ | 2003 |
|
RU2235308C1 |
| ЛАЗЕР | 1997 |
|
RU2164724C2 |
| ЗВЕЗДОЧКА ЦЕПНОЙ ПЕРЕДАЧИ | 1998 |
|
RU2158862C2 |
Изобретение относится к измерительной технике и может быть использовано для определения пористости различных материалов. Сущность: способ заключается в том, что перед образцом и после образца создают замкнутые герметичные пространства. В замкнутом герметичном пространстве перед образцом создают гармонические колебания газа с изменяющейся частотой, измеряют изменения амплитуды давления газа перед образцом и после образца, вычисляют разность амплитуд и определяют три значения частоты из условия равенства разности амплитуд и по отношениям амплитуд в замкнутом пространстве после образца и до образца, соответствующим определенным значениям частот, определяют активную пористость. Технический результат: повышение точности измерения пористости материалов. 2 ил.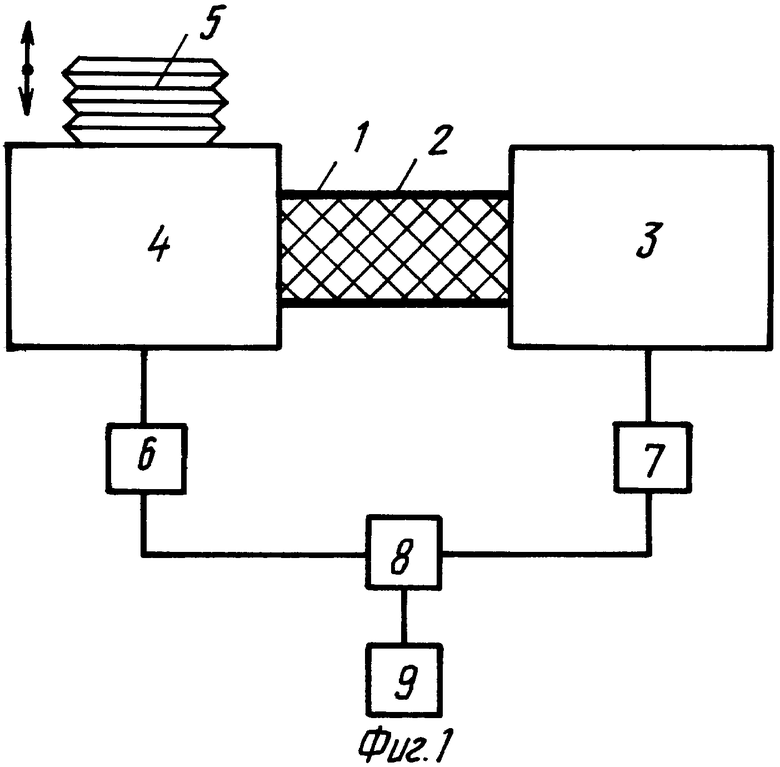
Способ определения активной пористости материалов, включающий ламинарную фильтрацию газа через заключенный в обечайку из газонепроницаемого материала образец из замкнутого пространства перед образцом в замкнутое пространство после него путем создания в замкнутом пространстве перед образцом гармонических колебаний давления газа определенной частоты и амплитуды и измерения амплитуды колебаний давления газа в замкнутом пространстве после образца, отличающийся тем, что гармонические колебания давления газа в замкнутом пространстве перед образцом осуществляют с изменяющейся частотой, измеряют изменение амплитуды давления газа в замкнутом пространстве перед образцом и после образца, вычисляют разность амплитуд и определяют три значения частоты из условия равенства разности амплитуд, определяя активную пористость материалов, эквивалентный радиус пор и коэффициент, учитывающий извилистость пор и потери давления на входе в образец и выходе из него в результате совместного решения на ЭВМ трех уравнений: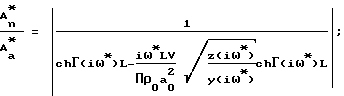
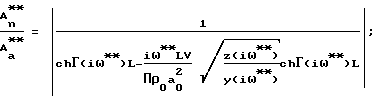
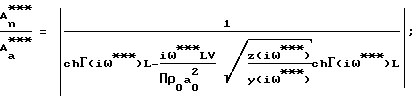 ;
;
где 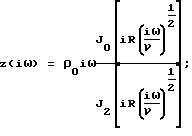
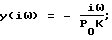
Г(iω) = [z(iω)•y(iω)]1/2;
ω*, ω**, ω***-
соответственно три значения частоты, при которых обеспечивается одинаковое значение 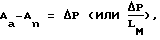 где Аа - амплитуда колебаний давления в замкнутом пространстве перед образцом;
где Аа - амплитуда колебаний давления в замкнутом пространстве перед образцом;
Аn - амплитуда колебаний давления в замкнутом пространстве после образца;
ΔP - перепад давлений на образце;
LM - толщина исследуемого материала;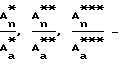 соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***;
соответственно отношение амплитуд в замкнутом пространстве после образца и до образца при ω*, ω**, ω***;
L = βLм, где β - коэффициент, учитывающий извилистость пор и потери давления на входе и выходе из образца;
R - эквивалентный радиус пор;
П - значение активной пористости;
ρ0 - плотность газа в установившемся состоянии;
i - комплексное число;
К - коэффициент адиабаты;
ν - коэффициент кинематической вязкости;
J0, J2 - функции Бесселя;
ch(iω), sh(iω)- эллиптические синус и косинус;
V - газовый объем пространства после образца;
а0 - скорость звука.
| Способ определения пористости материалов | 1989 |
|
SU1679287A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОРИСТОСТИ ЯДЕРНЫХ МЕМБРАН | 1996 |
|
RU2107279C1 |
| US 4854157 А, 08.08.1989 | |||
| US 4537062 А, 27.08.1985. | |||
Авторы
Даты
2002-03-20—Публикация
1999-10-01—Подача