Изобретение относится к метрологии, к измерительным приборам различного вида измерений и может применяться для проведения эталонных измерений.
В настоящее время для измерений используется принцип действия, основанный на реализации ряда основных измерительных преобразователей программным путем. Например, измерение среднеквадратического значения напряжения переменного тока реализуется виртуальным мультиметром в программно реализованном измерительном преобразователе, основанном на численном интегрировании, а не в традиционном измерительном преобразователе, основанном, например, на стабилитроне (см пат. РФ №1649460, кл. G 01 R 19/00 от 1991 г.).
Наиболее близким к изобретению является способ создания виртуального средства измерений, описанный в каталогах фирмы “National Instruments” с 1995 по 2003 год [1-2].
Основным недостатком прототипа является недостаточная точность измерений, такие измерения предназначены, как правило, для проведения измерений рабочей точности. Измерения подобного рода недостаточно универсальны и используются, как правило, для данной конкретной единицы физической величины в данном конкретном диапазоне значений.
Технический результат данного изобретения заключается в повышении точности и универсальности виртуальных средств измерений. Технический результат достигается тем, что способ определения значения измеряемой величины, изменяющейся во времени, заключается в том, что для нескольких моментов времени определяют значения, по крайней мере, двух вспомогательных величин, для каждой из которых заведомо известно наличие связи между ней и истинным значением измеряемой величины, после чего формируют в устройстве хранения данных массивы данных значений вспомогательных величин в указанные моменты времени, для каждой из вспомогательных величин задают неоднозначно определенную функциональную зависимость значения измеряемой величины от значения соответствующей вспомогательной величины, представляющую собой функцию с незаданными постоянными коэффициентами, после чего вычисляют значения измеряемой величины в указанные моменты времени и совместно с вычислением значения измеряемой величины для каждой из вспомогательных величин определяют однозначно определенную функциональную зависимость значения измеряемой величины от значения вспомогательной величины путем вычисления значений коэффициентов соответствующих функций, таких, что значения однозначно определенных функциональных зависимостей, рассчитанные для вычисленных значений измеряемой величины, по крайней мере, приближенно равны значениям вспомогательных величин, сведения о которых сформированы в устройстве хранения информации, после чего сведения о вычисленных значениях измеряемой величины для требуемых моментов времени передают на устройство вывода информации. Под термином “незаданные” постоянные коэффициенты подразумевается функция, в которой подлежат определению коэффициенты этой функции после решения соответствующей системы уравнений.
Способ характеризуется также тем, что по крайней мере, одна вспомогательная величина взаимно однозначно зависит от скорости изменения истинного значения измеряемой величины во времени, а по крайней мере, одна другая вспомогательная величина взаимно однозначно зависит от истинного значения измеряемой величины.
В предложенном способе для каждой из вспомогательных величин задают значение допустимой погрешности, а значения однозначно определенных функциональных зависимостей, рассчитанные для вычисленных значений измеряемой величины, признаются приближенно равными значениям вспомогательных величин, сведения о которых сформированы в устройстве хранения данных, при абсолютном значении разности указанных значений, не превосходящем значение допустимой погрешности. Предпочтительно, чтобы по крайней мере одна неоднозначно определенная функциональная зависимость представляла собой математический ряд с неопределенными коэффициентами.
Кроме того, значения по крайней мере двух различных вспомогательных величин формируют путем выборки данных из одного потока данных в различные моменты времени.
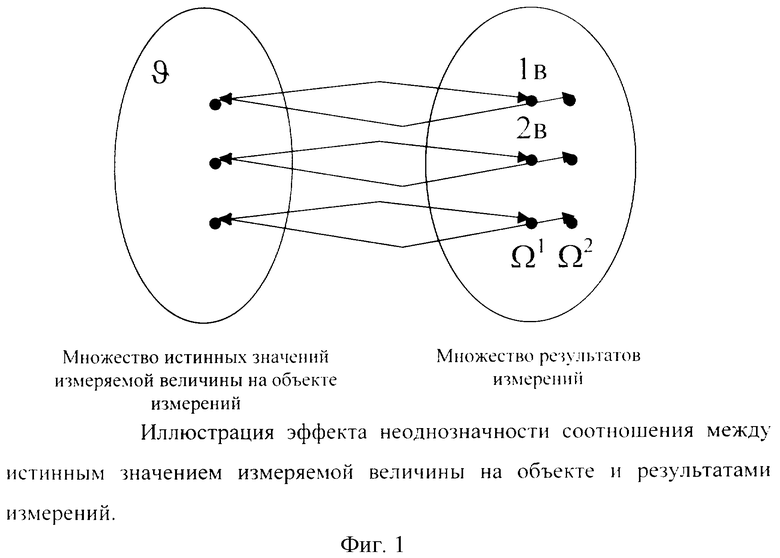
В основе предложенного способа лежит эффект неоднозначности Эффект неоднозначности, лежащий в основе указанного технического результата, иллюстрируется на фиг.1.
Основной проблемой повышения точности технических измерений на основе математических методов обработки результатов измерений является устранение систематической составляющей погрешности измерений, которая, как правило, в среднем составляет более 90% совокупной погрешности измерений. Традиционные математические методы обработки рассматривают множество результатов измерений как однородную совокупность Ω и поэтому не позволяют уменьшать систематическую составляющую погрешности без проведения дополнительных высокоточных измерений. Заявленный способ рассматривает виртуальные эталонные измерения, используя два разнородных множества результатов измерений (Ω 1 Ω 2 на фиг.1) и на этой основе уменьшает кроме случайной еще и систематическую составляющую погрешности измерений.
Действительно, если представить результаты измерений как некую функцию неизвестных случайной и систематической составляющей погрешности измерений, то уравнение относительно полного множества результатов измерений является неразрешимым. Однако, рассматривая результаты измерений как два разнородных множества, получаем систему из двух уравнений относительно двух неизвестных: случайной и систематической составляющей погрешности измерений. Данная система разрешима, что позволяет с учетом известных результатов измерений и вычисленных погрешностей оценить истинное значение измеряемой величины. При этом, например, коэффициенты функциональной зависимости относительно неизвестных случайной и систематической составляющих погрешности измерений определяют на основе многократных измерений с монотонно изменяющимся (убывающим или возрастающим) определяющим параметром. При этом в качестве двух разнородных множеств результатов измерений (Ω 1 Ω 2 на фиг.1) могут использоваться, например, соответственно:
1. множество результатов многократных измерений, выполненных при монотонно изменяющейся (возрастающей или убывающей) измеряемой величине на объекте измерений;
2. множество априорной информации о значении измеряемой величины на объекте в каждый момент времени измерений.
Основным ограничением при реализации виртуальных эталонных измерений является наличие достоверной априорной информации о значении измеряемой величины на объекте измерений в каждый момент времени измерений. Такая априорная информация, как правило, весьма часто присутствует в процессе измерений. Так, например, при измерении метрологических характеристик калибратора напряжения постоянного тока можно использовать априорную информацию, соответствующую показаниям, установленным в настоящий момент на калибраторе (1 В, 2 В и т.д. фиг.1). В случае, если требуемая априорная информация об объекте измерений отсутствует, ее можно получить на основе дополнительных невысокоточных измерений. Например, при эталонном измерении расхода жидкости в трубопроводе для реализации виртуального эталона можно использовать показания дополнительного (второго) расходомера рабочей точности. При этом результирующее повышение точности измерения расхода до эталонного уровня обеспечит весьма значительный технико-экономический эффект и в этом случае.
Следовательно, установление факта неоднозначности соотношения между истинным значением измеряемой величины на объекте и результатами измерений и позволяет сформировать и решить указанную систему из двух взаимно независимых уравнений и на этой основе обеспечить эталонную точность измерений с учетом как случайной, так и систематической погрешности. Рассмотрим физическое происхождение указанного эффекта неоднозначности соответствия между значением измеряемой величины на объекте и результатами измерений.
Взаимодействие объекта измерений и средств измерений (СИ) в процессе измерений осуществляется в потенциальном поле объекта измерений, что сопровождается превращением потенциальной энергии между двумя точками с разными потенциалами на объекте измерений в другие формы энергии в средстве измерений. При этом измеритель возмущает объект измерений и вносит погрешности в результат измерений.
Основным смыслом процедуры измерения является перевод замкнутой взаимообратной (изоморфной в понятиях абстрактной алгебры) системы “объект измерений - СИ” в однонаправленную (гомоморфную) систему. Этому идеальному состоянию с однонаправленными (гомоморфными) связями “объект измерений - СИ” соответствует истинное значение измеряемой величины. Действительное значение измеряемой величины отличается от истинного на величину погрешности измерений.
Пусть на объекте измерений за время измерений ti наблюдается множество значений измеряемой величины S и на выходе измерительного прибора регистрируется множество результатов измерений J. Пусть
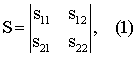
где S11, S21 - значения измеряемой величины в первой точке на объекте измерений с потенциалом ϕ 1, например на первом (положительном) контакте источника ЭДС постоянного тока в момент времени t1, t2 соответственно;
S12, S22 - значения измеряемой величины во второй точке на объекте измерений с потенциалом -ϕ 1, например на втором (отрицательном) контакте источника ЭДС постоянного тока в момент времени t1, t2.
Тогда
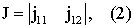
где j11, j12 - значения напряжения постоянного тока в момент времени t1, t2.
В этом примере измерительный прибор (вольтметр постоянного тока) описывается линейным оператором Т
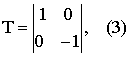
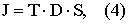
где D - линейный оператор, описывающий характер преобразования (например, увеличение напряжения на входном усилителе, либо уменьшение на входном делителе и т.д.). Следует отметить, что практически во всех случаях проведения технических измерений речь идет о преобразовании потенциальной энергии (два разных потенциала) с объекта измерений в измерительном приборе, поэтому линейный оператор вида (3) является общей формой записи преобразований сигнала измерительной информации в измерительных приборах.
При этом (4) фактически является формой преобразования координат, наиболее часто реализуемой в процессе технических измерений.
В процессе реальных технических измерений присутствуют возмущения линейного оператора Т (3) за счет внешних воздействующих факторов
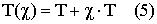
где χ - некоторое малое возмущение за счет внешних воздействующих факторов.
Известно, что линейные операторы вида Т(χ ) характеризуются неоднозначными собственными функциями с двумя ветвями [2], приводится результат аналитического исследования возмущения собственных значений возмущенного оператора (3) вида
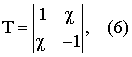
Собственные значения
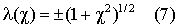
оператора Т(χ ) вида (6) суть ветви одной двузначной аналитической функции ±(1+χ 2)1/2, то есть в его области определения имеются так называемые исключительные точки χ =±i, в которых приращение собственных значений при расщеплении представляет собой бесконечно большую величину по сравнению с изменением самого оператора Т(χ ). В [2] дана оценка для радиуса сходимости рядов теории возмущений. Радиус сходимости r0=1.
Неоднозначность собственных значений (7) возмущенного оператора (6) проявляется в процессе восстановления функциональной зависимости по результатам измерений. Поэтому рассмотрим многократные измерения, когда значение физической величины на объекте монотонно изменяется (возрастает или убывает). Погрешности многократных измерений представляют собой сумму двух составляющих: симметричной относительно истинного значения измеряемой величины случайной и несимметричной систематической составляющей. При этом симметричная относительно истинного значения измеряемой величины случайная составляющая достаточно легко уменьшается применением традиционных математических методов обработки результатов измерений, рассматривающих однородное множество результатов измерений, соответствующее замкнутой взаимообратной (изоморфной в понятиях абстрактной алгебры) системе “объект измерений - СИ”. Для уменьшения несимметричной относительно истинного значения измеряемой величины систематической составляющей погрешности необходимо рассматривать множество результатов измерений как неоднородную совокупность, соответствующую однонаправленной (гомоморфной в понятиях абстрактной алгебры) системе “объект измерений - СИ”. При этом одна часть неоднородной совокупности результатов измерений может условно соответствовать информации (показаниям) объекта измерений, вторая - соответственно показаниям средства измерений. Применяя математические методы восстановления функциональной зависимости по результатам измерений относительно указанных выборок, можно уменьшить не только случайную, но и систематическую составляющую погрешности. Такие алгоритмы обработки результатов измерений переводят систему “объект измерений - СИ” из замкнутой взаимообратной (изоморфной в понятиях абстрактной алгебры) в однонаправленную (гомоморфную в понятиях абстрактной алгебры) систему. Поскольку, как отмечалось выше, этому идеальному состоянию с однонаправленными (гомоморфными) связями “объект измерений - СИ” соответствует истинное значение измеряемой величины, то указанное алгоритмическое информационное преобразование можно считать эталонным. Действительно, несмотря на свою информационную природу алгоритм восстановления функциональной зависимости по результатам измерений относительно указанных выше выборок соответствует основным признакам эталона. К таким признакам эталона относятся неизменность, воспроизводимость и сличаемость. Все эти три признака обеспечиваются за счет его приближения к истинному значению измеряемой величины вследствие однонаправленного (гомоморфного) характера связей “объект измерений - СИ”.
Основным ограничением при реализации способа создания виртуального эталона является наличие достоверной априорной информации о значении измеряемой величины на объекте в каждый момент времени измерений. Такая априорная информация как правило всегда присутствует в процессе измерения метрологических характеристик средств измерений. Например, при измерении метрологических характеристик калибратора напряжения постоянного тока можно использовать априорную информацию, соответствующую показаниям, установленным в настоящий момент на калибраторе (1 В, 2 В и т.д. фиг.1.). В случае, если требуемая априорная информация об объекте измерений отсутствует, ее можно получить на основе дополнительных невысокоточных измерений.
Основным достоинством описанного способа создания виртуального эталона является то, что при его реализации не нужно использовать эталоны для проведения измерений.
Рассмотрим конкретный пример реализации способа создания виртуального эталона, удаленного от места проведения измерений. Предварительно устанавливается выполнение правил проведения эталонных измерений с точки зрения законодательной метрологии в месте проведения измерений. При положительном заключении о порядке выполнения законодательных правил проведения эталонных измерений в удаленном месте проведения измерений оператор проводит соответствующие измерения по указанной на сервере, где располагается виртуальный эталон методики. При этом набор эталонных измерений ограничен имеющимся на сервере кадастром видов, средств и методик измерений. Например, при измерении метрологических характеристик калибратора напряжения постоянного тока на основании установленного кадастра выбирается тип вольтметра (рабочего средства измерения), диапазон измерений и конкретные значения поверяемых точек (значений измеряемого напряжения, выдаваемого калибратором). Далее, основываясь на установленной выше неоднозначности соотношений между показаниями калибратора и результатами измерений вольтметра, оценивается истинное значения измеряемой величины в каждой точке измерений. Если проводившая измерения лаборатория аккредитована на право проведения данного вида эталонных измерений, то результат измерений, полученный с удаленного компьютера (с сервера), фиксируется с точки зрения законодательной метрологии (например, ставится клеймо поверителя).
Анализ результатов экспериментальных исследований и моделирования на Персональной электронно-вычислительной машины.
(ПЭВМ) дает основание предположить практическую реализуемость заявленного способа для большого числа видов измерений в широком диапазоне значений измеряемой физической величины. За счет возможности тиражирования программного обеспечения достигается значительное уменьшение стоимости и трудоемкости эталонных измерений, а за счет его универсальности и гибкости - соответственно универсальность самого способа.
Необходимое и достаточное условия существования неоднозначности соотношения между истинным значением измеряемой величины на объекте и результатами измерений, что является основой описанного выше способа построения виртуального эталона, обосновывается следующим образом:
Сформулируем достаточные условия неоднозначности соотношения между истинным значением измеряемой величины на объекте и результатами измерений. Для этого рассмотрим модель измерений, имеющих информационную составляющую (в сигнале измерительной информации). Если бы сигнал измерительной информации имел чисто энергетическое представление, то
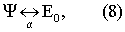
где ψ - сигнал измерительной информации;
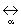 - изоморфизм энергетических связей;
- изоморфизм энергетических связей;
E0 - полная энергия взаимодействий сигнала измерительной информации.
Поскольку существует такое натуральное число М0>Е0, то
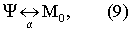
т.е. ψ - ограниченное множество.
Пусть S - множество возможных исходов измерений, определенным образом ограниченное, например, метрологическими характеристиками измерительной техники. Тогда при полном отсутствии неэнергетических связей в сигнале измерительной информации
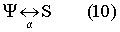
При наличии в сигнале измерительной информации информационной составляющей, не связанной изоморфно с ограниченной полной энергией взаимодействия в силу неограниченной ψ , в общем виде отсутствует изоморфизм между сигналами измерительной информации и S - множеством возможных исходов измерений.
В этом случае выполнение условия ограниченности множества Ψ можно достичь применением второго измерителя, тогда
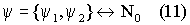
где ψ 1,ψ 2 - сигнал измерительной информации от измерителей 1 и 2. При этом для двух измерителей несмотря на наличие в сигнале измерительной информации информационной составляющей, не связанной с ограниченной полной энергией, выполняется условие изоморфизма между ψ и множеством возможных исходов измерений S
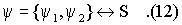
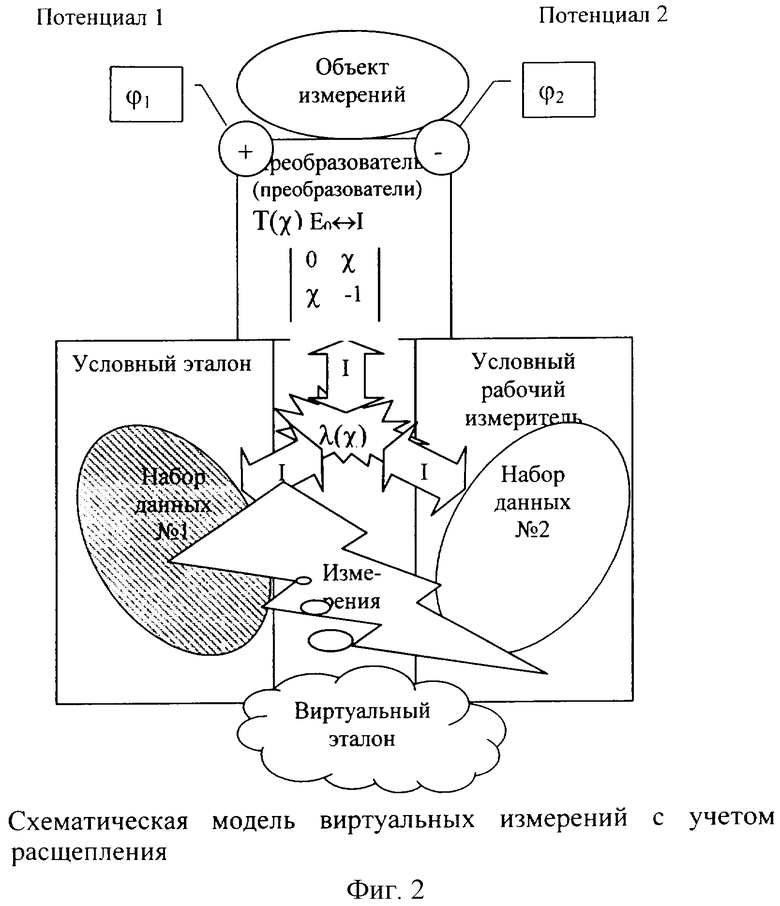
Рассмотрим модель виртуальных измерений с учетом расщепления 2(1), схематическое изображение модели приведено на фиг.2. На фиг.2 измерительный прибор преобразует потенциальную энергию (два потенциала разных знаков) с объекта измерений в измерительном преобразователе, характеризующимся линейным оператором. Для модели измерений на фиг.2 связи между объектом измерений и преобразователем (преобразователями) физической величины в информационную форму имеют взаимообратный энергетический характер. Под эталонным информационным преобразованием (вычислительным алгоритмом) будем понимать такое преобразование (алгоритм вычислений), который переводит взаимообратные связи между объектом измерений и измерительным преобразователем в однонаправленные от объекта измерений к измерительному преобразователю. Выражаясь другими словами, эталонное информационное преобразование осуществляет редукцию к идеальной системе объект измерений - измеритель, когда измеритель не оказывает обратного влияния в среде измерений, где существуют упомянутые энергетические связи, на объект измерений и не вносит погрешности в результат измерений значения физической величины на объекте.
Пусть φ - абстрактно-логическое математическое отображение состояний объекта измерений Q на измеритель S. При реальных условиях взаимодействия объекта измерений и измерителя φ - изоморфизм.
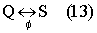
Тогда эталонное информационное преобразование (вычислительный алгоритм) θ переводит φ в однонаправленное преобразование ϕ
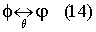
такое, что
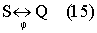
При этом ясно, что эталонное информационное преобразование (вычислительный алгоритм) θ - само по себе не изоморфизм. Данное требование накладывает столь значительные ограничения на класс эталонных информационных преобразований, что, пожалуй, отфильтровывает от понятия эталонное информационное преобразование (вычислительный алгоритм) все известные виды алгоритмов математической обработки данных измерений, которые без всякого сомнения являются изоморфизмами. Информационное преобразование (вычислительный алгоритм) на основе расщепления отвечает требованию и может считаться эталонным. Перейти от приведенных выше рассуждении абстрактной математической логики к понятиям метрологии дает возможность использование классификации погрешности измерений на систематическую и случайную.
Действительно, все известные информационные преобразования (вычислительные алгоритмы) с точки зрения метрологии уменьшают только случайную составляющую погрешности измерений, симметричную относительно эталона, не затрагивая систематическую погрешность измерений, несимметричную относительно эталона. Для уменьшения совокупной погрешности измерений, включающую как случайную, так и систематическую составляющую, необходимо использовать несимметричное информационное преобразование (вычислительный алгоритм) на основе расщепления 2 (4), что позволяет, как показано на фиг.2, условно разделить относительно него информацию (набор данных) на два класса №1 - условный эталон и №2 - условный рабочий измеритель. Тогда вследствие несимметричности расщепления 2(1) условный эталон (набор данных №1) будет отличаться по своей погрешности (как случайной, так и систематической) от условного рабочего измерителя (набора данных №2). При этом, проводя измерения относительно условного эталона (набора данных №1) информации с условного рабочего измерителя (набора данных №2), уменьшим совокупную погрешность измерений (случайную и систематическую) и сформируем такое информационное преобразование (вычислительный алгоритм), который и можно назвать виртуальным эталоном (фиг.2).
Если поставить целью найти математическое представление эталонного информационного преобразования (вычислительного алгоритма) Т, то он должен обладать следующим набором свойств:
- свойство симметричности относительно подмножества случайных составляющих погрешности измерений;
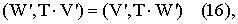
где W’, V’ - подмножество случайных составляющих погрешности измерений на выходе преобразователя (фиг.2) и эталонного информационного преобразования (вычислительного алгоритма) Т.
- свойство несимметричности относительно подмножества систематических составляющих погрешности измерений W, V на выходе преобразователя (фиг.2) и эталонного информационного преобразования (вычислительного алгоритма) Т. Перечисленному выше набору свойств удовлетворяет линейный оператор вида Т(χ ), который одновременно отвечает требованиям принципа редукции измерений. Таким образом, выше было показано необходимое условие существования расщеплений сигнала измерительной информации, в случае если он имеет информационно-энергетическую природу (сигнала измерительной информации виртуальных СИ), и сформулировано вытекающее из этого понятие виртуального эталона.
Исследуем достаточное условие существования расщеплений сигнала измерительной информации, в случае если он имеет информационно-энергетическую природу. Для этого покажем существование расщеплений в модели информационно-энергетического сигнала измерительной информации.
От объекта измерений А сигнал измерительной информации через некоторую среду, в которой происходят измерения, ϕ поступает на вход измерительной части виртуального СИ (Г), откуда значение измеряемой физической величины поступает в вычислительную часть виртуального средства измерений (СИ) (В), преобразующую его в требуемую форму. Для построения математической модели указанных физических объектов из цепи передачи сигнала измерительной информации поставим каждому из них во взаимно однозначное соответствие некоторые множества, определенные как множества состояний за время измерений tи. Столь простое математическое представление состояний объектов в цепи передачи сигнала измерительной информации является естественным в виртуальном СИ, где время измерений практически всегда дискретно. Представим время измерений в виде множества Т
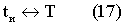
Поскольку модель измерений виртуального СИ допускает математическое представление состояния объектов в цепи передачи сигнала измерительной информации как множеств, воспользуемся этим допущением, которое в дальнейшем специально оговариваться не будет. Тогда следующие соотношения за время измерений tи будут взаимно однозначны: А↔ α , Ф↔ ϕ , Г↔ γ , В↔ β , где α , ϕ , γ , β - множества состояний объектов за время tи.
В объектах цепи передачи сигнала измерительной информации А, Ф и Г, как указывалось выше, физически присутствуют измеряемые и используемые в процессах преобразования при измерениях физические величины, что неразрывно связано с понятием энергии (Е). Воспользуемся для математического описания энергетических состояний моделью множества состояний, возникающих вследствие дискретности времени измерений: Е↔ е, где е - множество энергетических состояний за время tи.
Тогда существуют следующие взаимно однозначные соответствия между множествами:

где ~ - отношение эквивалентности.
Учитывая дискретность времени измерения в виртуальном СИ (17), математическую модель измерительной информации (I) в сигнале измерительной информации запишем как I↔ i, где i - множество информационных состояний за время tи.
Особенностью модели виртуального СИ является "комбинаторное" определение информации как некоторой совокупности данных. Такое определение возникает из представления о роли компьютера в измерениях только как инструмента преобразования значения физической величины.
Этому представлению об информации в нашей модели виртуального СИ соответствует важное представление о счетности множества i, которым и будем пользоваться для дальнейших рассуждений.
Поскольку в модели виртуального СИ допускается существование информации, не связанной с конкретными измерениями за время tи (например, заданной до измерений), а значит и с физическим представлением об энергии, становится понятным следующее выражение:
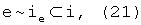
где ie - эквивалентное множеству энергетических состояний подмножество информационных состояний.
Для дальнейших рассуждений очень важно, что множество
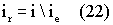
конечно.
Действительно, из счетности множества i~N, где N - множество натуральных чисел, и (15) следует, что
ie~N.
Поставим во взаимно однозначное соответствие элементы множества Т и множества i, тогда вследствие их счетности
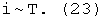
Поскольку Т - одномерно по условию, i и ie в общем случае бесконечные и счетные одновременно и
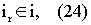
из (22), то ir - конечно.
Что и требовалось доказать.
Теперь мы имеем все необходимые математические объекты и операции для определения математической модели измерений виртуального СИ. Пусть Х - математическая модель, состоящая из объектов множеств (α ,
ϕ , γ , β ) и одной операции, приписывающей каждому из множеств свойства счетности по (18)-(21).
Пусть Y - математическая модель, состоящая из множеств (i, ie, ir) и операций (22), (24). Тогда для того, чтобы модели Х и Y были изоморфны относительно рассматриваемых операций, необходимо соответственно задать свойства образованных при этом отражений.
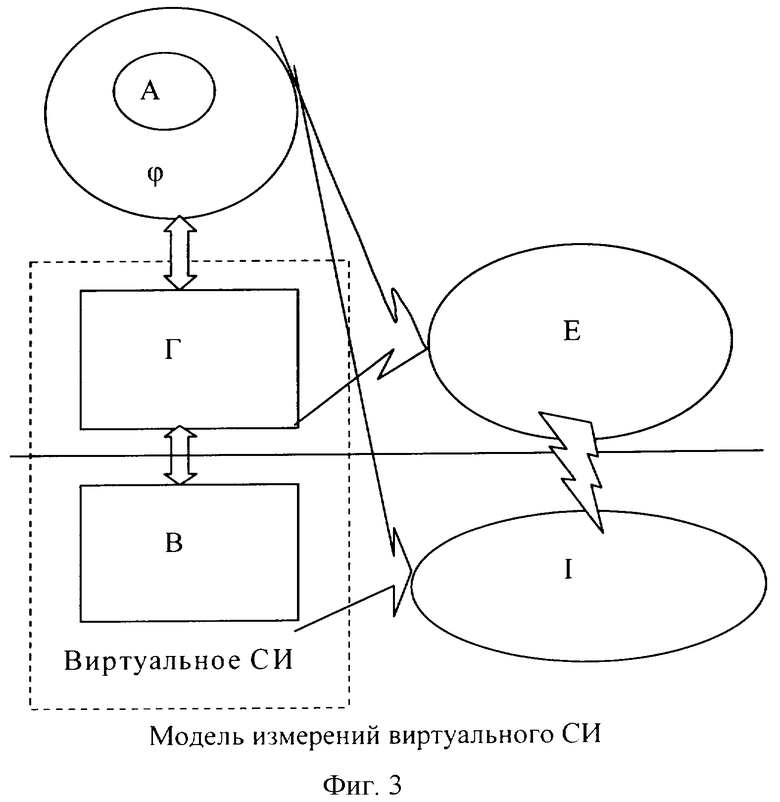
Зададим эти свойства, исходя из физического смысла модели измерений виртуального СИ на фиг. 3.
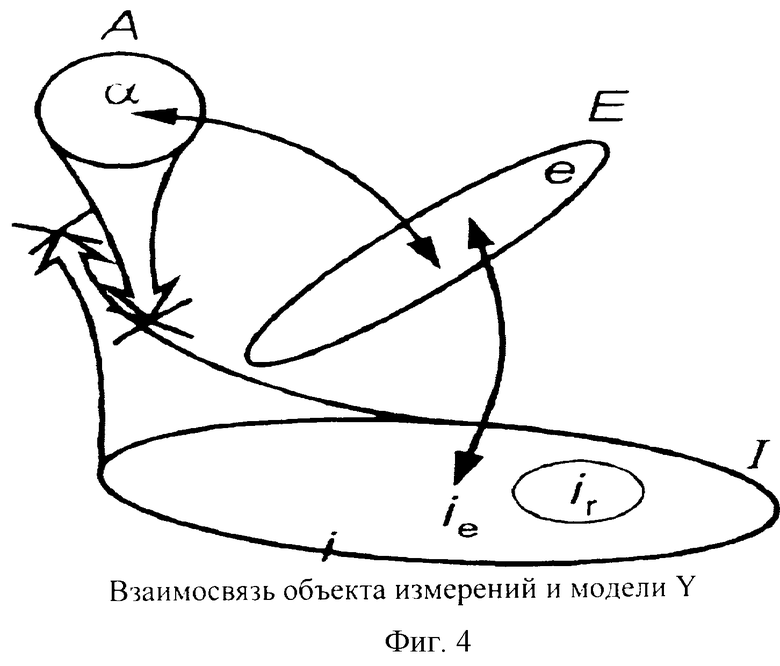
Физическая величина на объекте измерений имеет чисто энергетическую природу, и ее взаимосвязь с элементами модели Y может быть представлена моделью на фиг. 4, где показано, что по смыслу измерения никакую априорную информацию об объекте измерения нельзя использовать как апостериорную без проведения измерений, которые всегда связаны с физическими энергетическими превращениями. Это важное ограничение в физической модели измерений записывается в математической форме взаимодействия счетных множеств α и ie в виде
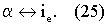
Для остальных математических объектов из Х их отображение в Y записывается в виде
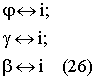
Поскольку, исходя из смысла модели измерений виртуального СИ, физическая величина на объекте измерений имеет чисто энергетическую природу, и ее взаимосвязь с элементами модели Y может быть представлена моделью на фиг.3, где показано, что по смыслу измерения никакую априорную информацию об объекте измерения нельзя использовать как апостериорную без проведения измерений, которые всегда связаны с физическими энергетическими превращениями. Это важное ограничение в физической модели измерений записывается в математической форме взаимодействия счетных множеств α и ie в виде (25). Рассмотрим какие основные принципы построения виртуальных систем эталонной точности вытекают из этого положения.
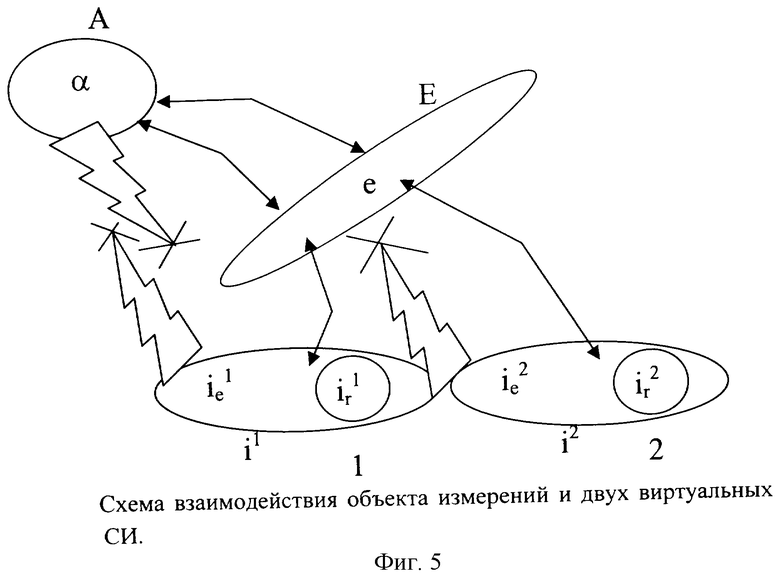
На фиг.5 показана схема взаимодействия объекта измерений и двух виртуальных СИ. Если рассматривать измерительную систему, состоящую из двух виртуальных СИ, измеряющих на объекте измерений А, то согласно определению подмножества ie, ie 1, ie 2 и свойства (26)
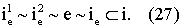
С другой стороны следует отметить, что 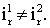
Пусть ℘ - мера возможности, различающая множества ir 1 и ir 2. Инвариантность шкалы значений возможности относительно группы непрерывных монотонных преобразований, оставляющих неподвижными точки 0 и 1, определяет принцип относительности, согласно которому в теории возможностей каждый исследователь при построении модели может использовать “свою” шкалу (в отличие от “абсолютной шкалы” значений вероятности) L (“индивидуальную систему отсчета”), но при этом модель должна быть инвариантна относительно преобразований шкалы L, а содержательно истолкованы могут быть лишь те выводы, которые не зависят от выбора шкалы. Именно эти свойства возможности и обусловили ее применение для определения относительного различия между множествами ir 1 и ir 2
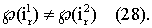
С другой стороны, согласно (10),
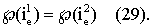
Пусть вычислительная часть виртуального СИ программируется таким образом, что модель возможностей, определяемая соотношениями (28), (29), инвариантна для преобразования шкалы возможностей из множества i на β .
Целью функционирования вычислительной части виртуального СИ является получение наиболее точного отражения множества состояний α объекта измерений в ЭВМ измерительной системы на множестве β 0 ⊂β .
Пусть β 0 ⊂β , тогда для идеального виртуального СИ математически это запишется как
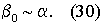
Выражение (30) фактически является формализованной записью цели функционирования вычислительной части идеального виртуального СИ.
Тогда из (25)и (26) следует, что
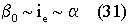
и для β r=β /β 0
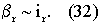
Сравним, исходя из цели функционирования вычислительной части виртуального СИ (30) (его точности), предполагая, что вычислительная часть виртуального СИ программируется таким образом, что модель возможностей, определяемая соотношениями (28), (29), инвариантна для преобразования шкалы возможностей из множества i на β результат измерений на объекте А, выполняемых одним и двумя виртуальными СИ.
С точки зрения шкалы возможностей ℘ возможность идеального по точности функционирования вычислительной части виртуального СИ, когда измерения на объекте выполняются двумя виртуальными СИ
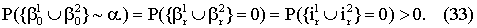
А для одного виртуального СИ выражение (23) запишется в виде
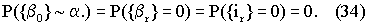
Таким образом, возможность идеального по точности функционирования вычислительной части виртуального СИ, когда измерения на объекте выполняются двумя виртуальными СИ, вследствие конечности множеств 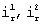 и соответственно
и соответственно 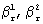 , больше нуля. С другой стороны, возможность идеального по точности функционирования вычислительной части виртуального СИ, когда измерения на объекте выполняются одним виртуальным СИ согласно (34)равна нулю.
, больше нуля. С другой стороны, возможность идеального по точности функционирования вычислительной части виртуального СИ, когда измерения на объекте выполняются одним виртуальным СИ согласно (34)равна нулю.
Данная теоретическая модель является непосредственным признаком достаточного условия гипотезы “возмущения” сигнала измерительной информации в том случае, когда в нем кроме энергетической присутствует информационная составляющая. Теоретической моделью данного возмущения в линейном случае служит модель возмущений линейных операторов Т. Като [2].
Безусловно данная теоретическая модель нуждается в серьезной проверке. Однако основные теоретические выводы, следующие из данной модели о резком повышении точности обработки при обработке результатов измерений по указанной схеме за счет учета систематической составляющей погрешности и о том, что порядок использования исходных данных при создании виртуального эталона несимметричен, вследствие описанной выше несимметричности расщепления подтверждаются реальными экспериментальными результатами.
Литература
1. Каталоги фирмы “National Instruments” за 1995-2003 годы.
2. Като Т. Теория возмущения линейных операторов./Пер с англ. - М.: Мир, 1972.
Изобретение относится к метрологии, к измерительным приборам и может применяться для проведения эталонных измерений. Способ основан на многократных измерениях исследуемых величин, причем в основе способа лежит неоднозначность соответствия между истинным значением измеряемой величины и результатами измерений. Значения исследуемой величины обрабатывают с использованием этой неоднозначности, для чего измеряют значения двух вспомогательных величин. Для каждой из этих величин задают неоднозначно определенную функциональную зависимость измеряемого истинного значения величины от значения соответствующей вспомогательной величины, представляющую собой функцию с постоянными коэффициентами. Коэффициенты определяются на основе множества измерений изменяющихся во времени вспомогательных величин, после чего вычисляют измеряемые истинные значения величины. Изобретение позволяет уменьшить систематическую составляющую погрешности измерений без проведения дополнительных высокоточных измерений. За счет многократности измерений уменьшается также и случайная погрешность измерения. 4 з.п. ф-лы, 5 ил.
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ОДНОТИПНЫХ СРЕДСТВ ИЗМЕРЕНИЙ В ГРУППЕ | 1997 |
|
RU2123190C1 |
| СПОСОБ ОТБОРА ЭТАЛОНОВ ИЗ СОВОКУПНОСТИ ОДНОТИПНЫХ СРЕДСТВ ИЗМЕРЕНИЙ | 1997 |
|
RU2123707C1 |
| Цифровая система измерения и обработки | 1986 |
|
SU1352507A2 |
| Способ измерения электрических и неэлектрических параметров | 1988 |
|
SU1649460A1 |
Авторы
Даты
2005-05-20—Публикация
2003-06-09—Подача