Изобретение относится к контрольно-измерительной технике, к автоматическим и автоматизированным системам разработки интеллектуальных датчиков путем «обучения» в процессе изготовления и может быть использовано в приборостроении при разработке, изготовлении и диагностике интеллектуальных датчиков и измерительных систем различного типа.
Согласно ГОСТ Р 8.673-2009 ГСИ «Датчики интеллектуальные и системы измерительные интеллектуальные. Основные термины и определения», интеллектуальные датчики - это адаптивные датчики, содержащие в себе изменяемые по внешним сигналам алгоритмы работы и параметры, и в которых, кроме этого, реализована функция метрологического самоконтроля. Предлагаемый интеллектуальный датчик измерений требует вычислительной обработки внутри датчика. В составе датчика могут применяться сенсоры (чувствительные элементы, первичные измерительные преобразователи - ПИП) для измерения любых физических величин. Выбор измеряемой физической величины и соответствующего сенсора производится на стадии конструирования. После изготовления и калибровки датчик обеспечивает измерение физической величины с заданной метрологической точностью во всех ожидаемых условиях эксплуатации. Для адаптации к условиям эксплуатации и точного измерения физической величины датчик содержит обучаемые в процессе калибровки интеллектуальные алгоритмы. Индивидуальное обучение алгоритмов каждого датчика данного типа уменьшает отбраковку экземпляров датчика после их изготовления, что позволяет упростить конструкцию и технологические процессы изготовления датчиков, снизить их стоимость. Датчик является законченным метрологически самоконтролируемым изделием, что повышает его надежность и упрощает обслуживание. Конструкция объекта измерения не сказывается на работе датчика, удешевляется установка.
В предлагаемом изобретении под интеллектуальным датчиком понимают датчик со встроенной электроникой, включающей в себя: первичный измерительный преобразователь (сенсор), АЦП, цифровой процессор и цифровой интерфейс с поддержкой сетевых протоколов для коммуникации. Интеллектуальный датчик, благодаря функции самоидентификации, способен восстанавливать измеряемый параметр во всех эксплуатационных диапазонах измеряемой величины, физических и климатических условий измерений.
Инженерная задача определения отклонений параметров функции преобразования (математической модели) датчиков от номинальных значений часто решается как задача параметрической идентификации. Определение параметров известной математической модели датчика, как правило, линейной, осуществляется для последующей алгоритмической компенсации его систематических погрешностей. Под математической моделью датчика при калибровке понимают некоторую функцию преобразования датчика, ставящую в соответствие измеряемому физическому воздействию на входе датчика некоторый «сигнал» на его выходе в установившемся режиме работы в форме, удобной для последующего использования (например, ток, напряжение, цифровой код и т.п.). Линейность функции преобразования датчика, с одной стороны, позволяет существенно упростить процедуры калибровки, но, с другой стороны, достигается достаточно сложными конструкторскими приемами и отбраковкой большого числа датчиков, характеристики моделей которых не отвечают общим для данного типа датчиков техническим условиям. Параметры линейных моделей датчиков, прошедших процедуру отбраковки, для повышения точности измерений дополнительно доуточняются индивидуально для каждого датчика как раз в процессе выполнения процедуры калибровки, что обеспечивает алгоритмическую компенсацию систематических погрешностей этого датчика при последующем его функционировании в рабочих режимах.
В составе интегрированных блоков для измерения векторного значения некоторой физической величины применяются несколько датчиков. Модель (функцию преобразования) большинства применяемых на практике одиночных датчиков и «векторных» датчиков стремятся получить в линейной параметрической форме вида
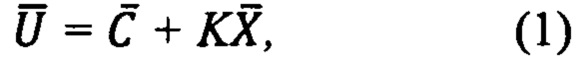
где 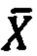 - вектор входных сигналов датчика, т.е. измеряемая векторная физическая величина, воздействующая на датчик;
- вектор входных сигналов датчика, т.е. измеряемая векторная физическая величина, воздействующая на датчик; 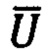 - вектор сигналов на выходе датчика, соответствующий (пропорциональный) вектору входных сигналов, K - матричный коэффициент пропорциональности векторов выходных и входных сигналов датчика, называемый масштабным коэффициентом,
- вектор сигналов на выходе датчика, соответствующий (пропорциональный) вектору входных сигналов, K - матричный коэффициент пропорциональности векторов выходных и входных сигналов датчика, называемый масштабным коэффициентом, 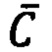 - вектор «нулевых сигналов», называемых «смещением нуля», измеряемых на выходе датчика при отсутствии векторного сигнала на его входе, точнее, при заведомо известном нулевом векторе сигналов на входе датчика. Такая модель, по сути, представляет собой полином минимальной (первой) степени для аппроксимации значений векторного выходного сигнала и требует идентификации лишь двух параметров -
- вектор «нулевых сигналов», называемых «смещением нуля», измеряемых на выходе датчика при отсутствии векторного сигнала на его входе, точнее, при заведомо известном нулевом векторе сигналов на входе датчика. Такая модель, по сути, представляет собой полином минимальной (первой) степени для аппроксимации значений векторного выходного сигнала и требует идентификации лишь двух параметров - 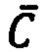 и К. Следует иметь в виду, что для случая векторного датчика матрица К может быть не обязательно диагональной.
и К. Следует иметь в виду, что для случая векторного датчика матрица К может быть не обязательно диагональной.
Простота линейной модели позволяет определять (идентифицировать) ее параметры с использованием достаточно простой процедуры калибровки и даже надежно и с известной точностью предсказывать (на основе паспортных данных) показания датчика вообще без калибровки, если требования к точности его показаний не высоки и лежат в пределах погрешностей, характерных для множества датчиков данного типа. Еще одним достоинством линейной функции преобразования вида (1) является то, что восстановление и предсказание значений измеряемой датчиком физической величины осуществляется по весьма просто получаемой из (1) обратной функции преобразования датчика
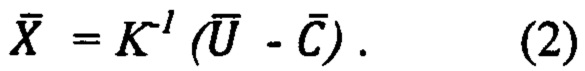
Однако, чтобы обеспечить линейность модели приходится платить дорогую цену за сложные конструкторские ухищрения (специально направленные на обеспечение линейности датчика) и за высокий коэффициент отбраковки датчиков. Это является недостатком подавляющего большинства всех современных датчиков, измеряющих самые разные физические величины. Достаточно простые способы избавления датчиков от этого недостатка до настоящего времени малоизвестны.
Существует патент РФ №2540449 «Способ формирования статуса результата измерений интеллектуального датчика», МПК G01D 3/00, опубликован 10.02.2015.
Задача, на решение которой направлено заявляемое изобретение, заключается в разработке универсального способа оценки метрологического состояния датчика физической величины в режиме непрерывного технологического процесса. В целях формирования статуса результата измерений интеллектуального датчика формируют верхнее и нижнее пороговые значения опорного сигнала, причем нижнее пороговое значение меньше единицы, а верхнее больше, сравнивают значения опорного сигнала с пороговыми значениями, причем, если значение опорного сигнала находится в диапазоне между верхним и нижним пороговыми значениями или равно им, измерению присваивают статус - подтвержденное, а в случае выхода за границы, определяемые верхним и нижним пороговыми значениями, - недостоверное.
Данное изобретение не предоставляет возможность определения конкретных значений тех или иных погрешностей в характеристиках измеряемых величин датчика и последующей их компенсации.
Цель изобретения - получение интеллектуального датчика упрощенной процедурой разработки на основе применения предложенной новой технологии его индивидуальной калибровки и обучения, обеспечивающей как восстановление воздействующей на датчик физической величины с заданной точностью во всем диапазоне ожидаемых условий рабочего функционирования, так и уникальное для датчика конкретного типа избирательное повышение чувствительности в интересующем диапазоне изменения измеряемой физической величины.
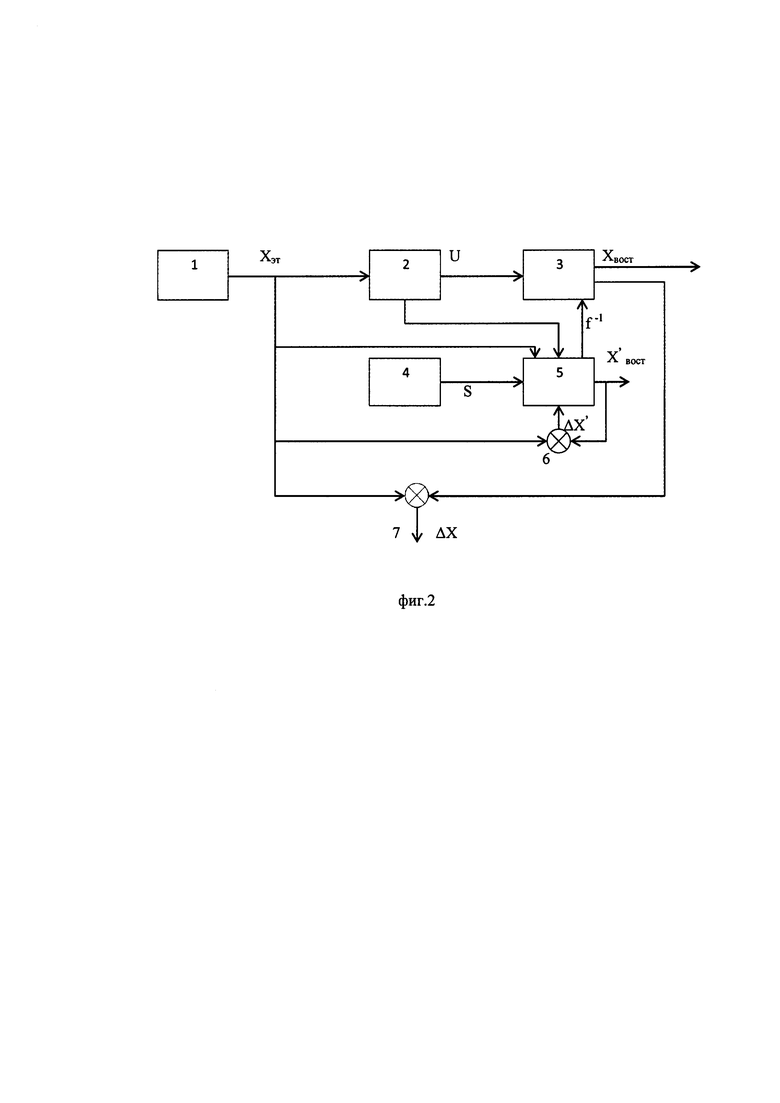
Для достижения поставленной цели предлагаемая система для разработки интеллектуального датчика, включающая первичный измерительный преобразователь (ПИП), процессор, отличающаяся тем, что дополнительно содержит генератор эталонного сигнала, задатчик структуры искусственной нейронной сети (ИНС), автоматизированное рабочее место (АРМ) обучения-калибровки, первое и второе вычитающее устройства, к выходу генератора эталонного сигнала подключен вход ПИП, к второму выходу которого подключен первый вход процессора, к выходу генератора эталонного сигнала подключены также первый вход АРМ, первый вход первого вычитающего устройства, и первый вход второго вычитающего устройства, с вторым и четвертым входами АРМ соединены выходы структуры ИНС и первый выход ПИП соответственно, к второму выходу АРМ подключен второй вход процессора, к первому выходу АРМ подключен второй вход первого вычитающего устройства, к выходу которого подключен третий вход АРМ, с вторым входом второго вычитающего устройства соединен первый выход процессора, выход второго вычитающего устройства используют для контроля качества обучения, второй выход процессора является выходом интеллектуального датчика (фиг. 2).
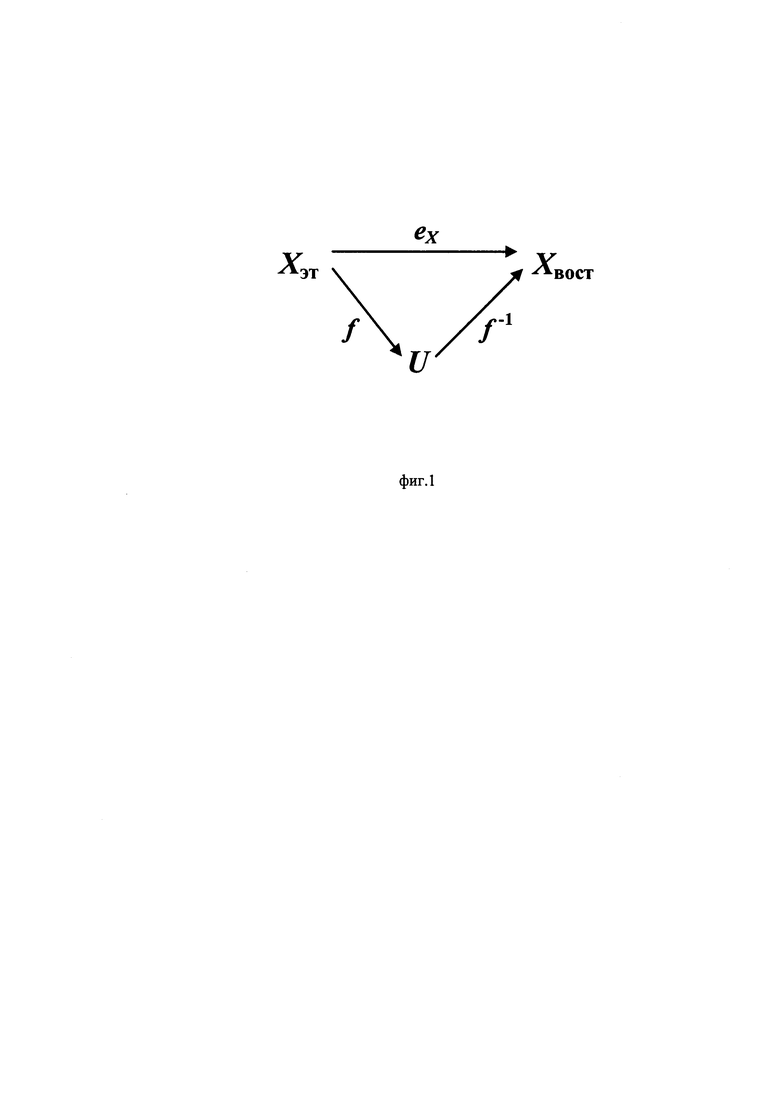
Сущность изобретения поясняется диаграммой (фиг. 1) и чертежом (фиг. 2), где на фиг. 1 представлена коммутативная диаграмма отображений в задаче калибровки, на фиг. 2 представлена структурная схема интеллектуального датчика.
Система для разработки интеллектуального датчика содержит: генератор эталонного сигнала 1, первичный измерительный преобразователь 2, процессор 3, задатчик структуры искусственной нейронной сети 4, автоматизированное рабочее место обучения 5 (формирователь f-1), первое вычитающее устройство 6, второе вычитающее устройство 7.
Генератор эталонного сигнала 1 предназначен для организации подачи эталонного сигнала измеряемой физической величины.
Первичный измерительный преобразователь 2 - это чувствительный элемент датчика, который преобразует эталонный сигнал физической величины с помощью функции преобразования f в цифровой сигнал U на выходе ПИП.
Процессор 3 предназначен для восстановления в процессе работы датчика преобразованного сигнала физической величины обратной функцией преобразования f-1, сформированной в процессе обучения датчика при его калибровке.
Структуру ИНС для начальной калибровки задают задатчиком 4, исходя из характеристик чувствительного элемента (ПИП) калибруемого датчика и требований к точности воспроизведения датчиком измеряемой физической величины.
АРМ обучения 5, в состав которого входит нейропроцессор с загруженной в него из задатчика 4 искусственной нейронной сетью, служит для формирования и обучения искусственной нейронной сети, формализующей функцию f-1.
Вычитающее устройство 6 формирует разность ΔХ= Хэт - Xвост между эталонным сигналом физической величины Хэт и текущим восстановленным сигналом X'вост при обучении нейронной сети - при формировании обратной функции преобразования f-1.
Вычитающее устройство 7 формирует разность ΔХ= Хэт - Xвост между эталонным сигналом Хэт и текущим восстановленным сигналом Xвост после формирования в АРМ 5 функции f-1 и ее прошивки в процессор 3 датчика для контроля качества обучения нейронной сети путем подачи с генератора 1 во всем диапазоне измеряемой физической величины дополнительных эталонных сигналов, не использовавшихся при обучении.
Описание работы
Традиционная задача калибровки может рассматриваться как частный случай классической задачи параметрической идентификации модели датчика для всего множества установившихся режимов его работы, то есть - задача определения статической характеристики датчика, называемой в разных прикладных задачах метрологии [9, 10] также функцией преобразования датчика. Для избавления от недостатка, обусловленного необходимостью обеспечения линейности модели датчика, задачу идентификации его модели и, соответственно, задачу калибровки, общий принцип изоморфизма [1, 6] позволяет рассматривать в более широкой, фундаментальной постановке. В предложенной системе датчики не отбраковываются и их модели существенно индивидуальны (уникальны), нелинейны, а в наиболее общем случае и вообще не известны. Здесь ставят задачу идентификации (в общем случае - задачу непараметрической идентификации) модели датчика по известным данным, поступающим на его вход, и данным, непосредственно измеряемым на выходе. Такая задача в классической теории систем [7] известна как задача реализации модели датчика, рассматриваемого в качестве «черного ящика», по известным данным. Однако длительное время такая задача практически не имела решения, т.к., как указывал в [7] Р. Калман, не удавалось в достаточно общем виде не только доказать, но и сформулировать «теорему о реализации».
В отличие от традиционно применяемых датчиков, у которых функция преобразования (1) почти всегда линейна и обязательно всегда обратима в обычном смысле, у «интеллектуальных» датчиков, функционирующих на основе общего принципа изоморфизма, функция преобразования f (фиг. 1) может быть не только нелинейной, но и необратимой в обычном смысле. На f накладывается лишь одно требование-ограничение - она должна быть мономорфным отображением вида f: Xэт→U. Это условие легко выполнить при калибровке (оно выполняется и для обычных «линейных датчиков»): каждому значению эталонного сигнала Хэт должно строго соответствовать одно единственное значение выходного сигнала U и, наоборот, в множестве значений выходного сигнала U должно существовать подмножество U* ⊂U таких значений сигнала U, каждому из которых обязательно соответствует единственное значение калибровочного эталонного сигнала из множества Xэт. Тогда обязательно будет существовать эпиморфное отображение f-1: U→Xвост, позволяющее восстанавливать значения сигналов из множества Хвост, точно и взаимно однозначно отображающих соответствующие сигналы из множества Хэт.
В рамках новой парадигмы в теории систем [6], основанной на общем принципе изоморфизма, теорема о реализации доказана в форме основной (фундаментальной) леммы [6]. На основе этой леммы применительно к задаче калибровки можно построить коммутативную диаграмму, показанную на фиг. 1, где обозначены: eX - изоморфное в обычном смысле отображение (в данном случае единичное), характеризующее желаемое тождество между некоторым известным эталонным сигналом Xэт, подаваемым на вход калибруемого «интеллектуального» датчика, и восстановленным на его выходе сигналом Хвост; f - неизвестная функция преобразования (измерительная характеристика) входного сигнала Xэт датчика в сигнал U на его выходе (на выходе «чистого» датчика (первичного измерительного преобразователя), т.е. до «интеллектуальной» обработки сигнала); f-1 - функция восстановления измеряемой датчиком физической величины Хвост, представляющая собой обратную функцию преобразования датчика, характеризующую некоторую процедуру «интеллектуальной» обработки его выходного сигнала U.
В соответствии с теоремой о реализации (основной леммой), доказанной в [6], в рамках коммутативной диаграммы на фиг. 1 должны выполняться условия:
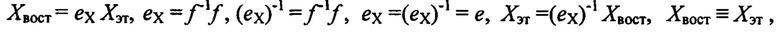
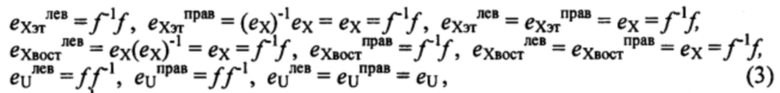
где f-1 - обратное с точностью до изоморфизма eХ отображение-изоморфизм к отображению f, характеризующему неизвестную функцию преобразования (модель) датчика; 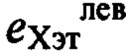 ,
, 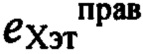 ,
, 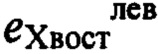 ,
, 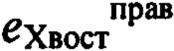 ,
, 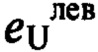 ,
, 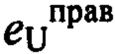 - соответственно левая и правая единицы на множествах сигналов Xэт, Хвост, U. Причем, в соответствии с условиями и результатами доказательства основной (фундаментальной) леммы [6], матричные единицы
- соответственно левая и правая единицы на множествах сигналов Xэт, Хвост, U. Причем, в соответствии с условиями и результатами доказательства основной (фундаментальной) леммы [6], матричные единицы 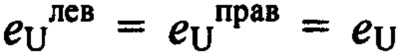 , определяемые на множестве U в рамках коммутативной диаграммы, не обязательно должны быть обычными единичными матрицами. Несмотря на кажущуюся громоздкость выражений (3), в использовании их на практике при калибровке датчиков нет необходимости.
, определяемые на множестве U в рамках коммутативной диаграммы, не обязательно должны быть обычными единичными матрицами. Несмотря на кажущуюся громоздкость выражений (3), в использовании их на практике при калибровке датчиков нет необходимости.
Как следует из доказательства основной леммы в [6], отображение f будет в этом случае изоморфным с точностью до изоморфизма eX: Xэт→Xвост. Доказательство рассматриваемого утверждения об обязательном существовании эпиморфного отображения f-1 и изоморфности отображения f внутри коммутативной диаграммы опирается на доказательство основной леммы, подробно изложенное в [6].
Далее, в качестве модели обратной функции преобразования f-1 выбирается искусственная нейронная сеть, обучаемая на полученных в результате проведения калибровочных экспериментов примерах таким образом, чтобы каждому уникальному значению выходного сигнала датчика из множества U строго отвечало единственное восстановленное значение физической величины из множества Xвост, точно соответствующее тому значению входной физической величины на множестве Xэт, которому точно соответствует значение сигнала из множества U, вызвавшее указанный отклик нейронной сети (значение сигнала из множества Хвост). После обучения нейронной сети на всем множестве калибровочных сигналов-примеров для проверки точности модели f-1 может быть проведена серия контрольных экспериментов с подачей на вход датчика таких значений сигналов, которые не вошли в множество Xэт обучающих эталонных входных сигналов. При необходимости для повышения точности работы «интеллектуального» датчика нейронная сеть может быть дообучена на результатах дополнительных экспериментов, позволяющих сформировать промежуточные обучающие точки-сигналы. Такая процедура обучения позволяет получить изоморфное отображение eX:Xэт→Xвост и в неявной форме (в форме нейронной сети) - обратную функцию преобразования f-1, позволяющую восстанавливать с заданной точностью реальные значения физической величины, действующей на вход датчика.
Нейронная сеть (обратная функция преобразования f-1), сформированная и обученная в процессе проведения калибровочных экспериментов (фиг. 2), должна записываться в память процессора «интеллектуального» датчика и в дальнейшем использоваться в процессе его рабочего функционирования. Обратим внимание также на то, что необходимость идентификации самой функции преобразования датчика f, а также необходимость решения сложной системы алгебраических уравнений (3) для определения обратной функции преобразования f-1 при рассмотренном подходе отсутствует. Функция f может оставаться вообще неизвестной. К функции преобразования f «интеллектуального» датчика предъявляется лишь традиционное и для обычного «линейного» датчика требование - высокая стабильность f при длительных сроках эксплуатации. При этом f может изменяться (трансформироваться) при изменении в широких пределах ожидаемых условий эксплуатации датчика. В этом случае искусственная нейронная сеть должна быть обучена применительно ко всем этим условиям будущего применения датчика путем проведения дополнительных калибровочных экспериментов. Кроме того, у конструкторов, в отличие от традиционного подхода, связанного с необходимостью обеспечения линейности функции f, появляется свобода выбора таких ее видов, которые обеспечивают, например, избирательное калибровочных экспериментов. Кроме того, у конструкторов, в отличие от традиционного подхода, связанного с необходимостью обеспечения линейности функции f, появляется свобода выбора таких ее видов, которые обеспечивают, например, избирательное повышение чувствительности датчика в некоторых, интересующих разработчика, диапазонах изменения измеряемой физической величины. Если таких требований нет, конструктор в принципе может вообще не задаваться каким-либо видом функции f, ориентируясь лишь на приемлемую чувствительность датчика во всем диапазоне изменения измеряемой физической величины. Если же возникнет необходимость идентификации самой функции преобразования датчика f, то для этого может быть использована либо та же искусственная нейронная сеть, что и в случае идентификации обратной функции преобразования f-1, либо некоторая другая. В этом случае процедура обучения, исходя из изоморфного отображения eU:U→Uвост, позволяет получить в неявной форме (в форме нейронной сети) - функцию преобразования f, позволяющую восстанавливать с заданной точностью значения Uвост сигнала датчика, непосредственно наблюдаемые на его выходе. Отметим, что обычно при калибровке идентифицировать функцию преобразования f не требуется, так как она не используется в рабочем режиме функционирования откалиброванного датчика для восстановления физической величины, действующей на его вход.
Процесс обучения «интеллектуального» датчика можно кратко описать следующим образом (фиг. 2). В процессе калибровки ставятся эксперименты, позволяющие получить для каждого значения эталонного сигнала Xэт некоторое единственное значение сигнала из множества U выходных сигналов датчика (например, некоторый уникальный цифровой код). Генератор эталонного сигнала задает эталонные сигналы Xэт, на выходе ПИП получаются кодовые сигналы U. Параллельно этому эталонный сигнал Xэт поступает на автоматизированное рабочее место (АРМ) обучения-калибровки (процессор), в котором происходит обучение искусственной нейронной сети (ИНС), поступившей в АРМ из задатчика структуры нейронной сети. Чтобы обучить нейросеть, необходимо сформировать на ее выходе (на выходе АРМ) такой же вектор X'вост, как и на ее входе Хэт (на входе АРМ). Весовые коэффициенты нейросети необходимо настроить так, чтобы входной сигнал совпадал с выходным. На вход первого вычитающего устройства подается эталонный сигнал и сравнивается с восстановленным сигналом Х'вост, полученным на выходе из АРМ. Цикл повторяется до достижения ΔХ' заданного порогового значения. Для обучения системы создается структура ИНС Sинс, которая загружается в АРМ из задатчика структуры ИНС.
По окончании обучения нейросети генератор эталонных сигналов подает на вход ПИП известный контрольный вектор, значения которого сравниваются с полученными значениями восстановленного сигнала на выходе датчика. Если разность между контрольными и восстановленными значениями сигнала больше допустимой, то на выходе появляется ошибка обучения ΔХ, превышающая порог. В этом случае структура ИНС может быть скорректирована, либо может быть расширено множество обучающих примеров для прежней структуры ИНС. В любом случае дополнительная процедура обучения должна быть построена таким образом, чтобы ошибка ΔХ стала меньше пороговой (допустимой). Если ошибка меньше допустимой, то обучение считается законченным, в противном случае обучение нейросети с использованием АРМ продолжается до тех пор, пока ошибка ΔХ не сведется к допустимой (близкой к нулю). Обученная ИНС прошивается в процессор интеллектуального датчика.
Таким образом предложена система разработки интеллектуального датчика, опирающаяся на общий эффект от применения двух технологий - технологии идентификации систем на основе общего принципа изоморфизма [1-6] и технологии разработки и обучения искусственных нейронных сетей [12].
На множестве значений выходного сигнала U датчика допускается существование некоторых «зашумленных» значений сигнала, ни одно из которых не отвечает какому-либо эталонному значению сигнала из множества Хэт. Тем не менее, «интеллектуальная» обработка зашумленных значений сигнала U посредством обратной функции преобразования f-1: U→Хвост позволит восстановить точные значения сигнала Хвост, однозначно отвечающие соответствующим значениям сигнала из множества Хэт посредством выделения в U указанного выше подмножества U* ⊂ U.
Указанное утверждение и его доказательство справедливы лишь в том случае, когда изоморфность отображения eХ:Xэт→Xвост обеспечена заранее, например, путем «обучения» интеллектуального датчика в процессе калибровки. Процесс обучения позволяет одновременно решить две задачи: сформировать обратную функцию преобразования f-1 датчика, то есть решить задачу калибровки его модели, и получить изоморфное отображение eX:Xэт→Xвост, обеспечивающее существование этой обратной функции.
Техническим результатом является упрощение процедур разработки датчиков на основе применения предложенной в изобретении новой технологии их индивидуальной калибровки и обучения, в результате которой может быть получен «интеллектуальный» датчик, обеспечивающий как восстановление воздействующей на него физической величины с заданной точностью во всем диапазоне условий рабочего функционирования, так и уникальное для датчика конкретного типа избирательное повышение чувствительности в интересующем диапазоне изменения измеряемой физической величины. Полученные результаты позволяют разработать принципиально новые способы конструирования и калибровки датчиков различного назначения.
Литература
1. Кулабухов B.C. Принцип изоморфности в задаче реализации и его приложения к анализу свойств систем управления // В сборнике: XII Всероссийское совещание по проблемам управления ВСПУ-2014. Институт проблем управления им. В.А. Трапезникова РАН. 2014. С. 438-448. URL: http://vspu2014.ipu.ru/prcdngs
2. Кулабухов B.C. Изоморфные наблюдатели состояния и робастная фильтрация сигналов систем // Радиотехника. 2017. №8. С. 50-55.
3. Кулабухов B.C. Синтез регуляторов для следящих систем на основе принципа изоморфности // Мехатроника, автоматизация, управление. 2017. Том 18, №8. С. 507-515.
4. Kulabukhov V. Linear Isomorphic Regulators // CMTAI2016. MATEC Web of Conf. 2017. T. 99. C. 03008.(doi:10.1051/matecconf/20179903008)
URL:https://www.matec-conferences.org/articles/matecconf/pdf/2017/13/matecconf_cmtai2017_03008.pdf
5. Kulabukhov V. S. Isomorphic observers of the linear systems state // Workshop on Materials and Engineering in Aeronautics (MEA2017) 15-16 November 2017, Moscow, Russian Federation. doi:10.1088/1757-899X/312/l/012016. p.012016. URL: http://iopscience.iop.org/issue/1757-899X/312/1
6. Кулабухов B.C. Общий принцип изоморфизма в теории систем // Cloud of Science. 2018. Т.5. №3. С. 400-472. URL: https://cloudofscience.ru/sites/default/files/pdf/CoS_5_400.pdf
7. Калман Р.Е. Идентификация систем с шумами // УМН. 1985. Т. 40. Вып.4 (244). С. 27-41.
8. Цыпкин Я.З. Информационная теория идентификации. - М.: Наука. Физматлит, 1995. - 336 с.
9. URL: https://search.rsl.ru/ru/record/01006744194
10. ГОСТ Р 8.879-2014 Государственная система обеспечения единства измерений. Методики калибровки средств измерений. Общие требования к содержанию и изложению.
11. Хайкин С. Нейронные сети. Полный курс. 2-е изд. Пер. с англ. - М.: Издательский дом «Вильямс», 2006. - 1104 с.
12. Кулабухов B.C. Модель нейробионической сети для бортовых систем искусственного интеллекта // В сборнике: III Всероссийская научно-техническая конференция «Моделирование авиационных систем». Сборник тезисов докладов. ФГУП «ГосНИИАС», 21-22 ноября 2018 г., г. Москва. С. 339-341.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ калибровки интеллектуальных датчиков | 2019 |
|
RU2730367C1 |
| Способ идентификации нелинейных систем | 2019 |
|
RU2714612C1 |
| МЕТОД РЕЗЕРВИРОВАНИЯ КАНАЛОВ КОНСТРУКТИВНО-ФУНКЦИОНАЛЬНЫХ МОДУЛЕЙ БОРТОВЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЕЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА ОСНОВЕ ИНТЕЛЛЕКТУАЛЬНОЙ ДИАГНОСТИЧЕСКОЙ СИСТЕМЫ В УСЛОВИЯХ ИНТЕГРИРОВАННОЙ МОДУЛЬНОЙ АВИОНИКИ | 2021 |
|
RU2778366C1 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ ИНФОРМАЦИОННО-ПРЕОБРАЗУЮЩИХ ЭЛЕМЕНТОВ БОРТОВОГО ОБОРУДОВАНИЯ ВОЗДУШНОГО СУДНА НА ОСНОВЕ МАШИННОГО ОБУЧЕНИЯ | 2022 |
|
RU2802976C1 |
| Система оперативного управления движением транзитных поездов | 2019 |
|
RU2723051C1 |
| ОБЪЕКТОВАЯ КОММУНИКАЦИОННО-ИНФОРМАЦИОННАЯ СИСТЕМА И СПОСОБ ЕЁ ПРОЕКТИРОВАНИЯ | 2022 |
|
RU2792329C1 |
| Способ подавления шума на рентгеновском изображении с помощью искусственной нейронной сети | 2022 |
|
RU2822515C2 |
| СПОСОБ И СИСТЕМА ПЛАНИРОВАНИЯ ПРОФИЛАКТИЧЕСКОГО ОБСЛУЖИВАНИЯ И РЕМОНТА ТЕХНОЛОГИЧЕСКОГО ОБОРУДОВАНИЯ НА ОСНОВЕ АКУСТИЧЕСКОЙ ДИАГНОСТИКИ С ПРИМЕНЕНИЕМ НЕЙРОННЫХ СЕТЕЙ | 2021 |
|
RU2764962C1 |
| СПОСОБ И СИСТЕМА УПРАВЛЕНИЯ ЭЛЕКТРОННЫМИ УСТРОЙСТВАМИ С ПОМОЩЬЮ ЭЛЕКТРОМИОГРАФИЧЕСКОГО УСТРОЙСТВА СЧИТЫВАНИЯ | 2017 |
|
RU2683859C1 |
| Система для управления работой участка железной дороги с построением единого расписания | 2020 |
|
RU2742959C1 |
Изобретение относится к контрольно-измерительной технике, в частности к автоматическим и автоматизированным системам разработки интеллектуальных датчиков путем «обучения» в процессе калибровки, и может быть использовано в приборостроении при разработке, изготовлении и диагностике интеллектуальных датчиков и измерительных систем различного типа. Система для разработки интеллектуального датчика содержит: генератор эталонного сигнала, первичный измерительный преобразователь, процессор, задатчик структуры искусственной нейронной сети, автоматизированное рабочее место обучения (формирователь f-1), первое и второе вычитающие устройства, соединенные между собой в соответствии с блок-схемой на фиг. 2. Система разработки интеллектуального датчика опирается на общий эффект от применения двух технологий - технологии идентификации систем на основе общего принципа изоморфизма и технологии разработки и обучения искусственных нейронных сетей. Техническим результатом является упрощение процедур разработки датчиков на основе применения предложенной в изобретении новой технологии их индивидуальной калибровки и обучения, в результате которой может быть получен «интеллектуальный» датчик, обеспечивающий как восстановление воздействующей на него физической величины с заданной точностью во всем диапазоне условий рабочего функционирования, так и уникальное для датчика конкретного типа избирательное повышение чувствительности в интересующем диапазоне изменения измеряемой физической величины. 2 ил.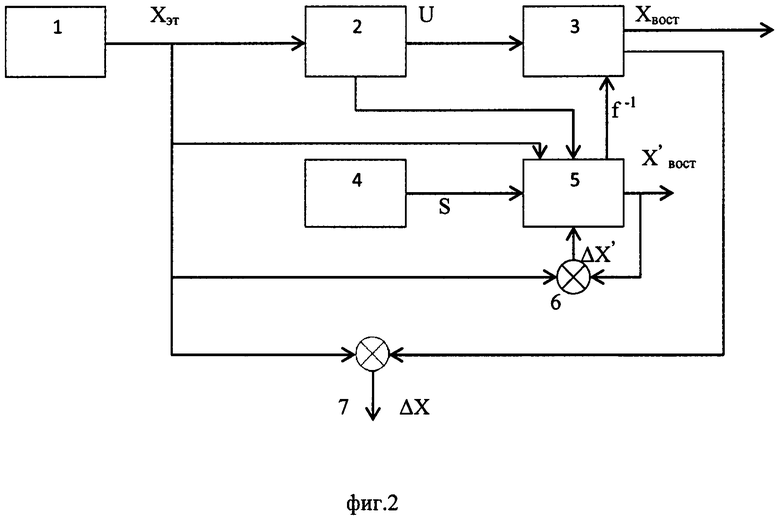
Система для разработки интеллектуального датчика, включающая первичный измерительный преобразователь (ПИП), процессор, отличающаяся тем, что дополнительно содержит генератор эталонного сигнала, задатчик структуры искусственной нейронной сети (ИНС), автоматизированное рабочее место (АРМ) обучения-калибровки, первое и второе вычитающие устройства, к выходу генератора эталонного сигнала подключен вход ПИП, к второму выходу которого подключен первый вход процессора, к выходу генератора эталонного сигнала подключены также первый вход АРМ, первый вход первого вычитающего устройства и первый вход второго вычитающего устройства, с вторым и четвертым входами АРМ соединены выходы структуры ИНС и первый выход ПИП соответственно, к второму выходу АРМ подключен второй вход процессора, к первому выходу АРМ подключен второй вход первого вычитающего устройства, к выходу которого подключен третий вход АРМ, с вторым входом второго вычитающего устройства соединен первый выход процессора, выход второго вычитающего устройства используют для контроля качества обучения, второй выход процессора является выходом интеллектуального датчика.
| Бесконтактный электромагнитный датчик для измерения крутящего момента, передаваемого вращающимся валом | 1960 |
|
SU148932A1 |
| RU 2017111461 A, 05.10.2018 | |||
| СПОСОБ ФОРМИРОВАНИЯ СТАТУСА РЕЗУЛЬТАТА ИЗМЕРЕНИЙ ИНТЕЛЛЕКТУАЛЬНОГО ДАТЧИКА | 2013 |
|
RU2540449C1 |
| US 20130041783 A1, 14.02.2013 | |||
| US 20160350671 A1, 01.12.2016 | |||
| US 20160274553 A1, (ROCKWELL AUTOMATION TECHNOLOGIES, INC.) 22.09.2016. | |||
Авторы
Даты
2020-02-11—Публикация
2019-06-10—Подача