Изобретение относится к радиотехнике и может использоваться для измерения разности времени прихода и разности частоты приема сигналов с разнесенных приемных позиций без привлечения априорной информации о структуре сигнала и о модулирующем сообщении.
Измерение разности времени прихода (РВП) и разности частоты приема (РЧП) сигналов с разнесенных приемных позиций имеет большое значение в системах дальней космической связи с космическими аппаратами (КА) типа Mars Polarlander, Mars Pathfinder [1] или с КА типа Voyager и Galileo [2], в том числе для определения параметров движения таких КА.
Известен ряд аналоговых способов измерения РВП и РЧП сигналов с разнесенных приемных позиций [3-6], основанных на нахождении аргументов максимума двумерной кросс-корреляционной функции, потенциально дающих статистически оптимальные максимально правдоподобные оценки разностей времени и частоты прихода сигналов. Однако потенциальная точность способов [3-6] нереализуема на практике ввиду отсутствия плавно регулируемых эталонов времени и частоты [7, 8].
Известен ряд цифровых способов измерения РВП сигналов с разнесенных приемных позиций [8], основанных на нахождении аргумента максимума кросс-корреляционной функции или аргумента минимума разностных кросс-корреляционных функций, позволяющих реализовать потенциальную точность способов [3-6] за счет исключения погрешности дискретности путем параболической интерполяции окрестностей максимума или минимума соответствующих функций. Однако цифровые способы измерения РВП сигналов с разнесенных приемных позиций [8-9] неприменимы при наличии движения источника сигнала или приемной позиции, что имеет место в системах дальней космической связи с космическими аппаратами. Другим недостатком цифровых способов измерения, представленных в работе [8], является низкая вычислительная эффективность на больших размерах выборки данных, поскольку они основаны на прямом вычислении кросс-корреляционных функций (при таком методе нахождения кросс-корреляционных функций количество операций умножения пропорционально квадрату длины (n) выборки данных, подобная пропорциональность обычно обозначается как O(n2)).
В патентах [10-12] представлен ряд цифровых способов совместного измерения РВП и РЧП сигналов с разнесенных приемных позиций, основанных на нахождении аргументов максимума дискретной двумерной кросс-корреляционной функции (ДДККФ), которые позволяют производить измерения при наличии движения источника сигнала или приемной позиции. Основная цель, поставленная автором патентов [10-12], посвящена снижению потоков информации, передаваемых между разнесенными приемными позициями, и компенсации систематической погрешности, возникающей при корреляции компрессированного и опорного сигналов. Однако в способах совместного измерения РВП и РЧП [10-12] не решены вопросы исключения погрешности дискретности (корреляционная зависимость между РВП и РЧП [13] не позволяет очевидным способом распространить на совместные измерения подходы, изложенные в [8]), и вопросы повышения вычислительной эффективности, так как кросс-корреляционные функции в способах [10-12] порождаются не прямым методом через свертку двух последовательностей данных, как и в [8], а за счет n-кратного повторения (для обеспечения поиска аргумента максимума в частотной области), количество операций умножения увеличивается и пропорционально кубу длины (n) выборки данных, т.е. O(n3).
Наиболее близким к предлагаемому способу измерения РВП и РЧП сигналов, по совокупности используемых действий над сигналом, является способ [14], основанный на нахождении аргументов максимума ДДККФ (вычислительно существенно более эффективный, чем аналоги), принятый за прототип.
Согласно этому способу:
1. Принимают сигнал на двух разнесенных приемных позициях.
2. Преобразуют сигнал, полученный от одной приемной позиции, в первый цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
3. Преобразуют сигнал, полученный от другой приемной позиции, во второй цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
4. Преобразуют с использованием быстрого преобразования Фурье (БПФ) упомянутый первый цифровой поток данных на смежных отрезках времени в значения первого спектра, который представляет сигнал как ряд значений функции частоты.
5. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных на смежных отрезках времени в значения второго спектра, который представляет сигнал как ряд значений функции частоты.
6. Поточечно взаимно перемножают значения первого и второго спектров на смежных отрезках времени для порождения совокупности кросс-спектров как функции времени.
7. Преобразуют каждую частоту, из указанной совокупности кросс-спектров как функции времени, в множество значений РЧП (для поиска аргумента максимума РЧП).
8. Выбирают из указанного множества значений РЧП те, которые соответствуют сигналу, представляющему интерес.
9. Суммируют указанные значения кросс-спектров по каждому из выбранных значений РЧП через вычисление обратного БПФ для нахождения РВП как аргумента максимума найденных сумм.
По существу способ, описанный выше [14], реализует вычислительно эффективное по сравнению с аналогами [10-12] нахождение аргументов максимума ДДККФ с использованием при вычислении ДДККФ быстрых преобразований Фурье на основании теоремы Винера-Хинчина [15], определяющей взаимосвязь между спектром и корреляционной функцией сигнала.
С учетом того, что полная выборка данных длины (n) в способе-прототипе разбивается на k смежных сегментов для получения разрешения в области неопределенности по допплеровскому сдвигу, как указано в третьем абзаце первого столбца восьмой страницы описания прототипа [14] с последующим вычислением спектров и соответствующих им кросс-спектров для каждого из смещенных во времени смежных сегментов выборки данных, можно оценить объем вычислительных затрат на нахождение двумерной кросс-корреляционной функции в способе-прототипе.
Нахождение Фурье-образа для одной выборки данных длиной n требует реализовать порядка O(n·logn) операций умножения [16-17]. С учетом того, что из каждой выборки данных от двух приемных позиций формируют k смежных сегментов, для каждого из которых находят Фурье-образ, общий объем операций умножения, требуемых для нахождения Фурье-образов входных данных, составляет О(2·k·n·logn). Для нахождения соответствующих кросс-спектров требуется О(k·n) операций умножения. Вычисление ДДККФ через обратное БПФ полученных k кросс-спектров требует О(k·n·logn) операций умножения. Таким образом, в способе-прототипе на нахождение ДДККФ требуется всего порядка О(3·k·n·logn+k·n) операций умножения, что намного меньше, чем в аналогах. Так, например, для выборки данных длиной n=1024 при k=32 в способе-прототипе на нахождение ДДККФ потребуется всего порядка одного миллиона О(3·32·1024·log1024+32·1024)=О(3·32·1024·10+32·1024)=О(995072) операций умножения. В предельном случае k=n количество операций умножения возрастает только до 30 миллионов. В то время как в аналогах [10-12] потребуется порядка миллиарда (О(n3)) операций умножения.
Несмотря на существенное снижение вычислительных затрат по сравнению с аналогами одним из недостатков способа-прототипа является недостаточная вычислительная эффективность. Другим недостатком способа-прототипа является, как и у аналогов [10-12], погрешность дискретности определения аргументов максимума, поскольку корреляционная зависимость между РВП и РЧП [13] не позволяет очевидным способом распространить на совместные измерения подходы по ее исключению, изложенные в [8].
Устройство-прототип [14] содержит первое средство приема сигналов, подключенное к устройству определения аргументов максимума ДДККФ, выход которого является выходом устройства-прототипа, через последовательно включенные первый аналого-цифровой преобразователь (АЦП), первый процессор БПФ, вычислитель кросс-спектров и второй процессор БПФ. Между вторым средством приема сигналов и вторым входом вычислителя кросс-спектров последовательно включены второй АЦП и третий процессор БПФ.
Недостатком устройства-прототипа является недостаточное быстродействие определения РЧП и РВП сигналов. Другим недостатком устройства-прототипа является недостаточная точность определения РЧП и РВП, обусловленная наличием погрешности дискретности определения аргументов максимума ДДККФ.
Техническим результатом изобретения является повышение вычислительной эффективности за счет использования уточненных спектральных свойств дискретного преобразования Фурье цифрового сигнала, преобразованного по частоте, позволяющих исключить необходимость сегментации данных на смежные подмножества и вычисление Фурье-образов для указанных подмножеств сигнала.
Технический результат достигнут тем, что в способе измерения разностей времени прихода и частоты приема сигналов, включающем прием сигнала на двух разнесенных приемных позициях, аналого-цифровое преобразование сигнала, полученного от одной приемной позиции, в первый цифровой поток данных, представляющий сигнал в цифровой форме как ряд значений функции времени, аналого-цифровое преобразование сигнала, полученного от другой приемной позиции, во второй цифровой поток данных, преобразование первого цифрового потока данных с использованием быстрого преобразования Фурье (БПФ) в значения первого спектра, представляющего сигнал как ряд значений функции частоты S1(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных, преобразование второго цифрового потока данных с использованием БПФ в значения второго спектра, представляющего второй принятый сигнал как ряд значений функции частоты S2(k), взаимное перемножение значений спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала, порождающее кросс-спектр, вычисление дискретной двумерной кросс-корреляционной функции (ДДККФ) сигнала через обратное БПФ множества кросс-спектров, определение разности времени прихода и частоты приема сигналов как аргументов максимума ДДККФ сигнала, согласно изобретению, спектр одного из сигналов Si(k), где i=1, 2 - номер одного из двух спектров, преобразуют по частоте на величины m, выбираемые согласно требованиям по разрешению РЧП, из целочисленного ряда значений от единицы до (N-1), где N - длина обрабатываемого цифрового потока данных, с созданием последовательности преобразованных по частоте спектров Si,m(k), полученной из исходных спектральных составляющих сигнала по следующему правилу:
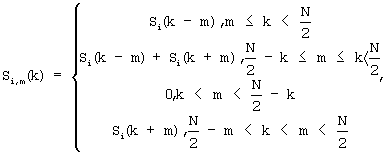
значения спектров Si,m(k) преобразованных по частоте сигналов взаимно перемножают с комплексно сопряженными значениями спектра второго из двух исходных сигналов для порождения множества кросс-спектров.
Другим техническим результатом изобретения является исключение погрешности дискретности за счет использования того факта, что окрестность главного максимума двумерной кросс-корреляционной функции сигнала имеет форму эллиптического параболоида [13, стр.8-9], и за счет разработки оптимального, в среднеквадратическом смысле, аналитического метода оценки параметров эллиптического параболоида и определения аргументов его максимума, основанного на проективных преобразованиях.
Технический результат достигнут тем, что в способе измерения разностей времени прихода и частоты приема сигналов в окрестности аргументов максимума ДДККФ сигнала выбирают конечное множество точек указанной функции, включающее точку максимума и, как минимум, две точки, расположенные с противоположных сторон относительно аргумента максимума РВП, и две точки, расположенные с противоположных сторон относительно аргумента максимума РЧП, значения ДДККФ для выбранных точек объединяют в вектор-столбец z, из единиц формируют вектор-столбец 1 такой же размерности, как вектор z, объединяют векторы 1 и z в двухстолбцовую матрицу G, первым столбцом которой ставят единичный вектор 1, а вторым - вектор z, псевдообращают матрицу G, обозначая псевдообратную матрицу как G+, где надстрочный индекс + обозначает операцию псевдообращения матриц, умножают матрицу G справа на псевдообратную ей матрицу G+, формируют проектор 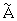 , как разность между матрицей тождественного преобразования и результатом умножения, аргументы, соответствующие РВП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец x, а квадраты компонент вектора x аналогично объединяют в вектор-столбец q, аргументы, соответствующие РЧП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец у, а квадраты компонент вектора у аналогично объединяют в вектор-столбец v, векторы-столбцы x, у, v в перечисленном порядке объединяют в трехстолбцовую матрицу F, находят оценку наименьших квадратов трехмерного вектора-столбца
, как разность между матрицей тождественного преобразования и результатом умножения, аргументы, соответствующие РВП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец x, а квадраты компонент вектора x аналогично объединяют в вектор-столбец q, аргументы, соответствующие РЧП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец у, а квадраты компонент вектора у аналогично объединяют в вектор-столбец v, векторы-столбцы x, у, v в перечисленном порядке объединяют в трехстолбцовую матрицу F, находят оценку наименьших квадратов трехмерного вектора-столбца 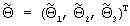 , где надстрочный индекс т обозначает операцию транспонирования матрицы, согласно следующему правилу:
, где надстрочный индекс т обозначает операцию транспонирования матрицы, согласно следующему правилу: 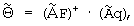 половинное значение первой компоненты вектора
половинное значение первой компоненты вектора 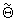 делят на частоту выборки сигнала Fs и получают уточненное значение
делят на частоту выборки сигнала Fs и получают уточненное значение 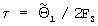 РВП сигнала, а половинное значение второй компоненты вектора
РВП сигнала, а половинное значение второй компоненты вектора 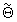 , взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение
, взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение 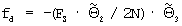 РЧП сигнала.
РЧП сигнала.
Способ реализуется устройством измерения разностей времени прихода и частоты приема сигналов, содержащим первое средство приема сигналов, подключенное к устройству определения аргументов максимума дискретной двумерной кросс-корреляционной функции сигнала, выход которого является выходом устройства измерения, через последовательно включенные первый аналого-цифровой преобразователь (АЦП), первый процессор БПФ, вычислитель кросс-спектров и второй процессор БПФ, между вторым средством приема сигналов и вторым входом вычислителя кросс-спектров последовательно включены второй АЦП и третий процессор БПФ, согласно изобретению, между выходом первого процессора БПФ и третьим входом вычислителя кросс-спектров включено арифметическое устройство (АУ), преобразующее значения Si(k) спектра одного из двух сигналов по частоте на величины m, выбираемые из целочисленного ряда значений от единицы до (N-1), и создающее на выходе множество спектров Si,m(k) по следующему правилу:
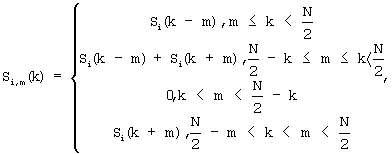
где Si,m(k) - множество преобразованных по частоте на величины m спектров одного из сигналов, N - длина обрабатываемого цифрового потока данных, i - номер одного из двух принимаемых сигналов, k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.
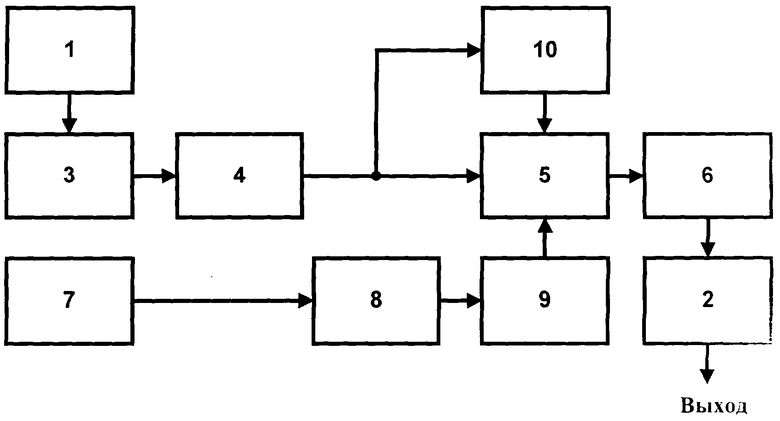
На чертеже приведена структурная схема устройства, в котором реализуется предложенный способ.
Согласно предлагаемому способу:
1. Принимают сигнал на двух разнесенных приемных позициях.
2. Преобразуют сигнал, полученный от одной приемной позиции, в первый цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
3. Преобразуют сигнал, полученный от другой приемной позиции, во второй цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
4. Преобразуют с использованием быстрого преобразования Фурье (БПФ) упомянутый первый цифровой поток данных в значения первого спектра, который представляет сигнал как ряд значений функции частоты S1(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.
5. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S2(k).
6. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.
7. Спектр одного из сигналов Si(k), где i=1, 2 - номер одного из двух спектров, преобразуют по частоте на величины m, выбираемые согласно требованиям по разрешению РЧП, из целочисленного ряда значений от единицы до (N-1), где N - длина обрабатываемого цифрового потока данных, с созданием последовательности преобразованных по частоте спектров Si,m(k), полученной из исходных спектральных составляющих сигнала по следующему правилу:
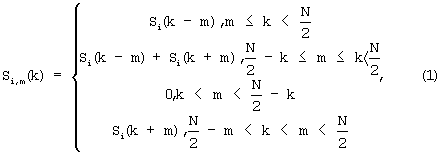
где i - номер одного из двух принимаемых сигналов значения.
8. Значения спектров Si,m(k) преобразованных по частоте сигналов взаимно перемножают с комплексно сопряженными значениями спектра второго из двух исходных сигналов для порождения множества кросс-спектров.
9. Вычисляют дискретную двумерную кросс-корреляционную функцию (ДДККФ) сигнала с использованием обратного БПФ множества кросс-спектров
10. Определяют разности времени прихода и частоты приема сигналов как аргументы максимума ДДККФ сигнала.
В известном способе, для построения дискретной двумерной кросс-корреляционной функции сигнала с использованием множества сдвинутых по частоте спектров одного из сигналов Si,m(k), указанные спектры получают посредством многократного БПФ сдвинутых на величины m смежных отрезков из цифрового потока данных, полученного в результате аналого-цифрового преобразования принятого сигнала, то есть в результате прямого применения известной для преобразования Фурье теоремы о запаздывании сигнала во временной области [15-16].
Покажем, что применение правила (1) также приводит к получению множества сдвинутых по частоте спектров одного из сигналов Si,m(k).
Если в непрерывном времени действительный сигнал s(t) переносится по частоте на величину g Гц, то в результате получается сигнал
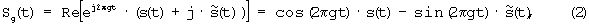
где 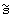 (t)=HT(s(t)) - преобразование Гильберта от s(t).
(t)=HT(s(t)) - преобразование Гильберта от s(t).
Преобразование Фурье (FT) для (2) в силу линейности имеет вид
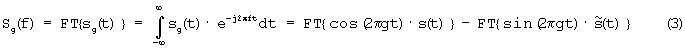 Для упрощения (3) примем во внимание известные свойства преобразований Фурье и Гильберта [15-16, 19]
Для упрощения (3) примем во внимание известные свойства преобразований Фурье и Гильберта [15-16, 19]

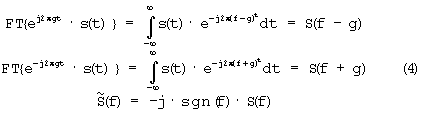
где 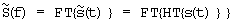 , а функция sgn(f) по определению [19] равна
, а функция sgn(f) по определению [19] равна
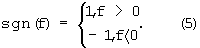
Тогда для первого слагаемого в (3) получим
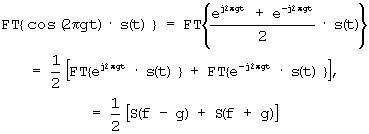
а для второго слагаемого выражения (3)
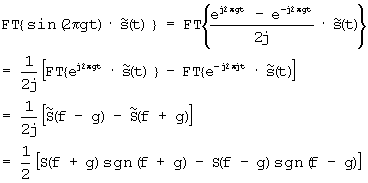
подставив полученное в выражение (3), имеем
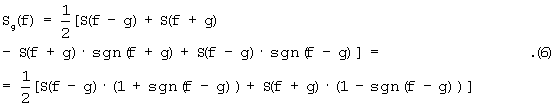
С учетом определения (5) выражение (6) можно переписать в виде
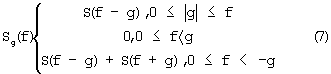
На основе полученных результатов для действительного сигнала s(t) в непрерывном времени, для дискретной последовательности 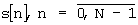 в дискретном времени, ниже устанавливаются аналогичные спектральные свойства.
в дискретном времени, ниже устанавливаются аналогичные спектральные свойства.
Если для дискретной последовательности s[n} соответствующую периодически продолженную последовательность обозначить как 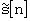 , то ее дискретное преобразование Фурье определяется как
, то ее дискретное преобразование Фурье определяется как
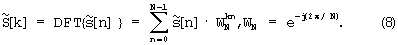
Пусть 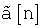 - дискретный аналог аналитического сигнала, использованного внутри круглых скобок выражения (2), тогда, следуя [18, 19],
- дискретный аналог аналитического сигнала, использованного внутри круглых скобок выражения (2), тогда, следуя [18, 19],
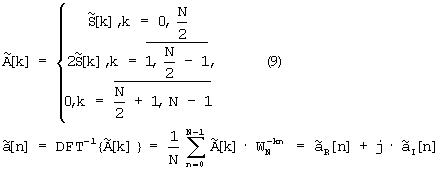
где 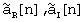 - действительные последовательности, причем
- действительные последовательности, причем 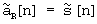 .
.
Данный результат можно использовать для получения преобразованной по частоте на величину 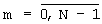 последовательности, определяемой как
последовательности, определяемой как
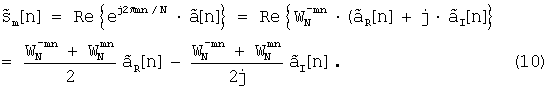
В силу определений (8) в дискретном времени имеет место равенство
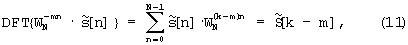
которое аналогично равенствам (4) для непрерывного времени. Поэтому, вследствие свойства дискретного преобразования Гильберта [18, стр.257], в текущих обозначениях
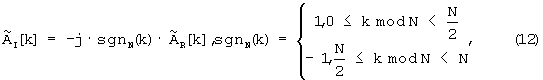
где обозначение kmodN означает целочисленный остаток от деления индексной переменной k на размер обрабатываемого цифрового потока данных N, и с учетом того, что 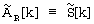 можно записать
можно записать
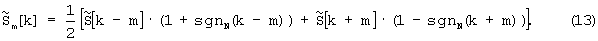
Последнее выражение на основе определения целочисленной знаковой функции sgnN(k), представленного в (12), легко преобразуется к виду (1), что позволяет получать преобразованные по частоте на величины m спектры сигнала посредством переобозначения индексных переменных согласно правилу (1) без сегментации данных и без БПФ для каждого сегмента данных, как в способе-прототипе. Это позволяет исключить порядка О(2·k·n·logn) операций умножения, здесь k обозначает количество требуемых сегментов данных, повысить вычислительную эффективность и, в предельном случае k=n, уменьшить примерно в три раза количество требуемых операций умножения и, по сравнению с представленным выше примером для способа-прототипа, сократить их количество с 30 до 10 миллионов операций.
Согласно второму варианту предлагаемого способа, исключающему погрешности дискретности:
1. Принимают сигнал на двух разнесенных приемных позициях.
2. Преобразуют сигнал, полученный от одной приемной позиции, в первый цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
3. Преобразуют сигнал, полученный от другой приемной позиции, во второй цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени.
4. Преобразуют с использованием быстрого преобразования Фурье (БПФ) упомянутый первый цифровой поток данных в значения первого спектра, который представляет сигнал как ряд значений функции частоты S1(k), где k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.
5. Преобразуют с использованием БПФ упомянутый второй цифровой поток данных в значения второго спектра, который представляет сигнал как ряд значений функции частоты S2(k).
6. Взаимно перемножают значения спектра одного из сигналов с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра.
7. Спектр одного из сигналов Si(k), где i=1, 2 - номер одного из двух спектров, преобразуют по частоте на величины m, выбираемые согласно требованиям по разрешению РЧП, из целочисленного ряда значений от единицы до (N-1), где N - длина обрабатываемого цифрового потока данных, с созданием последовательности преобразованных по частоте спектров Si,m(k), полученной из исходных спектральных составляющих сигнала по следующему правилу:
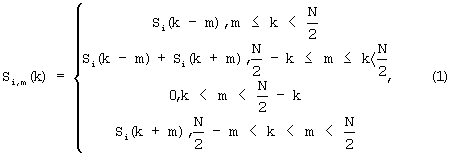
где i - номер одного из двух принимаемых сигналов значения.
8. Значения спектров Si,m(k) преобразованных по частоте сигналов взаимно перемножают с комплексно сопряженными значениями спектра второго из двух исходных сигналов для порождения множества кросс-спектров.
9. Вычисляют дискретную двумерную кросс-корреляционную функцию (ДДККФ) сигнала с использованием обратного БПФ множества кросс-спектров
10. Определяют разности времени прихода и частоты приема сигналов как аргументы максимума ДДККФ сигнала.
11. В окрестности аргументов максимума ДДККФ сигнала выбирают конечное множество точек указанной функции, включающее точку максимума и, как минимум, две точки, расположенные с противоположных сторон относительно аргумента максимума РВП, и две точки, расположенные с противоположных сторон относительно аргумента максимума РЧП.
12. Значения ДДККФ для выбранных точек объединяют в вектор-столбец z.
13. Из единиц формируют вектор-столбец 1 такой же размерности, как вектор z.
14. Объединяют векторы 1 и z в двухстолбцовую матрицу G, первым столбцом которой ставят единичный вектор 1, а вторым - вектор z.
15. Псевдообращают матрицу G, обозначая псевдообратную матрицу как С+, где надстрочный индекс + обозначает операцию псевдообращения матриц.
16. Умножают матрицу G справа на псевдообратную ей матрицу G+.
17. Формируют проектор 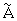 , как разность между матрицей тождественного преобразования и результатом умножения.
, как разность между матрицей тождественного преобразования и результатом умножения.
18. Аргументы, соответствующие РВП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец x.
19. Квадраты компонент вектора x аналогично объединяют в вектор-столбец q.
20. Аргументы, соответствующие РЧП для выбранных точек ДДККФ, упорядоченные так же, как и компоненты вектора z, объединяют в вектор-столбец y.
21. Квадраты компонент вектора y аналогично объединяют в вектор-столбец v.
22. Векторы-столбцы x, у, v в перечисленном порядке объединяют в трехстолбцовую матрицу F.
23. Находят оценку наименьших квадратов трехмерного вектора-столбца 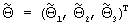 , где надстрочный индекс г обозначает операцию транспонирования матрицы, согласно следующему правилу:
, где надстрочный индекс г обозначает операцию транспонирования матрицы, согласно следующему правилу:
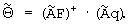
24. Половинное значение первой компоненты вектора 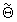 делят на частоту выборки сигнала Fs получают уточненное значение
делят на частоту выборки сигнала Fs получают уточненное значение 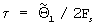 РВП сигнала.
РВП сигнала.
25. Половинное значение второй компоненты вектора 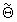 , взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение
, взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение 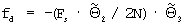 РЧП сигнала.
РЧП сигнала.
Известно [17-18], что дискретное представление непрерывной функции неизбежно приводит к возникновению шумов квантования, создающих погрешности дискретности с дисперсией ошибки 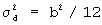 , где b - шаг квантования. Вариант предлагаемого способа, исключающий погрешности дискретности при оценке параметров двумерной кросс-корреляционной функции С12(τ,fd), основан на том, что в окрестности максимума функция С12(τ,fd) имеет форму эллиптического параболоида [13] вида [21], оценив параметры которого в результате решения системы линейных уравнений, можно уточнить значения РВП и РЧП, полученные как аргументы максимума ДДККФ, поскольку ДДККФ является выборочной от функции С12(τ,fd).
, где b - шаг квантования. Вариант предлагаемого способа, исключающий погрешности дискретности при оценке параметров двумерной кросс-корреляционной функции С12(τ,fd), основан на том, что в окрестности максимума функция С12(τ,fd) имеет форму эллиптического параболоида [13] вида [21], оценив параметры которого в результате решения системы линейных уравнений, можно уточнить значения РВП и РЧП, полученные как аргументы максимума ДДККФ, поскольку ДДККФ является выборочной от функции С12(τ,fd).
Каноническое уравнение эллиптического параболоида в декартовой системе координат OXYZ [21, стр.101]
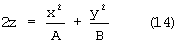
описывает поверхность с минимумом в точке (0,0)T, поэтому для наших целей (14) будет преобразовано к виду
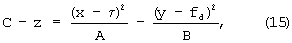
где С - значение параболоида по оси z в точке максимума, τ - аргумент максимума по оси x, соответствующий в данном случае истинной величине РВП, fd - аргумент максимума по оси у, соответствующий в данном случае истинной величине РЧП.
Исходное уравнение (15) можно переписать в функциональном виде
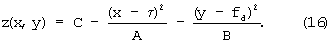
Здесь функция z(x,y) по существу представляет двумерную кросс-корреляционную функцию в других обозначениях.
Введем обозначение ρ=А/В и приведем уравнения (15)-(16) к линейному, относительно неизвестных пока параметров параболоида (16) τ, fd, A, B, C, виду
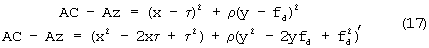
или по-другому
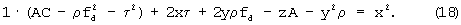
Уравнение (18) можно переписать в векторном виде следующим образом:
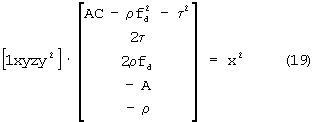
Введем обозначения для векторов правой части уравнения (19)
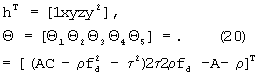
Пусть выбраны точки ДДККФ, являющейся, в дискретном времени, выборочной функцией для двумерной кросс-корреляционной функции C12(τ,fd), которая в окрестности максимума описывается эллиптическим параболоидом [13, стр.8-9], тогда вектора-строки вида hT и свободные члены уравнения (19) являются известными величинами, а вектор-столбец 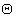 - вектором неизвестных параметров. Поэтому, если выбрано достаточное количество таких, линейно-независимых, строк hT, чтобы создать переопределенную систему уравнений (19), то может быть получена оптимальная оценка наименьших квадратов пятимерного вектора
- вектором неизвестных параметров. Поэтому, если выбрано достаточное количество таких, линейно-независимых, строк hT, чтобы создать переопределенную систему уравнений (19), то может быть получена оптимальная оценка наименьших квадратов пятимерного вектора 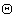 , компоненты которого связаны с искомыми параметрами эллиптического параболоида выражениями (20).
, компоненты которого связаны с искомыми параметрами эллиптического параболоида выражениями (20).
Для формирования необходимой системы уравнений (19) выбираются точка максимума ДДККФ, найденная в результате выполнения первых десяти операций предлагаемого способа, и еще, как минимум, четыре точки ДДККФ (две точки, расположенные с противоположных сторон относительно аргумента максимума РВП, и две точки, расположенные с противоположных сторон относительно аргумента максимума РЧП), тогда однозначно решается система линейных уравнений (19), позволяющая в бесшумном случае найти истинные значения РВП τ и РЧП fd, а при наличии шумов найти их среднеквадратические оценки.
Пусть выбранные Р точек ДДККФ упорядочены в произвольном порядке по номерам 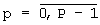 , каждая с координатами (xp,yp,zp)Т где, согласно принятым выше обозначениям, координата xp точки р соответствует ее аргументу по оси РВП ДДККФ, координата yp - ее аргументу по оси РЧП ДДККФ, а координата zp - значению ДДККФ для точки р, тогда их координаты и квадраты их координат можно объединить в Р-мерные векторы-столбцы
, каждая с координатами (xp,yp,zp)Т где, согласно принятым выше обозначениям, координата xp точки р соответствует ее аргументу по оси РВП ДДККФ, координата yp - ее аргументу по оси РЧП ДДККФ, а координата zp - значению ДДККФ для точки р, тогда их координаты и квадраты их координат можно объединить в Р-мерные векторы-столбцы
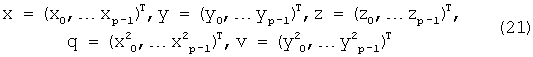
которые аналогично вектору hT объединяются в матрицу Н
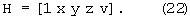 .
.
Сформированная на основе матрицы Н система уравнений имеет следующее решение:
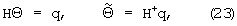
и позволяет, посредством операции псевдообращения матрицы Н [22-24] и умножения псевдообратной матрицы H+ справа на столбец свободных членов q, с учетом соотношений (20), найти уточненные оценки значений РВП τ и РЧП fd. При этом значение уточненной оценки РВП τ, для перехода из области дискретного времени в область непрерывного времени, необходимо разделить на частоту выборки сигнала Fs, а значение уточненной оценки РЧП fd необходимо умножить на величину, равную Fs/N. Последнее очевидно, так как дискретный шаг между точками ДДККФ по оси РВП составляет величину, равную 1/Fs, а по оси РЧП - величину, равную Fs/N.
Различные варианты выполнения операции псевдообращения прямоугольных матриц детально изложены в работах [22-27]. Пример практической реализации операции псевдообращения в широко распространенном пакете прикладных программ MATLAB Release 13 описан в его документации [28, рр.2-91-2-93].
Несмотря на то, что выражение (22) позволяет найти уточненные оценки значений РВП τ и РЧП fd, высокая размерность вектора (20) оцениваемых параметров 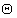 приводит к большой обусловленности матрицы Н [22], обозначаемой как cond(H), и влечет снижение потенциально достижимой точности оценивания уточненных значений РВП τ и РЧП fd.
приводит к большой обусловленности матрицы Н [22], обозначаемой как cond(H), и влечет снижение потенциально достижимой точности оценивания уточненных значений РВП τ и РЧП fd.
Одной из основных особенностей предлагаемого способа является исключение из числа оцениваемых параметров  (20) величин
(20) величин  4,
4,  5, оценка которых не является обязательной для определения координат двумерной кросс-корреляционной функции С12(τ,fd). Сокращение размерности вектора оцениваемых параметров снижает размерность задачи и позволяет улучшить обусловленность системы.
5, оценка которых не является обязательной для определения координат двумерной кросс-корреляционной функции С12(τ,fd). Сокращение размерности вектора оцениваемых параметров снижает размерность задачи и позволяет улучшить обусловленность системы.
К сожалению, нет очевидного решения с уменьшением размерности задачи. Для сокращения размерности вектора оцениваемых параметров произведем ряд преобразований с системами линейных уравнений (19) и (23). При этом разобьем пятистолбцовую матрицу Н на две подматрицы меньшей размерности
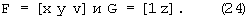
Переопределим вектор оцениваемых параметров следующим образом:
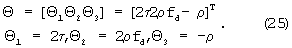
Введем определение вектора мешающих параметров
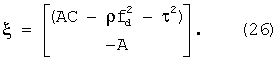
Тогда можно записать систему уравнений, тождественную системе линейных уравнений (23)
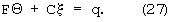
Если систему уравнений (27) умножить слева на проектор [22, 23]
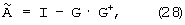
ортогональный пространству, натянутому на столбцы матрицы G [22, 26, 27], такой, что 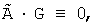 где I - матрица тождественного преобразования [23], то из системы уравнений (27) получится следующая система уравнений:
где I - матрица тождественного преобразования [23], то из системы уравнений (27) получится следующая система уравнений:
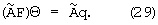
Таким образом, в результате операции проективного преобразования (28) система уравнений (29) является уже системой с тремя неизвестными вместо пяти и ее обусловленность существенно меньше [22] обусловленности системы уравнений (23), что подтверждается результатами вычислительных экспериментов
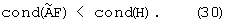
Поэтому потенциально достижимая точность оценивания уточненных значений РВП τ и РЧП fd на основе решения системы уравнений (29) будет выше при условии, что ранг матрицы 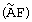 равен трем
равен трем
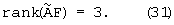
Тогда оценка наименьших квадратов вектора-столбца 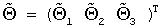 из линейной системы уравнений (28) имеет вид
из линейной системы уравнений (28) имеет вид
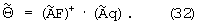
С учетом выражений (25) и с учетом того, что, как и для системы уравнений (29), значение уточненной оценки РВП τ, для перехода из области дискретного времени в область непрерывного времени, необходимо разделить на частоту выборки сигнала Fs, а значение уточненной оценки РЧП fd необходимо умножить на величину, равную Fs/N, окончательные выражения указанных оценок имеют вид
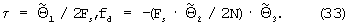
Полученная на основе выведенных здесь преобразований над сигналом последовательность действий и реализует патентуемый способ.
Устройство, реализующее предложенный способ измерения разностей времени прихода и частоты приема сигналов (смотри чертеж), содержит первое средство приема сигналов 1, подключенное к устройству определения аргументов максимума дискретной двумерной кросс-корреляционной функции 2, через последовательно включенные первый АЦП 3, первый процессор БПФ 4, вычислитель кросс-спектров 5 и второй процессор БПФ 6. Выход устройства 2 является выходом устройства измерения. Между вторым средством приема сигналов 7 и вторым входом вычислителя кросс-спектров 5 последовательно включены второй АЦП 8 и третий процессор БПФ 9. Между выходом первого процессора БПФ 4 и третьим входом вычислителя кросс-спектров 5 включено арифметическое устройство 10.
Предлагаемое устройство работает следующим образом. На одной из двух разнесенных приемных позиций принимают сигнал первым средством приема сигналов 1, а на другой из двух разнесенных приемных позиций принимают сигнал вторым средством приема сигналов 7. С выхода первого средства приема сигналов 1 принятый сигнал подают на вход первого АЦП 3 и преобразуют сигнал, полученный от одной приемной позиции, в первый цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени. С выхода второго средства приема сигналов 7 принятый сигнал подают на вход второго АЦП 8 и преобразуют сигнал, полученный от другой приемной позиции, во второй цифровой поток данных, который в цифровой форме представляет сигнал как ряд значений функции времени. В первом процессоре БПФ 4 преобразуют первый цифровой поток данных, полученный с выхода первого АЦП 3, в значения первого спектра, который представляет сигнал как ряд значений функции частоты S1(k). В третьем процессор БПФ 9 преобразуют второй цифровой поток данных, полученный с выхода второго АЦП 8, в значения второго спектра, который представляет сигнал как ряд значений функции частоты S2(k). В вычислителе кросс-спектров 5 взаимно перемножают поступившие по первым двум входам от процессоров БПФ 4 и 9 значения спектра первого сигнала с комплексно сопряженными значениями спектра другого сигнала для порождения кросс-спектра без преобразования частоты сигналов. Кроме этого, в вычислителе кросс-спектров 5 взаимно перемножают поступившие на его третий вход с выхода процессора БПФ 4 через АУ 10 значения множества спектров Si,m(k), полученные в АУ 10 согласно правилу (1) из значений спектра первого сигнала, с комплексно сопряженными значениями спектра другого сигнала для порождения множества кросс-спектров с преобразованием частоты сигналов. После этого второй процессор БПФ 5 вычисляет ДДККФ с использованием обратного БПФ множества кросс-спектров, поступивших на его вход с выхода вычислителя кросс-спектров 5. И, наконец, устройство определения аргументов максимума ДДККФ 2 по поступившей на его вход с выхода второго процессора БПФ 5 функции определяет разности времени прихода и частоты приема сигналов как аргументы максимума ДДККФ и выдает измеренные величины на выходе устройства.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Harcke L. and G. Wood, Laboratory and Flight Performance of the Mars Pathfinder (15, 1/6) Convolutionally Encoded Telemetry Link, TDA PR 42-129, January-March 1997, pp.1-11, May 15, 1997.
2. Rebold Т.А., М. Tinto, S.W. Asmar and E.R. Kursinski, Neptune Revisited: Synthesizing Coherent Doppler From Voyager’s Noncoherent Downlink, TDAPR 42-131, July-September 1997, pp.1-19, November 15, 1997.
3. Кnарр С.Н. and Carter G.С., Estimation of time delay in the presence of source or receiver motion, J. Acoust. Soc. Amer., vol.61, no.6, pp.1545-1549, June 1977.
4. Adams W.В., Kuhn J.P. and Whyland W.P., Correlator compensation requirements for passive time-delay estimation with moving source or receivers, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-28, pp.158-168, Apr.1980.
5. Stuller J. A., Maximum-likelihood estimation of time-varying delay-Part I, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-35, pp. 300-313, Mar. 1987.
6. Jin Q., Wong K.M. and Luo Z.Q.Т., The estimation of time delay and doppler stretch of wideband signals, IEEE Trans. Signal Processing, vol.43, pp.904-916, Apr. 1995.
7. Одуан К., Гино Б., Измерение времени. Основы GPS, M., Техносфера, 2002, 400 с.
8. Jacovitti G. and Scarano G., Discrete time techniques for time delay estimation, IEEE Trans. Signal Processing, vol.41, pp.525-533, Feb. 1993 (аналоги).
9. US Patent №6201499, Hawkes K.D., Koehler J.L., Time difference of arrival measurement system, МПК 7: G 01 S 001/24, March 13, 2001 (аналог).
10. US Patent №5570099, DesJardins G.A., TDOA/FDOA technique for locating a transmitter, МПК 7: G 01 S 003/16; G 01 S 005/04; G 01 S 015/00; G 01 S 003/80, October 29, 1996 (аналог).
11. Japan Patent №7191125, DesJardins G.A., Improved TDOA/FDOA technique for locating a transmitter, МПК 7: G 01 S 5/06, July 28, 1995 (аналог).
12. European Patent №0649033 A2, DesJardins G.A., Improved TDOA/FDOA technique for locating a transmitter, МПК 7: G 01 S 5/06, April 19, 1995 (аналог).
13. Moura Jose M.F., Baggeroer A.B., Passive Systems Theory with Narrow-band and linear Constrraints: Part 1 - Spatial Diversity, IEEE Journal on Ocean Engineering, vol.OE-3, pp.5-13, №1, Jan. 1978.
14. US Patent №5874916, DesJardins G.A., Frequency selective TDOA/FDOA cross-correlation, February 23, 1999 (Способ и устройство-прототип).
15. Радиотехнические цепи и сигналы, - под ред. К.А.Самойло. - М.: “Радио и связь”, 1982.- 528 с.
16. Блейхут Р., Быстрые алгоритмы цифровой обработки сигналов, М., Мир,1989, 448 с.
17. Рабинер Л., Гоулд Б., Теория и применение цифровой обработки сигналов, М., Мир, 1978, 848 с.
18. Оппенгейм A.B., Шафер Р.В., Цифровая обработка сигналов, М., Связь, 1979, 416 с.
19. Бендат Дж., Пирсол А., Прикладной анализ случайных данных, М., Мир,1989, 540 с.
20. Френкс Л., Теория сигналов, М., Сов.радио, 1974, 344 с.
21. Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М., Наука, 1974, 320 с.
22. Альберт А., Регрессия, псевдоинверсия, рекуррентное оценивание, М., Наука, 1977, 223 с.
23. Гантмахер Ф.Р., Теория матриц. М., Наука, 1988, 552 с.
24. Кириченко Н.Ф., Лепеха Н.П., Псевдообращение в задачах управления и наблюдения. Автоматика, М., Наука, 1993, №5, с.69-81.
25. Кириченко Н.Ф., Псевдообращение матриц и их рекуррентность в задачах моделирования и управления. Проблемы управления и информатики, М., Наука, 1995, №1, с.114-127.
26. Меуеr C.D., Matrix Analysis and Applied Linear Algebra, SIAM, 2001, 700 р.
27. Кириченко М.Ф., В.Т.Матвiэнко В.Т., Аналiз та синтез керованих систем, Учбовий посiбник, К., ВПЦ “Киiвський унiверситет”, 2000, 53 с.
28. MATLAB Function Reference: Volume 3 P-Z, pp.2-91-2-93, Revised for Version 6.5, Mathworks Inc., 2002, 858 p.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2483318C2 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2476985C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2524843C2 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2476986C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2483319C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ РАДИОПЕРЕДАТЧИКОВ С ИСПОЛЬЗОВАНИЕМ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СИСТЕМ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВАРИАНТЫ) | 2005 |
|
RU2321017C2 |
| СПОСОБ КОМПЬЮТЕРНО-ИНТЕРФЕРОМЕТРИЧЕСКОГО ОБНАРУЖЕНИЯ-ПЕЛЕНГОВАНИЯ СИГНАЛОВ С РАСШИРЕННЫМ СПЕКТРОМ | 2005 |
|
RU2291456C1 |
| Многоканальное устройство для определения координат множества одновременно действующих источников акустических сигналов | 1984 |
|
SU1201753A1 |
| Способ определения плановых координат воздушной цели с помощью многопозиционной радиолокационной системы, встроенной в пространственно-распределенную систему радиопомех | 2023 |
|
RU2810525C1 |
| СПОСОБ ПРОСТРАНСТВЕННОЙ ПОЛЯРИЗАЦИОННО-ЧУВСТВИТЕЛЬНОЙ ЛОКАЛИЗАЦИИ МНОГОЛУЧЕВЫХ РАДИОСИГНАЛОВ | 2008 |
|
RU2385467C1 |
Изобретение относится к радиотехнике и может использоваться для измерения разности времени прихода и разности частоты приема сигналов с разнесенных приемных позиций без привлечения априорной информации о структуре сигнала и о модулирующем сообщении. Технический результат заключается в повышении вычислительной эффективности и в исключении погрешности дискретности. Устройство содержит два средства приема сигналов, устройство определения аргументов максимума дискретной двумерной кросс-корреляционной функции (ДДККФ) сигнала, два аналого-цифровых преобразователя (АЦП), три процессора быстрого преобразования Фурье (БПФ), вычислитель кросс-спектров и арифметическое устройство. Способ основан на вычислении ДДККФ с использованием обратного БПФ множества кросс-спектров, причем спектр одного из сигналов, для порождения указанного множества кросс-спектров, преобразуют посредством переобозначения индексных переменных. 2 н. и 1 з.п. ф-лы, 1 ил.
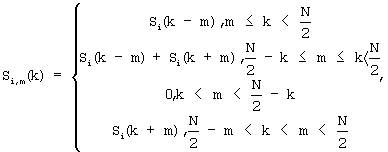
значения спектров Si,m(k) преобразованных по частоте сигналов взаимно перемножают с комплексно сопряженными значениями спектра второго из двух исходных сигналов для порождения множества кросс-спектров.
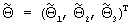 , где надстрочный индекс T обозначает операцию транспонирования матрицы, согласно следующему правилу:
, где надстрочный индекс T обозначает операцию транспонирования матрицы, согласно следующему правилу: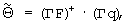
половинное значение первой компоненты вектора 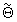 делят на частоту выборки сигнала Fs и получают уточненное значение
делят на частоту выборки сигнала Fs и получают уточненное значение 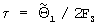 , РВП сигнала, а половинное значение второй компоненты вектора
, РВП сигнала, а половинное значение второй компоненты вектора 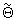 , взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение
, взятой с противоположным знаком, умножают на частоту выборки сигнала и на значение третьей компоненты указанного вектора, делят на размер N обрабатываемого цифрового потока данных и получают уточненное значение 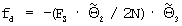 РЧП сигнала.
РЧП сигнала.
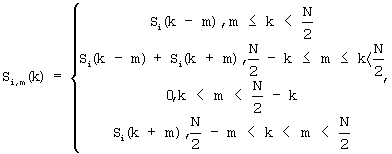
где Si,m(k) - множество преобразованных по частоте на величины m спектров одного из сигналов, N - длина обрабатываемого цифрового потока данных, i - номер одного из двух принимаемых сигналов, k - целочисленная индексная переменная, изменяющаяся в пределах длины данных.
| US 5874916 А, 23.02.1999 | |||
| Способ контроля работы устройства для электростатической записи | 1977 |
|
SU649033A1 |
| ФАЗОВЫЙ ПАРАМЕТРИЧЕСКИЙ ГИДРОЛОКАТОР | 1995 |
|
RU2097785C1 |
| US 6201499 B1, 13.05.2001 | |||
| US 5168459 A, 01.12.1992. | |||
Авторы
Даты
2005-07-10—Публикация
2003-06-30—Подача