Изобретение относится к области вычислительной техники и может быть использовано в модулярных нейрокомпьютерах.
Известно устройство для определения позиционных характеристик непозиционного кода (А.С. RU 1142827, G 06 F 5/20, Бюл. №8 1985 г.), содержащее три входных регистра, два дешифратора, сумматор по модулю и элемент ИЛИ.
Недостатком данного устройства является то, что оно способно определить только одну позиционную характеристику.
Наиболее близким техническим решением к предоставленному является устройство для определения позиционных характеристик непозиционного кода (патент RU №2020756, 5 Н 03 М 7/18 RU), содержащее n входных регистров (n - число оснований системы остаточных классов) и k блоков умножения на константу (k - число рабочих оснований), причем входы остатков числа соединены с входами соответствующих регистров, отличающееся тем, что с целью расширения функциональных возможностей за счет работы устройства в избыточной системе остаточных классов с числами, представленными в прямом и дополнительном кодах, в него введены сумматор по модулю, коммутатор, блок преобразования кода в системе остаточных классов в полиодический код, блок определения знака числа и сумматор, выход которого соединен с выходом позиционного кода числа устройства.
Недостаток этого устройства - низкая скорость преобразования и малое число определяемых непозиционных характеристик.
Цель изобретения - повысить скорость вычисления позиционных характеристик, уменьшить объем оборудования и расширить функциональные возможности устройства, а именно, определение: абсолютных величин числа, переполнения машинного диапазона, определения знака числа и сравнение чисел.
Поставленная цель достигается тем, что устройство содержит три ступени нейронных сетей конечного кольца (НСКК).
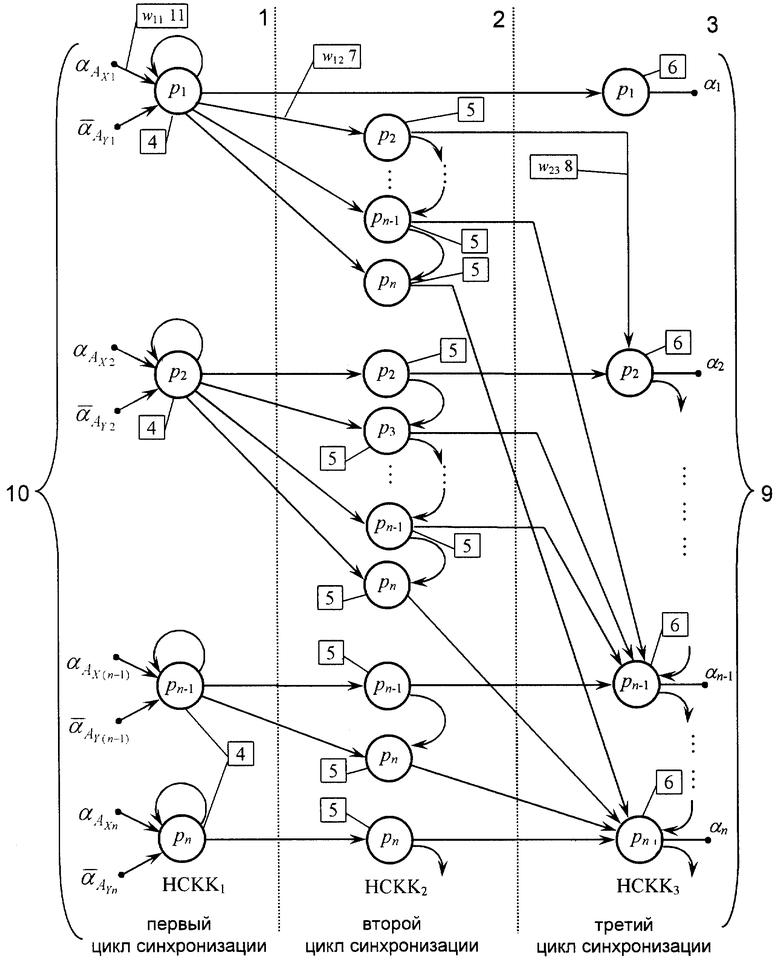
На чертеже представлена структурная схема нейронной сети для вычисления позиционных характеристик непозиционного кода, которая содержит нейронную сеть конечного кольца HCKK1 1 с подсетями по модулям системы остаточных классов 4, НСКК2 2 с подсетями по модулям обобщенной позиционной системы счисления 5, НСКК3 3 с подсетями по модулям обобщенной позиционной системы счисления 6, весовыми коэффициентами между подсетями w11 11, w12 7, w23 8, а также входы 10 и выходы 9.
В настоящее время система остаточных классов (СОК) привлекает все более пристальное внимание из-за ее способности поддерживать высокоскоростную арифметику при параллельной обработке данных. СОК определяется набором модулей рi из относительно простых чисел. Если {p1, p2,... ,pk} - набор модулей pi и наибольший общий делитель (pi, pj)=1, для i, j=1, 2,... k, i≠ j, тогда для целого числа А∈ Zp и Р=p1·p2·...·pk существует единственное представление в СОК
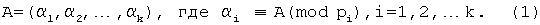
Основными операциями, выполняемыми в СОК (кроме модульных), являются операции немодульного типа. К ним относятся операции вычисления позиционных характеристик. К немодульным операциям относятся операции вычисления абсолютных величин чисел, сравнения между собой чисел, определения знака чисел и переполнения разрядной сетки, а также преобразования чисел из позиционной системы счисления (ПСС) в СОК и обратного преобразования из СОК в ПСС и обобщенную позиционную систему счисления (ОПСС).
Известно, что сравнение величины целых чисел можно осуществить путем вычитания одного числа из другого и определения знака разности чисел.
К сожалению, проблема этим не решается, поскольку разряды числа, представленные в СОК, не несут информации о знаке числа, поэтому для определения знака числа необходимо перейти к определению таких позиционных характеристик, которые бы позволили определить знак числа.
Если дано представление А=(α 1, α 2,... , α k), то для того, чтобы установить знак числа, которое оно представляет, достаточно решить задачу о принадлежности этого числа к той или иной половине диапазона [0, Р], к первой [0, P/2] - число положительное или ко второй [Р/2, Р-1] - число отрицательное. Эта задача решается сравнением данного представления с представлением Р/2 при условии, что рn=2.
С целью повышения скорости вычисления позиционных характеристик рассмотрим способ, основанный на использовании ОПСС. При этом преобразовании выполняются только операции модулярной арифметики по модулю pi. Число в ОПСС представляется в виде
А=a1+a2·р1+а3·р1·р2+... +аn·р1·р2·...·рn-1 (2)
где ai=0÷ рi-1 для i=1, 2,... ,n; an - старший коэффициент числа;
р1, р2,... ,рn - основания ОПСС.
Диапазон представимых чисел равен Р=р1·р2·...·рn. Если принять р1, p2,... ,рn одновременно основаниями СОК и ОПСС, тогда диапазоны представления чисел совпадают.
Представление числа в ОПСС имеет вид
А=[а1,а2,... ,аn], (3)
где аi - коэффициенты ОПСС, 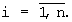
В предлагаемом изобретении преобразование числа из СОК в ОПСС базируется на выражении
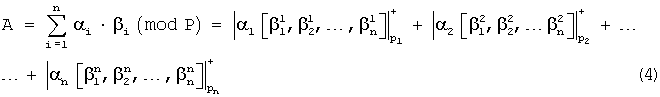
где α i - разряды числа, представленного в СОК; i=1, 2,... , n;
β i=[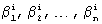 ] - ортогональные базисы, представленные в ОПСС.
] - ортогональные базисы, представленные в ОПСС.
Тогда
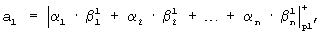
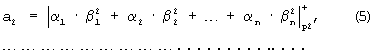
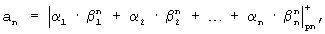
где ai - коэффициенты ОПСС, i=[1, n].
Значение результатов аi образуется путем суммирования по модулю pi всех цифр α i·β i j, j=[1, n] без учета переноса в n-м разряде.
Если выбрать p1>р2>... >рn, а рn=2, тогда старший коэффициент ОПСС an может принимать два значения: 0 или 1. И знак числа будет совпадать со значением старшего коэффициента ОПСС an, т.к. весь диапазон делится на два интервала: первый - [0, Р/2-1] и второй - [P/2, P-1]. Число, которое попадает в первый интервал, будем считать положительным, а во второй интервал - отрицательным, тогда при an=0 - число положительное, а при аn=1 - отрицательное.
Рассмотрим пример сравнения двух чисел, представленных в СОК. Пусть в качестве оснований СОК использованы числа р1=5, p2=3, p3=2, тогда Р=5· 3· 2=30. Ортогональные базисы В1=6, В2=10, В3=15.
Сравним два числа Ax=7=(2, 1, 1), АY=9=(4, 0, 1).
Для сравнения чисел необходимо:
1. Найти разность чисел.
Представим АY в дополнительном коде, тогда 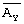 =(p1-4, p2-0, p3-1) =(1,0,1). Операцию вычитания заменим операцией сложения числа, представленного в дополнительном коде, тогда получим Аr=АX+
=(p1-4, p2-0, p3-1) =(1,0,1). Операцию вычитания заменим операцией сложения числа, представленного в дополнительном коде, тогда получим Аr=АX+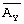 .
.
Ax=(2,1,1)
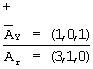
2. Определим знак числа
Представим базисы B1, B2 и В3 в ОПСС, согласно выражению (2):
B1=[1,1,0]; B2=[0,2,0]; B3=[0,0,1].
Согласно (4, 5) вычислим α i·β i, тогда α 1·β 1=3· B1=[3, 0, 1]; α 2·β 2=1· В2=[0, 2, 0]; α 3·β 3=0· B3=0. Найдем старший коэффициент ОПСС Аr=α 1β 1+α 2β 2+α 3β 3, так как α 3β 3=0, то получим
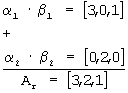
где a1=3, a2=2, a3=1.
Так как старший коэффициент ОПСС а3=1, то знак разности чисел АX и АY равен 1, т.е. число отрицательное, поэтому число АX<АY.
Предложенный параллельный способ определения коэффициентов является универсальным, т.к. он позволяет определять: равенство двух чисел, знак числа, абсолютное значение чисел и переполнение разрядной сетки ЭВМ.
Данный способ является полностью параллельным и позволяет определять позиционные характеристики путем выполнения модульных операций по модулю рi, что выгодно отличает его от известных.
Итак, для выполнения операции сравнения необходимо три цикла синхронизации: В первом цикле синхронизации выполняется операция сложения чисел, во втором цикле синхронизации выполняется операция вычисления αi·βi и в третьем цикле синхронизации вычисляются коэффициенты ОПСС.
Параллельный способ сравнения чисел легко реализуется на нейронных сетях (НС) конечного кольца (НСКК). Если число входов (синаптических весов) нейронов, используемых для организации и функционирования НС, согласованно с числом модулей СОК и ОПСС, то НС становиться натуральным представлением СОК и ОПСС.
Структура нейронной сети для вычисления позиционных характеристик чисел представляет собой многослойную сеть прямого распространения, состоящую из подсетей НСКК 1, 2, 3. На входы 10 НС (нейроны 4) подаются сравниваемые числа АX и АY (в дополнительном коде), представленные в СОК, а на выходе 9 (нейроны 6) формируются коэффициенты ОПСС и знак разности Ах и АY - 0 или 1, в зависимости от величины сравниваемых чисел. Если АX≥АY, то входной сигнал сети равен 0, АX<АY, то выходной сигнал равен 1. При вычислении коэффициентов ОПСС используется только один вход НС.
Процедура сравнения чисел заключается в следующем. На первый слой HCKK1 (нейроны 4) поступают значения остатков сравниваемых чисел 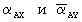 . Синаптические веса w11 11 равны 1. HCKK1 выполняет операцию сложения разрядов чисел
. Синаптические веса w11 11 равны 1. HCKK1 выполняет операцию сложения разрядов чисел 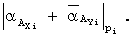 Результат суммирования с выхода HCKK1 (нейроны 4) поступает на входы НСКК2 (нейроны 5). Синаптические веса входов НСКК2 w12 7 определяются выражением (4) и равны bi i для i=1, 2,... ,n. НСКК2 реализует вычислительную модель
Результат суммирования с выхода HCKK1 (нейроны 4) поступает на входы НСКК2 (нейроны 5). Синаптические веса входов НСКК2 w12 7 определяются выражением (4) и равны bi i для i=1, 2,... ,n. НСКК2 реализует вычислительную модель 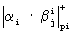 . На выходах НСКК2 (нейроны 5) формируются значения
. На выходах НСКК2 (нейроны 5) формируются значения 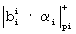 и подаются на входы НСКК3 (нейроны 6), которые с синаптическими весами w23 8, равными 1, реализуют вычислительную модель (5). Выходы 9 НСКК3 (нейроны 6) представляют собой коэффициенты ОПСС в выражении (3). Старший коэффициент an определяет знак разности двух чисел. Если an=0, то AX≥АY, и если аn=1, то АX<AY. При вычислении остальных позиционных характеристик используется только один вход подсети 1 (нейроны 4)
и подаются на входы НСКК3 (нейроны 6), которые с синаптическими весами w23 8, равными 1, реализуют вычислительную модель (5). Выходы 9 НСКК3 (нейроны 6) представляют собой коэффициенты ОПСС в выражении (3). Старший коэффициент an определяет знак разности двух чисел. Если an=0, то AX≥АY, и если аn=1, то АX<AY. При вычислении остальных позиционных характеристик используется только один вход подсети 1 (нейроны 4)
Коэффициенты a1, а2,... ,an используют для определения позиционных характеристик. Важно отметить, что время преобразования определяется тремя циклами синхронизации при сравнении чисел и двумя циклами синхронизации при вычислении других позиционных характеристик при любом количестве модулей СОК.
Рассмотренная параллельная НС идеально подходит к структуре программируемых логических интегральных схем (ПЛИС) типа Xilinx. Большая интеграция позволяет реализовать параллельно работающие нейроны, которые отождествлены с модулями СОК. При этом обмен данными между нейронами осуществляется внутри такой ПЛИС с высокой скоростью.
Предложенный новый параллельный способ и его нейросетевая реализация могут быть применены для преобразования из остаточного представления в двоичное, определения переполнения диапазона, знака числа, сравнения чисел, а также для вычисления пороговой функции активации в динамических нейронных сетях, что открывает новые перспективы, которые ранее было сложно осуществить при создании специализированных процессоров, быстрых адаптивных цифровых фильтров и отказоустойчивых вычислительных структур.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ НЕЙРОКОМПЬЮТЕРАХ | 2003 |
|
RU2256213C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
Заявленное изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах. Техническим результатом является повышение скорости преобразования, уменьшение объема оборудования и расширение функциональных возможностей устройства, а именно, определение: абсолютных величин числа, переполнения машинного диапазона, определения знака числа и сравнение чисел. Для этого сеть содержит три нейронные сети конечного кольца (НСКК), первая нейронная сеть осуществляет операцию сложения разрядов чисел, вторая нейронная сеть осуществляет операцию умножения, а третья нейронная сеть осуществляет определение позиционных характеристик непозиционного входного кода. 1 ил.
Нейронная сеть для вычисления позиционных характеристик непозиционного кода, содержащая три нейронные сети конечного кольца, каждая из которых включает n подсетей (n - число модулей системы остаточных классов), первая нейронная сеть выполняет операцию сложения разрядов
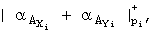 ,
,
где 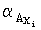 - i-й разряд исходного числа Ах в прямом коде;
- i-й разряд исходного числа Ах в прямом коде;
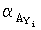 - i-й разряд исходного числа Аy в дополнительном коде,
- i-й разряд исходного числа Аy в дополнительном коде,
вторая нейронная сеть реализует вычислительную модель
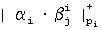
с учетом переноса между разрядами, кроме старшего разряда, перенос которого игнорируется,
где 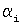 - i-й разряд числа, представленного в СОК;
- i-й разряд числа, представленного в СОК;
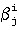 - j-й разряд ортогонального базиса, представленного в обобщенной позиционной системе счисления по основанию pi,
- j-й разряд ортогонального базиса, представленного в обобщенной позиционной системе счисления по основанию pi,
третья нейронная сеть конечного кольца реализует математическую модель
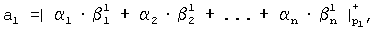
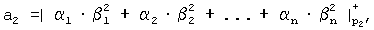
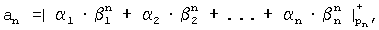
где 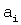 – коэффициенты обобщенной позиционной системы счисления, с учетом переноса между разрядами, кроме старшего разряда, перенос которого игнорируется, i = [1, n], отличающаяся тем, что в ней выходы первой нейронной сети соединены с входом второй нейронной сети, выходы которой соединены с входом третьей нейронной сети для вычисления позиционных характеристик непозиционного входного кода.
– коэффициенты обобщенной позиционной системы счисления, с учетом переноса между разрядами, кроме старшего разряда, перенос которого игнорируется, i = [1, n], отличающаяся тем, что в ней выходы первой нейронной сети соединены с входом второй нейронной сети, выходы которой соединены с входом третьей нейронной сети для вычисления позиционных характеристик непозиционного входного кода.
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 1991 |
|
RU2020756C1 |
| Устройство для определения позиционных признаков непозиционного кода | 1983 |
|
SU1142827A1 |
| SU 1488968 A1, 23.06.1989 | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| КЛЕЙ-РАСПЛАВ | 0 |
|
SU357212A1 |
| US 4825401 A, 25.04.1989. | |||
Авторы
Даты
2005-07-27—Публикация
2003-06-24—Подача