Изобретение относится к вычислительным модулярным нейрокомпьютерным системам и предназначено для выполнения операции деления над числами, представленными в системе остаточных классов (СОК).
Известно устройство для деления чисел в системе остаточных классов (Овчаренко Л.А., Лопатин Д.С. Деление числа в модулярном коде на основание системы счисления // Телекоммуникации. - 2002. - №6. - С.7-10), содержащее табличные вычислители, когерентный преобразователь модулярного кода, устройство отображения и сумматор по модулю.
Недостатком данного устройства является большой объем оборудования и низкая скорость деления чисел.
Наиболее близким к данному изобретению техническим решением является устройство, представленное в виде "Нейронной сети для округления и масштабирования чисел, представленных в системе остаточных классов" (Решение о выдаче патента по заявке №2003115586/09(016529) от 26.05.2003), содержащее входной слой нейронов, нейронную сеть конечного кольца (НСКК) определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n+1, n - нейронных сетей конечного кольца вычисления масштабированного числа.
Недостатком устройства является большой объем оборудования и низкая скорость округления.
Однако такие нейронные сети предназначены для округления и масштабирования чисел, представленных в системе остаточных классов.
Целью данного изобретения является расширение возможностей известной нейронной сети для выполнения операции деления чисел, повышения скорости деления и уменьшения объема оборудования.
Поставленная цель достигается тем, что в нейронную сеть введена нейронная сеть конечного кольца для определения остатка делителя. Таким образом, нейронная сеть для деления чисел, представленных в системе остаточных классов, будет состоять из входного слоя 2 с нейронами 3, нейронной сети для вычисления остатка делителя 4, состоящей из нейронных сетей конечного кольца 5 по модулям СОК р1, р2,...,pn делимого и нейронных сетей конечного кольца 6 по модулю делителя, нейронных сетей конечного кольца 14 для вычисления произведений 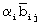 , нейронной сети конечного кольца 11 для выполнения финального шага при выполнении делителя остатка и выходной нейронной сети частного 7, состоящей из НСКК 8.
, нейронной сети конечного кольца 11 для выполнения финального шага при выполнении делителя остатка и выходной нейронной сети частного 7, состоящей из НСКК 8.
Структура нейронной сети зависит от внешних параметров, которые определяются модулями делимого, делителя и частного. Функционирование нейронной сети определяется весовыми коэффициентами, которые являются константами СОК и определяются заранее. Обучение сети не требуется.
Число А представляется в СОК набором наименьших неотрицательных остатков α1,α2,...,αn от деления А на попарно простые числа р1,p2,...,рn, называемые модулями (основаниями). При этом число А записывается в СОК в следующей форме
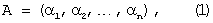
где 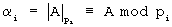 .
.
Число А лежит в пределах - Р≤А<Р, где Р=р1·р2·...·рn.
При выполнении этого условия представление (1) взаимно однозначно с обычным представлением А в позиционной системе счисления, т.е. по (α1,α2,...,αn) можно определить А.
Деление числа в СОК сводится к отбрасыванию от делимого соответствующим образом подобранного остатка, определяющегося делителем. Ниже выводится алгоритм деления числа А на число D с отбрасыванием остатка в предположении, что D либо целое положительное число, попарно простое с p1,р2,...,рn, либо целое положительное число, представляющее собой произведение чисел, попарно простых с p1,р2,...,рn. Алгоритм деления получается, исходя из следующих рассуждений.
Если А делится на D без остатка, то операция деления является модульной операцией и сравнительно просто реализуется на НСКК. Поэтому алгоритм деления в качестве вспомогательной операции включает операцию нахождения числа 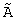 , которое делится на D без остатка. Операция нахождения
, которое делится на D без остатка. Операция нахождения 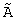 заменяет операцию отбрасывания остатка от деления. При нахождении
заменяет операцию отбрасывания остатка от деления. При нахождении 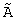 используется алгоритм определения остатка делителя путем расширения системы оснований, где в качестве расширяемого основания используется делитель. Пусть
используется алгоритм определения остатка делителя путем расширения системы оснований, где в качестве расширяемого основания используется делитель. Пусть

Тогда
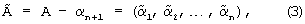
где 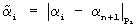 .
.
Из выражения (3) видно, что 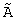 делится без остатка на D.
делится без остатка на D.
Рассмотрим алгоритм определения остатка делителя.
Пусть СОК состоит из оснований р1, р2, ..., рn. Диапазон чисел этой системы будет 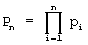 . Добавим к числу оснований СОК делитель D=рn+1. Диапазон этой системы равен
. Добавим к числу оснований СОК делитель D=рn+1. Диапазон этой системы равен 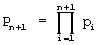 . Тогда любое число А из диапазона [0, Pn+1) в обобщенной позиционной системе счисления (ОПСС) представим как
. Тогда любое число А из диапазона [0, Pn+1) в обобщенной позиционной системе счисления (ОПСС) представим как 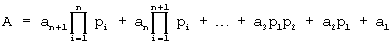 , где аi - коэффициенты обобщенной позиционной системы счисления.
, где аi - коэффициенты обобщенной позиционной системы счисления.
Если число А будет лежать в первоначальном диапазоне [0, Рn), то в обобщенной позиционной системе цифра an+1=0. Этот факт и используется для получения остатка делителя от деления числа А на новое основание СОК рn+1, которое отождествляется с делителем.
Пусть число А имеет представление (α1,α2,...,αn) по основаниям p1,p2,...,рn. Добавим новое основание pn+1=D, тогда число 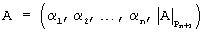 в системе оснований р1,р2,...,рn, D=pn+1, где
в системе оснований р1,р2,...,рn, D=pn+1, где 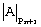 - остаток от деления числа А на рn+1, т.е. искомая цифра по новому основанию, равному делителю D.
- остаток от деления числа А на рn+1, т.е. искомая цифра по новому основанию, равному делителю D.
Для определения этой цифры используется метод перевода числа из СОК в ОПСС, включая неизвестную цифру 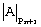 в проводимые операции. При этом мы параллельно получаем цифры в ОПСС a1,a2,...,аn и выражение для цифры an+1=0. Из полученных соотношений и определяем остаток числа по модулю делителя
в проводимые операции. При этом мы параллельно получаем цифры в ОПСС a1,a2,...,аn и выражение для цифры an+1=0. Из полученных соотношений и определяем остаток числа по модулю делителя 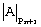 .
.
Расширим число А в системе оснований р1,р2,...,рn, рn+1, тогда
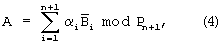
где 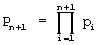 - диапазон расширенной системы оснований,
- диапазон расширенной системы оснований,
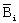 - ортогональные базисы расширенной системы оснований.
- ортогональные базисы расширенной системы оснований.
Представим ортогональные базисы 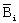 в обобщенной позиционной системе счисления, тогда
в обобщенной позиционной системе счисления, тогда

где 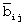 - коэффициенты ОПСС; i,j=1,2,...,n.
- коэффициенты ОПСС; i,j=1,2,...,n.
На основании (5) запишем выражение (4) в виде
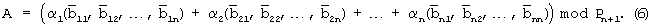
Из выражения (6) можно определить коэффициенты обобщенной позиционной системы счисления аi числа А, тогда
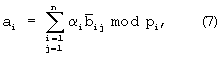
где αi - вычеты числа А по рi;
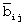 - ортогональные базисы, представленные в ОПСС.
- ортогональные базисы, представленные в ОПСС.
Цифра аi в представлении ОПСС получается суммированием по модулю pi всех произведений 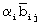 и переносом, генерируемым при формировании ai-1. Перенос генерируется как число раз, когда сумма цифр в ОПСС переполняется по модулю pi. Этот перенос используется для формирования цифр ai+1. Последний перенос, генерируемый при получении последней цифры числа в ОПСС, отбрасывается. Рассмотренный метод выполняется в параллельном режиме. Цифры αi,
и переносом, генерируемым при формировании ai-1. Перенос генерируется как число раз, когда сумма цифр в ОПСС переполняется по модулю pi. Этот перенос используется для формирования цифр ai+1. Последний перенос, генерируемый при получении последней цифры числа в ОПСС, отбрасывается. Рассмотренный метод выполняется в параллельном режиме. Цифры αi, 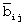 принимают от 0 до pi-1, причем
принимают от 0 до pi-1, причем 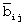 являются константами, поэтому произведение
являются константами, поэтому произведение 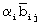 можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений
можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений 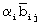 являются вычеты αi числа А по модулю pi.
являются вычеты αi числа А по модулю pi.
Для иллюстрации определения констант приведем пример 1.
Пример 1. Пусть p1=2, p2=3, p3=5, D=7, Рn+1=2·3·5·7=210, B1=105, B2=70, В3=126, B4=120.
Далее на основании (5) определим 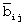 :
:
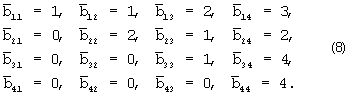
Пример 2. Пусть задана система модулей р1=2, р2=3, р3=5, тогда Рn=2·3·5=30. И пусть задано число X=23=(1, 2, 3). Расширим систему оснований, где в качестве рn+1 возьмем делитель D=7. Необходимо определить остаток по основанию, равному делителю.
Пусть X=23=(1, 2, 3, |A|7) в системе оснований р1=2, р2=3, р3=5, р4=D=7.
Воспользуемся константами 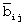 , приведенными в (8), которые заданы матрицей
, приведенными в (8), которые заданы матрицей
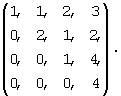
Процесс решения задачи приведем в таблице 1.
Так как 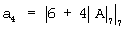 , но по условию a4=0, т.е. 4|A|7=-6 или
, но по условию a4=0, т.е. 4|A|7=-6 или 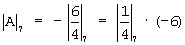 . Мультипликативная обратная величина
. Мультипликативная обратная величина 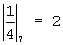 , и так как число 6 отрицательное, возьмем его дополнение по модулю 7.
, и так как число 6 отрицательное, возьмем его дополнение по модулю 7.
Итак, вычет числа А по модулю p4=D=7 определяется выражением |A|7=2·(7-6)=2.
Так как результат образования цифры в СОК по новому основанию pn+1=D зависит только от первых цифр, то операцию определения вычетов можно проводить сразу по нескольким делителям, попарно простым с основаниями СОК.
Преимущество предложенного метода определения вычетов исходного числа по нескольким делителям состоит в том, что:
- все вычисления выполняются в параллельных каналах по отдельным модулям;
- не требуется вычисления большого количества дополнительных величин, необходимо только наличие констант  и мультипликативных величин по расширенным основаниям;
и мультипликативных величин по расширенным основаниям;
- возможно получение расширенного представления вычетов числа сразу по нескольким дополнительным основаниям, что не влияет на быстродействие всей операции расширения.
На основании проведенных расширений алгоритм деления числа А на число D с отбрасыванием остатка можно представить как последовательность следующих операций:
определение αn+1 на основе вычислительной модели (7);
вычисление 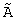 на основе вычислительной модели (3);
на основе вычислительной модели (3);
нахождение частного от деления 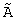 на D
на D
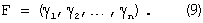
Эта операция представляет собой совокупность модульных операций, реализующих выражение
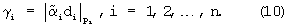
В случае, если pi - простые числа
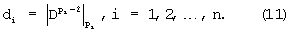
Величины d1,d2,...,dn не зависят от А и они вычисляются заранее по заданному D, т.е. числа d1,d2,...,dn являются константами операции. Алгоритм деления числа А на число D, являющееся произведением чисел, попарно простых с р1,р2,...,рn, может быть представлен как последовательность алгоритмов деления числа на числа, попарно простые с p1,p2,...,pn.
Пример 3. Пусть задана система оснований, как в примере 1. Требуется число А=(1, 2, 3) разделить на D=7.
В примере 2 вычислен остаток по модулю D и он равен α4=2.
После этого вычисляются 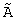 по формуле (3)
по формуле (3)
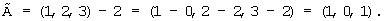
Далее вычисляем по формуле (11) d1=|70|2=1, d2=|71|3=1 и d3=|73|5=3.
Наконец, по формуле (10) вычисляем частное F=(|1·1|2, |1·0|3, |1·3|5)=(1, 0, 3).
Нетрудно проверить, что F=23:7≈3→(1, 0, 3).
Предложенный алгоритм деления отличается от известного тем, что его реализация полностью состоит из модульных операций по модулю pi и его можно легко реализовать нейронными сетями конечного кольца.
На чертеже представлена схема нейронной сети для деления чисел, представленных в СОК.
Принцип работы данного изобретения излагается ниже.
Нейронная сеть, приведенная на чертеже, позволяет выполнять операции деления исходного числа (α1,α2,...,αn) 1 на число D, соответствующее расширяемому модулю pn+1.
Остатки делимого (α1,α2,...,αn) 1 по системе оснований р1,р2,...,рn поступают на вход нейронов 3 входного слоя 2, остаток делителя с учетом переносов 10 формируется нейронной сетью 4, состоящей из НСКК 5, 6, 14, финальный шаг которого вычисляется НСКК 11, а результат (частное) в остатках появляется на выходе нейронной сети частного 7, выходы 9.
С выходов нейронов 3 входного слоя 2 остатки делимого (α1,α2,...,αn) по модулям р1,р2,...,рn поступают на вход нейронной сети 4, состоящей из НСКК 5, 6, по соответствующим модулям. Весовые коэффициенты 12 нейронов НСКК 5, 6, выполняющие роль распределенной памяти, определяются значениями  . НСКК 5, 6 вычисляют значение
. НСКК 5, 6 вычисляют значение 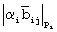 с учетом переносов 10. Выходные значения НСКК 5, 6 с весовыми коэффициентами 13, равными 1, подаются на вход НСКК 14 для выполнения суммирования значений
с учетом переносов 10. Выходные значения НСКК 5, 6 с весовыми коэффициентами 13, равными 1, подаются на вход НСКК 14 для выполнения суммирования значений 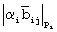 .
.
Результаты суммирования с выхода НСКК 14 по модулю D (делителя), соответствующему остатку делителя, в дополнительном коде подаются на вход нейронной сети НСКК 11 для выполнения финального шага, весовой коэффициент которого 15 определяется мультипликативной величиной 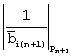 . На выходе НСКК 11 формируется остаток делителя, равный
. На выходе НСКК 11 формируется остаток делителя, равный 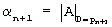 , который поступает на первые входы нейронной сети 7 НСКК 8. На вторые входы НСКК 8 с входного слоя поступают остатки делимого α1,α2,...,αn. Весовые коэффициенты 16 НСКК 8 определяются выражением
, который поступает на первые входы нейронной сети 7 НСКК 8. На вторые входы НСКК 8 с входного слоя поступают остатки делимого α1,α2,...,αn. Весовые коэффициенты 16 НСКК 8 определяются выражением 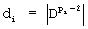 , где i=1,2,...,n. Используя распределительный закон алгебры, выходные НСКК 8 реализуют вычислительную модель
, где i=1,2,...,n. Используя распределительный закон алгебры, выходные НСКК 8 реализуют вычислительную модель 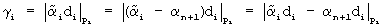 , на выходах которой формируется частное 9.
, на выходах которой формируется частное 9.
Время деления числа определяется двумя циклами синхронизации: один цикл для формирования остатка делителя и один цикл для формирования частного.
Работа выполнена по гранту А 04-2.8-755.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОКРУГЛЕНИЯ И МАСШТАБИРОВАНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271570C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах для быстрого деления чисел, представленных в системе остаточных классов. Техническим результатом является повышение скорости выполнения операции деления, а также сокращение оборудования. Указанный результат достигается за счет того, что нейронная сеть содержит входной слой, нейронные сети конечного кольца для определения остатка делителя и нейронные сети конечного кольца для вычисления частного от деления двух чисел. 1 табл., 1 ил.
Нейронная сеть для деления чисел, представленных в системе остаточных классов, содержащая входной слой нейронов, выходы которых разветвлены на входы нейронных сетей конечного кольца, входящих в состав выходной нейронной сети частного и на входы нейронных сетей конечного кольца по модулям р1,р2,...рn,рn+1, входящих в состав нейронной сети для вычисления остатка делителя, которая реализует вычислительную модель αn+1=|A|D, где А - исходное число, представленное в системе остаточных классов, D - делитель, D=рn+1, отличающаяся тем, что в нейронную сеть для вычисления остатка делителя введены нейронная сеть конечного кольца для вычисления суммы произведений 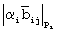 , где αi - остатки исходного числа А по модулю рi,
, где αi - остатки исходного числа А по модулю рi, 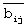 - ортогональные базисы, представленные в обобщенной позиционной системе счисления, i,j=1,2,...n, и нейронная сеть конечного кольца с весовым коэффициентом, равным обратной мультипликативной величине
- ортогональные базисы, представленные в обобщенной позиционной системе счисления, i,j=1,2,...n, и нейронная сеть конечного кольца с весовым коэффициентом, равным обратной мультипликативной величине 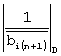 для выполнения финального шага при вычислении остатка от делителя, вход которой соединен с инверсным выходом нейронной сети конечного кольца для вычисления суммы произведений
для выполнения финального шага при вычислении остатка от делителя, вход которой соединен с инверсным выходом нейронной сети конечного кольца для вычисления суммы произведений 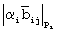 по модулю делителя D, на вход которой подаются значения
по модулю делителя D, на вход которой подаются значения 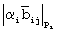 с выходов нейронных сетей конечного кольца по модулям р1,р2,...рn,рn+1, выход нейронной сети конечного кольца для выполнения финального шага при вычислении остатка от делителя соединен с первыми входами нейронных сетей конечного кольца, входящих в состав выходной нейронной сети частного, на вторые входы которых поступают остатки исходного числа по модулям р1,р2,...рn, которая реализует вычислительную модель
с выходов нейронных сетей конечного кольца по модулям р1,р2,...рn,рn+1, выход нейронной сети конечного кольца для выполнения финального шага при вычислении остатка от делителя соединен с первыми входами нейронных сетей конечного кольца, входящих в состав выходной нейронной сети частного, на вторые входы которых поступают остатки исходного числа по модулям р1,р2,...рn, которая реализует вычислительную модель 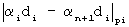 , где
, где 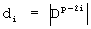 , причем di являются константами операции, вычисляемыми заранее по заданному делителю D и не зависящими от исходного числа А, на выходной нейронной сети частного получают результат от деления исходного числа на заданный делитель.
, причем di являются константами операции, вычисляемыми заранее по заданному делителю D и не зависящими от исходного числа А, на выходной нейронной сети частного получают результат от деления исходного числа на заданный делитель.
| RU 2003115586 А, 27.11.2004 | |||
| Устройство для деления чисел в системе остаточных классов | 1985 |
|
SU1287152A1 |
| Устройство для деления в системе остаточных классов | 1983 |
|
SU1141400A1 |
| US 5155699 A, 13.10.1992. | |||
Авторы
Даты
2007-08-27—Публикация
2005-05-11—Подача