Изобретение относится к вычислительной технике, и в частности к модулярным нейрокомпьютерным средствам, и предназначено для выполнения операции масштабирования модулярных чисел, т.е. чисел, представленных в системе остаточных классов (СОК).
Известно устройство для округления чисел в системе остаточных классов (АС СССР №398949, кл. G06F 7/52, 1973 г.), содержащее входной регистр, блоки хранения констант, сумматоры констант по основаниям рабочего и дополнительного диапазонов, блоки вычисления неточных рангов и блок коррекции округления.
Недостатком данного устройства является большой объем оборудования, низкая скорость округления и ограниченная функциональная возможность.
Наиболее близким к данному изобретению техническим решением является нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов, содержащая входной слой нейронов, нейронную сеть конечного кольца определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n-l, нейронную сеть конечного кольца вычисления разности чисел между входными остатками и остатками по основанию n+1, n-нейронных сетей конечного кольца вычисления масштабированного числа.
Недостатком устройства является большой объем оборудования, ограниченная функциональная возможность, которая заключается в том, что масштабирование модулярных чисел реализуется только для случая, если коэффициент масштабирования модулярных чисел равен одному из модулей системы остаточных классов. Однако на практике требуется чтобы коэффициент масштабирования был равен произведению модулей.
В данном изобретении предлагается использовать коэффициент масштаба, равный произведению нескольких множителей.
Целью изобретения является уменьшение объема оборудования, повышение скорости масштабирования чисел и расширение функциональных возможностей.
Поставленная цель достигается тем, что нейронная сеть ускоренного масштабирования модулярных чисел содержит входной слой 2 с нейронами 3, нейронные сети конечного кольца (НСКК) по модулям СОК 4 и НСКК 5 по модулю разности чисел ΔС(A)=рi-pj. Структура НСКК зависит от внешних параметров, которые определяются модулями СОК. Функционирование нейронной сети ускоренного масштабирования модулярных чисел определяется структурой НСКК по модулям СОК, весовыми коэффициентами и выходным значением НСКК по модулю разности чисел. НСКК обучается путем установки весовых коэффициентов, которые являются константами и определяется выбранными модулями СОК, поэтому режим классического обучения сети не используется.
Известен ряд алгоритмов для масштабирования чисел СОК. Ранние попытки масштабирования разбиваются на две категории: масштабирование одним модулем, подразумевающее, что число СОК подвергается делению на один из модулей или масштабирование на произведение модулей, при этом процесс масштабирования происходит итерационно. Тем не менее, эти методы являются медленными и требуют обработки чисел с большей длиной слова вне СОК.
Метод ускоренного приблизительного масштабирования чисел на произведение модулей СОК с модулями рi и динамическим диапазоном 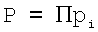 основан на применении в качестве масштабного коэффициента подмножества
основан на применении в качестве масштабного коэффициента подмножества 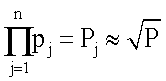 .
.
Если задан ряд положительных целых чисел р1, р2, …, рn, называемых в дальнейшем основанием системы, то под системой счисления в остаточных классах будем понимать такую систему, в которой целое положительное число представляется в виде набора остатков (вычетов) по выбранным основаниям
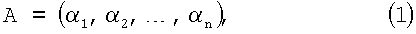
причем образование цифр осуществляется следующим процессом
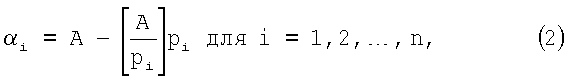
то есть цифра i-го разряда αi числа А есть наименьший неотрицательный остаток от деления А на рi.
Объем диапазона представимых чисел определяется
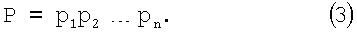
Для обратного перевода используется метод, основанный на применении ортогональных базисов, при этом число А представляются в виде
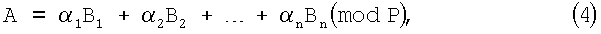
где Bi ортогональные базисы СОК и могут быть представлены в виде
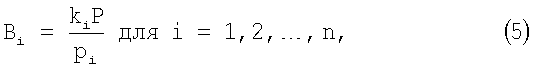
где ki целое положительное число, которое называется весом ортогонального базиса.
Причем ki должно выбираться таким образом, чтобы имело место следующее сравнение
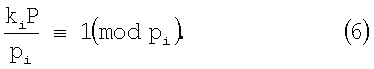
Для вычисления ki необходимо найти 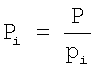 .
.
Так как Рi составлено из Рi множителей взаимно простых чисел с рi, то Рi не будет нацело делиться на рi, в результате деления получим некоторый остаток, который обозначим через δi. Тогда в соответствии с (6) ki определяется как решение сравнения
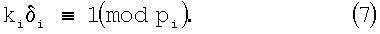
Ввиду сравнительной малости величин оснований для набора модулей рi составлены таблицы решений сравнений (7), в которых по величине δi находится соответствующее ki.
Рассмотрим метод масштабирования чисел СОК, основанный на центральной функции. Метод состоит из выведения центра внутри СОК, при этом все вычисления сокращаются до результатов внутри модулей СОК.
Масштабирование числа СОК на основе китайской теоремы об остатках
Введено понятие центральной функции, которая определяется для целого А как
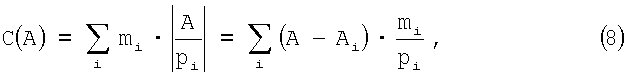
где Аi обозначает А по модулю рi, а mi обозначает i-ый вес (значение).
Полагая Аn=Р в (8), получим

Разделив левую и правую части на Р, получим
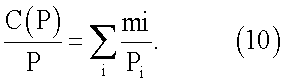
Для получения небольших значений С(P) необходимо, чтобы некоторые значения mi были отрицательными. Подставляя (10) в (8), получим
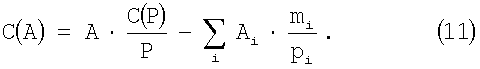
Значения mi можно определить выражением (10), если взять обе стороны по модулю рj
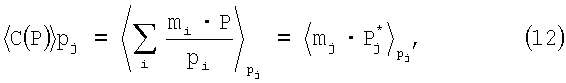
где 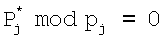 для всех pi за исключением pj. Из (12) определим
для всех pi за исключением pj. Из (12) определим
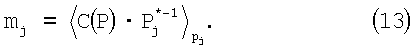
При выбранных значениях С(Р) некоторые mj могут быть отрицательными, что обеспечивает С(Р)<<Р. Заметим, что если С(Р) является составной рj, то соответствующее значение mj=0. Область центральной функции G(P) определяется как
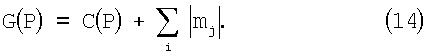
Теперь Китайская теорема об остатках для преобразования чисел СОК обратно в позиционные (то есть десятичные или двоичные) может быть выражена как
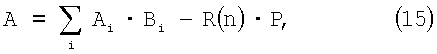
где R(n) известна как функция ранга, а Bi, обозначает i-ый базис СОК, тогда
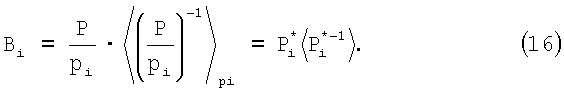
Подстановка (15) в (11) дает
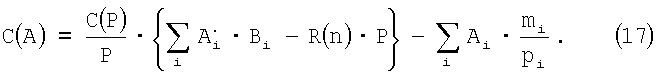
Упрощение и реконструкция (17) дает
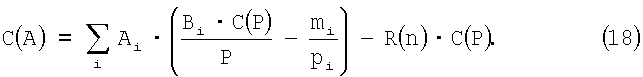
Устанавливая A=Вi в (11), получаем
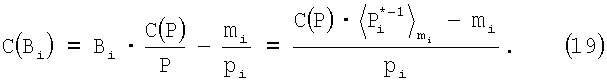
Откуда
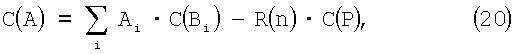
которое известно как Китайская теорема об остатках центральной функции. Тем не менее, вследствие невыполнимости вычисления R(n) независимо, предпочтительная форма теоремы об остатках центральной функции выглядит как
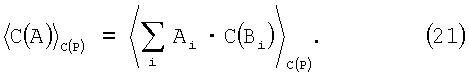
Пример. Рассмотрим СОК с набором модулей pi={2,3,5,7,11,13}, тогда Р=30,030, а Рi={1,2,1,6,6,3}. Далее выберем С(Р)=3·5·11=165. Затем из (13) вычислим значения mi:
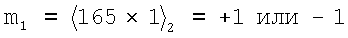
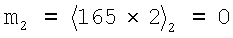

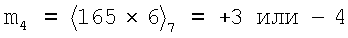
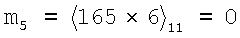

Для минимизации центральной функции необходимо выбрать значения mi с небольшими размерами. В этом примере выберем набор значений mi={-1,0,0,3,0,1}, а его правомерность можно проверить выражением (9)
С(Р)=-1×15015+3×4290+1×2310=165.
Альтернативная установка значений mi={1,0,0,-4,0,1} также возможна, правомерность которой определяется как
С(Р)=1×15015+-4×4290+1×2310=165
Метод приблизительного масштабирования модулярных чисел
Метод приблизительного масштабирования определяется в пределах представления СОК, не выходя в другие формы представления (позиционные или обобщенные позиционные системы счисления).
Из равенства (11) видно, что С(A) можно вычислить внутри СОК, что и определяет приблизительную масштабную версию А
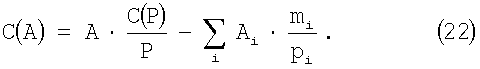
Это достигается разделением набора модулей на два подмножества наборов, которые определяют Рj и Рk так, что PjPk=P и Pj|Pk≈1. Затем можно выполнить масштабирование с помощью Рj или Рk (другими словами, извлечение С(А) из С(Р)=Рj или С(Р)=Рk).
Сначала установим 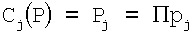 . Затем из (22) находим
. Затем из (22) находим
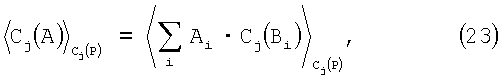
для набора модулей рj, который создал Рj. Но Рj это составляющая Сj(Р), так что
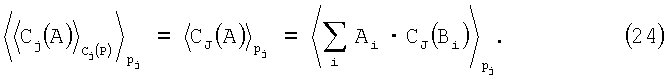
Тем не менее, для набора модулей рk, который образует Рk, не делит PJ, поэтому подобное упрощение невозможно
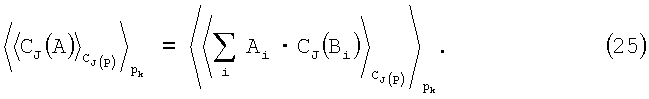
Таким образом, равенство (23) можно вычислить внутри набора модулей рj, но (24) нет. Подобно, если 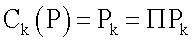
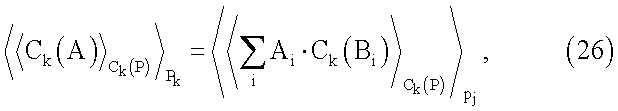
который можно вычислить внутри набора модулей рk. Отсюда 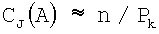 можно вычислить внутри набора модулей рJ, но не набора модулей pk, к тому же
можно вычислить внутри набора модулей рJ, но не набора модулей pk, к тому же 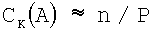 можно вычислить внутри модуля набора модулей рk, но не подстановки рj. Тем не менее, если использовать разницу между центрами ΔС(A)=Сj(А)-СK(A), то можно вычислить СK(А) набора модулей рk, расширяя внутри
можно вычислить внутри модуля набора модулей рk, но не подстановки рj. Тем не менее, если использовать разницу между центрами ΔС(A)=Сj(А)-СK(A), то можно вычислить СK(А) набора модулей рk, расширяя внутри
CJ(А) наборы модулей рk. Другими словами, добавляя ΔС(A) (или вычитая) к значениям одного набора модулей масштабных остатков, доступно СJ(А) или СK(А} по всем остаткам, а масштабное значение А можно получить внутри СОК. Простое выражение для ΔС(A) можно получить из(20) как
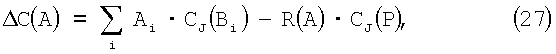
которое можно упростить для практического использования
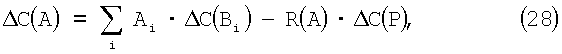
где
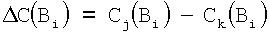 , а
, а 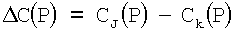 .
.
Из-за сложности определения значения R(A) из остатков лучше использовать выражение (28) в виде
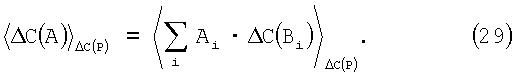
Это выражение очень удобное для оценки ΔС(A), так как оно имеет малый модуль ΔС(Р).
Численный пример и нейросетевая реализация ускоренного масштабирования модулярных чисел
Провести масштабирование числа А=1859107, представленного в системе остаточных классов (СОК) по модулям р1=7, р2=11, p3=13, p4=17, p5=19, p6=23 А=(5,8,3,4,14,17) на число Рj=p1·p4·p6=7·17·23=2737 или Рk=р2·р3·р5=11·13·19=2717, которые представляют подмножество модуля 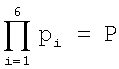 .
.
При этом общий диапазон представления числа в СОК определится как P=p1·p2·p3·p4·p5·p6=7·11·13·17·19·23=7436429, а разность между выбранными подмножествами ΔP(Р)=Рj-Рk=2737-2717=20.
Для нахождения ортогональных базисов Bi (i=1,2,…,n) определим
 и
и 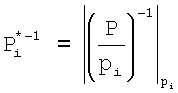 ,
,
тогда значение Pi *=(1062347, 676039, 572033, 437437, 391391, 323323), Рi *-1=(6,1,2,12,2,2), а Bi=(6374282, 676039, 1144066, 5259244, 782782, 646646).
Используя вычислительную модель (13), определим весовые коэффициенты mi для Сj(Р)=Рj и Сk(Р)=Рk.
Для 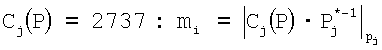 , отсюда mi=(0,-2,1,0,2,0), и для Сk(Р)=2717, mi=(-1,0,0,-2,-6).
, отсюда mi=(0,-2,1,0,2,0), и для Сk(Р)=2717, mi=(-1,0,0,-2,-6).
Теперь выразим Сj, Сk и ΔР(Bi) через ортогональные базисы СОК, тогда на основе  получим
получим
Cj(Bi)=(2346, 249, 421, 1932, 288, 238),
Сk(Bi)=(2329, 247, 418, 1918, 286, 236), ΔP(Bi)=(17, 2, 3, 14, 2, 2).
Выполним масштабирование числа А=(5, 8, 3, 4, 14, 17) с помощью 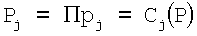 и
и 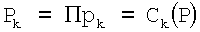 на основе китайской теоремы об остатках, результат которой необходимо взять по модулю рi (i=1,2,…,n), поэтому предварительно представим Рj и Рk по модулям выбранной СОК:
на основе китайской теоремы об остатках, результат которой необходимо взять по модулю рi (i=1,2,…,n), поэтому предварительно представим Рj и Рk по модулям выбранной СОК:
Сj1(Bi)mod7=(1,4,1,0,1,0);
Cj2(Bi)mod17=(0,11,13,11,16,0);
Cj3(Bi)mod23=(0,19,7,0,12,8);
Ck(Bi)mod11=(8,5,0,4,0,5);
Ck(Bi)mod13=(2,0,2,7,0,2);
Ck(Bi)mod19=(11,0,0,18,1,8),
тогда:
Cj(A)mod7=(5·1+8·4+3·1+4·0+14·1+17·0)mod7=5
Cj(A)mod17=(5·0+8·11+3·13+4·11+14·16+17·0)mod17=4
Cj(A)mod23=(5·0+8·19+3·7+4·0+14·12+17·8)mod23=l7
Ck(A)mod11=(5·8+8·5+3·0+4·4+14·0+17·5)mod11=5
Ck(A)mod13=(5·2+8·0+3·2+4·7+14·0+17·2)mod13=0
Ck(A)mod19=(5·11+8·0+3·0+4·18+14·1+17·8)mod19=11
Параллельно вычислим 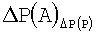 :
:
ΔP(A)mod20=(5·17+8·2+3·3+4·14+14·2+17·2)mod20=8.
Наконец, проведем сложение ΔР(A) с Сk(А), тогда
Cj(A)mod11=Ck(A)+ΔP(A)mod11=5+8=13=2mod11
Cj(A)mod13=Ck(A)+ΔP(A)mod13=0+8=8mod13
Cj(A)mod19=Ck(A)+ΔP(A)mod19=11+8mod19=0.
Итак, значение модулярного числа А=1859107 (или (5,2,8,4,0,17) в СОК формате) после приблизительного масштабирования на число 2717 равно Сj(A)=(5,2,8,4,0,17). Проверим путем обратного преобразования в десятичное, используя китайскую теорему об остатках

Действительно, при приблизительном масштабировании числа А=1859107 на число 2717 получим число  .
.
На чертеже представлена нейронная сеть для ускоренного масштабирования модулярных чисел для шести модулей, используемых в числовом примере. Принцип работы данного изобретения изложен ниже.
Нейронная сеть для ускоренного масштабирования модулярных чисел представляет собой набор n-НСКК 4 по модулям pi, где i=1,2,…,n, и НСКК 5 по модулю разности чисел ΔС(A)=Рj-Pk.
Информация в виде остатков масштабируемого числа А=(α1,α2,α3,α4,α5,α6) 1 поступает на входы НСКК 4 по модулям рi и НСКК 5 по модулю ΔС(A). Выходы НСКК 4 по модулям рi представляют результат масштабирования чисел Аm 6, выходы 7. Разряды (остатки) чисел в реальной схеме представлены в двоичном коде. Для упрощения схемы остатки будем рассматривать в десятичном коде. Весовые коэффициенты ΔС(Bi) 9, Сj(Вi) 10, Ck(Bi) 11 (синаптические веса) НСКК 4, 5 определяются константами выбранной системы остаточных классов и поступают на первые входы умножителей 12, которые представляют собой просмотровые таблицы, выполненные в виде табличных ROM (постоянные запоминающие устройства). Там, где весовые коэффициенты равны 0, входные шины для НСКК 4 не показаны.
Нейронный слой 2 нейроны 3 обеспечивают прием разрядов масштабируемого числа А 1, которые затем поступают на первые (информационные) входы умножителей 12, а на вторые (синаптические) входы умножителей 12 поступают значения весовых коэффициентов 9, 10, 11.
Информационные входы являются адресными входами табличных умножителей, содержимое которых предварительно вычислено и сохранено в просмотровых таблицах соответственно AiCi(Bi), AiCk(Bi) и АiΔC(Bi). Организация просмотровых таблиц определяется двоичным представлением значений модулей pi и ΔС(Р) соответственно l и l' и выражается формулами l=[log pi] и l′=[log ΔC(P)]. Выходные значения умножителей суммируются в HCKKmod7-HCKKmod23 и НСКК ΔР(Вi), где реализуются вычислительные модели (24-26).
Организация и функционирование НСКК приведены в патенте №2279132, опубликованные 10.07.2005, Бюл.19. Финальным шагом является суммирование выходного значения НСКК ΔC(P), в нашем примере НСКК mod20, выход 7, с содержимым НСКК mod11, НСКК mod13 и HCKK mod19. На выходах HCKKmod7-HCKKmod23 формируются значения разрядов масштабированного числа 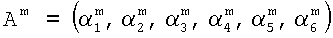 , 6.
, 6.
Время суммирования определяется 0[logn]+1 циклами синхронизации. Заметим, что два соответствующих коэффициента в HCKK mod7 - HCKK mod23 С(Bi)=0, поэтому используется n-2 входов HCKK mod7 - HCKK mod23.
Время масштабирования модулярного числа на произведение модулей в предложенной схеме определяется временем масштабирования на один модуль в известных схемах. Время масштабирования чисел на произведение модулей в известных схемах определяется итерационным методом и линейно зависит от числа модулей, на произведение которых осуществляется масштабирование.
Выше было сказано, что масштабирование модулярных чисел на произведение модулей может быть выполнено в рамках представления чисел в СОК без использования итераций. Этим обеспечивается высокая скорость масштабирования модулярных чисел. Масштабированное число 6 появляется на выходах НСКК mod7 - HCKK mod23, выходы 7.Операция масштабирования на коэффициент масштабирования, равного произведению модулей, выполняется за 3 цикла синхронизации.
В известном изобретении масштабирование осуществляется только на один из модулей, и если их использовать для масштабирования на коэффициент масштаба, равный произведению модулей, то процесс будет итерационным и время масштабирования определяется числом модулей СОК, входящих в масштабный коэффициент. Количество итераций линейно зависит от числа модулей, входящих в масштабный коэффициент, что и отличает это изобретение от известного. Изобретение предназначено для ускоренного масштабирования модулярных чисел в модулярных нейрокомпьютерах.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОКРУГЛЕНИЯ И МАСШТАБИРОВАНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271570C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для выполнения операции масштабирования модулярных чисел. Техническим результатом является уменьшение объема оборудования, повышение быстродействия и расширение функциональных возможностей устройства. Устройство содержит входной слой нейронов, на которые подаются остатки масштабируемого числа А по модулям pi, где i=1, 2, …, n, нейронные сети конечного кольца по модулям pj, нейронные сети конечного кольца по модулям рk, где модули pj и рk являются подмножествами набора модулей рi, разделенных таким образом, чтобы Pj/Pk≈1, где Pj и Рk - произведения модулей указанных подмножеств, нейронную сеть конечного кольца разности по модулю разности чисел ΔC(A)=Pj-Pk, табличные умножители. 1 ил.
Нейронная сеть ускоренного масштабирования модулярных чисел, содержащая входной слой нейронов, на которые подаются остатки масштабируемого числа А по модулям pi, где i=1, 2, …, n, нейронные сети конечного кольца по модулям pj, нейронные сети конечного кольца по модулям рk, где модули pj и рk являются подмножествами набора модулей Pi, разделенных таким образом, чтобы Pj/Pk≈1, где Pj и Рk - произведения модулей указанных подмножеств, нейронную сеть конечного кольца разности по модулю разности чисел ΔC(A)=Pj-Pk, табличные умножители, при этом, выходы нейронов входного слоя соединены с первыми входами табличных умножителей, на вторые входы которых поступают значения весовых коэффициентов Cj(Bi), Ck(Bi) и ΔC(Bi), на выходах табличных умножителей формируются выражения AiCj(Bi), AiCk(Bi) и AiΔC(Bi), которые поступают на первые входы нейронных сетей конечного кольца по модулям pj, pk и ΔС(А) соответственно, реализующих вычислительные модели
 ,
, 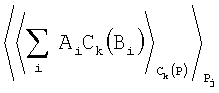 и
и 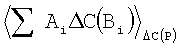 ,
,
вторые входы нейронных сетей по модулям рk соединены с выходом нейронной сети конечного кольца разности по модулю ΔС(А), и реализующие вычислительную модель 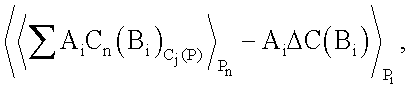 масштабированное число формируется на выходах нейронных сетей конечного кольца по модулям pi.
масштабированное число формируется на выходах нейронных сетей конечного кольца по модулям pi.
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОКРУГЛЕНИЯ И МАСШТАБИРОВАНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271570C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
| УСТРОЙСТВО ДЛЯ МАСШТАБИРОВАНИЯ ЧИСЛА В МОДУЛЯРНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 2002 |
|
RU2246753C2 |
| УСТРОЙСТВО ДЛЯ ОКРУГЛЕНИЯ ЧИСЛА В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 0 |
|
SU398949A1 |
| JP 7129530 A, 19.05.1995 | |||
| US 6243490 A, 05.06.2001. | |||
Авторы
Даты
2009-06-20—Публикация
2007-06-13—Подача