Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах для реализации преобразования кодов.
Известно устройство для преобразования кода из системы остаточных классов в двоичный позиционный код (А.С. 813408, G06F 5/02), содержащее входной регистр, дешифратор, преобразователь кодов из системы остаточных классов в полиадический код, группу элементов ИЛИ, элементы задержки и сумматор. Недостатком устройства является его сложность.
Наиболее близкой по технической сущности к заявленному устройству является нейронная сеть для преобразования остаточного кода в двоичный позиционный код (патент RU 2318238 G06N 3/04, опубликовано 27.02.08, Бюл. №6), содержащая входной слой нейронов, n - нейронных сетей конечного кольца и сумматор.
Недостатком этой нейронной сети является ограниченное функциональное применение: достоверное преобразование из остаточного кода в двоичный позиционный код осуществляется только при правильных значениях всех разрядов остаточного кода.
Целью настоящего изобретения является расширение функциональных возможностей преобразователя остаточного кода в двоичный позиционный код.
Необходимо, чтобы сеть могла правильно преобразовать остаточный код в двоичный при наличии ошибочных разрядах, т.е. без их исправления, что ведет к увеличению скорости преобразования, так как из цикла обнаружения ошибок, их локализации, исправления и преобразования из системы остаточных классов в двоичный код исключается шаг исправления ошибки.
В пороговых (k, t) - схеме множество S делится на m - частей посредством таких алгебраических преобразований, что только по n≤m истинным частям можно восстановить S, где в качестве S используется либо ключ (секрет) в пороговых криптографических схемах, либо обычный кортеж числа, представленного в системе остаточных классов. Данное свойство схемы разделения секрета или кортежа числа дополняется следующим требованиям: если предъявлены k+j=t долей секрета (кортежа), из которых е<j могут отсутствовать или быть ложными (искаженными), то пороговая схема обеспечивает восстановление секрета (кортежа) по подлинным k+j - е частям, что дает возможность контроля над предоставлением полученного результата сторонам с ложными (искаженными) частями секрета (кортежа).
Поставленная цель достигается тем, что в преобразователь введены постоянное запоминающее устройство формирования весовых коэффициентов при реконфигурации нейронных сетей конечного кольца и постоянное запоминающее устройство формирования поправки выходного двоичного кода. Таким образом, нейронная сеть с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код будет состоять из входного слоя нейронных сетей, выполняющих роль регистров, параллельного преобразователя остаточного кода в полиадический, постоянных запоминающих устройств, параллельного взвешенного сумматора (Нейронная сеть для преобразования остаточного кода в двоичный позиционный код, RU, патент 2318238 C1 G06N 3/04), постоянного запоминающего устройства формирования весовых коэффициентов при реконфигурации нейронных сетей конечного кольца и постоянного запоминающего устройства формирования поправки выходного двоичного кода. Функционирование нейронной сети с пороговой (k, t) структурой для преобразования остаточного кода в двоичный рассмотрим на принципе безопасного хранения криптографических ключей, так как функционирование этой сети в случае использования ее для преобразования остаточного кода в двоичный при локализации искаженных разрядов осуществляется аналогично.
Использование криптографического разделения секрета позволяет конструировать ключ из отдельных элементов данных, имеющихся у различных участников или абонентов распределенной вычислительной системы. Секретный ключ восстанавливается путем сбора этих элементов, количество которых достаточно для восстановления исходного ключа.
Принцип разделения секрета основан на применении Китайской теоремы об остатках (КТО).
КТО представляет собой схему разделения секрета без всяких модификаций. Пусть р1,р2,…,рt попарно простые положительные целые числа и 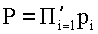 . Рассмотрим теперь КТО для целых чисел относительно этих модулей. Предположим, что мы имеем секрет, который является целым числом s с 0≤s≤Р. Секрет s может быть разделен среди t сторон следующим образом. Пусть р1,р2,…,рt обозначают t сторон, которые собираются разделить секрет. Мы даем рi остаток si=smodpi как секретную информацию, которая известна только рi. КТО t частей информации si является достаточным для определения первоначального секрета s, но любой набор с меньшим чем t числом остатков si не могут определить оригинал s. Это схема разделения секрета, но не пороговая схема.
. Рассмотрим теперь КТО для целых чисел относительно этих модулей. Предположим, что мы имеем секрет, который является целым числом s с 0≤s≤Р. Секрет s может быть разделен среди t сторон следующим образом. Пусть р1,р2,…,рt обозначают t сторон, которые собираются разделить секрет. Мы даем рi остаток si=smodpi как секретную информацию, которая известна только рi. КТО t частей информации si является достаточным для определения первоначального секрета s, но любой набор с меньшим чем t числом остатков si не могут определить оригинал s. Это схема разделения секрета, но не пороговая схема.
(k,t) - Пороговая схема разделения секрета определена следующим образом. Пусть t сторон рi разделяют секрет s со следующими свойствами:
каждая сторона имеет часть si о секрете s, который не известен другой стороне;
секрет s может быть «легко» вычислен из любых k частей si;
k-1 частей si не дают никакой информации о секрете s.
В терминах информационной терминологии вышеупомянутое второе условие означает, что взаимная информация между s и любыми k остатками si является равной самой информации s, то есть 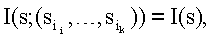 , где 1≤i1<i2<…<ik≤t. Общепринятое определение для требования во втором условии - существование полиномиального алгоритма для вычисления s из любых k частей s1. Вышеупомянутое третье условие говорит о том, что взаимная информация между s и любыми k-1 частями равна нулю, то есть
, где 1≤i1<i2<…<ik≤t. Общепринятое определение для требования во втором условии - существование полиномиального алгоритма для вычисления s из любых k частей s1. Вышеупомянутое третье условие говорит о том, что взаимная информация между s и любыми k-1 частями равна нулю, то есть 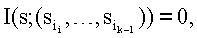 где 1≤i1<i2<…<ik-1≤t.
где 1≤i1<i2<…<ik-1≤t.
Рассмотрим принцип восстановления ключа в пороговых криптосистемах.
Пусть К - ключ, который требуется сохранить в распределенной системе обработки информации, состоит из n компонентов. Под компонентами подразумеваются: аппаратные средства - ЭВМ, программное обеспечение, данные и пользователи. При этом требуется, чтобы любые L пользователей из тех n (n>L), которые получили информацию о ключе, могли бы вместе восстановить ключ, но никакая группа из L - 1 пользователей или менее не могла этого сделать.
Для решения этой задачи сформулируем условия выбора оснований СОК, которые распределены между пользователями криптосистемы. Выберем упорядоченный вектор оснований СОК q<p1<р2<…<рn. Числа рi для i=1,2,…,n взаимно простые, т.е. (рi,pj)=1 для i≠j. Каждому пользователю криптосистемы приписывается свое большое число рi(i=1,2,…n). Выберем q<К такое, что (q,pj)=1 для всех i=1,2,…n. Произведение L наименьших чисел рi, т.е. р1,р2…pL>qpn-L+2pn-L+2…pn. Если R=p1p2…pL, тогда 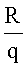 должно быть больше, чем произведение любых
должно быть больше, чем произведение любых
L-1 чисел рi.
Выберем случайное число r в интервале 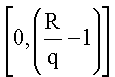 и вычислим К′=К+rq, чтобы K′ попало в интервал [0,R-1]. Для восстановления ключа К пользователю необходима информация в виде r и Кi≡К′ modpi, i=1,2,…n.
и вычислим К′=К+rq, чтобы K′ попало в интервал [0,R-1]. Для восстановления ключа К пользователю необходима информация в виде r и Кi≡К′ modpi, i=1,2,…n.
Центр распределения ключей генерирует по идентификатору, поступившему от любого пользователя, случайное числа r и вычисляет К′. Если один из пользователей сети хочет узнать ключ сеанса связи каких-либо пользователей, то он может получить его на основании r и К′, полученных от центра распределения ключей.
Информация, полученная от центра распределения ключей, должна быть аутентифицирована с помощью его собственного ключа. Передающая и принимающая сторона восстанавливают ключ, который знают только один. Для этой цели центр распределения ключей по запросу пользователя вычисляет и передает числа r и К′, по которому пользователь определяет ключ сеанса связи, используемый только в одном случае.
Пример 1. Для простоты вычислений будем использовать небольшие числа, хотя на практике применяются очень большие числа. Пусть ключ К=9, число пользователей сети L=2, число всех пользователей n=3. Выберем взаимно простые числа q=13, р1=17,
р2=19, р3=23. Проверим условие R=p1p2>qp3=17·19>13·23=323>299, условие выполняется. Выберем случайное число r в интервале 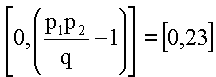 , например r=2. Найдем К′=K+qr=9+2·13=35. Распределяемые числа r и
, например r=2. Найдем К′=K+qr=9+2·13=35. Распределяемые числа r и 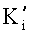 передаются всем пользователям, которые определяются как Ki≡K′I mod pi,i=1,2,…,n. Итак, Кi≡35mod17=1, K2≡35mod19=16, К3≡35mod23=12. По любым двум их этих чисел можно восстановить ключ К, а в общем случае количество выборок
передаются всем пользователям, которые определяются как Ki≡K′I mod pi,i=1,2,…,n. Итак, Кi≡35mod17=1, K2≡35mod19=16, К3≡35mod23=12. По любым двум их этих чисел можно восстановить ключ К, а в общем случае количество выборок 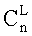 определяется сочетанием из n элементов по L - подмножество мощности L исходного конечного множества мощности n. Число сочетаний из n элементов по L обозначается
определяется сочетанием из n элементов по L - подмножество мощности L исходного конечного множества мощности n. Число сочетаний из n элементов по L обозначается 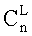 и равно
и равно 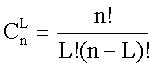 .
.
Например, для K1 и К3 имеем K′1≡1(mod17), K′3≡12(mod17). На основании Китайской теоремы об остатках восстановим К и определим ключ

Используя метод ортогональных базисов, восстановим ключ К. Вначале определим К′≡(К1В1+K1B3)mod(p1p3), где B1 и В3 - ортогональные базисы. По определению ортогональные базисы могут быть представлены в виде: B1=m1p3,B3=m3p1, где m1 и m3 - веса базисов соответственно B1 и B3. Причем m1 и m3 выбираются из сравнений m1p3=1modp1,m3p1=1modp3. Ввиду малости величин оснований решим сравнения путем подбора m1 и m3, m1=3 и m3=19. Тогда В1=3·23=69, В3=19·17=323, K′=1·16+12·323≡394mod391=35. Отсюда K=35-2·13=9. Таким образом, восстановленный ключ К=9.
Недостаток рассмотренного метода заключается в том, что приходится иметь дело с большими числами 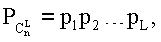 ,где i=[1,L] и, кроме того, действия сложения и умножения надо выполнять в позиционной системе счисления, а полученный результат необходимо вводить в диапазон вычитаемой величины, кратной
,где i=[1,L] и, кроме того, действия сложения и умножения надо выполнять в позиционной системе счисления, а полученный результат необходимо вводить в диапазон вычитаемой величины, кратной  .
.
Кроме того, применение КТО для восстановления числа требует сложных вычислений в модулярном нейрокомпьютере, так как элементарные процессоры выполняют операции по модулю рi, где i=1,2,…n, а не по модулю 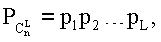 как требуется по КТО.
как требуется по КТО.
Для отображения К' необходимы сумматоры по модулю рi. Эту нежелательную особенность можно обойти при помощи отображения СОК на ассоциированное представление со смешанным основанием, а затем и на двоичное представление. Коэффициенты Кi могут быть представлены с помощью L цифр со смешанными основаниями. Отображение из СОК в обобщенную позиционную систему счисления (ОПСС) может быть определено рекурсивно с помощью операций по малым модулям рi.
Для перехода от вычислений по модулю  к вычислению по модулям рi предлагается метод восстановления чисел на основе совместного использования КТО и ОПСС.
к вычислению по модулям рi предлагается метод восстановления чисел на основе совместного использования КТО и ОПСС.
Пусть задана система оснований p1,p2,…pn с диапазоном Р=p1·p2·…·pn и ортогональными базисами B1, В2,…,Вn, веса которых m1,m2,…,mn, которые определяются как

где mi - веса ортогональных базисов.
Тогда КТО можно представить в виде
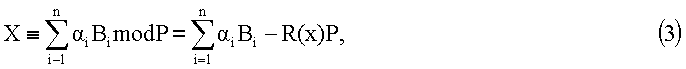
где α - остатки (вычеты) числа Х по mod pi; R(x) - ранг числа.
Представим ортогональные базисы Bi в ОПСС, тогда
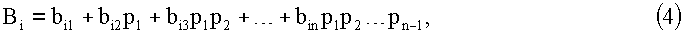
bij- коэффициенты ОПСС; i,j=1,2,…,n.
На основании (4) запишем ХОПСС выражение (3) в виде
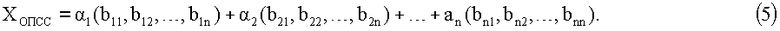
Так как Bi mod pi=0, ∀j>i, то перед первым значащим разрядом будет i-1 нулей.
Для удобства вычислений базисы можно представить в виде матрицы
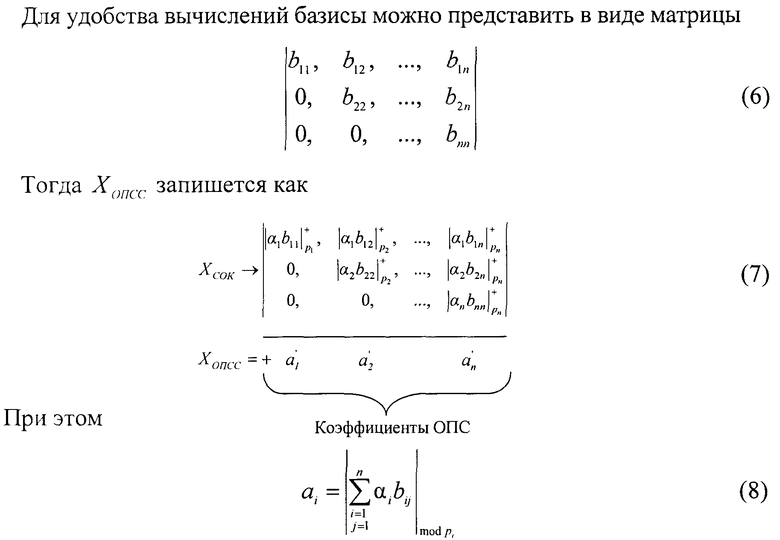
При использовании традиционной вычислительной базы произведения αibij mod pi, можно поместить в память, а адресами будут являться остатки α′1.
Если вычислительная база представлена в нейросетевом базисе, тогда в качестве весовых коэффициентов нейронной сети будут выступать bij, а в качестве входных сигналов - остатки α′i.
Для выборки всех цифр ОПСС требуется две операции: одна операция выборки из памяти и одна операция для суммирования. По сравнению с известным методом Гарнера выигрыш определяется выражением  Для реализации этого метода в нейропроцессоре необходимо иметь средства для выполнения модульных операций, например, нейронные сети конечного кольца по рi основаниям, где i=1,2,…n.
Для реализации этого метода в нейропроцессоре необходимо иметь средства для выполнения модульных операций, например, нейронные сети конечного кольца по рi основаниям, где i=1,2,…n.
Пример 2. Пусть основания системы p1=3, р2=5, р3=7, p4=2. Дано число х=(2,3,0,1), представленное в СОК по выбранным модулям. Найти представление этого числа в ОПСС, то есть х=[α′1,α′2,α′3,α′4]. На основании выражения (5) определим ортогональные базисы СОК: B1=70, В2=126, В3=120, B4=105. Представим базисы Bi в ОПСС, тогда bij:
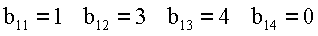
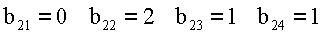
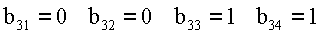
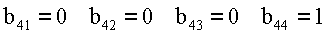
В связи с тем, что константы bij определяются выбором системы
модулей СОК, то их с учетом переноса в i - разрядах можно поместить в память, тогда процесс преобразования можно представить в виде

Для определения всех цифр ОПСС требуются две операции: одна операция для выборки из памяти и одна операция для суммирования. По сравнению с последовательным итерационным процессом выигрыш равен n-1, где n - число модулей СОК.
Полученные значения коэффициентов ОПСС α′i числа х используем для образования двоичного кода.
На чертеже представлена нейронная сеть с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код.
Нейронная сеть с пороговой структурой (k, t) для преобразования остаточного кода в двоичный позиционный код содержит входной слой нейронов 2, n - нейронных сетей конечного кольца (НСКК), n - постоянных запоминающих устройств (ПЗУ) 4, сумматор 5 входной нейронной сети 1, выход нейронной сети 6, весовые коэффициенты w 7, постоянное запоминающее устройство формирования весовых коэффициентов при реконфигурации нейронных сетей конечного кольца 8, постоянное запоминающее устройство поправки выходного двоичного разряда 9, сигнала реконфигурации 10 и сигнала поправки 11.
Блок нейронных сетей конечного кольца (НСКК Pi) вычисляет разрядные цифры в представлении ОПС и состоит из n НСКК. Из чертежа видно, что остаточные числа
К'i (i=1,2,…,n) числа подаются 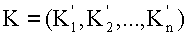 падаются параллельно через входной слой нейронов на входы всех НСКК рi, которые имеют n2 синаптических весов. Подключения синаптических весов на чертеже показаны точками. НСКК pi реализует треугольную матрицу (9) путем сложения цифр в представлении ОПС, описанному выше, т.е. данные в i-канале будут суммироваться с учетом переносов в канале по модулю рi в представлении ОПСС. Перенос представляет собой число раз, превышающее величину модуля рi, который поступает к (i+1) каналу. Поскольку в каждой строке имеется (i-1) нулей перед первым значащим элементом, а сумма чисел может переноситься (n-1) раз, то абсолютная величина каждого переноса ограничивается величиной (n-1)
падаются параллельно через входной слой нейронов на входы всех НСКК рi, которые имеют n2 синаптических весов. Подключения синаптических весов на чертеже показаны точками. НСКК pi реализует треугольную матрицу (9) путем сложения цифр в представлении ОПС, описанному выше, т.е. данные в i-канале будут суммироваться с учетом переносов в канале по модулю рi в представлении ОПСС. Перенос представляет собой число раз, превышающее величину модуля рi, который поступает к (i+1) каналу. Поскольку в каждой строке имеется (i-1) нулей перед первым значащим элементом, а сумма чисел может переноситься (n-1) раз, то абсолютная величина каждого переноса ограничивается величиной (n-1)
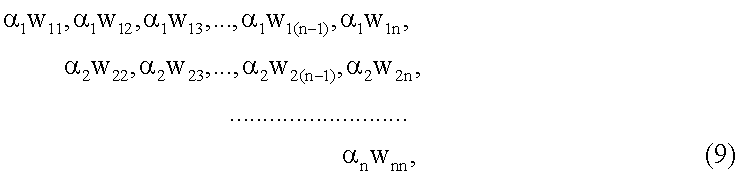
где wij=bij.
Для восстановления ключа, представленного в позиционной системе счисления, используется реконфигурационная структура, которая определяется конфигурацией используемых каналов 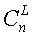 на данной сети. При формировании структуры, когда происходит реконфигурация сети, возникают две задачи: первая задача связана с исключением i-каналов, а вторая - с коррекцией весовых коэффициентов wij. Структура нейронной сети зависит от номеров исключаемых каналов и адаптируется к нему посредством загрузки весовых коэффициентов wij. В то время когда часть сети остается неактивной (исключаемой из системы), весовые коэффициенты между нейронами входного слоя и нейронами скрытого слоя НСКК не используются нейронной сетью и равны нулю. Весовые коэффициенты между нейронами скрытого слоя и нейронами выходного слоя НСКК не активизированных нейронов также равны нулю, а нейроны выходного слоя не активированной части нейронной сети имеют высокое значение (преимущественно ∞), т.е. можно считать, что они исключаются из общей системы.
на данной сети. При формировании структуры, когда происходит реконфигурация сети, возникают две задачи: первая задача связана с исключением i-каналов, а вторая - с коррекцией весовых коэффициентов wij. Структура нейронной сети зависит от номеров исключаемых каналов и адаптируется к нему посредством загрузки весовых коэффициентов wij. В то время когда часть сети остается неактивной (исключаемой из системы), весовые коэффициенты между нейронами входного слоя и нейронами скрытого слоя НСКК не используются нейронной сетью и равны нулю. Весовые коэффициенты между нейронами скрытого слоя и нейронами выходного слоя НСКК не активизированных нейронов также равны нулю, а нейроны выходного слоя не активированной части нейронной сети имеют высокое значение (преимущественно ∞), т.е. можно считать, что они исключаются из общей системы.
Посредством коммутации весовых коэффициентов нейронная сеть осуществляет реконфигурацию системы и ее настройку в соответствии с изменением констант СОК. Определенные активированные части нейронной сети активируют другие части, при этом весовые коэффициенты определены из новых констант СОК. В процессе реконфигурации активные нейроны целенаправленно активируют определенные части нейронной сети, просто и быстро приспосабливаясь к определенным внешним параметрам. Таким образом, в процессе вычисления весовые коэффициенты активированной части нейронной сети адаптируются к требованиям внешних параметров. Исходя из этого вычисления нейронная сеть не содержит каких-либо сложных условий реконфигурации системы и вследствие этого происходит быстрое определение значений величины выбранного варианта сети.
Функционирование нейронной сети зависит от весовых коэффициентов между слоями, которые определяются заранее и хранятся в ПЗУф формирования весовых коэффициентов.
Процесс вычисления коэффициентов ОПСС осуществляется активацией определенных входов НСКК, которые выбраны с помощью весовых коэффициентов. Таким образом, реконфигурация сети осуществляется весовыми коэффициентами нейронных связей на активированных входах нейронной сети.
Весовые коэффициенты определяются заранее и помещаются в ПЗУф формирования весовых коэффициентов при реконфигурации, и в зависимости от поступающих сигналов выдаются необходимые весовые коэффициенты для конкретных вариантов, соответственно определяя структуру нейронной сети, в которой при определенных внешних параметрах достигается надежное и быстрое вычисление двоичного кода ключа.
НСКК pi преобразуют числа 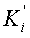 , представленные в остаточном коде в код ОПСС, при этом число представляется в виде, соответствующем ОПСС, следующим образом
, представленные в остаточном коде в код ОПСС, при этом число представляется в виде, соответствующем ОПСС, следующим образом 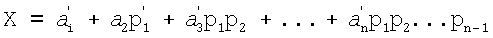 , где
, где 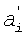 - называется коэффициентом ОПСС, причем 0≤
- называется коэффициентом ОПСС, причем 0≤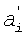 ≤рi. Весовой коэффициент, связанный с каждой цифрой ОПСС
≤рi. Весовой коэффициент, связанный с каждой цифрой ОПСС 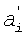 равен p1p2…pi-1. Такая система имеет тот же диапазон представления, что и СОК
равен p1p2…pi-1. Такая система имеет тот же диапазон представления, что и СОК
Р=р1р2…рn. Коэффициенты кода ОПСС являются адресами памяти, где хранятся значения произведений 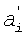 p1p2…pi-1. Двоичные эквиваленты значений
p1p2…pi-1. Двоичные эквиваленты значений 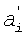 p1p2…pi-1, хранящиеся в памяти, поступают на вход сумматора, где по остаткам восстанавливается двоичное число. Для определения кода ключа на вход сумматора поступает поправка, представляющая произведение чисел - rq, которая формируется ПЗУn, а адресом является число r.
p1p2…pi-1, хранящиеся в памяти, поступают на вход сумматора, где по остаткам восстанавливается двоичное число. Для определения кода ключа на вход сумматора поступает поправка, представляющая произведение чисел - rq, которая формируется ПЗУn, а адресом является число r.
Распределенные числа 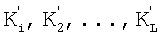 , представленные в СОК своими остатками
, представленные в СОК своими остатками 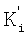 (вход 1), по модулям pi (i=1,2,…,L) поступают на входной слой нейронов 2, а число r 11 поступает на адресные входы ПЗУn. Выбранный вариант реконфигурации
(вход 1), по модулям pi (i=1,2,…,L) поступают на входной слой нейронов 2, а число r 11 поступает на адресные входы ПЗУn. Выбранный вариант реконфигурации 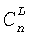 определяется сигналом реконфигурации 10, подаваемым на вход ПЗУф. Входной слой связан с L НСКК. При выбранных модулях СОК структура нейронной сети зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w=wij=bij7, определенных выражением (4, 6). НСККPi i=1,L реализуют вычислительную модель (7), на выходах которых формируются коэффициенты ОПСС
определяется сигналом реконфигурации 10, подаваемым на вход ПЗУф. Входной слой связан с L НСКК. При выбранных модулях СОК структура нейронной сети зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w=wij=bij7, определенных выражением (4, 6). НСККPi i=1,L реализуют вычислительную модель (7), на выходах которых формируются коэффициенты ОПСС 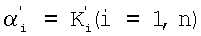 числа х. Коэффициенты
числа х. Коэффициенты 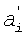 являются входными адресами ПЗУ pi 4, где хранятся двоичные эквиваленты Kip1p2…pi-1. Считанные из ПЗУ pi двоичные коды, соответствующие произведению Kip1p2…pi-1, суммируются взвешенным сумматором 5, на выходе которого формируется двоичный код 6. Время преобразования кода определяется L-тактами синхронизации. Структура преобразователя, реализованная на СБИС, требует n - НСКК по модулям pi, каждое из которых хранит pi слов разрядностью, эквивалентной числу (pi-1)p1p2…pi-1, и одного параллельного сумматора с ускоренным переносом. Сумматор может быть реализован по типу дерева, тогда время преобразования определяется выражением [logn]+1, где n - число модулей СОК.
являются входными адресами ПЗУ pi 4, где хранятся двоичные эквиваленты Kip1p2…pi-1. Считанные из ПЗУ pi двоичные коды, соответствующие произведению Kip1p2…pi-1, суммируются взвешенным сумматором 5, на выходе которого формируется двоичный код 6. Время преобразования кода определяется L-тактами синхронизации. Структура преобразователя, реализованная на СБИС, требует n - НСКК по модулям pi, каждое из которых хранит pi слов разрядностью, эквивалентной числу (pi-1)p1p2…pi-1, и одного параллельного сумматора с ускоренным переносом. Сумматор может быть реализован по типу дерева, тогда время преобразования определяется выражением [logn]+1, где n - число модулей СОК.
Кроме того, на вход сумматора подается число - rq в дополнительном коде, выбранном по адресу r 11 из ПЗУn. Дополнительный код использован для замены операции вычитания операцией сложения при реализации модели (1).
Рассмотрим числовую интерпретацию примера 1, реализованную архитектурой, приведенной на чертеже. Число всех пользователей n=3, а число пользователей сети
L=1. При этом распределяемые числа 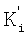 поступают на вход нейронов входного слоя, а r - на вход ПЗУn в качестве адресных входов. На вход ПЗУф поступает сигнал реконфигурации. В соответствии с
поступают на вход нейронов входного слоя, а r - на вход ПЗУn в качестве адресных входов. На вход ПЗУф поступает сигнал реконфигурации. В соответствии с 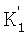 =1,
=1, 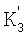 =12 ПЗУф осуществляет конфигурацию нейронной сети путем подачи соответствующих весовых коэффициентов, которые определяются на основе значений
=12 ПЗУф осуществляет конфигурацию нейронной сети путем подачи соответствующих весовых коэффициентов, которые определяются на основе значений 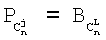 , где L=2,3,…, n-1; j∈{2,3,…,L}; L⊂n;
, где L=2,3,…, n-1; j∈{2,3,…,L}; L⊂n;
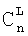 - число сочетаний из n по L. На основе (4)
- число сочетаний из n по L. На основе (4) 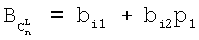 определим bij, тогда b11=1, b13=4 и b21=0, b23=19. Представим bij в виде таблицы на основе (6), тогда
определим bij, тогда b11=1, b13=4 и b21=0, b23=19. Представим bij в виде таблицы на основе (6), тогда
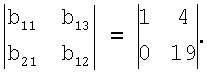
Выражение для данной конфигурации системы K'=b1+b217, тогда получим значения для коэффициентов ОПСС
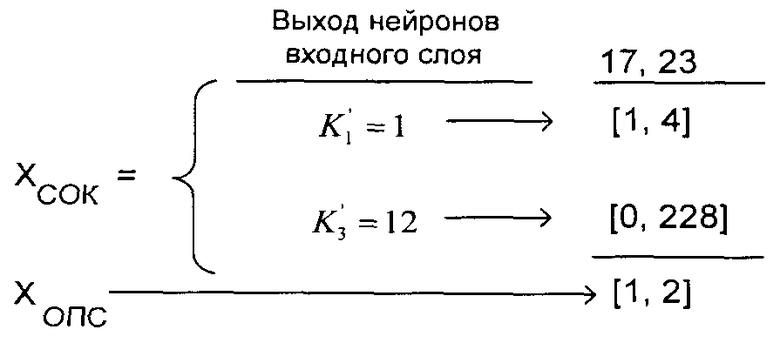
Итак, K'=1+2·17=35.
Значения Xопс=[1, 2] являются адресными входами ПЗУ1 и ПЗУ3. На выходе ПЗУ1 формируется число, равное 1, а на выходе ПЗУ3 - число, равное 2·17=34. В сумматоре эти значения суммируются 1+34=35, из которого вычисляется значение rq=2·13=26. Все операции в сумматоре выполняются в дополнительном коде. Так как используются положительные целые числа, то дополнительный код числа равен самому числу. Итак, код ключа равен К=35-26=9.
Нейронная сеть с пороговой (n, t) структурой для преобразования остаточного кода в двоичный позиционный код работает следующим образом.
Входное число 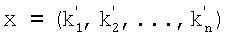 1, представленное в СОК своими остатками
1, представленное в СОК своими остатками  по модулям pi(i=1,2,…,n), поступает на входной слой 2. Входной слой связан с n НСКК в соответствии с заданной реконфигурацией, которая зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w 7, формируемых ПЗУф 8 по сигналу реконфигурации 10 и определяемых выражением (4). НСКК pi 3 реализует вычислительную модель (7), на выходе которых формируются коэффициенты ОПСС
по модулям pi(i=1,2,…,n), поступает на входной слой 2. Входной слой связан с n НСКК в соответствии с заданной реконфигурацией, которая зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w 7, формируемых ПЗУф 8 по сигналу реконфигурации 10 и определяемых выражением (4). НСКК pi 3 реализует вычислительную модель (7), на выходе которых формируются коэффициенты ОПСС 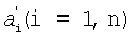 числа x. Коэффициенты
числа x. Коэффициенты 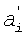 являются адресными входами ПЗУpi 4, где хранятся двоичные эквиваленты
являются адресными входами ПЗУpi 4, где хранятся двоичные эквиваленты 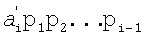 . Считанные из ПЗУpi двоичные коды, соответствующие произведениям
. Считанные из ПЗУpi двоичные коды, соответствующие произведениям 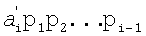 суммируются взвешенным сумматором 5 с учетом поправки - rq, формируемой ПЗУn 9 по сигналу поправки 11. На выходе 6 формируется двоичный код ключа. Время преобразования определяется n+1 тактами синхронизации. Структура нейронной сети с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код требует n - НСКК по модулям рi, n - ПЗУpi, каждое из которых хранит рi слов разрядностью, эквивалентной числу pi-1p1p2…pi-1, одного параллельного сумматора с ускоренным переносом, одного постоянного запоминающего устройства формирования весовых коэффициентов при реконфигурации, хранящего
суммируются взвешенным сумматором 5 с учетом поправки - rq, формируемой ПЗУn 9 по сигналу поправки 11. На выходе 6 формируется двоичный код ключа. Время преобразования определяется n+1 тактами синхронизации. Структура нейронной сети с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код требует n - НСКК по модулям рi, n - ПЗУpi, каждое из которых хранит рi слов разрядностью, эквивалентной числу pi-1p1p2…pi-1, одного параллельного сумматора с ускоренным переносом, одного постоянного запоминающего устройства формирования весовых коэффициентов при реконфигурации, хранящего 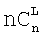 весовых коэффициентов, и постоянного запоминающего устройства формирования поправки, емкость которого определяется произведением
весовых коэффициентов, и постоянного запоминающего устройства формирования поправки, емкость которого определяется произведением 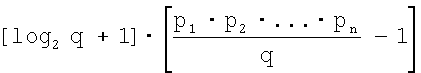 .
.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОКРУГЛЕНИЯ И МАСШТАБИРОВАНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271570C2 |
Изобретение относится к нейронной сети с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код, которая является схемой восстановления позиционного числа по сокращенной системе модулей остаточных классов независимо от того, что часть модулей искажена и они отбрасываются либо часть модулей просто игнорируется. Техническим результатом является расширение функциональных возможностей преобразователя остаточного кода в двоичный позиционный код. Для этого нейронная сеть с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код содержит входной слой нейронов, n - нейронных сетей конечного кольца для преобразования остаточного кода в код обобщенной позиционной системы счисления, n - постоянных запоминающих устройств для хранения двоичных эквивалентов коэффициентов обобщенной позиционной системы счисления, параллельный сумматор, постоянное запоминающее устройство формирования весовых коэффициентов для выбора необходимой конфигурации нейронных сетей конечного кольца и постоянное запоминающее устройство для формирования поправки выходного двоичного кода. 1 ил.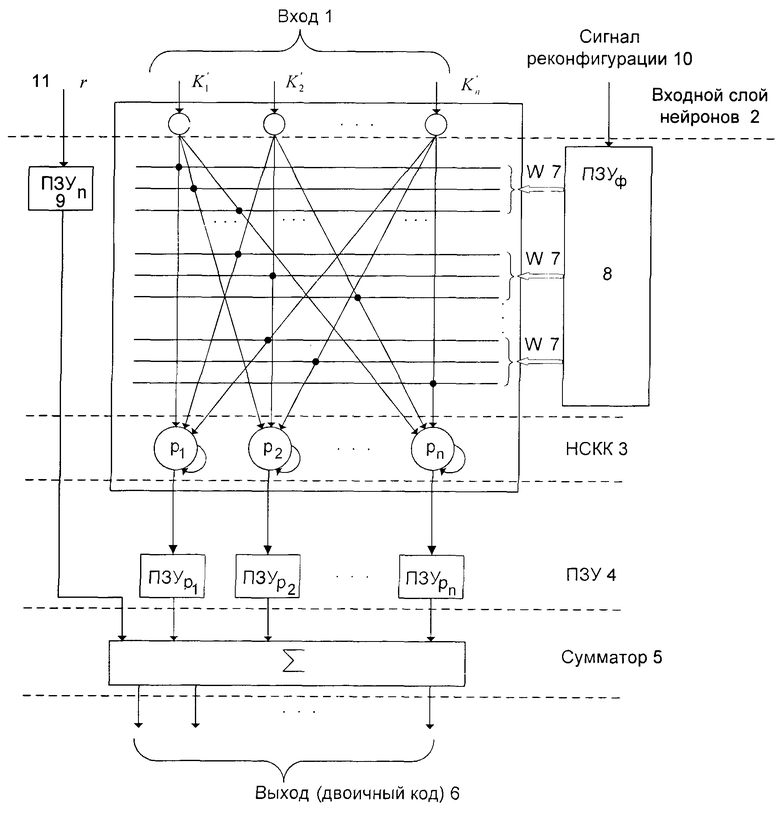
Нейронная сеть с пороговой (k, t) структурой для преобразования остаточного кода в двоичный позиционный код, содержащая входной слой нейронов, n нейронных сетей конечного кольца (НСКК), предназначенных для формирования коэффициентов обобщенной позиционной системы счисления (ОПСС), n постоянных запоминающих устройств для хранения двоичных эквивалентов значений α'i р1 р2…рi-1 (i=1, 2, …, n) и сумматор, причем входной слой нейронов связан n нейронными сетями конечного кольца, выходы которых связаны с адресными входами упомянутых n постоянно запоминающих устройств для хранения двоичных эквивалентов, причем сумматор предназначен для суммирования двоичных эквивалентов, считанных из n постоянно запоминающих устройств, и формирования на своих выходах двоичного позиционного кода, отличающаяся тем, что в нее введены постоянное запоминающее устройство формирования весовых коэффициентов при реконфигурации нейронных сетей конечного кольца, причем на вход упомянутого постоянного запоминающего устройства формирования весовых коэффициентов поступает выбранный вариант реконфигурации 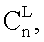 а на выходах постоянного запоминающего устройства формирования весовых коэффициентов формируется набор весовых коэффициентов, которые поступают на НСКК для выбора конфигурации из L НСКК в соответствии с конкретной выборкой сочетаний
а на выходах постоянного запоминающего устройства формирования весовых коэффициентов формируется набор весовых коэффициентов, которые поступают на НСКК для выбора конфигурации из L НСКК в соответствии с конкретной выборкой сочетаний 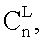 где L - подмножество конечного множества n, и постоянное запоминающее устройство формирования поправки rq выходного двоичного кода, r - случайное число поправки, q - модуль системы остаточных классов, при этом на вход упомянутого постоянного запоминающего устройства поправки rq поступает случайное число r, а сумматор осуществляет упомянутое суммирование двоичных эквивалентов, считанных из n постоянно запоминающих устройств, с учетом поправки rq, формируемой постоянным запоминающим устройством формирования поправки rq выходного двоичного кода.
где L - подмножество конечного множества n, и постоянное запоминающее устройство формирования поправки rq выходного двоичного кода, r - случайное число поправки, q - модуль системы остаточных классов, при этом на вход упомянутого постоянного запоминающего устройства поправки rq поступает случайное число r, а сумматор осуществляет упомянутое суммирование двоичных эквивалентов, считанных из n постоянно запоминающих устройств, с учетом поправки rq, формируемой постоянным запоминающим устройством формирования поправки rq выходного двоичного кода.
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЗИЦИОННУЮ СИСТЕМУ СЧИСЛЕНИЯ | 2004 |
|
RU2275741C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЗИЦИОННЫЙ КОД | 2002 |
|
RU2235423C2 |
| КЛЕЙ-РАСПЛАВ | 0 |
|
SU357212A1 |
Авторы
Даты
2010-01-27—Публикация
2008-05-30—Подача