Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерных системах.
Известно устройство для контроля и исправления ошибок в избыточном модулярном коде (патент №2022472, кл. Н03М 13/00, RU, 1999), состоящее из входного преобразователя кода, выходного преобразователя, блока группы элементов сравнения, блока группы элементов ИЛИ, блока элементов И.
Однако данное устройство обладает следующими недостатками:
низкое быстродействие, большие аппаратные затраты и малые функциональные возможности, так как в устройстве используется один избыточный модуль, коррекция ошибки осуществляется по большому модулю, равному диапазону контрольных чисел.
Наиболее близким по технической сущности к заявленному устройству является устройство для обнаружения и исправления ошибок в системе остаточных классов (А.С. №714399, G06F 11/08, 1980), содержащее два блока модульной свертки, причем первый выход регистра соединен со входом первого и второго блоков модульной свертки и с первым входом третьего сумматора, выходы первого и второго блоков модульной свертки соединены соответственно с первыми входами первого и второго сумматоров, второй и третий выходы регистра соединены соответственно со вторыми входами первого и второго сумматоров и со вторым и третьим входами третьего сумматора, выход блока памяти соединен с четвертым входом третьего сумматора, выход которого является выходом устройства.
Недостатком известного устройства является сложность, которая объясняется наличием двух блоков модульной свертки, низким быстродействием, которое пропорционально количеству модулей системы остаточных классов и малыми функциональными возможностями.
Целью настоящего изобретения является упрощение устройства, повышение быстродействия и расширение функциональных возможностей.
Поставленная цель достигается тем, что устройство содержит нейронную сеть 8, состоящую из нейронных сетей конечного кольца 4, 5 и 6 и нейронных сетей конечного кольца 27, 28, которые формируют остатки по контрольным модулям системы остаточных классов, выходы 9 которых соединены с первыми входами нейронных сетей конечного кольца 10, 11 вычисления синдрома ошибки, вторые входы которых соединены с выходами нейронов 23 избыточных модулей αn+1 и αn+2, выходы нейронных сетей конечного кольца 10, 11, шины 12 и 13 связаны со входами блока памяти 14 для выбора из нее констант ошибок, выходы 15, которые поступают на шины 16, 17 и 18, определяющие номер неисправного модуля (канала), и на вход элемента ИЛИ 19, выход 20 которого определяет наличие ошибки, кроме того, выходы блока памяти 14 поступают на первые входы нейронных сетей конечного кольца 21, а на вторые входы которых поступают остатки неправильного числа α1, α2,...,αn. Исправленное число с выходов нейронных сетей конечного кольца 21 поступает на выходы 22 устройства.
Рассмотрим метод коррекции ошибок.
Пусть дано контролируемое число А=(α1, α2,...,αn, αn+1, αn+2), где
αi=Amodpi∀i=1, 2,..., n+2, р1,р2,...,рn,рn+1,рn+2 - основания СОК с двумя избыточными основаниями рn+1, рn+2.
Принцип обнаружения, локализации и исправления ошибки основан на функциональном объединении всех трех операций в одну операцию. Данный метод основан на определении цифр по избыточным основаниям на основании цифр по рабочим основаниям и сравнении их с изначально известными цифрами по избыточным основаниям. Если вычисленные цифры α'n+1 и α'n+2 по контрольным разрядам равны исходным цифрам αn+1 и αn+2 этих разрядов, то ошибки нет, если они не равны, то необходимо определить синдром ошибки, равный разности этих цифр δ1=(αn+1-α'n+1)mod pn+1 и δ2=(αn+2-α'n+2)mod pn+2, по значениям которых определяется константа ошибки. Далее суммируя константу ошибки с неправильным числом, которая подобрана таким образом, что неявное место ошибки в числе устраняется. Для локализации ошибки необходимо поразрядно сравнить откорректированное число с ошибочным, и в случае, если αi-αi'≠0, определяется ошибочный разряд. Изложенный метод позволяет обнаружить, локализовать и исправить ошибку по одному из информационных каналов.
Вычисление α'n+1 и α'n+2 проведем на основе метода расширения системы оснований, который базируется на использовании китайской теоремы об остатках и обобщенной позиционной системе счисления. Рассмотрим вначале расширение на одно основание, а затем обобщим расширение на два основания.
Пусть задана система оснований р1, р2,..., рn с диапазоном Р=р1·p2·...·рn, ортогональными базисами В1, В2,...,Вn, веса которых m1, m2,..., mn и определяются из сравнения  Расширим систему оснований, добавляя основание рn+1, тогда диапазон системы станет Pn+1=pn+1·P, ортогональные базисы системы
Расширим систему оснований, добавляя основание рn+1, тогда диапазон системы станет Pn+1=pn+1·P, ортогональные базисы системы 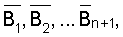 их веса
их веса 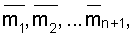 причем
причем 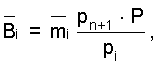
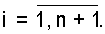 Задача состоит в определении цифры αn+1 числа А по основанию рn+1.
Задача состоит в определении цифры αn+1 числа А по основанию рn+1.
Тогда число А в системе оснований р1, р2,..., рn, рn+1 будет иметь вид
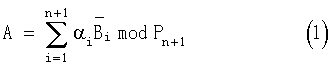
где 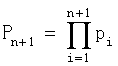 - диапазон расширенной системы оснований;
- диапазон расширенной системы оснований;
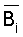 - ортогональные базисы расширенной системы оснований.
- ортогональные базисы расширенной системы оснований.
Представим ортогональные базисы 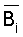 в обобщенной позиционной системе счисления, тогда
в обобщенной позиционной системе счисления, тогда
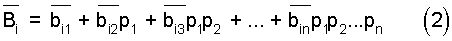
где 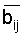 - коэффициенты ОПСС;
- коэффициенты ОПСС;
i, j=1,2,...,n.
На основании (2) запишем выражение (1) в виде
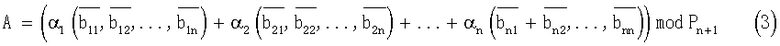
Из выражения (3) можно определить коэффициенты αi числа А, тогда
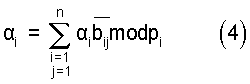
где αi - вычеты числа А по mod pi;
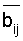 - ортогональные базисы, представленные в ОПСС.
- ортогональные базисы, представленные в ОПСС.
Цифры αi в представлении ОПСС получаются суммированием по модулю pi всех произведений  и переносом, генерируемым при формировании αi-1. Перенос генерируется как число раз, когда сумма цифр в ОПСС переполняется по модулю pi. Этот перенос используется для формирования цифр αi+1. Последний перенос, генерируемый при получении последней цифры числа в ОПСС, отбрасывается. Предлагаемый метод выполняется в параллельном режиме. Выигрыш в быстродействии данного метода с итеративным методом очевиден, поскольку он уменьшает время преобразования с 2(n+1) циклов синхронизации до трех циклов.
и переносом, генерируемым при формировании αi-1. Перенос генерируется как число раз, когда сумма цифр в ОПСС переполняется по модулю pi. Этот перенос используется для формирования цифр αi+1. Последний перенос, генерируемый при получении последней цифры числа в ОПСС, отбрасывается. Предлагаемый метод выполняется в параллельном режиме. Выигрыш в быстродействии данного метода с итеративным методом очевиден, поскольку он уменьшает время преобразования с 2(n+1) циклов синхронизации до трех циклов.
Цифры αi, 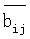 принимают значения от 0 до pi-1, причем
принимают значения от 0 до pi-1, причем 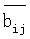 являются константами, поэтому произведение αi
являются константами, поэтому произведение αi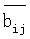 можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений αi
можно поместить в ПЗУ или в весовые коэффициенты связей между нейронами. Адресами произведений αi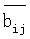 являются вычеты αi числа А по модулю pi.
являются вычеты αi числа А по модулю pi.
Пример 1. Пусть р1=2, р2=3, р3=5, p4=7, Pn+1=2·3·5·7=210, B1=105, B2=70, B3=126, В4=120.
Тогда на основании (2) определим 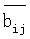 :
:

Рассмотрим перевод числа из СОК в ОПСС.
Пусть А=11=(1, 2, 1, 4). Тогда в ПЗУ поместим значения αi, 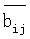 :
:
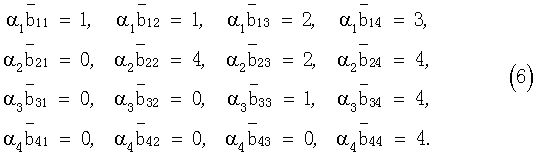
Преобразование числа A из СОК в ОПСС имеет вид

При сложении цифр по каждому модулю с учетом переноса получим число А, представленное в ОПС как А=[1,2,1,0].
Рассмотрим метод определения вычета по расширенному основанию. Пусть СОК состоит из оснований р1, р2,...,pn. Объем диапазона этой системы будет  Добавим к числу оснований СОК новое основание pn+1. Объем диапазона этой системы
Добавим к числу оснований СОК новое основание pn+1. Объем диапазона этой системы 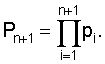 Тогда любое число А из диапазона [0, Рn+1] в обобщенной позиционной системе счисления можно представить в виде
Тогда любое число А из диапазона [0, Рn+1] в обобщенной позиционной системе счисления можно представить в виде
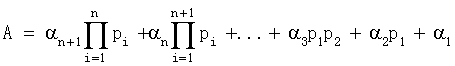
Если число А будет лежать в первоначальном диапазоне [0; Р], то в ОПСС цифра αn+1=0. Если αn+1≠0, тогда значение числа А выходит за пределы динамического диапазона. Факт αn+1=0 используется для получения остатка (вычета) от деления числа А на новое основание СОКрn+1.
Пусть число А имело представление (α1, α2,..., αn) по основаниям р1, p2,..., рn. Добавляем новое основание pn+1, тогда число 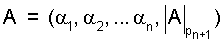 в системе оснований p1, р2,..., рn, pn+1, где
в системе оснований p1, р2,..., рn, pn+1, где 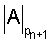 - остаток от деления числа А на рn+1, т.е. искомая цифра по новому основанию.
- остаток от деления числа А на рn+1, т.е. искомая цифра по новому основанию.
Для определения этой цифры используем метод перевода числа из СОК в ОПСС, включая неизвестную цифру 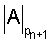 в проводимые операции. При этом мы параллельно получим цифры ОПСС α1, α2,...,αn и выражение для цифры αn+1. Но так как по условию число А∈[0;P], то цифра αn+1=0.
в проводимые операции. При этом мы параллельно получим цифры ОПСС α1, α2,...,αn и выражение для цифры αn+1. Но так как по условию число А∈[0;P], то цифра αn+1=0.
Из полученного соотношения и определяем искомую цифру 
Пример 2. Пусть задана система модулей р1=2, р2=3, p3=5, тогда P=2·3·5=30. И пусть задано число А=11=(1, 2, 1). Расширим систему оснований, добавляя р4=7. Тогда А=11=(1, 2, 1, |А|7) в системе оснований p1=2, р2=3, р3=5, р4=7.
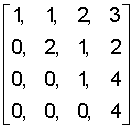
Набор констант bij приведен в (5) и задается матрицей
Процесс решения задачи приведен в таблице 1.
После сложения цифр по модулю pi получим А=[1, 2, 1, 5+4|A|7], но так как α4=|5+4·|А|7|7, но по условию α4=0, т.е. 4·|А|7=-5 или 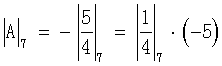 . Мультипликативная обратная величина
. Мультипликативная обратная величина 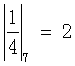 , и так как число 5 отрицательное, возьмем его дополнение по модулю 7. Итак, вычет числа А по модулю 7 определяется выражением |А|7=2·(7-5)=4.
, и так как число 5 отрицательное, возьмем его дополнение по модулю 7. Итак, вычет числа А по модулю 7 определяется выражением |А|7=2·(7-5)=4.
Тогда расширенное представление числа будет A=11=(1, 2, 1, 4). Так как результат образования цифры в СОК по новому основанию рn+1 зависит только от информационных разрядов, то операцию расширения вычетов можно проводить сразу по нескольким дополнительно введенным основаниям.
Пример 3. Пусть задана система оснований (модулей) СОК р1=2, р2=3, р3=5. Расширим систему оснований, добавляя р4=7, р5=11. Тогда в выражение (5) добавляется еще один столбец и одна строка, а именно
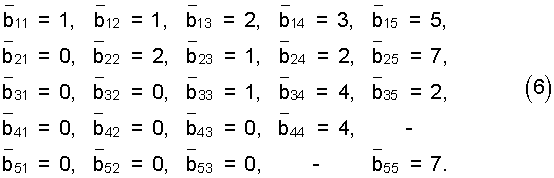
Пусть задано число А=17=(l,2,2,|A|7, |А|11), необходимо найти остатки по основаниям р4=7, р5=11.
Процесс решения приведен в таблице 2.
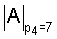
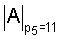
После сложения цифр по модулю pi получим
А=[1,2,2,2+4|А|7,2+7|А|11],
но так как α4=2+4|A|7,а α5=2+7|A|11, и по условию α4=0 и α5=0, тогда
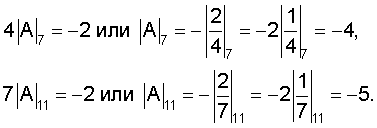
Мультипликативные величины 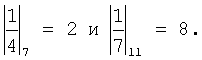
Так как |А|7=-4, а |А|11=-5 возьмем их дополнения, т.е. |A|7=7-4=3, а |A|11=11-5=6.
Тогда расширенное представление числа будет равно информационному числу, т.е. А=(1,2,2,3,6)11, и это говорит о том, что число А безошибочное.
Преимущества предложенного метода расширения системы вычетов состоит в том, что:
- все вычисления выполняются в параллельных каналах по отдельным модулям, причем каждый модуль отождествляется с отдельным каналом;
- не требуется вычисления большого количества дополнительных величин, необходимо только наличие констант  и мультипликативных величин по расширенным основаниям;
и мультипликативных величин по расширенным основаниям;
- возможно получение расширенного представления вычетов числа сразу по нескольким дополнительным основаниям, что не влияет на быстродействие всей операции расширения.
Применим этот метод для обнаружения, локализации и исправления ошибки.
Коррекция ошибок в СОК основана на представлении числа в расширенной системе. В качестве расширенных оснований возьмем избыточные (контрольные) основания. Допустим, в процессе обработки и хранения данных в вычислительной системе остатки чисел по избыточным основаниям, с одной стороны, абсолютно верны, а с другой стороны, они вычисляются на основе остатков по неизбыточным (информационным) основаниям, непосредственно перед контролем данных. Если вычисленные избыточные остатки равны исходным, то ошибки в информационных основаниях не произошло, в противном случае - произошла ошибка по информационным основаниям. На основании этой информации устраняется ошибка и определяется неисправный модуль.
Введенное ограничение на абсолютную верность избыточных оснований обеспечивается абсолютной надежностью каналов по избыточным модулям, которую можно обеспечить известными структурными технологиями (например, использованием обычных корректирующих кодов или мажоритарной схемы).
Пример 4. Исходные данные такие же, как и в примере 3.
Допустим, произошла ошибка по третьему информационному основанию, тогда ошибочное число 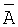 будет иметь вид
будет иметь вид 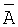 =(1,2,3,3,6).
=(1,2,3,3,6).
Избыточные разряды по четвертому и пятому основаниям равны соответственно 3 и 6, и они абсолютно верны.
На основании информационных остатков определим синдром ошибки δ.
Метод обнаружения, исправления и локализации ошибок в СОК представляется следующим образом.
Контролируемое число α1, α2,...,αn, αn+1, αn+2 делится на две части: информационную, в которую входят остатки по информационным основаниям α1, α2,..., αn, и контрольную часть, в которую входят остатки по избыточным (контрольным) основаниям αn+1, αn+2.
Далее по остаткам информационных каналов определяем остатки по избыточным основаниям. Воспользуемся таблицей 2, тогда третья строка будет иметь вид не [0, 0, 2, 8, 4], а [0, 0, 3, 12, 6].
При выполнении операции согласно таблице 2 получим

Отсюда
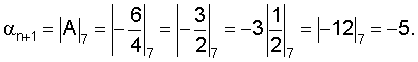

Используя найденные остатки, определяем синдром ошибки:
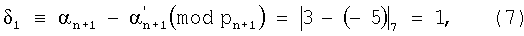
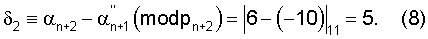
По величинам δ1, δ2 формируются константы ошибок таким образом, что при их сложении с информационными разрядами контролируемого числа А имевшая место ошибка в числе устраняется. Заметим, что если контролируемое число не будет содержать ошибки, то величины δ1 и δ2 равны нулю.
Для локализации ошибки необходимо провести сравнение разрядов исходного числа с исправленным числом и по тому разряду, где сравнение не выполняется, определяется ошибочный разряд.
Определим константы ошибок для данного примера и сведем их в таблицу 3.
Константы ошибок для СОК с основаниями р1=2, р2=3, р3=5, p4=7, p5=11
1,4
3,10
6,6
5,1
6,9
2,10
3,2
В соответствии с δ1=1, δ2=5 таблицы 2 определяется величина ошибки (0,0,4), которая складывается с контролируемым числом 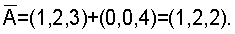
По величине ошибки (0,0,4) локализуется ошибочный разряд, им будет разряд по modp3. Использование синдрома ошибки позволяет все процедуры по обнаружению, локализации и исправлению ошибок объединить в одну процедуру, что позволяет уменьшить время коррекции ошибок и повысить эффективность.
На чертеже приведена нейронная сеть для обнаружения, локализации и исправления ошибок в системе остаточных классов. Нейронная сеть состоит из входного слоя нейронов 2, 23, входного слоя 24, предназначенного для хранения остатков числа по рабочим и контрольным основаниям в течение времени обнаружения ошибки, вход которой соединен со входами 1(α1, α2,..., αn) и входами 25(αn+1, αn+2) нейронной сети; нейронной сети 8, предназначенной для вычисления остатков чисел по контрольным основаниям, входы которой соединены с выходами нейронов 2, хранящими остатки по рабочим основаниям; нейронных сетей конечного кольца 10, 11, предназначенных для вычисления синдромов ошибки по контрольным основаниям, первые входы которых соединены соответственно с выходами нейронной сети вычисления остатков по контрольным основаниям, а вторые - соответственно с выходами нейронов 23, хранящие остатки по контрольным основаниям, входы которых подключены к шине 25; блок памяти 14, предназначенный для хранения констант, вход которого соединен с выходами нейронных сетей конечного кольца 10, 11; нейронных сетей конечного кольца 21, предназначенных для получения исправленного числа путем суммирования неправильного числа с константой ошибки, первые входы которых соединены соответственно с выходами блока памяти, шины 15, которые являются выходными шинами 16, 17 и 18, формирующие номера неисправных модулей и входом элемента ИЛИ 19, выход 20 которого формирует сигнал "есть ошибка", а вторые - с выходами нейронов 2, а выходные сигналы 22 нейронных сетей конечного кольца 21 являются выходами нейронной сети исправления ошибок.
Работа нейронной сети для обнаружения, локализации и исправления ошибок в системе остаточных классов осуществляется следующим образом.
На входы 1, 25 нейронов 2 и 23 нейронной сети для обнаружения, локализации и исправления ошибки в системе остаточных классов подается контролируемое число А=(α1, α2,...,αn, αn+1, αn+2). С выходов нейронов 2 остатки по рабочим основаниям с весовыми коэффициентами wij 3 поступают на вход нейронной сети 8 вычисления остатков по контрольным модулям. Нейронная сеть 8 состоит из совокупности нейронных сетей конечного кольца 4, 5, 6. Весовые коэффициенты wij 3 и wjk 7 нейронов нейронных сетей конечного кольца, выполняющие роль распределенной памяти, определяются соответственно  и wjk=1. Нейронные сети конечного кольца 4, 5 и 6 реализуют вычислительную модель, представленную в таблице 2.
и wjk=1. Нейронные сети конечного кольца 4, 5 и 6 реализуют вычислительную модель, представленную в таблице 2.
Выходные сигналы НСКК 5 и 6 последней строки поступают на вход НСКК 27 и 26, с весовыми коэффициентами wkl 29, равные  где l - количество расширяемых модулей и принимает значение 1,2,....
где l - количество расширяемых модулей и принимает значение 1,2,....
Выходные сигналы 9 НСКК 27 и 28 будут отрицательными значениями: -α'n+1 и -α'n+2, которые поступают соответственно на входы 9 НСКК 10 и 11, а на вторые входы поступают значения αn+1 и αn+2 по шинам соответственно 30 и 31. НСКК 10 и 11 реализуют вычислительную модель:
δ1=αn+1-(-α'n+1);
δ2=αn+2-(-α'n+2).
Выходные значения НСКК 10 и 11 по шинам 12 и 13, соответствующим синдромам ошибки, поступают на входы блока памяти 14 и выбирают оттуда соответствующую константу согласно таблице 3. Эти константы с выхода блока памяти 14 по шинам 15 поступают на соответствующую шину 16, 17 и 18, которые показывают номер неисправного модуля, а также на вход элемента ИЛИ 19, выход 20 которого показывает наличие ошибки. На входы НСКК 21 поступает сигнал с выхода блока памяти, а на вторые входы поступают соответственно выходные сигналы рабочих каналов, нейроны 3, выходная шина 26, где суммируются с константами ошибок, подобранными таким образом, что при ее сложении с контролируемым числом А имевшая место ошибка в числе устраняется. На выходе НСКК 21 выходная шина 22 формирует исправленное число.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ ПЕРЕПОЛНЕНИЯ ДИНАМИЧЕСКОГО ДИАПАЗОНА, ОПРЕДЕЛЕНИЯ ОШИБКИ И ЛОКАЛИЗАЦИИ НЕИСПРАВНОСТИ ВЫЧИСЛИТЕЛЬНОГО КАНАЛА В ЭВМ, ФУНКЦИОНИРУЮЩИХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2483346C1 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
Нейронная сеть для обнаружения, локализации и исправления ошибок в системе остаточных классов относится к вычислительной технике и может быть использована в модулярных нейрокомпьютерных системах. Техническим результатом является повышение скорости коррекции ошибок, сокращение оборудования, а также расширение функциональных возможностей. Для этого нейронная сеть содержит входной слой, нейронные сети конечного кольца для определения синдрома ошибок, блок памяти для хранения констант, нейронные сети для вычисления правильного результата и элемент ИЛИ для определения наличия ошибки. 1 ил., 3 табл.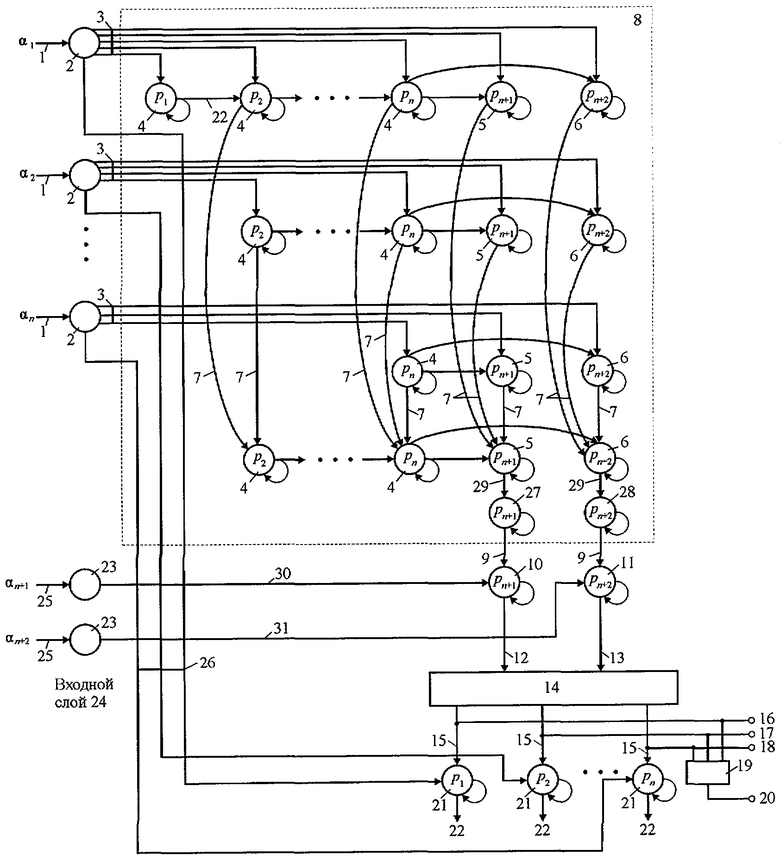
Нейронная сеть для обнаружения, локализации и исправления ошибок в системе остаточных классов (СОК), содержащая входной слой нейронов, на входы которых подается контролируемое число А=(α1, α2, ..., αn, αn+1, αn+2), где αi=Amod pii=1, 2, ..., n+2, р1, ... рn - рабочие основания СОК, рn+1, рn+2 - контрольные основания СОК, блок памяти, элемент ИЛИ, n выходных нейронных сетей конечного кольца, отличающаяся тем, что, ней выходы нейронов входного слоя по рабочим основаниям разветвлены соответственно на первые входы выходных нейронных сетей конечного кольца, предназначенных для получения исправленного числа путем суммирования неправильного числа с константой ошибки, и на входы нейронной сети, предназначенной для вычисления остатков α'n+1 и α'n+2 по контрольным основаниям, выходы которой соединены с входами нейронной сети формирования отрицательных значений остатков по контрольным основаниям, выходы которой подключены соответственно к первым входам нейронных сетей конечного кольца определения синдрома ошибки δ1=|αn+1-(-α'n+1)|p+1 и δ2=|αn+2-(-α'n+2)|p+2, выходы нейронов входного слоя по контрольным основаниям подключены соответственно на вторые входы нейронных сетей конечного кольца определения синдрома ошибки, выходы которых соединены с адресными входами блока памяти, в котором хранятся константы, определяемые синдромами ошибок δ1 и δ2, выходы блока памяти подключены к шинам определения основания по которому произошла ошибка и к элементу ИЛИ, формирующему сигнал «есть ошибка», а также соответственно к вторым входам n выходных нейронных сетей конечного кольца, выходы которых являются выходами нейронной сети обнаружения, локализации и исправления ошибок в СОК.
| Устройство для обнаружения и исправления ошибок в системе остаточных классов | 1977 |
|
SU714399A1 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ И ИСПРАВЛЕНИЯ ОШИБОК В ИЗБЫТОЧНОМ МОДУЛЯТОРНОМ КОДЕ | 1991 |
|
RU2022472C1 |
| Устройство для контроля ошибок в избыточном модулярном коде | 1986 |
|
SU1363484A1 |
| Устройство для обнаружения и исправления ошибок арифметических операций | 1977 |
|
SU744583A1 |
Авторы
Даты
2007-06-20—Публикация
2005-05-04—Подача