Изобретение относится к информационно-измерительной технике и может быть использовано для преобразования аналоговых входных сигналов в аналоговые выходные сигналы, при котором соотношения между амплитудами и фазами частотных компонентов входного сигнала остаются неизменными лишь в пределах определенного диапазона частот (в области нижних частот (НЧ); в области высших частот (ВЧ); в определенной полосе частот (ПЧ).
Известен помехоустойчивый метод измерения [Авторское свидетельство СССР №13771, МКИ Н03К 13/00, БИ №10, 1981], основанный на интегрировании измеряемой величины за время Т, равное или кратное номинальному периоду наложенной на сигнал периодической помехи, которое производят формированием весовой функции с единичным весом в течение трех временных промежутков длительностью 

 разделенных паузами длительностью
разделенных паузами длительностью  с нулевыми значениями весовой функции.
с нулевыми значениями весовой функции.
Таким образом, учитывая, что подавление помех (повышение помехоустойчивости) является одной из целей фильтрации сигналов путем интегрирования фильтруемого сигнала, процедуру фильтрации можно представить в виде интегрального соотношения в виде свертки входного (фильтруемого) сигнала Х(t)

Существенным недостатком этого «Помехоустойчивого способа измерения», обеспечивающего повышение помехоподавления, т.е. повышение точности фильтрации измерительных сигналов (на языке указанной монографии Гутникова B.C.), является принципиальная невозможность обеспечить единообразную зависимость коэффициента передачи фильтра от частоты в окрестностях точек его максимумов.
Действительно, частотная характеристика G(f) фильтра, реализующего ВФ в виде ступенчатой функции времени с длительностью ступеней Т2, может рассматриваться [Фильтрация измерительных сигналов. Гутников B.C.: Энергоатомиздат. Ленинградское отделение, 1990, стр.99-100] как свертка дискретной функции, содержащей Nδ-импульсов, и одиночного прямоугольного импульса, имеющего единичную амплитуду и длительность Т2. Соответственно этому частотная характеристика G(f) фильтра, реализующего такую ВФ, может быть найдена как произведение спектров дискретной функции Gg(f) и одиночного П-образного (прямоугольного) импульса GП(f):

где an - амплитуды ступеней ступенчатой весовой функции (весовые коэффициенты). Так как функция

представляющая спектр прямоугольного импульса, обязательно имеет нули на гармониках с номерами  , где К=1; 2; 3;…, то частотная характеристика G(f) рассматриваемого фильтра имеет нули на тех же гармониках фильтруемого сигнала, а значит, эти гармоники входного сигнала будут отсутствовать в составе частотных компонентов выходного сигнала, т.е. пропускание гармоник входного сигнала на выход фильтра с одинаковым коэффициентом передачи в определенной полосе частот невозможно.
, где К=1; 2; 3;…, то частотная характеристика G(f) рассматриваемого фильтра имеет нули на тех же гармониках фильтруемого сигнала, а значит, эти гармоники входного сигнала будут отсутствовать в составе частотных компонентов выходного сигнала, т.е. пропускание гармоник входного сигнала на выход фильтра с одинаковым коэффициентом передачи в определенной полосе частот невозможно.
Наличие нулей АЧХ в полосе пропускания фильтра делает невозможным решение задачи получения АЧХ фильтра с эквидистантными максимумами равной амплитуды на основе интеграла свертки.
Существенным недостатком этого фильтра является необходимость реализации интеграла свертки, т.е. интеграла от произведения входного сигнала на весовую функцию, т.к. процедуры перемножения и последующего интегрирования требуют большого объема технических средств, а выделение отдельной гармоники потребует удвоенного их объема.
Известен синхронный полосовой фильтр [Патент РФ на изобретение №1658377, МКИ 5 H03H 19/00, БИ №23, 1991], реализующий способ синхронной фильтрации.
Способ синхронной фильтрации основан на последовательном воздействии выборок фильтруемого сигнала на резистор и N цепей из последовательно соединенных конденсатора и 2-х ключей, на управляющие входы которых подаются выходные импульсы распределителя импульсов, вход которого соединен с выходом тактового генератора, чем обеспечивается идентичность условий заряда каждой из N «запоминающих» емкостей через вторые ключи перед очередным воздействием соответствующей выборки фильтруемого сигнала.
Недостатком способа является наличие реализационных погрешностей, обусловленных невозможностью точно коммутировать выборки фильтруемого сигнала по соответствующим «запоминающим» емкостям (так называемые синхронные помехи), а также свойствен принципиально неустранимый недостаток, обусловленный необходимостью разбиения непрерывного сигнала на отдельные выборки для организации фильтрации путем заряда «запоминающих» емкостей.
Действительно, разбиением непрерывного сигнала на последовательность коротких выборок производится преобразованием спектра фильтруемого сигнала в спектр суперпозиции запаздывающих относительно друг друга последовательностей импульсов, форма которых определяется поведением фильтруемого сигнала внутри интервала выборки τ (интервала стробирования). Спектр стробированного сигнала [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.304-305] характеризуется появлением гармоник частоты повторения стробирующих прямоугольных импульсов единичной амплитуды (отсутствовавших в спектре фильтруемого сигнала), около каждой из которых располагается симметрично спектр фильтруемого сигнала, т.е. спектр фильтруемого сигнала преобразуется в периодическую структуру из копий спектра фильтруемого сигнала, расположенных симметрично относительно гармоник последовательности прямоугольных стробирующих импульсов единичной амплитуды.
Из этого богатого набора копий спектра фильтруемого сигнала для создания выходного эффекта фильтрации используется только оригинал, расположенный симметрично относительно частоты ω=0. Выходной эффект создается набором последовательно коммутируемых «запоминающих» емкостей С, которые с единственным резистором R образуют фильтры нижних частот (RC цепочки), выделяющие из последовательностей модулированных в результате стробирования импульсов постоянную составляющую и частотные компоненты фильтруемого сигнала.
Для рассматриваемого фильтра нижних частот (ФНЧ), образуемого резистором R и каждой из N «запоминающих» емкостей С в течение каждого интервала выборки, его АХЧ определяется как модуль комплексного частотного коэффициента передачи
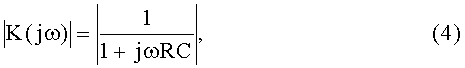
а поэтому энергия выходного сигнала ФНЧ определяется следующим образом:

где Wвх(ω) - энергетический спектр стробированного сигнала на входе ФНЧ.
Выходной энергетический спектр

а потому при воздействии на входе ФНЧ идеального низкочастотного сигнала, энергетический спектр которого отличен от нуля и равен W0 лишь в пределах интервала частот 0<ω<ωВ энергия выходного сигнала

где τ=RC - постоянная времени ФНЧ.
Энергия фильтруемого сигнала 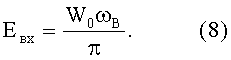
Отношение этих энергий Eвых/Eвх=arctgωВτ/(ωВτ) стремится к нулю с ростом как постоянной времени τ, так и высшей граничной частоты спектра фильтруемого сигнала ωВ, а потому реальный синхронный фильтр неизбежно искажает фильтруемый сигнал.
Существенно при этом, что увеличение высшей граничной частоты спектра фильтруемого сигнала wB до значений, превышающих  , где τВ - фиксированное значение постоянной времени RC - цепи при входных воздействиях, не содержащих частотных компонентов с частотами выше
, где τВ - фиксированное значение постоянной времени RC - цепи при входных воздействиях, не содержащих частотных компонентов с частотами выше  , при которых происходит соприкосновение копий спектра, сопровождается наложением копий спектра, что нарушает истинные соотношения между амплитудами и фазами частотных компонентов, попадающих в полосу пропускания каждого из N фильтров нижних частот, образующих эквивалентный синхронный фильтр. А так как в структуре известных реализаций способа синхронной фильтрации отсутствуют элементы контроля текущего значения высшей граничной частоты ωВ фильтруемых сигналов, то результат фильтрации не может считаться неискаженным.
, при которых происходит соприкосновение копий спектра, сопровождается наложением копий спектра, что нарушает истинные соотношения между амплитудами и фазами частотных компонентов, попадающих в полосу пропускания каждого из N фильтров нижних частот, образующих эквивалентный синхронный фильтр. А так как в структуре известных реализаций способа синхронной фильтрации отсутствуют элементы контроля текущего значения высшей граничной частоты ωВ фильтруемых сигналов, то результат фильтрации не может считаться неискаженным.
Известен способ фильтрации электрических сигналов [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.346 (гребенчатые фильтры)], заключающийся в том, что входной (подлежащий фильтрации) электрический сигнал суммируют с сигналами обратной связи, получаемыми путем задержки выходного сигнала фильтра на фиксированные интервалы времени, кратность величин которых определяется числом элементов задержки (2n отводов линии задержки), а результат суммирования подвергают усилению в такой мере, чтобы частично скомпенсировать его ослабление в процессе задержки в цепи обратной связи (но не вызвать самовозбуждение фильтра).
Существенным недостатком этого способа является принципиальная невозможность обеспечить единообразную зависимость коэффициента передачи фильтра от частоты в окрестностях точек его максимумов из-за различия фазочастотных характеристик.
Действительно, коэффициент передачи гребенчатого фильтра, реализующего рассматриваемый способ фильтрации, согласно выражению (14.15) источника информации [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.346] имеет вид

где K0 - коэффициент передачи основного элемента (не зависит от частоты ω;
β0 - коэффициент передачи масштабного усилительного звена в цепи обратной связи (не зависит от частоты ω);
τ0 - время задержки идеального устройства задержки сигналов (линии задержки).
Для амплитудно-частотной характеристики (АЧХ) рассматриваемого гребенчатого фильтра имеем:

Для фазочастотной характеристики (ФХЧ) рассматриваемого гребенчатого фильтра имеем:

Из выражения (10) следует, что максимумы АЧХ соответствуют значениям частоты  , где К=0; 1; 2; … При этом
, где К=0; 1; 2; … При этом  , т.е. достигает максимального значения и мало изменяется при отклонениях τ0 от несовершенства технологии изготовления линий задержки или воздействия дестабилизирующих факторов на первичные параметры линии задержки L и С (индуктивность и емкость на единицу длины линии задержки), определяющие волновое сопротивление линии
, т.е. достигает максимального значения и мало изменяется при отклонениях τ0 от несовершенства технологии изготовления линий задержки или воздействия дестабилизирующих факторов на первичные параметры линии задержки L и С (индуктивность и емкость на единицу длины линии задержки), определяющие волновое сопротивление линии  и величину задержки
и величину задержки 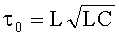 , т.е. время пробега волной расстояния L, равного длине линии.
, т.е. время пробега волной расстояния L, равного длине линии.
С учетом современных технологических и схемотехнических возможностей легко обеспечить малую относительную нестабильность коэффициентов усиления K0 и β0 (порядка сотых долей процента [Интегральная электроника в измерительных устройствах. Гутников B.C. Л.: Энергоатомиздат. Ленингр. Отделение, 1988, стр.20-21]). Поэтому модуль коэффициента передачи в окрестности значений частоты 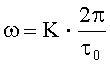 имеет стабильное значение, а причиной отклонений от этих значений является только технологический (из-за несовершенства технологии изготовления линий задержки) разброс значений τ0. Так, для изменения cosωτ0 относительно значения, равного 1, на величину 0,01, т.е. до уровня 0,99 аргумент ωτ0 должен измениться на величину
имеет стабильное значение, а причиной отклонений от этих значений является только технологический (из-за несовершенства технологии изготовления линий задержки) разброс значений τ0. Так, для изменения cosωτ0 относительно значения, равного 1, на величину 0,01, т.е. до уровня 0,99 аргумент ωτ0 должен измениться на величину  или
или 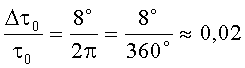 . Такое относительное отклонение τ0 сопровождается существенными изменениями угла фазового сдвига частотных компонентов фильтруемого сигнала в окрестностях максимумов АЧХ. Действительно, на основании выражения (11) для изменений угла фазового сдвига в рассматриваемом случае имеем:
. Такое относительное отклонение τ0 сопровождается существенными изменениями угла фазового сдвига частотных компонентов фильтруемого сигнала в окрестностях максимумов АЧХ. Действительно, на основании выражения (11) для изменений угла фазового сдвига в рассматриваемом случае имеем:

Для β0K0=0,9;  и с учетом
и с учетом 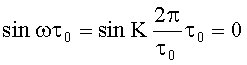 и
и  имеем:
имеем:

Отсюда следует, что неизбежный технологический разброс времен задержки между отводами отдельных секций линии задержки создает неустранимые фазовые сдвиги на частотах, соответствующих максимумам АЧХ гребенчатого фильтра. Вследствие этого форма выходных сигналов таких фильтров отличается от формы входных сигналов, т.е. фильтрация с их помощью не является идеальной. Этот способ выбран в качестве прототипа.
Таким образом, рассмотренные аналоги не обеспечивают решение задачи высокоточной фильтрации электрических сигналов, а тем более физического выделения отдельно взятой гармоники (непрерывного гармонического колебания) из входного сигнала.
Однако выделение отдельной гармоники (фильтрация входного сигнала для целей получения информации об изменениях его параметров) является важной задачей.
Техническим результатом заявляемого способа является принципиальная возможность выделения отдельно взятого гармонического колебания из входного сигнала без использования процедур перемножения входного сигнала на весовую функцию и последующего интегрирования результата перемножения, требующих большого объема оборудования.
Задача, на решение которой направлено техническое решение, достигается тем, что в известном способе фильтрации электрических сигналов [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.346 (гребенчатые фильтры)], заключающемся в том, что входной (подлежащий фильтрации) электрический сигнал суммируют с инвертированным равноамплитудным полиномом, представляющим собой сумму из N гармонических колебаний кратных частот и равных амплитуд и воспроизводимым в виде амплитудно-моделированного колебания, отличающийся тем, что закон изменения огибающей определяется отношением мгновенных значений синусоидальных колебаний равных амплитуд, частота делимого в N/2 раз выше частоты повторения измерительного сигнала f0, а частота делителя равна половине частоты повторения равноамплитудного полинома f0, чем обеспечивается низкочастотная фильтрация входного сигнала, а для выделения из него отдельно взятого гармонического колебания суммирование входного сигнала с инвертированными равноамплитудными полиномами 
 и
и  производят одновременно в соответствии с системой уравнений:
производят одновременно в соответствии с системой уравнений:

где Uвх(t) - входной сигнал;  - равноамплитудный полином, представляющий собой сумму из Nmax, гармонических колебаний, амплитуда каждого из которых равна ANmax; Uвыx2(t) - выходное напряжение дифференциального усилителя 2, являющееся результатом низкочастотной фильтрации входного сигнала.
- равноамплитудный полином, представляющий собой сумму из Nmax, гармонических колебаний, амплитуда каждого из которых равна ANmax; Uвыx2(t) - выходное напряжение дифференциального усилителя 2, являющееся результатом низкочастотной фильтрации входного сигнала.

где Uвых3(t)=Uвых2(t) - выходное напряжение дифференциального усилителя 3; 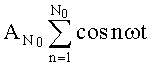 - равноамплитудный полином, представляющий собой сумму из N0 гармонических колебаний, амплитуда каждого из которых равна
- равноамплитудный полином, представляющий собой сумму из N0 гармонических колебаний, амплитуда каждого из которых равна  ; Uвых4(t) - выходное напряжение дифференциального усилителя 4.
; Uвых4(t) - выходное напряжение дифференциального усилителя 4.
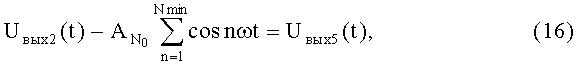
где Uвых5(t) - выходное напряжение дифференциального усилителя 5;  - равноамплитудный полином, представляющий собой сумму из ANmin гармонических колебаний, амплитуда каждого из которых равна
- равноамплитудный полином, представляющий собой сумму из ANmin гармонических колебаний, амплитуда каждого из которых равна  .
.

где  - выходное гармоническое колебание частоты N0ωt с амплитудой
- выходное гармоническое колебание частоты N0ωt с амплитудой  , что обеспечивает выделение (фильтрацию) из входного сигнала гармонического колебания частоты N0ω.
, что обеспечивает выделение (фильтрацию) из входного сигнала гармонического колебания частоты N0ω.
На фигуре показана структурная схема устройства, реализующего способ фильтрации измерительных сигналов.
Здесь:
1 - источник сигнала;
2-6 - дифференциальные усилители;
7-9 - формирователи равноамплитудных полиномов на основе операционного усилителя, переключением резисторов в цепи обратной связи которого обеспечивается изменение коэффициента передачи;
10 - блок синхронизации.
Изменение характера преобразований над подлежащими фильтрации измерительными сигналами возможно на основе преобразования Абеля [Математический анализ (функции, пределы, ряды, цепные дроби). Данилов В.Л. и др. СМБ, Физматгиз, 1961, стр.185]:

где UК=U1+U2+…UК для k=1, 2,…, N.
Обозначая Un=cosnx, Vn=Аn, запишем преобразование Абеля для полинома по косинусам:

Переходя к гармоническим функциям времени, перепишем (19) в следующем виде:

Правая часть (20) содержит член  , т.е. равноамплитудный полином с амплитудами составляющих его гармонических колебаний, равными разности амплитуд (AN-1-AN), что позволяет представить левую часть (20) следующим образом:
, т.е. равноамплитудный полином с амплитудами составляющих его гармонических колебаний, равными разности амплитуд (AN-1-AN), что позволяет представить левую часть (20) следующим образом:

Это означает обращение в ноль частотного компонента AN cos Nωt и обеспечивает воспроизведение  , т.е. низкочастотную фильтрацию входного сигнала
, т.е. низкочастотную фильтрацию входного сигнала 
При этом эффект фильтрации достигается формированием одного равноамплитудного полинома, что не требует выполнения процедур перемножения входного сигнала и весовой функции и последующего интегрирования результата перемножения.
Полагаем, что номеру гармоники N соответствует высшая граничная частота Fmax=Nf=Nmaxf, выбранная из информационных или энергетических соображений, а потому для получения измерительной информации используем гармоники с номерами N0=Nmax-1 и Nmin=N0-1.
Покажем, что указанные гармоники обеспечивают физическое выделение гармонического колебания без использования процедур перемножения входного сигнала на весовую функцию с последующим интегрированием произведения.
Действительно, входной сигнал  может быть представлен в виде
может быть представлен в виде
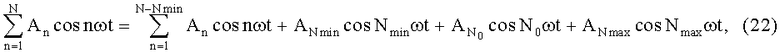
который позволяет реализовать процедуру фильтрации следующим образом:




Фильтрация измерительных сигналов осуществляется следующим образом. Подлежащий фильтрации измерительный сигнал с выхода источника 1 поступает на вход блока синхронизации 10 и одновременно на первый вход дифференциального усилителя 2, на второй вход которого с выхода формирователя 7 подается равноамплшудный полином  .
.
Выходное напряжение усилителя 2 представляет собой результат низкочастотной фильтрации входного сигнала

Одновременно точно такое же напряжение вырабатывается на выходе дифференциального усилителя 3 Uвых3(t)=Uвых2(t). Одновременно на первый вход дифференциального усилителя 4 поступает выходное напряжение усилителя 3, а на второй его вход с выхода формирователя 9 подается равноамплитудный полином  . Выходное напряжение усилителя 4 имеет вид:
. Выходное напряжение усилителя 4 имеет вид:
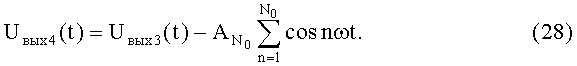
Одновременно выходное напряжение дифференциального усилителя 2 поступает на первый вход дифференциального усилителя 5, на второй вход которого с выхода формирователя 8 подается равноамплитудный полином  . Выходное напряжение усилителя 5 имеет вид:
. Выходное напряжение усилителя 5 имеет вид:

Поступающие на входы дифференциального усилителя 6 выходные напряжения усилителей 4 и 5 создают выходное напряжение

Таким образом, по сравнению с прототипом, заявляемый способ обеспечивает принципиальную возможность выделения отдельно взятого гармонического колебания из входного сигнала без использования процедур перемножения входного сигнала на весовую функцию и последующего интегрирования результата перемножения, требующих большого объема оборудования.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2003 |
|
RU2251791C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИСХОДНЫХ СИГНАЛОВ | 2003 |
|
RU2259591C2 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ТРАКТА СВЯЗИ | 1992 |
|
RU2069935C1 |
| Цифровое устройство формирования огибающей выходных сигналов передатчиков радиолокационных систем | 2018 |
|
RU2711507C2 |
| Радиопередающее устройство с цифровой коррекцией нелинейности | 2019 |
|
RU2731135C1 |
| СПОСОБ ИЗМЕРЕНИЯ УХОДА ЧАСТОТЫ НЕСУЩЕЙ В СИГНАЛЕ ДАЛЬНЕГО ЭХА В КОММУТИРУЕМОМ ДВУХПРОВОДНОМ КАНАЛЕ ТЕЛЕФОННОЙ СЕТИ ОБЩЕГО ПОЛЬЗОВАНИЯ | 2007 |
|
RU2345373C1 |
| УСТРОЙСТВО ПЕРЕДАЧИ ОДНОПОЛОСНОГО СИГНАЛА | 2006 |
|
RU2329597C1 |
| СПОСОБ ПЕРЕДАЧИ ОДНОПОЛОСНОГО СИГНАЛА | 2006 |
|
RU2332781C1 |
| СПОСОБ СИНТЕЗА ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ ПО ЗАДАННОЙ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ | 2001 |
|
RU2241306C2 |
| Способ формирования предварительно искаженного сигнала | 2019 |
|
RU2726184C1 |
Изобретение относится к информационно-измерительной технике и может быть использовано для преобразования аналоговых входных сигналов в аналоговые выходные сигналы. Техническим результатом является точное выделение отдельно взятого гармонического колебания, частота которого кратна частоте повторения измерительного сигнала. Способ заключается в том, что входной измерительный сигнал Uвx(t), подлежащий фильтрации, суммируют одновременно с инвертированными равноамплитудными полиномами 

 представляющими собой суммы из NMAX, N0 и NMIN гармонических колебаний кратных частот и равных амплитуд, равноамплитудные полиномы воспроизводятся в виде амплитудно-модулированных колебаний, закон изменения огибающей каждого из которых определяется отношением мгновенных значений синусоидальных колебаний равных амплитуд, при этом частота делимого в N раз выше частоты повторения фильтруемого сигнала, а частота делителя равна частоте повторения фильтруемого сигнала. 1 ил.
представляющими собой суммы из NMAX, N0 и NMIN гармонических колебаний кратных частот и равных амплитуд, равноамплитудные полиномы воспроизводятся в виде амплитудно-модулированных колебаний, закон изменения огибающей каждого из которых определяется отношением мгновенных значений синусоидальных колебаний равных амплитуд, при этом частота делимого в N раз выше частоты повторения фильтруемого сигнала, а частота делителя равна частоте повторения фильтруемого сигнала. 1 ил.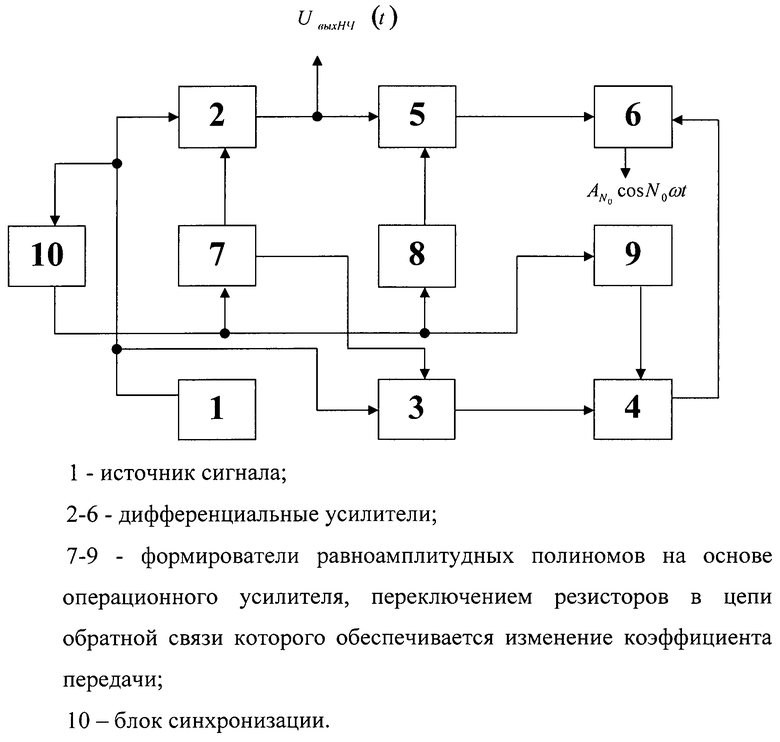
Способ фильтрации измерительных сигналов, заключающийся в том, что входной измерительный сигнал Uвх(t), подлежащий фильтрации, суммируют одновременно с инвертированными равноамплитудными полиномами  ,
,  и
и  , представляющими собой суммы из NMAX, N0 и NMIN гармонических колебаний кратных частот и равных амплитуд в соответствии с системой уравнений:
, представляющими собой суммы из NMAX, N0 и NMIN гармонических колебаний кратных частот и равных амплитуд в соответствии с системой уравнений:
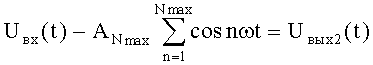 ;
;
 , где Uвых3(t)=Uвых2(t);
, где Uвых3(t)=Uвых2(t);
 ;
;

где Uвых2(t) - выходное напряжение дифференциального усилителя 2;
Uвых3(t) - выходное напряжение дифференциального усилителя 3;
Uвых4(t) - выходное напряжение дифференциального усилителя 4;
Uвых5(t) - выходное напряжение дифференциального усилителя 5;
 - выходное напряжение дифференциального усилителя 6,
- выходное напряжение дифференциального усилителя 6,
а равноамплитудные полиномы воспроизводятся в виде амплитудно-модулированных колебаний, закон изменения огибающей каждого из которых определяется отношением мгновенных значений синусоидальных колебаний равных амплитуд, при этом частота делимого в N раз выше частоты повторения фильтруемого сигнала, а частота делителя равна частоте повторения фильтруемого сигнала.
| БАСКАКОВ С.И | |||
| Радиотехнические цепи и сигналы | |||
| - М.: «Высшая школа», 2003, с.354 | |||
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2003 |
|
RU2251791C2 |
| Синхронный полосовой фильтр | 1989 |
|
SU1658377A1 |
| Помехоустойчивый способ измерения | 1979 |
|
SU813771A1 |
| US 4992967 A, 12.02.1991 | |||
| Устройство для резки полупроводниковых материалов | 1971 |
|
SU450260A1 |
Авторы
Даты
2012-09-27—Публикация
2010-05-20—Подача