Изобретение относится к приборостроению.
Цель изобретения - снижение погрешности измерений.
Известен итерационный способ [1] автоматической коррекции погрешностей измерительных устройств. В этом случае измеряемый сигнал Uвх через коммутатор и АЦП заносится в ЭВМ, где приближенно вычисляется цифровой эквивалент в виде кода. После чего эталонное значение сигнала, примерно соответствующее Uвх, формируется в ЭВМ в цифровом виде и после преобразования цифроаналоговым преобразователем подается через коммутатор вместо Uвх для уточнения параметров измерительного канала. Таким образом, определяются (калибруются) параметры измерительной цепи в точке, почти совпадающей с измеряемым сигналом. При этом возможно несколько итерационных процедур. Недостатком такого метода является затрата больших вычислительных мощностей, поскольку при измерении для каждого значения сигнала необходимо производить калибровку.
Известен способ калибровки измерительных систем [2] (стр.77, рис. 3.12), являющийся ближайшим аналогом, путем попеременного ввода в измерительный канал измеряемых и фиксированных эталонных сигналов, автоматического определения в интервалах между эталонными сигналами реальной рабочей преобразовательной характеристики системы по значениям эталонных сигналов путем интерполяции значений измеряемого сигнала в соответствии с опорными эталонными значениями.
Перед началом работы и в процессе измерений (например, напряжений) периодически производится подключение ко входу набора эталонных значений сигнала. Принципиально возможно в этом случае превратить нестабильную измерительную систему в прецизионную, когда погрешности измерений практически будут соответствовать погрешности задания эталонных сигналов. Но недостатком способа является то, что под воздействием дестабилизирующих факторов (температурный дрейф, нестабильность питающих напряжений и т.п.) параметры датчика и/или измерительного канала могут значительно изменяться. В этом случае может оказаться, что использование заранее заданного набора образцовых мер не сможет обеспечить заданную погрешность измерений и необходимо будет проводить коррекцию узлов аппроксимации (эталонных значений сигнала). В результате, выбор оптимальных эталонных значений сигнала становится идентичным поиску полинома наилучшего приближения функции на основании имеющегося полинома в соответствии с обобщенной теоремой Чебышева, когда все n+2 экстремальные значения погрешностей ΔL на интервале интерполяции (в нашем случае измерений) поочередно меняют знак и равны между собой по абсолютной величине [3, 4]. (Пример в [4] на стр.228-229, рис. 4.6.1).
В то же время поиск полинома наилучшего приближения является длительным процессом с большими затратами вычислительных мощностей и больше применим при однократном использовании для нахождения наилучших полиномов для аппроксимации часто используемых функций, например sinβ, 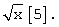
В связи с этим рассмотрим упрощенные методы поиска полиномов наилучшего приближения для аналитических функций и распространим его на способы калибровки измерительного канала с быстрым поиском наиболее оптимальных значений эталонных калибровочных сигналов (узлов аппроксимации) с автоматическим одновременным учетом всех дестабилизирующих факторов без непосредственного определения их значений и с автоматической коррекцией результатов измерений.
Перед калибровкой измерительных систем исследуют вид преобразовательных характеристик датчиков, коэффициентов передачи измерительных трактов. В этом случае, например, снимается набор характеристик датчиков с учетом их разброса от влияния различных дестабилизирующих факторов и определяется усредненное аппроксимирующее аналитическое выражение. Исследуются характерные точки для аппроксимируемой функции, разброс значений конечных разностей, производных относительно среднего значения. Это обеспечивает уменьшение погрешностей метода при выборе степени аппроксимирующего полинома наилучшего приближения и значений аргумента в узлах аппроксимации (эталонных значений сигнала) для калибруемой системы. В этом случае сравнительно большие вычислительные затраты будут необходимы только на этапе предварительных расчетов для целой партии измерительных приборов и для одного прибора на этапе его первой калибровки перед сдачей потребителю в эксплуатацию. Вычислительные затраты в процессе эксплуатации прибора непосредственно на калибровку при проведении измерений и воздействий на преобразовательную характеристику датчиков дестабилизирующих факторов поэтому необходимо минимизировать. Поиск оптимальных эталонных значений сигнала для калибровки измерительных систем соответствует поиску узлов аппроксимации полинома наилучшего приближения при интерполяции функциональных зависимостей [3, 4]. Поэтому необходимо исследовать упрощенные методы поиска полиномов наилучшего приближения. Тем более что во многих работах при аппроксимации функций используют не полином наилучшего приближения, а обычные полиномы Чебышева, Ньютона или модифицированный ряд Тейлора [5]. В то же время обычный полином Чебышева дает, например, для функций sinβ при β∈[0°; 90°] различия в максимальных значениях погрешностей на концах интервала в 2 раза, а для функций 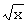
 в десятки раз. Для иллюстрации методов и алгоритмов предлагаемого способа калибровки предварительно проведем сравнительную оценку полиномов Тейлора, Ньютона и Чебышева степени n по отношению к "идеальному" полиному наилучшего приближения функции в соответствии с обобщенной теоремой Чебышева, когда все n+2 экстремальные значения погрешностей на интервале интерполяции β∈[a, b] поочередно меняют знак и равны между собой по абсолютной величине [3].
в десятки раз. Для иллюстрации методов и алгоритмов предлагаемого способа калибровки предварительно проведем сравнительную оценку полиномов Тейлора, Ньютона и Чебышева степени n по отношению к "идеальному" полиному наилучшего приближения функции в соответствии с обобщенной теоремой Чебышева, когда все n+2 экстремальные значения погрешностей на интервале интерполяции β∈[a, b] поочередно меняют знак и равны между собой по абсолютной величине [3].
Оценка максимальной погрешности интерполяции для полинома Чебышева Ln(β) степени n имеет вид
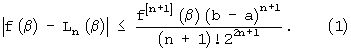
Выбор узлов производится в соответствии с выражением:
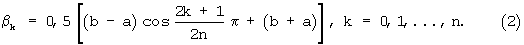
Оптимизацию коэффициентов обычного полинома Чебышева n-й степени необходимо проводить, когда имеет место сравнительно быстрое изменение производной f[n+1](β) на интервале интерполяции. В этом случае экстремальные значения погрешностей могут отличаться между собой по абсолютной величине в десятки раз. Методы уточнения узлов интерполяции полиномов первой-третьей степени на интервале [а, b] при адаптации измерительной системы к изменяющимся условиям проиллюстрируем на примере приближенного поиска полинома наилучшего приближения для функции sinβ. При b=0 и a=Н интервал интерполяции будет соответствовать Н. Для обычной формулы Ньютона, где расстояния между узлами интерполяции h равны, и H=nh - получим
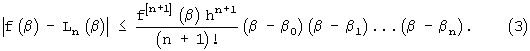
Из выражения (2) следует, что погрешность для полинома Чебышева будет в 22n+l раза меньше, чем для полинома такой же степени, определенного в соответствии с формулой Тейлора для интервала интерполяции Н. Для формулы Ньютона выигрыш несколько меньше и определяется выражением:(β-β0)(β-β1)...(β-βn) [3]. В то же время для полинома Чебышева по сравнению с полиномом Ньютона вводится нулевой член, что ведет к дополнительным программно-аппаратурным затратам. Необходимо оценить его влияние на значение погрешности интерполяции.
Задача оптимизации алгоритма калибровки состоит в том, чтобы при сравнительно больших единичных программно-аппаратурных затратах, относящихся к этапу разработки измерительной системы и подбору степени аппроксимирующего полинома наилучшего приближения, узлов интерполяции эталонных значений сигнала калибровки обеспечить минимальные программно-аппаратурные затраты при многократных периодических калибровках непосредственно в процессе измерений. При этом с учетом медленного или быстрого изменения производной f[n+1], экстремальных значений погрешностей в характерных точках под воздействием дестабилизирующих факторов на интервале аппроксимации Н следует с минимальными вычислительными затратами определять необходимость изменения коэффициентов полинома при заданных узлах интерполяции по определенным критериям и при необходимости проводить и коррекцию расположения узлов.
1. Случай кусочно-линейной интерполяции
Для полинома
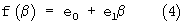
узлы Чебышева на интервале β∈[0, Н], соответствующем отрезку [0, а], будут расположены симметрично относительно его середины. При n=1, к=0,1 и а=Н получим в соответствии с выражением (2) βmа1=(0,5+0,5cosπ/4)H=0,85355H, βmа0=0,14645H
Максимальное значение погрешности для полинома Чебышева равно
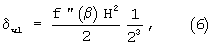
то есть в 23 раза меньше, чем для ряда Тейлора. При этом нет необходимости производить оптимизацию коэффициентов полинома путем изменения значений аргумента в узлах аппроксимации, если f″(β)=const. При f(β)=var узлы аппроксимации должны сдвигаться к значениям аргумента, где вторая производная f″(β) имеет наибольшее значение.
Для формулы Ньютона текущее значение погрешности аппроксимации в соответствии с выражением (3) при βмл=β-β0 и β-β1= (βмл-h)
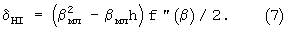
При f″(β)=const, βмл=0,5h максимальное значение погрешности аппроксимации равно δHI=125h2f″(β), то есть в четыре раза меньше, чем для ряда Тейлора. Логично дополнительно провести экстраполяцию формулы Ньютона влево и вправо от значений аргумента βмл=0 и βмл=h на величину 0,207h, когда в соответствии с выражением (7) экстремальные значения погрешности δHI еще не будут превышать максимального значения δHIM=0,125h2f″(β). Таким образом, при увеличении интервала интерполяции до значения 1,414h максимальное значение погрешности для формулы Ньютона будет в (1,414)2·4=8 раз меньше, чем для ряда Тейлора.
Интересно отметить, что если перенормировать расстояние между узлами интерполяции для полинома Чебышева 0,85355Н-0,14645H=0,7071H в соответствующее расстояние между узлами для полинома Ньютона, то получим для формулы Ньютона расширенный интервал аппроксимации HHl=1,414h, где значения аргумента в узлах аппроксимации, текущие и максимальные значения погрешностей в полиномах Чебышева и Ньютона равны.
Выбор эталонных значений функции при β=0,14645H, β=0,85355H и f″β=const для полинома Ньютона фактически обеспечивает расчет коэффициентов полинома наилучшего приближения Чебышева. Для сокращения одной операции алгебраического сложения в выражении (4) необходимо исключить нулевой член е0. При этом уменьшается эквивалентный интервал интерполяции HHI=1,207h и по сравнению с рядом Тейлора для полинома Ньютона с экстраполяцией только вправо погрешность будет меньше только в 5,83 раза. Первый узел должен быть при f(0)=0 и расстоянии между узлами интерполяции h=0,8285H. Фактически же интервал интерполяции будет равен Н.
Когда производная f″(β)≠const, то оптимальной с точки зрения определения минимального значения погрешности при линейной аппроксимации считается, например, следующий алгоритм. Аппроксимирующий полином выбирается так, чтобы он совпадал с градуируемой кривой в начальной и конечной точках. Определяется максимальное значение погрешности δHIM. После чего аппроксимирующий полином поднимается на величину δHIM/2 (п.4, стр.228, рис. 4.6.1.). Но такой алгоритм в связи с определением промежуточных значений требует больших вычислительных затрат и при проведении измерений за ограниченный временной интервал не пригоден.
В связи с этим, зная примерно значение второй производной и ее разброс под влиянием дестабилизирующих факторов относительно среднего значения, можно путем моделирования на ЭВМ рационально выбрать узлы аппроксимации и оценить максимальное значение погрешности с учетом разброса значений f″(β). Тем более что значения производной обычно изменяются меньше чем на порядок.
При кусочно-линейной интерполяции для функции sinβ в случае использования ряда Тейлора y=β практически максимальное значение погрешности определим при β=π/2 δTI=0,57.
Для функции sinβ в случае использования ряда Тейлора y=β практически максимальное значение погрешности определим при β=π/2 δTI=0,57. Для формулы Ньютона y=0,636619β и максимальное значение погрешности δHI=0,21, т.е. в 0,57/0,21=2,7 раза меньше, чем для ряда Тейлора. Практически для полинома Чебышева при y=0,073587+0,671315β имеем значение погрешности в 0,57/0,128=4,45 раза меньше, чем для ряда Тейлора (фиг.1). Полином наилучшего приближения для функции sinβ y=0,636619β+0,105257, полученный путем моделирования дает погрешность 0,105, что в 5,43 раза лучше, чем для ряда Тейлора, и только на 22% лучше, чем для обычного полинома Чебышева.
Полином наилучшего приближения y=0,724612β без нулевого члена дает значение погрешности δ=0,138, что в 4,13 раз лучше, чем для ряда Тейлора. Эксперименты показывают, что при изменении второй производной в узлах аппроксимации примерно в 3 раза максимальное значение погрешности для полинома Чебышева удалось уменьшить только в 1,22 раза.
Интересно отметить, что среднее арифметическое всех абсолютных экстремальных значений погрешности для полинома Чебышева равно 0,1032 и с погрешностью 1,7% совпадает с максимальным значением погрешности для полинома наилучшего приближения (см. фиг.1).
Из выражения (7) фактически представляющего собой текущее значение погрешности для полинома Чебышева за пределами интервала интерполяции h и из графиков следует, что около узлов интерполяции значение погрешности в функции аргумента изменяется практически по линейному закону. Таким образом, можно предложить упрощенный алгоритм перевода полинома Чебышева в полином наилучшего приближения путем выравнивания экстремальных значений погрешностей только на концах интервала, пригодный и для калибровки измерительных систем при воздействии дестабилизирующих факторов.
В этом случае, не определяя максимальное значение погрешности внутри интервала аппроксимации H, вычисляют среднее значение погрешности по абсолютным значениям погрешностей на концах интервала и вводят поправки на смещение обоих узлов интерполяции исходя из соответствующих приращений погрешностей
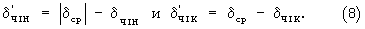
Для диффузии sinβ получено среднее значение δср=(0,128+0,0735)/2=0,10075. Это значение только на 4% отличается от оптимального 0,105.
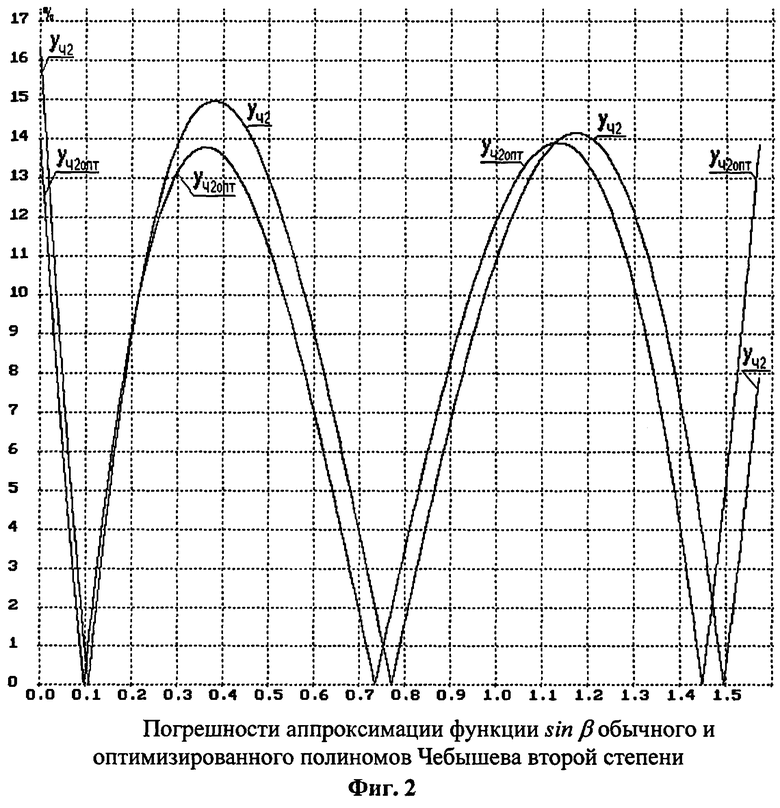
2. Случай полинома второй степени
Для полинома второй степени
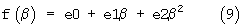
Определим узлы аппроксимации в соответствии с выражением (2) β1=0,066987 Н, β2=0,5 Н, β3=0,933012 Н. Экстремальные значения погрешности будут на интервале Н четыре раза менять знак. В соответствии с (3) теоретическое максимальное значение погрешности в полиноме Чебышева будет в 32 раза меньше, чем для ряда Тейлора.
Для формулы Ньютона на интервале аппроксимации Н=2h текущее значение погрешности метода при квадратичной аппроксимации можно приближенно оценить выражением
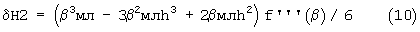
При β=1,577h и β=1,423h получим одинаковые по абсолютной величине максимальные значения погрешностей:
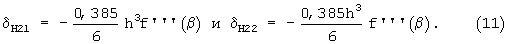
Для ряда Тейлора, когда интервал аппроксимации H=2h, максимальное значение погрешности: δT2=f'''(β)(2h)3/3!=8h3f'''(β)/6 будет в 20,78 раз больше, чем для формулы Ньютона.
Если экстраполировать полином Ньютона в соответствии с выражением (10) влево и вправо от значений аргумента β=0 и β=2h на величину 0,165h, когда экстремальные значения погрешности δH2 еще не будут превышать максимальных, то оказывается, что при увеличении интервала интерполяции до значения 2,31h максимальное значение погрешности для формулы Ньютона по сравнению с рядом Тейлора можно уменьшить в (2,31)3/0,385=32 раза.
Если перенормировать расстояние между узлами интерполяции для полинома Чебышева 0,5Н-0,066987Н=0,433013Н в соответствующее расстояние между узлами для полинома Ньютона, то получим для формулы Ньютона расширенный интервал интерполяции Нн=2,3094h. Таким образом, если исключить нулевой член в полиномах Чебышева или Ньютона (без экстраполяции влево), то по сравнению с рядом Тейлора отношение максимальных значений погрешностей будет равно только (2,155)3/0,385=26.
При применении ряда Тейлора оценку сверху погрешности метода для функции sinβ при f″(0)=0 практически невозможно произвести.
Для обычного полинома Чебышева у=-0,016222+β(1,188109-0,340131β) и полинома наилучшего приближения у=-0,013843+β(1,1744843-0,331410β) максимальные значения погрешностей (фиг.2.) соответственно равны 0,0162 и 0,01384.
Для полинома Чебышева без нулевого члена или Ньютона с экстраполяцией только вправо узлы интерполяции β0=0, β1=H/2,16=0,46296H, β2=0,92593Н, а сам полином у=β(1,145419-0,318005β) имеет максимальное значение погрешности 0,0195. Полином наилучшего приближения у=β(1,136553-0,311139β) имеет максимальное значение погрешности 0,0176.
Для полинома Чебышева математическое ожидание абсолютных значений экстремальных погрешностей равно 0,01373 и отличается от максимального для полинома наилучшего приближения на 1,6%.
Цель изобретения - снижение погрешности измерений.
Поставленная цель достигается тем, что в способе калибровки измерительных систем путем попеременного ввода в измерительный канал измеряемых и фиксированных эталонных сигналов, автоматического определения в интервалах между эталонными сигналами реальной рабочей преобразовательной характеристики системы по значениям эталонных сигналов путем интерполяции значений измеряемого сигнала в соответствии с опорными эталонными значениями, дополнительно при воздействии дестабилизирующих факторов периодически в процессе между измерениями по эталонным значениям, отличающимся от предыдущих, определяются погрешности измерительного канала в характерных и (или) эмпирически полученных точках диапазона измерений и в соответствии с их соотношением автоматически оставляются без изменений или корректируются эталонные значения входного измеряемого сигнала (узлы аппроксимации), по которым воспроизводится многочлен степени n наилучшего равномерного приближения, интерполирующий и экстраполирующий по значениям эталонных сигналов передаточную характеристику измерительной системы и обеспечивающий в соответствии с обобщенной теоремой Чебышева на интервале измерений по крайней мере n+1 или n+2 точки х1∈[х0, хn+1], в которых погрешности измерений L принимают поочередно с учетом неустранимых погрешностей ΔL равные максимальные значения +(L±ΔL) и -(L±ΔL).
По второму варианту, дополнительно при интерполяции и экстраполяции передаточной характеристики полиномом первой степени при воздействии дестабилизирующих факторов периодически определяются погрешности на концах диапазона измерения и в соответствии с разностями их среднего значения и значений погрешностей на концах интервала производится смещение эталонных значений, расчет новых значений коэффициента передачи и смещение нуля измерительного канала с выравниванием и уменьшением максимальных значений погрешностей на концах интервала измерений.
По третьему варианту, дополнительно при интерполяции и экстраполяции передаточной характеристики полиномом первой степени при воздействии дестабилизирующих факторов периодически определяются погрешности на концах диапазона измерения и в характерных точках, где знак значения погрешности противоположен знакам погрешностей на концах диапазона, и в соответствии со средним значением погрешностей и их соотношением по предварительно эмпирически подобранным функциональным зависимостям на соответствующую величину смещаются значения двух эталонных сигналов, определяющих узлы аппроксимации аппроксимируемого полинома, по которым определяются параметры измерительного канала, обеспечивающие коррекцию рабочей характеристики канала для аппроксимации измеряемых сигналов полиномом наилучшего приближения.
По четвертому варианту, дополнительно при интерполяции и экстраполяции передаточной характеристики полиномом второй степени при воздействии дестабилизирующих факторов периодически определяются погрешности на концах диапазона измерения и еще в двух характерных точках внутри диапазона, где знак значения погрешности противоположен знакам погрешностей на концах диапазона, и в соответствии с соотношением и средним значением погрешностей по эмпирически подобранным функциям на соответствующую величину смещаются значения трех эталонных сигналов, определяющих узлы аппроксимации и интерполяции полинома второй степени.
По пятому варианту, дополнительно при интерполяции и экстраполяции передаточной характеристики полиномом первой степени при воздействии дестабилизирующих факторов периодически определяются погрешности на концах диапазона измерения и (или) в характерных точках, где знак значения погрешности противоположен знакам погрешностей на концах интервала и в соответствии с соотношением погрешностей по предварительно эмпирически подобранным функциональным зависимостям или таблицам определяются параметры измерительного канала, обеспечивающие аппроксимацию и интерполяцию полиномом наилучшего приближения.
Таким образом, в случае кусочно-линейной интерполяции в соответствии с выражением (4) предлагаются два алгоритма калибровки в процессе измерений: 1) с коррекцией коэффициентов полинома без изменения узлов аппроксимации, 2) с коррекцией узлов аппроксимации при сравнительно больших изменениях f″(β) под влиянием дестабилизирующих факторов.
Исходя из приращений погрешностей 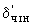 =0,10075-0,0735=0,027,
=0,10075-0,0735=0,027, 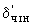 =0,128-0,10075=0,0272 проводится смещение узлов аппроксимации на 0,085 (радиан) в начале, и на 0,04 в конце интервала аппроксимации. Из фиг.1 следует, что такая аппроксимация практически соответствует полиному наилучшего приближения (фиг.3).
=0,128-0,10075=0,0272 проводится смещение узлов аппроксимации на 0,085 (радиан) в начале, и на 0,04 в конце интервала аппроксимации. Из фиг.1 следует, что такая аппроксимация практически соответствует полиному наилучшего приближения (фиг.3).
Для случая полинома второй степени предлагается проводить выравнивание экстремальных значений погрешностей на краях интервала Н путем соответствующего сдвига крайних узлов интерполяции. Например, среднее значение погрешности для крайних точек будет равно 0,01353 (см. фиг.2.) и отличается от 0,013843 только на 2,5%.
На рисунках показано:
- фиг.1 - сравнение двух вариантов полинома Чебышева первой степени - обычного (1) и оптимизированного (2) с приведением к шкале погрешностей;
- фиг.2 - сравнение двух вариантов для полинома Чебышева второй степени;
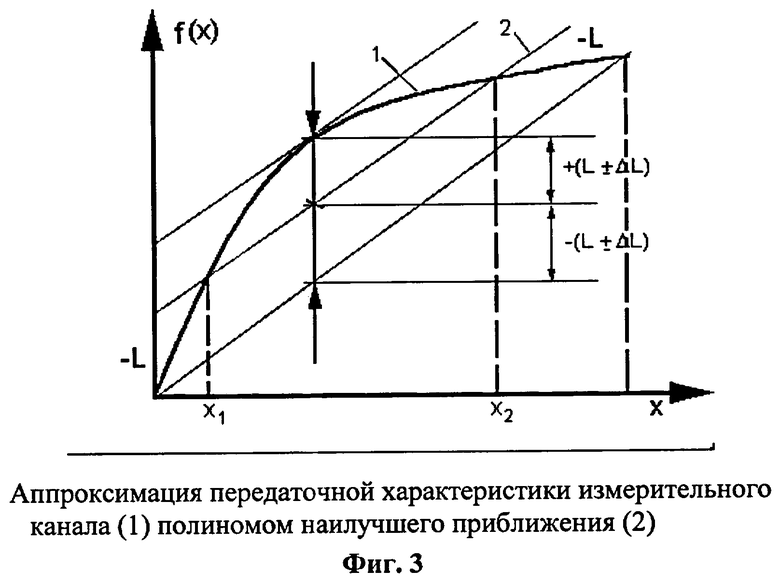
- фиг.3 - варианты аппроксимации передаточной характеристики измерительного канала в обычном случае и полиномом наилучшего приближения;
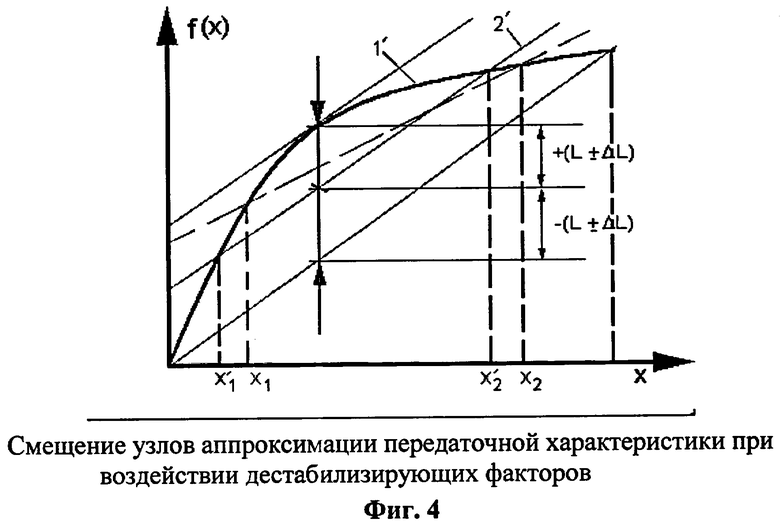
- фиг.4 - смещение узлов аппроксимации при наличии дестабилизирующих воздействий.
Принцип реализации заявляемого способа кратко может быть показан следующим образом. На вход приемного устройства подаются полезные (измеряемые) и эталонные (калибровочные) сигналы. В промежутках между подачей калибровочных сигналов путем интерполяции значений измеряемого сигнала в соответствии с опорными эталонными значениями осуществляется автоматическое определение реальной преобразовательной характеристики приемного канала. Поскольку под влиянием дестабилизирующих факторов, таких как температурные перепады, изменения давления и т.п., может наблюдаться смещение характеристики передаточного канала, что неизбежно приводит и к изменению преобразования эталонных сигналов, то в тех точках характеристики, которые являются характерными или эмпирически заранее найденными, определяются погрешности, после чего находится их соотношение и в зависимости от того, какой характер носит это соотношение, осуществляется смещение (коррекция) эталонных значений входного измеряемого сигнала (коррекция узлов аппроксимации) или же такого смещения не осуществляется. При этом коррекция осуществляется с учетом того, что эталонные значения должны удовлетворять условию воспроизведения многочлена наилучшего равномерного приближения, интерполирующего или экстраполирующего по значениям этих эталонных сигналов передаточную характеристику приемного тракта таким образом, чтобы погрешности поочередно принимали значения, разные по знаку, но одинаковые по абсолютной величине.
На фиг.3 приведена передаточная характеристика измерительного канала (1) полиномом наилучшего приближения (2) при эталонных значениях сигналов х1 и х2. На фиг.4 передаточная характеристика при воздействии дестабилизирующих факторов 11 изменила свою форму и вместо общепринятого способа калибровки с заданием эталонных значений х1 и х2 в соответствии с предлагаемым способом необходимо изменить значения эталонных сигналов на х1 и х3, чтобы значительно уменьшить погрешность при х=0. Пунктиром на фиг.4 показана передаточная характеристика при прежних, не измененных значениях эталонных сигналов х1 и х2.
Литература
1. Алиев Т.М. и др. Итерационные методы повышения точности измерений. - М.: Энергоатомиздат, 1968.
2. Чекушкин В.В., Ромашов В.В., Тарануха В.М. Автоматизированные системы контроля и управления радиоэлектронными средствами. - Муром: МИ ВлГУ, - 120 с.
3. Березин И.С., Жидков Н.П. Методы вычислений. T.1. - М.: Физматгиз, 1962.
4. Бахвалов Н.С. Численные методы. - М.: Наука, 1975 г.
5. Чекушкин В.В. Реализация преобразования представлений ортогональных составляющих сигналов в амплитуду и фазу // Измерительная техника, - 2001 г., № 4. С.18-21.
6. Сопельников В.М. и др. Цифроаналоговые преобразователи для воспроизведения тригонометрических функций // Изм. техн., - 2001 г., № 3. С.17-19.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КАЛИБРОВКИ ИЗМЕРИТЕЛЬНЫХ СИСТЕМ | 2010 |
|
RU2476896C2 |
| СПОСОБ И УСТРОЙСТВО ВЫЧИСЛЕНИЯ КВАДРАТНОГО КОРНЯ | 2008 |
|
RU2438160C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ | 2015 |
|
RU2602989C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ТАБЛИЧНО-АЛГОРИТМИЧЕСКИМ МЕТОДОМ | 1996 |
|
RU2136041C1 |
| Способ имитации траекторий движения объектов | 2015 |
|
RU2617144C1 |
| СПОСОБ ИЗМЕРЕНИЯ ДАВЛЕНИЯ, КАЛИБРОВКИ И ДАТЧИК ДАВЛЕНИЯ НА ОСНОВЕ НАНО- И МИКРОЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ | 2012 |
|
RU2498250C1 |
| СПОСОБ ЛИНЕАРИЗАЦИИ ГРАДУИРОВОЧНОЙ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНОГО ПРЕОБРАЗОВАТЕЛЯ | 2011 |
|
RU2468379C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЭФФЕКТИВНОЙ ПЛОЩАДИ РАССЕЯНИЯ НАЗЕМНЫХ ОБЪЕКТОВ РАДИОЛОКАТОРОМ С СИНТЕЗИРОВАННОЙ АПЕРТУРОЙ АНТЕННЫ | 2006 |
|
RU2308050C1 |
| СПОСОБ ИНТЕРПОЛЯЦИИ ЦИФРОВОГО ИЗОБРАЖЕНИЯ | 2007 |
|
RU2367019C2 |
| СПОСОБ ИЗМЕРЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ | 1999 |
|
RU2169940C1 |
Изобретение относится к измерительной технике, а именно к автоматической коррекции погрешностей измерительных устройств. Технический результат - повышение точности измерения. Для достижения данного результата при воздействии дестабилизирующих факторов периодически в процессе между измерениями осуществляют измерение на основе оценки эталонных значений. При этом в характерных и(или) эмпирически полученных точках диапазона измерений, в соответствии с их соотношением, автоматически запоминают или корректируют эталонные значения входного измеряемого сигнала. На основе соответствующих значений получают аппроксимации, по которым воспроизводится функция наилучшего равномерного приближения, интерполирующая и экстраполирующая значения эталонных сигналов. 4 з.п. ф-лы, 4 ил.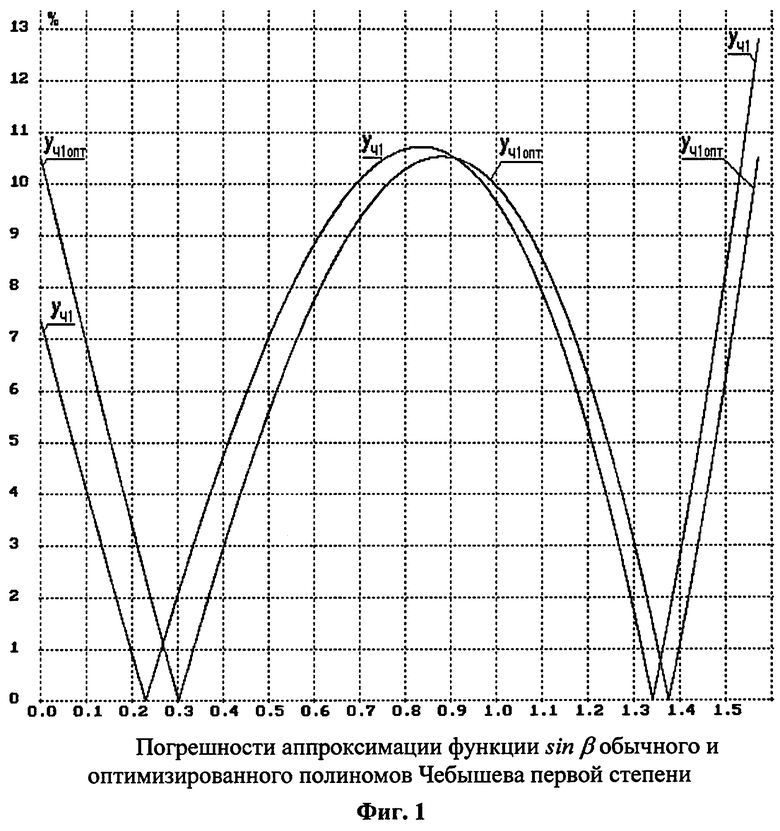
| Чекушкин В.В., Ромашов В.В., Тарануха В.М | |||
| Автоматизированные системы контроля и управления радиоэлектронными средствами | |||
| - Муром: МИ ВлГУ, с.120 | |||
| Способ калибровки амплитудных шкал измерительных приборов | 1987 |
|
SU1525644A1 |
| Способ измерения значений погрешностей измерителей напряжения | 1973 |
|
SU636566A1 |
| Способ определения статистической погрешности измерительных устройств | 1981 |
|
SU991342A2 |
| Способ многоканальной регистрации результатов измерений и устройство для его осуществления | 1990 |
|
SU1747905A1 |
| Устройство для автоматизированной поверки измерительных приборов | 1982 |
|
SU1051478A2 |
Авторы
Даты
2005-10-20—Публикация
2002-01-28—Подача