Предлагаемое изобретение относится к области боеприпасов, в частности к авиационным бомбам
При полете летательных аппаратов (ЛА) для бомбардировки наземных целей имеют место навигационные ошибки, которые не позволяют сбросить авиационные бомбы (АБ) в заданные точки с первого захода. Также возникает необходимость поражения площадных целей. В этом случае необходимо одновременно использование нескольких бомб, которые сбрасывают в одной точке и поражают разные цели.
Существующие неуправляемые АБ, состоящие из корпуса с крестообразными стабилизаторами и боевой части с взрывчатым устройством [1], не имеют возможности управления или изменения аэродинамических характеристик. Таким образом, точка приземления определяется только условиями сброса и конструктивными характеристиками бомбы. Устранение навигационных ошибок, а также площадное бомбометание на одном пролете самолета при использовании существующих АБ невозможно. Решение этих задач значительно расширило область функционального применения этих бомб.
Основными функциональными элементами управления АБ КАБ-500Л, влияющими на ее динамику полета, являются планер с крестообразным стабилизатором и дестабилизатором, система управления, состоящая из лазерного координатора цели, автопилота и рулевых приводов, а также источника питания и боевой части с взрывателем.
Наличие системы управления с приводами, отклоняющими задние кромки стабилизаторов, позволяет корректировать траекторию. Недостатком бомб типа КАБ является необходимость непрерывной подсветки цели лазерным лучом до момента взрыва бомбы. Также невозможно одновременное наведение на цель больше одной бомбы. Таким образом, невозможно поражение площадных целей. Снижение стоимости и исключение указанных выше недостатков привело бы к более широкому ее применению.
Известны разовые бомбовые кассеты [1], состоящие из корпуса, вышибного заряда с взрывателем и набора мелких бомб. Устройство позволяет поражать площадные цели, но наведение на конкретные объекты (цели) на выбранной площади невозможно, т.к. бомбы неуправляемые. Придание им свойств корректируемых бомб повысило бы эффективность их применения.
Создание бомб с корректируемой траекторией, имеющими возможность поражать несколько индивидуальных целей при одновременном сбросе, а также производить корректируемое площадное бомбометание, вместе с тем не требующими «подсветки» с самолета-носителя, и является задачей данного изобретения.
Задача решаема при создании бомбы с корректируемыми аэродинамическими характеристиками. В предлагаемой бомбе на задних кромках стабилизаторов устанавливают рули с приводами. В качестве приводов предлагается использовать типовые приводы, применяемые в КАБ-500Л [2]. Отличие заключается в том, что устанавливаются приводы электрического принципа действия. Источник энергии на бомбе отсутствует. Питание электропривода осуществляется через электроразъем до момента отделения бомбы.
Для контроля положения рулей устанавливают датчики обратной связи. Таким образом, новизна изобретения в принципе бомбометания:
- предварительный расчет положения рулей для заданного отклонения траектории;
- отклонение рулей выполняют до момента отцепки бомбы:
- бомбометание с фиксированным положением рулей.
Возможность решения терминальной задачи при фиксированном положении рулей показано в Приложении 1. Требования к траектории отсутствуют. В этом случае решение терминальной задачи - попадания АБ в заданную точку, в качестве которой выбирают цель, возможно, методом программного управления [3] при единственном заранее рассчитанном положении рулей.
На чертеже показаны устройства, осуществляющие работу предлагаемого устройства.
Предлагаемая бомба состоит из элементов обычной неуправляемой бомбы: корпуса (отсеки I, II, III), взрывателя 2, связанного с детонатором, боевого заряда, дестабилизатора 3, узлов подвески 5, стабилизатора 6, рулей 7, установленными на задних кромках плоскостей стабилизатора, которые соединены с электроприводами 1 и датчиками положения рулей, соединенными через электрический разъем 4 с вычислителем прицельной системы ЛА.
Сущность предлагаемого устройства состоит в следующем. При достижении ЛА области досягаемости АБ цели с помощью бортовых систем измеряют взаимное положение координат ЛА и цели. С помощью бортовых датчиков в ЛА измеряют вектор путевой скорости и вектор скорости ветра. Данную информацию вводят в вычислитель, входящий в состав прицельно-навигационного комплекса ЛА. На основании алгоритмов, изложенных в Приложении 1, непрерывно вычисляют необходимое отклонение рулей АБ и сигналы, пропорциональные отклонению рулей, подают на приводы АБ. Положение рулей АБ контролируют с помощью датчиков обратных связей, соединенных с рулями АБ. В момент отцепки АБ от ЛА электропитание рулей прекращается, и их положение остается неизменным в течение всего времени полета ЛА.
Результатом решения данной проблемы является расширение задач, решаемых с помощью предлагаемой бомбы по сравнению с неуправляемыми АБ при незначительных по стоимости доработках.
Приведем основные:
Задача 1. Установление бокового промаха, обусловленного навигационными ошибками, ошибками самолетовождения и пилотирования.
Задача 2. Поражение одной цели несколькими АБ при одном пролете над целью или около нее при условии выполнения ограничений на область достижимости. Данная задача возникает при поражении особо прочных или подземных целей. В этом случае из различных точек траектории полета ЛА сбрасывают несколько АБ в одну и ту же точку (цель). Два сигнала управления при сбросе каждой АБ рассчитывают по алгоритму, изложенному в Приложении 1.
Задача 3. Площадное поражение целей. В вычислителе параллельно решают число задач управления, равное числу поражаемых целей, координаты точки сброса задают одинаковыми, а также координаты целей для каждой АБ. Вычисление сигналов отклонения рулей для каждой АБ вычисляют на основании алгоритма, изложенного в Приложении 1.
Работа устройства
В вычислителе прицельной системы определяют необходимое положение рулей для достижения заданной цели с учетом высоты и скорости полета носителя, величины ветра и аэродинамических характеристик АБ. Сигналы, пропорциональные необходимому положению рулей, усиливают по мощности и подаются на приводы управления рулей. Положение рулей контролируется датчиками положения рулей, выполняющих роль датчиков обратной связи. После отделения АБ от носителя происходит отключение электроприводов и датчиков обратной связи от вычислителя прицельной системы, т.е. положение рулей остается неизменным на всей траектории полета АБ. При достижении цели посредством взрывателя происходят подрыв боевого заряда и поражение цели.
Отклонение рулей изменяет аэродинамические характеристики стабилизатора, что обеспечивает изменение моментов, действующих на плоскости стабилизатора, а следовательно, изменение траектории снижения АБ. Противоположные плоскости отклоняются синхронно. Поэтому конструктивно можно вместо четырех электроприводов иметь лишь два.
Преимущества
1. Предлагаемая АБ обладает свойствами управляемой, но в отличие от нее не имеет координатора, автопилота, источника питания. Вследствие этого имеет существенно низшую стоимость, близкую к стоимости неуправляемых АБ.
2. Не требует подсветки цели ЛА при помощи станции целеуказания.
3. При тех же размерах, что и КАБ, обладает большей боевой эффективностью за счет коррекции траектории. В то же время в сравнение с КАБ-500 Л уменьшены масса и объем аппаратуры наведения из-за отсутствия координатора, автопилота и источника питания, что можно использовать для увеличения боевого заряда.
4. При одновременном применении нескольких АБ предлагаемой конструкции позволяет заменить разовые бомбовые кассеты и разовые бомбовые связки [1].
Приложение 1
Оптимизация начальных условий на основе метода АКОР С ФОР
Аббревиатуры в заголовке означают соответственно: АКОР - аналитическое конструирование оптимальных регуляторов; ФОР - функционал обобщенной работы [3] с.417.
Рассмотрим следующую постановку задачи. Пусть объект задан системой уравнений
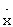 =f(x,t)+ϕ(x,t)u, х(t0)=x0,
=f(x,t)+ϕ(x,t)u, х(t0)=x0,
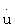 =ϑ, u(t0)=u0. (1)
=ϑ, u(t0)=u0. (1)
Необходимо достичь минимума функционала вида
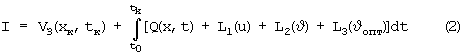
при ограничениях (1) за счет выбора такого значения вектора управляющих факторов и, при котором оптимальное значение вектора управления υопт=0.
Рассмотрим практически важный случай, когда все функции в (1) представлены квадратичными формами [3], с.323.
Введем функцию «стоимости» V(у,t), представляющую собой квадратичную форму
V(у,t)=уT(t)P(t)у(t), у=[xT,uT]T, (3)
динамика которой описывается уравнением
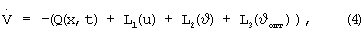
с граничным условием V(tк)=Vз(xк,tк).
Здесь у - новый вектор состояния, имеющий компоненты с заданными начальными условиями (х0) и оптимизируемыми начальными условиями (вектор управляющих факторов и). В соответствии с (2) и (4) функция V(у,t) также будет зависеть от υ и υопт. Граничные условия для у(tк) недоопределены. Потребуем, чтобы выполнялось условие
V(ук,tу)=V(xк,tк)+V(uк,tк)=Vз(xк,tк)+V(u0,tк), (5)
то есть значение вектора и в начальный, и конечный моменты времени совпадают.
Таким образом, приходим к выводу, что данная постановка задачи возможна в единственном частном случае, когда значение функции V(у,t) в момент tк зависит от вектора u(t0). В этом случае формула (5) всегда будет иметь вид
V(ук,tк)=Vз(xк,u0,tк).
Запишем полную производную функции V(у,t) через частные производные
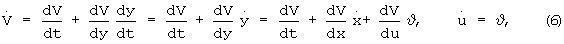
Объединяя (6) и (4), с учетом (1) получим
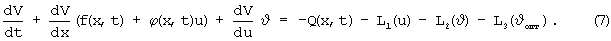
Данное уравнение в частных производных определяет зависимость функции V(x,t) от начальных условий и оптимизируемых управлений на множествах возможных значений векторов u и υ.
Выполним операцию минимизации по данным аргументам правой и левой частей уравнения (7)
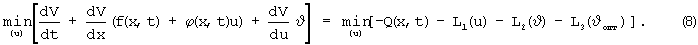 Отсюда
Отсюда 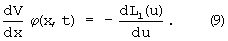
Задав L1 в виде квадратичной формы вида
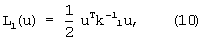
получим в точке экстремума по u
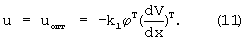
Подставим (11) в (7) с учетом (10) и получим
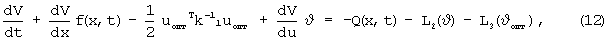
минимизированное по u.
Аналогичным образом выполним минимизацию по вектору υ. Точка экстремума из (8) определяется выражением
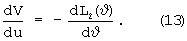
С учетом квадратичной формы L2 выражение (13) запишем в виде
ϑ=ϑопт=-k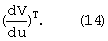
Подставляя (14) в (12), получим уравнение
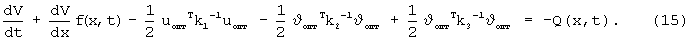 Здесь принято допущение, что L3(υопт) по структуре аналогична L2(υ).
Здесь принято допущение, что L3(υопт) по структуре аналогична L2(υ).
Объединяя слагаемые с υопт, запишем
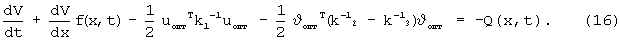 Рассмотрим наиболее часто встречающийся на практике случай, когда матрицы k2=k3.
Рассмотрим наиболее часто встречающийся на практике случай, когда матрицы k2=k3.
Траектория x(t), являющаяся функцией времени и удовлетворяющая уравнению (16), обозначим х0 и перепишем уравнение в виде
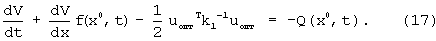
Заметим, что функция х0 удовлетворяет уравнению объекта (1) при u=uопт, υ=υопт. Решение уравнения (17) связано со значительными сложностями, так как требует значения х0, uопт, а в силу уравнения (1), и υопт. Кроме того, уравнение (17) имеет граничное условие на правом конце и требует решения в обратном времени, а функция х0 определяется интегрированием в прямом времени уравнения (1).
При выводе (11) и (14) было учтено, что функции u(t) и Uопт(t) в соответствии с (1) изменяются по закону
u(t)=u0+ut, t∈[t0,tk] (18)
Только в этом случае минимизация по вектору u как вектору параметров и по υ как вектору управления будет справедлива. В общем случае необходимо учитывать связь между u и υ в дифференциальной форме. Для решения задачи (2) и вычисления значений uопт и υопт воспользуемся известным методом характеристик [3], [4].
Гамильтонова система канонических уравнений имеет вид [3]
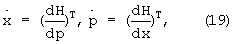
где х - вектор состояния, Н - гамильтониан системы, рT - (dV/dx)T - вектор-столбец частных производных искомой функции V(x,t) по компонентам вектора х∈Х с соответствующими граничными условиями для t=tк.
Для объекта (1) и функционала (2) данная система имеет вид
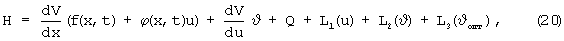
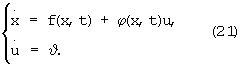
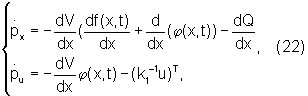
где рx=dV/dx, pu=dV/du.
Пусть вектор управляемых параметров оптимален u=uопт. Тогда система (20), (21), (22) имеет вид
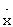 =f(x,t)+ϕ(x,t)uопт,
=f(x,t)+ϕ(x,t)uопт,
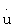 =ϑопт,
=ϑопт,
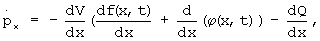
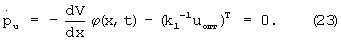
Подстановка uопт, вычисленного по формуле (11), приводит к тому, что последнее выражение в (22) приводится к виду 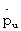 =0. Учитывая то, что по постановке задачи V(tк) не зависит от вектора u, граничные условия для рu также нулевые. Тогда из (6) следует
=0. Учитывая то, что по постановке задачи V(tк) не зависит от вектора u, граничные условия для рu также нулевые. Тогда из (6) следует
ϑ=ϑопт=-k2pu T=0. (24)
Поскольку данное условие выполняется только при u=uопт, то оно может служить критерием того, насколько полученное значение u близко к оптимальному.
Рассмотрим вычислительный алгоритм решения задачи с использованием прогнозируемой модели [3] с.471, [4] с.104.
Полная производная функции V(x,f) в силу уравнения (2) будет определяться выражением
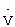 =-Q(x,τ)-L1(uм)-L2(ϑм)-L3(ϑопт),
=-Q(x,τ)-L1(uм)-L2(ϑм)-L3(ϑопт),
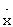 =f(xм,τ)+ϕ(хм,τ)uм,
=f(xм,τ)+ϕ(хм,τ)uм,
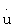 м=ϑм,
м=ϑм,
uм=-k1ϕT(xм,τ)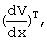
ϑм=-k2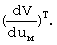 (26)
(26)
Последние два уравнения в (26) справедливы, в соответствии с (17), лишь на траектории х0 (оптимальной траектории), которая задается парой векторов uм=uопт, υм=υопт=0. Поэтому для поиска uопт можно использовать итерационную процедуру типа квазилинеаризации при υм=0. Система (26) для произвольной i-й итерации будет иметь вид
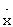 =f(xi,τ)+ϕ(хi,τ)ui,
=f(xi,τ)+ϕ(хi,τ)ui,
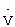 i=-Q(xi,τ)-L1(ui),
i=-Q(xi,τ)-L1(ui),
ui+1=-k1ϕT(xi,τ)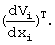 (27)
(27)
Величина υi может не вычисляться, поскольку при υi=0, ui=ui+1. Тогда заключение сходимости можно сделать на основе вычисления разности Δui=ui-ui+1.
Как следует из (15)-(17), применение прогнозирующей модели с нулевым вектором управления в данном случае вполне обосновано. Это следует из того обстоятельства, что υопт=0. Данный подход и алгоритм, его реализующий, позволяют вычислить в момент t0 такое значение u(t0), которое, являясь неизменным на всей траектории, решает терминальную задачу.
Литература
1. Авиационное вооружение./Под ред. Д.И.Гладкова. - М.: Воениздат, 1987.
2. Корректируемая авиабомба КАБ-500Л с полуактивной лазерной системой наведения./Под ред. И.Е.Казанова. - М.: ВВИА, 1983.
3. Справочник по теории автоматического управления./Под ред. А.А.Красовского. - М.: Наука, 1986.
4. Буков В.Н. Адаптивные прогнозирующие системы управления полетом. М.: Наука, 1987.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ПОСАДКИ КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2003 |
|
RU2272757C2 |
| КОМБИНИРОВАННАЯ СИСТЕМА УПРАВЛЕНИЯ КОРРЕКТИРУЕМОЙ АВИАЦИОННОЙ БОМБОЙ | 2011 |
|
RU2489675C2 |
| СИСТЕМА УПРАВЛЕНИЯ КОРРЕКТИРУЕМОЙ АВИАЦИОННОЙ БОМБОЙ, ПРЕДНАЗНАЧЕННОЙ ДЛЯ ПОРАЖЕНИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ ПРОТИВНИКА | 2011 |
|
RU2488769C2 |
| Способ управления планирующей авиабомбой | 2018 |
|
RU2676775C1 |
| КРУГЛОСУТОЧНАЯ ВСЕПОГОДНАЯ ВЫСОКОТОЧНАЯ КОРРЕКТИРУЕМАЯ АВИАБОМБА, СТАБИЛИЗИРОВАННАЯ ПО КРЕНУ, С АВТОМАТОМ ГЛОБАЛЬНОЙ СПУТНИКОВОЙ НАВИГАЦИИ | 2006 |
|
RU2317515C1 |
| АВИАЦИОННАЯ БОМБА, СТАБИЛИЗИРОВАННАЯ ПО КРЕНУ, С ИНЕРЦИАЛЬНО-СПУТНИКОВОЙ СИСТЕМОЙ НАВЕДЕНИЯ | 2006 |
|
RU2339904C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ПАРАМЕТРОВ ТРАЕКТОРИИ БОМБЫ | 2002 |
|
RU2212620C1 |
| САМОНАВОДЯЩАЯСЯ АВИАЦИОННАЯ БОМБА, СТАБИЛИЗИРОВАННАЯ ПО КРЕНУ | 2003 |
|
RU2247314C1 |
| СПОСОБ УЧЕТА ВЕТРА ПРИ ПРИМЕНЕНИИ АВИАЦИОННЫХ БОМБ | 2019 |
|
RU2727280C1 |
| Способ управления планирующей авиабомбой при ветре | 2018 |
|
RU2681749C1 |
Изобретение относится к области боеприпасов, к авиационным бомбам. Сущность изобретения заключается в том, что авиационная бомба с корректируемыми аэродинамическими характеристиками состоит из корпуса, боевого заряда, взрывателя, стабилизатора. Стабилизатор имеет рули, соединенные с электроприводами, входы которых соединены с выходами вычислителя прицельной системы летательного аппарата, датчики обратной связи соединены с входами вычислителя прицельной системы летательного аппарата через электрический разъем. Техническим результатом изобретения является снижение себестоимости бомбы и расширение области применения. 1 ил.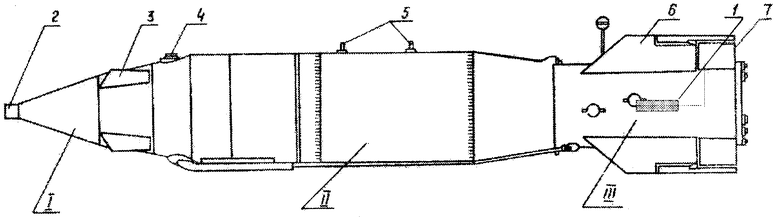
Авиационная бомба с корректируемыми аэродинамическими характеристиками, состоящая из корпуса, боевого заряда, взрывателя, стабилизатора, отличающаяся тем, что стабилизатор снабжен рулями, соединенными с электроприводами, входы которых соединены с выходами вычислителя прицельной системы летательного аппарата и датчиками обратной связи, соединенными с входами вычислителя прицельной системы летательного аппарата через электрический разъем.
| Проблемы создания корректируемых и управляемых авиационных бомб./Под ред | |||
| B.C | |||
| ШАХИДЖАНОВА | |||
| - М.: Инженер, 10.04.2003, с.88-89 | |||
| АВИАЦИОННАЯ КОРРЕКТИРУЕМАЯ БОМБА С ТЕЛЕВИЗИОННОЙ ГОЛОВКОЙ САМОНАВЕДЕНИЯ, СТАБИЛИЗИРОВАННАЯ ПО КРЕНУ | 1999 |
|
RU2147724C1 |
| КОРРЕКТИРУЕМАЯ, САМОНАВОДЯЩАЯСЯ АВИАЦИОННАЯ БОМБА, СТАБИЛИЗИРОВАННАЯ ПО КРЕНУ | 1999 |
|
RU2156954C1 |
Авторы
Даты
2005-12-10—Публикация
2003-12-22—Подача