Предлагаемое изобретение относится к области космической техники и предназначено для обеспечения точного и мягкого приземления искусственных объектов в случаи нештатных ситуаций.
Пилотируемые и беспилотные космические летательные аппараты (КЛА) имеют высокую степень надежности. Наряду с этим в истории космонавтики имеют место случаи нештатных ситуаций. Таковыми являются непредусмотренные программой полета ситуации или условия, в которых оказывается КЛА. В этих условиях возникает необходимость срочной посадки (приземления) КЛА из любой точки траектории полета.
Произвольная точка земной поверхности (населенные пункты, горы, пустыня, тундра, удаленные морские акватории и т.д.) может быть малопригодной для посадки. В связи с этим возникает необходимость управления процессом спуска КЛА для обеспечения посадки в определенных точках земной поверхности.
Известно устройство для сбрасывания тяжелых грузов с летательных аппаратов, содержащее пороховой двигатель, парашютную систему, снабженную фалом рифления для изменения скорости спуска посредством изменения площади миделя купола парашюта [1] (прототип). Известно также устройство для сбрасывания тяжелых грузов с летательных аппаратов [2], состоящее из управляемой парашютной системы, соединенной с платформой.
Недостатком первого устройства (прототип) является невозможность посадки в заданную точку земной поверхности из произвольного положения КЛА на орбите. Использование второго устройства для КЛА малоэффективно из-за невозможности использования аэродинамического руля направления в верхних слоях атмосферы. Также в этом случае увеличиваются массогабаритные характеристики, связанные с рулем и платформой. Невозможен учет ветра по высотам.
Задачей предлагаемого изобретения является расширение области начальных условий спуска КЛА при возникновении нештатной ситуации. Задача достигается тем, что парашютная система имеет четыре симметричные относительно центра масс КЛА точки подвески. При этом длина каждой фалы зависит от сигналов управления, формируемым алгоритмом, изложенным в Приложении 1.
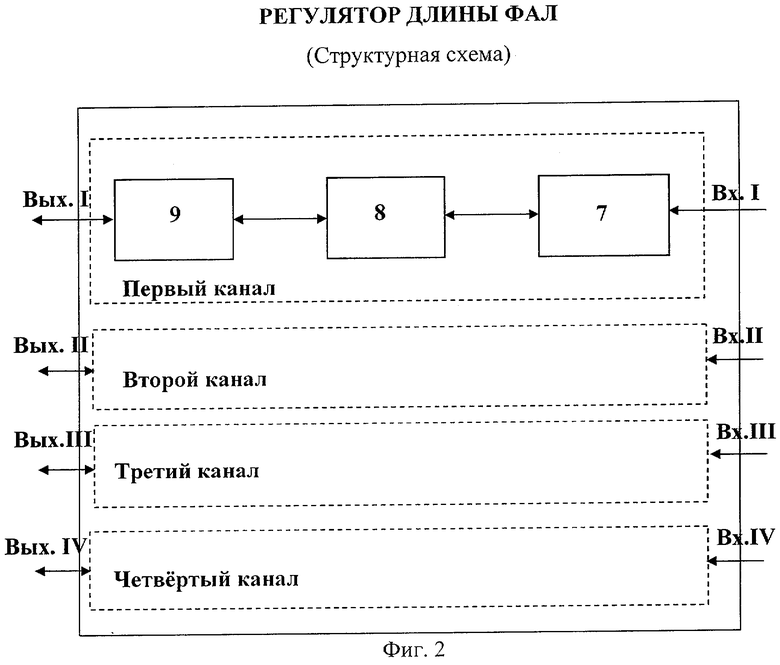
Структурная схема предлагаемого устройства представлена на фиг.1. На фиг.2 представлена структурная схеме регулятора длины фал.
Устройство посадки КЛА содержит парашютную систему (ПС) (1), состоящую из купола или системы куполов, посредством строп (2) соединенную с устройством управления и отцепа (3) купола (системы куполов).
Устройство управления и отцепа (3) посредством четырех фал соединено с КЛА через блок регулятора длины фал (4). Устройство управления (6) выдает управляющие сигналы, пропорциональные длинам фал (вых.I-вых.IV) в блок регулятор длины фал (4), а также сигналы, пропорциональные площади сечения миделя парашюта (вых.V), подаваемые на устройство регулирования длины фала рифления (5). С вых.VI устройства управления (6) дискретный сигнал сброса ПС поступает на устройство (3).
Устройства (1), (2), (5) описаны в прототипе. Устройство (3) содержит четыре независимых соединителя строп (2) с фалами. Каждый соединитель содержит замок, открываемый по команде с вых.VI устройства управления (6). Регулятор длины фал (4) является сложным устройством, содержащим четыре независимых канала. Структурная схема данного устройства представлена на фиг.2. Все четыре канала идентичны, т.е. являются одинаковыми по устройству, параметрам и характеристикам. Рассмотрим элементы канала. Элемент (9) представляет катушку или барабан, соединенный через шестерню с редуктором (8). Редуктор является выходом фиксатора (7), который функционирует в соответствии с сигналом на вх.1. Все устройства широко известны.
Устройство управления (6) на фиг.1 может быть выполнено как в аналоговом виде, так и в цифровом. Оно представляет собой вычислитель, либо блок бортовой вычислительной системы КЛА, но отдельный вычислитель является более предпочтительным в плане надежности.
Вычислитель может состоять из вычислительного устройства (ВУ), постоянного запоминающего устройства (ПЗУ) и усилителей мощности (УМ).
Вычислитель использует сигналы, пропорциональные координатам выбранной (заданной) точки посадки из ПЗУ, а также сигналы, пропорциональные координатам КЛА и его скорости. Алгоритм работы ВУ определяется формулами (26) или (27) (см. Приложение 1). Вычисленные сигналы, пропорциональные длинам фал и площади миделя купола, подают в УМ, сигналы которых являются выходными сигналами устройства управления.
Представленные на фиг.1 связи между устройствами (1), (2), (3) и устройствами (1), (5) являются механическими (силовыми), остальные связи являются электрическими (обозначены стрелками). Конструктивно можно выделить парашютную систему и собственно корпус КЛА, соединенных между собой системой регулирования фалов, благодаря чему достигается цель изобретения.
Устройство работает следующим образом.
Перед полетом КЛА рассчитывают координаты всех допустимых точек приземления. Их число должно быть достаточным для начала спуска из любой точки траектории и в любой момент времени. При этом учитываются в ограниченных пределах возможные отклонения от штатной или заданной траектории полета.
Координаты точек приземления и границы областей космического пространства, из которых возможно приземление КЛА в каждую из допускаемых точек приземления фиксируют в устройстве управления (6). После команды на спуск КЛА в (6) на основе алгоритмов, изложенных в Приложении 1, рассчитывают необходимые длины всех четырех фал, которые с выходов I, II, III и IV поступают на входы I, II, III и IV регулятора длины фал, изображенного па фиг.1 блоком (4).
Увеличение длины фалов от минимального до заданного значения происходит за счет силы натяжения, создаваемой ПС и регулируемой фиксатором (7), изображенным на фиг.2. При заданной длине фалов устройство управления и отцепа (7) обеспечивает движение в выбранную точку приземления. Устройство управления (6) регулирует скорость снижения через устройство (5) (фиг.1).
Регулятор длины фалов, изображенный на фиг.2, может быть выполнен либо как общий блок, содержащий четыре независимых устройства, либо в виде четырех автономных устройств, выполненных конструктивно отдельно.
ПРИЛОЖЕНИЕ 1
ОПТИМИЗАЦИЯ НАЧАЛЬНЫХ УСЛОВИЙ НА ОСНОВЕ МЕТОДА АКОР С ФОР
Аббревиатуры в заголовке означают соответственно: АКОР - аналитическое конструирование оптимальных регуляторов; ФОР - функционал обобщенной работы [3] с.417.
Рассмотрим следующую постановку задачи. Пусть объект задан системой уравнений
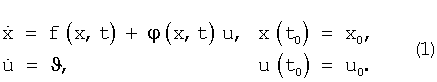
Необходимо достичь минимума функционала вида
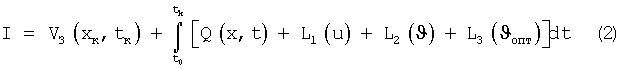
при ограничениях (1) за счет выбора такого значения вектора управляющих факторов u, при котором оптимальное значение вектора управления υопт=0.
Рассмотрим практически важный случай, когда все функции в (1) представлены квадратичными формами [3], с.323.
Введем функцию "стоимости" V(y,t), представляющую собой квадратичную форму
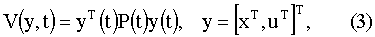
динамика которой описывается уравнением
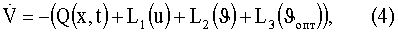
с граничным условием 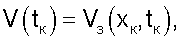
здесь y - новый вектор состояния, имеющий компоненты с заданными начальными условиями (х0) и оптимизируемыми начальными условиями (вектор управляющих факторов u). В соответствии с (2) и (4) функция V(y,t) также будет зависеть от υ и υопт. Граничные условия для y(tк) недоопределены. Потребуем, чтобы выполнялось условие
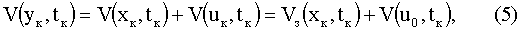
то есть значения вектора u в начальный и конечный моменты времени совпадают.
Таким образом, приходим к выводу, что данная постановка задачи возможна в единственном частном случае, когда значение функции V(y,t) в момент tк зависит от вектора u(t0). В этом случае формула (5) всегда будет иметь вид
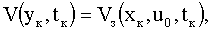
запишем полную производную функции V(y,t) через частные производные
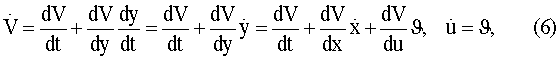
объединяя (6) и (4), с учетом (1) получим
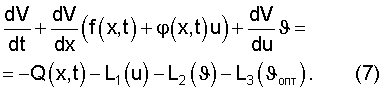
Данное уравнение в частных производных определяет зависимость функции V(x,t) от начальных условий и оптимизируемых управлений на множествах возможных значений векторов u и υ.
Выполним операцию минимизации по данным аргументам правой и левой частей уравнения (7)
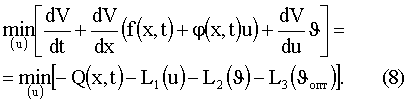
Отсюда
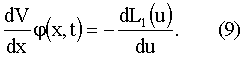
Задав L1 в виде квадратичной формы вида
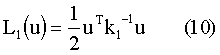
получим в точке экстремума по u
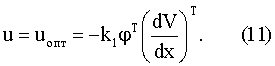
Подставим (11) в (7) с учетом (10) и получим
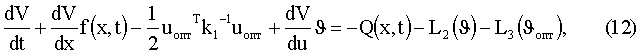
минимизированное по u.
Аналогичным образом выполним минимизацию по вектору υ. Точка экстремума из (8) определяется выражением
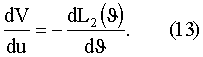
С учетом квадратичной формы L2 выражение (13) запишем в виде
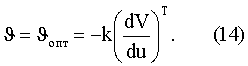
Подставляя (14) в (12), получим уравнение
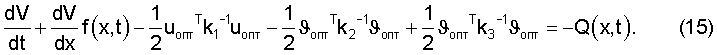
Здесь принято допущение, что L3(υопт) по структуре аналогична L2(υ). Объединяя слагаемые с υопт, запишем
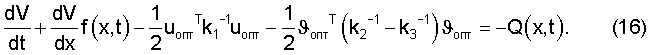
Рассмотрим наиболее часто встречающийся на практике случай, когда матрицы k2=k3.
Траектория x(t), являющаяся функцией времени и удовлетворяющая уравнению (16), обозначим х0 и перепишем уравнение в виде
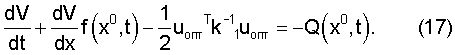
Заметим, что функция х0 удовлетворяет уравнению объекта (1) при u=uопт, υ=υопт. Решение уравнения (17) связано со значительными сложностями, так как требует значения х0, uопт, а в силу уравнения (1) и υопт. Кроме того, уравнение (17) имеет граничное условие на правом конце и требует решения в обратном времени, а функция х0 определяется интегрированием в прямом времени уравнения (1).
При выводе (11) и (14) было учтено, что функции u(t) и uопт(t) в соответствии с (1) изменяются по закону
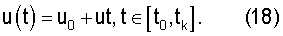
Только в этом случае минимизация по вектору u как вектору параметров и по υ как вектору управления будет справедлива. В общем случае необходимо учитывать связь между u и υ в дифференциальной форме. Для решения задачи (2) и вычисления значений uопт и υопт воспользуемся известным методом характеристик [3, 4].
Гамильтонова система канонических уравнений имеет вид [3]
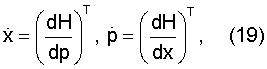
где х - вектор состояния, H - гамильтониан системы, рT - (dV/dx)T - вектор-столбец частных производных искомой функции V(x,t) по компонентам вектора х∈Х с соответствующими граничными условиями для t=tk.
Для объекта (1) и функционала (2) данная система имеет вид
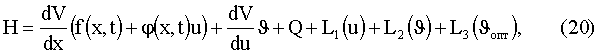
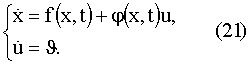
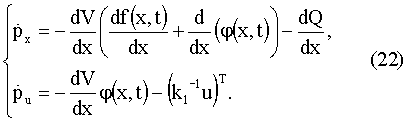
где 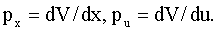
Пусть вектор управляемых параметров оптимален u=uопт. Тогда система (20), (21), (22) имеет вид
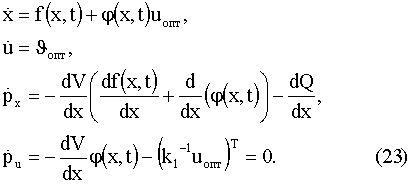
Подстановка uопт, вычисленного по формуле (11), приводит к тому, что последнее выражение в (22) приводится к виду 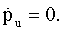 Учитывая то, что по постановке задачи V(tk) не зависит от вектора u, граничные условия для рu также нулевые. Тогда из (6) следует
Учитывая то, что по постановке задачи V(tk) не зависит от вектора u, граничные условия для рu также нулевые. Тогда из (6) следует
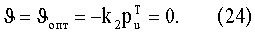
Поскольку данное условие выполняется только при u=uопт, то оно может служить критерием того, насколько полученное значение u близко к оптимальному.
Рассмотрим вычислительный алгоритм решения задачи с использованием прогнозируемой модели [3] с.471, [4] с.104.
Полная производная функции V(x,t) в силу уравнения (2) будет определяться выражением
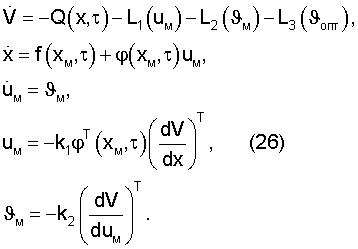
Последние два уравнения в (26) справедливы, в соответствии с (17), лишь на траектории х0 (оптимальной траектории), которая задается парой векторов uм=uопт, υм=υопт=0. Поэтому для поиска uопт можно использовать итерационную процедуру типа квазилинеаризации при υм=0. Система (26) для произвольной i-й итерации будет иметь вид
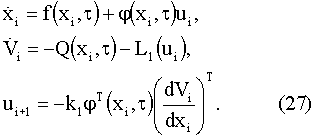
Величина υi может не вычисляться, поскольку при υi=0, ui=ui+1. Тогда заключение сходимости можно сделать на основе вычисления разности 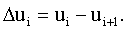
Как следует из (15)-(17), применение прогнозирующей модели с нулевым вектором управления в данном случае вполне обосновано. Это следует из того обстоятельства, что υопт=0. Данный подход и алгоритм, его реализующий, позволяют вычислить в момент t0 такое значение u(t0), которое, являясь неизменным на всей траектории, решает терминальную задачу.
Литература
1. Авторское свидетельство RU №2015071, кл. B 64 D 1/08, 1/14 (прототип).
2. Беляев Ю. Средства десантирования грузов с самолетов ВВС. - Зарубежное военное обозрение. / Под ред. В.И.Кожемякина. - М.: Красная звезда, 1989, №9. - 80 с.
3. Красовский А.А. Справочник по теории автоматического управления. - М.: Наука, 1987.
4. Буков В.Н. Адаптивные прогнозирующие системы управления полетом. - М.: Наука, 1987.
| название | год | авторы | номер документа |
|---|---|---|---|
| ТРЕНАЖЕР ПАРАШЮТИСТА-ДЕСАНТНИКА И СПОСОБ ДИНАМИЧЕСКОГО СОПРОВОЖДЕНИЯ ОБУЧЕНИЯ НА НЕМ | 2016 |
|
RU2653900C1 |
| АВИАЦИОННАЯ БОМБА С КОРРЕКТИРУЕМЫМИ АЭРОДИНАМИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ | 2003 |
|
RU2265792C2 |
| Способ подготовки парашютистов и устройство его реализующее | 2019 |
|
RU2730759C1 |
| СИСТЕМА ПАРАШЮТИРОВАНИЯ - 4 И СПОСОБ ЕЁ РАБОТЫ | 2014 |
|
RU2576852C1 |
| СИСТЕМА ПАРАШЮТИРОВАНИЯ И СПОСОБ ЕЁ РАБОТЫ | 2013 |
|
RU2527633C1 |
| Многокупольная крыльевая система | 2020 |
|
RU2770501C2 |
| БЕСПИЛОТНЫЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ С ПАРАШЮТНОЙ СИСТЕМОЙ ПОСАДКИ | 2020 |
|
RU2754278C1 |
| СПОСОБ ПАРАШЮТНОЙ ПОСАДКИ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА И БЕСПИЛОТНЫЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ С ЭЛЕКТРОДВИЖИТЕЛЕМ И ПАРАШЮТНОЙ СИСТЕМОЙ ПОСАДКИ | 2014 |
|
RU2592963C2 |
| СИСТЕМА ПАРАШЮТИРОВАНИЯ (ВАРИАНТЫ) | 2013 |
|
RU2533618C1 |
| СПОСОБ ЗАХОДА НА ПОСАДКУ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА В АВАРИЙНЫХ УСЛОВИЯХ | 2019 |
|
RU2725640C1 |
Изобретение относится к космической технике и предназначено для обеспечения точного и мягкого приземления искусственных объектов, главным образом в нештатных ситуациях. Устройство посадки космического летательного аппарата (КЛА) содержит парашютную систему, соединенную с КЛА посредством строп через устройство управления и отцепа. Последнее обеспечивает изменение длины фала рифления купола парашюта и сброс парашютной системы. Парашютная система содержит четыре фала, соединенных с КЛА через блок регулятора длины фалов в симметричных относительно центра масс КЛА точках подвески. Фалы соединены со стропами посредством четырех независимых соединителей с замками, открываемыми по команде устройства управления и отцепа. Регулятор длины фалов содержит четыре идентичных канала, включающих, каждый барабан, редуктор и фиксатор. Фиксаторы соединены с устройством управления и отцепа указанными четырьмя фалами. Длина этих фалов изменяется по сигналам с указанного устройства управления в соответствии с алгоритмом, обеспечивающим посадку КЛА в заданной точке. Технический результат изобретения состоит в расширении допустимой области начальных условий спуска КЛА главным образом при возникновении нештатной ситуации. 2 ил.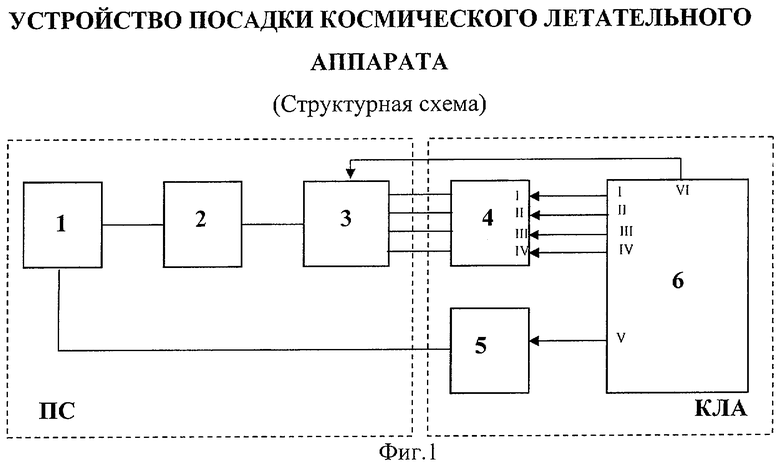
Устройство посадки космического летательного аппарата (КЛА), содержащее парашютную систему, соединенную с КЛА посредством строп через устройство управления и отцепа, обеспечивающее изменение длины фала рифления купола парашюта и сброс парашютной системы, причем парашютная система содержит четыре фала, соединенных с КЛА через блок регулятора длины фалов в симметричных относительно центра масс КЛА точках подвески и со стропами посредством четырех независимых соединителей строп с замками, открываемыми по команде устройства управления и отцепа, указанный регулятор длины фалов содержит четыре идентичных канала, включающих каждый барабан, редуктор и фиксатор, при этом фиксаторы соединены с устройством управления и отцепа указанными четырьмя фалами, длина которых изменяется по сигналам с указанного устройства управления в соответствии с алгоритмом, обеспечивающим посадку КЛА в заданной точке.
| УСТРОЙСТВО ДЛЯ СБРАСЫВАНИЯ ТЯЖЕЛЫХ ГРУЗОВ С ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 1992 |
|
RU2015071C1 |
| УПРАВЛЯЕМАЯ ПАРАШЮТНАЯ СИСТЕМА ДЛЯ ДОСТАВКИ ГРУЗОВ | 1993 |
|
RU2039680C1 |
| УПРАВЛЯЕМАЯ ПАРАШЮТНАЯ СИСТЕМА | 1996 |
|
RU2111898C1 |
| СПОСОБ ОБРАБОТКИ ТЯЖЕЛОГО ОСТАТКА НА ОСНОВЕ УГЛЕВОДОРОДОВ | 2013 |
|
RU2634727C2 |
Авторы
Даты
2006-03-27—Публикация
2003-12-22—Подача