СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ЛИНЕЙНОГО ТЕПЛОВОГО РАСШИРЕНИЯ Российский патент 2006 года по МПК G01N25/00 

Изобретение относится к способам определения коэффициента теплового расширения твердых тел в широком диапазоне температур.

Известен способ определения термического коэффициента линейного расширения, заключающийся в том, что исследуемое вещество наносят в виде слоя на две подложки и измеряют деформацию изгиба образцов и температуру (Авторское свидетельство СССР №693191, М. Кл. G 01 N 25/16, 25.10.1979).

Известен способ определения температурного коэффициента линейного расширения твердых материалов, включающий измерение приращения температуры исследуемого образца и его удлинения путем регистрации электрической емкости конденсаторного датчика перемещений (Авторское свидетельство СССР №1449880, М. Кл. G 01 N 25/16, 07.01.89 г.).

Известен способ определения теплового расширения твердых веществ в широком диапазоне температур, включающий нагрев исследуемого образца, а также измерение его температуры и удлинения (Авторское свидетельство СССР №575551, М. Кл. G 01 N 25/16, 05.10.1977).

Недостатком способов являются ограниченные функциональные возможности.

Наиболее близким по достигаемому результату является способ, по которому образец нагревают ступенчато, измеряют параметры образца в холодном и нагретом состояниях и вычисляют коэффициент линейного теплового расширения (Авторское свидетельство СССР №913195, М. Кл. G 01 N 25/16, 15.03.1982).

Недостатком является трудоемкость способа и ограниченные функциональные возможности.

Технический результат изобретения - снижение трудоемкости способа, возможность прогнозирования коэффициента линейного теплового расширения материала путем расчета по формуле, а также расширение функциональных возможностей за счет расширения диапазона температур. Причем коэффициент линейного теплового расширения материала рассчитывается при различных уровнях температур по сравнению с прототипом.

Технический результат изобретения достигается за счет того, что в способе определения коэффициента линейного теплового расширения, по которому его вычисляют по формуле, в отличие от прототипа определяют период кристаллической решетки для нитевидного монокристалла рентгеноструктурным методом, а затем по формуле

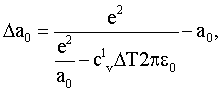
где Δа₀ - изменение периода кристаллической решетки вследствие теплового воздействия;

е=1,6*10^-19, Кл - величина взаимодействующих зарядов, равная заряду электрона;

π=3,14;

ε₀=8.85*10^-12 Кл²/нм² - электрическая постоянная;

а₀ - период кристаллической решетки;

ΔT - изменение температуры;

с¹ _v - теплоемкость атома при постоянном объеме,

рассчитывают зависимость изменения периода кристаллической решетки от температуры, а коэффициент теплового расширения кристаллической решетки определяется как

α=Δa₀/(2a₀ΔT).

Кроме того, период кристаллической решетки можно определить по справочным данным (Кристаллография и дефекты кристаллической решетки. Учебник для вузов /Новиков И.И., Розин К.М. М.: Металлургия, 1990, 336 с.).

Пример конкретной реализации способа

Для рентгеноструктурного анализа изготавливаются образцы. Монолитные образцы в форме шлифов изготавливают из исследуемого материала обычными механическими способами и перед съемкой подвергают электролитической полировке для снятия наклепа. Плоские шлифы подготавливают для съемки с помощью электролитического травления для снятия деформированного слоя. При съемке на просвет образцы должны электролитически утоньшаться до тонкой фольги.

Для определения периодов кристаллической решетки необходимо измерить межплоскостные расстояния, проиндицировать дифракционные отражения и, зная связь между межплоскостным расстоянием, индексами отражающих плоскостей и периодами решетки, рассчитать последние (С.С.Горелик, Л.Н.Расторгуев, Ю.А.Скаков. Рентгенографический и электронно-оптический анализ. М.: Металлургия, 1970, 366 с.).

Методами прецизионного определения периода кристаллической решетки могут служить следующие:

- асимметричная съемка с расчетом по последним линиям;

- метод съемки на больших расстояниях в широком расходящемся пучке;

- метод съемки с независимым эталоном;

- безэталонный метод при обратной съемке и др.

исследуемого материала (Н.Н.Качанов, Л.И.Миркин. Рентгеноструктурный анализ. М.: Машгиз, 1960, 216 с.).

Расчет изменения периода кристаллической решетки вследствие повышения температуры основан на учете изменения энергии связи двух разноименных зарядов в кристаллической решетке. Зависимость изменения периода кристаллической решетки от температуры имеет следующий вид

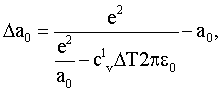
где Δа₀ - изменение периода кристаллической решетки вследствие теплового воздействия;

е=1,6*10^-19, Кл - величина взаимодействующих зарядов, равная заряду электрона;

π=3,14;

ε₀=8.85*10^-12 Кл²/нм² - электрическая постоянная;

a₀ - период кристаллической решетки;

ΔT - изменение температуры;

с¹ _v - теплоемкость атома при постоянном объеме. В соответствии с законом Дюлонга и Пти

с¹ _v=c_v/Na=3k=4.1421*10^-23 Дж/К,

где N_A - число Авогадро; k - постоянная Больцмана.

Для кристаллической решетки коэффициент теплового расширения определяется как

α=Δa₀/(2a₀ΔT).

Результаты расчета для некоторых металлов при ΔТ=20° приведены в таблице.

ТаблицаСимвол элементаВеличина коэффициента α, К^-1расчетнаяэкспериментальнаяпогрешность %Cu1,627*10^-51,67*10^-52,6Au1,836*10^-51,45*10^-526,6Fe1,291*10^-51,21*10^-56,6

Экспериментальные значения использованы из справочника (Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. - М.: Наука, 1982, с.71). Из таблицы видно, в частности, что расхождение результатов расчета коэффициента линейного теплового расширения для меди составляет 2,6%.

Таким образом, заявляемое изобретение позволяет снизить трудоемкость за счет расчета по формуле, в свою очередь, расчет в широком диапазоне температур расширяет функциональные возможности способа.

Изобретение относится к способам определения коэффициента теплового расширения твердых тел в широком диапазоне температур. В способе предварительно определяют период кристаллической решетки для нитевидного монокристалла рентгеноструктурным методом. Рассчитывают зависимость изменения периода кристаллической решетки от температуры и с учетом указанной зависимости определяют искомый коэффициент. Технический результат - снижение трудоемкости способа. 1 табл.

Способ определения коэффициента линейного теплового расширения, по которому вычисляют коэффициент линейного теплового расширения по формуле, отличающийся тем, что предварительно определяют период кристаллической решетки для нитевидного монокристалла рентгеноструктурным методом, а затем по формуле

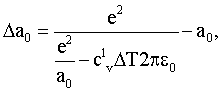
где Δа₀ - изменение периода кристаллической решетки вследствие теплового воздействия;

е=1,6·10^-19, Кл - величина взаимодействующих зарядов, равная заряду электрона;

π=3,14;

ε₀=8.85·10^-12 Кл²/нм² - электрическая постоянная;

а₀ - период кристаллической решетки;

ΔT - изменение температуры;

c¹ _v - теплоемкость атома при постоянном объеме,

рассчитывают зависимость изменения периода кристаллической решетки от температуры, а коэффициент линейного теплового расширения кристаллической решетки определяют как α=Δa₀/(2a₀ΔT).