Предлагаемое изобретение относится к области спутниковой радионавигации, геодезии, связи и может быть использовано для автономного мгновенного определения пользователями значений координат местоположения, составляющих вектора скорости фазовых центров антенн спутниковых источников радиоизлучения, координат местоположения и составляющих вектора скорости фазовых центров антенн аппаратуры пользователей, угловой ориентации в пространстве и пеленга, а также для интеграции действующих в настоящее время спутниковых систем узкоцелевого назначения в многоцелевую глобальную интегрированную спутниковую систему (ГИСС), создающей глобальное информационное пространство для предоставления пользователям услуг навигации, геодезии, связи, наблюдения, управления и целого ряда других услуг в реальном масштабе времени, в любое время суток, в любой точке Земного шара и на самом высоком уровне.
Известен способ определения координат местоположения, составляющих вектора скорости навигационных искусственных спутников Земли (НИСЗ) и пользователей спутниковых радионавигационных систем (СРНС), реализованный, например, в СРНС второго поколения американской Global Positioning System (GPS) [1].
Каждый спутник GPS, а их в системе 24, непрерывно излучают радиосигналы и передают собственные навигационные сообщения, содержащие служебную информацию, информацию о времени, эфемеридах, параметрах для введения поправок, о составляющих вектора скорости спутников и т.д. Навигационной аппаратурой пользователей (НАП) осуществляют одновременный прием навигационных радиосигналов от четырех НИСЗ, измеряют псевдодальности между навигирующимися пользователями и НИСЗ и производят расчеты, необходимые для решения навигационной задачи.
Формирование массивов навигационной информации, а также загрузку их в память электронно-вычислительных средств соответствующих НИСЗ производят наземными контрольными станциями (КС), контролирующими орбиты НИСЗ, расхождения шкал времени НИСЗ с системным временем и прогнозирование эфемерид каждого НИСЗ.
Используя информацию навигационных сообщений, принятых НАП, и измерения псевдодальностей до четырех выбранных НИСЗ, устанавливают функциональные зависимости между известными значениями координат НИСЗ и неизвестными значениями координат пользователей СРНС. Определение координат пользователей сводится к решению систем из четырех навигационных уравнений с четырьмя неизвестными.
В результате решения системы навигационных уравнений определяют четыре неизвестных: три координаты местоположения пользователя (XП, YП, ZП) и поправку к его шкале времени (поправку к его часам).
Геометрическим эквивалентом конечного алгоритма решения навигационной задачи этого известного способа является построение относительно используемых НИСЗ четырех поверхностей положения, точка пересечения которых и является искомым положением пользователей.
Аналогичным образом с использованием результатов измерений, но уже квазискоростей, определяют три составляющих вектора скорости пользователя (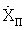 ,
, 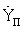 ,
, 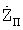 ) и поправку к частоте местного эталона частоты.
) и поправку к частоте местного эталона частоты.
Недостатками известного способа являются:
- необходимость нахождения в зоне радиовидимости навигирующегося пользователя одновременно четырех НИСЗ;
- необходимость содержания в СРНС 24 и более НИСЗ;
- наличие наземной сети КС, осуществляющих определение координат местоположения НИСЗ (эфемерид);
- прогнозирование и закладка на борт эфемерид каждого НИСЗ;
- низкая точность навигационных определений.
Известен также способ определения координат местоположения, составляющих вектора скорости фазовых центров антенн спутниковых источников навигационных сигналов и фазовых центров антенн НАП СРНС (Патент РФ №2210788) [2], в котором навигационной аппаратурой (НА), установленной на каждом спутнике, принимают непрерывно излучаемые наземными навигационными радиомаяками (ННРМ) навигационные радиосигналы, промодулированные навигационной информацией, дальномерными кодами и содержащие в своем составе координаты местоположения фазовых центров антенн ННРМ, время и информацию для введения поправок по частоте, по времени, измеряют на мерных интервалах дальности, разности дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн НА НИСЗ, измеряют скорости изменения дальности в серединах и на краях мерных интервалов, разности скоростей навигационных сигналов, затем модулируют измеренной информацией несущие принятых навигационных сигналов, усиливают их и ретранслируют в направлении Земли, которые принимают НАП установленной на пользователях СРНС, измеряют на краях и в серединах мерных интервалов дальности, разности дальностей между фазовыми центрами антенн НИСЗ и фазовыми центрами НАП, скорости изменения дальностей, разности скоростей изменения дальностей, выделяют информации о координатах местоположения фазовых центров антенн ННРМ, о поправках к частотам и задержкам, время и по измеренной, выделенной информации определяют:
- модули вектора положения фазового центра приемной антенны НА НИСЗ;
- модули вектора положения фазового центра антенны источника навигационного радиосигнала (ИНС) НИСЗ;
- значение косинуса угла между векторами базами, соединяющими начала и концы мерных интервалов, и векторами дальностей, соединяющими положения фазового центра антенны ННРМ и положения фазового центра приемной антенны НА НИСЗ;
- значения косинуса угла между векторами базами, соединяющими начала и концы мерных интервалов, и векторами дальностей, соединяющими положения фазового центра антенны НАП и положения фазового центра антенны ИНС НИСЗ;
- модули вектора баз;
- модули вектора положения фазового центра антенны ННРМ;
- модули вектора положения фазового центра антенны НАП СРНС;
- значения углов между вектором дальности, соединяющим положения фазового центра антенны ННРМ и положения фазового центра антенны НА НИСЗ, и вектором положения фазового центра антенны ННРМ;
- значения углов между вектором дальности, соединяющим положения фазового центра антенны НАП СРНС и положения фазового центра антенны ИНС НИСЗ, и вектором положения фазового центра антенны НАП, затем устанавливают системы функциональных зависимостей между известными значениями координат фазовых центров антенн ННРМ и неизвестными значениями координат фазовых центров антенн НА НИСЗ, определяют значения координат и составляющих вектора скорости фазовых центров антенн НА, ИНС НИСЗ, а потом устанавливают системы функциональных зависимостей между известными значениями координат, составляющих вектора скорости фазовых центров антенн ИНС НИСЗ и неизвестными значениями координат, составляющих вектора скорости фазовых центров антенн НАП и определяют координаты местоположения, составляющие вектора скорости фазового центра антенн НАП пользователей СРНС путем решения системы навигационных уравнений.
Недостатками известного способа, взятого в качестве прототипа, являются:
- низкая точность навигационных измерений и определений, достоверность и надежность, обусловленные ретрансляцией спутниками навигационной информации и дальномерных кодов наземных навигационных радиомаяков (ННРМ);
- невозможно навигироваться пользователям с использованием несущих частот радиосигналов других спутниковых систем;
- невозможно определить пользователями свою ориентацию в пространстве, пеленг при приеме спутниковых радиосигналов на одну слабонаправленную антенну;
- сложно проводить интеграцию спутниковых систем узкоцелевого назначения в многоцелевую.
Известный способ (прототип) характеризуется следующей совокупностью действий:
- навигационные радиосигналы, несущие которых промодулированы дальномерными кодами и навигационной информацией, а также информацией для введения поправок по частоте и времени, излучают ННРМ;
- навигационной аппаратурой, установленной на спутниках, принимают излученные ННРМ радиосигналы, измеряют с применением дальномерных кодов дальности, разности дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн навигационной аппаратуры, установленной на спутниках, а также измеряют с помощью системы слежения за несущей (ССН) значения приращений дальностей, обусловленные доплеровскими сдвигами частот, значения частот Доплера, скорости изменения дальностей, разности скоростей изменения дальностей, модулируют измеренной информацией несущие ретранслируемых радиосигналов, усиливают их и излучают в направление Земли;
- НАП СРНС принимают ретранслируемые спутниковыми источниками навигационных сигналов (СИНС) навигационные радиосигналы, измеряют с применением дальномерных кодов дальности, разности дальностей между фазовыми центрами антенн СИНС и фазовыми центрами антенн НАП, а также измеряют с помощью ССН значения приращений дальностей, обусловленные доплеровскими сдвигами частот, значения частот Доплера, скорости изменения дальностей, разности скоростей изменения дальностей выделяют навигационную информацию о координатах местоположения фазовых центров антенн ННРМ, информацию о частотно-временных поправках к частотам, задержкам, время и информацию, измеренную СНА, затем по измеренной и выделенной НАП СРНС информации определяют:
- модули вектора положения фазового центра антенны СНА как отношение геоцентрической гравитационной постоянной к произведению квадрата скорости света на разность между единицей и отношением квадрата частоты навигационного радиосигнала, принимаемого СНА, к квадрату частоты навигационного радиосигнала, излучаемого ННРМ, умноженной на квадрат суммы из единицы и отношения радиальной скорости фазового центра антенны СНА в серединах мерных интервалов относительно фазового центра антенны ННРМ к скорости света;
- модули вектора положения фазового центра антенны спутникового источника навигационного радиосигнала как отношение геоцентрической гравитационной постоянной к произведению квадрата скорости света на разность между единицей и отношением квадрата частоты навигационного радиосигнала, принимаемого НАП, к квадрату частоты навигационного радиосигнала, излучаемого СИНС, умноженной на квадрат разности между единицей и отношением радиальной скорости фазового центра антенны СИНС в серединах мерных интервалов относительно фазового центра антенны НАП к скорости света;
- значения косинуса угла между векторами базами, соединяющими начала и концы мерных интервалов, и векторами дальностей, соединяющими положения фазового центра антенны ННРМ и положения фазового центра антенны СНА, а также значения угла как отношения произведений значений радиальной скорости фазового центра антенны СНА, находящегося в серединах мерных интервалов относительно фазового центра антенны ННРМ на значения частоты навигационного радиосигнала, излучаемого ННРМ, к произведению скорости света на корень квадратный из разности квадратов значения частоты навигационного радиосигнала, излучаемого ННРМ, и квадратов значения частоты навигационного радиосигнала, принимаемого СНА, умноженной на квадрат суммы из единицы и отношения значения радиальной скорости фазового центра антенны СНА, находящегося в серединах мерных интервалов, относительно фазового центра антенны ННРМ к скорости света и как арксинус отношений соответственно;
- значения косинуса угла между векторами базами, соединяющими начала и концы мерных интервалов, и векторами дальностей, соединяющими положения фазового центра антенны НАП и положения фазового центра антенны СИНС, а также значения его угла как отношения произведений значений радиальной скорости фазового центра антенны СИНС, находящегося в серединах мерных интервалов относительно фазового центра антенны НАП, на значения частоты навигационного радиосигнала, излучаемого СИНС, к произведению скорости света на корень квадратный из разности квадратов значений частоты навигационного радиосигнала, излучаемого СИНС, и квадратов значений частоты навигационного радиосигнала, принимаемого НАП, умноженной на квадрат разности между единицей и отношением значения радиальной скорости фазового центра антенны СИНС, находящегося в серединах мерных интервалов, относительно фазовых центров антенн НАП к скорости света и как арккосинус отношений соответственно;
- модули вектора базы как произведение отношений разности дальностей между фазовым центром антенны ННРМ и фазовым центром антенны СНА на мерных интервалах, умноженные на скорость света к радиальной скорости фазового центра антенны СНА, относительно фазового центра антенны ННРМ, умноженной на значение частоты навигационного радиосигнала, излучаемого ННРМ, на корень квадратный из разности квадрата значений частоты навигационного радиосигнала, излучаемого ННРМ, и квадрата значений частоты навигационного радиосигнала, принимаемого СНА, и умноженной на квадрат суммы из единицы и отношения значений радиальной скорости фазового центра антенны СНА, находящегося в серединах мерных интервалов, относительно фазового центра антенны ННРМ к скорости света;
- модули вектора базы как произведение отношений разности дальностей между фазовым центром антенны СИНС и фазовым центром антенны НАП на мерных интервалах, умноженные на скорость света к радиальной скорости фазового центра антенны СИНС, относительно фазового центра антенны НАП, умноженной на значения частоты навигационного радиосигнала, переизлучаемого СИНС, на корень квадратный из разности квадрата значений частоты навигационного радиосигнала, переизлучаемого ИСЗ, и квадрата значений частоты навигационного радиосигнала, принимаемого НАП, умноженной на квадрат разности из единицы и отношения значений радиальной скорости фазового центра антенны СИНС, находящегося в серединах мерных интервалов, относительно фазового центра антенны НАП к скорости света;
- разности дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн СНА, а также разности дальностей между фазовыми центрами антенн СИНС и фазовыми центрами антенн НАП путем выделения информации о приращениях фаз несущих навигационных радиосигналов, обусловленных доплеровскими сдвигами частот в целях управления частотами генераторов управляемых напряжением ССН в СНА и НАП;
- дальность между фазовым центром антенны СИНС и фазовым центром антенны НАП как отношения произведений значений радиальной скорости фазового центра антенны СИНС в серединах мерных интервалов относительно фазового центра антенны НАП, измеренные с помощью НАП, и квадрата модуля вектора базы, определяемого мерным интервалом, к произведению разности радиальных скоростей на краях мерных интервалов на разность дальностей, умноженные на квадрат синуса арккосинуса отношения значений разностей дальностей, измеренных путем выделения информации о приращениях фаз несущих навигационных радиосигналов, обусловленных доплеровскими сдвигами частот в цепи управления генератора, управляемого напряжением ССН НАП, к значениям модуля вектора базы;
- дальность между фазовым центром антенны ННРМ и фазовым центром антенны СНА как отношение произведений значений радиальной скорости фазового центра антенны СНА в серединах мерных интервалов относительно фазового центра антенны ННРМ, измеренные с помощью ССН СНА, и квадрата модуля вектора базы, определяемого мерным интервалом, к произведению разности радиальных скоростей на краях мерных интервалов на разность дальностей, умноженные на квадрат синуса арккосинуса отношения значений разностей дальностей, измеренных путем выделения информации о приращениях фаз несущих навигационных радиосигналов, обусловленных доплеровскими сдвигами частот в цепях управления генераторов, управляемых напряжением ССН СНА, к значениям модуля вектора базы;
- дальность между фазовым центром антенны ННРМ и фазовым центром антенны СНА как отношения разности дальностей между фазовым центром антенны ННРМ и фазовым центром антенны СНА, измеренные с помощью ССН как приращения дальности на мерном интервале, умноженные на квадрат скорости света, к разности скорости изменения дальностей на мерном интервале, умноженной на квадрат значения частоты навигационного радиосигнала, излучаемого ННРМ, и разность дальностей, умноженные на разности квадратов значений частоты навигационного радиосигнала, излучаемого ННРМ, и квадратов значений частоты навигационного радиосигнала, принимаемого СНА, умноженные на квадрат суммы из единицы и отношения значений радиальной скорости фазового центра антенны СНА к скорости света, вторично умноженные на синус арккосинус отношения произведений значений радиальной скорости фазового центра антенны СНА на значения частоты навигационного радиосигнала, излучаемого ННРМ, к произведениям разности дальностей и скорости света, умноженные на корень квадратный из разности квадрата значений частоты навигационного радиосигнала, излучаемого ННРМ, и квадрата значений частоты навигационного радиосигнала, принимаемого СНА, умноженные на квадрат суммы из единицы и отношения значений радиальной скорости фазового центра антенны СНА к скорости света;
- дальность между фазовым центром антенны СИНС и фазовым центром антенны НАП как отношения разности дальностей между фазовым центром антенны СИНС и фазовым центом антенны НАП, измеренные с помощью ССН, как приращения дальности на мерном интервале, умноженные на квадрат скорости света, к разности скорости изменения дальностей на мерном интервале, умноженной на квадраты значений частоты навигационного радиосигнала, излучаемого СИНС, и разность дальностей, умноженные на разности квадрата значения частоты навигационного радиосигнала, излучаемого СИНС, и квадратов значений частоты навигационного радиосигнала, принимаемого НАП, умноженные на квадрат разности из единицы и отношения значения радиальной скорости фазового центра антенны СИНС к скорости света, вторично умноженные на синус арккосинус отношений произведения значений радиальной скорости фазового центра антенны СИНС на значения частоты навигационного радиосигнала, излучаемого СИНС, к произведениям разности дальностей и скорости света, умноженные на корень квадратный из разности квадрата значений частоты навигационного радиосигнала, излучаемого СИНС, и квадрата значений частоты навигационного радиосигнала, принимаемого НАП, умноженные на квадрат разности из единицы и отношения значения радиальной скорости фазового центра антенны СИНС к скорости света;
- устанавливают системы функциональных зависимостей между известными значениями координат фазовых центров антенн ННРМ, а также известными координатами размещения начала прямоугольной геоцентрической системы координат и неизвестными значениями координат фазовых центров антенн СИНС, определяют значения координат и составляющих вектора скорости фазовых центров антенн СИНС путем решения систем навигационных уравнений, затем устанавливают системы функциональных зависимостей между известными значениями координат, составляющих вектора скорости фазовых центров антенн СИНС, известными координатами размещения начала прямоугольной геоцентрической системы координат и неизвестными значениями координат, составляющих вектора скорости фазовых центров антенн НАП и определяют координаты местоположения, составляющие вектора скорости фазового центра антенн НАП СРНС путем решения соответствующих систем уравнений.
Технической задачей (целью) настоящего изобретения является автономное мгновенное определение пользователями-абонентами координат своего местоположения составляющих вектора скорости, угловой ориентации в пространстве и пеленга по фазе несущей радиосигналов наземных радиомаяков, ретранслируемых спутниками.
Поставленная цель достигается за счет новой совокупности действий и применения новых алгоритмов решения навигационной задачи.
Геометрическая интерпретация сущности предлагаемого способа иллюстрируется на фигурах 1, 2, 3.
На фигуре 1 приведена геометрическая схема, иллюстрирующая навигационные измерения и определения координат фазового цента антенн спутников по фазе несущих радиосигналов, излучаемых двумя наземными радиомаяками.
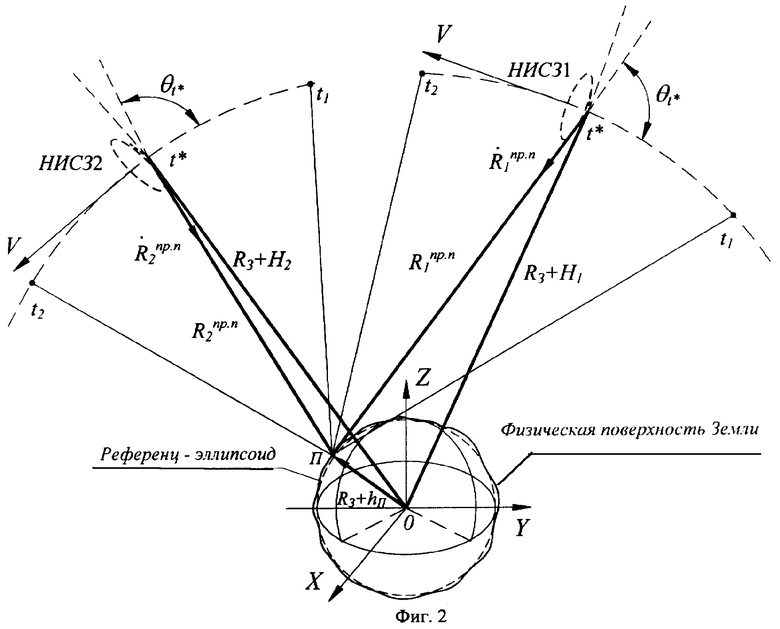
На фигуре 2 приведена геометрическая схема, иллюстрирующая навигационные измерения и определения координат фазового центра антенн пользователей по фазе несущих радиосигналов наземных радиомаяков, ретранслируемых двумя спутниками.
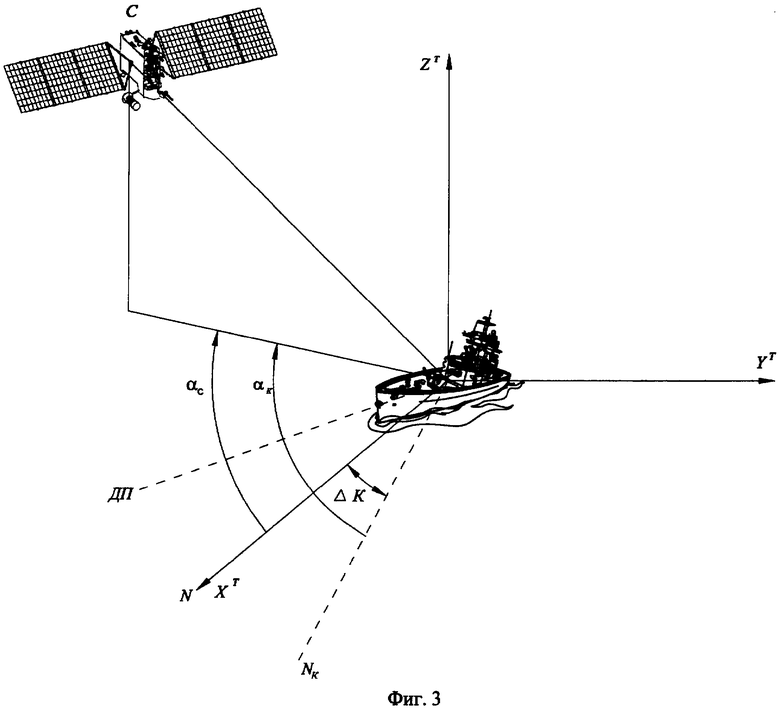
На фигуре 3 приведена геометрическая схема, иллюстрирующая связь измеренных значений азимутов с использованием компаса и спутников с поправкой курсоуказания в системе координат, связанной с судном,
где ДП - дирекционный пеленг;
N - истинное направление на север;
Nк - направление на север, измеренное компасом;
XT, YT, ZT - оси топоцентрической системы координат.
Сущность предлагаемого способа заключается в следующем.
Сетью простейших автоматических радиомаяков, размещенных на поверхности Земли таким образом, чтобы в зоне радиовидимости каждого спутника непрерывно находилось два радиомаяка, непрерывно излучающих несущие радиосигналов. В качестве радиомаяков могут быть использованы, например, существующие действующие, стационарные терминалы связных спутниковых систем или радиомаяки, непрерывно излучающие несущие радиосигналов.
Основные требования: непрерывно излучаемые радиосигналы радиомаяков излучали достаточную мощность несущих для уверенного приема приемными устройствами спутниковых ретрансляторов; ретранслируемые сигналы имели информацию о принадлежности сигналов к соответствующим радиомаякам, и были известны координаты местоположения радиомаяков (фазовых центров антенн) с достаточной точностью, которые при производстве аппаратуры пользователей (АП) записываются в их запоминающие устройства.
Приемными устройствами спутниковых ретрансляторов (ПУСР) непрерывно принимаются несущие радиосигналов от двух радиомаяков и более, находящихся в зоне радиовидимости, и информацией о изменении принимаемых частот несущих, имеющейся в цепях управления частотами генераторов, управляемых напряжением схем слежения за несущими (ССН) на краях и в серединах одних и тех же мерных интервалов в системах отсчета времени спутников, модулируются несущие радиосигналов, усиливаются и затем излучаются (ретранслируются) в направлении Земли. При этом сигналы радиомаяками могут излучаться в одном частотном диапазоне, а ретранслироваться спутниками в другом.
Для определения координат и скорости навигирующимися пользователями производится одновременный прием, но уже ретранслированных сигналов радиомаяков от двух спутников выделяется информация о принадлежности сигналов соответствующим радиомаякам и информация ССН об изменениях принимаемых несущих сигналов ПУСР, а также фиксируется информация об изменении значений несущих на краях и в серединах мерных интервалов, имеющиеся в цепях управления генераторов управляемых напряжением (ГУН) ССН АП.
Выделенная и зафиксированная информация в АП позволяет произвести вычисления навигационных параметров, которые в свою очередь позволяют установить навигационные зависимости между известными значениями направляющих косинусов векторов положения радиомаяков и неизвестными значениями направляющих косинусов векторов положения спутников. В результате решения системы навигационных уравнений в аппаратуре абонентов определяются значения и направляющих косинусов векторов положения спутников. Затем устанавливаются функциональные зависимости между известными значениями направляющих косинусов векторов положения спутников и неизвестными значениями направляющих косинусов векторов положения пользователей. Далее определяются координаты местонахождения пользователей без знания координат спутников с использованием только известных координат радиомаяков, записанных в запоминающие устройства АП при изготовлении аппаратуры.
При применении предложенного способа автономного определения абонентами своего местоположения отпадает необходимость также передавать каждым спутником собственные сообщения, на основе которых в действующей в настоящее время НАП производится решение навигационной задачи.
В основу предложенного способа автономного местоопределения спутников и пользователей положена дифференциальная радиально-скоростная методика измерений приращений фаз, обусловленных доплеровским сдвигом частоты. Современная радиально-скоростная дифференциальная методика базируется на измерениях доплеровских смещений частоты, которые приобретают излученные колебания номинальной частоты на трассе распространения между оконечными пунктами, находящимися в относительном движении с применением спутниковых линейных интерферометров и систем слежения за несущими частотами сигналов, принимаемыми приемными устройствами спутников и пользователей спутниковых систем.
При измерениях с применением дифференциальной радиально скоростной методики мерный интервал сравнительно мал (единицы секунд) и за время ТM измерение приращений фаз (приращений дальностей), обусловленных доплеровским сдвигом частоты, можно считать линейным. Разделив результат измерений приращений фаз на ТM, получим значение доплеровской частоты (радиальной скорости), пропорциональное мгновенному значению, а разделив на волновое число 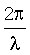 , получим значение разности дальностей за время мерного интервала ТM.
, получим значение разности дальностей за время мерного интервала ТM.
Классическое представление принципа работы интерферометра - измерение разности фаз колебаний, принимаемых двумя антеннами, разнесенными в пространстве (радиопеленгатор). Однако прием может осуществляться и на одну антенну, но тогда излучение принимаемого сигнала должно осуществляться разнесенными антеннами (фазовый радиомаяк). Демонстрацией работы интерферометра на базе второго принципа является прием пользователями спутниковых систем на мерных интервалах радиосигналов, излучающих движущимися спутниками. Расстояние, пройденное антенной спутника (фазовым центром) за мерный интервал, называется базой (базовым расстоянием d). Пользователи спутниковых систем удалены от центров баз на расстояния, во много раз превышающие d. В этом случае направления прихода сигналов спутников на мерных интервалах можно считать параллельными и можно записать разность расстояний в виде [3]:
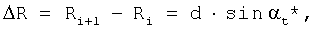
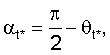
i=1,2,...,
где αt* - угол между направлением на пользователя (фазовый центр антенны АП) и нормалью к базе, проходящей через ее центр; π=3,1415....
Направление «пользователь - спутник» определяется направляющим углом θt*, отсчитываемый относительно базы. Направление часто характеризуется также величиной cosθt*, которая носит название направляющий косинус [4], [5].
Зная величину базы и измеряя тем или иным способом разность расстояний ΔR, можно определить направление на пеленгуемый спутник (источник излучения).
При фазовом методе измеряется разность фаз Δϕ колебаний. Если длина волны принимаемых колебаний равна λ, то
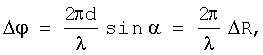
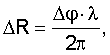
где 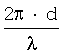 носит название крутизны пеленгационной характеристики или чувствительности [3].
носит название крутизны пеленгационной характеристики или чувствительности [3].
Поскольку разность фаз Δϕ пропорциональна направляющему косинусу угла прихода волны, определение направления фазовым методом сводится к измерению разности фаз (разности дальностей).
Таким образом, чувствительность спутникового интерферометра, а следовательно, и точность пеленгования, точность измерения радионавигационных параметров растут с увеличением отношения d/λ (увеличением мерного интервала).
Для уменьшения погрешностей, обусловленных флюктуацией фазы за счет среды, в которой распространяются радиоволны, а также за счет отсчетов фазы необходимо чтобы размер базы превышал эффективный радиус корреляции неоднородностей среды.
Геометрическая интерпретация измерений радионавигационных параметров с применением спутниковых линейных интерферометров и радиально-скоростной дифференциальной методики предлагаемого способа иллюстрируется на фигурах 1, 2.
Поверхности положения для радиальной скорости представляют собой конусы, уравнения которых [5]
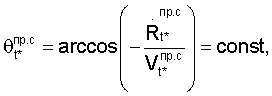
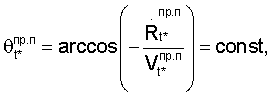
где 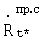 ,
,  ,
, 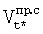 ,
, 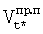 - радиальные скорости и линейные скорости кругового движения спутников, измеренные с применением информации ГУН ССН ПУСР и ГУН ССН АП об изменении несущих частот принимаемых сигналов соответственно.
- радиальные скорости и линейные скорости кругового движения спутников, измеренные с применением информации ГУН ССН ПУСР и ГУН ССН АП об изменении несущих частот принимаемых сигналов соответственно.
Оси этих конусов направлены по вектору скорости спутников, а вершины в момент измерения радиальной скорости находятся в фазовых центрах антенн спутников. По мере приближения спутников к пользователю радиальная скорость, оставаясь отрицательной, убывает по значению, угол θ увеличивается (конус «разворачивается»). В момент максимального приближения спутников к пользователю угол θ=90° конус вырождается в плоскость. Затем радиальная скорость становится положительной, θ>90° (конус «выворачивается наизнанку»).
Пространственное визирование с использованием спутниковых фазовых радиомаяков (линейных интерферометров) позволяет обозначить угловое положение линии, соединяющие фазовый центр антенн радиомаяков и фазовый центр антенн спутников, а также фазовый центр антенн спутников и фазовый центр антенн пользователей. Процессу пространственного пеленгования отвечает множество поверхностей, с которыми можно совместить линии визирования. Поверхностями положения в этом случае могут быть только те из них, которые имеют линейные образующие - линейчатые поверхности, например конические поверхности.
Линии визирования удобно задавать направляющими углами α, β, γ, заключенными между этими линиями и координатными осями. Вместо углов возможно употреблять значения их косинусов (cosα, cosβ и cosγ), что удобно для нахождения через эти направляющие косинусы соответствующих слагающих координат по осям. Из направляющих углов только два являются независимыми, а третий определяется через них.
Одним из видов навигационных измерений является метод измерения приращений фаз несущих навигационных радиосигналов с использованием радиально-скоростной дифференциальной методики.
Для измерения радионавигационного параметра (набега фаз колебаний несущих частот радиосигналов, обусловленных доплеровским сдвигом частоты) с применением радиально-скоростной дифференциальной методики обработки фазовых измерений, используются ССН ПУСР и ССН АП.
ССН предназначены для слежения за фазой несущих, выделения информации и измерения доплеровских сдвигов частот. Для обеспечения быстрой синхронизации по несущей используется кольцо цифровой фазовой автоматической подстройки частоты (ЦФАПЧ). Кольцо фазовой подстройки частоты отслеживает изменение частоты входного сигнала. Информации об изменении частоты входного сигнала имеется в цепи управления частотой подстраиваемого ГУН, с помощью которой частота генерируемого им сигнала поддерживается равной частоте входного сигнала.
Кольцо ЦФАПЧ относительно просто и с высокой точностью позволяет измерить на мерном интервале набег нециклической фазы выходного колебания (т.е. фазы, изменяющейся в пределах, не ограниченных интервалом длиной 2π). Это дает возможность применять относительно простые квазиоптимальные алгоритмы измерений приращений фаз по сигналу, замаскированному шумом [6].
Измеренные значения набега фаз с помощью ССН ПУСР 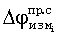 и ССН АП
и ССН АП 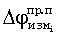 включают в себя как основную (рабочую) составляющую фазы
включают в себя как основную (рабочую) составляющую фазы 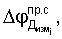
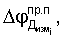 обусловленные эффектом Доплера, так, дополнительную составляющую фазы
обусловленные эффектом Доплера, так, дополнительную составляющую фазы 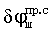 ,
, 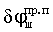 , вызванные рассогласованием временных шкал в радиолиниях «радиомаяки спутники», «спутники - пользователи» соответственно
, вызванные рассогласованием временных шкал в радиолиниях «радиомаяки спутники», «спутники - пользователи» соответственно
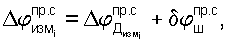
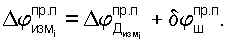
При радиально-скоростном дифференциальном режиме измерений можно считать, что неизвестные приращения фаз, обусловленные нестабильностью частот опорных генераторов оконечных пунктов радиоизмерительных трасс, сохраняются на протяжении измерительного сеанса постоянными и в процессе измерений разностей фаз они взаимно скомпенсируются. Поэтому в выражениях, определяющих значения измеренных разностей фаз (приращений фаз), они отсутствуют.
С целью более существенного уменьшения дисперсии фазовых измерений технология измерения набега фаз с помощью рассматриваемой методики предусматривает еще и вторичное усреднение, близкое к оптимальному. Вторичное усреднение измерений производится путем измерения усредненных значений 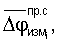
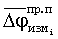 набега фаз на первой и на второй половинах мерного интервала и образования затем их разностей (двойных разностей фаз).
набега фаз на первой и на второй половинах мерного интервала и образования затем их разностей (двойных разностей фаз).
В этом случае в измеренных значениях разностей набега фаз, учитывая, что неизвестные расхождения временных шкал сохраняются на протяжении измерительного сеанса постоянными, взаимно скомпенсируются и также в конечных измеренных значениях радионавигационного параметра будут отсутствовать.
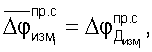
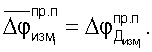
Таким образом, рассмотренная дифференциальная радиально-скоростная методика измерений разности набега фаз колебаний несущих частот навигационных радиосигналов с двойным усреднением на мерных интервалах позволяет практически мгновенно производить высокоточные измерения текущих значений радионавигационных параметров, являющимися основой вначале для определения навигационных параметров, а затем и установления функциональных навигационных зависимостей (алгоритмов) решения навигационной задачи.
Основное достоинство скоростного дифференциального радиального метода измерений навигационных параметров - отсутствие в измерениях систематических погрешностей, погрешностей, обусловленных расхождением шкал времени и частот генераторов радиомаяков - спутников, спутников - пользователей (абонентов).
Алгоритм оценки доплеровских сдвигов частоты (разности фаз несущих частот, обусловленных доплеровским сдвигом частоты) при измерении навигационных параметров используется дважды. Первый раз измеряется 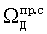 в радиолинии «радиомаяк - спутник» и второй раз измеряется
в радиолинии «радиомаяк - спутник» и второй раз измеряется  в радиолинии «спутник - пользователь»
в радиолинии «спутник - пользователь»
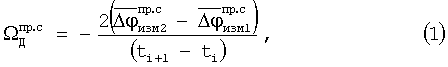
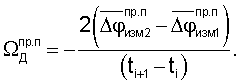
Реальные измеренные значения приращений дальностей ΔRпр.с, ΔRпр.п, радиальных скоростей 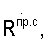
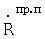 спутниковой аппаратурой и аппаратурой пользователей соответственно будут определяться выражениями
спутниковой аппаратурой и аппаратурой пользователей соответственно будут определяться выражениями
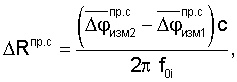
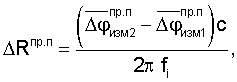

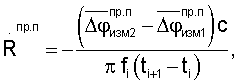
где f0i - частота колебаний радиосигналов, излучаемых радиомаяками; fi - частота колебаний радиосигналов, ретранслируемых спутниками; с - скорость света.
По измеренным значениям радионавигационных параметров с применением спутниковой навигационной аппаратуры и аппаратуры пользователей производится вычисление непосредственно самих навигационных параметров, определяющих как алгоритмы навигационных определений, так и предложенный способ в целом.
Способ автономного мгновенного определения пользователями-абонентами координат местонахождения, составляющих вектора скорости, угловой ориентации в пространстве и пеленга по фазе несущей радиосигналов наземных радиомаяков, ретранслируемых спутниками, основан на последовательном измерении навигационных параметров, выражающих расстояния между фазовыми центрами антенн радиомаяков - фазовыми центрами антенн спутников и расстояния между фазовыми центрами антенн спутников - фазовьми центрами антенн пользователей, а также на измерении модулей векторов положения спутников и пользователей (расстояний от точки размещения начала геоцентрической системы координат до фазовых центров антенн спутников и фазовых центров антенн пользователей) и определение по соответствующим измерениям значения направляющих косинусов. Они могут реализовываться в варианте, когда в зоне радиовидимости каждого спутника находятся два радиомаяка, а в зоне радиовидимости каждого пользователя - два спутника, расстояния до которых измеряется одновременно при соответствующем учете на мерном интервале их относительного движения.
Предложенный способ позволяет реализовать два алгоритма решения навигационной задачи: дальномерный и угломерный.
Исходными данными для решения навигационной задачи предложенного способа являются координаты радиомаяков (фазовых центров антенн), значения которых не изменяются и записываются в запоминающие устройства каждого комплекта АП в процессе их изготовления и информация об изменении принимаемых частот несущих радиомаяков и спутниковых ретрансляторов, имеющихся в цепях управления ГУН ССН ПУСР и АП. Вычисленные затем соответствующие навигационные параметры позволяют в свою очередь установить системы навигационных уравнений между известными значениями направляющих косинусов местных геоцентрических радиус-векторов и неизвестными значениями направляющих косинусов геоцентрических радиус-векторов. В процессе решения систем уравнений определяются непосредственно значения направляющих косинусов радиус-векторов положения спутников или значения координат фазовых центров антенн спутников. Далее устанавливаются системы навигационных уравнений между уже известными значениями направляющих косинусов геоцентрических радиус-векторов (векторов положения спутников) и неизвестными значениями направляющих косинусов радиус-вектора положения пользователя.
Для определения значений направляющих косинусов геоцентрических радиус-векторов системы уравнений имеют вид
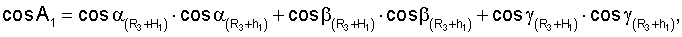
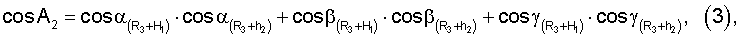
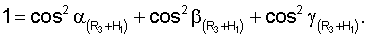
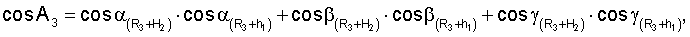
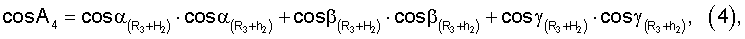
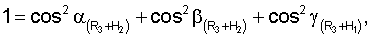
где
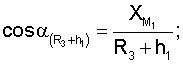
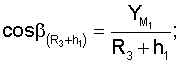
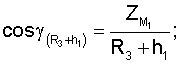
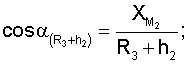
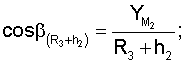
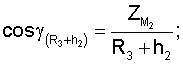
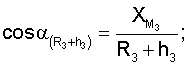
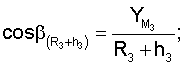
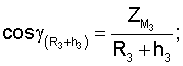
ХМ1, YМ1, ZМ1,...X** М3, YМ3 **, Z** М3 - значения координат первого и второго и третьего (в зоне радиовидимости спутника могут находиться и другие радиомаяки) опорных наземных радиомаяков соответственно;
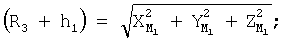
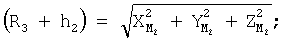
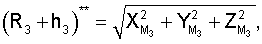
где cosA1, cosA2, cosA3 **, cosA4 ** - значения косинусов углов между геоцентрическим радиус-вектором (R3+Нi)пр.с и местными геоцентрическими радиус-векторами (R3+h1), (R3+h2), (R3+h3)** соответственно; H1, H2 - высоты спутников; h1, h2, h3 ** - высоты фазовых центров антенн радиомаяков над поверхностью Земли.
По теореме синусов
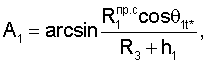
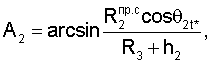
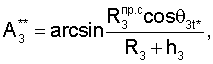
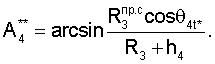
Для определения значений направляющих косинусов местного геоцентрического радиус-вектора и координат местоположения пользователей при приеме пользователями радиосигналов от двух спутников по известным значениям направляющих косинусов геоцентрических радиус-векторов устанавливаются системы навигационных уравнений
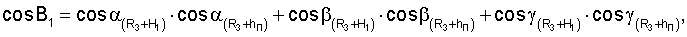
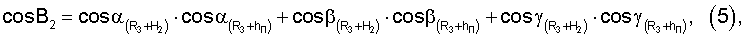
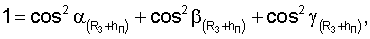
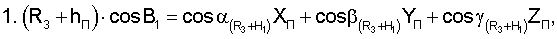
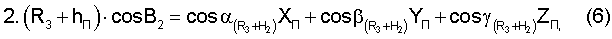
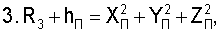
где cosB1, cosB2 - значения косинусов углов между геоцентрическими радиус-векторами (R3+H1)пр.п, (R3+H2)пр.п и местным геоцентрическим вектором R3+hП
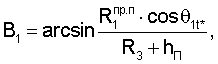
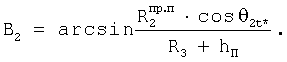
В результате решения систем уравнений (5), (6) определяют значения направляющих косинусов вектора положения пользователя и координаты местонахождения ХП, YП, ZП.
Уравнение 1, 2 системы (6) в отдельности представляет собой уравнение плоскости в пространстве, а в совокупности уравнения 1, 2 представляют собой прямую. Следовательно, геометрическим эквивалентом решения системы уравнения в целом является точка пересечения прямой с шаровой поверхностью радиусом (R3+hП), координаты которой и являются координатами местоположения фазового центра антенны пользователя.
Система уравнений (6) является реализацией алгоритма дальномерного метода решения навигационной задачи, а система уравнений (5) - угломерного метода.
В соответствии с алгоритмом угломерного метода решения навигационной задачи значения ХП, YП, ZП можно определить, использовав известные значения направляющих косинусов местного геоцентрического радиус-вектора (R3+hП).
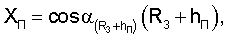
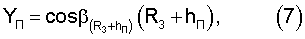
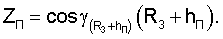
Аналогичным образом через известные значения направляющих косинусов вектора положения спутника можно определить координаты спутников
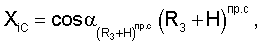
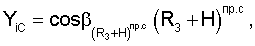
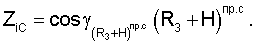
Составляющие вектора линейной скорости, а также составляющие векторов угловой скорости и углового ускорения спутников относительно осей геоцентрической системы координат определяются соответственно из выражений
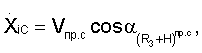

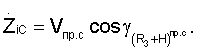

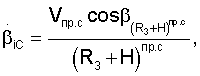
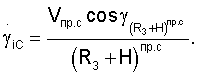
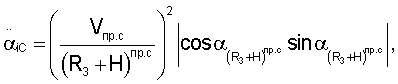
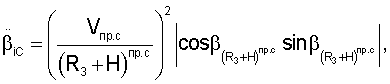
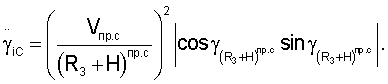
Значения направляющих косинусов топоцентрических векторов определяются из выражений
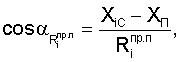
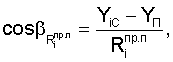
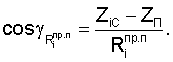
Значения составляющих вектора скорости пользователей определяются из решения системы уравнений, полученных после дифференцирования уравнений системы (6).
Как видно из решения навигационной задачи по определению координат пользователей для их нахождения достаточно знать значение координат фазовых центров антенн ННРМ. Координаты спутников в явном виде не применяются. Они косвенно присутствуют в значениях направляющих косинусов векторов положения спутников. Следовательно, нет необходимости их определения не только наземными средствами и передачи их пользователям с использованием спутниковых радиолиний, но и определять их вообще.
Таким образом предложенный способ позволяет определить местоположение пользователей-абонентов с использованием как алгоритма дальномерного метода, так и алгоритма угломерного метода без знания координат местоположения центров антенн источников излучения радиосигналов спутников.
При дифференциальном радиально-скоростном режиме измерений радионавигационных параметров с двойным усреднением измерений неизвестные приращения фаз, обусловленные нестабильностью частот генераторов оконечных пунктов радиоизмерительных трасс, а также дополнительные составляющие фаз, вызванные рассогласованием временных шкал в радиолиниях «радиомаяки-спутники», «спутники-пользователи» сохранятся на протяжении измерительных сеансов длительностью порядка нескольких секунд постоянными и в процессе измерений двойных разностей фаз они практически взаимно скомпенсируются. Следовательно, при фазовых измерениях по несущей частоте взаимная временная привязка спутниковых радиосигналов орбитальной группировки не требуется. Синхронизируются только часы (шкалы времени) спутников. Навигационная задача решается в шкале времени пользователей.
Определение значений направляющих косинусов векторов положения спутников и значений направляющих косинусов векторов положения пользователей разнесены по времени по шкале времени пользователей не более чем на несколько секунд. Для приведения их к единому времени (моменту решения навигационной задачи) направляющие косинусы спутников прогнозируются в АП, т.е. вычисляются их текущие значения на момент определения координат пользователей. Закон движения спутников на интервале времени несколько секунд можно считать линейным.
Одновременно результаты навигационных измерений и определений с применением угломерного метода позволяют определить составляющие линейной скорости, составляющие векторов угловой скорости и углового ускорения спутников относительно осей геоцентрической системы координат (8).
Некоторые пользователи наряду со знанием координат и составляющих вектора скорости нуждается в знании ориентации собственных осей в пространстве. Определение ориентации продольной оси движущихся пользователей относительно направления на истинный север сводится к измерению истинного курса, продольной оси относительно горизонта - к измерению дифферента или тангенса, поперечной оси относительно горизонта - к измерению курса. Все эти величины необходимы для морского и воздушного судовождения, некоторые - для топогеодезических работ.
При наличии на пользователях гироскопической или магнитной системы курсоуказания измерение истинной ориентации продольной оси по данным спутниковых систем и сравнение этих результатов с данными гирокомпаса или магнитного компаса позволит проложить маршрут движения и проконтролировать его. Трехмерная ориентация в пространстве нужна также спутникам, ракетным системам, стартовым устройствам ракетных систем.
Для ориентации пользователей в пространстве с использованием спутниковых систем измеряемыми навигационными параметрами являются углы между осями пользователей и прямой, соединяющей определенные точки пользователей и спутников (фазовые центры антенн АП и антенны источников навигационных радиосигналов спутников).
Для получения информации об ориентации пользователей спутниковых систем в пространстве необходима пеленгация спутников (пользователей).
В процессе пеленгации с использованием предложенных алгоритмов определяются направляющие косинусы углов α, β и γ геоцентрического и местного геоцентрического векторов, значения которых связаны с движением пользователя, вращением Земли и движением спутников.
Прямоугольные координаты и составляющие вектора скорости, например, пользователя в геоцентрической экваториальной системе координат связаны с географическими ϕ, γ и угловыми координатами известными соотношениями [3]:
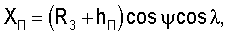
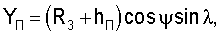
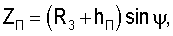
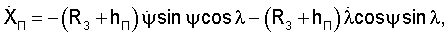
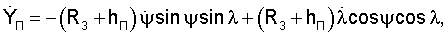
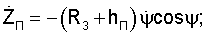
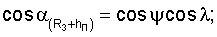
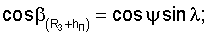
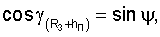
где (R3+hП) - модуль местного геоцентрического вектора (вектора положения пользователя); 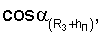
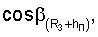
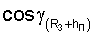 - направляющие косинусы вектора положения пользователя; ψ - геоцентрическая широта;
- направляющие косинусы вектора положения пользователя; ψ - геоцентрическая широта; 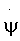 ,
, 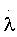 - скорости изменения геоцентрической широты и долготы.
- скорости изменения геоцентрической широты и долготы.
Геоцентрическая широта связана с географической широтой выражением:
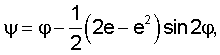
где е - эксцентриситет земного эллипсоида.
Известные значения направляющих косинусов векторов положения пользователей в геоцентрической системе координат, в свою очередь, позволяют найти значения углов ψ, λ из решения системы уравнений, а затем и скорости изменения геоцентрической широты и долготы путем дифференцирования выражений, определяющих их значения
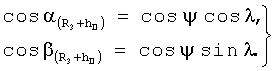
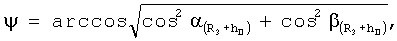
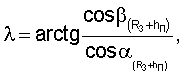
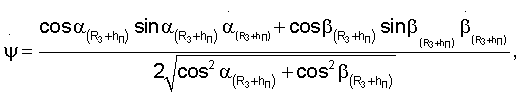
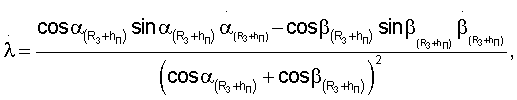
где 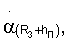
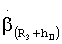 - скорости изменения угловых параметров местного геоцентрического вектора, определяемые выражениями (5) после их дифференцирования.
- скорости изменения угловых параметров местного геоцентрического вектора, определяемые выражениями (5) после их дифференцирования.
Используя формулы перехода из геоцентрической системы координат в топоцентрическую, пересчитывают значения направляющих косинусов векторов 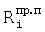 в геоцентрической системе координат в значения в топоцентрической системе координат в соответствии с выражениями [7].
в геоцентрической системе координат в значения в топоцентрической системе координат в соответствии с выражениями [7].
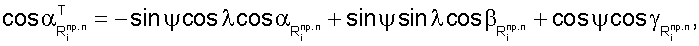
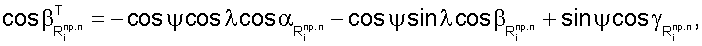
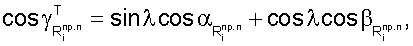
В то же время
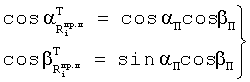
Совместное решение уравнений позволяют найти значения углов азимута αП и места βП пользователей в топоцентрической системе координат.
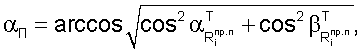
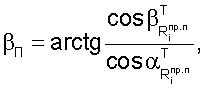
Условие пеленгации пользователя подвижным спутником требует непрерывной компенсации тем или иным способом отклонения плоскости пеленгации. Нарушение условий пеленгации происходит вследствие возмущающих вращательных и поступательных движений пользователей и движения спутников на небесной сфере.
Одним из вариантов непрерывной компенсации условий пеленгации (погрешностей), обусловленных вращательными и поступательными движениями пользователей фазовыми характеристиками используемых антенн, подстилающей поверхностью являются, например, технические решения, опубликованные в [8].
Знание значений направляющих косинусов вектора положения пользователя в геоцентрической системе координат и в системе координат пользователей позволяет определить углы между ортами двух систем. А знание значений углов, например, между ортами судовой системы координат с началом в центре масс, направленными соответственно по правому борту, носу и вверх, и ортами геоцентрической системы координат с началом в центре масс Земли, направленными соответственно по меридиану на север и вертикально вверх по отношению к поверхности Земли, является практически исчерпывающей информацией для определения ориентации пользователя в пространстве. Вычисленные значения направляющих косинусов векторов положения спутников и пользователей одновременно позволяют определить не только ориентацию в пространстве, но и составляющие их угловых скоростей и ускорений путем дифференцирования выражений их определяющих, а также решить задачу курсоуказания.
Для того чтобы произвести определение курса движения судна с требуемой погрешностью необходимо произвести определение (проверку) поправки компаса. Условимся, что под поправкой компаса будем понимать угол в горизонтальной плоскости между плоскостью истинного меридиана и осью любого (магнитного, гироскопического и др.) судового хранителя направления.
Определение поправки курсоуказания с применением алгоритма угломерного метода производится путем сличения отнесенных к одному моменту измерений измеренных значений αП с использованием, например, навигационных радиосигналов спутников системы GPS диапазона частот L1 или L2 и измеренных значений αк с помощью компаса.
Поправка компаса определяется из выражения
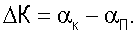
Геометрическая интерпретация определения поправки курсоуказания по навигационным радиосигналам спутников системы GPS иллюстрируется на фигуре 3.
Результирующая погрешность навигационных определений пользователей зависит от множества факторов, полный учет которых едва ли возможен.
В значительной мере погрешность определяются типом сигнала, используемого в навигационной системе, а в основном погрешностью эфемерид, окружающей средой, в которой распространяются навигационные сигналы, и погрешностью измерения навигационных параметров непосредственно аппаратурой ПУСР и АП.
Основой для вычислений приращений дальностей, радиальных скоростей, линейных скоростей кругового движения спутников, модулей топоцентрических, геоцентрических и местных геоцентрических векторов базовых расстояний, значений угловых скоростей базовых расстояний, значений косинусов углов между радиальным движением спутников и вектором линейной скорости являются фазовые измерения, измерения значений доплеровских частот аппаратурой ПУСР и АП по приращениям фаз несущих навигационных радиосигналов радиомаяков и спутников. Измерение приращений фаз производится с использованием радиально-скоростной дифференциальной методики. Режим измерений с применением ССН аппаратуры ПУСР и АП приращений фаз эквивалентен режиму измерений двойных разностей хода радиосигналов между фазовыми центрами антенн радиомаяков, АП и двумя положениями фазовых центров спутниковых антенн спутниковым линейным интерферометром, создающим на концах мерных интервалов два источника излучения сигналов, разнесенных во времени и в пространстве. Поэтому оценку погрешностей навигационных измерений и определений следует производить из расчета погрешностей фазовых измерений спутниковым интерферометром.
Погрешности фазовых измерений спутниковым интерферометром приращений фаз в общем случае обусловлены неточностями определения частот принимаемых аппаратурой ПУСР и АП радиосигналов (доплеровских сдвигов частоты), ошибками при разрешении неоднозначности фазовых измерений, нестабильностью принимаемых частот, многолучевостью распространения сигналов, влиянием ионосферы, тропосферы и погрешностями углов визирования спутников, обусловленными вычислительным процессом, а также характеристиками ПУСР и АП.
Измерения приращений фаз спутниковым интерферометром являются реализацией режима относительных измерений, положительной особенностью которых является то, что при их измерениях погрешности, имеющие систематический характер, взаимно компенсируются. По существу относительные измерения являются одной из разновидностей дифференциального режима использования интерферометрических измерений для определения навигационных параметров, в ходе реализации которого за счет компенсации систематических погрешностей и обеспечивается высокая точность фазовых измерений.
Эффективность компенсации зависит от выходных характеристик цифровых следящих систем приемных устройств спутников и АП, в частности от характеристик цифровых ССН, поскольку именно шумовая погрешность ограничивает эффект компенсации сильно коррелированных погрешностей.
Измерение значений доплеровского сдвига частоты навигационных радиосигналов в современных отечественных и зарубежных приемоиндикаторах спутниковых систем основано на измерениях приращений фаз несущих частот с использованием цифровых систем ССН, позволяющих весьма просто и относительно точно измерять набег нециклической фазы выходных колебаний (т.е. фазы, изменяющейся в пределах, не ограниченных интервалом 2π). Следовательно, проблемы разрешения неоднозначности фазовых измерений нет. Это дает возможность применять относительно простые квазиоптимальные алгоритмы фазовых измерений значений доплеровского сдвига частоты по сигналу, замаскированному шумом [6]. Среднеквадратическое значение погрешности слежения следящих систем, например, на частотах американской GPS, имеющих полосу слежения 20 Гц, обусловленной спектральной плотностью фазовых шумов, составляет не более 0.1 радиана [9].
Нестабильность принимаемых частот (нестабильность приращений фаз) в аппаратуре ПУСР и АП можно представить как сумму постоянной в течение сеанса измерений (но неизвестной) и флуктационных составляющих. Первая при образовании вторых разностей фаз практически устраняется, доля вторых сводится к величине порядка 0,1 радиана [10].
Погрешности, обусловленные многолучевостью, сводятся также к незначительным величинам, как за счет применения направленных антенн с правой круговой поляризацией, в результате которой отраженные сигналы принимаются при малых углах возвышения с меньшим усилением и в основном имеют левую поляризацию, так и за счет компенсации систематических погрешностей в процессе навигационных измерений и обработки измерений.
Влияние ионосфер и тропосферы, а также сказывающее влияние на движение спутников лобовое сопротивление и аномалии гравитационного поля незначительно, поскольку приращения фаз, обусловленные условиями распространения радиоволн на мерных интервалах, отличаются мало и в процессе измерений разностей фаз большая часть их взаимно компенсируется. Использование первичного и вторичного усреднений фазовых измерений позволяет большую часть как шумовой погрешности, так и оставшиеся части погрешностей, связанных с влиянием условий распространения (ионосфера, тропосфера, многолучевость), с влиянием лобового сопротивления на движение спутников, нестабильностью фазовых сдвигов в приемных устройствах, влияние ускорений и гравитационных полей спутников и АП свести к минимуму.
По своему происхождению причины погрешностей могут быть самые разные, но самой весомой является погрешность, обусловленная энергетическим потенциалом радиолинии, отношением 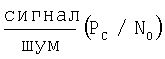 - шумовая погрешность.
- шумовая погрешность.
Для оценки шумовой погрешности измерений приращений дальностей (σΔR), значений доплеровских сдвигов частоты (σ Ωд), радиальной скорости 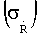 можно использовать выражение для дисперсии фазы (ε2 ф) схем ССН [11].
можно использовать выражение для дисперсии фазы (ε2 ф) схем ССН [11].
Среднеквадратические значения погрешности измерений приращений фаз определяются выражением
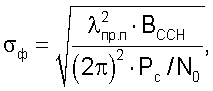
где ВССН - ширина полосы системы слежения за несущей.
Среднеквадратическое значение погрешности измерения приращений дальностей, например, в GPS 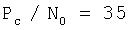 дБГц и BCCH=20 Гц на несущей частоте (λ=19 см) составит 0.079 радиан. Погрешность измерения приращений дальностей как приращений фаз несущей за определенный интервал времени увеличивается в
дБГц и BCCH=20 Гц на несущей частоте (λ=19 см) составит 0.079 радиан. Погрешность измерения приращений дальностей как приращений фаз несущей за определенный интервал времени увеличивается в 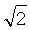 раз. Поэтому среднеквадратическая погрешность измерения приращений дальностей по фазе несущей, обусловленной шумом σΔRш=0,34 см.
раз. Поэтому среднеквадратическая погрешность измерения приращений дальностей по фазе несущей, обусловленной шумом σΔRш=0,34 см.
Измерение радиальной скорости основано также на измерениях приращений фаз на несущей частоте. Если интервал времени, в течение которого измеряется приращение фазы несущей равным одной секунды, а фазу выразить через длину волны, то погрешность измерения радиальной скорости составит 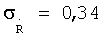 см/с.
см/с.
Погрешности квантования измеряемых приращений дальности при цифровой реализации ССН в предположении равномерного их распределения (σΔRкв) равны 0,25 см [11].
Источниками погрешностей вычислительного процесса в ПУСР и АП являются ограниченная разрядность процесса, математические аппроксимации и приближение выполнение команд с временной задержкой. Используя вычислители, способные выполнять расчеты с удвоенной точностью и с плавающей запятой, можно получить среднеквадратическую погрешность обработки приращений дальностей не более (σΔRв) 0,3 см.
Таким образом, в первом приближении можно утверждать, что доминирующее влияние на точность измерений радионавигационных параметров с использованием фазовых измерений спутниковым интерферометром оказывают помехи шумового типа и собственные шумы приемников, погрешности, обусловленные квантованием и вычислительным процессом.
Результирующая погрешность измерения приращений дальностей определяется квадратичным суммированием составляющих согласно формуле
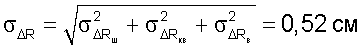
Рассмотрим погрешности навигационных измерений применительно к рассмотренной дифференциальной радиально-скоростной методики измерения радионавигационных параметров выражений (2), (3) двойных разностей фаз.
В соответствии с формулой полного дифференциала измеряемых величин 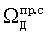 ,
, 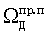 ,
, 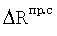 ,
,  ,
,  ,
, 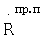 выражений (1), (2) получим для конечных приращений
выражений (1), (2) получим для конечных приращений
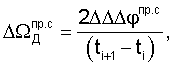
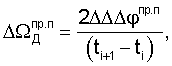
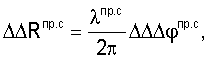
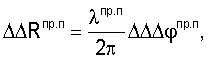
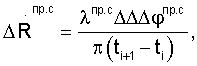
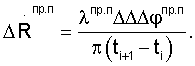
Погрешности измерений двойных разностей фаз могут быть вызваны как погрешностями слежения ССН, так и погрешностями определения длин волн, мерных интервалов.
Обычно случайные погрешности измерений по радиоканалам «радиомаяки-спутники» и «спутники-пользователи» независимы, а их среднеквадратические значения одинаковы  Поэтому среднеквадратические значения погрешностей измерений радионавигационных параметров с использованием радиально-скоростной методики можно найти по формулам
Поэтому среднеквадратические значения погрешностей измерений радионавигационных параметров с использованием радиально-скоростной методики можно найти по формулам
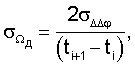
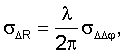
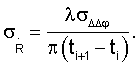
В соответствии с формулой полного дифференциала выражений определяемых величин 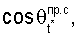
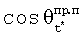 [3] с учетом (1) среднеквадратическая погрешность углов визирования θt* оценивается как
[3] с учетом (1) среднеквадратическая погрешность углов визирования θt* оценивается как
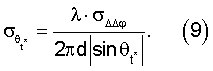
Таким образом, погрешность пеленгования спутниковым интерферометром уменьшается с увеличением отношения сигнала к шуму, длительности мерного интервала и с уменьшением полосы слежения ССН.
С учетом выше приведенной информации о среднеквадратической погрешности фазовых измерений, равной 0,079 радиан на односекундном мерном интервале, среднеквадратическая погрешность углов визирования 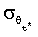 спутниковым фазовым интерферометром, например, на частотах GPS составит не более 0,123 угл. с. (на односекундном мерном интервале d≈4 км). Соответственно, на мерном интервале, равном 10 с, погрешность составит 0,0123 угл. с.
спутниковым фазовым интерферометром, например, на частотах GPS составит не более 0,123 угл. с. (на односекундном мерном интервале d≈4 км). Соответственно, на мерном интервале, равном 10 с, погрешность составит 0,0123 угл. с.
Рассмотрим погрешности измерения дальностей и погрешности навигационных определений спутников, пользователей, например, по радиосигналу GPS с применением радиально-скоростной дифференциальной методике фазовых измерений навигационных параметров.
Значения искомых дальностей 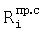 ,
,  вычисляются по приращениям
вычисляются по приращениям 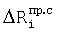 ,
, 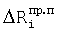 и значениям
и значениям 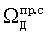 ,
, 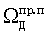 ,
, 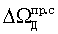 , которые в свою очередь косвенно измеряются по одним и тем же фазовым измерениям на несущих частотах. Поэтому их случайные погрешности зависимы и равны между собой.
, которые в свою очередь косвенно измеряются по одним и тем же фазовым измерениям на несущих частотах. Поэтому их случайные погрешности зависимы и равны между собой.
Применяя принципы равного влияния погрешностей фазовых измерений на среднеквадратические значения погрешностей измерения дальностей, погрешности последних можно определить, использовав выражение [12]
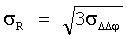
Погрешность измерения дальностей как погрешность, обусловленная фазовыми приращениями несущей частоты за определенные мерные интервалы, также увеличиваются в 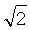 раз. Чтобы учесть все неучтенные и остаточные погрешности фазовых измерений, увеличим среднеквадратическую погрешность измерения дальностей еще в два раза.
раз. Чтобы учесть все неучтенные и остаточные погрешности фазовых измерений, увеличим среднеквадратическую погрешность измерения дальностей еще в два раза.
Тогда
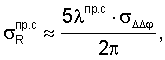
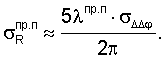
При равенстве длины волн несущих λпр.с=λпр.п=19 см среднеквадратическое значение погрешности определения дальностей между фазовыми центрами антенн радиомаяков-спутников, спутников-пользователей равно 1,2 см. Соответственно, предельное значение погрешности измерения дальностей (3 σR) равно 3,6 см.
Среднеквадратическая погрешность навигационных определений при применении дальномерной методики определяется как произведение предельных значений среднеквадратической погрешности измерения навигационного параметра (дальности) на соответствующее значение геометрического фактора (ГФ). Принимая номинальную величину ГФ, равную 3-5, предельная среднеквадратическая погрешность навигационных определений пользователей при применении дальномерной методики соответственно составит (10,8-18) см (без учета погрешностей определения, координат местоположения фазовых центров антенн спутников).
В случае применения этой же дальномерной методики для определения координат спутников предельное значение погрешности определения местоположения пользователей соответственно составит (15,23÷25,4) см, т.е. увеличится в 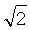 раз.
раз.
Измерения приращений фаз (приращения дальностей) в АП с применением цифровых ССН производится с использованием дифференциальной (радиально-скоростной) методики обработки измерений. Поэтому в навигационных системах уравнений отсутствуют погрешности, обусловленные расхождением шкал времени пользователей и спутников. Следовательно, для определения координат местоположения, составляющих вектора скорости пользователей GPS с применением алгоритмов автономного функционирования достаточно, чтобы в зоне радиовидимости каждого пользователя находилось не менее одного-трех спутников, а в зоне радиовидимости каждого спутника размещалось не менее одного-трех радиомаяков.
Для уменьшения случайных составляющих погрешностей навигационных определений и погрешностей, обусловленных шумом, необходимо увеличивать размеры базовых расстояний d (мерных интервалов) и соотношение 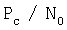 (отношение мощности сигнала к мощности шума) и уменьшать полосу слежения систем слежения за несущими навигационных радиосигналов ВССН.
(отношение мощности сигнала к мощности шума) и уменьшать полосу слежения систем слежения за несущими навигационных радиосигналов ВССН.
Глобальный дефект увеличения вертикальной составляющей погрешности определения местоположения пользователей в алгоритме угломерного метода (26) устраняется путем использования в системе уравнений измеренного значения местного геоцентрического радиус-вектора (R3+hП).
Рассмотрим вопрос об источниках погрешностей и погрешности навигационных определений алгоритмов угломерного метода.
Дифференцируя выражения (5), (6), (7) и переходя к конечным приращениям, получим выражения, определяющие погрешности определения местоположения пользователей и спутников, а также погрешности определения составляющих вектора угловой скорости и составляющих углового ускорения спутников относительно осей геоцентрической системы координат.
Погрешности установления функциональных зависимостей уравнений систем (3), (4) определяются погрешностями измерений спутниковыми линейными интерферометрами узлов визирования 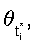 выражение (9) и составляют на мерных интервалах 1 с и 10 с 5,975·10-7 и 5,975·10-8 радиан соответственно. Допуская, что вычислительный процесс значений направляющих косинусов геоцентрического радиус-вектора (R3+Н) и радиус-вектора положения пользователей (R3+hП) вносит дополнительную погрешность, равную
выражение (9) и составляют на мерных интервалах 1 с и 10 с 5,975·10-7 и 5,975·10-8 радиан соответственно. Допуская, что вычислительный процесс значений направляющих косинусов геоцентрического радиус-вектора (R3+Н) и радиус-вектора положения пользователей (R3+hП) вносит дополнительную погрешность, равную 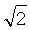 . Тогда средние среднеквадратические значения погрешностей определения углов
. Тогда средние среднеквадратические значения погрешностей определения углов 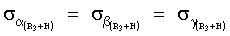 и
и 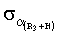 ,
, 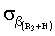 ,
, 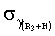 на мерных интервалах 1 с и 10 с соответственно составят 8,42·10-7, 8,42·10-8 и 1,19·10-6, 1,19·10-7 радиан. Это значит, что с такими средними погрешностями привязаны соответствующие радиус-вектора к осям геоцентрической системы координат, в том числе и к меридиану, направленному на север. Т.е. среднеквадратическое значение погрешности определения направления истинного меридиана с использованием спутниковых линейных интерферометров составит 1,19·10-6 радиан (0,258 угл. с) на 1 с мерном интервале и 1,19·10-7 радиан (0,0258 угл. с) на 10 с мерном интервале. Следовательно, предельная погрешность определения поправки курсоуказания спутниковыми интерферометрами с использованием приема приемоиндикатором спутниковых радиосигналов на одну антенну на мерном интервале, равном 1 с составит 1 угл. с. Соответственно, на мерном интервале, равном 10 с предельная погрешность поправки курсоуказания составит 0,1 угл. с.
на мерных интервалах 1 с и 10 с соответственно составят 8,42·10-7, 8,42·10-8 и 1,19·10-6, 1,19·10-7 радиан. Это значит, что с такими средними погрешностями привязаны соответствующие радиус-вектора к осям геоцентрической системы координат, в том числе и к меридиану, направленному на север. Т.е. среднеквадратическое значение погрешности определения направления истинного меридиана с использованием спутниковых линейных интерферометров составит 1,19·10-6 радиан (0,258 угл. с) на 1 с мерном интервале и 1,19·10-7 радиан (0,0258 угл. с) на 10 с мерном интервале. Следовательно, предельная погрешность определения поправки курсоуказания спутниковыми интерферометрами с использованием приема приемоиндикатором спутниковых радиосигналов на одну антенну на мерном интервале, равном 1 с составит 1 угл. с. Соответственно, на мерном интервале, равном 10 с предельная погрешность поправки курсоуказания составит 0,1 угл. с.
Как видно из систем уравнений (3), (4), (5), для того чтобы определить координаты местонахождения пользователей с применением угломерного метода решения навигационной задачи, определение (значение) координат спутников не требуется.
Средние значения предельных погрешностей навигационных определений с применением алгоритма угломерного метода при 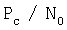 - отношении мощности сигнала к спектральной плотности мощности шума приведена в таблице.
- отношении мощности сигнала к спектральной плотности мощности шума приведена в таблице.
Таблица. Средние значения предельных погрешностей навигационных определений с использованием разработанного алгоритма угломерного метода при отношении
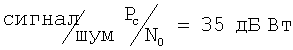 .
.
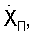
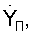
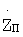 с использованием дальномерного метода (6):
с использованием дальномерного метода (6):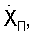
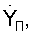
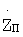 с применением алгоритма угломерного метода (5):
с применением алгоритма угломерного метода (5):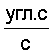
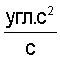
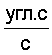
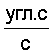 .
.
Техническая задача (цель) достигается за счет новой последовательности и совокупности действий над излучаемыми сигналами ННРМ, над принимаемыми сигналами приемными устройствами спутниковых ретрансляторов, над ретранслируемыми и над принимаемыми НАП ретранслированными спутниками радиосигналами, путем применения новых алгоритмов навигационных измерений и решения навигационных задач, которые и являются отличительными признаками предложенного способа:
- навигационную информацию в составе координат местоположения фазовых центров антенн ННРМ, времени и информацию для введения поправок по частоте, по времени, а также информацию по принадлежности к определенному ННРМ не передают в составе излучаемых ННРМ сигналов и не ретранслируют спутниками-ретрансляторами, а записывают в запоминающие устройства НАП на заводах изготовителях при ее изготовлении;
- определяют значения дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами спутниковых антенн приемных устройств спутников ретрансляторов (ПУСР) как произведения отношений квадратов значений радиальной скорости движения фазовых центров спутников приемных антенн к ускорениям радиальной скорости на квадраты значений тангенсов углов между радиальным движением и вектором скорости спутников;
- определяют значения дальностей между фазовыми центрами спутниковых антенн, ретранслирующих сигналы ННРМ, и фазовыми центрами антенн НАП как произведения отношений квадратов значений радиальной скорости движения фазовых центров спутниковых антенн, ретранслирующих сигналы ННРМ, к ускорениям радиальной скорости на квадраты значений тангенсов углов между радиальным движением и вектором скорости спутников;
- определяют значения косинусов углов между геоцентрическими радиус-векторами (векторами положения спутников (R3+Нi)пр.с) и местными геоцентрическими радиус-векторами (векторами положения фазовых центров антенн ННРМ (R3+hi)) как арксинусы отношений произведений значений дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн ПУСР и значений косинусов углов 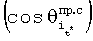 между радиальным движением фазового центра антенны ПУСР и вектором скорости спутников к значениям модулей векторов положения фазовых центров антенн ННРМ;
между радиальным движением фазового центра антенны ПУСР и вектором скорости спутников к значениям модулей векторов положения фазовых центров антенн ННРМ;
- определяют значения косинусов углов между векторами положения спутников и вектором положения фазового центра антенны НАП как арксинусы отношений произведений значений дальностей между фазовыми центрами антенн спутников, через которые ретранслируют сигналы ННРМ, и фазовыми центрами антенн НАП и значений косинусов углов 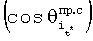 между радиальным движением и векторами скорости спутников к значениям модуля вектора положения фазового центра антенны НАП;
между радиальным движением и векторами скорости спутников к значениям модуля вектора положения фазового центра антенны НАП;
- устанавливают систему функциональных зависимостей (систему навигационных уравнений) между известными значениями направляющих косинусов векторов положения фазовых центров антенн ННРМ и неизвестными значениями направляющих косинусов геоцентрических радиус-векторов (3), (4);
- определяют значения направляющих косинусов геоцентрических радиус-векторов (R3+Нi)пр.с путем решения систем уравнений (3), (4);
- устанавливают систему функциональных зависимостей (систему навигационных уравнений) между известными значениями направляющих косинусов геоцентрических радиус-векторов и неизвестными значениями направляющих косинусов вектора положения фазового центра антенны НАП;
- определяют значения направляющих косинусов вектора положения фазового центра антенны НАП путем решения системы уравнений (5);
- используя выражения, связывающие известные значения направляющих косинусов вектора положения фазового центра антенны ПАП с географическими долготой λ и с широтой ψ определяют значения λ и ψ, а затем определяют значения синусов, косинусов углов λ как синусы, косинусы арктангенсов отношений значений проекций векторов положения фазовых центров антенн НАП на ось OY к значениям проекций векторов положения фазового центра антенн НАП на ось ОХ на одном и том же мерном интервале, а также синусы, косинусы углов ψ на том же мерном интервале как синусы, косинусы арккосинусов корней квадратных из сумм квадратов отношений проекций векторов положения фазовых центров антенн НАП на оси OX, OY геоцентрической системы координат к их модулям;
- используя формулы перехода из геоцентрической системы координат в топоцентрическую, пересчитывают значения направляющих косинусов векторов дальностей между фазовыми центрами антенн спутниковых источников радиосигналов и фазовыми центрами антенн НАП в значения направляющих косинусов в топоцентрической системе координат, определяют значения углов азимута и углов места направления истинного меридиана как арксинусы корней квадратных их сумм квадратов отношений проекций векторов положения фазовых центров антенн НАП на оси ОХТ, OYТ топоцентрической системы координат к их модулям и как арктангенсы отношений значений проекций векторов положения фазовых центров антенн НАП на ось OYТ к значениям проекций векторов положения фазовых центров антенн НАП на ось ОХТ, а затем определяют значения поправки курсоуказания в топоцентрической системе координат путем сличения отнесенных к одному моменту измерений измеренных значений углов азимута с использованием радиосигналов спутников и измеренных значений углов азимута с помощью компаса путем взаимного вычитания.
Положительный эффект использования предложенного технического решения заключается в следующем.
Стратегия определения местоположения спутников (эфемерид) является ключевым вопросом создания любой спутниковой навигационной системы. Поэтому возможность навигироваться пользователями с высокой точностью с использованием навигационных измерений по фазе несущей радиосигналов наземных радиомаяков, ретранслируемых спутниками и по координатами местонахождения фазовых центров антенн ННРМ без знания эфемерид, а также определять с высокой точностью угловые параметры путем приема спутников радиосигналов на одну антенну НАП, являются большими преимуществами предлагаемого способа.
Помимо точности, к числу важных выходных параметров предложенного способа относятся достоверность и надежность.
Под достоверностью понимается способность системы обнаруживать свое неправильное функционирование и оповещать об этом пользователей для того, чтобы исключить использование этой системы в тех случаях, когда ее эксплуатационные параметры выходят за пределы установленных допусков.
Под надежностью понимается вероятность того, что в течение определенного временного интервала в любой точке пространства навигационная система обеспечивает пользователей информацией, достаточной для определения местоположения с требуемой точностью.
Надежность обеспечивается тем, что навигационная информация не определяется и не закладывается наземными контрольно-измерительными станциями (КИС) на борт каждого спутника, не ретранслируется спутниками пользователям и дальномерные коды не используются, а достоверность обеспечивается контролем уровней принимаемых НАП спутниковых радиосигналов непосредственно во время навигационного сеанса.
Предлагаемые технические решения открывают реальные возможности для интегрирования эксплуатируемых в настоящее время спутниковых систем узкоцелевого назначения в многоцелевую ГИСС навигации, геодезии, связи, наблюдения и управления и решения вопроса эффективного использования спутниковыми системами невосполнимого мирового ресурса, каким являются радиочастотной спектр и спутниковые орбиты.
Одновременно предлагаемый способ позволяет упростить наземные средства и решить проблему автономного функционирования спутниковых систем.
Дороговизна спутниковых систем особенно обусловлена дороговизной наземного сегмента, его высокими эксплуатационными расходами. Автономное функционирование систем позволит снизить экономические затраты на управление спутниковыми системами. Таким образом, экономический эффект применения предлагаемого способа достигается за счет снижения эксплуатационных расходов.
Потребности жизни и деятельности человека, а также конкуренция заставляют операторов мобильной связи настойчиво бороться за расширение номенклатуры предоставляемых услуг, в том числе и позицирования с применением спутниковых систем.
Причем актуальность предоставления навигационных услуг с использованием спутниковых систем возрастает с каждым годом. Так, например, 19.02.2003 г. московские власти нашли средство борьбы с транспортными пробками. В столице стартовал первый этап программы по внедрению системы спутниковой навигации. Пока что речь идет о 140 рейсовых автобусах и 20 машин «Скорой помощи». Столичные власти также собираются предложить услуги спутниковой навигации всем желающим москвичам. Следовательно, не только в зарубежных странах, но и в России практически сформировался заказ на предоставления пользователям навигационных услуг с применением спутниковых систем. Поэтому предлагаемый способ соответствует требованиям «промышленная применяемость».
Таким образом, предложенный способ автономного мгновенного определения пользователями-абонентами координат своего местоположения, составляющих вектора скорости, угловой ориентации в пространстве и пеленга по фазе несущей радиосигналов наземных радиомаяков, ретранслируемых спутниками, соответствует критериям новизны, изобретательскому уровню, промышленной применяемости и дает при использовании положительный эффект, заключающийся в повышении точности навигационных измерений и определений, достоверности надежности, в эффективности использования радиочастотного спектра и спутниковых орбит, а также в снижении эксплуатационных расходов спутниковых систем.
ЛИТЕРАТУРА
1. B.C.Шебшаевич. Сетевые спутниковые радионавигационные системы. - М.: Радио и связь, 1993.
2. А.Н.Армизонов. Способ определения координат местоположения, составляющих вектора скорости фазовых центров антенн спутниковых источников навигационных сигналов и фазовых центров антенн навигационной аппаратуры пользователей СРНС. Патент №2210788 (МПК G 01 S 5/00), 2001 г.
3. Ю.М.Казаринов, Ю.А.Коломенский и др. Радиотехнические системы. - М.: Советское радио, 1968.
4. П.А.Агаджанов, Н.М.Барабанов и др. Космические траекторные измерения. - М.: Советское радио, 1969.
5. B.C.Волосов, Ю.С.Дубинко и др. Судовые комплексы спутниковой навигации. - Ленинград, Судостроение, 1976.
6. Цифровые радиоприемные системы. Справочник под редакцией М.И.Жодзишского. - М.: Радио и связь, 1990.
7. B.C. Шебшаевич. Введение в теорию космической навигации. - М.: Радио и связь, 1971.
8. Н.Е.Армизонов, А.Г.Козлов. Фазовые характеристики и фазовые центры антенн навигационной аппаратуры пользователей спутниковых радионавигационных систем. // Радиотехника. - 2000. - №5.
9. Глобальная спутниковая система ГЛОНАСС. Интерфейсный контрольный документ. - М.: КНИЦ, 2002 (пятая редакция).
10. А.П.Манин, Л.М.Романов. Методы и средства относительных определений в системе NAVSTAR. Зарубежная радиоэлектроника №1. - М.: Радио и связь, 1989.
11. B.C.Шебшаевич и др. Бортовые устройства спутниковой навигации. - М.: Транспорт, 1988.
12. Г.А.Бурмистров. Основы способа наименьших квадратов. - М.: Издательство литературы по геологии и охране недр, 1963.
Предлагаемое изобретение относится с области спутниковой радионавигации, геодезии, связи и может быть использовано для автономного мгновенного определения пользователями значений координат местоположения, составляющих вектора скорости фазовых центров антенн спутниковых источников радиоизлучения, координат местоположения и составляющих вектора скорости фазовых центров антенн аппаратуры пользователей, угловой ориентации в пространстве и пеленга. Достигаемый технический результат - высокая точность навигационных определений - определяется использованием фазовых измерений приращений дальностей по несущим частотам радиосигналов, ретранслируемых спутниками. Отличие заявленного способа от известного заключается в том, что навигационную информацию о положении фазовых центров антенн наземных радионавигационных маяков (ННРМ), информацию для введения поправок по частоте и времени записывают в запоминающие устройства навигационной аппаратуры пользователя (НАП) при ее изготовлении, что навигационной аппаратурой (НА), установленной на спутниках, принимают навигационные радиосигналы от двух и более ННРМ, а НАП принимают ретранслированные сигналы от двух спутников. 3 ил., 1 табл.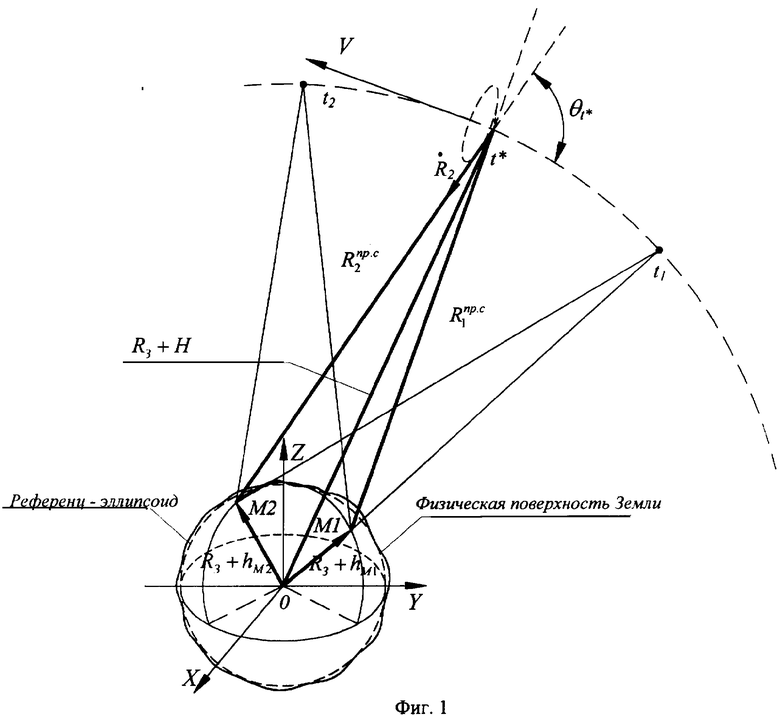
Способ автономного мгновенного определения пользователями-абонентами координат своего местоположения, составляющих вектора скорости, угловой ориентации в пространстве и пеленга по фазе несущей радиосигналов наземных радиомаяков, ретранслируемых спутниками, согласно которому наземные навигационные радиомаяки (ННРМ) непрерывно излучают навигационные радиосигналы, а навигационной аппаратурой (НА), установленной на каждом спутнике, принимают излученные ННРМ навигационные радиосигналы, информацией об изменении частот принимаемых несущих модулируют несущие излучаемых радиосигналов, усиливают их и ретранслируют в направлении Земли, принимают ретранслированные сигналы навигационной аппаратурой пользователей (НАП) определяют: значения дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн спутников, значения дальностей между фазовыми центрами антенн спутников и фазовым центром антенн НАП, затем устанавливают системы функциональных зависимостей, отличающийся тем, что навигационную информацию о положении фазовых центров антенн ННРМ, информацию для введения поправок по частоте, по времени записывают в запоминающие устройства НАП при ее изготовлении; НА установленной на спутниках, принимают навигационные радиосигналы от двух и более ННРМ, а НАП принимают ретранслированные сигналы от двух спутников и определяют:
значения дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн спутников как произведения отношений квадратов значений радиальной скорости движения фазовых центров спутниковых приемных антенн к ускорениям радиальной скорости на квадраты значений тангенсов углов между радиальным движением и вектором скорости спутников;
значения дальностей между фазовыми центрами антенн спутников и фазовым центром антенн НАП как произведения отношений квадратов значений радиальной скорости движения фазовых центров спутниковых антенн, ретранслирующих сигналы ННРМ к ускорениям радиальной скорости на квадраты значений тангенсов углов между радиальным движением и вектором скорости спутников;
значения косинусов углов между векторами положения фазовых центров антенн спутников и векторами положения фазовых центров антенн ННРМ как арксинусы отношений произведений значений дальностей между фазовыми центрами антенн ННРМ и фазовыми центрами антенн спутников и значений косинусов углов  между радиальным движением фазовых центров антенн спутников и вектором скорости спутников к значениям модулей векторов положения фазовых центров антенн ННРМ;
между радиальным движением фазовых центров антенн спутников и вектором скорости спутников к значениям модулей векторов положения фазовых центров антенн ННРМ;
значения косинусов углов между векторами положения фазовых центров антенн спутников и вектором положения фазового центра антенны НАП как арксинусы отношений произведений значений дальностей между фазовыми центрами антенн спутников, через которые ретранслируют сигналы ННРМ и фазовыми центрами антенн НАП и значений косинусов углов 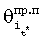 между радиальным движением фазовых центров спутниковых антенн, излучающих радиосигналы, и вектора линейной скорости спутников к значениям модуля вектора положения фазового центра антенны НАП;
между радиальным движением фазовых центров спутниковых антенн, излучающих радиосигналы, и вектора линейной скорости спутников к значениям модуля вектора положения фазового центра антенны НАП;
устанавливают две системы функциональных зависимостей между неизвестными значениями направляющих косинусов векторов положения фазовых центров антенн двух спутников и известными значениями направляющих косинусов векторов положения фазовых центров антенн двух ННРМ, как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны первого спутника и значений направляющих косинусов соответствующих узлов вектора положения фазового центра антенны первого ННРМ, равную значению косинуса угла между ними, как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны первого спутника и значений направляющих косинусов соответствующих углов вектора положения фазового центра антенны второго ННРМ, равную значению косинуса угла между ними, как сумму квадратов значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны первого спутника, равную единице, первую и как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны второго спутника и значений направляющих косинусов соответствующих углов вектора положения фазового центра антенны первого ННРМ, равную значению косинуса угла между ними, как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны второго спутника и значений направляющих косинусов соответствующих углов вектора положения фазового центра антенны второго ННРМ, равную значению косинуса угла между ними, как сумму квадратов значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны второго спутника, равную единице, вторую и путем решения первой и второй систем определяют значения направляющих косинусов углов α, β, γ вектора положения фазовых центров антенн первого и второго спутников;
устанавливают систему функциональных зависимостей между известными значениями направляющих косинусов векторов положения фазовых центров антенн первого и второго спутников и неизвестными значениями направляющих косинусов вектора положения фазового центра антенны пользователя как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны первого спутника и значений направляющих косинусов соответствующих углов вектора положения фазового центра антенны пользователя, равную значению косинуса угла между ними, как сумму произведений значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны второго спутника и значений направляющих косинусов соответствующих углов вектора положения фазового центра антенны пользователя, равную значению косинуса угла между ними и как сумму квадратов значений направляющих косинусов углов α, β, γ вектора положения фазового центра антенны пользователя, равную единице, и путем решения системы определяют значения направляющих косинусов углов α, β, γ вектора положения центра антенны пользователя,
по известным значениям направляющих косинусов векторов положения фазовых центров антенн НАП определяют:
координаты местоположения пользователя;
составляющие вектора скорости пользователя;
значения долготы λ и широты ψ местонахождения фазового центра антенны НАП, пересчитывают известные значения направляющих косинусов векторов положения фазового центра антенны НАП в значения направляющих косинусов векторов в топоцентрической системе координат и определяют
значения углов азимута и углов места пользователя в топоцентрической системе координат;
угловую ориентацию пользователя в пространстве, вычисляя значения поправки курсоуказания путем взаимного вычитания отнесенных к одному моменту измерений в топоцентрической системе координат значений углов азимута, измеренных с использованием радиосигналов спутниковых радионавигационных систем, и значений углов азимута, измеренных с помощью компаса.
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ, СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ ФАЗОВЫХ ЦЕНТРОВ АНТЕНН СПУТНИКОВЫХ ИСТОЧНИКОВ НАВИГАЦИОННЫХ СИГНАЛОВ И ФАЗОВЫХ ЦЕНТРОВ АНТЕНН НАВИГАЦИОННОЙ АППАРАТУРЫ ПОЛЬЗОВАТЕЛЕЙ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 2001 |
|
RU2210788C2 |
| ГЛОБАЛЬНАЯ КОСМИЧЕСКАЯ СИСТЕМА ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И РАДИОНАВИГАЦИИ, РАДИОМАЯК И ПРИЕМНИК, ИСПОЛЬЗУЕМЫЕ В ДАННОЙ СИСТЕМЕ | 1996 |
|
RU2182341C2 |
| JP 2000206224, 28.07.2000 | |||
| US 6111538 A, 29.08.2000. | |||
Авторы
Даты
2006-10-27—Публикация
2004-09-20—Подача