Изобретение относится к области космической радионавигации, геодезии и может быть использовано для определения курсового угла и координат местоположения объектов, а также для измерений траекторий искусственных спутников Земли и создания на подвижных объектах высокоточной опорной системы координат.
Известен способ определения местоположения и определения угловой ориентации на плоскости с использованием интерферометров с короткой базой, образованной двумя пространственно разнесенными антеннами, определяющих разность фаз несущих частот принятых сигналов двух навигационных искусственных спутников Земли (НИСЗ).
Недостатками известного способа являются: ошибки, обусловленные эфемеридными данными; ошибки, обусловленные погрешностями определения координат центра базовой линии; ошибки, обусловленные угловым перемещением антенн; ошибки при разрешении неоднозначности фазовых измерений; ошибки, обусловленные нестабильностью частоты радиосигналов НИСЗ и генераторов объектов.
Известен также способ по измерениям псевдодальности, измеренные с помощью четырех приемников сигналов НИСЗ, антенны которых установлены на объектах таким образом, что они образуют прямоугольную систему координат.
Недостатками этого способа являются ошибки, обусловленные эфемеридными данными и погрешностями определения координат центра баз (центра координат); ошибки, обусловленные нестабильностью частот радиосигналов НИСЗ и генераторов объектов; ошибки, обусловленные угловым перемещением антенн в процессе движения объектов; невозможность построения опорной системы координат на подвижном объекте, например, на качающем надводном корабле.
Цель изобретения - повышение точности определения курсового угла, координат местоположения объектов по радиосигналам космических аппаратов (КА) спутниковых радионавигационных систем (СРНС) и создания на подвижных объектах высокоточной опорной системы координат.
Это достигается тем, что при предлагаемом способе для определения курсового угла, координат местоположения объектов, создания на подвижных объектах высокоточной опорной системы координат и повышения помехозащищенности навигационных радиолиний производится одновременный прием каждым антенно-приемным устройством взаимно ортогональных пар, одно из которых в паре является ведущим, а другое ведомым, одночастотного навигационного радиосигнала одного и того же спутника, выделение в ведомых приемных устройствах колебаний с частотой, равной разности частот Доплера, принятые ведущими и ведомыми антенно-приемными устройствами путем использования в качестве гетеродинных сигналов в преобразователях ведомых антенно-приемных устройств сигналов генераторов управляющих напряжением систем фазовой автоподстройки частот (ФАПЧ) ведущих антенно-приемных устройств, определение отношения разности доплеровских приращений и определение курсового угла, координат местоположения объектов.
Известный способ характеризуется следующей совокупностью действий над принимаемыми спутниковыми радионавигационными сигналами: прием четырьмя антенно-приемными устройствами двухчастотных навигационных радиосигналов НИСЗ; выделение каждым приемным устройством доплеровского сдвига частоты путем использования сигналов генераторов управляющих напряжением систем ФАПЧ; определение набега фазы колебаний с частотой Доплера путем интегрирования их на мерном интервале; определение координат местоположения объектов; определение курсового угла объектов.
Физическая сущность известного решения (прототипа) заключается в выделении каждым приемным устройством из принятых радиосигналов соответствующих НИСЗ доплеровского сдвига частоты и определении набега фазы колебаний с частотой Доплера (разности дальности (Δ R) на мерном интервале
ΔR = 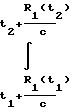 Fд(t)·dt=
Fд(t)·dt= 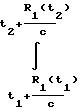 (fo-fп)dt =
(fo-fп)dt =
= (fo-fп)·(t2-t1) +  [R1(t2)-R1(t1)] где t1 и t2 - время передачи временных меток НИСЗ;
[R1(t2)-R1(t1)] где t1 и t2 - время передачи временных меток НИСЗ;
R1(t1) и R1(t2) - расстояние между фазовыми центрами антенн определяющегося объекта и НИСЗ;
Fд (t) - частота Доплера;
fп - частота принимаемого сигнала;
fп = fи ± Δ fи + Δ fио + Δ fтр + Δ fгр +
+Δ fвч + Δ fпч + Δ fтш ± Δ fугл + Δ fдр, где fи - частота сигнала, излучаемая НИСЗ;
± Δ fп - нестабильность излучаемой частоты;
Δ fио, Δ fтр - неизвестные сдвиги частоты, обусловленные распространением сигналов в ионосфере и тропосфере;
Δ fгр - неизвестный сдвиг частоты, обусловленный гравитационными силами;
Δ fтш, Δ fпч, Δ fвч - нестабильность частоты, обусловленная высокочастотными трактами приемных устройств, промежуточными и температурой;
Δ fугл - приращение частоты за счет углового движения антенн (угловое перемещение антенн относительно центра масс объекта);
Δ fдр - нестабильность частоты, обусловленная другими факторами;
с - скорость света;
fо - частота сигнала опорного генератора (генератора объекта);
fo = fи + Δ fo ± Δ f, где fо - известный постоянный сдвиг частоты (частотная подставка);
±Δ f - нестабильность опорного генератора.
С учетом изложенного выражение пример вид:
ΔR = [(fи+Δfo± Δf)-(fи± Δfи+ Δfио+Δfтр+Δfтр+Δfвч+Δfпч+ +Δfтш± Δfугл+Δfдр)]· (t2-t1)+  [R1(t2)-R1(t1)] (1)
[R1(t2)-R1(t1)] (1)
Выражая дальности через координаты, получим навигационное уравнение
ΔR = 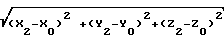 _
_ 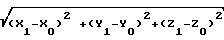 (2) где X1, Y1, Z1, Х2, Y2, Z2 - координаты фазового центра антенны спутника в моменты времени t1 и t2 соответственно;
(2) где X1, Y1, Z1, Х2, Y2, Z2 - координаты фазового центра антенны спутника в моменты времени t1 и t2 соответственно;
Хо, Yo, Zо - неизвестные координаты фазовых центров антенн объекта.
Уравнение (2) содержит три неизвестные координаты Хо, Yo, Zо. Цикл измерений каждым антенно-приемным устройством по соответствующему НИСЗ позволит определить координаты Хо, Yo, Zо.
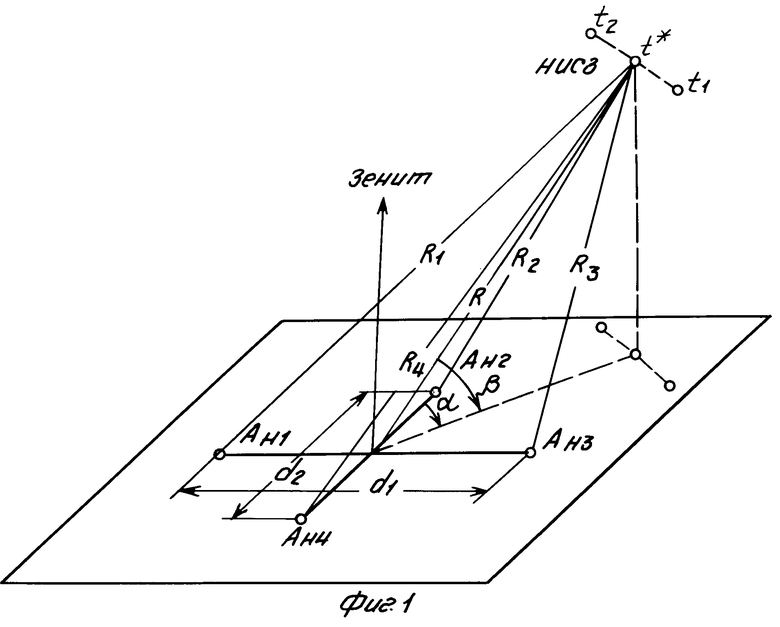
Зная координаты фазовых центров антенн, образующих прямоугольную систему координат из двух взаимно ортогональных разнесенных в пространстве пар антенн Ан1 - Ан3, Ан2 - Ан4, базы которых соответственно d1 = d2 = d перпендикулярны друг другу (см. фиг.1), а также координаты фазового центра антенны НИСЗ в моменты времени t1, t*, t2 определяются расстояния R1(t*), R3(t*) и R2(t*), R4(t*).
По определяющимся расстояниям определяются разности расстояний Δ R1,3(t*) и Δ R2,4(t*), которые связаны с азимутом α и углом места β НИСЗ следующими соотношениями:
ΔR1,3(t*)= 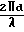 · sinα·cosβ (3)
· sinα·cosβ (3)
ΔR2,4(t*)= 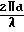 · cosα·cosβ (4)
· cosα·cosβ (4)
Определив разности дальностей ΔR1,3(t*), Δ R2,4(t*) можно найти курсовой угол из совместного решения уравнений (3), (4).
α= arctg 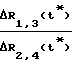 (5)
(5)
Предлагаемый способ характеризуется следующей совокупностью действий:
одновременный прием четырьмя приемными устройствами одночастотного навигационного радиосигнала одного и того же НИСЗ, антенны которых пространственно взаимно ортогонально разнесены между собой, образуя прямоугольную систему координат, оси которой параллельны осям объекта;
выделение колебаний с частотой, равной разности доплеровских сдвигов частоты в каждой ортогональной паре, принятых антенно-приемными устройствами, одно из которых в каждой паре является ведущим, а другое ведомым, путем использования в ведомых приемных устройствах в качестве гетеродинных сигналов сигналов генераторов управляющих напряжением ФАПЧ ведущих приемных устройств;
измерение разностей доплеровских сдвигов частоты;
измерение отношения разностей доплеровских приращений;
определение курсового угла;
определение координат местоположения объекта.
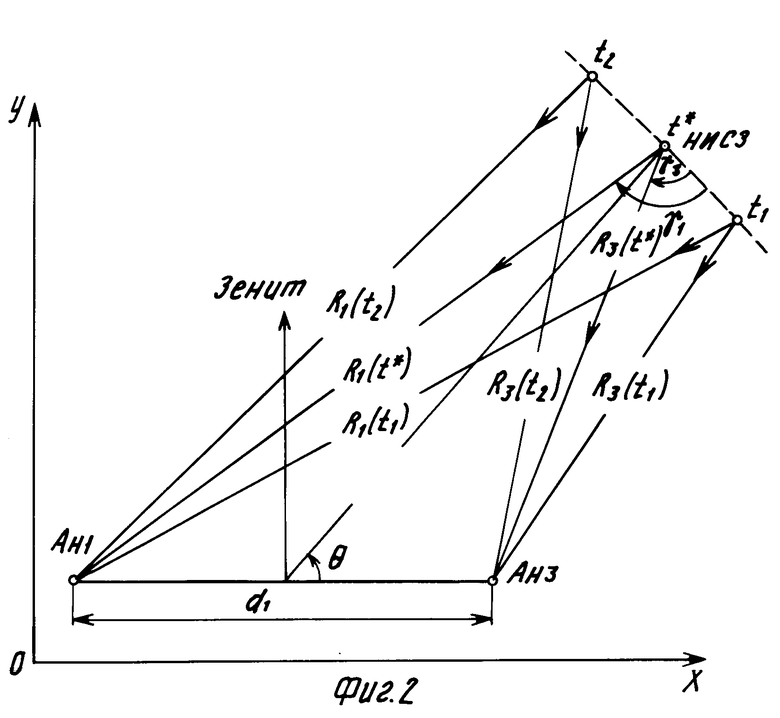
Геометрическая интерпретация предлагаемого способа поясняется на примере одной ортогональной базовой линии, образованной двумя разнесенными антеннами Ан1 и Ан3 (см. фиг.2) и других положений НИСЗ.
Точками t1, t*, t2 обозначены положения НИСЗ на орбите, являющиеся границами отсчетов навигационного параметра. Использование теоремы косинусов и разложения в ряд а членами не выше второго порядка для двух положений позволяет получить:
Для антенны Ан1: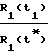 ≈ 1 +
≈ 1 + 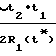 · cosγ1+
· cosγ1+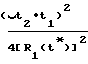 ·
· 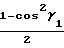
 ≈ 1 -
≈ 1 - 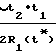 · cosγ1+
· cosγ1+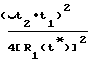 ·
· 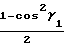
ΔR1(t*)= R1(t2)-R1(t1)=  t2·t1·cosγ1
t2·t1·cosγ1
Для антенны Ан3: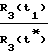 ≈ 1 -
≈ 1 - 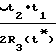 · cosγ3+
· cosγ3+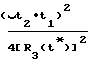 ·
· 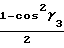
 ≈ 1 +
≈ 1 + 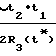 · cosγ3+
· cosγ3+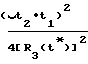 ·
· 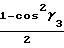
ΔR3(t*)= R3(t2)-R3(t1)=  t2·t1·cosγ3
t2·t1·cosγ3
Таким образом каждая разность хода ΔR1(t*), Δ R3(t*) дает информацию о проекции пути пройденного НИСЗ из точки t1 в точку t2 на направление прямых R1(t*), R3(t*), соединяющих точку t* с фазовыми центрами антенн Ан1 и Ан3 определяющегося объекта.
Вторично используя теорему косинусов и разложения в ряд с членами не выше второго порядка для НИСЗ, находящегося в точке t*, можно получить:
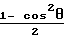
Для антенны Ан1: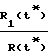 ≈ 1 +
≈ 1 + 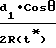 +
+ 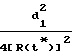 ·
· 
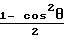
Для антенны Ан3: ≈ 1 -
≈ 1 - 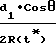 +
+ 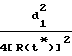 ·
· 
Как отмечалось, дальности R1(t*) и R3(t*) содержат в себе проекции пути, пройденного НИСЗ из точки t1 в точку t2. Поэтому, беря разницу Δ R1,3(t*) = R1(t*) - R3(t*), находим информацию о проекции разности дальностей между фазовым центром антенны НИСЗ в точке t* и фазовыми центрами антенн определяющегося объекта
ΔR1,3(t*)= [R1(t2)-R1(t1)] - [R3(t2)-R3(t1)]=
=  t2·t1(cosγ1-cosγ3) = R1(t*) -R3(t*) (6)
t2·t1(cosγ1-cosγ3) = R1(t*) -R3(t*) (6)
Двойная разность дальностей Δ R1,3(t*) дает информацию о проекции базовой линии на направление к прямой R(t*), соединяющей среднюю точку базы (базовой линии) с фазовым центром антенны НИСЗ в момент времени t*,
t* = 
Аналогично выводятся соотношения для второй ортогональной пары, образованной пространственно-разнесенными антеннами Ан2 и Ан4.
ΔR2,4(t*)= [R2(t2)-R2(t1)] - [R4(t2)-R4(t1)]=
=  t2·t1(cosγ2-cosγ4) = R2(t*) -R4(t*) (7)
t2·t1(cosγ2-cosγ4) = R2(t*) -R4(t*) (7)
α= arctg 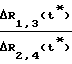 =
= 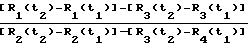 (8)
(8)
Таким образом алгоритм определения курсового угла объекта предлагаемого способа по радиосигналу одного и того же спутника с использованием взаимно ортогональных пар антенно-приемных устройств, выражение (8) есть алгоритм, использующий двойную разность дальностей от фазовых центров антенн интерферометра определяющегося объекта до фазового центра антенны НИСЗ для двух его положений t1 и t2.
Навигационному параметру - двойной разности дальностей соответствует измеряемый радионавигационный параметр - разность доплеровских сдвигов частоты (Fд1 - Fд3) и (Fд2 - Fд4) взаимно ортогональных пар.
Аналитически с учетом того, что число излучаемых циклов между временными метками t1 и t2 равно числу принятых циклов между t1+ 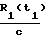 , t2+
, t2+ 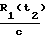 и t1+
и t1+ 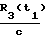 , t2+
, t2+ 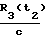 , это будет иллюстрироваться следующим образом:
, это будет иллюстрироваться следующим образом:
ΔR1,3(t*) = 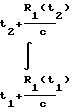 Fд1(t)·dt
Fд1(t)·dt 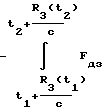 (t)·dt =
(t)·dt =
= 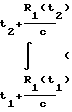 fo-fп1)dt -
fo-fп1)dt - 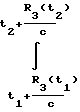 (fo-fпз)dt =
(fo-fпз)dt =
= 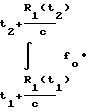 dt
dt 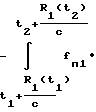 dt -
dt -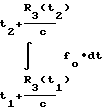
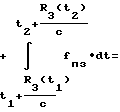 (9)
(9)
= {(fo-fи)·(t2-t1)+ 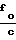 [R1(t2)-R1(t1)]} -
[R1(t2)-R1(t1)]} -
= {(fo-fи)·(t2-t1)+ 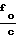 [R3(t2)-R3(t1)]} где с - скорость света;
[R3(t2)-R3(t1)]} где с - скорость света;
fп1, fп3 - частоты, принимаемые антеннами Ан1, Ан3 соответственно и определяемые частотой излучаемой НИСЗ (fи) и доплеровским сдвигом из-за движения спутника и определяющегося объекта.
t1+ 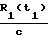 , t2+
, t2+ 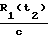 , t1+
, t1+ 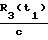 , t2+
, t2+ 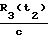 - времена приема временных меток потребителем, которое передавались в моменты времени t1 и t2;
- времена приема временных меток потребителем, которое передавались в моменты времени t1 и t2;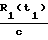 ,
, 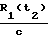 ,
, 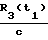 ,
, 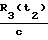 - соответствующие задержки на участках R1(t1), R1(t2), R3(t1), R3(t2) (расстояния фазовый центр антенн НИСЗ - фазовые центры антенн определяющегося объекта).
- соответствующие задержки на участках R1(t1), R1(t2), R3(t1), R3(t2) (расстояния фазовый центр антенн НИСЗ - фазовые центры антенн определяющегося объекта).
Аналогично выводятся соотношения для второй ортогональной пары, образованной антеннами Ан2 и Ан4
ΔR2,4(t*)= {(fo-fи)·(t2-t1)+ 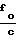 [R2(t2)-R2(t1)]} -
[R2(t2)-R2(t1)]} -
- {(fo-fи)·(t2-t1)+ 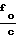 [R4(t2)-R4(t1)]} (10)
[R4(t2)-R4(t1)]} (10)
С учетом выражения (5), выражение для курсового угла запишется следующим образом:
α= arctg 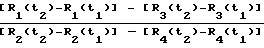 (11)
(11)
Сравнивая выражение (8) геометрической интерпретации работы предлагаемого способа, определяющее курсовой угол, с выражением (11) аналитической интерпретации, видим, что они идентичны.
Как отмечалось выше, каждой двойной разности дальности, определяющей курсовой угол, соответствует разность доплеровских сдвигов частоты. Причем, разность доплеровских сдвигов частоты определяется не аналитически, а выделяется аппаратурно путем использования в ведомых приемных устройствах в качестве гетеродинных сигналов сигналов генераторов управляющих напряжением ФАПЧ ведущих приемных устройств.
Физика выделения разности доплеровских сдвигов частоты, принятая каждым антенно-приемным устройством (ведущими и ведомыми), заключается в следующем. Вследствие того, что антенны взаимно ортогональных пар пространственно разнесены между собой, приращения частоты принимаемого радиосигнала одного и того же НИСЗ, обусловленные эффектом Доплера, будут разными. Системы ФАПЧ ведущих приемных устройств ортогональных пар, отслеживая измененные частоты принимаемого сигнала, изменяют соответственно частоты генераторов, управляющих напряжением (ГУН) ведущих приемных устройств так, чтобы на выходах смесителей частоты выделенных сигналов были постоянными.
Одновременно сигналы ГУН ведущих приемных устройств поступают на преобразователи ведомых приемных устройств.
В процессе преобразования в смесителях ведомых устройств неизвестные сдвиги частоты, обусловленные нестабильностью сигналов НИСЗ, условиями распространения радиоволн, а также гравитационными и другими силами, условиями, описываемые соответственно выражениями
(fи ± Fд1 ± Δ fи + Δ fио + Δ fтр + Δ fгр +
+ fвч + Δ fпч + Δ fтш ± Δ fугл + Δfдр) -
- (fг ± Fд3 ± Δ fи + Δ fио + Δ fтр + Δ fгр +
+ fвч + Δ fпч + Δ fтш ± Δ fугл + Δ fдр) =
= fпр ± (Fд1 + Fд3) и
(fи ± Fд2 ± Δ fи + Δ fио + Δ fтр + Δ fгр +
+ fвч + Δ fпч + Δ fтш ± Δ fугл + Δ fдр) -
- (fг ± Fд4 ± Δ fи + Δ fио + Δ fтр + Δ fгр +
+ Δ fвч + Δ fпч + Δ fтш ± Δ fугл + fдр) =
= fпр ± (Fд2 - Fд4), исключатся и на выходах преобразователей выделятся сигналы промежуточной частоты, значения которых изменяются прямо пропорционально разностям доплеровских сдвигов частоты, принятых ведущими и ведомыми приемными устройствами каждой ортогональной пары. Частотным компаратором на один вход которого поступает промежуточная частота с одного ведомого антенно-приемного устройства, а на другой вход - с другого, производится измерение отношения разностей доплеровских сдвигов частоты.
Отношение разностей доплеровских сдвигов частоты выделение во взаимно ортогональных парах антенно-приемных устройств и есть навигационный параметр, определяющий курсовой угол определяющегося объекта и функциональную зависимость (навигационное уравнение) между известными координатами НИСЗ и неизвестными координатами объекта. При аналитической интерпретации двойной разности дальностей вывод уравнений (9), (10) для измерения двойной разности дальностей на мерном интервале t1 и t2 необходимо измерить набег фазы колебаний с частотой, равной разности доплеровских сдвигов частоты на интервалах t1+
t1+ 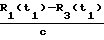 ; t2+
; t2+ 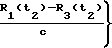
и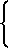 t1+
t1+ 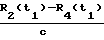 ; t2+
; t2+ 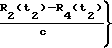 для каждой ортогональной пары соответственно. Набег фазы колебаний с частотой, равной разности доплеровских сдвигов частоты на интервале t1и t2, можно получить с использованием измерений самой разностной частоты, а именно:
для каждой ортогональной пары соответственно. Набег фазы колебаний с частотой, равной разности доплеровских сдвигов частоты на интервале t1и t2, можно получить с использованием измерений самой разностной частоты, а именно:
Δ ϕ = Δ Fд(t*) (t2 - t1) (12)
С учетом выражения (12), выражение (8) примет вид
α= arctg 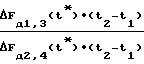 =
= 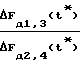 (13)
(13)
Уравнение (13) является прямым измерением отношения выделенных значений разностей доплеровских сдвигов частоты в каждой ортогональной паре антенно-приемных устройств на момент времени 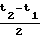 , в котором отсутствуют погрешности измерения радионавигационного параметра за счет условий распространения радиоволн, углового перемещения антенн, погрешности, обусловленные кратковременной нестабильности частоты спутникового и опорного генераторов, погрешности, обусловленные гравитационным эффектом, радиотрактами и антеннами приемного устройства, а также другими эффектами более высокого порядка малости.
, в котором отсутствуют погрешности измерения радионавигационного параметра за счет условий распространения радиоволн, углового перемещения антенн, погрешности, обусловленные кратковременной нестабильности частоты спутникового и опорного генераторов, погрешности, обусловленные гравитационным эффектом, радиотрактами и антеннами приемного устройства, а также другими эффектами более высокого порядка малости.
Определение курсового угла позволяет реализовать например, азимутальный или разностно-азимутальный метод определения координат местоположения объектов
cosα = 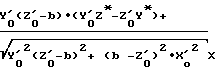
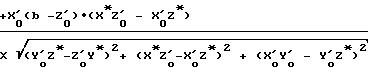 где Х'о , Y'o , Z'o - неизвестные координаты объекта (координаты точки пересечения баз);
где Х'о , Y'o , Z'o - неизвестные координаты объекта (координаты точки пересечения баз);
b - малая полуось референц-эллипсоида;
X*,Y*,Z* - координаты фазового центра антенн спутника в точке t*.
Физическая сущность предлагаемого решения по выделению разностей доплеровских сдвигов частоты эквивалентна работе следящей системы, отслеживающей в двух взаимно ортогональных плоскостях направления фазовый центр антенны спутника - центр пересечения баз (центр выбранной системы координат) объекта, в которой компенсируется приращение частоты за счет углового движения антенн как НИСЗ, так и определяющегося объекта.
Поэтому система из четырех приемных устройств, антенны которых пространственно разнесены между собой, образуя прямоугольную систему координат, позволяет реализовать построение на подвижном объекте высокоточной опорной системы координат.
Отличительные признаки предложенного способа:
одновременный прием каждым антенно-приемным устройством взаимно ортогональных пар, одно из которых в паре является ведущим, а другое - ведомым одночастотного навигационного радиосигнала одного и того же НИСЗ;
выделение в ведомых приемных устройствах колебаний с частотой, равной разности частот Доплера, принятых ведущими и ведомыми антенно-приемными устройствами, путем использования в качестве гетеродинных сигналов в преобразователях ведомых антенно-приемных устройств сигналов генераторов управляющих напряжением систем фазовой автоподстройки частоты ведущих антенно-приемных устройств;
измерение отношения разностей доплеровских приращений частоты;
определение курсового угла объекта;
определение координат местоположения.
Таким образом, предложенный способ определения курсового угла и координат местоположения объекта по радионавигационным сигналам космических аппаратов спутниковых радионавигационных систем с помощью четырех антенно-приемных устройств, антенны которых установлены на объекте таким образом, что они образуют прямоугольную систему координат, оси которой параллельны осям объекта, обладает новизной, существенными отличиями и дает при использовании положительный эффект, заключающийся в повышении точности определения курсового угла и координат местоположения, а также создания на подвижном объекте высокоточной опорной системы координат и повышения помехозащищенности навигационной радиолинии.
Использование: космическая радионавигация, геодезия для определения курсового угла и координат местоположения объектов, а также для измерений траекторий искусственных спутников Земли и создания на подвижных объектах высокоточной опорной системы координат. Сущность изобретения: способ заключается в определении курсового угла и координат местоположения объектов по радионавигационным сигналам космических аппаратов спутниковых радионавигационных систем и интегрального доплеровского или фазового метода измерений радионавигационного параметра и двойной разности фаз прохождения фронтом волны навигационного радиосигнала одного и того же спутника до двух пространственно разнесенных антенн. Повышение точности измерений обеспечивается за счет исключения из измерений с точностью до значения коэффициента взаимной корреляции погрешностей, обусловленных нестабильностью сигналов генераторов спутников, опорных генераторов, условиями распространения радиоволн, тепловым шумом, нелинейностью фазовых диаграмм антенн и их углового перемещения относительно центра масс объекта. 2 ил.
СПОСОБ ОПРЕДЕЛЕНИЯ КУРСОВОГО УГЛА И КООРДИНАТ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТОВ ПО РАДИОНАВИГАЦИОННЫМ СИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ спутниковых радионавигационных систем, при котором принимают каждым из четырех антенно-приемных устройств, установленных на объектах, навигационные радиосигналы спутников, при этом антенны четырех антенно-приемных устройств образуют прямоугольную систему координат, оси которой параллельны осям объектов, выделяют сигнал с частотой Доплера путем использования сигналов генераторов, управляющих напряжением систем фазовой автоподстройки частоты, определяют набег фаз колебаний с частотой Доплера путем интегрирования их на мерных интервалах определения координат фазовых центров антенн и определяют курсовой угол и координаты местоположения объектов, отличающийся тем, что производят одновременный прием каждым антенно-приемным устройством взаимно ортогональных пар, одно из которых в паре является ведущим, а другое - ведомым, одночастотного навигационного радиосигнала одного и того же спутника, выделяют в ведомых приемных устройствах сигнал с частотой, равной разности частот Доплера, принятых ведущими и ведомыми антенно-приемными устройствами, путем использования в качестве гетеродинных сигналов в преобразователях ведомых антенно-приемных устройств сигналов генераторов, управляющих напряжением систем фазовой автоподстройки частоты ведущих антенно-приемных устройств, и определяют набег фаз колебаний с частотой, равной разности частот Доплера, путем умножения их средних значений на мерный интервал.
| Applications of Navstar GPS fo presion attitude determination | |||
| Roht | |||
| Ben | |||
| D., Singh Ram-Nandan P | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Geod Sattel | |||
| Position., Austin, Tex., 28 Apr-28, May, 1986, Vol2" S.I., S.A., 1345-1359. | |||
Авторы
Даты
1994-10-30—Публикация
1992-04-27—Подача