Изобретение относится к области вооружения и военной техники, в частности к защите боевой машины (БМ) от средств воздушного нападения (СВН), например, с помощью пулеметных (пушечных) установок.
Известен способ стрельбы БМ, заключающийся в обнаружении и опознавании цели, захвате цели на сопровождение, сопровождении цели прицельно-навигационной системой с выдачей необходимых параметров в бортовой вычислитель, определении угловых поправок стрельбы соответственно в вертикальном и горизонтальном каналах α и β из соотношений

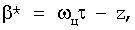
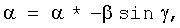
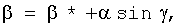
 ,
,
где α - угол прицеливания;
γ - угол крена;
tпол - полетное время снаряда на дальность;
ωц - относительная угловая скорость движения цели в горизонтальной плоскости;
Dy, D - соответственно упрежденная и текущая дальность до цели;
z - поправка на деривацию;
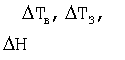 - отклонение соответственно температуры воздуха и заряда, давления воздуха от нормального;
- отклонение соответственно температуры воздуха и заряда, давления воздуха от нормального;
Δν0 - отклонение начальной скорости снаряда от номинального значения,
отработке этих поправок силовыми приводами пулеметной (пушечной) установки (ПУ) и стрельбе по цели /1/.
Для реализации этого способа существует подсистема, включающая прицельно-навигационную систему, бортовой аналоговый вычислитель, силовые приводы, пулеметную (пушечную) установку /2/.
Недостатком этого способа и реализующей его системы является большая систематическая ошибка при стрельбе по скоростным, в частности, воздушным целям, обусловленная неучетом в стрельбовом алгоритме угловой скорости линии визирования в вертикальной плоскости, неучетом скорости сближения цели с носителем.
Кроме того, при существующей приборной реализации прицелов, в частности прицела 1К13-2 111, сопроводительная стрельба в ближней зоне не возможна из-за ограничений по угловой скорости линии визирования (ωmax=3-6 град/с) и ограничений по углу прокачки линии визирования в вертикальной плоскости (ε<30°).
Поэтому наиболее близким техническим решением, выбранным в качестве прототипа, является способ стрельбы БМ по целям, включающий обнаружение и распознавание цели, сопровождение с определением координат и параметров цели, определение угловых поправок из математических выражений, суммирование их соответственно по горизонтальному и вертикальному каналам с учетом угла крена и постоянное отклонение во время стрельбы с учетом выработанных угловых поправок стволов ПУ относительно линии визирования /3/.
Для реализации этого способа на БМ известна система огневой защиты, которая содержит последовательно соединенные обзорно-прицельную и бортовую вычислительную систему, которая включает в свой состав устройство определения углов упреждения, содержащее в том числе блок формирования угла упреждения Δβ, блок формирования угла упреждения Δε, блок формирования упрежденной дальности DУ, блок поправки на баллистический ветер по горизонтальному каналу, блок поправки на продольный ветер по вертикальному каналу, далее силовые приводы установки и пулеметную или пушечную установку, а также навигационную систему и блок данных о внешней среде, выходы которых соединены с вычислительной системой.
Недостатком приведенного способа и реализующей его системы является снижение точности и соответственно эффективности стрельбы БМ из-за невозможности обеспечения в настоящее время аппаратурными способами потребной точности определения угловых скоростей линии визирования, по крайней мере, в рамках существующих габаритно-массовых и стоимостных ограничений на систему.
Задачей предлагаемого способа и реализующей его системы является повышение точности и соответственно эффективности стрельбы БМ в особенности по высокоскоростным, в частности, воздушным целям путем повышения точности определения угловой скорости линии визирования.
Поставленная задача решается тем, что в известном способе стрельбы боевой машины (БМ) по скоростной цели, включающем обнаружение и распознавание цели, сопровождение с определением координат и параметров цели, определение угловых поправок, суммирование их соответственно по горизонтальному и вертикальному каналам с учетом угла крена и постоянное отклонение во время стрельбы с учетом выработанных угловых поправок стволов пушечной установки (ПУ) относительно линии визирования, отличающийся тем, что перед определением угловых поправок находят угловую скорость линии визирования 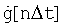 дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах из следующего соотношения
дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах из следующего соотношения
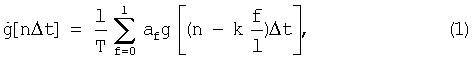
где 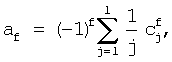
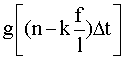 - угол наклона линии визирования в момент времени
- угол наклона линии визирования в момент времени 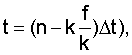
где Δt - интервал времени между моментами поступления информации об углах наклона линии визирования - дискрета, 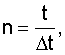
f - порядковый номер "узловой" точки - укрупненной дискреты Δt' 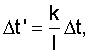
Т - время наблюдения, T должно быть кратно целому числу укрупненных дискрет Δt', т.е. должно выполняться условие 
l - порядок приближения воспроизводимой производной угла наклона линии визирования, l=[1, 2...6],
k - количество шагов дискретизации на T, 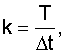
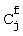 - биномиальные коэффициенты,
- биномиальные коэффициенты, 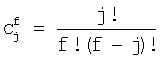 , причем
, причем 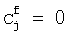 при j>f.
при j>f.
Поставленная задача решается также тем, что в известном способе стрельбы боевой машины (БМ) по скоростной цели, включающем обнаружение и распознавание цели, сопровождение с определением координат и параметров цели, определение угловых поправок, суммирование их соответственно по горизонтальному и вертикальному каналам с учетом угла крена и постоянное отклонение во время стрельбы с учетом выработанных угловых поправок стволов ПУ относительно линии визирования, в случае неопределенности условий относительного перемещения цели перед определением угловых поправок предварительно накапливают информацию об угле наклона линии визирования g(t) в виде m+1 точек по каждому каналу, затем аппроксимируют функцию g[nΔt] полиномом m-го порядка, далее определяют систематическую и случайную ошибки воспроизводимой производной угла наклона линии визирования, выбирают порядок приближения l на следующий интервал прогнозирования угловых скоростей, исходя из рационального соотношения систематической и случайной ошибок, и угловую скорость линии визирования 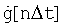 соответственно в горизонтальном и вертикальном каналах определяют дифференцированием углов наклона линии визирования
соответственно в горизонтальном и вертикальном каналах определяют дифференцированием углов наклона линии визирования 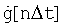 из следующего соотношения
из следующего соотношения
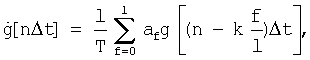
где 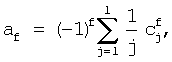
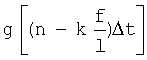 - угол наклона линии визирования в момент времени
- угол наклона линии визирования в момент времени 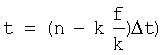 ,
,
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования, 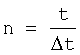 ,
,
f - порядковый номер "узловой" точки - укрупненной дискреты Δt' 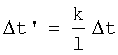 ,
,
Т - время наблюдения,
l - порядок приближения производной,
k - количество шагов дискретизации на T, 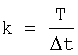 ,
,
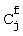 - биномиальные коэффициенты,
- биномиальные коэффициенты, 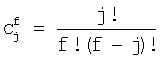 , причем
, причем 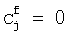 при j>f.
при j>f.
Поставленная задача решается также тем, что в известном способе стрельбы боевой машины (БМ) по скоростной цели систематическую ошибку 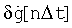 определяют по зависимости
определяют по зависимости
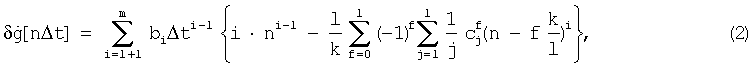
где bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm,
Т - время наблюдения, T должно быть кратно целому числу укрупненных дискрет Δt', т.е. должно выполняться условие

l - порядок приближения производной,
k - число шагов дискретизации на T, 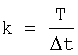 ,
,
f - порядковый номер "узловой" точки - укрупненной дискреты Δt' 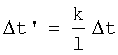 ,
,
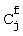 - биномиальные коэффициенты
- биномиальные коэффициенты
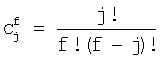 ,
, 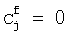 при j>f.
при j>f.
Поставленная задача решается также тем, что в известном способе стрельбы БМ по скоростной цели систематическую ошибку 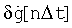 определяют в виде суммы числового ряда
определяют в виде суммы числового ряда
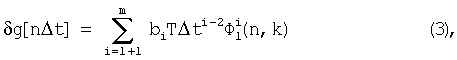
где 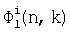 - сумма степенного ряда функций вида
- сумма степенного ряда функций вида
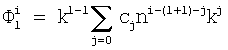 от номера текущего шага n и параметра k,
от номера текущего шага n и параметра k,
сj - предварительно рассчитанные коэффициенты cj=cj(l,i), i=1, ..., m,
bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Pm,
Т - время наблюдения,
l - порядок приближения производной,
k - число шагов дискретизации на T, 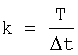 ,
,
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования, 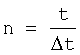 .
.
Поставленная задача решается также тем, что случайную ошибку 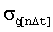 определяют в виде
определяют в виде
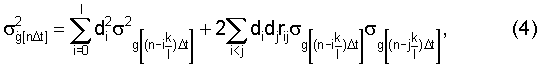
где 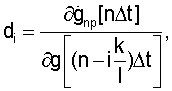
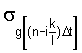 - среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени 
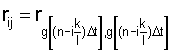 - коэффициент корреляции между
- коэффициент корреляции между 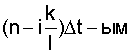 и
и 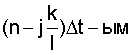 сечениями случайной последовательности g[nΔt].
сечениями случайной последовательности g[nΔt].
Поставленная задача решается также тем, что в известном способе стрельбы боевой машины (БМ) по скоростной цели случайную ошибку 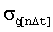 определяют в виде
определяют в виде
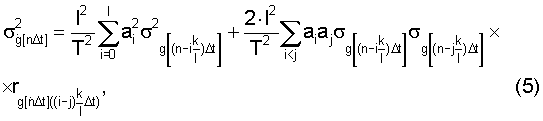
где ai=af - коэффициент при f-ом члене дифференцирующего фильтра,
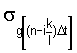 - среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени 
 - коэффициент корреляции между
- коэффициент корреляции между 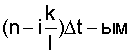
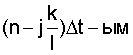 сечениями случайной последовательности g[nΔt].
сечениями случайной последовательности g[nΔt].
Поставленная задача решается также тем, что в известном способе стрельбы боевой машины (БМ) по скоростной цели рациональное соотношение систематической и случайной ошибок устанавливается из соотношения
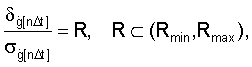
где (Rmin, Rmax) - диапазон рационального соотношения систематических и случайных ошибок, определяемый из условия обеспечения максимального значения критерия эффективности стрельбы,
причем если R<Rmin, то l=l-1, если R>Rmax, то l=l+1, иначе l=l.
Поставленная задача решается также тем, что в известной системе стрельбы БМ по цели, содержащей последовательно соединенные обзорно-прицельную систему, бортовую вычислительную систему, включающую устройство формирования углов упреждения, содержащее в том числе блок формирования угла упреждения Δβ, блок формирования угла упреждения Δε, блок формирования упрежденной дальности DУ, блок поправки на баллистический ветер по горизонтальному каналу, блок поправки на продольный ветер по вертикальному каналу, входы которых соединены с выходами обзорно-прицельной системы через соответствующие входы вычислительной системы, далее силовые приводы установки и пулеметную или пушечную установку, а также навигационную систему и блок данных о внешней среде, выходы которых соединены с вычислительной системой, в вычислительную систему дополнительно введен блок формирования угловой скорости, входы которого соединены с первым - вторым выходами обзорно-прицельной системы, первый его выход - со входами блока формирования угла упреждения по горизонтальному каналу Δβ, блока формирования упрежденной дальности Dy, блока поправки на баллистический ветер по горизонтальному каналу, второй выход - со входами блока формирования угла упреждения по вертикальному каналу Δε, блока формирования упрежденной дальности Dy, блока поправки на продольный ветер по вертикальному каналу.
Поставленная задача решается также тем, что в известной системе стрельбы БМ по цели блок формирования угловой скорости содержит последовательно соединенные накопительное устройство, (l+1) параллельно соединенных множительных устройств, сумматор, (l+2)-е множительное устройство.
Именно организованная таким образом стрельба с помощью предлагаемых систем обеспечивает согласно способу повышение точности определения угловой скорости линии визирования, а в конечном счете, повышение точности и эффективности стрельбы, в частности, по скоростной, в особенности воздушной цели.
Тем самым достигается цель изобретения. Это позволяет сделать вывод о том, что заявляемые изобретения связаны между собой единым изобретательским замыслом.
Сопоставительный анализ заявленных решений с прототипом показывает, что заявляемый способ отличается от известного тем, что согласно изобретению перед определением угловых поправок находят угловую скорость линии визирования 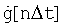 дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах (п.1 формулы, вар.1 способа). Для этого предварительно во время сопровождения цели назначают порядок приближения 1 воспроизводимой производной угла наклона линии визирования, исходя из условий перемещения цели относительно БМ - l=[1, 2...6].
дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах (п.1 формулы, вар.1 способа). Для этого предварительно во время сопровождения цели назначают порядок приближения 1 воспроизводимой производной угла наклона линии визирования, исходя из условий перемещения цели относительно БМ - l=[1, 2...6].
В случае неопределенности условий относительного перемещения цели перед определением угловых поправок предварительно накапливают информацию об угле наклона линии визирования g(t) в виде m+1 точек по каждому каналу с тем, чтобы далее аппроксимировать функцию g[nΔt] полиномом m-го порядка (п.2 формулы, вар.2).
Основным приемом при выводе зависимости, используемой далее для определения систематической ошибки 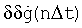 , являлась аппроксимация входного сигнала g(nΔt) некоторым степенным полиномом
, являлась аппроксимация входного сигнала g(nΔt) некоторым степенным полиномом 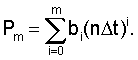 Тогда погрешность вычисления систематической ошибки определения производной
Тогда погрешность вычисления систематической ошибки определения производной 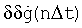 в значительной степени сводится к ошибке, возникающей за счет аппроксимации функции g(nΔt).
в значительной степени сводится к ошибке, возникающей за счет аппроксимации функции g(nΔt).
Входная дифференцируемая функция g(nΔt) аппроксимировалась полиномом разных порядков m=1-6. На фиг.1-2 представлены в качестве примера реальные (из блока относительного движения) входные функции - зависимости соответственно углов наклона линии визирования β(t), ε(t) по траектории и аппроксимирующие их зависимости при разных порядках полиномов Рm - m=1-6.
Как следует из графиков фиг.1-2, в зависимости от динамичности входного (дифференцируемого) сигнала для обеспечения потребной точности аппроксимации требуются различные значения степени m полинома Рm.
На вход ДФ подавались входные сигналы, представленные вышеприведенными полиномами Рm, полученными путем аппроксимации реального сигнала об углах β(t), ε(t), поступающих с блока относительного движения.
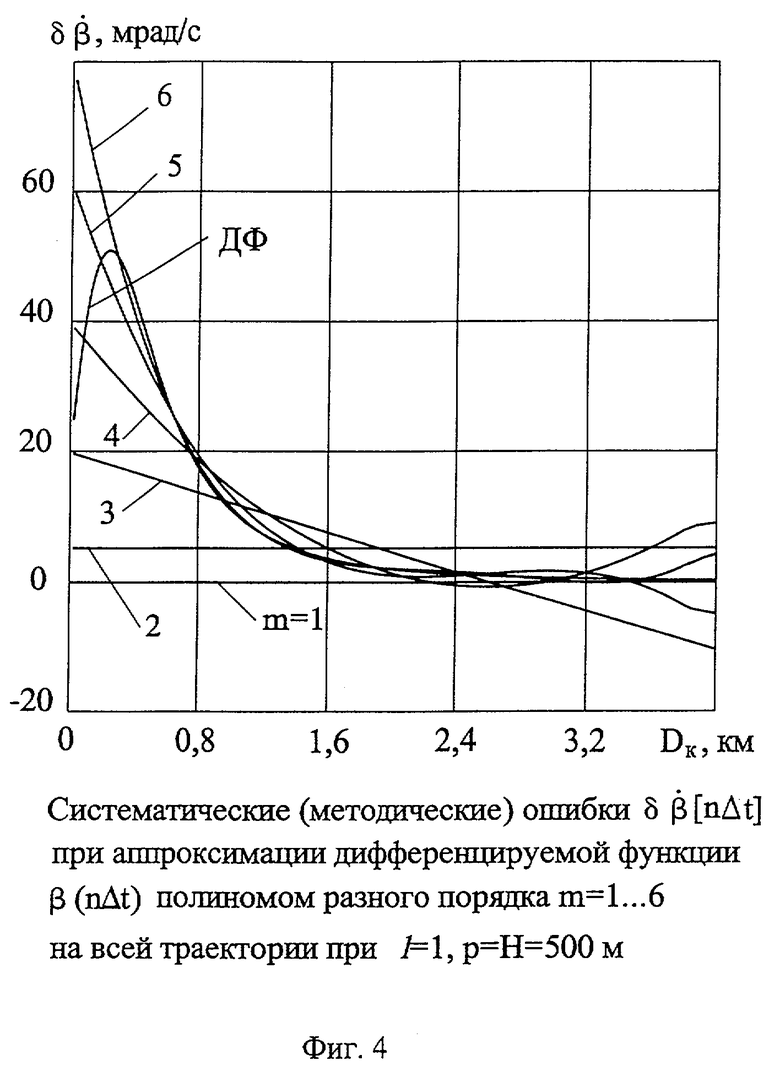
На фиг.3 и 4 приведены погрешности определения методических ошибок 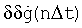 при аппроксимации угла разворота линии визирования в горизонтальной плоскости относительно продольной оси носителя - функции β(t) - на всей траектории полиномами разных порядков m при воспроизведении производной с помощью ДФ первого (l=1) и второго (l=2) порядков приближения.
при аппроксимации угла разворота линии визирования в горизонтальной плоскости относительно продольной оси носителя - функции β(t) - на всей траектории полиномами разных порядков m при воспроизведении производной с помощью ДФ первого (l=1) и второго (l=2) порядков приближения.
Для сравнения приведены и сами систематические (методические ошибки) δg(nΔt), см. фиг.6 (l=1), 7 (l=2), рассчитываемые по аналитическим зависимостям (2, 3) при поступлении на вход ДФ угла наклона линии визирования, аппроксимированного функцией 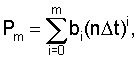 а для сравнения - и при поступлении на вход ДФ реального сигнала (обозначено ДФ).
а для сравнения - и при поступлении на вход ДФ реального сигнала (обозначено ДФ).
Другими словами, полученные значения погрешности определения систематической ошибки 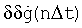 представляют собой разность систематических ошибок, полученных при их прямом (имитационном) моделировании и полученных по аналитическим зависимостям, и соответственно включают в себя как методические ошибки воспроизведения производной с помощью ДФ, так и ошибки аппроксимации входного сигнала полиномом Рm, см. фиг.7.
представляют собой разность систематических ошибок, полученных при их прямом (имитационном) моделировании и полученных по аналитическим зависимостям, и соответственно включают в себя как методические ошибки воспроизведения производной с помощью ДФ, так и ошибки аппроксимации входного сигнала полиномом Рm, см. фиг.7.
Как показывает анализ графиков, систематическая ошибка, рассчитываемая по аналитическим зависимостям, тем больше, чем больше порядок аппроксимирующего полинома, т.е. чем более динамичным является сигнал, см. фиг.4, 6.
Однако при повышении порядка m полинома Рm он точнее отображает реальный сигнал. И повышением порядка m полинома Рm можно свести ошибку определения систематической ошибки 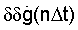 к бесконечно малой величине даже при больших временах наблюдения, сопоставимых с временем сопровождения цели на траектории. Так, уже при m=6 при l=1 max
к бесконечно малой величине даже при больших временах наблюдения, сопоставимых с временем сопровождения цели на траектории. Так, уже при m=6 при l=1 max 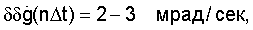 при при l=2 max
при при l=2 max 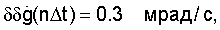 т.е. в десятки раз меньше по сравнению с малым порядком аппроксимирующего полинома m(m=1-2).
т.е. в десятки раз меньше по сравнению с малым порядком аппроксимирующего полинома m(m=1-2).
Очевидно также, что систематические ошибки существенно (на порядок) снижаются с повышением порядка ДФ.
А, самое главное, систематические ошибки сильно уменьшаются при уменьшении времени наблюдения и времени экстраполяции. Фиг.8-9 (l=1), 10-11 (l=2) аналогичны вышеописанным графикам на фиг.3-6. Отличие заключается в том, что время наблюдения (и время прогнозирования функции g(t)) уменьшено до Tн=Tпрогн=1 с.
Анализ значений погрешности определения систематической ошибки 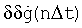 показывает, что при аппроксимации входной функции β(nΔt) полиномом выше m=3-4 можно достаточно точно прогнозировать систематическую ошибку воспроизведения производной
показывает, что при аппроксимации входной функции β(nΔt) полиномом выше m=3-4 можно достаточно точно прогнозировать систематическую ошибку воспроизведения производной  , используя аналитические зависимости (2, 3), причем в реальном масштабе времени например посекундно.
, используя аналитические зависимости (2, 3), причем в реальном масштабе времени например посекундно.
Таким образом, вышеприведенные результаты исследования показывают, что даже для такого динамичного сигнала как угловая скорость линии визирования можно оценивать систематическую ошибку его дифференцирования по предлагаемым далее аналитическим зависимостям с приемлемой точностью 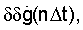 регулируя уровень погрешности подбором степени m аппроксимирующего полинома, на малые интервалы времени, в реальном масштабе времени.
регулируя уровень погрешности подбором степени m аппроксимирующего полинома, на малые интервалы времени, в реальном масштабе времени.
Следует заметить, что вычислительные возможности современных, а тем более перспективных бортовых вычислителей вряд ли ограничивают порядок аппроксимирующего полинома m.
Это создает предпосылки для того, чтобы непосредственно в процессе сопровождения цели и стрельбы по ней в бортовом вычислителе БМ находить оптимальные, адаптивные к реальным условиям (дальность, параметр и высота пролета цели, скорости цели и носителя и т.п.) тип и параметры ДФ, т.е. производить его структурно-параметрический синтез.
Поэтому согласно изобретению далее, используя накопленные по каждому каналу m+1 точек, аппроксимируют функцию g(t) полиномом m-го порядка, а затем определяют ошибки воспроизводимой производной из соотношений - систематическую 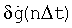 - зависимости (2) или (3), а случайную
- зависимости (2) или (3), а случайную 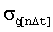 - (4) или (5).
- (4) или (5).
Систематическую ошибку 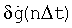 рассчитывают по зависимости (2) (зависимый п.3 формулы)
рассчитывают по зависимости (2) (зависимый п.3 формулы)
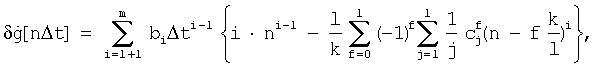
где bi - коэффициеты аппроксимации функции g[nΔt] степенным полиномом Рm,
Т - время наблюдения (T должно быть кратно целому числу укрупненных дискрет Δt', т.е. должно выполняться условие  ,
,
l - порядок приближения производной (или число учитываемых членов разложения при расчете первой производной),
k - число шагов дискретизации на T, 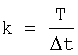 ,
,
f - порядковый номер "узловой" точки - укрупненной дискреты Δt' 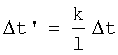 ,
,
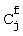 - биномиальные коэффициенты,
- биномиальные коэффициенты, 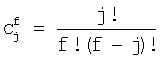 ,
, 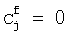 при j>f.
при j>f.
Однако вышеприведенная общая зависимость для расчета систематической ошибки 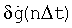 (2) не очень удобна для конкретного программирования. Очевидно, при малых порядках ДФ l целесообразно использовать заранее вычисленные значения коэффициентов
(2) не очень удобна для конкретного программирования. Очевидно, при малых порядках ДФ l целесообразно использовать заранее вычисленные значения коэффициентов 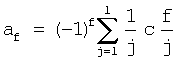 , т.е. учитывать конкретный вид ДФ. И тогда она может быть представлена в виде (4)
, т.е. учитывать конкретный вид ДФ. И тогда она может быть представлена в виде (4)
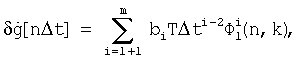
где 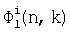 - сумма степенного ряда функций вида
- сумма степенного ряда функций вида
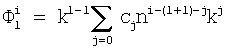 от номера текущего шага n и параметра k,
от номера текущего шага n и параметра k,
сj - предварительно рассчитанные коэффициенты cj=cj(l,i), i=1, 2...m.
(Значения сj в 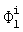 приведены в таблицах 1 и 2 соответственно для l=1, 2...)
приведены в таблицах 1 и 2 соответственно для l=1, 2...)
bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm,
Т - время наблюдения,
l - порядок приближения производной (или число учитываемых членов разложения при расчете первой производной), Т
k - число шагов дискретизации на Т, 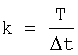 ,
,
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования,
В таблицах 1, 2 в качестве примера представлены значения 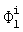 для l=1, 2.
для l=1, 2.
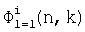
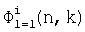 , n≥k
, n≥k
Вид функции 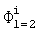

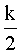
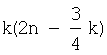

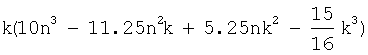
Вышеприведенным способом предлагается рассчитывать систематическую ошибку в зависимом п.4 формулы изобретения.
Зависимости (2) и (3) позволяют проследить, как накапливается систематическая ошибка в зависимости от порядка фильтра (l), динамичности входного сигнала (m), от величины постоянной времени (T) и шага дискретности (Δt).
В качестве примечания заметим, что зависимости, предлагаемые для определения систематической 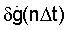 и случайной
и случайной 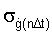 ошибок, являются авторскими и представляют собой базу методического аппарата для оценки точности метода численного дифференцирования.
ошибок, являются авторскими и представляют собой базу методического аппарата для оценки точности метода численного дифференцирования.
Случайную ошибку 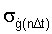 определяют согласно зависимому п.5 формулы по зависимости (4)
определяют согласно зависимому п.5 формулы по зависимости (4)

где 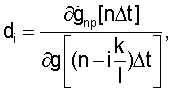
 - среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени 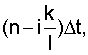
 - коэффициент корреляции между
- коэффициент корреляции между 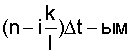 и
и 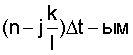 сечениями случайной последовательности g[nΔt].
сечениями случайной последовательности g[nΔt].
Выражение (4) (1-й вариант для СКО, п.5 формулы) получено согласно основным положениям теории вероятностей /4/, при этом в соответствии с выражением (1) l-е приближение первой производной рассматривалось как линейная комбинация l+1 значений входной случайной последовательности g[nΔt], g[n-1)Δt]...g[(n-k)Δt], каждое из которых представляет собой случайную величину.
Совокупность таких значений g[nΔt], взятых на времени наблюдения Т (2 - при ДФ 7-го порядка (l=1), 3 - при ДФ 2-го порядка (l=2), 4 - при ДФ 3-го порядка (l=3)...l+1 - при ДФ l-го порядка) представляет собой систему l+1 случайных величин (например, при  ) с математическим ожиданием соответственно
) с математическим ожиданием соответственно 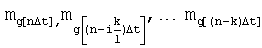 и корреляционный матрицей
и корреляционный матрицей
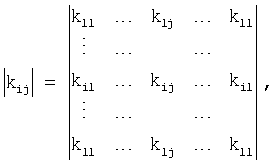
где kij - коэффициент корреляции между i-ым и j-ым значениями числовой последовательности, i=1, ..., l, j=1, ..., l,
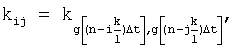
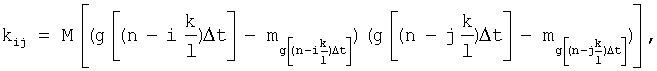
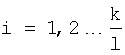 ,
,  .
.
В соответствии с видом зависимости для ДФ первого порядка, см. (1)
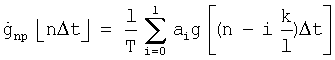
случайная величина 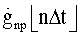 есть линейная форма (функция) случайного аргумента
есть линейная форма (функция) случайного аргумента 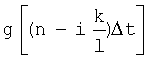 .
.
Например, при l=3
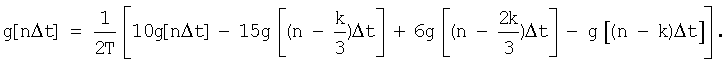
Вследствие линейного характера функции (1) можно определять ее числовую характеристику - дисперсию - без учета производных высшего порядка (выше первого), не прибегая к линеаризации функции, то есть точно.
Тогда дисперсия (квадрат СКО) сигнала на выходе ДФ согласно /4/ может быть представлена в виде
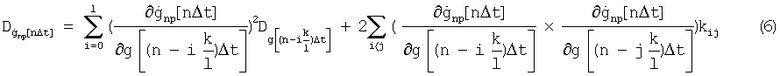
kij - взаимный коэффициент корреляции соответственно между i-ым j-ым сечениями случайной последовательности g[nΔt],
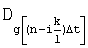 - дисперсия дифференцируемой случайной последовательности (на входе ДФ).
- дисперсия дифференцируемой случайной последовательности (на входе ДФ).
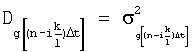
Таким образом, получена используемая в п.5 зависимость для определения случайной ошибки.
В п.6 формулы изобретения для расчета среднеквадратического отклонения 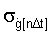 используется второй вариант зависимости для СКО
используется второй вариант зависимости для СКО 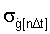 - зависимость (5).
- зависимость (5).
Получаемую после ДФ последовательность  будем теперь рассматривать как сумму случайных функций
будем теперь рассматривать как сумму случайных функций 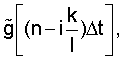 i=1,2,...l, каждая из которых берется с соответствующим коэффициентом аi точнее это линейная форма функций
i=1,2,...l, каждая из которых берется с соответствующим коэффициентом аi точнее это линейная форма функций 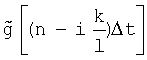
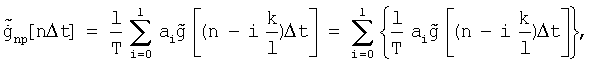
где 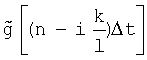 - значение входной функции
- значение входной функции 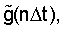 взятое в некоторые моменты времени nΔt,
взятое в некоторые моменты времени nΔt, 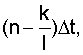
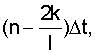
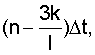 ... (n-k)Δt.
... (n-k)Δt.
Для 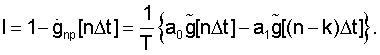
Тогда математическое ожидание сформированной таким образом новой случайной функции 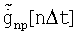 в соответствии с положениями теории вероятностей равно сумме математических ожиданий слагаемых
в соответствии с положениями теории вероятностей равно сумме математических ожиданий слагаемых
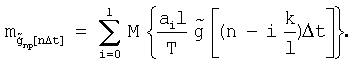
Вынося за скобку постоянные величины, получаем
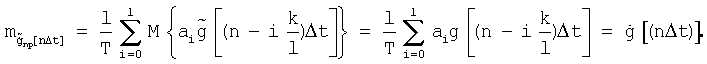
В соответствии с положениями теории случайных функций о сложении случайных функций /4/ корреляционная функция выходной величины - функции 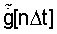 равна сумме корреляционных функций
равна сумме корреляционных функций 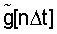 плюс сумма взаимных корреляционных функций (корреляционных функций связи) всех возможных сочетаний исходных функций. Далее для краткости будем опускать знак случайной функции "˜" (тильда).
плюс сумма взаимных корреляционных функций (корреляционных функций связи) всех возможных сочетаний исходных функций. Далее для краткости будем опускать знак случайной функции "˜" (тильда).
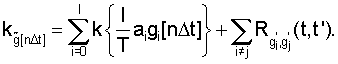
Взаимная корреляционная функция 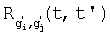 характеризует связь между i-ым и j-ым сечениями случайной функции
характеризует связь между i-ым и j-ым сечениями случайной функции 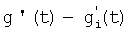 и
и 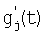 и по определению является математическим ожиданием произведения
и по определению является математическим ожиданием произведения 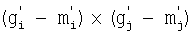 .
.
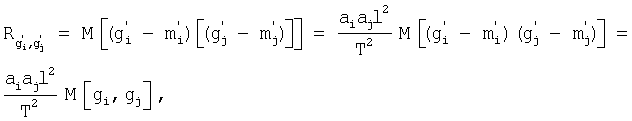
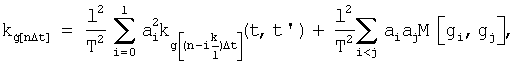
где 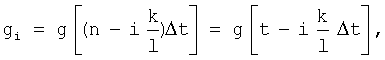
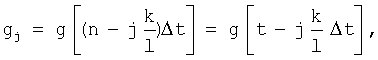
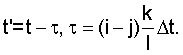
Учитывая, что функции gi, gj под знаком математического ожидания это сечения одной функции g(t), но взятые в моменты времени соответственно 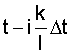 и
и  где t'-t=τ, можно перейти от взаимной корреляционной функции к автокорреляционной функции
где t'-t=τ, можно перейти от взаимной корреляционной функции к автокорреляционной функции 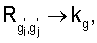 но уже по новому аргументу
но уже по новому аргументу 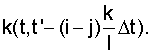
Тогда, предполагая стационарность функции g(t) k(t,t')=k(τ), можно записать

где 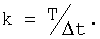
В результате корреляционную функцию воспроизводимой с помощью ДФ первой производной l-го порядка приближения 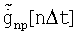 можно записать в виде
можно записать в виде

где l - порядок ДФ,
Т - время наблюдения,
ai, aj - коэффициенты, определяемые порядком l ДФ, см. зависимость (1).
В таблицу 3 сведены значения ai, используемые при воспроизведении первой производной ДФ-ом порядка l (l=1-6).
Значения коэффициентов аi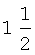
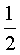
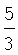
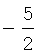
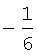
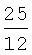

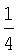
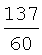
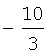
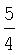
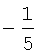

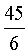
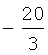
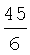
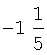
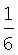
Учитывая, что 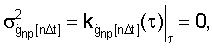 запишем выражение для СКО ошибок определения воспроизводимой с помощью ДФ производной
запишем выражение для СКО ошибок определения воспроизводимой с помощью ДФ производной 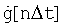 с учетом симметричности корреляционной матрицы относительно главной диагонали
с учетом симметричности корреляционной матрицы относительно главной диагонали
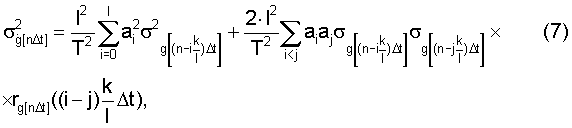
где 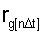 - нормированный коэффициент корреляции между соответствующим i-ым и j-ым сечениями исходной функции g[nΔt].
- нормированный коэффициент корреляции между соответствующим i-ым и j-ым сечениями исходной функции g[nΔt].
Сравнивая зависимости (6) и (7) (или соответственно ранее приведенные зависимости 4 и 5), можно убедиться, что разными путями мы пришли к одной зависимости для расчета СКО воспроизводимой производной  получаемой на выходе ДФ разного порядка l (в смысле степени приближения первой производной).
получаемой на выходе ДФ разного порядка l (в смысле степени приближения первой производной).
Выражения (6) и (7) в количественной мере устанавливают зависимость уровня шумов, транслированных на выход ДФ, во-первых, от уровня шумов (случайной помехи) сигнала на входе ДФ, характеризуемого их дисперсией (СКО) - 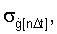 а также их внутренней (частотной) структурой (характеризуемой, в частности, декрементом затухания α и коэффициентом периодичности β), а во-вторых, зависит от структуры ДФ (порядка l) и его параметров (постоянной времени T и частоты опроса Δt).
а также их внутренней (частотной) структурой (характеризуемой, в частности, декрементом затухания α и коэффициентом периодичности β), а во-вторых, зависит от структуры ДФ (порядка l) и его параметров (постоянной времени T и частоты опроса Δt).
На фиг.12 представлены зависимости среднеквадратического отклонения шумов на выходе ДФ разных порядков l=1...6 при входном сигнале, "зашумленном" помехами разной статистической структуры - типа "белого шума" и с корреляционной функцией типа 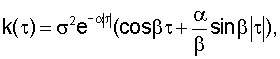 характерной для ошибок сопровождения оператором, при реальной (полученной опытным путем) зависимости уровня этих ошибок от дальности (σβ,ε(D) при заданных значениях параметра и высоты пролета цели возрастают с уменьшением дальности).
характерной для ошибок сопровождения оператором, при реальной (полученной опытным путем) зависимости уровня этих ошибок от дальности (σβ,ε(D) при заданных значениях параметра и высоты пролета цели возрастают с уменьшением дальности).
Для сравнения в таблицу 4 сведены рассчитанные по полученным аналитическим зависимостям значения так называемого коэффициента усиления шума 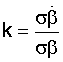 для разных порядков l ДФ при "развязанном" сигнале помехи (α→∞) и для рассматриваемого нами
для разных порядков l ДФ при "развязанном" сигнале помехи (α→∞) и для рассматриваемого нами 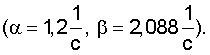
Расчетные значения коэффициента усиления "зашумленности" сигнала k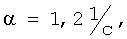
Примечание. В знаменателе во второй строке приведены значения времени наблюдения Т (T≈1 с. Δt=0,1 с).
Сравнивая коэффициенты усиления шума k из таблицы 3.4.2, можно заметить, что наличие корреляционной связи между сечениями 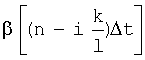 и
и 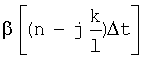 позволяет снизить случайную ошибку на выходе ДФ в нашем случае определения угловой скорости линии визирования в несколько раз. Причем снижение тем больше, чем выше порядок l ДФ.
позволяет снизить случайную ошибку на выходе ДФ в нашем случае определения угловой скорости линии визирования в несколько раз. Причем снижение тем больше, чем выше порядок l ДФ.
Так, если при ДФ второго порядка (l=2) коэффициент усиления ("подчеркивания" шумов) составляет при сигнале помехи типа "белого" шума (α→∞) k=5,1, при сигнале помехи типа случайного процесса с корреляционной функцией 
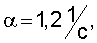 β=2,088 - k=2,9, то при ДФ шестого порядка (l=6) снижается соответственно с k=62,9 до k=5,4.
β=2,088 - k=2,9, то при ДФ шестого порядка (l=6) снижается соответственно с k=62,9 до k=5,4.
Для наших практических целей анализ приведенных в таблице данных позволяет сделать следующие выводы:
1. Наличие корреляционной связи между сечениями исходного (дифференцируемого) процесса β[nΔt] дает возможность повышать порядок ДФ и благодаря этому снижать уровень систематической (динамической) ошибки до приемлемых уровней даже при достаточно динамичном характере входного сигнала, каковым является, например, сигнал об углах линии визирования β(t), ε(t) (в отличие, к примеру, от сигнала о дальности до цели D(t)). Таким образом, неизбежное при повышении порядка ДФ l возрастание случайных ошибок отчасти компенсируется сильной корреляционной связью ошибок углов наклона линии визирования.
2. При реализуемых в результате этого уровнях и Частотном спектре случайных ошибок  вполне допустимо (целесообразно) обойтись без сглаживания выходного сигнала
вполне допустимо (целесообразно) обойтись без сглаживания выходного сигнала 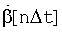 , которое неизбежно внесет дополнительную систематическую ошибку.
, которое неизбежно внесет дополнительную систематическую ошибку.
3. Предварительный анализ существующего уровня и структуры ошибок сопровождения цели оптическим каналом и аппаратурных ошибок в углах разворота линии визирования, определяемых как классом точности датчиков углов (в БМП-3 - ДУ ВН, ДУГ ГН и курсовой датчик башни), так и погрешностями, вносимыми при модуляции (демодуляции) сигнала, позволяют сделать вывод о возможности обеспечения приемлемой точности определения угловых скоростей линии визирования с помощью ДФ порядка l=2-4 без последующего сглаживания (Tн=1-2 с, Δt≈0,1 с).
Эти уровни ошибок воспроизведения угловых скоростей в гарантированной постановке примерно соответствуют требуемым для обеспечения планируемых уровней эффективности стрельбы по скоростным, в частности, воздушным целям. Таким образом, неаппаратурными (математическими, алгоритмическими) способами можно обеспечить заявленные ранее высокие уровни эффективности стрельбы, и, прежде всего, по скоростным воздушным целям.
4. Анализ проведенных расчетов по оценке входной (дифференцируемой) функции показывает существенно различающиеся уровни ошибок (систематических и случайных) при предлагаемом способе воспроизведения производной в различных условиях боевого применения.
Это свидетельствует о необходимости постоянного (в процессе сопровождения и стрельбы) выбора структуры и параметров ДФ, т.е. формирования и контроля ДФ, адаптивного к условиям пролета цели (параметр, высота, скорости цели и носителя).
Разработанный методический аппарат для оценки точности воспроизведения производной позволяет реализовать адаптивный ДФ и соответственно осуществить стрельбу оптимальным (наиболее рациональным) способом.
Поэтому далее выбирают порядок приближения l на следующий интервал прогнозирования угловых скоростей, исходя, например, из рационального соотношения систематической и случайной ошибок
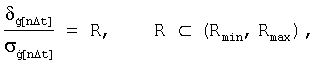
причем если R<Rmin, то l=l-1, если R>Rmax, то l=l+1, иначе l=l.
А угловую скорость линии визирования 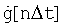 соответственно в горизонтальном и вертикальном канале определяют дифференцированием углов наклона линии визирования g[nΔt] из следующего соотношения
соответственно в горизонтальном и вертикальном канале определяют дифференцированием углов наклона линии визирования g[nΔt] из следующего соотношения
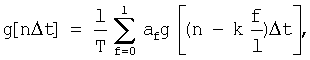
где 
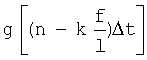 - угол наклона линии визирования в вертикальном или горизонтальном канале в момент времени
- угол наклона линии визирования в вертикальном или горизонтальном канале в момент времени 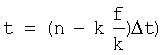 .
.
Выражение (1) получено из выражения, представленного в литературе по теории автоматического регулирования, в частности /5, 6/

где 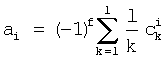 - биномиальные коэффициенты,
- биномиальные коэффициенты, 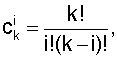 причем
причем 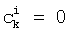 при i>k.
при i>k.
Как следует из выражения (1), с повышением степени приближения l 1-й производной пропорционально увеличивается минимально необходимое время наблюдения входного дифференцируемого сигнала 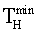 при фиксируемом шаге дискретизации его Δt
при фиксируемом шаге дискретизации его Δt
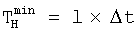
На практике из физических соображений часто бывает необходимо фиксировать Тн, т.е. разнести последнее (текущее) g[nΔt] и первое g[(n-k)Δt] по времени учитываемые значения g[nΔt] на заданном времени наблюдения Тн или сместить первое значение g[nΔt] на k шагов дискретизации Δt от текущего.
Для этого следует учесть, что в общем случае
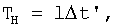

где l - порядок приближения ДФ 1-го порядка,
Δt' - интервал времени между соседними учитываемыми замерами (дискретами).
Тогда в общем виде можно записать выражение для l-го приближения 7-й производной в виде

где 
f - порядковый номер "узловой" точки (укрупненной дискреты) Δt', 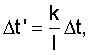
ТН - время наблюдения (необходимо так выбирать ТH, чтобы на нем укладывалось целое число этих укрупненных дискрет Δt', т.е. должно выполняться условие 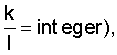
l - порядок приближения воспроизводимой производной,
k - количество шагов дискретизации на TH,  ,
,
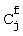 - биномиальные коэффициенты,
- биномиальные коэффициенты, 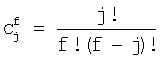 , причем
, причем 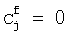 при f>j.
при f>j.
Сравнение заявляемых технических решений с прототипами позволяет установить соответствие критерию "новизна".
Анализ известных способов защиты объектов от СВН в данной области техники не позволил выявить в них совокупность признаков, отличающих заявляемое решение от прототипа.
Отдельные операции, входящие в заявляемый способ, широко известны. Однако при их введении в способ в указанной последовательности (связи) по предлагаемым соотношениям достигается желаемый эффект - повышение точности и эффективности стрельбы по воздушным целям.
При изучении технических решений в других областях техники признаки, отличающие заявляемое изобретение - систему стрельбы БМ по скоростной воздушной цели - также не были выявлены.
Это позволяет сделать вывод о соответствии предлагаемых решений критериям новизны и изобретательского уровня.
На фиг.1 представлены зависимости угла наклона линии визирования в горизонтальной плоскости β(t), реального и аппроксимируемого полиномом Рm (m=1...6).
На фиг.2 представлены зависимости угла наклона линии визирования в вертикальной плоскости ε(t), реального и аппроксимируемого полиномом Pm (m=1...6).
На фиг.3 представлены погрешности определения систематических (методических) ошибок 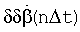 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=1, параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=1, параметре и высоте пролета p=Н=500 м.
На фиг.4 представлены систематические (методические) ошибки 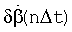 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=1, параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=1, параметре и высоте пролета p=Н=500 м.
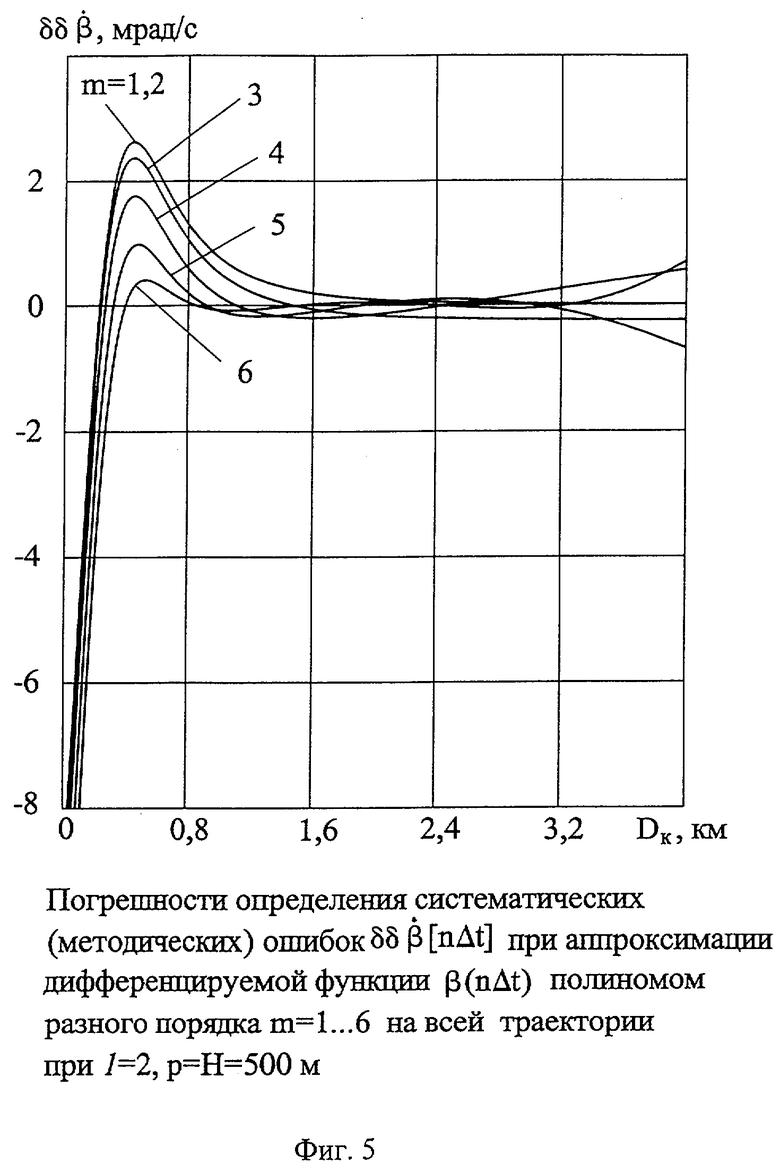
На фиг.5 представлены погрешности определения систематических (методических) ошибок 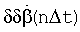 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ 1=2, параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ 1=2, параметре и высоте пролета p=Н=500 м.
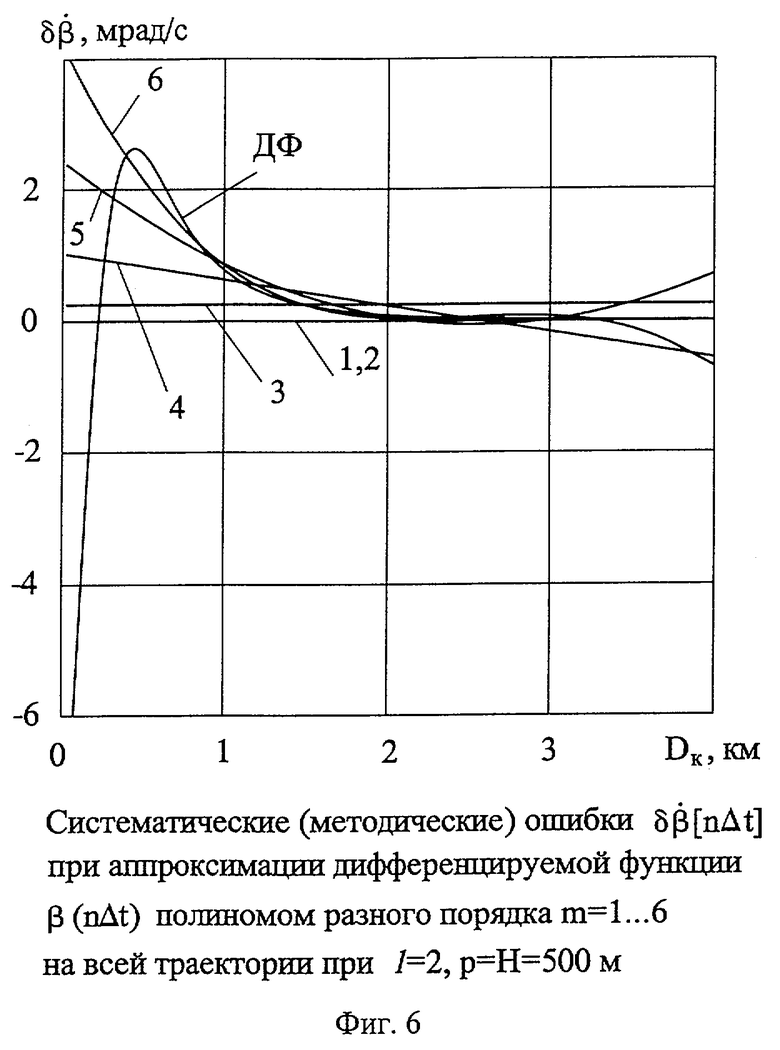
На фиг.6 представлены систематические (методические) ошибки 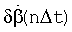 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=2, параметре и высоте пролета р=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) на всей траектории при порядке ДФ l=2, параметре и высоте пролета р=Н=500 м.
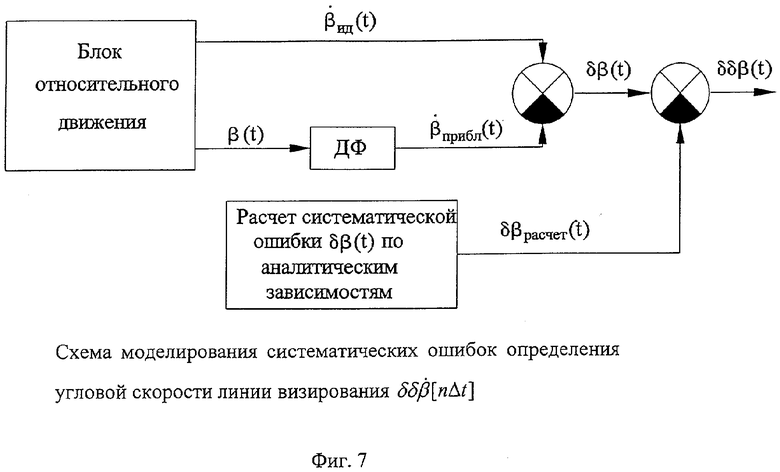
На фиг.7 представлена схема моделирования систематических ошибок определения угловой скорости линии визирования 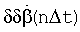 .
.
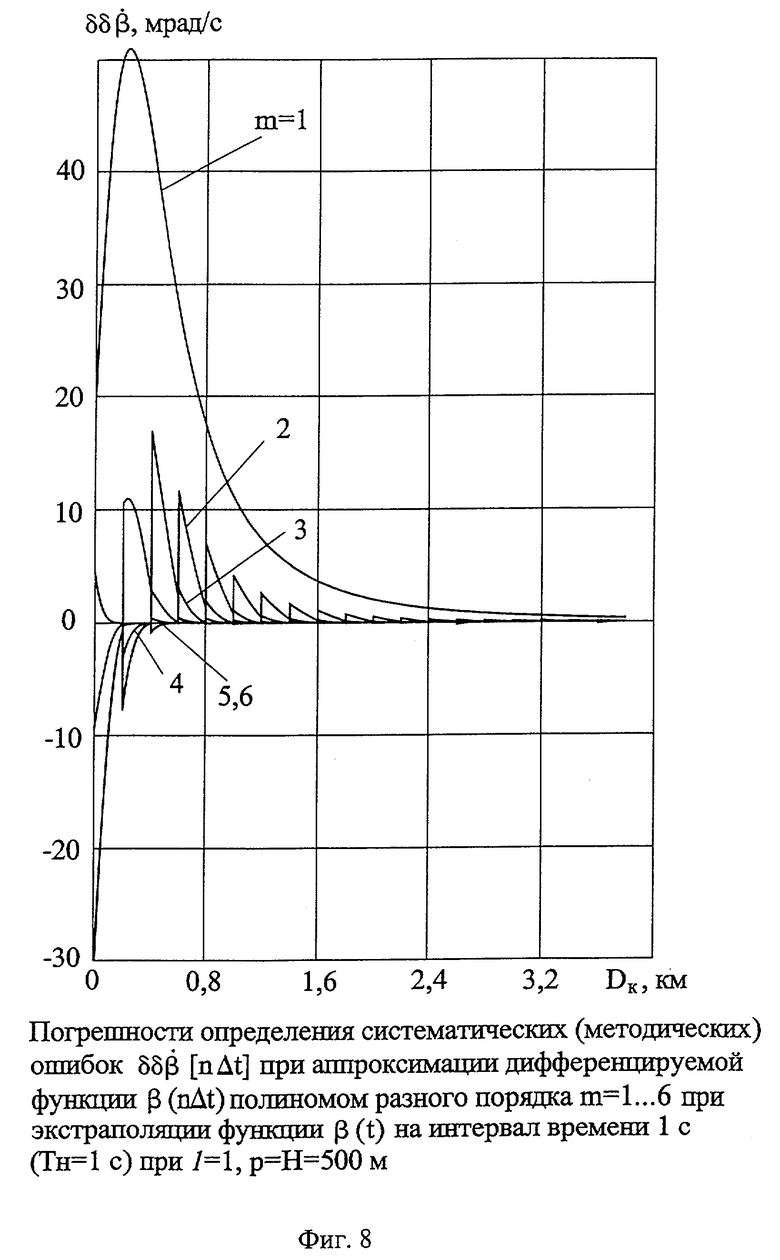
На фиг.8 представлены погрешности определения систематических (методических) ошибок 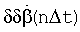 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при TH=Тпрогн=1 с для порядка ДФ 1=1, при параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при TH=Тпрогн=1 с для порядка ДФ 1=1, при параметре и высоте пролета p=Н=500 м.
На фиг.9 представлены систематические (методические) ошибки 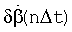 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при TH=Tпрогн=1 c для порядка ДФ l=1, при параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при TH=Tпрогн=1 c для порядка ДФ l=1, при параметре и высоте пролета p=Н=500 м.
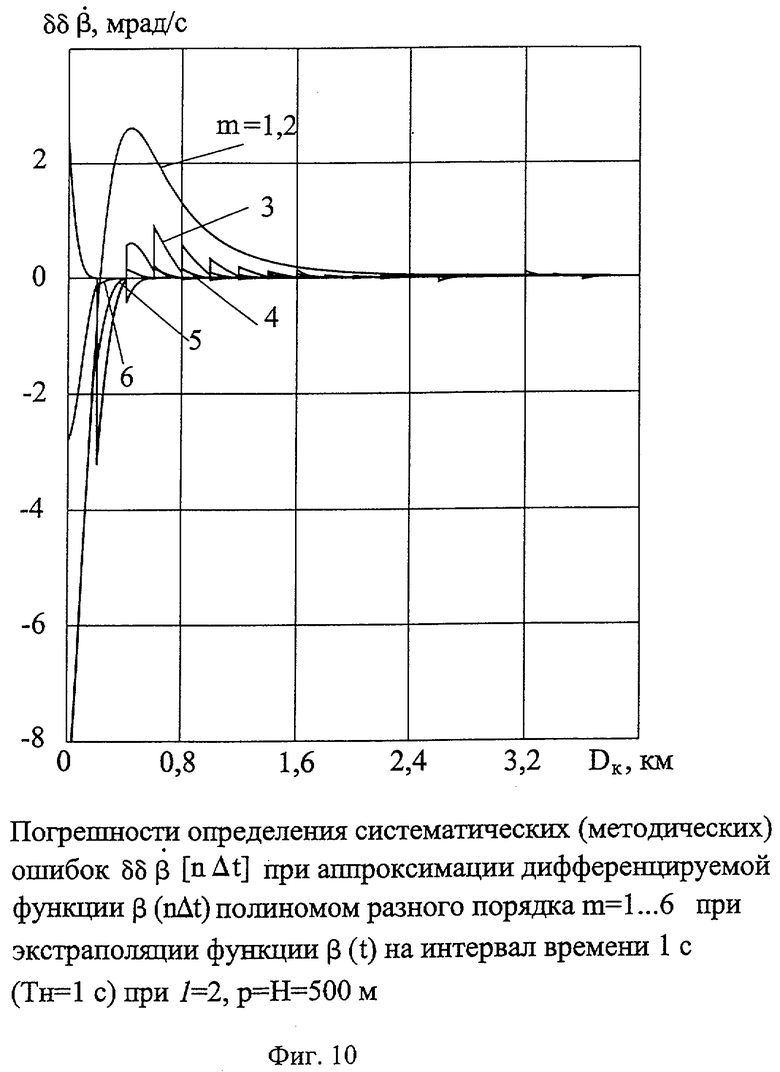
На фиг.10 представлены погрешности определения систематических (методических) ошибок 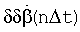 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при ТH=Тпрогн=1 c для порядка ДФ 1=2, при параметре и высоте пролета р=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при ТH=Тпрогн=1 c для порядка ДФ 1=2, при параметре и высоте пролета р=Н=500 м.
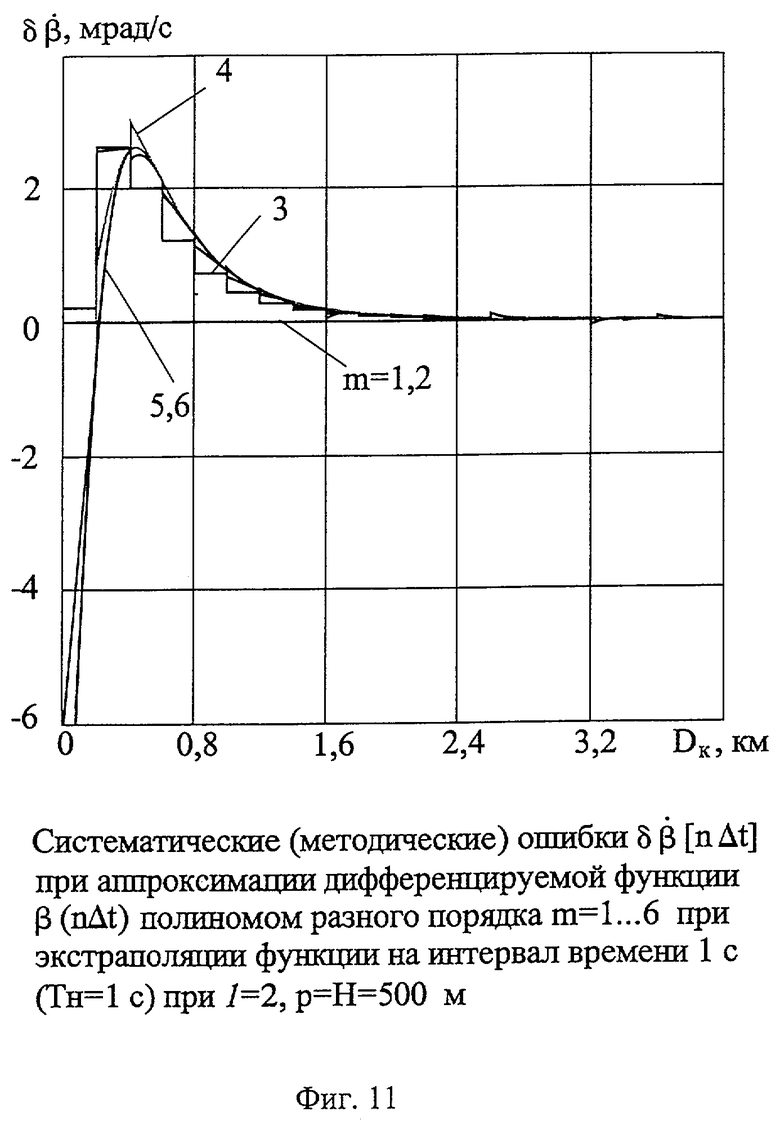
На фиг.11 представлены систематические (методические) ошибки 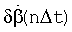 при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при ТH=Тпрогн=1 c для порядка ДФ l=2, при параметре и высоте пролета p=Н=500 м.
при аппроксимации дифференцируемой функции β(nΔt) полиномами разного порядка (m=1...6) при ТH=Тпрогн=1 c для порядка ДФ l=2, при параметре и высоте пролета p=Н=500 м.
На фиг.12 представлены зависимости среднеквадратического отклонения шумов на выходе ДФ разных порядков l=1...6 при входном сигнале, "зашумленном" помехами разной статистической структуры - типа "белого шума" и с корреляционной функцией типа 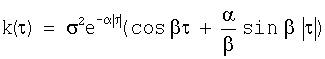 , характерной для ошибок сопровождения оператором, при заданной зависимости уровня ошибок углов наклона линии визирования от дальности σβ,ε(D).
, характерной для ошибок сопровождения оператором, при заданной зависимости уровня ошибок углов наклона линии визирования от дальности σβ,ε(D).
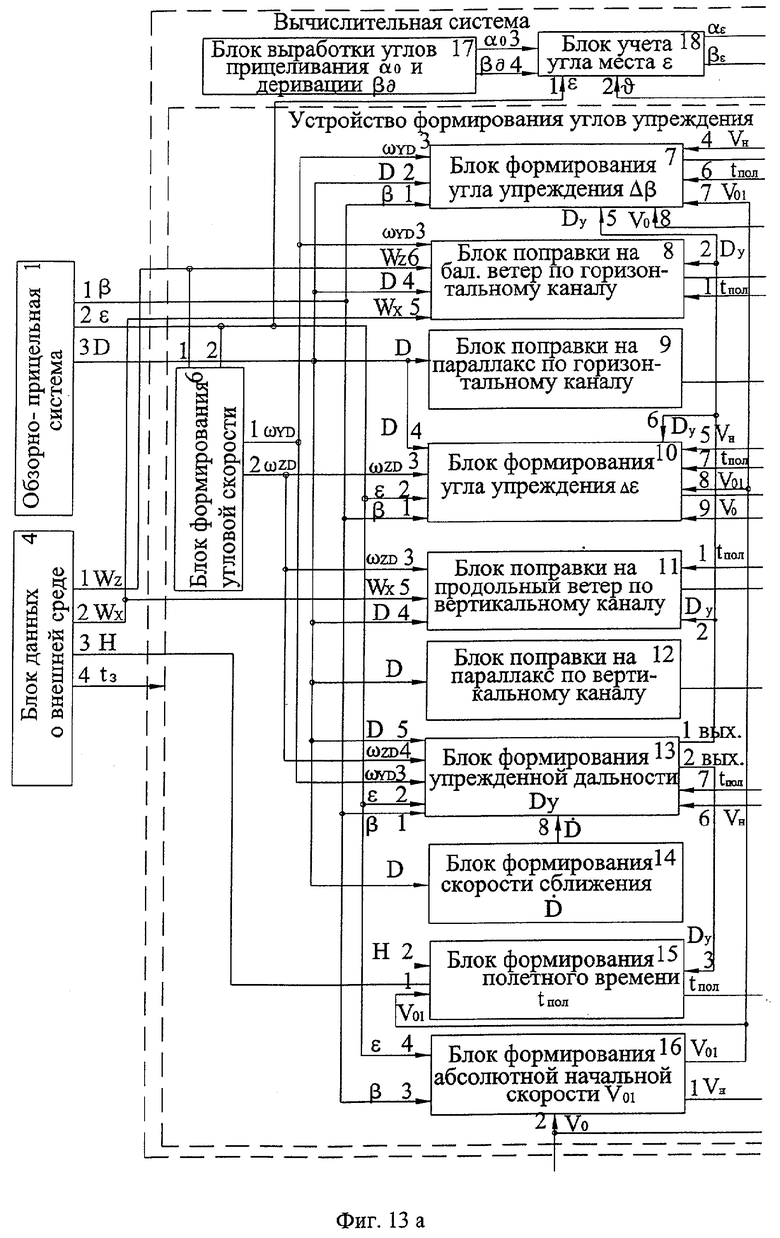
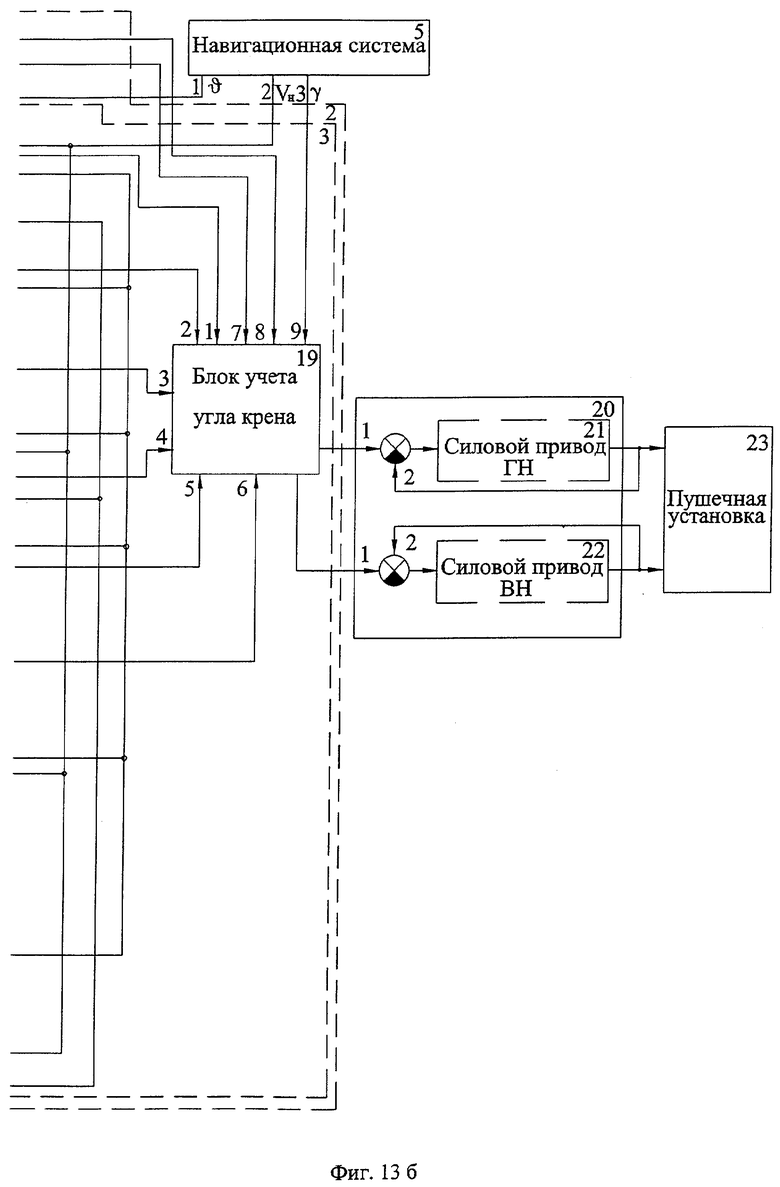
На фиг.13 (13 а и 13б) представлена функциональная схема системы стрельбы БМ по цели (вариант реализации) и место в ней заявляемого блока формирования угловой скорости линии визирования (пункт 5 формулы изобретения).
Система стрельбы БМ по цели содержит последовательно соединенные обзорно-прицельную систему 1, бортовую вычислительную систему 2, включающую в свой состав устройство определения углов упреждения 3, содержащее блок формирования угла упреждения Δβ 7, блок формирования угла упреждения Δε 10, блок формирования упрежденной дальности Dy 13, блок формирования скорости сближения 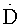 14, блок формирования полетного времени tпол 15, блок формирования абсолютной начальной скорости ν01 16, блок поправки на баллистический ветер по горизонтальному каналу 8, блок поправки на продольный ветер по вертикальному каналу 11, блок поправки на параллакс по горизонтальному каналу 9, блок поправки на параллакс по вертикальному каналу 12, блок формирования угловой скорости 6, входы которых соединены с выходами обзорно-прицельной системы через соответствующие входы вычислительной системы, далее силовые приводы установки 20 (силовой привод горизонтального 21 и вертикального 22 наведения) и пулеметную или пушечную установку 23, а также навигационную систему 5 и блок данных о внешней среде 4, выходы которых соединены с вычислительной системой 2. Кроме того, вычислительная система содержит последовательно соединенные блок выработки углов прицеливания α0 и деривации βд 17 и блок учета угла места ε 18, а также блок учета угла крена 19.
14, блок формирования полетного времени tпол 15, блок формирования абсолютной начальной скорости ν01 16, блок поправки на баллистический ветер по горизонтальному каналу 8, блок поправки на продольный ветер по вертикальному каналу 11, блок поправки на параллакс по горизонтальному каналу 9, блок поправки на параллакс по вертикальному каналу 12, блок формирования угловой скорости 6, входы которых соединены с выходами обзорно-прицельной системы через соответствующие входы вычислительной системы, далее силовые приводы установки 20 (силовой привод горизонтального 21 и вертикального 22 наведения) и пулеметную или пушечную установку 23, а также навигационную систему 5 и блок данных о внешней среде 4, выходы которых соединены с вычислительной системой 2. Кроме того, вычислительная система содержит последовательно соединенные блок выработки углов прицеливания α0 и деривации βд 17 и блок учета угла места ε 18, а также блок учета угла крена 19.
Первый и второй входы блока формирования угла упреждения Δβ соединены с первым и третьим выходами обзорно-прицельной системы, третий его вход - с первым выходом блока формирования угловой скорости, четвертый - со вторым выходом навигационной системы, пятый - с первым выходом блока формирования упрежденной дальности Dy, шестой - с выходом блока формирования полетного времени tпол, седьмой - с выходом блока формирования абсолютной начальной скорости ν01, восьмой - с задатчиком начальной скорости ν0.
Первый, второй и четвертый входы блока формирования угла упреждения Δε соединены соответственно с первым, вторым и третьим выходами обзорно-прицельной системы, третий - со вторым выходом блока формирования угловой скорости, пятый выход - со вторым выходом навигационной системы, шестой - с первым выходом упрежденной дальности, седьмой - с выходом блока формирования полетного времени, восьмой - с выходом блока формирования абсолютной начальной скорости, девятый - с задатчиком начальной скорости.
Первый и второй входы блока поправки на баллистический ветер по горизонтальному каналу соединены соответственно с выходами блоков формирования полетного времени и упрежденной дальности, третий - с первым выходом блока формирования угловой скорости, четвертый - с третьим выходом обзорно-прицельной системы, пятый и шестой - с первым и вторым выходами блока данных о внешней среде.
Первый и второй входы блока поправки на продольный ветер по горизонтальному каналу соединены соответственно с выходами блоков формирования полетного времени и упрежденной дальности, третий - со вторым выходом блока формирования угловой скорости, четвертый - с третьим выходом обзорно-прицельной системы, пятый - со вторым выходом блока данных о внешней среде.
Входы блоков поправки на параллакс по горизонтальному и вертикальному каналам соединены с третьим выходом обзорно-прицельной системы.
Первый, второй и пятый входы блока формирования упрежденной дальности соединены соответственно с первым, вторым и третьим выходами обзорно-прицельной системы, третий и четвертый входы - соответственно с первым и вторым входами блока формирования угловой скорости, шестой - со вторым выходом навигационной системы, седьмой - с выходом блока формирования полетного времени.
Вход блока формирования скорости сближения соединен с третьим выходом обзорно-прицельной системы, а выход - с восьмым входом блока формирования упрежденной дальности.
Первый вход блока формирования полетного времени соединен с выходом блока формирования абсолютной начальной скорости, второй - с третьим выходом блока данных о внешней среде, а третий его вход - со вторым выходом блока формирования упрежденной дальности.
Первый вход блока формирования абсолютной начальной скорости соединен со вторым выходом навигационной системы, второй - с задатчиком начальной скорости, третий и четвертый его входы - соответственно с первым и вторым выходами обзорно-прицельной системы.
Первый - второй входы блока формирования угловой скорости соединены с первым - вторым выходами обзорно-прицельной системы.
Выходы блоков формирования углов упреждения Δβ и Δε, блоков поправки на баллистический ветер по горизонтальному каналу и на продольный ветер по вертикальному каналу, блоков поправки на параллакс по горизонтальному и вертикальному каналам, входящих в состав устройства формирования углов упреждения, а также выход блока учета угла места и третий выход навигационной системы соединены с первым - девятым входами блока учета угла крена, первый и второй выходы которого соединены с первыми входами силовых приводов соответственно ГН и ВН.
На фиг.14 представлена структурная схема блока формирования угловой скорости линии визирования g[nΔt].
Для подтверждения технической реализуемости заявляемого способа (и соответствующей системы) ниже приведен пример функционирования системы.
После взятия на сопровождение атакующей воздушной цели типа самолета (или вертолета) из обзорно-прицельной системы в вычислительную систему (ВС) поступают непрерывно сигналы об углах визирования цели β и ε соответственно в двух плоскостях системы координат, связанной с носителем XHYHZH, а также дискретные замеры дальности D. С навигационной системы в ВС поступают также данные о носителе: скорость носителя, углы тангажа, крена и т.д.
Предварительно в ВС введены данные об оружии (баллистический коэффициент, относительная начальная скорость снаряда), а также данные о внешней среде.
Согласно изобретению (п.1) предварительно производят так называемую предпроцессорную обработку сигналов об углах наклона линии визирования соответственно в горизонтальной β(t) и вертикальной ε(t) плоскостях из следующего соотношения
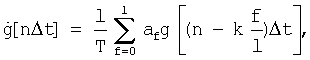
где  ,
,
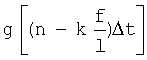 - угол наклона линии визирования в момент времени
- угол наклона линии визирования в момент времени 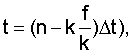
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования,
f - порядковый номер "узловой" точки (укрупненной дискреты),
T - время наблюдения (необходимо так выбирать Т, чтобы на нем укладывалось целое число этих укрупненных дискрет Δt', т.е. должно выполняться условие 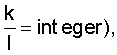
l - порядок приближения воспроизводимой производной угла наклона линии визирования, l=[1, 2...6],
k - количество шагов дискретизации на T, 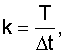
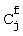 - биномиальные коэффициенты,
- биномиальные коэффициенты,  причем
причем 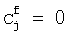 при j>f.
при j>f.
О степени динамичности сигнала формально можно судить по значениям скорости, параметра и высоты пролета цели относительно БМ.
В случае неопределенности условий относительного перемещения цели согласно п.2 изобретения, как отмечалось ранее, дополнительно перед определением угловых поправок предварительно накапливают информацию об углах наклона линии визирования g(t) в виде m+1 точек по каждому каналу, затем аппроксимируют функцию g(t) полиномом m-го порядка, далее определяют ошибки воспроизводимой производной угла наклона линии визирования из соотношений:
- систематическую 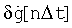 - в соответствии с п.3 формулы изобретения, зависимость (2)
- в соответствии с п.3 формулы изобретения, зависимость (2)
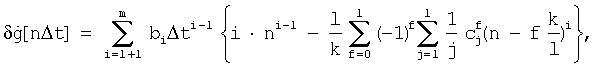
где bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm,
Т - время наблюдения, T должно быть кратно целому числу этих укрупненных дискрет Δt', т.е. должно выполняться условие  ,
,
l - порядок приближения производной,
k - число шагов дискретизации на Т, 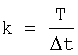 ,
,
f - порядковый номер "узловой" точки (укрупненной дискреты),
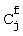 - биномиальные коэффициенты,
- биномиальные коэффициенты,
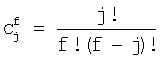 , причем
, причем 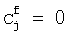 при j>f.
при j>f.
или согласно п.4 формулы изобретения - в виде суммы числового ряда (зависимость (3))
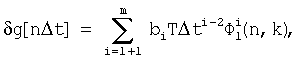
где 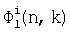 - сумма степенного ряда функций вида
- сумма степенного ряда функций вида
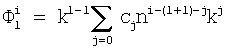 от номера текущего шага n и параметра k,
от номера текущего шага n и параметра k,
cj - предварительно рассчитанные коэффициенты
cj=сj (l,i), i=1,2...m.
(Значения сj, в 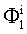 приведены в таблицах. 1 и 2 соответственно для l=1, 2...)
приведены в таблицах. 1 и 2 соответственно для l=1, 2...)
bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm,
Т - время наблюдения,
l - порядок приближения производной (или число учитываемых членов разложения при расчете первой производной),
k - число шагов дискретизации на T, 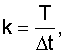
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования,
затем находят случайную ошибку 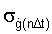 - по зависимости (4), п.5 формулы изобретения
- по зависимости (4), п.5 формулы изобретения
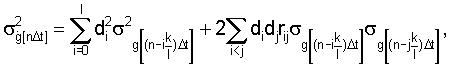
где 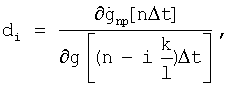
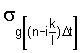 - среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени 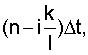
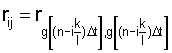 - коэффициент корреляции между
- коэффициент корреляции между 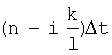 -ым и
-ым и  -ым сечениями функции g[nΔt],
-ым сечениями функции g[nΔt],
или в виде зависимости (5) по п.6 формулы изобретения
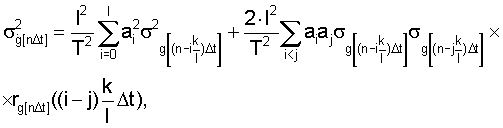
где ai=af - коэффициент при f-ом члене дифференцирующего фильтра,
 - среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонения случайной последовательности g[nΔt] в момент времени 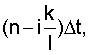
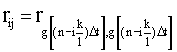 - коэффициент корреляции между
- коэффициент корреляции между  и
и 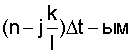 сечениями случайной последовательности g[nΔt].
сечениями случайной последовательности g[nΔt].
Далее устанавливается рациональное соотношение систематической и случайной ошибок из соотношения
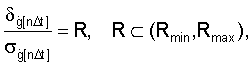
где (Rmin, Rmax) - Диапазон рационального соотношения систематических и случайных ошибок, определяемый из условия обеспечения максимального значения критерия эффективности стрельбы, причем если R<Rmin, то l=l-1, если R>Rmax, то l=l+1, иначе l=l.
Вопросы рационального соотношения ошибок стрельбы различной статистической структуры, обеспечения оптимального коэффициента корреляции достаточно широко представлены в специальной литературе, например /4, 7/.
Определенный таким образом порядок ДФ l используется в блоке формирования угловых скоростей линии визирования (см. п.9 формулы и фиг.14), с выходов которого сигналы поступают на вход ВС.
В блоке формирования угловой скорости в соответствии с зависимостью (1) из накопительного устройства выбираются (l+1) значений входной функции, каждая из которых домножается на соответствующий коэффициент аi (см. формулу (1), п.1, 2), полученные таким образом масштабированные функции складываются в сумматоре СУМ, а полученная сумма (линейная комбинация входных функций) домножается на коэффициент 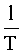 (отношение порядка ДФ 1 к времени наблюдения Т).
(отношение порядка ДФ 1 к времени наблюдения Т).
Комбинация выработанных в ВС поправок (с учетом угла крена) по каждому из каналов поступает на вход силового привода.
Достаточно подробно их вычисление приведено в литературе, в частности в более ранних патентах, например /3/.
Силовые приводы соответственно горизонтального и вертикального наведения, отрабатывая управляющие сигналы с учетом сигнала обратной связи, в каждый момент времени разворачивают стволы ПУ в нужном направлении.
Использование заявляемого способа и реализующей его системы обеспечит по сравнению с существующими следующие преимущества:
- повышение точности стрельбы и отсюда эффективности зенитного огня БМ по высокоскоростным воздушным целям, в особенности в ближней зоне стрельбы;
- снижение габаритно-массовых характеристик и стоимости системы за счет замены аппаратурных (датчиковых) средств математическими (алгоритмическими).
Данный способ определения угловой скорости линии визирования может быть использован как дублирующий и на уже существующих системах, например в информационно-управляющих системах летательных аппаратов, зенитных комплексов.
Источники информации
1. Изделие 1В539. Техническое описание ПБА 3.031.039 ТО Тула, КБП, 1985, стр.12-16.
2. Комплекс вооружения 2К23 боевой машины пехоты БМП-3. Техническое описание и инструкция по эксплуатации. Тула, КБП, 1991, стр.1-10.
3. Патент России № 2172463 (прототип).
4. Вентцель Е.С. Теория вероятностей. Изд. физ.-мат. литературы. - М., 1962, 564 с.
5. Бесекерский В.А., Изранцев В.В. Системы автоматического управления с микроЭВМ. - М.: Наука, 1987, 319 с.
6. В.А.Иванов, А.С.Ющенко Теория дискретных систем автоматического управления. - М.: Наука, 1983, 335 с.
7. Е.П.Калабухова Основы теории эффективности воздушной стрельбы и бомбометания (конспект лекций), ч.1., М., МАИ, 1975.





Изобретение относится к области вооружения и военной техники, в частности к защите боевой машины (БМ) от средств воздушного нападения, например, с помощью пулеметных (пушечных) установок. Техническим результатом является повышение точности и соответственно эффективности стрельбы БМ, в особенности по высокоскоростным, в частности, воздушным целям путем повышения точности определения угловой скорости линии визирования. По первому варианту осуществляют обнаружение и распознавание цели, сопровождение с определением координат и параметров цели, определение угловых поправок, суммирование их соответственно по горизонтальному и вертикальному каналам с учетом угла крена. Перед определением угловых поправок находят угловую скорость линии визирования дифференцированием углов наклона линии визирования соответственно в горизонтальном и вертикальном каналах. По второму варианту осуществляют обнаружение и распознавание цели, сопровождение с определением координат и параметров цели, определение угловых поправок, суммирование их соответственно по горизонтальному и вертикальному каналам с учетом угла крена. При этом перед определением угловых поправок предварительно накапливают информацию об угле наклона линии визирования в виде множества точек по каждому каналу. Затем аппроксимируют функцию, характеризующую линию визирования полиномом. Определяют систематическую и случайную ошибки воспроизводимой производной угла наклона линии визирования, выбирают порядок ее приближения на следующий интервал прогнозирования угловых скоростей, исходя из рационального соотношения систематической и случайной ошибок, и угловую скорость линии визирования соответственно в горизонтальном и вертикальном каналах. 3 н. и 6 з.п. ф-лы, 14 ил, 4 табл.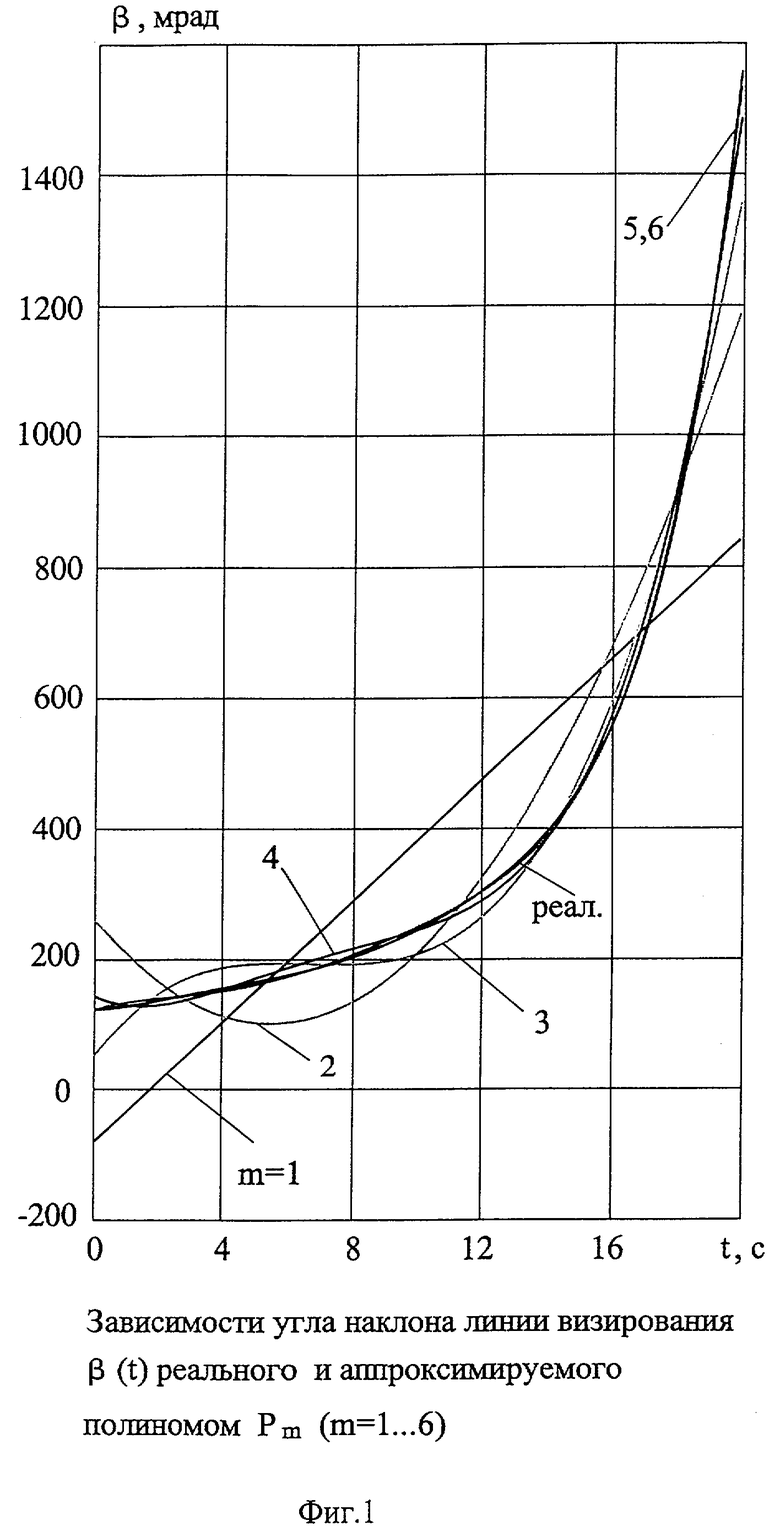
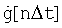 дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах из следующего соотношения:
дифференцированием углов наклона линии визирования g(t) соответственно в горизонтальном и вертикальном каналах из следующего соотношения:
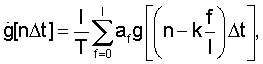
где 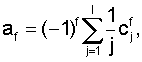
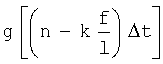 - угол наклона линии визирования в момент времени
- угол наклона линии визирования в момент времени
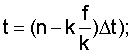
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования - дискрета, 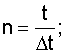
f - порядковый номер "узловой" точки - укрупненной дискреты Δt'
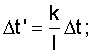
Т - время наблюдения, Т должно быть кратно целому числу укрупненных дискрет Δt', т.е. должно выполняться условие 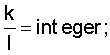
l - порядок приближения воспроизводимой производной угла наклона линии визирования, l=[1, 2...6];
k - количество шагов дискретизации на Т, 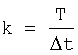
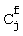 - биномиальные коэффициенты,
- биномиальные коэффициенты, 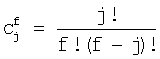 , причем
, причем 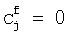
при j>f.
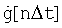 соответственно в горизонтальном и вертикальном каналах определяют дифференцированием углов наклона линии визирования
соответственно в горизонтальном и вертикальном каналах определяют дифференцированием углов наклона линии визирования 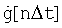 из следующего соотношения
из следующего соотношения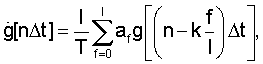
где 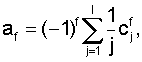
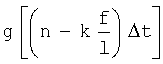 - угол наклона линии визирования в момент времени
- угол наклона линии визирования в момент времени
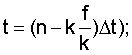
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования, 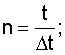
Т - время наблюдения;
l - порядок приближения производной;
k - количество шагов дискретизации на Т, 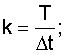
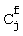 - биномиальные коэффициенты,
- биномиальные коэффициенты, 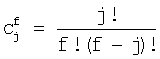 , причем
, причем 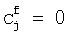
при j>f.
 определяют по зависимости
определяют по зависимости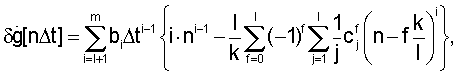
bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm;
Т - время наблюдения, Т должно быть кратно целому числу укрупненных дискрет Δt', т.е. должно выполняться условие

l - порядок приближения производной;
k - число шагов дискретизации на Т, 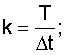
f - порядковый номер "узловой" точки - укрупненной дискреты;
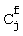 - биномиальные коэффициенты
- биномиальные коэффициенты
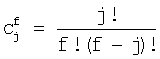 ,
, 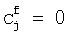 , при j>f.
, при j>f.
 определяют в виде суммы числового ряда
определяют в виде суммы числового ряда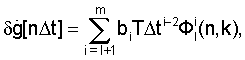
где 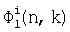 - сумма степенного ряда функций вида;
- сумма степенного ряда функций вида;
 от номера текущего шага n и параметра k;
от номера текущего шага n и параметра k;
cj - предварительно рассчитанные коэффициенты;
cj=cj(l,i), i=1, ..., m;
bi - коэффициенты аппроксимации функции g[nΔt] степенным полиномом Рm;
Т - время наблюдения;
l - порядок приближения производной;
k - число шагов дискретизации на T, 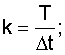
Δt - интервал времени между моментами поступления информации об углах наклона линии визирования, 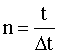 .
.
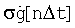 определяют в виде
определяют в виде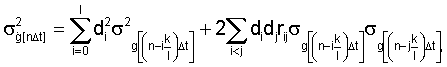
где  ,
, 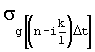 - среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени 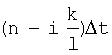 ,
,
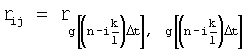 - коэффициент корреляции между
- коэффициент корреляции между  и
и 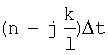 -ым сечениями случайной последовательности g[nΔt].
-ым сечениями случайной последовательности g[nΔt].
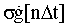 определяют в виде
определяют в виде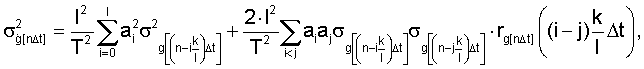
где ai=аf - коэффициент при f-ом члене дифференцирующего фильтра,
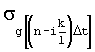 - среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени
- среднеквадратическое отклонение случайной последовательности g[nΔt] в момент времени 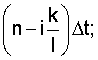
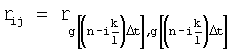 - коэффициент корреляции между
- коэффициент корреляции между  и
и  -ым сечениями случайной последовательности g[nΔt].
-ым сечениями случайной последовательности g[nΔt].
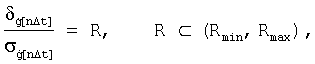
где (Rmin, Rmax) - диапазон рационального соотношения систематических и случайных ошибок, определяемый из условия обеспечения максимального значения критерия эффективности стрельбы, причем если R<Rmin, то l=l-1, если R>Rmax, то l=l+1, иначе l=l.
| СПОСОБ СТРЕЛЬБЫ БОЕВОЙ МАШИНЫ ПО ЦЕЛИ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1999 |
|
RU2172463C2 |
| СПОСОБ ЗАЩИТЫ БОЕВОЙ МАШИНЫ ОТ СРЕДСТВ ВОЗДУШНОГО НАПАДЕНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2087832C1 |
| АЛМАЗНЫЙ ИНСТРУМЕНТ ДЛЯ ПРАВКИ ШЛИФОВАЛЬНЫХ КРУГОВ | 2007 |
|
RU2354532C1 |
| 0 |
|
SU159392A1 |
Авторы
Даты
2006-12-27—Публикация
2005-05-13—Подача