Изобретение относится к измерительной технике и может быть использовано в акустике и радиотехнике для формирования с повышенной разрешающей способностью комплексных изображений углового спектра и определения азимутального и угломестного направлений на источники кратковременных когерентных волновых процессов различной природы (например, процессов распространения акустических, сейсмических и электромагнитных волн).
Достижение теоретически предельной точности формирования изображений и определения пространственных координат в условиях многолучевого распространения волн ограничивается существенной априорной неопределенностью относительно параметров среды распространения и несовершенством известных способов обработки сигналов, в настоящее время не решающих эффективно проблему пеленгования многолучевых сигналов.
Известен способ пеленгования многолучевых сигналов [1], включающий преобразование входных сигналов, принятых отдельными элементами антенной решетки, в цифровые данные, формирование оценочной ковариационной матрицы цифровых данных, разложение сформированной матрицы по ее собственным векторам, преобразование полученного разложения согласно одному из класса сверхразрешающих алгоритмов, основанных на анализе собственных значений, для определения направлений на источники, сигналы которых содержатся в цифровых данных.
Описанный способ теряет свою эффективность при решении задачи пеленгования когерентных сигналов близко расположенных источников в связи с тем, что он базируется на классе сверхразрешающих алгоритмов, основанных на анализе собственных значений пространственных корреляционных матриц и в основу которых закладываются предположения о некоррелированности принимаемых сигналов. К данному классу относятся алгоритмы классификации MUSIC (multiple signal classification), EV (eigenvector) [1]. Другим недостатком данного способа является сложность однозначного разделения собственных значений корреляционной матрицы на сигнальные и шумовые, что приводит к неоднозначности результатов и ошибкам пеленгования.
Известен способ пеленгования многолучевых сигналов [2], свободный от этих недостатков и принятый за прототип. Согласно этому способу:
1. Принимают многолучевой сигнал многоэлементной антенной решеткой.
2. Синхронно преобразуют ансамбль принятых сигналов xn(t), зависящих от времени t и номера n антенного элемента, в цифровые сигналы xn(ν), где ν - номер временного отсчета сигнала.
3. Преобразуют сигналы xn(ν) в сигнал комплексного амплитудно-фазового распределения (АФР) 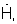 описывающий распределение амплитуд и фаз на элементах решетки. Запоминают сигнал
описывающий распределение амплитуд и фаз на элементах решетки. Запоминают сигнал 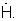
4. Преобразуют сигнал АФР 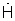 в сигнал комплексного углового спектра
в сигнал комплексного углового спектра 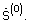 Для этого используют алгоритм псевдообращения
Для этого используют алгоритм псевдообращения 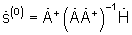 или алгоритм классического формирователя луча
или алгоритм классического формирователя луча 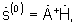 где
где 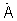 - предварительно сформированный и запомненный сигнал комплексной фазирующей функции, зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника,
- предварительно сформированный и запомненный сигнал комплексной фазирующей функции, зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника,  - матрица, эрмитово сопряженная с
- матрица, эрмитово сопряженная с 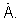
5. Используя сигнал комплексного углового спектра 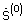 в качестве начального приближения, итерационно формируют зависящие от предыдущего решения взвешивающий сигнал
в качестве начального приближения, итерационно формируют зависящие от предыдущего решения взвешивающий сигнал  р<1 - показатель степени регуляризирующего функционала,
р<1 - показатель степени регуляризирующего функционала,  - m-й элемент вектора
- m-й элемент вектора 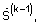 ε - малое число, k=1, 2,... - номер итерации, и сигнал очередного приближения углового спектра
ε - малое число, k=1, 2,... - номер итерации, и сигнал очередного приближения углового спектра  где γ - параметр регуляризации, до тех пор, пока энергия разности текущего и запомненного предыдущего угловых спектров не достигнет заданного малого значения.
где γ - параметр регуляризации, до тех пор, пока энергия разности текущего и запомненного предыдущего угловых спектров не достигнет заданного малого значения.
6. Вычисляют угловой спектр мощности 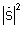 многолучевого сигнала, по локальным максимумам которого определяют азимут α и угол места β каждого луча приходящего сигнала.
многолучевого сигнала, по локальным максимумам которого определяют азимут α и угол места β каждого луча приходящего сигнала.
Способ-прототип относится к классу итерационных способов (способов последовательных приближений) синтеза изображений с неквадратичной регуляризацией (в силу условия р<1), в которых по известному приближению ищется следующее, более точное приближение. При этом на текущей итерации производится нелинейная фильтрация сигнала измеренного АФР 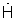 фильтром, характеристика
фильтром, характеристика  которого зависит от результата, полученного на предыдущей итерации
которого зависит от результата, полученного на предыдущей итерации 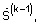 значений показателя степени регуляризирующего функционала р и параметра регуляризации γ.
значений показателя степени регуляризирующего функционала р и параметра регуляризации γ.
Недостатком способа-прототипа является наличие ложных составляющих (продуктов нелинейного преобразования сигнала) в синтезированном угловом спектре при наиболее типичных для практики входных отношениях сигнал/шум (не превышающих 30 дБ), что снижает точность и достоверность пеленгования, так как приводит к возникновению аномально больших ошибок при пеленговании многолучевых сигналов, с одной стороны, и отсутствием у данного способа операций их устранения, с другой.
Повышение точности и достоверности пеленгования при использовании способа-прототипа можно обеспечить несколькими известными путями [3]:
1. Когерентным усреднением множества синтезированных комплексных угловых спектров, полученных по множеству статистически независимых реализации входных данных.
2. Когерентным усреднением множества синтезированных комплексных угловых спектров, полученных по одной реализации входных данных, каждый раз специально искажаемой путем введения искусственного дополнительного шума или путем простого отбрасывания некоторой части измерений.
Первый путь может привести к размыванию ложных составляющих в синтезированном распределении углового спектра. Однако этот путь имеет ограниченное применение, так как требует множества статистически независимых реализации входных данных, что не реализуемо при пеленговании кратковременных сигналов естественного или искусственного происхождения, характеризующихся повышенной временной скрытностью.
Второй путь позволяет формировать угловой спектр пеленгуемого многолучевого сигнала с меньшим числом ложных составляющих по одной реализации входных данных, что существенно при пеленговании кратковременных сигналов. Это обусловлено тем, что ложные детали спектра более подвержены влиянию шума, следовательно, когерентное усреднение независимо искаженных спектров может приводить к размыванию ложных максимумов. Однако этот путь также имеет ограниченное применение, так как требует высоких входных отношений сигнал/шум.
Техническим результатом изобретения является повышение эффективности (точности и достоверности) пеленгования источников кратковременных сигналов в условиях многолучевого распространения волн различной природы.
Технический результат достигается тем, что в способе пеленгования многолучевых сигналов, включающем прием многолучевого сигнала многоэлементной антенной решеткой, синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера антенного элемента, в цифровые сигналы, преобразование цифровых сигналов в сигнал комплексного амплитудно-фазового распределения (АФР), описывающий распределение амплитуд и фаз на элементах решетки, и его запоминание, преобразование сигнала АФР в сигнал комплексного углового спектра, использование сигнала комплексного углового спектра в качестве начального приближения, согласно изобретению из сигнала начального приближения формируют множества сигналов нелинейно регуляризованных комплексных угловых спектров, идентифицируют множество сигналов регуляризованных спектров с минимальной дисперсией, усредняют сигналы регуляризованных спектров идентифицированного множества, находят их усредненный спектр мощности, по максимумам которого определяют амплитуду, азимут и угол места каждого луча принятого многолучевого сигнала.
Возможны частные случаи осуществления способа:
1. Формирование отдельного z-го, z=1,...,Z, множества сигналов, включающего Q сигналов нелинейно регуляризованных комплексных угловых спектров, осуществляют синтезом регуляризованных спектров при фиксированном значении показателя степени регуляризирующего функционала р и отличающихся значениях параметра регуляризации γ(q), q=1,...,Q - номер синтезируемого спектра.
Это обеспечивает возможность последующего выбора множества регуляризованных угловых спектров с минимальной дисперсией.
2. Синтез сигнала отдельного q-го нелинейно регуляризованного комплексного углового спектра осуществляют путем итерационного формирования зависящих от предыдущего решения взвешивающего сигнала
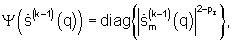 р<1,
р<1, 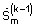 - m-й элемент вектора спектра
- m-й элемент вектора спектра  m=1, М - номер возможного направления прихода принимаемого сигнала, k=1, 2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра
m=1, М - номер возможного направления прихода принимаемого сигнала, k=1, 2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра 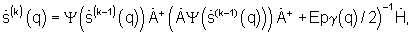 где
где 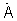 - идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра,
- идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра,  - сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
- сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
Это повышает эффективность разделения лучей многолучевых сигналов.
3. Идентификацию отдельного z-го множества сигналов регуляризованных угловых спектров как множества с минимальной дисперсией осуществляют путем когерентного усреднения сигналов комплексных угловых спектров каждого z-го множества и выбором множества с минимальной усредненной по пространству дисперсией угловых спектров.
Это обеспечивает оптимальный выбор параметров регуляризирующего функционала.
4. Сигнал усредненного углового спектра мощности получают путем усреднения сигналов модулей регуляризованных угловых спектров из множества с минимальной дисперсией.
Это повышает точность оценки углов прихода и амплитуды каждого луча принятого многолучевого сигнала.
5. Формирование множеств сигналов нелинейно регуляризованных комплексных угловых спектров осуществляют последовательно или параллельно во времени.
Это позволяет оптимизировать процесс пеленгования по быстродействию.
Операции способа поясняются следующими чертежами:
Фиг.1. Структурная схема устройства пеленгования многолучевых сигналов.
Фиг.2. Результаты моделирования процесса синтеза углового спектра мощности и определения параметров многолучевого сигнала:
а) множество регуляризованных азимутальных спектров мощности, сформированных при неоптимальном значении показателя степени регуляризирующего функционала р=p1;
б) множество регуляризованных азимутальных спектров мощности, сформированных при оптимальном значении показателя р=рopt,
в) средний спектр мощности, полученный из множества регуляризованных при значении р=рopt азимутальных спектров мощности с минимальной дисперсией.
Способ пеленгования многолучевых сигналов осуществляется следующим образом:
1. Принимают многолучевой сигнал источника акустического или электромагнитного излучения антенной решеткой из N элементов и формируют ансамбль сигналов xn(t), зависящих от времени t и номера антенного элемента n=1,..., N.
2. Синхронно преобразуют ансамбль принятых сигналов xn(t) в цифровые сигналы хn(ν), где ν - номер временного отсчета сигнала.
3. Преобразуют цифровые сигналы xn(ν) в сигнал комплексного амплитудно-фазового распределения (АФР) 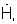 описывающий амплитуды и фазы сигналов, принятых элементами решетки. Запоминают сигнал АФР
описывающий амплитуды и фазы сигналов, принятых элементами решетки. Запоминают сигнал АФР 
Формирование сигнала АФР возможно применением ряда известных алгоритмов цифровой обработки сигналов во временной и частотной областях [4].
При использовании корреляционно-интерферометрического алгоритма в частотной области [2], обладающего рядом преимуществ, формируют сигналы комплексных спектральных плотностей  цифровых сигналов хn(ν), где Ft{...} - оператор дискретного Фурье-преобразования по времени,
цифровых сигналов хn(ν), где Ft{...} - оператор дискретного Фурье-преобразования по времени, 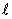 - номер частотной дискреты, 1≤
- номер частотной дискреты, 1≤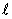 ≤L. После этого перемножением и усреднением сформированных спектральных плотностей
≤L. После этого перемножением и усреднением сформированных спектральных плотностей 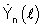 и комплексно сопряженной спектральной плотности
и комплексно сопряженной спектральной плотности 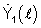 сигнала, измеренного на опорной антенне решетки с номером n=1, формируют АФР принятого сигнала в виде комплексного вектора
сигнала, измеренного на опорной антенне решетки с номером n=1, формируют АФР принятого сигнала в виде комплексного вектора 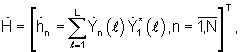 где (...)* - означает комплексное сопряжение.
где (...)* - означает комплексное сопряжение.
4. Генерируют и запоминают матрицу идеального двумерного сигнала 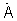 комплексной фазирующей функции размером N×M, зависящую от заданной частоты приема и описывающую возможные направления прихода сигнала от каждого потенциального источника, где М - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту αm и углу места βm, m=
комплексной фазирующей функции размером N×M, зависящую от заданной частоты приема и описывающую возможные направления прихода сигнала от каждого потенциального источника, где М - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту αm и углу места βm, m=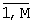 - номер направления. Отдельный элемент матрицы двумерного сигнала
- номер направления. Отдельный элемент матрицы двумерного сигнала 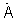 описывается соотношением
описывается соотношением  где rn, zn, αn - цилиндрические координаты антенных элементов решетки, λ - длина волны, соответствующая заданной частоте приема. Полагая в последнем соотношении rn=r, zn=0, получаем частный вид идеального сигнала, являющегося фазирующей функцией или вектором наведения плоской кольцевой антенной решетки.
где rn, zn, αn - цилиндрические координаты антенных элементов решетки, λ - длина волны, соответствующая заданной частоте приема. Полагая в последнем соотношении rn=r, zn=0, получаем частный вид идеального сигнала, являющегося фазирующей функцией или вектором наведения плоской кольцевой антенной решетки.
5. Используя сигнал АФР 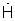 и сигнал фазирующей функции
и сигнал фазирующей функции 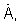 синтезируют начальное приближение углового спектра сигнала
синтезируют начальное приближение углового спектра сигнала 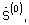 которое запоминают для использования на очередной итерации.
которое запоминают для использования на очередной итерации.
Для синтеза начального приближения углового спектра сигнала 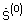 могут быть использованы различные алгоритмы. Рассмотрим алгоритм псевдообращения, который предусматривает вычисления по следующей формуле:
могут быть использованы различные алгоритмы. Рассмотрим алгоритм псевдообращения, который предусматривает вычисления по следующей формуле: 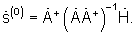
При этом выполняют следующие действия:
- умножают идеальный двумерный сигнал 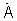 фазирующей функции на эрмитово сопряженный сигнал
фазирующей функции на эрмитово сопряженный сигнал 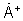 и получают двумерный сигнал
и получают двумерный сигнал 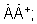
- обращая матрицу полученного двумерного сигнала 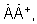 формируют взвешивающий сигнал АФР
формируют взвешивающий сигнал АФР  размерностью N×N;
размерностью N×N;
- умножая восстановленный вектор АФР 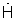 на взвешивающий сигнал АФР
на взвешивающий сигнал АФР 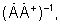 получают вектор взвешенного АФР
получают вектор взвешенного АФР 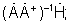
- умножая вектор взвешенного АФР 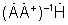 на сигнал фазирующей функции
на сигнал фазирующей функции 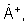 получают и запоминают
получают и запоминают 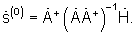
Возможно также применение классического алгоритма формирования луча 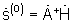 [2, 4].
[2, 4].
6. Формируют последовательно или параллельно во времени Z множеств сигналов нелинейно регуляризованных комплексных угловых спектров принятого многолучевого сигнала, используя сигнал 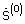 в качестве начального приближения.
в качестве начального приближения.
При этом формирование z-го, z=1,..., Z, множества сигналов, включающего Q сигналов нелинейно регуляризованных комплексных угловых спектров, осуществляют синтезом регуляризованных спектров при фиксированном значении показателя р и всех значениях параметра γ(q), q=1,..., Q - номер синтезируемого спектра. Другими словами, для каждого значения р формируют свой набор из Q угловых спектров.
Кроме того, синтез сигнала отдельного q-го нелинейно регуляризованного комплексного углового спектра z-го множества осуществляют путем итерационного формирования зависящих от предыдущего решения взвешивающего сигнала
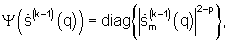 р<1 - показатель степени регуляризирующего функционала,
р<1 - показатель степени регуляризирующего функционала, 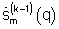 - m-й элемент вектора спектра
- m-й элемент вектора спектра 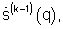 m=1, M - номер возможного направления прихода принимаемого сигнала, k=1, 2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра
m=1, M - номер возможного направления прихода принимаемого сигнала, k=1, 2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра 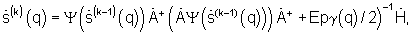 где
где 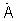 - идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра,
- идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра, 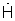 - сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
- сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
При этом в процессе синтеза сигнала каждого q-го углового спектра выполняют следующие действия:
- вычисляют сигнал углового спектра мощности 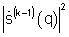 комплексного углового спектра сигнала
комплексного углового спектра сигнала  k≥1, полученного на предыдущей итерации. При вычислении сигнала углового спектра мощности на первой итерации используется хранящийся в памяти сигнал начального приближения углового спектра, то есть
k≥1, полученного на предыдущей итерации. При вычислении сигнала углового спектра мощности на первой итерации используется хранящийся в памяти сигнал начального приближения углового спектра, то есть  при k=1, на второй итерации используется хранящийся в памяти сигнал приближения, полученного на первой итерации, то есть
при k=1, на второй итерации используется хранящийся в памяти сигнал приближения, полученного на первой итерации, то есть 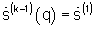 при k=2 и т.д.;
при k=2 и т.д.;
- возводя модуль полученного приближения углового спектра 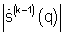 в степень (2 -р), формируют зависящий от предыдущего решения двумерный взвешивающий сигнал размером М×М в форме диагональной матрицы
в степень (2 -р), формируют зависящий от предыдущего решения двумерный взвешивающий сигнал размером М×М в форме диагональной матрицы  где р<1,
где р<1, 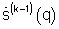 - m-й элемент вектора
- m-й элемент вектора 
Таким образом, на первой (k=1) и последующих {k=2, 3,...) итерациях взвешивающий сигнал 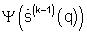 выражается через сигнал углового спектра
выражается через сигнал углового спектра 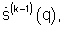 полученный на предыдущей итерации;
полученный на предыдущей итерации;
- используя полученный взвешивающий сигнал 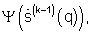 выбранное из конечного интервала значений γmin<γ(d)<γmax значение параметра регуляризации γ(d) и запомненные сигналы
выбранное из конечного интервала значений γmin<γ(d)<γmax значение параметра регуляризации γ(d) и запомненные сигналы  и
и 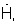 формируют взвешенный сигнал фазирующей функции
формируют взвешенный сигнал фазирующей функции 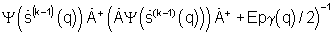 и зависящий от предыдущего решения текущий угловой спектр сигнала
и зависящий от предыдущего решения текущий угловой спектр сигнала 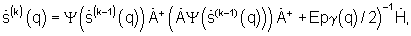 который запоминают для использования на очередной итерации;
который запоминают для использования на очередной итерации;
- сравнивают энергию разности сигналов угловых спектров 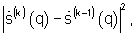 полученных на текущей и предыдущей итерации, с порогом δ. Значение порога выбирается, например, из условия
полученных на текущей и предыдущей итерации, с порогом δ. Значение порога выбирается, например, из условия 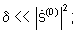
- при невыполнении условия 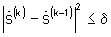 инициализируется очередная итерация синтеза углового спектра при выбранном значении параметра регуляризации γ(q), на которой повторяются операции формирования сигналов
инициализируется очередная итерация синтеза углового спектра при выбранном значении параметра регуляризации γ(q), на которой повторяются операции формирования сигналов  и
и 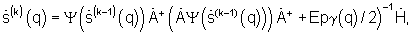 запоминания
запоминания 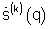 и сравнения энергии разности сигналов угловых спектров
и сравнения энергии разности сигналов угловых спектров 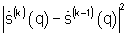 с порогом δ;
с порогом δ;
- при выполнении условия 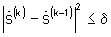 запомненное значение
запомненное значение 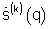 выбирается в качестве результата синтеза q-го углового спектра z-го множества
выбирается в качестве результата синтеза q-го углового спектра z-го множества 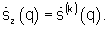
Отметим, что предложенный способ в отличие от прототипа обеспечивает более высокую вычислительную эффективность формирования сигнала текущего углового спектра 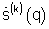 за счет сокращения вычислительных операций благодаря применению формулы
за счет сокращения вычислительных операций благодаря применению формулы 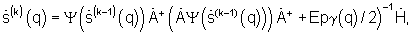 вместо формулы, приведенной в пункте 5 на странице 3 данного описания. При этом достигается многократное снижение размерности (N×N вместо М×М) обрабатываемых сигналов и соответствующее сокращение требуемого числа вычислительных операций. Так, при N=11 и шаге по азимуту, равном 0,5 градуса, получаем [M/6,6N)3=(720×1/(6,6×11))3≈103 раз для случая синтеза азимутального углового спектра и в (720×180/(6,6×11))3≈5,5×109 раз для случая синтеза углового спектра с тем же шагом по азимуту и углу места.
вместо формулы, приведенной в пункте 5 на странице 3 данного описания. При этом достигается многократное снижение размерности (N×N вместо М×М) обрабатываемых сигналов и соответствующее сокращение требуемого числа вычислительных операций. Так, при N=11 и шаге по азимуту, равном 0,5 градуса, получаем [M/6,6N)3=(720×1/(6,6×11))3≈103 раз для случая синтеза азимутального углового спектра и в (720×180/(6,6×11))3≈5,5×109 раз для случая синтеза углового спектра с тем же шагом по азимуту и углу места.
Таким образом, на данном этапе формируют Z множеств сигналов комплексных угловых спектров  Каждое z-e множество сигналов, включающее Q сформированных при различных значениях параметра регуляризации γ(q), q=1,..., Q, сигналов комплексных угловых спектров
Каждое z-e множество сигналов, включающее Q сформированных при различных значениях параметра регуляризации γ(q), q=1,..., Q, сигналов комплексных угловых спектров 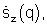 получают при фиксированном значении параметра р. Значения параметра р изменяются в интервале [ 10-5,10-1].
получают при фиксированном значении параметра р. Значения параметра р изменяются в интервале [ 10-5,10-1].
На фиг.2, а и б представлены примеры двух множеств сигналов угловых спектров мощности, сформированных при двух значениях параметра р из одной реализации принятого сигнала, содержащего два луча с равными амплитудами и направлениями прихода по азимуту α1 и α2.
Из фиг.2, а следует, что каждый угловой спектр мощности 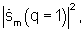
 первого множества, сформированного при неоптимальном значении параметра p=p1, содержит два максимума, соответствующие истинным направлениям прихода лучей принятого сигала (азимуты α1 и α2), и два ложных максимума. С другой стороны, из фиг.2, б следует, что каждый угловой спектр мощности второго множества, полученного при оптимальном значении параметра р=рopt, содержит только максимумы, соответствующие истинным азимутальным углам прихода сигналов первого α1 и второго α2 луча.
первого множества, сформированного при неоптимальном значении параметра p=p1, содержит два максимума, соответствующие истинным направлениям прихода лучей принятого сигала (азимуты α1 и α2), и два ложных максимума. С другой стороны, из фиг.2, б следует, что каждый угловой спектр мощности второго множества, полученного при оптимальном значении параметра р=рopt, содержит только максимумы, соответствующие истинным азимутальным углам прихода сигналов первого α1 и второго α2 луча.
Задачей следующего этапа обработки является идентификация и выбор множества сигналов регуляризованных угловых спектров с минимальной дисперсией, что необходимо для накопления полезных и снижения числа и уровня ложных составляющих в формируемом угловом спектре.
7. Идентифицируют отдельное z-e множество сигналов регуляризованных угловых спектров как множество с минимальной дисперсией путем когерентного усреднения сигналов комплексных угловых спектров каждого z-го множества  и выбора множества с минимальной усредненной по пространству дисперсией угловых спектров
и выбора множества с минимальной усредненной по пространству дисперсией угловых спектров 
 - элементы вектора
- элементы вектора 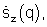
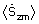 элементы вектора
элементы вектора 
8. Получают сигнал усредненного углового спектра мощности  путем усреднения сигналов квадратов модулей регуляризованных угловых спектров из множества с минимальной дисперсией.
путем усреднения сигналов квадратов модулей регуляризованных угловых спектров из множества с минимальной дисперсией.
9. По локальным максимумам усредненного спектра мощности 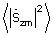 определяют амплитуду, азимут α и угол места β каждого луча принятого многолучевого сигнала.
определяют амплитуду, азимут α и угол места β каждого луча принятого многолучевого сигнала.
На фиг.2, в приведен усредненный азимутальный спектр мощности  полученный усреднением сигналов квадратов модулей регуляризованных азимутальных спектров множества с минимальной дисперсией, представленного на фиг.2, б. Из фиг.2, б следует, что множество угловых спектров, полученных при р=рopt, обладает минимальной дисперсией, так как соответствующие пики отдельных спектров имеют одинаковые (как у исходного сигнала) амплитуды и концентрируются на одинаковых азимутах. Из фиг.2, в следует, что усредненный азимутальный спектр мощности также содержит два равных по уровню пика, азимуты α1 и α2 которых соответствуют параметрам исходного двухлучевого сигнала.
полученный усреднением сигналов квадратов модулей регуляризованных азимутальных спектров множества с минимальной дисперсией, представленного на фиг.2, б. Из фиг.2, б следует, что множество угловых спектров, полученных при р=рopt, обладает минимальной дисперсией, так как соответствующие пики отдельных спектров имеют одинаковые (как у исходного сигнала) амплитуды и концентрируются на одинаковых азимутах. Из фиг.2, в следует, что усредненный азимутальный спектр мощности также содержит два равных по уровню пика, азимуты α1 и α2 которых соответствуют параметрам исходного двухлучевого сигнала.
10. Полученные двумерные пеленги (α, β) и амплитуда выделенных лучей отображаются на картографическом фоне, чем обеспечивается повышение информативности пеленгования.
Из приведенного описания следует, что операции формирования множества сигналов нелинейно регуляризованных комплексных угловых спектров принятого многолучевого сигнала могут выполняться как последовательно, так и параллельно во времени. Последнее означает, что предложенный способ может быть реализован как последовательными, так и параллельными устройствами обработки сигналов. При параллельной обработке скорость получения совокупности сигналов нелинейно регуляризованных комплексных угловых спектров повышается в Q×Z раз. Это повышение может быть существенным, если учесть возможные значения величин Q≈300 и Z≈104.
Рассмотрим работу устройства параллельной обработки, реализующего предложенный способ, на примере пеленгования многолучевых сигналов источников электромагнитных волн.
Устройство, реализующее предложенный способ, содержит последовательно соединенные N-элементную антенную решетку 1, N-канальный преобразователь частоты 2, N-канальный аналого-цифровой преобразователь (АЦП) 3, формирователь амплитудно-фазового распределения (АФР) 4, вычислитель начального приближения углового спектра 5, формирователь регуляризованных спектров 6, блок идентификации и усреднения 7 и блок измерения параметров лучей и отображения 8. В свою очередь, формирователь АФР 4 содержит N идентичных вычислителей, входы которых параллельно подключены к выходу АЦП 3, а выходы параллельно соединены с входом вычислителя 5. Кроме того, формирователь регуляризованных спектров 6 содержит Z идентичных блоков формирования 6(1),...,6(z),...,6(Z), каждый из которых, в свою очередь, содержит Q идентичных модулей формирования 6{z,1),...,6(z,q),...,6(z,Q), входы которых параллельно подключены к выходу вычислителя 5, а выходы параллельно соединены с входом блока идентификации и усреднения 7.
Антенная решетка может быть произвольной пространственной конфигурации: плоской прямоугольной, плоской кольцевой или объемной, в частности конформной.
Преобразователь частоты 2 выполнен с общим гетеродином. Общий гетеродин обеспечивает многоканальный когерентный прием сигналов, что является основным условием интерферометрической (топографической) регистрации комплексных сигналов передатчиков. Если разрядность и быстродействие АЦП достаточны для непосредственного аналого-цифрового преобразования входных сигналов, как, например, при синтезе углового спектра в KB диапазоне и в акустике, то вместо преобразователя 2 могут использоваться частотно-избирательный полосовой фильтр и усилитель. Другими словами, аналоговая часть устройства, реализующего предлагаемый способ, может быть построена по принципу прямого усиления.
Кроме этого, преобразователь 2 обеспечивает подключение опорной антенны (например, n=1) вместо всех антенн решетки для периодической калибровки каналов по внешнему источнику сигнала с целью устранения их амплитудно-фазовой неидентичности. Возможна калибровка по внутреннему источнику сигнала. При этом может быть использован генератор шума, выход которого также может подключаться вместо всех антенн для периодической калибровки каналов.
Каждый из модулей 6(z,1),...,6(z,q),...,6(z,Q), а также блок идентификации 7 могут быть реализованы в однопроцессорном и многопроцессорном вариантах.
Многопроцессорный вариант реализации каждого модуля 6(z,q) ускорит формирование сигнала углового спектра 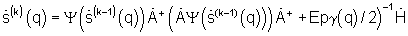 в N раз.
в N раз.
Работает устройство, реализующее способ пеленгования многолучевых сигналов, следующим образом.
Многочастотные временные сигналы xn(t) с выхода антенной системы 1 от антенн с номерами n=1...N, входящих в решетку, поступают на входы преобразователя 2 и когерентно переносятся на более низкую частоту.
Сформированный в преобразователе 2 ансамбль сигналов xn(t) синхронно преобразуется с помощью АЦП 3 в ансамбль цифровых сигналов xn(z). Цифровые сигналы xn(z) синхронно регистрируются в формирователе АФР 4.
В формирователе 4 из цифровых сигналов xn(z) формируются сигналы комплексных спектральных плотностей 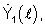 а также формируется и запоминается АФР принятого сигнала в виде комплексного вектора
а также формируется и запоминается АФР принятого сигнала в виде комплексного вектора 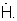
В вычислителе 5 с использованием сигнала АФР 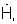 поступающего из формирователя 4, и предварительно сформированной с учетом требуемой частоты приема фазирующей функции
поступающего из формирователя 4, и предварительно сформированной с учетом требуемой частоты приема фазирующей функции  синтезируется и запоминается начальное приближение комплексного углового спектра сигнала
синтезируется и запоминается начальное приближение комплексного углового спектра сигнала 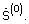 Полученный в вычислителе 5 сигнал
Полученный в вычислителе 5 сигнал  начального приближения транслируется в вычислитель 6.
начального приближения транслируется в вычислитель 6.
В каждом блоке 6(1),...,6(z),...,6(Z) формирователя 6 при фиксированном значении показателя р=рz параллельно находятся Q сигналов нелинейно регуляризованных комплексных угловых спектров z-го множества 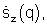 q=1,...,Q, которые поступают в блок 7.
q=1,...,Q, которые поступают в блок 7.
В блоке 7 выполняются следующие действия:
- когерентно усредняются сигналы комплексных угловых спектров 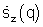 для получения сигнала среднего значения спектра
для получения сигнала среднего значения спектра 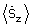 z-го множества;
z-го множества;
- определяется усредненная по пространству дисперсия угловых спектров σ2 z z-го множества;
- выбирается z-e множество сигналов комплексных угловых спектров 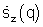 с минимальной усредненной по пространству дисперсией угловых спектров σ2 z;
с минимальной усредненной по пространству дисперсией угловых спектров σ2 z;
- усредняются сигналы квадратов модулей регуляризованных угловых спектров из множества с минимальной дисперсией для определения сигнала усредненного углового спектра мощности 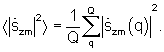
Полученный усредненный угловой спектр мощности  поступает в блок измерения и отображения 8.
поступает в блок измерения и отображения 8.
В блоке 8 по локальным максимумам усредненного спектра мощности  определяются амплитуда, азимут α и угол места β каждого луча принятого многолучевого сигнала, которые для повышения информативности пеленгования отображаются на картографическом фоне.
определяются амплитуда, азимут α и угол места β каждого луча принятого многолучевого сигнала, которые для повышения информативности пеленгования отображаются на картографическом фоне.
Таким образом, за счет дополнительной информации, получаемой из одной реализации входных данных, благодаря введению операций:
- формирования множества сигналов нелинейно регуляризованных комплексных угловых спектров;
- подгонки параметров регуляризирующего функционала с целью минимизации дисперсии сигналов регуляризованных угловых спектров;
- идентификации множества сигналов регуляризованных угловых спектров с минимальной дисперсией;
- когерентного усреднения сигналов регуляризованных угловых спектров с минимальной дисперсией,
минимизирующих число и уровень ложных спектральных составляющих в формируемом угловом спектре и, как следствие, значительно повышающих эффективность (точность и достоверность) пеленгования источников кратковременных сигналов в условиях многолучевого распространения волн различной природы, удается решить поставленную задачу с достижением технического результата.
Источники информации:
1. US, патент, № 6567034 В1, кл. G01S 7/36; G01S 13/00; G01S 5/02, 2003 г.
2. Шевченко В.Н. Оценивание углового положения источников когерентных сигналов на основе методов регуляризации // Радиотехника. - 2003. - №9. - С.3-10.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПЕЛЕНГОВАНИЯ С ПОВЫШЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТЬЮ | 2004 |
|
RU2285938C2 |
| СПОСОБ ПОЛЯРИЗАЦИОННО-НЕЗАВИСИМОГО ПЕЛЕНГОВАНИЯ МНОГОЛУЧЕВЫХ РАДИОСИГНАЛОВ | 2010 |
|
RU2431862C1 |
| СПОСОБ МНОГОСИГНАЛЬНОЙ ПЕЛЕНГАЦИИ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2008 |
|
RU2382379C2 |
| СПОСОБ ПРОСТРАНСТВЕННОЙ ПОЛЯРИЗАЦИОННО-ЧУВСТВИТЕЛЬНОЙ ЛОКАЛИЗАЦИИ МНОГОЛУЧЕВЫХ РАДИОСИГНАЛОВ | 2008 |
|
RU2385467C1 |
| СПОСОБ ПЕЛЕНГОВАНИЯ С ПОВЫШЕННОЙ ЭФФЕКТИВНОСТЬЮ | 2008 |
|
RU2381519C2 |
| СПОСОБ КОМПЬЮТЕРНО-ИНТЕРФЕРОМЕТРИЧЕСКОГО ОБНАРУЖЕНИЯ-ПЕЛЕНГОВАНИЯ СИГНАЛОВ С РАСШИРЕННЫМ СПЕКТРОМ | 2005 |
|
RU2291456C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГАЦИОННОЙ ПАНОРАМЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2012 |
|
RU2528177C2 |
| СПОСОБ КОМПЬЮТЕРНО-ИНТЕРФЕРОМЕТРИЧЕСКОГО ОБНАРУЖЕНИЯ-ПЕЛЕНГОВАНИЯ РАДИОСИГНАЛОВ С РАСШИРЕННЫМ СПЕКТРОМ | 2011 |
|
RU2470315C1 |
| СПОСОБ ПОЛЯРИЗАЦИОННО-ЧУВСТВИТЕЛЬНОГО ПЕЛЕНГОВАНИЯ РАДИОСИГНАЛОВ (ВАРИАНТЫ) | 2008 |
|
RU2393498C2 |
| СПОСОБ ПЕЛЕНГОВАНИЯ С ПОВЫШЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТЬЮ | 2010 |
|
RU2491569C2 |

Изобретение может быть использовано в акустике и радиотехнике для формирования с повышенной разрешающей способностью комплексных изображений углового спектра и определения азимутального и угломестного направлений на источники кратковременных когерентных волновых процессов различной природы. Техническим результатом изобретения является повышение точности и достоверности пеленгования источников кратковременных сигналов в условиях многолучевого распространения волн различной природы. Технический результат достигается за счет статистической информации, извлекаемой из одной реализации входных данных путем формирования множества сигналов нелинейно регуляризованных комплексных угловых спектров, минимизации дисперсии сигналов регуляризованных спектров, идентификации множества сигналов регуляризованных спектров с минимальной дисперсией и когерентного усреднения спектров с минимальной дисперсией. В результате минимизируется число и уровень ложных спектральных составляющих, повышается точность формирования углового спектра и возрастает эффективность пеленгования. 5 з.п. ф-лы, 2 ил.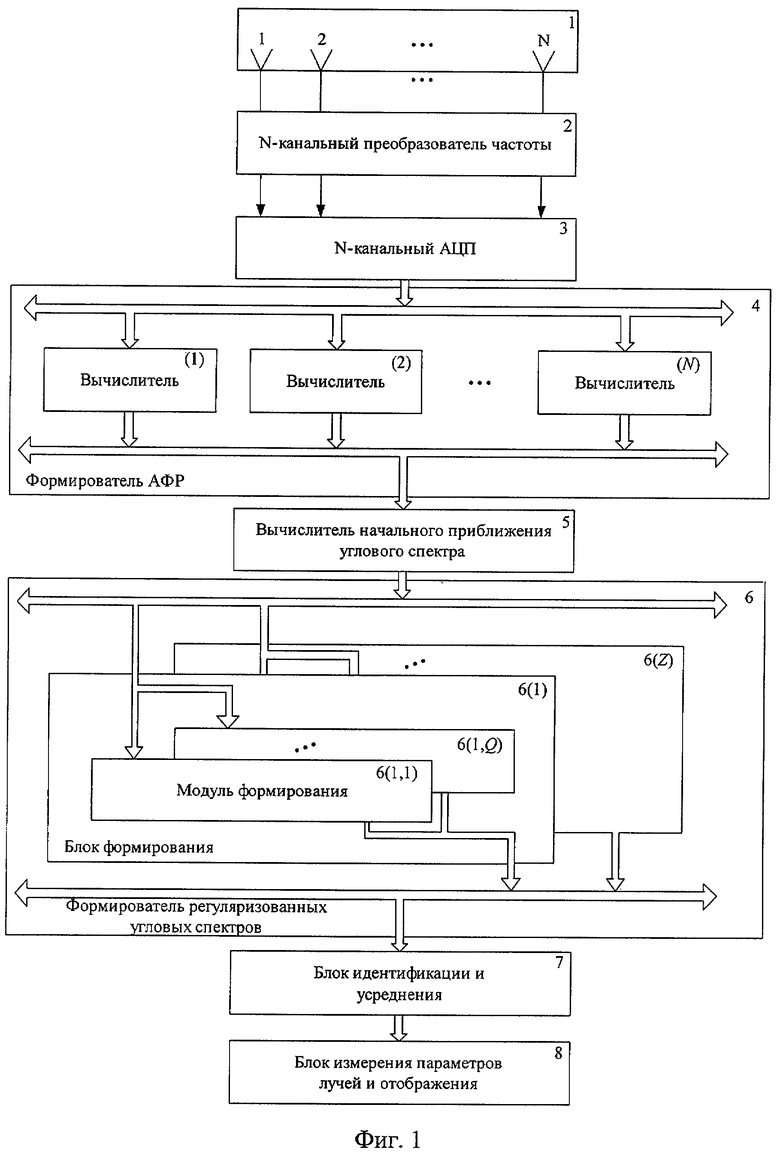
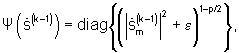
p<1, 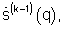 - m-й элемент вектора спектра
- m-й элемент вектора спектра 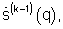
 - номер возможного направления прихода принимаемого сигнала, k=1,2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра
- номер возможного направления прихода принимаемого сигнала, k=1,2,... - номер итерации, и сигнала очередного приближения регуляризованного комплексного углового спектра 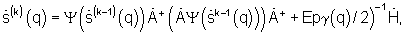
где 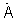 - идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра,
- идеальный двумерный сигнал комплексной фазирующей функции размером N×M, N - число элементов антенной решетки, Е - единичная N×N матрица, γ(q) - значение параметра регуляризации, используемого при формировании q-го спектра, 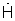 - сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
- сигнал АФР, до тех пор, пока энергия разности текущего и запомненного предыдущего приближения регуляризованных угловых спектров не достигнет заданного малого значения.
| ШЕВЧЕНКО В.Н | |||
| Оценивание углового положения источников когерентных сигналов на основе методов регуляризации | |||
| - Радиотехника | |||
| Способ и приспособление для нагревания хлебопекарных камер | 1923 |
|
SU2003A1 |
| СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ В УСЛОВИЯХ МНОГОЛУЧЕВОСТИ | 1997 |
|
RU2141675C1 |
| СПОСОБ ОБНАРУЖЕНИЯ И ОПРЕДЕЛЕНИЯ ДВУМЕРНОГО ПЕЛЕНГА И ЧАСТОТЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 2000 |
|
RU2190236C2 |
| СПОСОБ КВАЗИКОГЕРЕНТНОГО ПРИЕМА МНОГОЛУЧЕВОГО СИГНАЛА И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2002 |
|
RU2252493C2 |
| US 5486831 A, 23.01.1996 | |||
| US 5872776 A, 16.02.1999 | |||
| WO 9708566 A1, 06.03.1997. | |||
Авторы
Даты
2007-10-27—Публикация
2005-10-13—Подача