СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГАЦИОННОЙ ПАНОРАМЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ Российский патент 2014 года по МПК G01S5/04 

Область техники

Изобретение относится к радиотехнике, в частности к радиопеленгации.

Уровень техники

Многосигнальная пеленгация источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки при многолучевом распространении радиоволн, воздействии преднамеренных и непреднамеренных помех, отражениях сигнала от различных объектов и слоев атмосферы.

Задача радиопеленгации является некорректной. Большинство методов многосигнальной пеленгации на одной частоте, описанных в литературе, опираются на статистические методы проверки гипотез, на метод максимума правдоподобия, на сверхразрешающие методы (например MUSIC) и др. Однако задача пеленгации ИРИ как некорректная задача не может быть решена надежно ни статистическими методами, достоверность результата которых определяется точностью полученных оценок параметров сигналов, ни методом наименьших квадратов (МНК), в силу нелинейности и плохой обусловленности решаемой системы уравнений, ни сверхразрешающими методами, которые дают приемлемые результаты лишь при высоких соотношениях сигнал/шум и не обеспечивают разрешение ИРИ, имеющих близкие по значениям пеленги.

Известен способ пеленгации с повышенной разрешающей способностью [1], принятый за прототип. Согласно данному способу исходная постановка задачи сводится к линейной задаче путем введения сетки значений пеленгов в заданном диапазоне углов.

Несмотря на линейность задача остается некорректной. Следует обратить внимание, что количество узлов сетки много больше количества ИРИ, т.е. большинство элементов вектора амплитуд u в идеальном случае равны нулю.

В прототипе применен метод ℓ_p-регуляризации. В методе ℓ_p-регуляризации для нахождения решения строится функционал вида:

$$J\left(u,\lambda \right)={\Vert Au-y\Vert }_2^2+\lambda {\Vert u\Vert }_p^p,\mathrm{0,}<p\le 1;J\left(u,\lambda \right)\to \underset{u}{\min }\left(1\right)$$ .

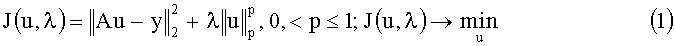
Регуляризирующий функционал вида (1) способствует получению вектора решения, большинство элементов которого равны нулю, а несколько элементов имеют относительно большие значения за счет формы функционала (1). Значение параметра регуляризации λ и показателя степени p определяет опытный квалифицированный оператор пеленгатора в процессе калибровки алгоритма.

Способ-прототип обладает следующими недостатками:

1. Длительный вычислительный процесс.

2. Требуются квалифицированные операторы пеленгатора, т.к. для обработки зарегистрированного сигнала необходимо подобрать значения параметра регуляризации λ и показателя степени p. Эта процедура требует большого опыта и квалификации оператора и отнимает много времени.

Указанные недостатки не позволяют применять способ-прототип в реальных условиях.

Раскрытие изобретения

Предлагаемый способ свободен от указанных недостатков и является параметрическим методом многосигнального пеленгования на одной частоте. Задача предлагаемого изобретения - повышение быстродействия, точности пеленгации и минимизация участия квалифицированного оператора пеленгатора в процессе определения пеленгационной панорамы.

Сигналы рассматриваются как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению.

Достигаемый технический результат - получение углового спектра (пеленгационной панорамы) нескольких ИРИ, уменьшение времени расчета пеленгов и повышение точности пеленгации при приеме радиосигналов нескольких источников радиоизлучения, работающих на одной частоте, с использованием антенных систем (АС), состоящих из слабонаправленных элементов (вибраторов). Повышение точности пеленгации достигается за счет введения переопределенного базиса и решения полученной системы линейных алгебраических уравнений (СЛАУ) оригинальным методом.

Способ определения пеленгационной панорамы источников радиоизлучения на одной частоте включает в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал амплитудно-фазового распределения (АФР) у, описывающий распределение амплитуд u и фаз φ сигналов на элементах АС, определение двумерного сигнала А комплексной фазирующей функции размером М×N, зависящего от заданной частоты приема и описывающего возможные направления прихода сигнала от каждого потенциального источника, где М - число элементов АС, N - число угловых направлений, соответствующих заданным потенциально возможным направлениям сигнала по азимуту θ_к и углу места β_к, где к=1, 2, …, N. При этом получение многосигнального углового спектра и вектора амплитуд сигналов u, представляющего собой распределение амплитуд по пеленгам θ_к и β_к, осуществляют путем формирования точечных оценок амплитуд u и пеленгов сигналов за счет использования функционала с заданным шагом обновления направления спуска по методу сопряженных градиентов, включающего в себя сумму разностей сигнала А, умноженного на амплитуду искомого сигнала АФР y, и произведения y_i на логарифм сигнала А, умноженного на амплитуду искомого сигнала АФР y, деленных на 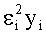$${\epsilon }_i^2{y}_i$$ , где ε_i - относительная погрешность значения y_i, точка минимума которого определяет точечные оценки параметров Θ, что позволяет определить для каждого пеленга в заданном диапазоне углов амплитуду u. По полученному многосигнальному угловому спектру строят пеленгационную панораму, по которой определяют количество, интенсивность и пеленги источников радиоизлучения.

Далее определяют интервальную оценку пеленгационной панорамы (углового спектра) на основе вычисленной корреляционной (ковариационной) матрицы ошибок найденных значений пеленгов (интервальные оценки пеленгов получают на основе теоремы Крамера-Рао - путем вычисления обратной матрицы, составленной из вторых производных минимизируемого функционала).

Перечень фигур

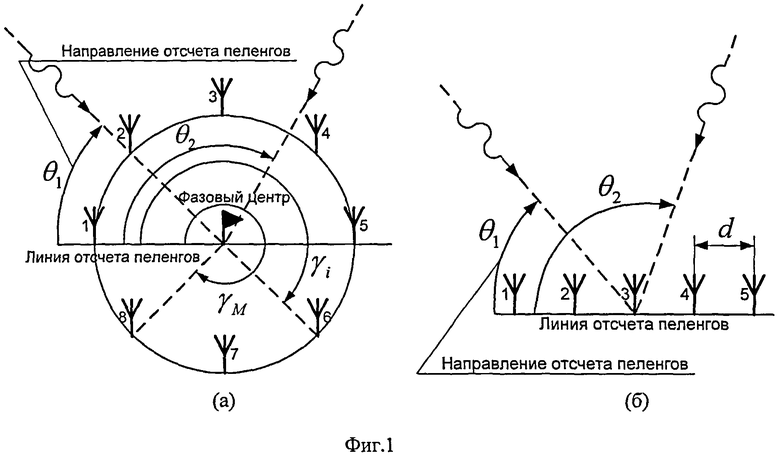
Фиг.1. Пространственные конфигурации АС: (а) - круговая, (б) - линейная.

Осуществление изобретения

В качестве АС рассматриваются две системы, состоящие из нескольких слабонаправленных элементов (вибраторов).

В круговой АС (фиг.1а) в качестве фазового центра (точки, относительно которой происходит измерение фаз сигналов, приходящих на элементы антенной системы), как правило, берется центр окружности. В линейной АС (фиг.1б) в качестве фазового центра выбирается один из вибраторов.

Ставится задача определения следующих параметров присутствующих в эфире ИРИ:

- количество ИРИ;

- амплитуды (мощности) излучаемых сигналов;

- азимутальные пеленги ИРИ;

- угломестные пеленги ИРИ.

Поскольку на результаты измерений неизбежно накладываются помехи, а также имеют место ошибки измерений, обусловленные используемой аппаратурой, необходимо получить не только точечные оценки искомых параметров, но и их ковариационные матрицы или, по крайней мере, дисперсии.

Рассмотрим задачу пеленгации в следующей постановке. В эфире присутствует K ИРИ с азимутальными пеленгами θ=[θ₁, θ₂ … θ_K]^T, угломестными пеленгами β=[β₁ β₂ … β_K]^T и амплитудами (мощностями) излучаемых сигналов u=[u₁, u₂ … u_K]^T ; y=[y₁, y₂ … y_M]^T - сигнал комплексного амплитудно-фазового распределения, описывающий амплитуды и фазы сигналов, принятых элементами АС, где М - количество элементов АС. Используемый вид модуляции (амплитудная, частотная, фазовая и др.) не имеет принципиального значения.

В общем случае математическая модель задачи имеет следующий вид:

$$A\left(\theta ,\beta ,t\right)u+n\left(t\right)=y\left(t\right),t=\left\{t_1;t_2;\dots ;t_T\right\}\left(2\right)$$ ,

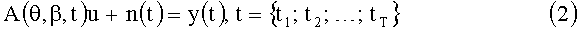
где n(t) - вектор аддитивной помехи, имеющей нулевое математическое ожидание и ковариационную матрицу вида σ²I, I - единичная матрица, σ - среднеквадратическое отклонение (СКО); матрица A(θ,β,t) (фазирующая функция) формируется с учетом вида сигналов пеленгуемых ИРИ и пространственной конфигурации антенной системы. Система (2) - система нелинейных уравнений относительно неизвестных θ, β и u. Для круговой антенной системы (рис.1а) матрица A(θ,β,t) имеет вид:

А(θ,β,t)=[а(θ₁,β₁,t) а(θ₂,β₂,t) … a(θ_K,β_K,t)],

где m-й элемент, m=1; 2; …; М, вектора-столбца a (θ_k,β_k,t) имеет вид

$$a_m\left({\theta }_k,{\beta }_k,t\right)=\exp \left\{j\left[2\pi {\sout{\int }}_{0}t+{\varphi }_k+\left(2\pi R/\lambda \right)\cos \left({\theta }_k-{\gamma }_m\right)d\cos {\beta }_k\right]\right\}\left(3\right)$$

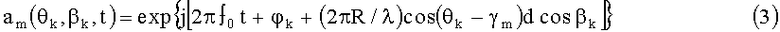
для линейной антенной системы (рис.1б) с фазовым центром, расположенным на вибраторе №1, матрица A (θ,е) имеет вид

$$a_m\left({\theta }_k,{\beta }_k,t\right)=\exp \left\{j\left[2\pi {\sout{\int }}_{0}t+{\varphi }_k+\left(m-1\right)\left(2\pi /\lambda \right)d\cos {\theta }_k\cos {\beta }_k\right]\right\}\left(4\right)$$ ,

где ƒ₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

φ_k - начальная фаза k-го сигнала,

R - радиус окружности, вдоль которой расположены элементы антенной системы,

λ - длина волны сигналов ИРИ,

d - расстояние между соседними элементами антенной системы,

γ_i, i=1; 2; …; М - угол между линией отсчета пеленгов и линией отсчета пеленгов и линией, проведенной через центр окружности и i-й элемент антенной системы (для круговой АС),

М - количество элементов в антенной системе.

В задаче уравнений (2) требуется определить для каждого из одновременно поступивших на АС сигналов амплитуду (мощность) u_k, азимутальный пеленг θ_k и уголоместный пеленг β_k. Задача является нелинейной.

Линеаризуем задачу (2) при помощи введения переопределенного базиса. Будем считать, что задан интервал возможных значений азимутальных пеленгов (например от 0° до 180°) и угломестных пеленгов (например от 0° до 90°). Введем на данном интервале сетку пеленгов 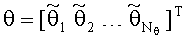$$\theta ={[{\tilde{\theta }}_1{\tilde{\theta }}_2\dots {\tilde{\theta }}_{N_{\theta }}]}^T$$ и сетку углов места $$\tilde{\beta }={[{\tilde{\beta }}_1{\tilde{\beta }}_2\dots {\tilde{\beta }}_{N_{\beta }}]}^T$$ .

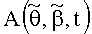
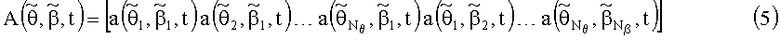
В системе (1) матрицу А(θ,β,t) заменим матрицей $$A\left(\tilde{\theta },\tilde{\beta },t\right)$$ ,

$$A\left(\tilde{\theta },\tilde{\beta },t\right)=\left[a\left({\tilde{\theta }}_1,{\tilde{\beta }}_1,t\right)a\left({\tilde{\theta }}_2,{\tilde{\beta }}_1,t\right)\dots a\left({\tilde{\theta }}_{N_{\theta }},{\tilde{\beta }}_1,t\right)a\left({\tilde{\theta }}_1,{\tilde{\beta }}_2,t\right)\dots a\left({\tilde{\theta }}_{N_{\theta }},{\tilde{\beta }}_{N_{\beta }},t\right)\right]\left(5\right)$$ ,

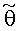
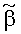
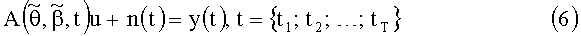
в которой неизвестными остаются только амплитуды, соответствующие азимутальным пеленгам $$\tilde{\theta }$$ и угломестным пеленгам $$\tilde{\beta }$$ . Получаем систему линейных алгебраических уравнений (СЛАУ) относительно вектора неизвестных u:

$$A\left(\tilde{\theta },\tilde{\beta },t\right)u+n\left(t\right)=y\left(t\right),t=\left\{t_1;t_2;\dots ;t_T\right\}\left(6\right)$$ .

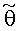
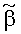
Количество элементов вектора амплитуд сигналов u (количество столбцов матрицы системы) увеличивается до произведения размерностей сеток азимутальных и угломестных пеленгов - N_θ×N_β. Теперь вектор и представляет собой распределение амплитуд (мощностей) по пеленгам $$\tilde{\theta }$$ и $$\tilde{\beta }$$ (угловой спектр или пеленгационная панорама). В идеальном случае (шумы отсутствуют) количество ненулевых элементов вектора u равно количеству фактически присутствующих в эфире ИРИ. Положение ненулевых элементов в векторе u (в сетке пеленгов) характеризует пеленги соответствующих ИРИ. Таким образом, введение сетки пеленгов решает не только проблему нелинейности задачи, но и проблему определения количества ИРИ. Решив систему линейных алгебраических уравнений (СЛАУ) (6) получаем необходимую информацию.

Несмотря на линейность, задача (6) является некорректной. Количество узлов сетки много больше количества ИРИ, т.е. большинство элементов вектора u в идеальном случае равны нулю. Тогда получим другой функционал для получения пеленгационной панорамы, свободный от недостатка прототипа с ℓ_p-регуляризацией.

Экспериментальные данные у=[y₁ y₂ … y_M]^T будем рассматривать как дискретные неотрицательные случайные безразмерные величины N_i=y_i/ Δy_i, где Δy_i, - наименьшая единица измерения случайной величины y_i. Распределение N_i в каждой точке аппроксимируем законом распределения Пуассона. 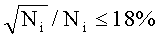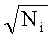Такая аппроксимация справедлива для широкого диапазона погрешностей значений N_i (при N_i≥30, что соответствует погрешности исходных данных $$\sqrt{N_i}/N_i\le 18\%$$ , распределение Пуассона близко к нормальному). Поскольку для случайных величин N_i, подчиняющихся распределению Пуассона, погрешность равна $$\sqrt{N_i}$$ , то, для того, чтобы относительная погрешность N_i была равна относительной погрешности ε_i значения y_i, величину Δy_i следует брать равной ε_i ²y_i.

Истинные значения исходных данных задачи связаны между собой соотношением Аθ = Y, где θ - вектор пеленгов, т.е. математическое ожидание случайной величины N_i будет равно N_mi=(Аθ)_i/(Δy_i,). Тогда совместная плотность вероятности получения совокупности статистически независимых величин {N_i}

$$P=\Pi \left(\exp \left(-N_{mi}\right)N_{mi}^{N_i}\right)/N_i!\left(7\right)$$ .

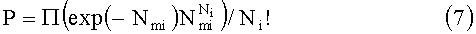
Согласно методу максимального правдоподобия (ММП) оценки искомых значений могут быть получены из условия максимума ln Р, а доверительные интервалы найденных оценок - из анализа закона распределения ln Р или же приближенно с помощью матрицы вторых производных от ln Р.

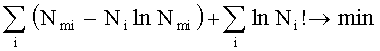
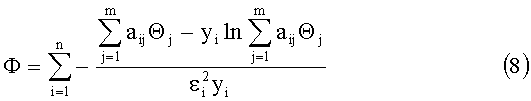
Из (7) имеем $${\displaystyle \sum _i\left(N_{mi}-N_i\ln N_{mi}\right)+}{\displaystyle \sum _i\ln N_i!\to \min }$$ . Последнее слагаемое является константой и в дальнейшем при поиске минимума (экстремума) может не рассматриваться. Возвращаясь к исходным данным получаем функционал

$$Ф={\displaystyle \sum _{i=1}^n-\frac{{\displaystyle \sum _{j=1}^m{a}_{ij}{\Theta }_j-y_i\ln {\displaystyle \sum _{j=1}^m{a}_{ij}{\Theta }_j}}}{{\epsilon }_i^2{y}_i}}\left(8\right)$$ ,

точка минимума которого определяет точечные оценки параметров Θ (прим.: обозначение Θ повторяет сходное по написанию обозначение θ (оба этих обозначения считаем одинаковыми)).

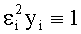
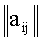
Если в функционале (8) положить $${\epsilon }_i^2{y}_i\equiv 1$$ и считать, что $$\Vert a_{ij}\Vert$$ - стохастическая матрица, при этом: 0<y_i<1, то придем к функционалу, для которого доказано, что он является строго выпуклым на выпуклом множестве М допустимых решений матричного пространства F, т.е. имеет единственную точку минимума [2].

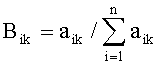
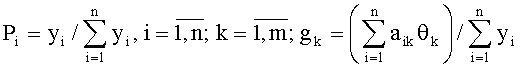
Исходные данные для последующего определения решения целесообразно нормировать следующим образом: вместо исходной системы уравнений берется нормированная (в относительных единицах) система: Bg = P, где $$B_{ik}=a_{ik}/{\displaystyle \sum _{i=1}^n{a}_{ik}}$$ ;

$$P_i=y_i/{\displaystyle \sum _{i=1}^n{y}_i,i=\overline{\mathrm{1,}n};k=\overline{\mathrm{1,}m};g_k=\left({\displaystyle \sum _{i=1}^n{a}_{ik}{\theta }_k}\right)/{\displaystyle \sum _{i=1}^n{y}_i}}$$ .

Функционал (8) записывается затем в новых переменных.

Регуляризирующий функционал вида (8) способствует получению вектора решения, большинство элементов которого равны нулю, а несколько элементов имеют относительно большие значения.

Нормировка функционала (8) позволяет получить решение задач одного класса за относительное малое число итераций. В результате этого значительно сокращается время расчета пеленгов по сравнению с прототипом.

Дисперсии оценок пеленгов определяются с помощью матрицы вторых производных от функционала (8). Аналитический вид формулы для дисперсий оценок показывает, что дисперсия увеличивается практически по линейному закону с увеличением значения θ от точки минимума и уменьшается с уменьшением значений θ. В то же время дисперсию оценок в точке минимума для СЛАУ Аθ = Y можно найти как (A^TA)^-1. Этот факт часто бывает полезным для анализа того, в «какой стороне» от точки минимума остановился итерационный процесс при заданных условиях - ограничениях. Для наших плохообусловленных систем этот факт важно знать, так как разные нулевые приближения в них могут привести к существенно различающимся точечным оценкам.

Устойчивость решения задач с помощью функционала (8) определяется дополнительным ограничением 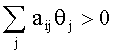$${\displaystyle \sum _j{a}_{ij}{\theta }_j>0}$$ , которое содержится в функционале, а также резким изменением скорости движения приближений к решению в окрестности точки минимума, что согласно [2] демпфирует неустойчивость некорректной задачи, и выбором оптимального числа итераций n₀, обеспечивает устойчивость решения.

Отыскание точки минимума функционала (8) проводилось с помощью метода сопряженных градиентов [2]. Метод сопряженных градиентов обеспечивает сходимость к точке минимума квадратичной функции за n итераций, где n - число переменных. Для произвольной функции используется идея квадратичной аппроксимации. Если через некоторое число шагов итераций произвольная функция станет квадратичной, то процедура сходится за конечное число шагов.

Представим функционал (8) в квадратичной форме

$$\widehat{O}\left(g\right)=\frac{1}{2}{g}^T\tilde{A}g+q^{T}g$$ ,

где $$\tilde{A}$$ - положительно определенная симметричная матрица. Зададимся точкой начального приближения g⁰ и построим первое приближение

$$g^1=g^0-{\alpha }_0\frac{\partial \widehat{O}\left(g^0\right)}{\partial g}=g^0-{\alpha }^0{d}^1$$ ,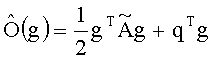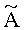

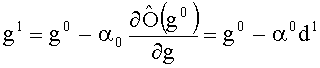
где α⁰ выбирается из равенства

$$\widehat{O}\left(g_0-{\alpha }^0{d}^1\right)=\underset{\alpha }{\min }\widehat{O}\left(g^0-\alpha d^1\right)$$ .

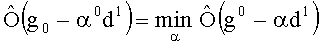
Для следующих шагов по методу сопряженных градиентов

g^s+1=g^s-α_sd^s+1,s=1,2,…,

где 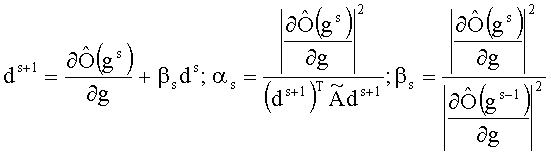$$d^{s+1}=\frac{\partial \widehat{O}\left(g^s\right)}{\partial g}+{\beta }_s{d}^s;{\alpha }_s=\frac{{\left|\frac{\partial \widehat{O}\left(g^s\right)}{\partial g}\right|}^2}{{\left(d^{s+1}\right)}^T\tilde{A}{d}^{s+1}};{\beta }_s=\frac{{\left|\frac{\partial \widehat{O}\left(g^s\right)}{\partial g}\right|}^2}{{\left|\frac{\partial \widehat{O}\left(g^{s-1}\right)}{\partial g}\right|}^2}$$ .

Анализ сходимости показывает, что метод сопряженных градиентов имеет квадратичную скорость сходимости [2]. При минимизации функционала (8) методом сопряженных градиентов в авторской компьютерной программе предусмотрено «обновление» направления. Направление выбирается вновь в точке g^s если функционал Ô(g^s) начал расти, или через заданное число m₀ итераций. Число итераций m₀ определяется дополнительно для различных классов задач. Например, для решения интегральных уравнений типа свертки с числом точек дискретизации более 100 m₀=10…15. При использовании метода сопряженных градиентов, в принципе, двигаясь по поверхности Ô(g), можно получить отрицательные значения g. Поэтому в авторской программе для таких случаев предусмотрена операция уменьшения шага движения до тех пор, пока не будет выполняться условие g≥0.

Процедура получения углового спектра (пеленгационной панорамы) в предлагаемом способе реализуется следующим образом.

1. Принимают многолучевой сигнал ИРИ антенной системой (АС), состоящей из M элементов и формируют ансамбль сигналов y_m(t), m=1; 2; …; M, зависящих от времени t.

2. Синхронно преобразуют ансамбль принятых сигналов y_m(t) в цифровые сигналы y_m(z), где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы y_m(z) в сигнал комплексного амплитудно-фазового распределения (АФР), описывающий амплитуды и фазы сигналов, принятых элементами АС. Восстанавливают вектор комплексных амплитуд сигналов y=[y₁ y₂ … y_M]^T, полученных с выхода каждого элемента АС.

4. Данные поступают в блок определения точки минимума функционала (8) с заданным шагом обновления направления спуска по методу сопряженных градиентов, т.е. находят значения пеленгов всех сигналов, поступивших на АС.

5. Пеленги поступают на блок вычисления дисперсий оценок пеленгов.

6. Вывод углового спектра (пеленгационной панорамы).

Приведенные процедуры не содержат ни параметров регуляризации, ни дополнительных сглаживающих операторов из l_р-регуляризации. Регуляризация решения обеспечивается формой (видом) функционала (8). Процедуры используют простейшие математические операции, чем обеспечивается малое время вычислительного процесса. При этом также минимизировано (практически отсутствует) участие квалифицированного оператора пеленгатора в процессе определения пеленгационной панорамы.

Пример реализации изобретения

Приведем результаты модельного расчета пеленга на компьютере с процессором с тактовой частотой 2 ГГц. Рассматривалась пеленгация двух ИРИ, работающих на частоте 20 МГц. Азимутальные пеленги - 30 и 50°, угломестные пеленги не вводились. Для сравнения модельные расчеты проводился по способу прототипа и по предлагаемому способу. Получены обоими способами значения азимутальных пеленгов 29.94 и 50,89°. Время расчета предлагаемым способом в 2 раза меньше, чем способом прототипа, к тому же это еще и без учета затрат времени квалифицированного оператора на подбор в способе прототипа параметров l_р-регуляризации

Источники информации

1. Патент RU 2382379, опубликовано 20.02.2010, МПК G01S 5/04

2. Грешилов А.А. Математические методы принятия решений: Учебное пособие для вузов. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2006, 584 с.

Изобретение относится к радиотехнике, в частности к радиопеленгации. Достигаемый технический результат - получение углового спектра нескольких ИРИ, уменьшение времени расчета пеленгов и повышение точности пеленгации. Сущность заявленного способа заключается в том, что осуществляют прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал амплитудно-фазового распределения (АФР) y, описывающий распределение амплитуд u и фаз φ сигналов на элементах АС, определение двумерного сигнала А комплексной фазирующей функции размером М×N, зависящего от заданной частоты приема и описывающего возможные направления прихода сигнала от каждого потенциального источника, где М - число элементов АС, N - число угловых направлений, соответствующих заданным потенциально возможным направлениям сигнала по азимуту θ_к и углу места β_к, где к=1, 2,…, N. При этом получение многосигнального углового спектра и вектора амплитуд сигналов u, представляющего собой распределение амплитуд по пеленгам θ_к и β_к, осуществляют путем формирования точечных оценок амплитуд u и пеленгов сигналов за счет использования функционала с заданным шагом обновления направления спуска по методу сопряженных градиентов, включающего в себя сумму разностей сигнала А, умноженного на амплитуду искомого сигнала АФР y, и произведения у_i на логарифм сигнала А, умноженного на амплитуду искомого сигнала АФР y, деленных на 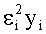$${\epsilon }_i^2{y}_i$$ , где ε_i - относительная погрешность значения y_i, точка минимума которого определяет точечные оценки параметров Θ, что позволяет определить для каждого пеленга в заданном диапазоне углов амплитуду u. По полученному многосигнальному угловому спектру строят пеленгационную панораму, по которой определяют количество, интенсивность и пеленги источников радиоизлучения. 1 з.п.ф-лы,1 ил.

1. Способ определения пеленгационной панорамы источников радиоизлучения на одной частоте, включающий в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал амплитудно-фазового распределения (АФР) y, описывающий распределение амплитуд u и фаз φ сигналов на элементах АС, определение двумерного сигнала А комплексной фазирующей функции размером M×N, зависящего от заданной частоты приема и описывающего возможные направления прихода сигнала от каждого потенциального источника, где M - число элементов АС, N - число угловых направлений, соответствующих заданным потенциально возможным направлениям сигнала по азимуту θ_к и углу места β_к, где к=1, 2, …, N, отличающийся тем, что получение многосигнального углового спектра и вектора амплитуд сигналов u, представляющего собой распределение амплитуд по пеленгам θ_к и β_к, осуществляют путем формирования точечных оценок амплитуд u и пеленгов сигналов за счет использования функционала с заданным шагом обновления направления спуска по методу сопряженных градиентов, включающего в себя сумму разностей сигнала А, умноженного на амплитуду искомого сигнала АФР y, и произведения y_i на логарифм сигнала А, умноженного на амплитуду искомого сигнала АФР y, деленных на 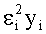$${\epsilon }_i^2{y}_i$$ где ε_i - относительная погрешность значения y_i, точка минимума которого определяет точечные оценки параметров Θ, что позволяет определить для каждого пеленга в заданном диапазоне углов амплитуду u, по полученному многосигнальному угловому спектру строят пеленгационную панораму, по которой определяют количество, интенсивность и пеленги источников радиоизлучения.

2. Способ по п.1, отличающийся тем, что определяют интервальную оценку углового спектра найденных пеленгов на основе вычисленной корреляционной (ковариационной) матрицы ошибок найденных значений пеленгов.