Изобретение относится к вычислительной технике и может быть использовано для высокоскоростного перевода чисел из полиномиальной системы классов вычетов (ПСКВ) в позиционный код с коррекцией ошибки.
Известно устройство для преобразования числа из системы остаточных классов (СОК) в позиционный код (АС СССР №1005028, G06F 5/02), содержащее позиционный накапливающий сумматор, выход которого является выходом устройства, и блок синхронизации, отличающееся тем, что с целью повышения быстродействия, оно содержит блок памяти констант, группу элементов И, сдвиговый регистр, группа входов которого является входом устройства, а управляющий вход подключен к первому выходу блока синхронизации, первые входы элементов И группы объединены и подключены к выходу младшего разряда сдвигового регистра, а вторые входы подключены к соответствующим информационным выходам блока памяти констант, управляющий вход которого подключен к второму выходу блока синхронизации, выходы элементов И группы подключены к соответствующим входам позиционного накапливающего сумматора.
Недостатком устройства является неспособность к коррекции ошибки.
Одним из наиболее перспективных методов обнаружения и коррекции ошибок является вычисление старших коэффициентов обобщенной полиадической системы (ОПС).
В работе (Справочник по цифровой вычислительной технике. /Под редакцией Б.Н.Маменовского. К., Технiка, 1974, 512 с.) на страницах 33-35 представлены методы вычисления коэффициентов ОПС. Данные методы характеризуются значительными временными затратами (время вычисления пропорционально числу оснований системы).
Сократить время вычисления старших коэффициентов ОПС можно за счет применения полиномиальной системы ПСКВ, а также псевдоортогональных базисов.
Если исходное число А представить в полиномиальной форме, а в качестве оснований выбрать минимальные многочлены расширенного поля Галуа, то это число можно представить в виде:
A(z)=(α1(z), α2(z),... αn(z)),
где αi(z)≡A(z)mod рi(z); pi(z) - минимальный многочлен.
Если в качестве рабочих оснований выбрать k минимальных многочленов ПСКВ (k<n), то данные основания определяют рабочий диапазон
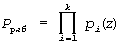
Если А(z)∈Рраб(z), то А(z) - разрешен.
Псевдоортогональные полиномы представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям
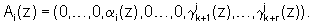
Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безызбыточной системы оснований полиномиальной системы классов вычетов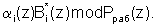 
Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z),...,pk(z) на r контрольных оснований pk+1(z),...,pk+r(z) и представим ортогональные полиномы 
в виде
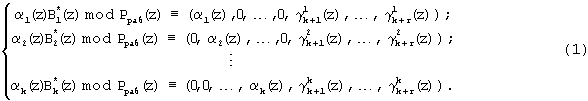
Выражение (1) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.
Согласно китайской теореме об остатках
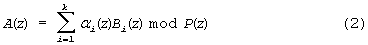
полином можно представить в виде
Тогда каждое слагаемое выражения (2) представляет собой
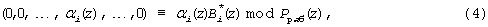
где 
- ортогональный базис безызбыточной системы оснований ПСКВ.
Подставив выражение (1) в равенство (3) и учитывая, что в процессе выполнения операции не бывает выход за пределы Рраб(z), получаем
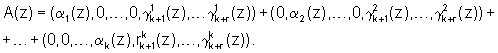
Следовательно, справедливо
Таким образом, на основании выражения (5) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (1), можно вычислить значения остатков по контрольным основаниям 
согласно
Затем на основании полученных значений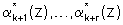 
и значений αk+1(z),...,αk+r(z), поступающих на вход устройства коррекции ошибок, можно определить разность согласно выражению
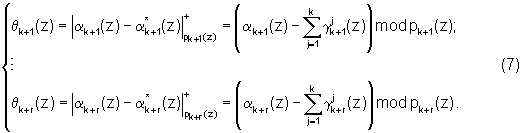
Если разность равна нулю, т.е.
θk+1(z)=0,...,θk+r(z)=0,
то исходный полином A(z)∈Pраб(z) является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины, определяемой выражением (7), осуществляется коррекция ошибки, т.е.
где (0,...,Δαi(z),...,0) - вектор ошибки модулярного кода; Δαi(z) - глубина ошибки по i-му модулю; 
Пусть задано расширенное поле Галуа GF(24), в котором определены следующие основания:
p1(z)=z+1; p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1; p4(z)=z4+z3+1; p5(z)=z4+z+1,
где р1(z), р2(z), p3(z) - рабочие основания, p4(z), p5(z) - контрольные основания ПСКВ.
Тогда согласно выражению 
имеем
Рраб(z)=z7+z6+z5+z2+z+1.
В полной системе оснований ПСКВ поля GF(24) определены ортогональные базисы:
B1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1,
B2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z,
B3(z)=z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z,
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3,
B5(z)=z12+z9+z8+z6+z4+z3+z2+z.
Используя сравнимость ортогональных базисов безызбыточной и полной системы по рабочему диапазону, определим значения ортогональных базисов безызбыточной системы оснований p1(z)=z+1; р2(z)=z2+z+1; p3(z)=z4+z3+z2+z+1. Тогда
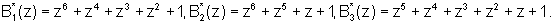
На основании полученных значений определим все псевдоортогональные полиномы для ПСКВ GF(24), учитывая невозможность выхода за пределы рабочего диапазона Рраб(z)=z7+z6+z5+z2+z+1. Полученные значения представлены в таблице 1.
Если полином A(z)∈Pраб, то справедливо
(α1(z), α2(z), α3(z))=(α1(z), α2(z), α3(z), α* 4(z), α* 5(z))=(α1(z), α2(z), α3(z), α4(z), α5(z)),
где левая часть равенства представлена по рабочим основаниям p1(z), p2(z), p3(z), средняя часть равенства получена на основании выражения (6), а правая - модулярная комбинация системы оснований p1(z), p2(z), p3(z), p4(z), p5(z) расширенного поля Галуа GF(24), поступившая на вход устройства для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов. Тогда имеем нормированное значение
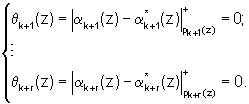
В противном случае
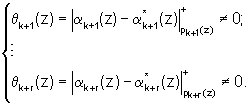
Полученный результат свидетельствует, что поступившая на вход устройства модульная комбинация A(z) содержит ошибку, которую необходимо подвергнуть коррекции. В таблице 2 представлены значения вектора ошибки (0,...,Δαi(z),...,0) - модулярного кода для различных значений синдрома ошибки для ПСКВ поля GF(24).
В расширенном поле Галуа GF(24) можно использовать обобщенную полиадическую систему счисления с основаниями
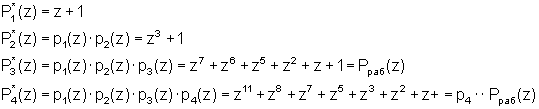
Тогда
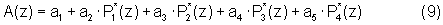
Из равенства (9) наглядно видно, что если А (z) ∈ Рраб (z), то есть ord A(z)<ord Рраб(z), то старшие коэффициенты ОПС, соответствующие контрольным основаниям, должны быть равны нулю, то есть
а4(z)=0 и а3(z)=0
В противном случае А(z) содержит ошибку, следовательно, для обнаружения и коррекции ошибки надо вычислить а4(z) и а5(z). Тогда вычисление старших коэффициентов ОПС через нормированный след осуществляется согласно выражению
j=k+1,...,k+r;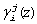 
- константа пересчета из ПСКВ в ОПС.
Для поля GF(24) с двумя контрольными основаниями р4(z)=z4+z3+1 и р5(z)=z4+z+1 имеем
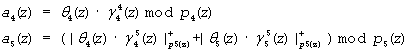
Значения констант пересчета приведены в таблицах 3 и 4.
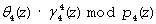
Представим ортогональные базисы в виде коэффициентов ОПС
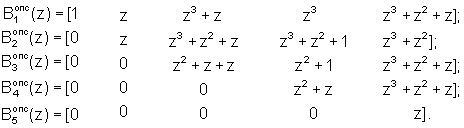
Если в качестве ортогональных базисов Вi(z) взять их представления в ОПС, то в результате выполнения выражения (10) определяются коэффициенты ОПС
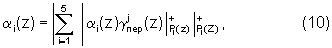
где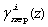 
- коэффициенты ОПС i-го ортогонального базиса с учетом переполнения (i-1)-го основания. При этом умножение вычетов αi(z) на соответствующие коэффициенты 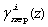осуществляется помодульно и поразрядно, при этом учитывается превышение модуля Pi(z) как перенос в старший коэффициент ОПС αi+1(z).
Пусть дан полином A(z)=z6+z5+z4+z+1, который принадлежит Pпол(z)=zl5+1. Тогда в коде ПСКВ A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z). Воспользуемся выражением (10) и значениями 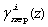из таблиц 3, 4 для определения коэффициентов ОПС контрольных оснований p4(z) и р5(z).
Таким образом, для полинома A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z) значения старших коэффициентов ОПС равны:
a4(z)=0, a5(z)=0,
что свидетельствует об отсутствии ошибки.
Допустим, что в принятой комбинации произошла ошибка по первому основанию и ее глубина равна Δa1(z)=1. Тогда имеем:
A*(z)=(0, z+1, z3+z2+z+1, z3+z2+z, z3+z).
Согласно выражению (1) и данным, представленным в таблице 1, получаем следующие псевдоортогональные полиномы Ai(z):
A1(z)=(0, z+1, 0, z3+z2+1, z3+z2+z);
A2(z)=(0, 0, z3+z2+z+1, z3, z2+z).
Используя выражение (6) определяем значения остатков по контрольным основаниям:
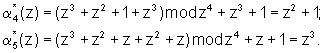
Согласно выражению (7) определяем:
θ4(z)=(z3+z2+z-z2+1)mod(z4+z3+1)=z3+z+1;
θ5(z)=(z3+z-z3)mod(z4+z+1)=z.
Таким образом
α4(z)=z+z3+z2+z2+z=z3
α5(z)=z3+1+z3+z2+z+1+z+z3+z2+z+z2=z3+z2+z
Δα2=z
Δα3=z
Δα3=z2
Δα3=z3
Δα4=z
Δα4=z2
Δα4=z3
Δα5=z
Δα5=z2
Δα5=z3
Из таблицы 5 в соответствии с α4(z)=z3 и α5(z)=z3+z2+z выбирается величина ошибки, которая складывается с A*(z)=(0, z+1, z3+z2+z+1, z3+z2+z, z3+z), в результате чего получаем A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z).
Ошибка в модулярном коде исправлена.
Техническим результатом изобретения является обеспечение повышения быстродействия и коррекции ошибки.
Повышение быстродействия достигается тем, что устройство содержит позиционный накапливающий сумматор, выход которого является выходом устройства, и блок синхронизации, содержащий блок памяти констант, группу элементов И, сдвиговый регистр, группа входов которого является входом устройства, а управляющий вход подключен к первому выходу блока синхронизации, первые входы элементов И группы объединены и подключены к выходу младшего разряда сдвигового регистра, а вторые входы подключены к соответствующим информационным выходам блока памяти констант, управляющий вход которого подключен к второму выходу блока синхронизации, выходы элементов И группы подключены к соответствующим входам позиционного накапливающего сумматора.
На фиг.1 представлена структура устройства для преобразования числа из ПСКВ в позиционный код с коррекцией ошибки.
Устройство содержит сдвиговый регистр 1, блок 2 синхронизации, блок 3 памяти констант, группу элементов И 4, позиционный накапливающий сумматор 5, вход 6 устройства, блок 7 обнаружения ошибки, блок 8 хранения данных, корректирующий сумматор по модулю два 9, выход 10 устройства.
Число в коде ПСКВ через вход 6 заносится на сдвиговый регистр 1, представляющий собой совокупность подрегистров для хранения вычетов по каждому из оснований ПСКВ. В дальнейшем регистр 1 рассматривается как единый регистр, содержимое которого в каждом такте сдвигается вправо в сторону "младших" разрядов на один разряд.
Блок 3 памяти констант содержит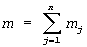 
констант разрядностью
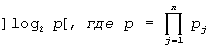
Работа устройства происходит по тактам. В каждом такте производится выдача очередной константы из блока памяти констант 3 величиной 2i-1·Bji в случае открытых элементов И группы - прибавление ее к содержимому позиционного накапливающего сумматора 5, работающего по модулю р, и сдвиг кода исходного числа в регистре 1 на один разряд вправо. Работа устройства заканчивается через m тактов и не зависит от величины исходного числа. Время работы известного устройства зависит от величины числа и колеблется от 0 до р.
Параллельно с занесением числа в коде ПСКВ на сдвиговый регистр оно поступает на блок обнаружения ошибки 7, где происходит обнаружение ошибки по следу полинома. Если число правильное, его след нормированный и равен нулю. В противном случае он не равен нулю и на вход корректирующего сумматора по модулю два 9 поступает Δкор, предварительно занесенное в блок 8 хранения данных. В корректирующем сумматоре по модулю два 9 происходит суммирование по модулю два значений А* и Δ кор, следовательно, на выход 10 устройства поступает исправленная комбинация.
Таким образом, введение в состав устройства блока 7 обнаружения ошибки, блока 8 хранения данных и корректирующего сумматора по модулю два 9 позволяет не классическим способом, а при помощи минимальных многочленов не только обнаружить, но и корректировать ошибку.
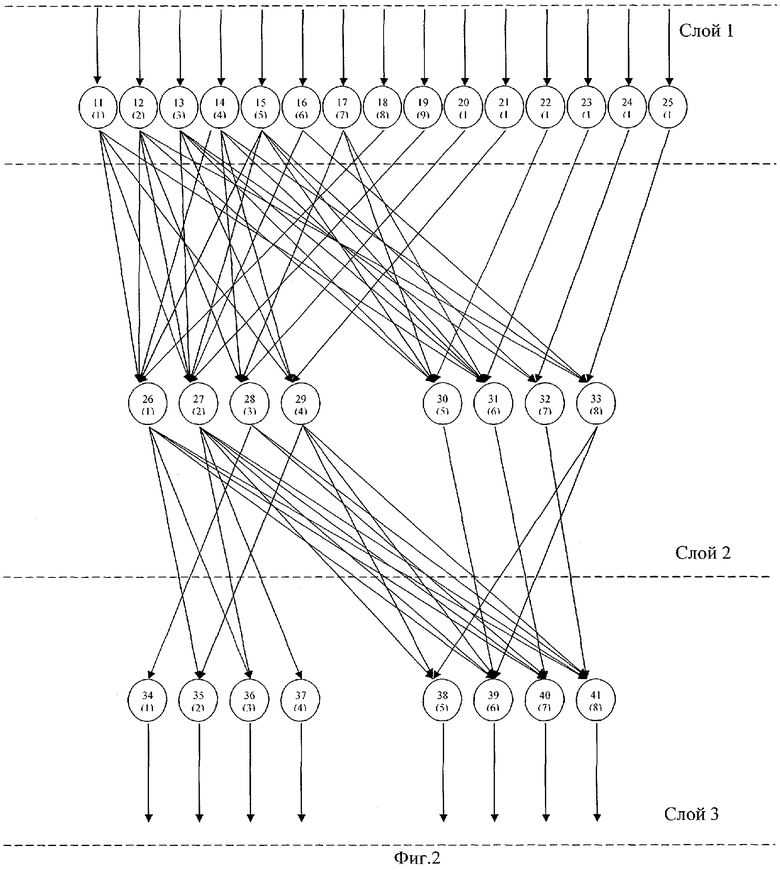
Блок 7 обнаружения ошибки представляет собой трехслойную нейронную сеть (фиг.2). Входной слой состоит из 15 нейронов, распределенных в соответствии с размерностью разрядных сеток модулей -1-2-4-4-4. Данные нейроны осуществляют разветвление входного вектора ((α1(z), α2(z), α3(z), α4(z), α5(z)), представленного в двоичной форме. Причем нейрон 11 предназначен для распределения нулевого разряда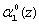 
первого основания. Нейроны 12, 13 предназначены для распределения нулевого 
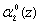и первого 
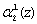разрядов второго основания соответственно. Нейроны 14-17 используются для приема и распределения 
, 
, 
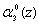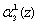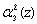и 
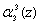разрядов третьего основания соответственно. Для перераспределения нулевого 
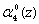, первого 
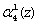, второго 
и третьего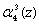 
разрядов четвертого основания p4(z) используются нейроны 18, 19, 20, 21 соответственно. Нейроны 22, 23, 24, 25 применяются для приема нулевого 
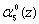, первого 
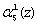, второго 
и третьего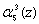 
разрядов пятого основания p5(z) соответственно.
Второй слой предназначен для вычисления нормированного следа и состоит из восьми нейронов, распределенных в соответствии с размерностью разрядных сеток коэффициентов (αi(z), i=4,5) ОПС 4-4. Нейроны 26-33 второго слоя выполняют базовую операцию суммирования по модулю два значений разрядов, поступающих с выходов соответствующих нейронов первого слоя, причем на нейрон 26 второго слоя поступают сигналы с нейронов 11, 12, 14, 15, 18 входного слоя, на нейрон 27 второго слоя - с нейронов 11, 12, 13, 15, 16, 19 входного слоя, на нейрон 28 второго слоя - с нейронов 12, 14, 17, 20 входного слоя, на нейрон 29 второго слоя - с нейронов 11, 13, 14, 21 входного слоя. Эти четыре нейрона второго слоя предназначены для вычисления константы пересчета θ4. На нейрон 30 второго слоя поступают сигналы с нейронов 12, 13, 15, 17, 22 входного слоя, на нейрон 31 второго слоя - с нейронов 11, 13, 14, 15, 17, 23 входного слоя, на нейрон 32 второго слоя - с нейронов 13, 15, 24 входного слоя, на нейрон 33 второго слоя - с нейронов 12, 14, 16, 25 входного слоя. Данные четыре нейрона второго слоя предназначены для вычисления константы пересчета θ5.
Третий слой предназначен для вычисления старших коэффициентов ОПС и также состоит из восьми нейронов, распределенных в соответствии с размерностью разрядных сеток коэффициентов (αi(z), i=4,5) ОПС 4-4. Нейроны 34-41 третьего слоя выполняют базовую операцию суммирования по модулю два значений разрядов, поступающих с выходов соответствующих нейронов второго слоя, причем на нейрон 34 третьего слоя поступают сигналы с нейрона 28 второго слоя, на нейрон 35 третьего слоя - с нейронов 26, 29 второго слоя, на нейрон 36 третьего слоя - с нейронов 26, 27 второго слоя, на нейрон 37 третьего слоя - с нейрона 27 второго слоя. Эти четыре нейрона третьего слоя предназначены для вычисления коэффициента ОПС а4. На нейрон 38 третьего слоя поступают сигналы с нейронов 27, 33 второго слоя, на нейрон 39 третьего слоя - с нейронов 26, 27, 30, 33 второго слоя, на нейрон 40 третьего слоя - с нейронов 26, 27, 31 второго слоя, на нейрон 41 третьего слоя - с нейронов 26, 27, 32 второго слоя. Данные четыре нейрона третьего слоя предназначены для вычисления коэффициента ОПС а5.
Сигналы с выхода третьего слоя поступают на входы блока 8 хранения данных.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2008 |
|
RU2393529C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ, ПРЕДСТАВЛЕННЫХ В РАСШИРЕННЫХ ПОЛЯХ ГАЛУА GF(2) | 2004 |
|
RU2258956C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2008 |
|
RU2390051C2 |
Изобретение относится к вычислительной технике и может быть использовано в устройствах преобразования чисел из полиномиальной системы классов вычетов в позиционный код. Техническим результатом является повышение быстродействия преобразования и расширение функциональных возможностей устройства за счет обеспечения коррекции ошибки. Устройство содержит сдвиговый регистр, блок синхронизации, блок памяти констант, группу элементов И, позиционный накапливающий сумматор, блок обнаружения ошибки, блок хранения данных, корректирующий сумматор по модулю два. Блок обнаружения ошибки выполнен в виде трехслойной нейронной сети. 1 з.п. ф-лы, 2 ил., 5 табл.
| Устройство для преобразования числа из системы остаточных классов в позиционный код | 1981 |
|
SU1005028A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| Устройство для обнаружения и исправления ошибок арифметических преобразований полиномиальных кодов | 1979 |
|
SU894711A1 |
| JP 63254829, 21.10.1988 | |||
| Светочувствительная композиция | 1977 |
|
SU1029125A1 |
