Изобретение относится к вычислительной технике и может быть использовано в процессорах цифровой обработки сигналов, в цифровых фильтрах для обнаружения и коррекции ошибки.
Известно устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов (ПСКВ) (Патент RU 2270475 С2, G06F 7/72, 2006 г.), выбранное в качестве прототипа, содержащее счетчик тактов, блок коррекции ошибки, преобразователь кода ПСКВ в позиционный код, модульный сумматор, два блока вычисления сумм парных произведений по произвольному основанию и один блок вычисления сумм парных произведений по контрольному основанию, каждый из которых содержит регистр, память, матричный умножитель, три группы буферных регистров и матричный сумматор, причем выход счетчика тактов соединен с адресными входами памяти первого, второго и третьего блоков вычисления сумм парных произведений по произвольному и контрольному основанию соответственно и входами разрешения работы преобразователя кода ПСКВ в позиционный код и блока коррекции ошибки, а в каждом из блоков вычисления сумм парных произведений выход регистра соединен с первым входом матричного умножителя, второй вход которого соединен с выходом памяти, а выходы - с входами буферных регистров первой группы, выходы которых соединены с входами первого слагаемого матричного сумматора, выходы которого соединены с входами буферного регистра второй группы, выходы которого соединены с входами буферного регистра третьей группы, выходы которого соединены с входами второго слагаемого матричного сумматора и соответственно с первым, вторым и третьим информационными входами блока коррекции ошибки, а выходы буферного регистра третьей группы первого, второго блоков вычисления сумм парных произведений по произвольному основанию соединены со входами преобразователя кода ПСКВ в позиционный код, второй выход которого соединен с четвертым входом блока коррекции ошибки, а первый выход преобразователя кода ПСКВ в позиционный код соединен с первым входом модульного сумматора, второй вход которого подключен к выходу блока коррекции ошибки, выход модульного сумматора соединен с выходом устройства. При этом блок коррекции ошибки содержит три регистра, семь нейронов входного слоя, предназначенных для осуществления перераспределения данных на три нейрона второго слоя и два нейрона счетчика тактов перехода, выходы которых соединены со входами трех нейронов выходного слоя, нейроны второго слоя, нейроны счетчика тактов перехода и нейроны выходного слоя предназначены для реализации базовой операции суммирования по модулю два, причем выход первого регистра соединен со входом первого нейрона входного слоя, выход второго регистра соединен со входами второго, третьего и четвертого нейронов входного слоя, выход третьего регистра соединен со входами пятого, шестого и седьмого нейронов входного слоя, а выходы первого нейрона входного слоя соединены со вторым и третьим нейронами второго слоя, выходы второго нейрона входного слоя соединены с первым, вторым и третьим нейроном второго слоя, выходы третьего нейрона входного слоя соединены с первым и третьим нейроном второго слоя и первым нейроном счетчика тактов переходов, выходы четвертого нейрона входного слоя соединены с первым нейроном второго слоя и первым и вторым нейроном счетчика тактов перехода, выход пятого нейрона входного слоя соединен с входом первого нейрона второго слоя, выход шестого нейрона входного слоя соединен с входом второго нейрона второго слоя, выход седьмого нейрона входного слоя соединен со входом третьего нейрона второго слоя, выход первого нейрона второго слоя и выход первого нейрона счетчика тактов переходов соединены со входами первого нейрона выходного слоя, выход второго нейрона второго слоя и выход второго нейрона счетчика тактов перехода соединены со входами второго нейрона выходного слоя, выход третьего нейрона второго слоя соединен со входом третьего нейрона выходного слоя, выходы первого, второго и третьего нейрона выходного слоя соединены с входом блока памяти, выход которого является выходом блока коррекции ошибки.
Недостатком данного устройства является то, что блок коррекции ошибки содержит избыточное количество аппаратных средств.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является сокращение аппаратных затрат.
Технический результат достигается за счет того, что число переходов за пределы рабочего диапазона определяется только значениями остатков по рабочим основаниям ПСКВ, которые можно заранее просчитать и учесть в структуре нейронной сети блока коррекции. Это позволяет отказаться от счетчика числа переходов и дополнительного слоя нейронной сети, находящихся в блоке коррекции ошибки прототипа.
В полиномиальной системе классов вычетов любой полином A(z) представляется как набор остатков
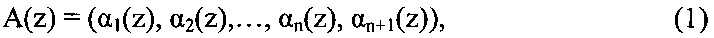
где αi(z)=rest(A(z)/pi(z)); pi(z) - минимальный многочлен, определяемый в расширенном поле Галуа GF (2v); n+1 - количество оснований ПСКВ; n - количество информационных оснований.
Согласно прототипа для определения ошибок в коде ПСКВ используется полиномиальная форма позиционной характеристики интервала, которая определяется

где 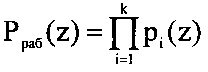 - рабочий диапазон.
- рабочий диапазон.
Так как операция деления в ПСКВ не выполняется, то выражение (2) сводится к совокупности модульных операций согласно
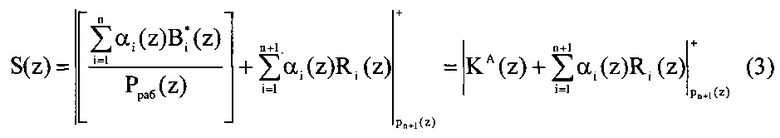
где 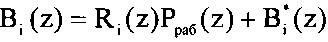 - ортогональный базис полной, состоящей из n+1 оснований, ПСКВ;
- ортогональный базис полной, состоящей из n+1 оснований, ПСКВ; 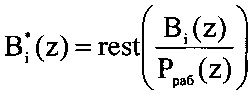 - ортогональный базис безызбыточной системы с основаниями p1(z), р2(z), …, pn(z);
- ортогональный базис безызбыточной системы с основаниями p1(z), р2(z), …, pn(z); 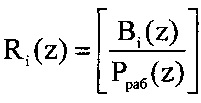 ;
; 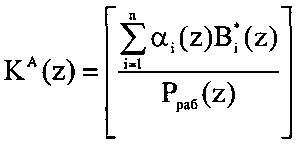 - количество переходов за величину рабочего диапазона Pраб(z), которое возникнет при переводе A(z) из модулярного кода в позиционный код на основе китайской теоремы об остатках.
- количество переходов за величину рабочего диапазона Pраб(z), которое возникнет при переводе A(z) из модулярного кода в позиционный код на основе китайской теоремы об остатках.
Одним из основных достоинств полиномиальной системы классов вычетов расширенного поля Галуа GF(2v), v=1, 2, …, является то, что операция суммирования осуществляется по модулю 2. Таким образом, при суммировании двух полиномов не может произойти выход за пределы рабочего диапазона, так как данная операция проводится поразрядно. Следовательно, значение KA(z) будет определяться только значениями произведений 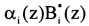 , i=1, …, n.
, i=1, …, n.
Тогда выражение (3) можно представить в виде
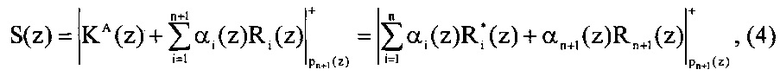
где 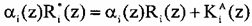 ;
; 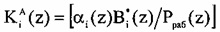 - количество переходов за рабочий диапазон Pраб(z), которое возникнет при значении остатка αi(z); i=1, …, п.
- количество переходов за рабочий диапазон Pраб(z), которое возникнет при значении остатка αi(z); i=1, …, п.
Следовательно, значение 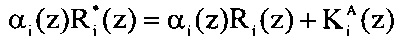 можно рассчитать заранее. Таким образом, нет необходимости в использовании счетчика числа переходов и дополнительного слоя нейронной сети.
можно рассчитать заранее. Таким образом, нет необходимости в использовании счетчика числа переходов и дополнительного слоя нейронной сети.
Например, пусть имеем поле Галуа GF(23), в котором определены минимальные многочлены, составляющие систему оснований ПСКВ p1(z)=z+1, p2(z)=z+z+1, p3(z)=z+z+1. В качестве контрольного основания используем многочлен p3(z). Тогда
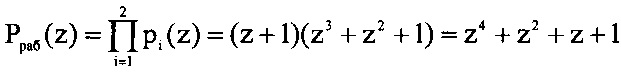 .
.
Вычислим ортогональные базисы полной ПСКВ
B1(z)=z6+z5+z4+z3+z2+z+1;
B2(z)=z6+z5+z3+1;
B3(z)=z4+z2+z+1.
При этом ортогональные базисы можно представить в виде
B1(z)=R1Pраб(z)+B1*=(z2+z)Pраб(z)+(z3+z2+1);
B2(z)=R2Pраб(z)+B2*=(z2+z+1)Pраб(z)+(z3+z2);
B3(z)=R3Pраб(z)=1Pраб(z).
Получаем систему безызбыточных оснований p1(z)=z+1, p2(z)=z3+z2+1, в которой определены ортогональные базисы B1*(z)=z3+z2+1, В2*(z)=z3+z2.
Значения 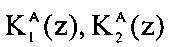 для различных значений α1(z) и α2(z) приведены в таблице 1.
для различных значений α1(z) и α2(z) приведены в таблице 1.

Значения 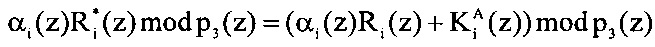 , i=1, 2, представлены в таблице 2.
, i=1, 2, представлены в таблице 2.


Пусть α2(z)=z. Вычислим значение 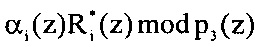 . Тогда получаем
. Тогда получаем
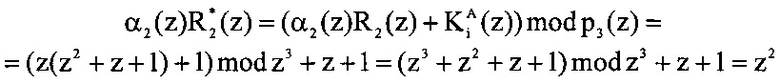 .
.
Возьмем полином A(z)=z3+z2+z+1, который принадлежит Pраб(z). В ПСКВ данный полином имеет вид A(z)=(0, z, z2). Определим значение S(z) согласно равенства (4)
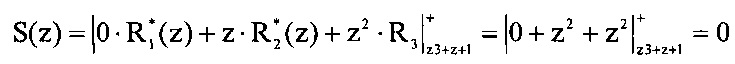
Так как полиномиальная форма позиционной характеристики интервал S(z)=0, то код ПСКВ не содержит ошибки.
Истинное значение полинома определяется следующим образом
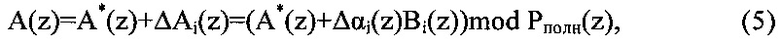
где A*(z) - значение полинома, поступившего на вход устройства; ΔAj(z) - корректирующее значение при возникновении по j-му основанию; j=1, 2; 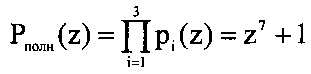 - полный диапазон.
- полный диапазон.
Глубина ошибки по основаниям и корректирующие значения ΔAj(z) на выходе памяти приведены в таблице 3.


Преобразователь кода ПСКВ в позиционный код определяет значение
A*(z)=(α1(z)B1(z)+α2(z)B2(z)+α3(z)B3(z))mod z7+1=
=(0(z6+z5+z4+z3+z2+z+1)+z(z6+z5+z3+1)+z2(z4+z2+z+1))mod z7+1=
=(z7+z6+z4+z+z6+z4+z3+z2)mod z7+1=z3+z2+z+1.
Тогда согласно (5) и данных таблицы 3 получаем
A(z)=A*(z)+ΔA1(z)=z3+z2+z+1+0=z3+z2+z+1.
Пусть ошибка произошла по первому основанию. Тогда A(z)=(1, z, z2). Определим значение S(z)
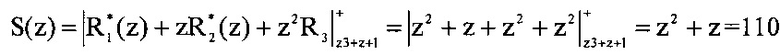 .
.
Таким образом, значение нулевого разряда полиномиальной формы позиционной характеристики интервал S0(z)=0, значение первого разряда полиномиальной форма позиционной характеристики интервал S1(z)=1, а вычисленное значение второго разряда полиномиальной формы позиционной характеристики интервал равно S2(z)=1.
Так как значение полиномиальной формы позиционной характеристики интервал S(z)≠0, то код ПСКВ содержит ошибку.
Произведем ее исправление. Преобразователь кода ПСКВ в позиционный код определяет значение
A*(z)=(α1(z)B1(z)+α2(z)B2(z)α3(z)B3(z))mod z7+1=
=((z6+z5+z4+z3+z2+z+1)+z(z6+z5+z3+1)+z2(z4+z2+z+1))mod z7+1=
=(z7+z6+z5+z4+1)mod z7+1=z6+z5+z4.
Тогда согласно выражения (5) и данных таблицы 3 имеем
A(z)=A*(z)+ΔAj(z)=(z6+z5+z4)+(z6+z5+z4+z3+z2+z+1)=z3+z2+z+1.
Ошибка исправлена.
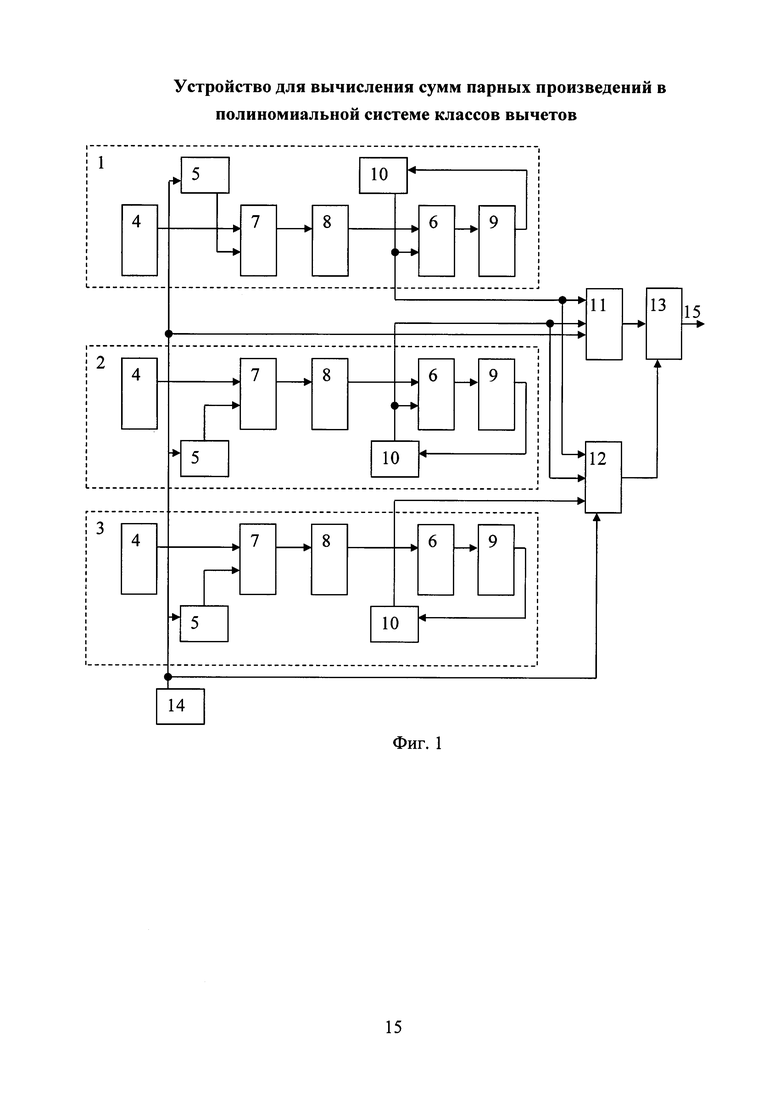
На фигуре 1 представлена функциональная схема устройства для вычисления сумм парных произведений, которая содержит блоки вычисления сумм парных произведений по произвольному основанию 1, 2 и по контрольному основанию 3, каждый из которых содержит регистр 4, память 5, матричный сумматор 6, матричный умножитель 7 и три группы буферных регистров 8, 9, 10; преобразователь 11 кода ПСКВ в позиционный код, блок коррекции ошибки 12, модульный сумматор 13, счетчик тактов 14 и выход устройства 15. Устройство работает следующим образом.
В регистры 4 блоков вычисления сумм парных произведений по произвольному основанию 1, 2 и по контрольному основанию 3 до начала работы записаны числа в коде ПСКВ. Счетчик тактов 14 формирует адреса для считывания коэффициентов, которые хранятся в коде ПСКВ в памяти 5 в блоках 1, 2, 3 вычисления сумм парных произведений. Содержимое регистров 4 в каждом из блоков вычисления сумм парных произведений по произвольному 1, 2 и по контрольному 3 основаниям перемножается с коэффициентами из памяти 5 с помощью матричных умножителей 7. Результат умножения записывается в первую группу буферных регистров 8, содержимое которых складывается с содержимым буферных регистров 10 третьей группы (в первом цикле происходит сложение с нулем). Сложение осуществляют матричные сумматоры 6 в каждом из блоков 1, 2, 3 вычисления сумм парных произведений. Сумма записывается в буферные регистры 9 второй группы, а затем передается в буферные регистры 10 третьей группы. С выходов буферных регистров 10 третьей группы блоков 1 и 2 вычисления сумм парных произведений по произвольному основанию результат подается на входы преобразователя 11 кода ПСКВ в позиционный код и на информационные входы блока коррекции ошибки 12. На третий информационный вход блока коррекции ошибки 12 подается информация с выходов буферного регистра 10 третьей группы блока 3 вычисления сумм парных произведений по контрольному основанию. Счетчик тактов 14 по окончании суммирования парных произведений выдает разрешающий сигнал на вход разрешения преобразователя 11 кода ПСКВ в позиционный код и блока коррекции ошибки 12. Результаты с выходов преобразователя 11 кода ПСКВ в позиционный код и блока 12 коррекции ошибки подаются на входы модульного сумматора 13, где и происходит сложение. Выход модульного сумматора 13 является выходом 15 устройств.
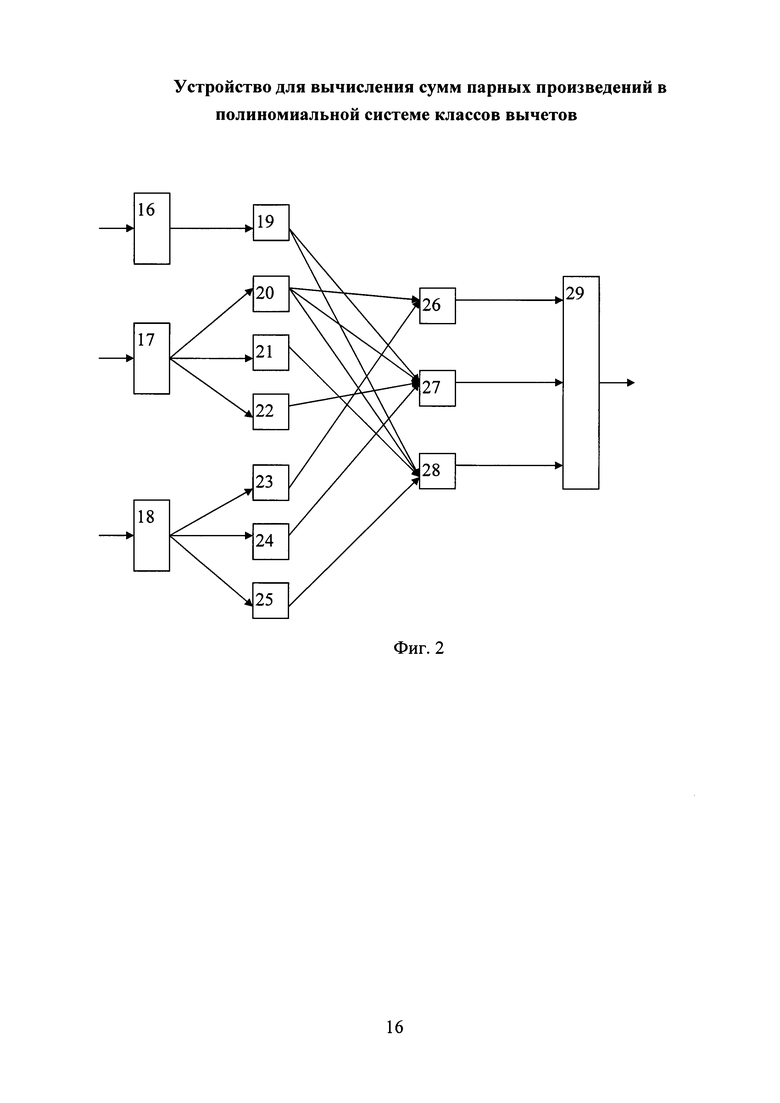
На фигуре 2 представлена функциональная схема блока коррекции ошибки 12. Блок коррекции ошибки 12 содержит три регистра 16-18, предназначенных для хранения остатков α1(z), α2(z), α3(z) соответственно, входной слой нейронной сети, который имеет архитектуру 1-3-3 и состоит из семи нейронов 19-25, трех нейронов 26-28 выходного слоя и блока памяти 29. Выход первого регистра 16 соединен с входом первого нейрона 19 входного слоя. Выход второго регистра 17 подключен к входам нейронов 20-22 входного слоя, при этом младший разряд остатка α02(z) подается на вход нейрона 20, а старший разряд остатка α22(z) подается на вход нейрона 22 (а 21?). Выход третьего регистра 18 подключен к входам нейронов 23-25 входного слоя, при этом младший разряд остатка α03(z) подается на вход нейрона 23, а старший разряд остатка α23(z) подается на вход нейрона 25 (что на 24?). Вход первого нейрона 26 выходного слоя подключен к выходам нейронов 20 и 23 входного слоя. Вход второго нейрона 27 выходного слоя подключен к выходам нейронов 19, 20, 22 и 24 входного слоя. Вход третьего нейрона 28 выходного слоя подключен к выходам нейронов 19, 20, 21 и 25 входного слоя. Выходы нейронов 26-28 выходного слоя подключены к входам блока памяти 29, выход которого является выходом блока коррекции ошибки 12.
Блок коррекции ошибки 12 работает следующим образом. Остатки α1(z), α2(z), α3(z) подаются соответственно на регистры 16, 17, 18, с выхода которых эти остатки поступают на соответствующие нейроны 19-25 входного слоя нейронной сети. Структура данного слоя имеет архитектуру 1-3-3. При этом младшие разряды остатков α1(z), α2(z), α3(z) подаются соответственно на нейроны 19, 20, 23. Старшие разряды остатков α2(z), α3(z) подаются соответственно на нейроны 22 и 25. Нейроны данного слоя в процессе вычисления значения полиномиальной формы позиционной характеристики интервал S(z) не участвуют, а осуществляют перераспределение данных на нейроны выходного слоя 26-28. Синаптические веса связей равны «1». При этом на выходе нейрона 26 будет вычисленное значение нулевого разряда полиномиальной формы позиционной характеристики интервал - S0(z). На выходе нейрона 27 будет вычисленное значение первого разряда полиномиальной формы позиционной характеристики интервал - S1(z). На выходе нейрона 28 будет вычисленное значение второго разряда полиномиальной формы позиционной характеристики интервал - S2(z).
Структура связей входного и выходного слоев нейронной сети представлена в таблице 4.
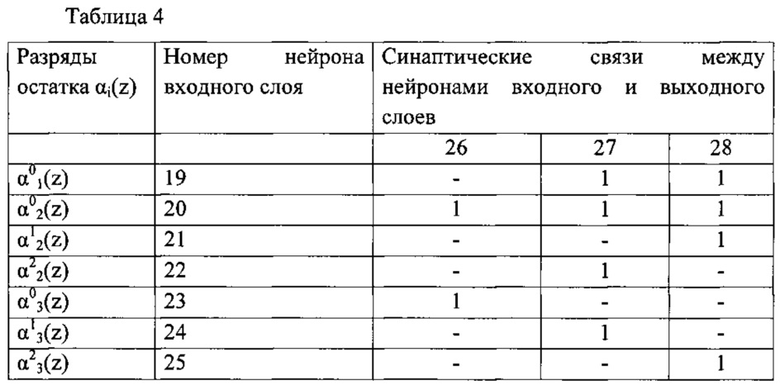
Нейроны 26-28 выходного слоя нейронной сети реализуют базовую операцию суммирования по модулю 2. С выходов данных нейронов значения полиномиальной формы позиционной характеристики интервал S(z) в двоичном коде поступают на вход блока памяти 29, на выходе которого появляется значение коррекции ΔAj(z), которое подается с выхода блока коррекции ошибки 12 на второй вход модульного сумматора 13, где и производится выполнение выражения (5).
Пусть на вход блока коррекции ошибки 12 поступила ошибочная комбинация A*(z)=(1, z, z2). Тогда полиномиальная форма позиционной характеристики интервал равна S(z)=z2+z=110. В таблице 5 приведено вычисление значения S(z) с помощью нейронной сети блока коррекции ошибки 12. При этом искаженная комбинация в двоичном коде представляется в виде A*(z)=(1, z, z2)=(1, 010, 100).
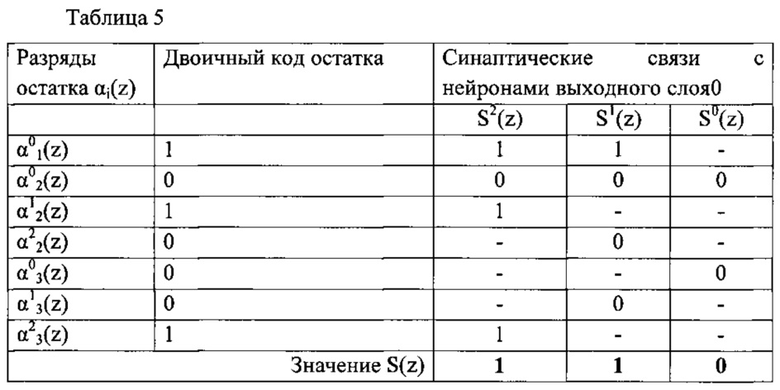
Таким образом, на выходе нейронной сети получен результат S(z)=z2+z. Данное вычисленное значение подается на вход блока памяти 29 блока коррекции ошибки 12. На выходе блока памяти 29 появится корректирующее значение ΔA1(z)=z6+z5+z4+z3+z2+z+1, которое с выхода блока коррекции 12 поступит на модульный сумматор 13. На выходе модульного сумматора 13 появится откорректированное значение
A(z)=z3+z2+z+1.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2008 |
|
RU2390051C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
Изобретение относится к вычислительной технике и может быть использовано в процессорах обработки сигналов, в цифровых фильтрах для обнаружения и коррекции ошибки. Техническим результатом, достигнутым при осуществлении заявленного изобретения, является сокращение аппаратных затрат. Указанный технический результат достигается за счет того, что число переходов за пределы рабочего диапазона определяется только значениями остатков по рабочим основаниям ПСКВ, которые можно заранее просчитать и учесть в структуре нейронной сети блока коррекции. Это позволяет отказаться от счетчика числа переходов и дополнительного слоя нейронной сети, находящихся в блоке коррекции ошибки прототипа. 2 ил., 5 табл.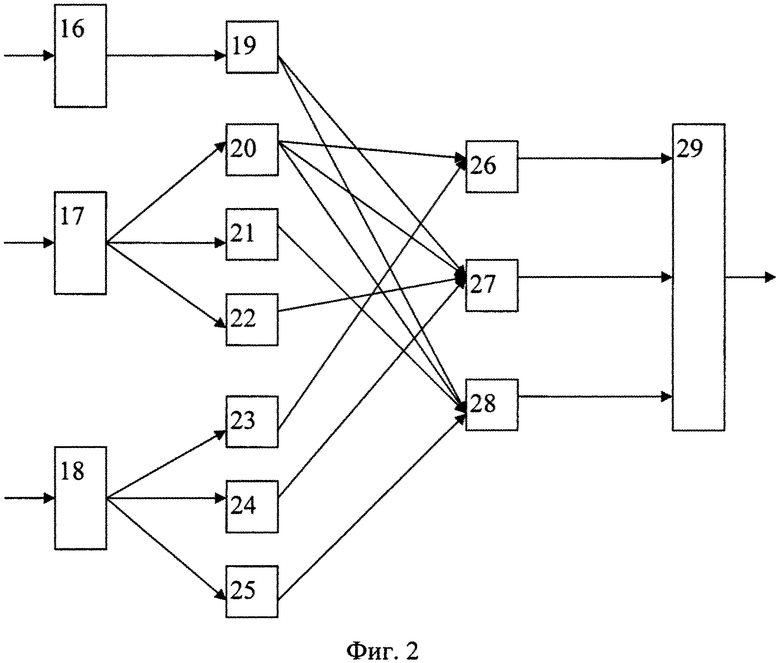
Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов, содержащее счетчик тактов, блок коррекции ошибки, преобразователь кода полиномиальной системы классов вычетов (ПСКВ) в позиционный код, модульный сумматор, два блока вычисления сумм парных произведений по произвольному основанию и один блок вычисления сумм парных произведений по контрольному основанию, каждый из которых содержит регистр, память, матричный умножитель, три группы буферных регистров и матричный сумматор, причем выход счетчика тактов соединен с адресными входами памяти первого, второго и третьего блоков вычисления сумм парных произведений по произвольному и контрольному основанию соответственно и входами разрешения работы преобразователя кода ПСКВ в позиционный код и блока коррекции ошибки, а в каждом из блоков вычисления сумм парных произведений выход регистра соединен с первым входом матричного умножителя, второй вход которого соединен с выходом памяти, а выходы - с входами буферных регистров первой группы, выходы которых соединены с входами первого слагаемого матричного сумматора, выходы которого соединены с входами буферного регистра второй группы, выходы которого соединены с входами буферного регистра третьей группы, выходы которого соединены с входами второго слагаемого матричного сумматора и соответственно с первым, вторым и третьим входами блока коррекции ошибки, а выходы буферного регистра третьей группы первого, второго блоков вычисления сумм парных произведений по произвольному основанию соединены со входами преобразователя кода ПСКВ в позиционный код, выход которого соединен с первым входом модульного сумматора, второй вход которого подключен к выходу блока коррекции ошибки, выход модульного сумматора соединен с выходом устройства, отличающееся тем, что блок коррекции ошибки содержит три регистра, семь нейронов входного слоя, имеющих архитектуру 1-3-3, три нейрона выходного слоя, реализующих операцию суммирования по модулю два, блок памяти, причем выход первого регистра соединен со входом первого нейрона входного слоя, выход второго регистра соединен с входами второго, третьего и четвертого нейронов входного слоя, выход третьего регистра соединен с входами пятого, шестого и седьмого нейронов входного слоя, при этом первый, второй и пятый нейроны входного слоя предназначены для приема младших разрядов первого, второго и третьего остатков кода и осуществления перераспределения данных на входы нейронов выходного слоя, которые предназначены для реализации базовой операции суммирования по модулю два, при этом вход первого нейрона выходного слоя соединен с выходами второго и пятого нейронов входного слоя, вход второго нейрона выходного слоя соединен с выходами первого, второго, четвертого и шестого нейронов входного слоя, вход третьего нейрона выходного слоя соединен с выходами первого, второго, третьего и седьмого нейронов входного слоя, выходы первого, второго, третьего нейронов выходного слоя соединены с входом блока памяти, выход которого является выходом блока коррекции ошибки.
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| Устройство для централизованного управления затворами силосов, амбаров и т.п. | 1930 |
|
SU27610A1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ | 1992 |
|
RU2012041C1 |
| JPS 6429125 (A), 31.01.1989. | |||
Авторы
Даты
2017-06-20—Публикация
2016-07-05—Подача