Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для вычисления коэффициентов обобщенной полиадической системы (ОПС), представленных в полях Галуа GF(2ν).
Известна нейронная сеть для вычисления коэффициентов обобщенной полиадической системы (ОПС), представленных в расширенных полях Галуа GF(2ν) ([1] Калмыков И.А., Лободин М.В., Алексишин Е.В., Щелкунова Ю.О. Нейронная сеть для вычисления коэффициентов обобщенной полиадической системы, представленной в расширенных полях Галуа // Патент РФ №2258956, G06N 3/04), содержащая два слоя по 15 нейронов в каждом, при этом первый слой 15 нейронов подключен к соответствующим входам 15 нейронов второго слоя.
Недостатком устройства является невозможность выполнения процедуры исправления ошибок, возникающих в процессе работы вычислительного устройства.
Основной задачей является расширение функциональных возможностей, которые позволят нейронной сети корректировать ошибки.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является расширение функциональных возможностей, позволяющих исправлять ошибки в коэффициентах ОПС, которые были получены из кодовой комбинации, представленной в полиномиальной системе классов вычетов (ПСКВ).
Указанный технический результат достигается за счет введения блока памяти и 7 корректирующих сумматоров по модулю два, с помощью которых происходит исправление ошибки.
В полиномиальной системе классов вычетов в качестве основания системы используются минимальные многочлены pi(z), i=1, 2, …, n, определенные в расширенных полях Галуа GF(2ν). Тогда любой полином A(z), удовлетворяющий условию

где degA(z) - степень полинома A(z); 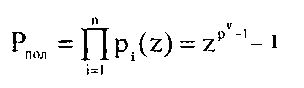 - полный диапазон, можно представить в виде n-мерного вектора
- полный диапазон, можно представить в виде n-мерного вектора
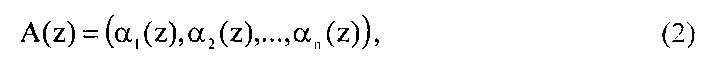
где 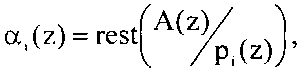 i=1, 2, …, n.
i=1, 2, …, n.
Используя коды ПСКВ, можно операцию сложения, вычитания и умножения двух операндов, представленных в полиномиальной форме A(z) и B(z), свести к выполнению этих операций над соответствующими остатками αi(z) и βi(z). При этом в ПСКВ эти операции производятся независимо по каждому из модулей pi(z), что указывает на параллелизм данной алгебраической системы. При этом, благодаря параллелизму алгебраической системы вычисления могут быть реализованы с помощью нейронных сетей ([2] - Калмыков И.А., Воронкин Р.А., Резеньков Д.Н, Емарлукова Я.В., Фалько А.А. Генетические алгоритмы в системах цифровой обработки сигналов // Нейрокомпьютеры: разработка и применение. - 2011. - №5. - С. 20-27).
Кроме того, особенность ПСКВ состоит еще и в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но также и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства класса вычетов. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из n оснований ПСКВ (k<n), то это позволит осуществить разбиение полного диапазона 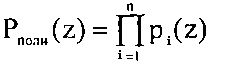 расширенного поля Галуа GF(pv) на два непересекающихся подмножества.
расширенного поля Галуа GF(pv) на два непересекающихся подмножества.
Первое подмножество называется рабочим диапазоном и определяется выражением
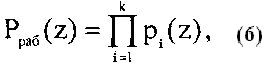
Многочлен A(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона Pполн(z), то есть принадлежит рабочему диапазону degA(z)<degPраб(z).
Второе подмножество GF(pv), определяемое произведением r=n-k контрольных оснований
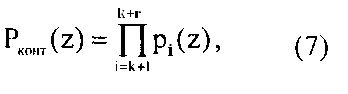
задает совокупность запрещенных комбинаций. Если A(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома A(z) относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация A(z)=(α1(z), α2(z), …, αk+r(z)) разрешенной или содержит ошибочные символы ([3] Калмыков И.А., Саркисов А.Б., Яковлева Е.М., Калмыков М.И. Модулярный систолический процессор цифровой обработки сигналов с реконфигурируемой структурой // Вестник Северо-Кавказского федерального университета. - 2013. - №2 (35). - С. 30-35.)
В [1] приведена нейронная сеть для перевода из модулярного кода ПСКВ в обобщенную полиадическую систему, в которой используются 5 неприводимых полиномов p1(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1, p4(z)=z4+z3+1, p5(z)=z4+z+1. Если положить, что первые три основания являются информационными, т.е. k=3, то рабочий диапазон будет определяться согласно (6) и равен
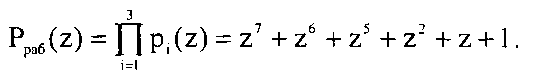
Оставшиеся два основания p4(z)=z4+z3+1 и p5(z)=z4+z+1 будем считать контрольными модулями, с помощью которых будут производиться поиск и коррекция ошибок, возникающих в кодах ПСКВ.
В этом случае любой полином, представленный в коде ПСКВ, чья степень будет меньше семи, т.е. degA(z)<7, является разрешенным, а его кодовая комбинация не содержит ошибки. В противном случае кодовая комбинация содержит ошибки.
Коэффициенты обобщенной полиадической системы позволяют осуществить поиск и коррекцию ошибок в кодах ПСКВ. Для данного примера полином A(z) можно представить в обобщенной полиадической системе как 
где 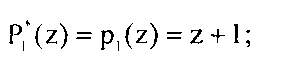
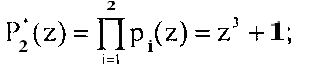
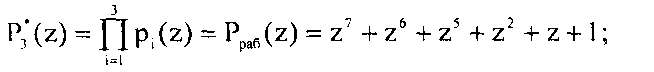
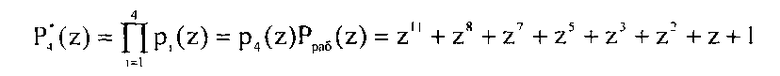
Ортогональные базисы такой системы равны:
B1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
B2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z;
B3(z)=z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z;
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3;
B5(z)=z12+z9+z8+z6+z4+z3+z2+z.
Представим ортогональные базисы в виде коэффициентов ОПС
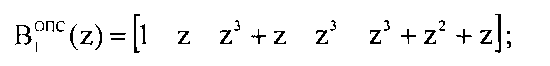
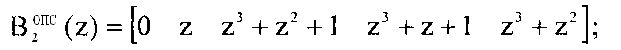
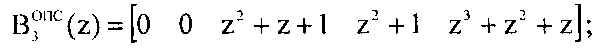
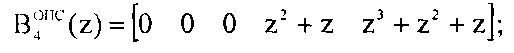

Согласно Китайской теореме об остатках полином A(z) определяется как
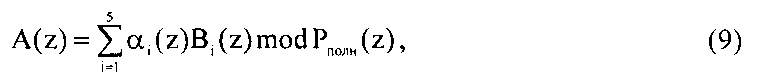
где 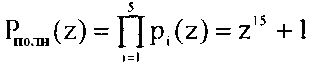 - полный диапазон ПСКВ.
- полный диапазон ПСКВ.
Если в качестве ортогональных базисов Bi(z) взять их представления в ОПС, то при умножении остатков αi(z) на последние можно получить коэффициенты ОПС
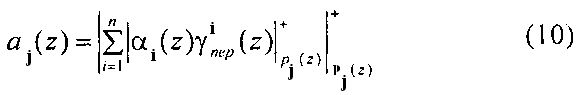
где 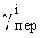
При этом умножение вычетов на соответствующие коэффициенты 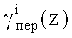
Из выражения (8) наглядно видно, что если полином A(z), представленный в ПСКВ, не содержит ошибки, то его степень не превысит степень рабочего диапазона. Следовательно, значения старших коэффициентов ОПС должны равняться нулю, т.е. a4(z)=0 и a5(z)=0.
Если полином A*(z), представленный в ПСКВ, содержит ошибку, то его значение будет определяться как
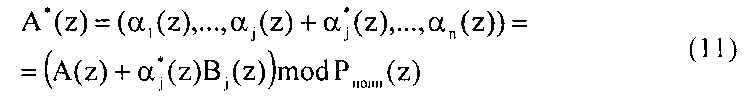
где 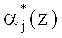
В результате этого результат ошибочного кода A*(z) при переводе в позиционный код окажется за пределами рабочего диапазона Ppaб(z). Следовательно, значения старших коэффициентов ОПС не будут равняться нулю. При этом по величине значений старших коэффициентов ОПС можно однозначно определить местоположение и глубину ошибки.
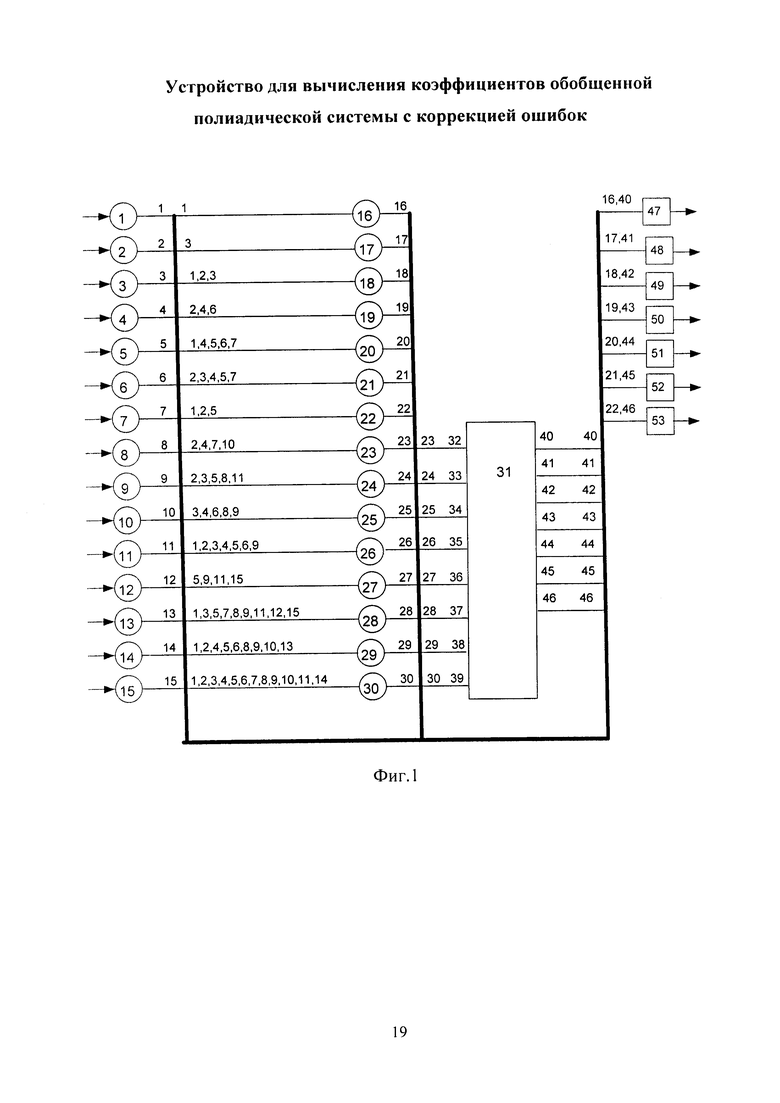
Чтобы осуществлять коррекцию ошибок в комбинации кода ПСКВ были введены два дополнительных слоя нейронов. Структура устройства представлена на фигуре 1. Устройство состоит из двухслойной нейронной сети (нейроны 1-15 образуют первый слой, нейроны 16-30 создают второй слой), блока памяти 31, имеющего восемь входов 32-39 и семь выходов 40-46, семи двухвходовых корректирующих сумматоров 47-53.
Рассмотрим двухслойную нейронную сеть, структура которой совпадает с прототипом [1]. Каждый слой содержит по 15 нейронов. Входной слой состоит из 15 нейронов, распределенных в соответствии с размерностью разрядных сеток модулей -1-2-4-4-4. Данные нейроны осуществляют разветвление входного вектора (α1(z), α2(z), α3(z), α4(z), α5(z)), представленного в двоичной форме. Причем нейрон 1 предназначен для распределения нулевого разряда 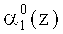
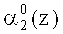
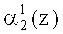
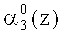
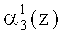
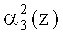

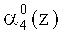
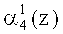
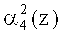
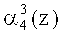

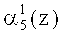
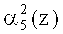

Второй слой нейронной сети содержит также 15 нейронов, распределенных в соответствии с размерностью разрядных сеток коэффициентов (ai(z), i=1, 2, 3, 4, 5) ОПС -1-2-4-4-4. Нейроны 16-30 второго слоя выполняют базовую операцию суммирования по модулю два значений разрядов, поступающих с выходов соответствующих нейронов первого слоя. Синаптические веса связей равны единице.
Нейрон 16 предназначен для приема данных, поступающих с выхода нейрона 1 входного слоя. Выход нейрона 16 соответствует нулевому разряду первого коэффициента ОПС a1(z).
Нейроны 17, 18 осуществляют вычисление нулевого и первого 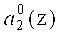 ,
, 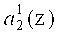 разрядов второго коэффициента ОПС соответственно. Причем вход нейрона 17 подключен к выходу нейрона 3. Вход нейрона 18 подключен к выходу нейронов 1, 2, 3.
разрядов второго коэффициента ОПС соответственно. Причем вход нейрона 17 подключен к выходу нейрона 3. Вход нейрона 18 подключен к выходу нейронов 1, 2, 3.
Нейроны 19, 20, 21, 22 осуществляют вычисление нулевого, первого, второго и третьего разрядов 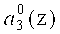 ,
, 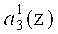 ,
, 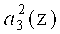 ,
, 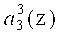 третьего коэффициента ОПС a3(z) соответственно. Причем нейрон 19 подключен к выходам нейронов 2, 4 и 6 первого слоя. Нейрон 20 - к выходам нейронов 1, 4, 5, 6 и 7. Вход нейрона 21 - к выходам нейронов 2, 3, 4, 5 и 7. Вход нейрона 22 - к выходам нейронов 1, 2, 5.
третьего коэффициента ОПС a3(z) соответственно. Причем нейрон 19 подключен к выходам нейронов 2, 4 и 6 первого слоя. Нейрон 20 - к выходам нейронов 1, 4, 5, 6 и 7. Вход нейрона 21 - к выходам нейронов 2, 3, 4, 5 и 7. Вход нейрона 22 - к выходам нейронов 1, 2, 5.
Нейроны 23, 24, 25, 26 осуществляют вычисление нулевого, первого, второго и третьего разрядов  ,
, 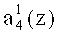 ,
, 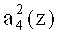 ,
,  четвертого коэффициента ОПС a4(z) соответственно. Причем входы нейрона 23 подключены к выходам нейронов 2, 4, 7, 10 первого слоя. Вход нейрона 24 - к выходам нейронов 2, 3, 5, 8, 11. Вход нейрона 25 - к выходам нейронов 3, 4, 6, 8, 9. Вход нейрона 26 - к выходам нейронов 1, 2, 3, 4, 5, 6, 9.
четвертого коэффициента ОПС a4(z) соответственно. Причем входы нейрона 23 подключены к выходам нейронов 2, 4, 7, 10 первого слоя. Вход нейрона 24 - к выходам нейронов 2, 3, 5, 8, 11. Вход нейрона 25 - к выходам нейронов 3, 4, 6, 8, 9. Вход нейрона 26 - к выходам нейронов 1, 2, 3, 4, 5, 6, 9.
Нейроны 27, 28, 29, 30 осуществляют вычисление нулевого, первого, второго и третьего разрядов 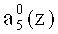 ,
, 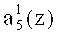 ,
,  ,
,  пятого коэффициента ОПС a5(z) соответственно. Причем вход нейрона 27 подключен к выходам нейронов 5, 9, 11 и 15 первого слоя. Вход нейрона 28 - к выходам нейронов 1, 3, 5, 7, 8, 9, 11, 12, 15. Вход нейрона 29 - к выходам нейронов 1, 2, 4, 5, 6, 8, 9, 10, 13.Вход нейрона 30 - к выходам нейронов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14 первого слоя.
пятого коэффициента ОПС a5(z) соответственно. Причем вход нейрона 27 подключен к выходам нейронов 5, 9, 11 и 15 первого слоя. Вход нейрона 28 - к выходам нейронов 1, 3, 5, 7, 8, 9, 11, 12, 15. Вход нейрона 29 - к выходам нейронов 1, 2, 4, 5, 6, 8, 9, 10, 13.Вход нейрона 30 - к выходам нейронов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14 первого слоя.
Блок памяти 31 имеет 8 входов. Первый вход 32 подключен к выходу нейрона 23. Второй вход 33 подсоединен к выходу нейрона 24. Третий вход 34 подключен к выходу нейрона 25. Четвертый вход 35 блока памяти 31 подключен к выходу нейрона 26. Пятый вход 36 блока памяти 31 подключен к выходу нейрона 27. Шестой вход 37 блока памяти 31 подключен к выходу нейрона 28. Седьмой вход 38 блока памяти 31 подключен к выходу нейрона 29. Восьмой вход 39 блока памяти 31 подключен к выходу нейрона 30. Таким образом, на первый вход 32 блока памяти 31 поступает значение нулевого разряда  четвертого коэффициента a4(z), на второй вход 33 - первый разряд
четвертого коэффициента a4(z), на второй вход 33 - первый разряд 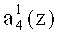 коэффициента ОПС a4(z), на третий вход 34 - второй разряд
коэффициента ОПС a4(z), на третий вход 34 - второй разряд 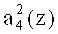 коэффициента ОПС a4(z), на четвертый вход 35 - третий разряд
коэффициента ОПС a4(z), на четвертый вход 35 - третий разряд 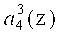 коэффициента ОПС a4(z). Значения нулевого, первого, второго и третьего разрядов
коэффициента ОПС a4(z). Значения нулевого, первого, второго и третьего разрядов 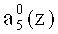 ,
, 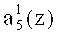 ,
,  ,
,  пятого коэффициента ОПС a5(z) поступают соответственно на пятый 36, шестой 37, седьмой 38 и восьмой 39 входы блока памяти 31.
пятого коэффициента ОПС a5(z) поступают соответственно на пятый 36, шестой 37, седьмой 38 и восьмой 39 входы блока памяти 31.
Первый вход корректирующего сумматора 47 подключен к выходу нейрона 16, а второй вход подсоединен к первому выходу 40 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 47 поступает нулевой разряд 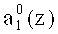 первого коэффициента ОПС a1(z), а на второй вход - корректирующее значение
первого коэффициента ОПС a1(z), а на второй вход - корректирующее значение 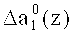 . В результате этого происходит исправление ошибки по нулевому разряду первого коэффициента а1(z).
. В результате этого происходит исправление ошибки по нулевому разряду первого коэффициента а1(z).
Первый вход корректирующего сумматора 48 подключен к выходу нейрона 17, а второй вход подсоединен ко второму выходу 41 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 48 поступает разряд  второго коэффициента ОПС a2(z), а на второй вход - корректирующее значение
второго коэффициента ОПС a2(z), а на второй вход - корректирующее значение 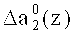 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
Первый вход корректирующего сумматора 49 подключен к выходу нейрона 18, а второй вход подсоединен ко второму выходу 42 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 49 поступает разряд 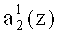 второго коэффициента ОПС a2(z), а на второй вход - корректирующее значение
второго коэффициента ОПС a2(z), а на второй вход - корректирующее значение 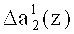 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
Первый вход корректирующего сумматора 50 подключен к выходу нейрона 19, а второй вход подсоединен ко второму выходу 43 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 50 поступает разряд 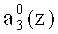 третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение
третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение 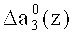 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
Первый вход корректирующего сумматора 51 подключен к выходу нейрона 20, а второй вход подсоединен ко второму выходу 44 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 51 поступает разряд 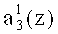 третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение
третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение 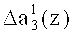 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
Первый вход корректирующего сумматора 52 подключен к выходу нейрона 21, а второй вход подсоединен ко второму выходу 45 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 52 поступает разряд 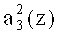 третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение
третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение 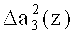 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
Первый вход корректирующего сумматора 53 подключен к выходу нейрона 22, а второй вход подсоединен ко второму выходу 46 блока памяти 31. Таким образом, на первый вход корректирующего сумматора 53 поступает разряд 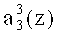 третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение
третьего коэффициента ОПС a3(z), а на второй вход - корректирующее значение 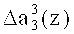 . В результате этого происходит исправление ошибки в данном разряде.
. В результате этого происходит исправление ошибки в данном разряде.
С выходов корректирующих сумматоров 47-53, которые являются выходами устройства, снимаются исправленные значения коэффициентов ОПС a1(z), a2(z), a3(z).
Блок памяти 31 предназначен для хранения констант коррекции, значение которых зависит от вычисленных величин старших коэффициентов ОПС. Зависимость значений старших коэффициентов ОПС a4(z) и a5(z) от местоположения и глубины ошибки в коде ПСКП приведены в таблице 1.

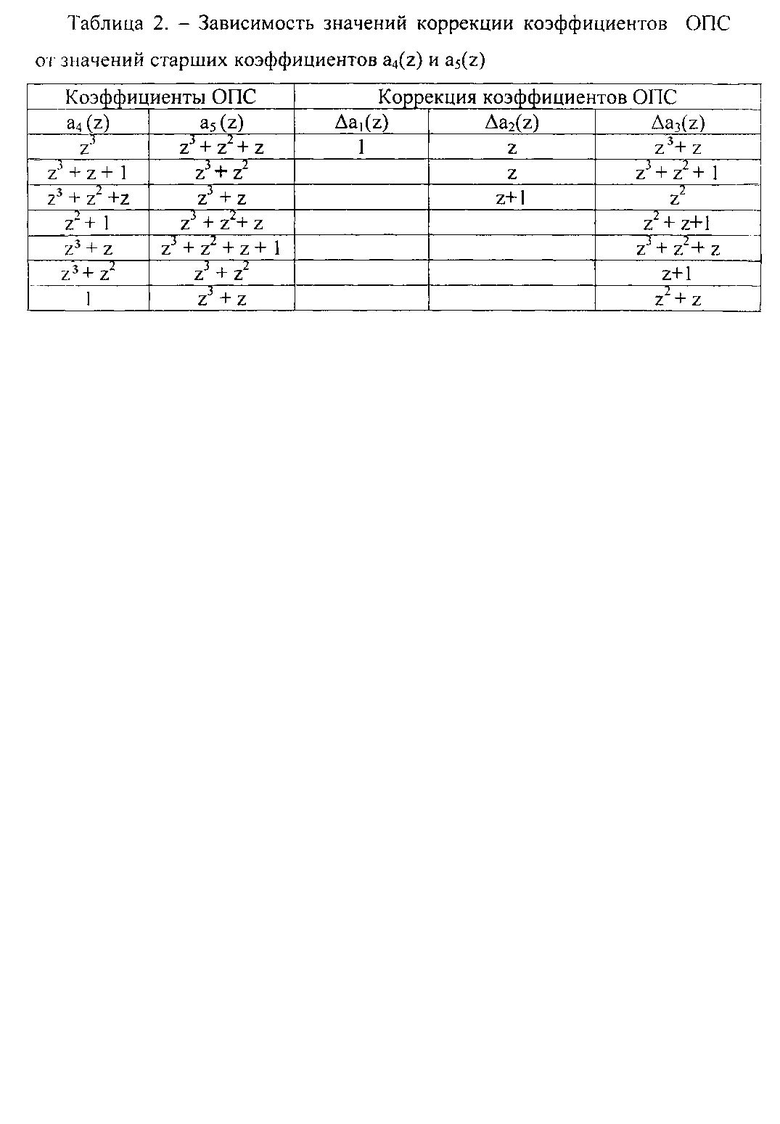
Зависимость между значениями старших коэффициентов a4(z), a5(z) и корректирующими значениями коэффициентов ОПС a1(z), a2(z), a3(z) приведена в таблице 2.
Рассмотрим работу устройства.
Пусть задан полином A(z)=z6+z5+z4+z+1, который принадлежит рабочему диапазону Ppaб(z). Тогда его код в ПСКВ имеет вид A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z) и при этом этот код не содержит ошибки. Воспользуемся выражением (10) и произведем вычисление коэффициентов ОПС. Так как полином A(z) принадлежит рабочему диапазону, то при переводе из ПСКВ в обобщенную полиадическую систему, согласно равенству (8), должны быть значения старших коэффициентов ОПС a4(z)=0 и a5(z)=0. В результате вычислений были получены следующие значения:
a1(z)=1, a2(z)=z+1, a3(z)=z3+z2+z+1, a4(z)=0, a5(z)=0.
Это свидетельствует о том, что данная кодовая комбинация, представленная в ПСКВ, не содержит ошибки.
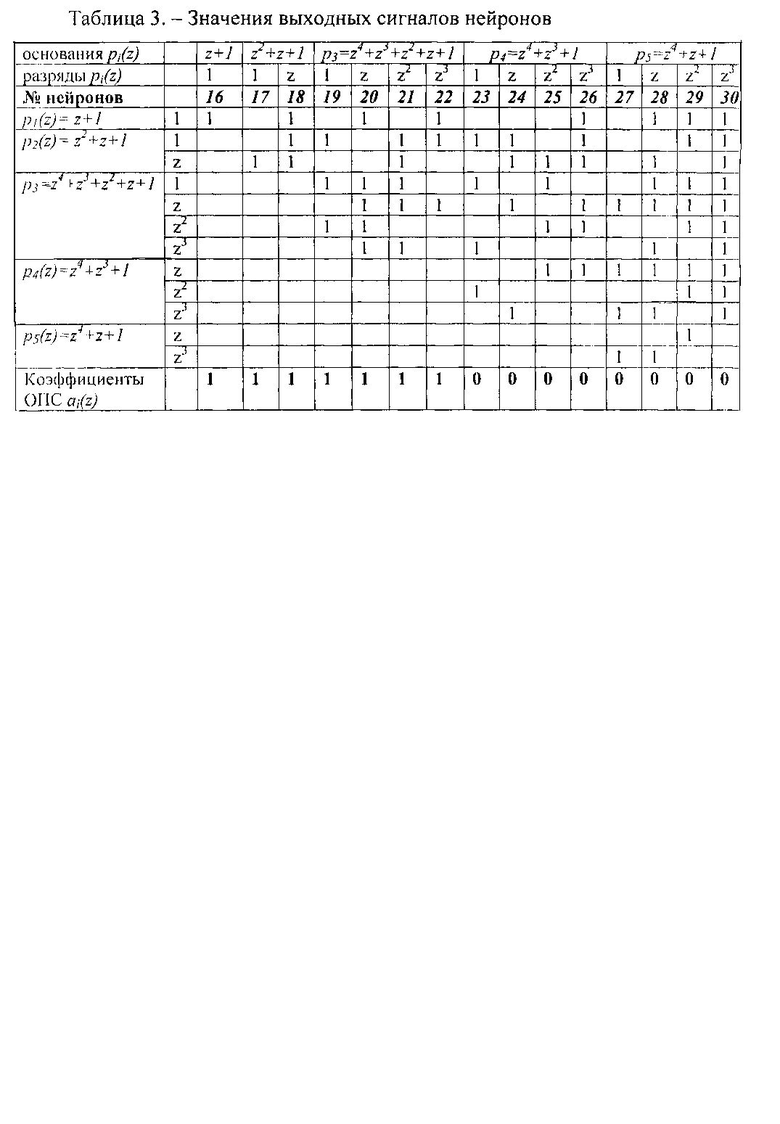
В прототипе [1] было показано, как можно провести расчет коэффициентов ОПС с использованием двухслойной нейронной сети прямого распространения. Воспользуемся таблицей 3, с помощью которой покажем работу первого и второго слоев нейронной сети. Рассмотрим получение сигнала на выходе нейрона 18, который соответствует первому разряду второго коэффициента ОПС  . Так как на его вход подается 3 единицы, то результат суммирования по модулю два (суммируем по столбцам) равен единице. Аналогичным образом вычисляются значения на выходах остальных нейронов второго слоя. Коэффициенты ОПС, полученные с помощью таблицы 3, совпали с вычисленными ранее.
. Так как на его вход подается 3 единицы, то результат суммирования по модулю два (суммируем по столбцам) равен единице. Аналогичным образом вычисляются значения на выходах остальных нейронов второго слоя. Коэффициенты ОПС, полученные с помощью таблицы 3, совпали с вычисленными ранее.
Так как старшие коэффициенты ОПС равны нулю, то это свидетельствуют, что кодовая комбинация ПСКВ не содержит ошибку, и ее не надо корректировать. В этом случае на входы блока памяти 31 поступают нулевые сигналы с выходов нейронов 23-26 и 27-30, которые соответствуют двоичному представлению коэффициентов a4(z) и a5(z), В результате этого с выходов 40-46 также снимается нулевой результат, который подается на корректирующие сумматоры 47-53. В соответствии с этим на выходах этих корректирующих сумматоров, выполняющих операцию суммирования по модулю, значения коэффициентов ОПС a1(z)=1, a2(z)=z+1, a3(z)=z3+z2+z+1, которые были получены с выходов нейронов 16-23 второго слоя, останутся без коррекции.
Пусть произошла ошибка в первом остатке кода ПСКВ и ее глубина равна 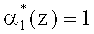
а 1(z)=0;
a 2(z)=1;
a 3(z)=z2+1;
a 4(z)=z3;
a 5(z)=z3+z2+z.
Работу на нейронной сети прямого распределения можно представить в виде таблицы 4.

Так как значения старших коэффициентов ОПС a 4(z)≠0 и a 5(z)≠0, то это свидетельствует о том, что кодовая комбинация содержит ошибку.
В соответствии с полученными значениями a 4(z)=z3 и a 5(z)=z3+z2+z единичный сигнал будет на выходе нейронов 26, 28, 29 и 30 второго слоя. Этот сигнал с выходов нейронов 26, 28, 29, 30 подается на четвертый 35, шестой 37, седьмой 38 и восьмой 39 входы блока памяти 31 соответственно.
В результате с выходов блока памяти 31, согласно данным, приведенным в таблице 2, будут сниматься корректирующие значения Δа1(z)=1, Δа2(z)=z, Δa3(z)=z3+z. Это значит, что сигналы появятся соответственно на первом 40, третьем 42, пятом 44 и седьмом 46 выходах блока памяти 31. Следовательно, эти сигналы поступят на вторые входы первого 47, третьего 49, пятого 51 и седьмого 53 корректирующих сумматоров.
В результате на выходе первого 47 корректирующего сумматора получаем
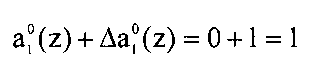
Ошибку исправили. Теперь откорректированное значение первого коэффициента ОПС a1(z)=1.
На выходе второго 48 корректирующего сумматора получаем сигнал

На выходе третьего 49 корректирующего сумматора получаем сигнал
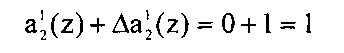
Произошло исправление ошибки. Теперь откорректированное значение первого коэффициента ОПС а2(z)=z+1.
На выходе четвертого 50 корректирующего сумматора получаем сигнал

Ошибка в разряде исправлена.
На выходе пятого 51 корректирующего сумматора получаем сигнал
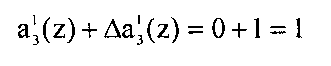
Ошибка в разряде исправлена.
На выходе шестого 52 корректирующего сумматора получаем сигнал
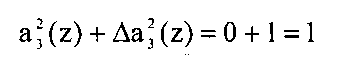
Ошибка в разряде исправлена.
На выходе седьмого 53 корректирующего сумматора получаем сигнал
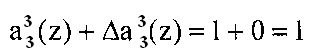
Ошибка исправлена. Теперь откорректированное значение третьего коэффициента ОПС равно a3(z)=z3+z2+z+1.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ, ПРЕДСТАВЛЕННЫХ В РАСШИРЕННЫХ ПОЛЯХ ГАЛУА GF(2) | 2004 |
|
RU2258956C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2008 |
|
RU2393529C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2008 |
|
RU2390051C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для вычисления коэффициентов обобщенной полиадической системы (ОПС), представленных в полях Галуа GF(2v). Техническим результатом является обеспечение возможности исправления ошибок в коэффициентах ОПС, которые были получены из кодовой комбинации, представленной в полиномиальной системе классов вычетов (ПСКВ). Устройство содержит двухслойную нейронную сеть, каждый слой которой содержит 15 нейронов, блок памяти и 7 корректирующих сумматоров по модулю два. 1 ил., 4 табл.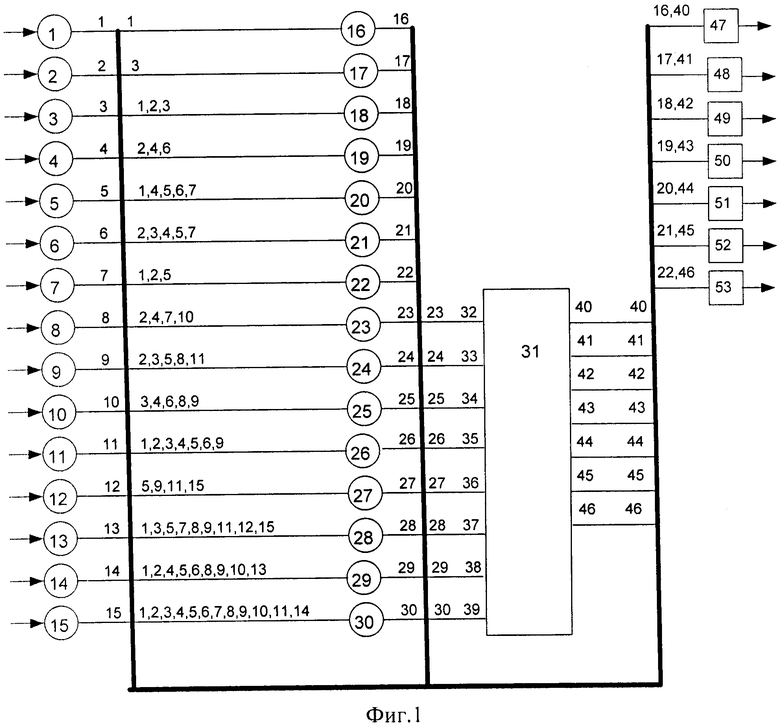
1. Устройство для вычисления коэффициентов обобщенной полиадической системы с коррекцией ошибок содержит нейронную сеть, которая имеет первый слой из пятнадцати нейронов, осуществляющий прием и распределение входного вектора, представленного в виде остатков αi(z), i=1, 2, …, n, и второй слой из пятнадцати нейронов, осуществляющих суммирование по модулю pi(z) произведения остатков на соответствующие им значения ортогональных базисов, представленных в обобщенной полиадической системе, причем вход первого нейрона второго слоя соединен с выходом первого нейрона первого слоя, вход второго нейрона второго слоя подключен к выходу третьего нейрона первого слоя, вход третьего нейрона второго слоя подключен к выходу первого, второго, третьего нейронов первого слоя, вход четвертого нейрона второго слоя соединен с выходами второго, четвертого, шестого нейронов первого слоя, вход пятого нейрона второго слоя соединен с выходами первого, четвертого, пятого, шестого, седьмого нейронов первого слоя, вход шестого нейрона второго слоя соединен с выходами второго, третьего, четвертого пятого, седьмого нейронов первого слоя, вход седьмого нейрона второго слоя соединен с выходами первого, второго, пятого нейронов первого слоя, вход восьмого нейрона второго слоя соединен с выходами второго, четвертого, седьмого, десятого нейронов первого слоя, вход девятого нейрона второго слоя соединен с выходами второго, третьего, пятого, восьмого, одиннадцатого нейронов первого слоя, вход десятого нейрона второго слоя соединен с выходами третьего, четвертого, шестого, восьмого, девятого нейронов первого слоя, вход одиннадцатого нейрона второго слоя соединен с выходами первого, второго, третьего, четвертого, пятого, шестого, девятого нейронов первого слоя, вход двенадцатого нейрона второго слоя соединен с выходами пятого, девятого, одиннадцатого, пятнадцатого нейронов первого слоя, вход тринадцатого нейрона второго слоя соединен с выходами первого, третьего, пятого, седьмого, восьмого, девятого, одиннадцатого, двенадцатого, пятнадцатого нейронов первого слоя, вход четырнадцатого нейрона второго слоя соединен с выходами первого, второго, четвертого, пятого, шестого, восьмого, девятого, десятого, тринадцатого нейронов первого слоя, вход пятнадцатого нейрона второго слоя соединен с выходами первого, второго, третьего, четвертого, пятого, шестого, седьмого, восьмого, девятого, десятого, одиннадцатого, четырнадцатого нейронов первого слоя, отличающаяся тем, что в нее дополнительно введены блок памяти и семь корректирующих сумматоров, при этом блок памяти имеет восемь входов и семь выходов, первый вход блока памяти соединен с выходом восьмого нейрона второго слоя, второй вход блока памяти соединен с выходом девятого нейрона второго слоя, третий вход блока памяти подключен к выходу десятого нейрона второго слоя, четвертый вход блока памяти подключен к выходу одиннадцатого нейрона второго слоя, пятый вход блока памяти подключен к выходу двенадцатого нейрона второго слоя, шестой вход блока памяти подключен к выходу тринадцатого нейрона второго слоя, седьмой вход блока памяти подключен к выходу четырнадцатого нейрона второго слоя, восьмой вход блока памяти подключен к выходу пятнадцатого нейрона второго слоя, при этом первый выход блока памяти подключен ко второму входу первого корректирующего сумматора, первый вход которого соединен с выходом первого нейрона второго слоя, второй выход блока памяти подключен ко второму входу второго корректирующего сумматора, первый вход которого соединен с выходом второго нейрона второго слоя, третий выход блока памяти подключен ко второму входу третьего корректирующего сумматора, первый вход которого подключен к выходу третьего нейрона второго слоя, четвертый выход блока памяти подключен ко второму входу четвертого корректирующего сумматора, первый вход которого подключен к выходу четвертого нейрона второго слоя, пятый выход блока памяти подключен ко второму входу пятого корректирующего сумматора, первый вход которого подключен к выходу пятого нейрона второго слоя, шестой выход блока памяти подключен ко второму входу шестого корректирующего сумматора, первый вход которого подключен к выходу шестого нейрона второго слоя, седьмой выход блока памяти подключен ко второму входу седьмого корректирующего сумматора, первый вход которого подключен к выходу седьмого нейрона второго слоя.
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ, ПРЕДСТАВЛЕННЫХ В РАСШИРЕННЫХ ПОЛЯХ ГАЛУА GF(2) | 2004 |
|
RU2258956C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| US 2011231465 A1, 22.09.2011 | |||
| US 4107783 A, 15.08.1978. | |||
Авторы
Даты
2016-05-20—Публикация
2015-05-14—Подача