Устройство относится к вычислительной технике и может быть использовано как для контроля и исправления ошибок при передаче информации, так и при проведении арифметических операций в ЭВМ.
Известно устройство спектрального обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов (ПСКВ) (патент RU 2301441, кл. G06F 7/72), содержащее три информационных входа и два контрольных входа, регистр, блок вычисления интервального полинома, блок спектрального анализа, постоянное запоминающее устройство, корректирующий сумматор, выход.
Недостатками известного устройства являются его сложность и значительные схемные затраты.
Технический результат, достигаемый при осуществлении заявленного изобретения, заключается в снижении аппаратурных затрат на определение местоположения и глубины ошибки в модулярном коде ПСКВ и последующей ее коррекции.
Указанный технический результат достигается за счет удаления из структуры постоянного запоминающего устройства, где хранятся корректирующие значения Δαкор(z), и введения в состав блока спектрального анализа, представляющего собой двухслойную нейронную сеть (НС) третьего и четвертого слоев нейронов.
Функциональная схема устройства представлена на фиг.1. Устройство содержит вход 1, на который подают код полинома

где αi(z) - остатки по рабочим и контрольным основаниям ПСКВ pi(z);
i=1÷n - количество оснований ПСКВ,
он подсоединен ко входу регистра 2, выход которого подключен ко входу блока вычисления интервального полинома 3, реализующего вычисление во временной области
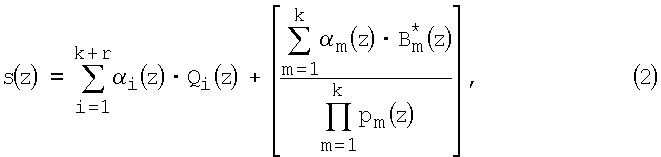
где Qi(z) - частное от деления ортогонального базиса Bi(z) на величину
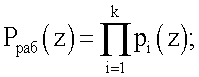
k - количество рабочих оснований ПСКВ;
r=n-k - количество контрольных оснований;
Bm *(z) - ортогональный базис безызбыточной ПСКВ.
Выход блока 3 подключен ко входу блока спектрального анализа 4, выход которого соединен со вторым входом корректирующего сумматора 5, первый вход которого подключен к выходу регистра 2, по которому осуществляется передача остатков модулярного кода ПСКВ по рабочим и контрольным основаниям. Выход корректирующего сумматора 5 является выходом 6 устройства.
Рассмотрим работу устройства. На вход 1 устройства подается три остатка по рабочим основаниям p1(z)=z+1; р2(z)=z2+z+1; р3(z)=z4+z3+z2+z+1 и двум контрольным основаниям p4(z)=z4+z3+1 и p5(z)=z4+z+1. В этом случае рабочий диапазон будет равен
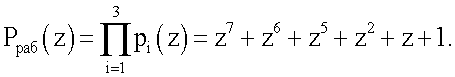
Известно, что если полином A(z), представленный в виде ПСКВ, принадлежит рабочему диапазону, то он не содержит ошибок.
В противном случае A(z)=(α1(z), α2(z), α3(z), α4(z), α5(z)) содержит ошибку.
При этом если модулярный код A(z) не содержит ошибок, то определенные спектральные составляющие интервального полинома (2), определяемые выражением
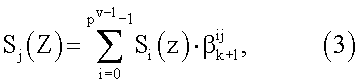
где Sj(Z) - j-ая спектральная составляющая полинома s(z);
βk+l - первообразный элемент расширенного поля GF(pv), порожденный полиномом pk+l(z); l=1, 2, …, r, j=0, …, pv-1-1,
будут равны 0.
Такими спектральными составляющими будут S1(Z1), S2(Z1), S4(Z1), S8(Z1), а также S7(Z1), S11(Z1), S13(Z1), S14(Z1). Данные спектральные составляющие интервального полинома s(z) соответствуют корням контрольных оснований p4(z) и p5(z) соответственно.
Появление ошибки в n-мерной комбинации A(z) по i-тому основанию и глубиной Δαi(z) приводит к смещению последнего во временной области на величину 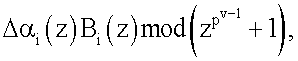
т.е.
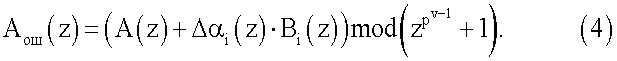
При этом наблюдается смещение спектра. В таблице 1 представлены смещения спектра при различных ошибках по всем основаниям ПСКВ расширенного поля Галуа GF(24).
Анализируя смещения первой гармоники S1 (Z), сложно составить соответствие между ее величиной и местоположением ошибки Δαi(z), которое приведено в таблице 2.
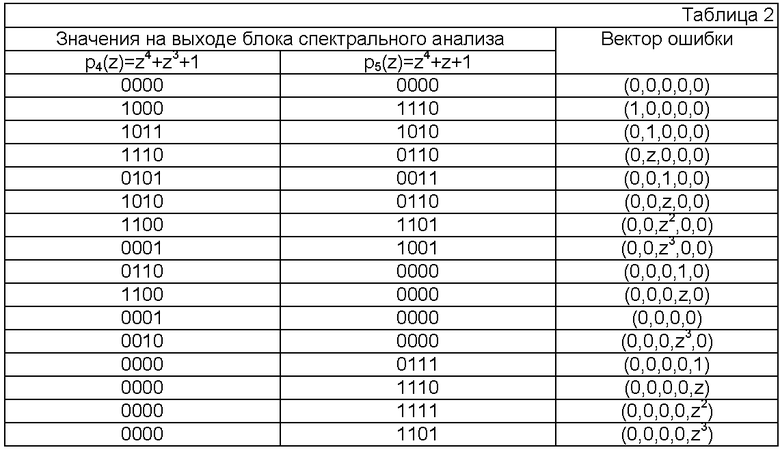
Анализ таблицы показывает, что определить значения Δαi(z) можно с использованием третьего слоя нейронов блока спектрального анализа.
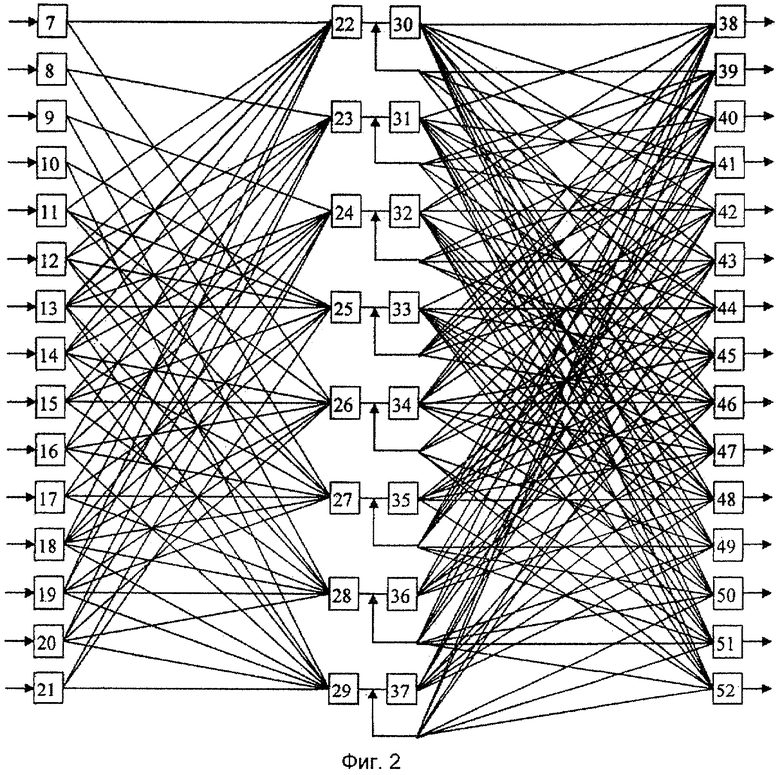
Структура блока спектрального анализа показана на фиг.2. Он представляет собой четырехслойную нейронную сеть, первый слой которой содержит пятнадцать нейронов 7-21, второй слой - восемь нейронов 22-29, третий слой - восемь нейронов 30-37, а четвертый слой - пятнадцать нейронов 38-52. Нейроны первого слоя осуществляют распределение значений, поступивших на их входы, нейроны второго слоя реализуют базовую операцию суммирования по модулю два, нейроны третьего слоя реализуют базовую операцию «НЕ», а нейроны четвертого слоя - операцию «логическое И». Причем входы нейрона 22 второго слоя соединены с выходами 7, 11, 12, 13, 14, 16, 18, 19 нейронов первого слоя. Входы нейрона 23 второго слоя соединены с выходами 8, 12, 13, 14, 15, 17, 19, 20 нейронов первого слоя. Входы нейрона 24 второго слоя соединены с выходами 9, 13, 14, 15, 16, 18, 20, 21 нейронов первого слоя. Входы нейрона 25 второго слоя соединены с выходами 10, 11, 12, 13, 15, 17, 18, 21 нейронов первого слоя. Выходы нейронов 22, 23, 24, 25 представляют собой соответственно нулевой, первый, второй и третий разряды первой спектральной составляющей S1 (Z1) по модулю p4(z)=z4+z3+1.
Входы нейрона 26 второго слоя соединены с выходами 7, 11, 14, 15, 16, 18, 19, 20 нейронов первого слоя. Входы нейрона 27 второго слоя соединены с выходами 8, 11, 12, 14, 16, 17, 18, 19 нейронов первого слоя. Входы нейрона 28 второго слоя соединены с выходами 9, 12, 13, 15, 17, 18, 19, 20 нейронов первого слоя. Входы нейрона 29 второго слоя соединены с выходами 10, 13, 14, 16, 18, 19, 20, 21 нейронов первого слоя. Выходы нейронов 26, 27, 28, 29 представляют собой соответственно нулевой, первый, второй и третий разряды первой составляющей S1 (Z1) по модулю p5(z)=z4+z+1.
Вход нейрона 30 третьего слоя соединен с выходом нейрона 22 второго слоя. Вход нейрона 31 третьего слоя соединен с выходом нейрона 23 второго слоя. Вход нейрона 32 третьего слоя соединен с выходом нейрона 24 второго слоя. Вход нейрона 33 третьего слоя соединен с выходом нейрона 25 второго слоя. Вход нейрона 34 третьего слоя соединен с выходом нейрона 26 второго слоя. Вход нейрона 35 третьего слоя соединен с выходом нейрона 27 второго слоя. Вход нейрона 36 третьего слоя соединен с выходом нейрона 28 второго слоя. Вход нейрона 37 третьего слоя соединен с выходом нейрона 29 второго слоя. Нейроны 30-37 третьего слоя реализуют операцию «логическое НЕ».
Входы нейрона 38 четвертого слоя соединены с выходами 25, 27, 28, 29 нейронов второго слоя и выходами 30, 31, 32, 34 нейронов третьего слоя. Входы нейрона 39 четвертого слоя соединены с выходами 22, 23, 25, 27, 29 нейронов второго слоя и выходами 32, 34, 36 нейронов третьего слоя. Входы нейрона 40 четвертого слоя соединены с выходами 23, 24, 25, 27, 28 нейронов второго слоя и выходами 30, 34, 37 нейронов третьего слоя. Входы нейрона 41 четвертого слоя соединены с выходами 22, 24, 26, 27 нейронов второго слоя и выходами 31, 33, 36, 37 нейронов третьего слоя. Входы нейрона 42 четвертого слоя соединены с выходами 23, 25, 27, 28 нейронов второго слоя и выходами 30, 32, 34, 37 нейронов третьего слоя. Входы нейрона 43 четвертого слоя соединены с выходами 24, 25, 26, 28, 29 нейронов второго слоя и выходами 30, 31, 35 нейронов третьего слоя. Входы нейрона 44 четвертого слоя соединены с выходами 22, 26, 29 нейронов второго слоя и выходами 31, 32, 33, 35, 36 нейронов третьего слоя. Входы нейрона 45 четвертого слоя соединены с выходами 23, 24 нейронов второго слоя и выходами 30, 33, 34, 35, 36, 37 нейронов третьего слоя. Входы нейрона 46 четвертого слоя соединены с выходами 24, 25 нейронов второго слоя и выходами 30, 31, 34, 35, 36, 37 нейронов третьего слоя. Входы нейрона 47 четвертого слоя соединены с выходами 22 нейронов второго слоя и выходами 31, 32, 33, 34, 35, 36, 37 нейронов третьего слоя. Входы нейрона 48 четвертого слоя соединены с выходами 23 нейронов второго слоя и выходами 30, 32, 33, 34, 35, 36, 37 нейронов третьего слоя. Входы нейрона 49 четвертого слоя соединены с выходами 26, 27, 28 нейронов второго слоя и выходами 30, 31, 32, 33, 37 нейронов третьего слоя. Входы нейрона 50 четвертого слоя соединены с выходами 27, 28, 29 нейронов второго слоя и выходами 30, 31, 32, 33, 34 нейронов третьего слоя. Входы нейрона 51 четвертого слоя соединены с выходами 26, 27, 28, 29 нейронов второго слоя и выходами 30, 31, 32, 33 нейронов третьего слоя. Входы нейрона 52 четвертого слоя соединены с выходами 26, 28, 29 нейронов второго слоя и выходами 30, 31, 32, 33, 35 нейронов третьего слоя.
Нейроны 38-52 четвертого слоя реализуют базовую операцию «логическое умножение». С выходов данных нейронов снимается значение Δαi(z)Bi(z)modPполн(z), i=1, 2, 3, 4, 5, представленное в модулярном коде.
При этом корректирующее значение Δα1 кор(z)=Δα1(z)В1(z)modPполн(z), где
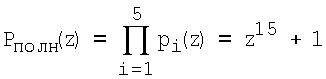 - полный диапазон; снимается с выхода нейрона 38 четвертого слоя. Корректирующее значение Δα2 кор(z)=Δα2(z)B2(z)modPполн(z) снимается с выходов нейронов 39 и 40 четвертого слоя. Корректирующее значение Δα3 кор(z)=Δα3(z)В3(z)modРполн(z) снимается с выходов нейронов 41-44 четвертого слоя. Корректирующее значение Δα4 кор(z)=Δα4(z)В4(z)modРполн(z) снимается с выходов нейронов 45-48 четвертого слоя. Корректирующее значение Δα5 кор(z)=Δα5(z)В5(z)modРполн(z) снимается с выходов нейронов 49-52 четвертого слоя. Данные значения Δαi кор(z)=Δαi(z)Bi(z)modPполн(z) представлены в двоичном коде, при этом снимаются с выходов 38, 40, 44, 48, 52 нейронов четвертого слоя. Выходы нейронов четвертого слоя являются выходом блока спектрального анализа.
- полный диапазон; снимается с выхода нейрона 38 четвертого слоя. Корректирующее значение Δα2 кор(z)=Δα2(z)B2(z)modPполн(z) снимается с выходов нейронов 39 и 40 четвертого слоя. Корректирующее значение Δα3 кор(z)=Δα3(z)В3(z)modРполн(z) снимается с выходов нейронов 41-44 четвертого слоя. Корректирующее значение Δα4 кор(z)=Δα4(z)В4(z)modРполн(z) снимается с выходов нейронов 45-48 четвертого слоя. Корректирующее значение Δα5 кор(z)=Δα5(z)В5(z)modРполн(z) снимается с выходов нейронов 49-52 четвертого слоя. Данные значения Δαi кор(z)=Δαi(z)Bi(z)modPполн(z) представлены в двоичном коде, при этом снимаются с выходов 38, 40, 44, 48, 52 нейронов четвертого слоя. Выходы нейронов четвертого слоя являются выходом блока спектрального анализа.
Устройство работает следующим образом. На вход 1 устройства подается модулярный код полинома A(z)=(α1(z), α2(z), α3(z), α4(z), α5(z)), который поступает на вход регистра 2, предназначенного для хранения принятой комбинации, данный модулярный код имеет 3 рабочих основания p1(z)=z+1, p2(z)=z2+z+1, р3(z)=z4+z3+z2+z+1, которые образуют диапазон
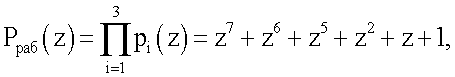
и два контрольных основания p4(z)=z4+z3+1 и p5(z)=z4+z+1. Пусть в качестве исходного полинома выбираем A(z)=z6+z+1, принадлежащий рабочему диапазону. Тогда данный полином представляется в виде кода ПСКВ A(z)=(1,z,1,z3+z2,z3+z2+z+1).
С выхода регистра 2 модулярный код поступает на вход блока вычисления интервального полинома 3. Для системы ПСКВ имеем ортогональные базисы
B1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
В2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z;
В3(z)=z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z;
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3;
B5(z)=z12+z9+z8+z6+z4+z3+z2+z.
Тогда
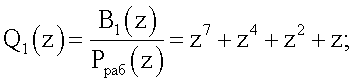
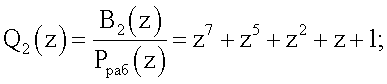
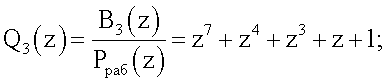
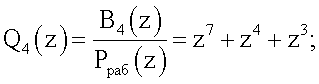
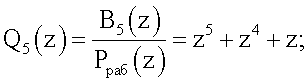
B1 *(z)=B1(z)modPраб(z)=z6+z4+z3+z2+1;
B2 *(z)=B2(z)modPраб(z)=z6+z5+z+1;
B3 *(z)=B3(z)modPраб(z)=z5+z4+z3+z2+1.
Согласно выражению (2) имеем s1(z)=z10+z9+z7+z6+z5+z2+z.
Данное значение интервального полинома подается на входы нейронов первого слоя блока спектрального анализа 4. В таблице 3 представлено распределение сигналов на выходе нейронов первого слоя.
Данные значения подаются на нейроны второго слоя, на выходе которого получается сигнал в соответствии сданными, представленными в таблицах 4, 5.


Полученный нулевой результат на выходе нейронов второго слоя поступает на соответствующие входы нейронов третьего и четвертого слоев. Так как данные нейроны реализуют базовую операцию «НЕ» и операцию логического умножения, то на выходах нейронов четвертого слоя будет нулевой результат. Этот сигнал с выхода блока спектрального анализа 4 поступает на второй вход корректирующего сумматора 5, на первый вход которого подается с регистра 2 модулярный код А(z). Корректирующий сумматор 5 реализует операцию
Aиспр(z)=A(z)+Δαкор(z)=(1,z,1,z3+z2,z3+z2+z+1)+(0,0,0,0,0)=
=(1,z,1,z3,+z2,z3+z2+z+1).
Полученное значение подается на выход устройства 6.
Допустим, что ошибка произошла по второму основанию p2(z)=z2+z+1, а ее глубина Δα2(z)=z. Тогда модулярная комбинация имеет вид
Aош(z)=(1,0,1,z3+z2,z3+z2+z+1).
Данный модулярный код ПСКВ через вход 1 поступает на регистр 2, с выхода которого подается на блок вычисления интервального полинома 3.
С выхода блока вычисления интервального полинома 3 выдается двоичный код интервального полинома
s(z)=z10+z9+z8+z7+z5+z+1.
Данное значение поступает на входы нейронов первого слоя блока спектрального анализа 4. Сигналы на выходе этих нейронов определяются таблицей 6.
Данные значения подаются на входы нейронов второго слоя, на выходе которых появляются сигналы в соответствии с таблицами 7 и 8.


Ненулевой результат спектральных составляющих по модулю p4(z)=z4+z3+1-s1(z)=1110=z3+z2+z, по модулю p5(z)=z4+z+1-s2(z)=0110=z2+z свидетельствует о том, что комбинация Аош(z) содержит ошибку. Данные сигналы поступают на входы нейронов третьего и четвертого слоев.
В таблице 9 представлены сигналы на выходе нейронов третьего слоя.

В таблице 10 представлены сигналы на выходе нейронов четвертого слоя.
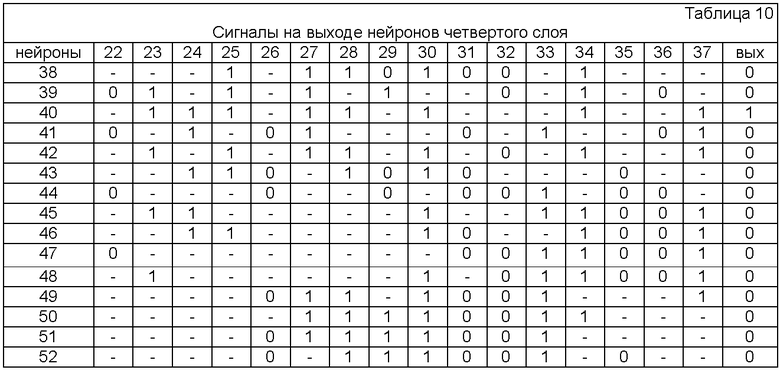
Полученный результат на выходе нейронов четвертого слоя соответствует
Δα2 кор(z)=(0,z,0,0,0).
Данный модулярный код с выхода блока спектрального анализа 4 поступает на второй вход корректирующего сумматора 5, на первый вход которого подается код ПСКВ из регистра 2. Корректирующий сумматор 5 реализует операцию
Aиспр(z)=A(z)+Δαкор(z)=(1,0,1,z3+z2,z3+z2+z+1)+(0,z,0,0,0)=
=(1,z,1,z3+z2,z3+z2+z+1).
Ошибка исправлена.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2008 |
|
RU2393529C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ, ПРЕДСТАВЛЕННЫХ В РАСШИРЕННЫХ ПОЛЯХ ГАЛУА GF(2) | 2004 |
|
RU2258956C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
Изобретение относится к вычислительной технике и, в частности, к модулярным нейрокомпьютерным средствам и предназначено для определения ошибок в кодовых конструкциях непозиционного кода полиномиальной системы классов вычетов (ПСКВ), представленных в расширенных полях Галуа GF(2v). Техническим результатом является снижение аппаратурных затрат. Устройство содержит регистр, блок вычисления интервального полинома, корректирующий сумматор, блок спектрального анализа, который является четырехслойной нейронной сетью, при этом первый слой предназначен для записи интервального полинома, представленного в виде двоичного кода, второй слой предназначен для вычисления первых спектральных составляющих по контрольным основаниям, третий слой - для инверсии полученных значений, а четвертый слой - для вычисления корректирующего значения, представленного в полиномиальной системе классов вычетов. 2 ил., 10 табл.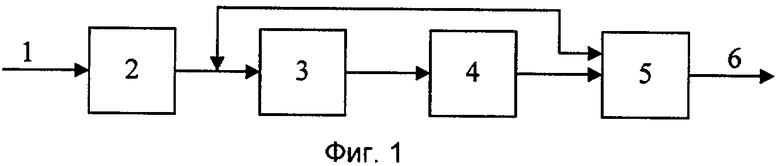
Устройство спектрального обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов содержит вход устройства, регистр, блок вычисления интервального полинома, блок спектрального анализа, корректирующий сумматор, выход которого является выходом устройства, причем вход регистра подключен ко входу устройства, а выход регистра подсоединен ко входу блока вычисления интервального полинома, выход которого подключен к входу блока спектрального анализа, кроме того, выход регистра подсоединен к первому входу корректирующего сумматора, отличающееся тем, что выход блока спектрального анализа подсоединен ко второму входу корректирующего сумматора, при этом блок спектрального анализа представляет собой четырехслойную нейронную сеть, первый слой которой содержит пятнадцать нейронов, второй слой - восемь нейронов, третий слой - восемь нейронов, четвертый слой - пятнадцать нейронов, при этом первый слой предназначен для записи интервального полинома, представленного в виде двоичного кода, второй слой предназначен для вычисления первых спектральных составляющих по контрольным основаниям, третий слой - для инверсии полученных значений, а четвертый слой - для вычисления корректирующего значения, представленного в полиномиальной системе классов вычетов, причем входы нейронов первого слоя являются входом блока спектрального анализа, а выходы нейронов четвертого слоя являются выходом блока спектрального анализа, при этом входы первого нейрона второго слоя подключены к выходам первого, пятого, шестого, седьмого, восьмого, десятого, двенадцатого, тринадцатого нейронов первого слоя, входы второго нейрона второго слоя подключены к выходам второго, шестого, седьмого, восьмого, девятого, одиннадцатого, тринадцатого, четырнадцатого нейронов первого слоя, входы третьего нейрона второго слоя подключены к выходам третьего, седьмого, восьмого, девятого, десятого, двенадцатого, четырнадцатого, пятнадцатого нейронов первого слоя, входы четвертого нейрона второго слоя подключены к выходам четвертого, пятого, шестого, седьмого, девятого, одиннадцатого, двенадцатого, пятнадцатого нейронов первого слоя, входы пятого нейрона второго слоя подключены к выходам первого, пятого, восьмого, девятого, десятого, двенадцатого, тринадцатого, четырнадцатого нейронов первого слоя, входы шестого нейрона второго слоя подключены к выходам второго, пятого, шестого, восьмого, десятого, одиннадцатого, двенадцатого, тринадцатого нейронов первого слоя, входы седьмого нейрона второго слоя подключены к выходам третьего, шестого, седьмого, девятого, одиннадцатого, двенадцатого, тринадцатого, четырнадцатого нейронов первого слоя, входы восьмого нейрона второго слоя подключены к выходам четвертого, седьмого, восьмого, десятого, двенадцатого, тринадцатого, четырнадцатого, пятнадцатого нейронов первого слоя, вход i-го нейрона третьего слоя, i=1…8, соединен с выходом i-го нейрона второго слоя, входы первого нейрона четвертого слоя подключены к выходам четвертого, шестого, седьмого, восьмого нейронов второго слоя и выходам первого, второго, третьего, пятого нейронов третьего слоя, входы второго нейрона четвертого слоя подключены к выходам первого, второго, четвертого, шестого, восьмого нейронов второго слоя и выходам третьего, пятого, седьмого нейронов третьего слоя, входы третьего нейрона четвертого слоя подключены к выходам второго, третьего, четвертого, шестого, седьмого нейронов второго слоя и выходам первого, пятого, восьмого нейронов третьего слоя, входы четвертого нейрона четвертого слоя подключены к выходам первого, третьего, пятого, шестого нейронов второго слоя и выходам второго, четвертого, седьмого, восьмого нейронов третьего слоя, входы пятого нейрона четвертого слоя подключены к выходам второго, четвертого, шестого, седьмого нейронов второго слоя и выходам первого, третьего, пятого, восьмого нейронов третьего слоя, входы шестого нейрона четвертого слоя подключены к выходам третьего, четвертого, пятого, седьмого, восьмого нейронов второго слоя и выходам первого, второго, шестого нейронов третьего слоя, входы седьмого нейрона четвертого слоя подключены к выходам первого, пятого, восьмого нейронов второго слоя и выходам второго, третьего, четвертого, шестого, седьмого нейронов третьего слоя, входы восьмого нейрона четвертого слоя подключены к выходам второго, третьего нейронов второго слоя и выходам первого, четвертого, пятого, шестого, седьмого, восьмого нейронов третьего слоя, входы девятого нейрона четвертого слоя подключены к выходам третьего, четвертого нейронов второго слоя и выходам первого, второго, пятого, шестого, седьмого, восьмого нейронов третьего слоя, входы десятого нейрона четвертого слоя подключены к выходу первого нейрона второго слоя и выходам второго, третьего, четвертого, пятого, шестого, седьмого, восьмого нейронов третьего слоя, входы одиннадцатого нейрона четвертого слоя подключены к выходу второго нейрона второго слоя и выходам первого, третьего, четвертого, пятого, шестого, седьмого, восьмого нейронов третьего слоя, входы двенадцатого нейрона четвертого слоя подключены к выходам пятого, шестого, седьмого нейронов второго слоя и выходам первого, второго, третьего, четвертого, восьмого нейронов третьего слоя, входы тринадцатого нейрона четвертого слоя подключены к выходам шестого, седьмого, восьмого нейронов второго слоя и выходам первого, второго, третьего, четвертого, пятого нейронов третьего слоя, входы четырнадцатого нейрона четвертого слоя подключены к выходам пятого, шестого, седьмого, восьмого нейронов второго слоя и выходам первого, второго, третьего, четвертого нейронов третьего слоя, входы пятнадцатого нейрона четвертого слоя подключены к выходам пятого, седьмого, восьмого нейронов второго слоя и выходам первого, второго, третьего, четвертого, шестого нейронов третьего слоя.
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| Устройство для обнаружения и исправления ошибок арифметических преобразований полиномиальных кодов | 1979 |
|
SU894711A1 |
| Устройство для пластикации и впрыска полимерных материалов | 1975 |
|
SU582749A3 |
| US 5136592 A, 04.08.1992 | |||
| JP 11126199 A, 11.05.1999. | |||
Авторы
Даты
2010-05-20—Публикация
2008-07-09—Подача