Устройство относится к области вычислительной техники, в частности может быть использовано как для контроля и исправления ошибки при передаче информации, так и при проведении арифметических операций в расширенных полях Галуа GF(2v).
Известно устройство для обнаружения и исправления ошибок (СССР №714399, 08.02.1980, G 06 F 11/08), содержащее регистр, два блока модульной свертки, предназначенных для вычисления остатков числа по контрольным основаниям, два модульных сумматора, предназначенных для вычисления синдрома ошибки по первому и второму контрольному основаниям, блок памяти, предназначенный для хранения констант, третий сумматор, предназначенный для получения исправленного числа путем суммирования ошибочного числа с константой ошибки.
Недостатком устройства является низкое быстродействие вследствие отдельного последовательного применения блоков модульной свертки, предназначенных для вычисления остатков числа по контрольным основаниям и сумматоров, для вычисления синдромов ошибки по первому и второму контрольным основаниям.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является повышение скорости обнаружения и коррекции ошибок.
Указанный технический результат достигается за счет применения полиномиальной системы классов вычетов (ПСКВ), в которой в качестве основания системы используется минимальные многочлены pi(z), i=1, 2, ..., k+r, определенные в расширенных полях Галуа GF(2v) и нейросетевых технологий, а также применения псевдоортогональных полиномов, определяемых в данной ПСКВ.
Особенность ПСКВ состоит в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но также и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства класса вычетов. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из n оснований ПСКВ (k<n), то это позволит осуществить разбиение полного диапазона Рполн(z) расширенного поля Галуа GF(pv) на два непересекающихся подмножества.
Первое подмножество называется рабочим диапазоном и определяется выражением
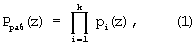
Многочлен A(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона Pполн(z), то есть принадлежит рабочему диапазону A(z)∈Pраб(z).
Второе подмножество GF(рv), определяемое произведением r=n-k контрольных оснований
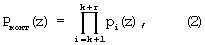
задает совокупность запрещенных комбинаций. Если A(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома A(z) относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация A(z)=(α1(z), α2(z), ..., αk+r(z)) разрешенной или содержит ошибочные символы.
В основу математической модели определения позиционной характеристики - нормированного следа полинома A(z) положена китайская теорема об остатках, согласно которой
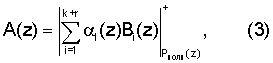
где 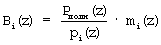 и
и 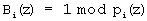 - ортогональный базис i-го основания; mi(z) - вес ортогонального базиса.
- ортогональный базис i-го основания; mi(z) - вес ортогонального базиса.
С другой стороны A(z) можно представить в виде суммы ортогональных полиномов 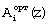 , у которых все остатки равны нулю за исключением основания pi(z)
, у которых все остатки равны нулю за исключением основания pi(z)
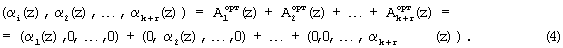
Тогда на основании равенств (3) и (4) очевидно, что
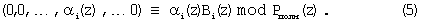
Если положить условие, A(z)∈Рраб(z), то справедливо
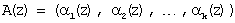
Согласно китайской теореме об остатках полином можно представить в виде
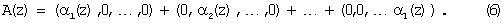
Тогда каждое слагаемое выражения (6) представляет собой
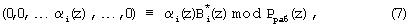
где  - ортогональный базис безизбыточной системы оснований ПСКВ.
- ортогональный базис безизбыточной системы оснований ПСКВ.
Наряду с ортогональными полиномами 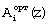 в модулярных кодах нашли широкое применение псевдоортогональные полиномы, которые представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям
в модулярных кодах нашли широкое применение псевдоортогональные полиномы, которые представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям
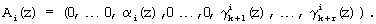
Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безизбыточной системы оснований полиномиальной системы классов вычетов 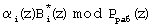 .
.
Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), ..., pk(z) на r контрольных оснований pk+1(z), ..., pk+r(z) и представим ортогональные полиномы 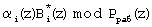 в виде
в виде
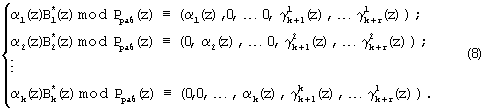
Выражение (8) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.
Подставив выражение (8) в равенство (6), и учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем

Следовательно, справедливо
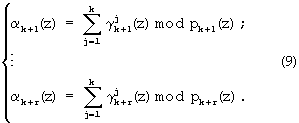
Таким образом, на основании выражения (9) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (8), можно вычислить значения остатков по контрольным основаниям 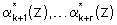 согласно
согласно
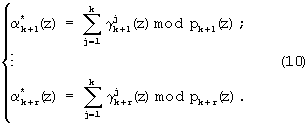
Затем на основании полученных значений 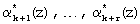 и значений αk+1(z), ..., αk+r(z), поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражению
и значений αk+1(z), ..., αk+r(z), поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражению
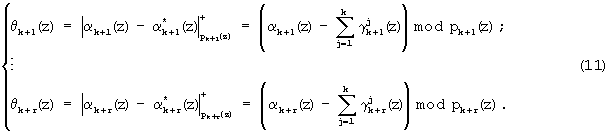
Если синдром ошибки равен нулю, т.е.
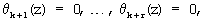
то исходный полином A(z)∈Pраб(z) является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.
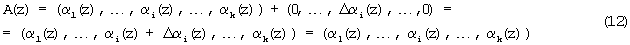 где (0, ..., Δα(z), ..., 0) - вектор ошибки модулярного кода; Δαi(z) - глубина ошибки по i-му модулю;
где (0, ..., Δα(z), ..., 0) - вектор ошибки модулярного кода; Δαi(z) - глубина ошибки по i-му модулю; 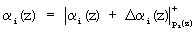 .
.
Структура устройства представлена на фигуре 1. Устройство состоит из регистра 2, предназначенного для хранения остатков по рабочим и контрольным основанием ПСКВ в течение времени обнаружения ошибки, вход которого соединен со входом 1 устройства, блока вычисления синдрома ошибки 3, входы которого соединены с выходами регистра 2, блокам памяти 4, предназначенного для хранения констант - векторов ошибки, входы которого подключены к выходам блока вычисления синдрома ошибки 3, сумматора 5, осуществляющего исправления ошибки путем суммирования исправленной (ошибкой) комбинации кода ПСКВ с вектором ошибки, первый, второй и третий входы которого соединены соответственно с тремя первыми выходами регистра 2 по которым передаются остатки рабочих оснований, а четвертый вход соединен с выходом блока памяти 4, выход сумматора 5 является выходом 6 устройства.
Работа устройство для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов осуществляется следующим образом. На вход 1 устройства для коррекции ошибок в ПСКВ подается контролируемое число, представленное в полиномиальной форме
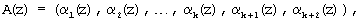
где αi(z) - остаток полинома A(z) по модулю pi(z); p1(z), p2(z), ..., pk(z) - рабочие основания системы ПСКВ; рk+1(z), pk+2(z) - контрольные основания. Данный код записывается в регистр 2. Затем с выхода регистра 2 код ПСКВ в двоичном виде поступает на вход блока вычисления синдрома ошибки 3, который представляет собой двухслойную нейронную сеть. Модулярный код ПСКВ A(z)=(α1(z), α2(z), ..., αk(z), αk+1(z), αk+2(z)) записывается нейронами первого слоя блока вычисления синдрома ошибки 3. С выхода нейронов первого слоя сигналы в двоичном виде поступают на второй слой нейронной сети, который осуществляет вычисление синдрома ошибки согласно выражению (11). С выхода нейронов второго слоя значение синдрома ошибки в двоичном коде θk+1(z), ..., θk+r(z) подается на вход блока 4 памяти, где осуществляется выбор оттуда соответствующей константы ошибки. Эта константа ошибки поступает на четвертый вход сумматора 5, где суммируется со значением A(z)=(α1(z), α2(z), ..., αk(z)), представленным по рабочим основаниям, поступившим с выходов регистра 3 на первые три входа сумматора 5. Исправленное значение A(z) согласно равенству (12) с выхода сумматора 5 подается на выход 6 устройства.
В качестве примера рассмотрим расширенное поле Галуа GF(24), в котором определены следующие основания:
p1(z)=z+1; р2(z)=z2+z+l; p3(z)=z4+z3+z2+z+1; p4(z)=z4+z3+1; p5(z)=z4+z+1, где p1(z), p2(z), р3(z) - рабочие основания, p4(z), p5(z) - контрольные основания ПСКВ. Тогда согласно выражению (1) имеем Pраб(z)=z7+z6+z5+z2+z+1.
В полной системе оснований ПСКВ поля GF(24) определены следующие ортогональные базисы:
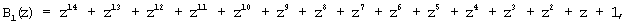
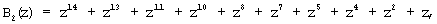
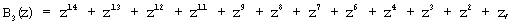
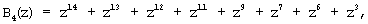
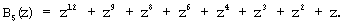
Используя сравнимость ортогональных базисов безызбыточной и полной системы по рабочему диапазону, определим значения ортогональных базисов безызбыточной системы оснований p1(z)=z+1; p2(z)=z2+z+1; p3(z)=z4+z3+z2+z+1. Тогда
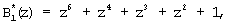
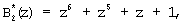
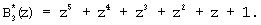
На основании полученных значений определим все псевдоортогональные полиномы для ПСКВ GF(24), учитывая невозможность выхода за пределы рабочего диапазона Рраб(z)=z7+z6+z5+z2+z+1. Полученные значения представлены в таблице 1.
Псевдоортогональные полиномы ПСКВ поля GF(24)
Если полином A(z)∈Pраб, то справедливо
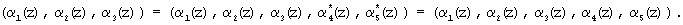
где левая часть равенства представлена по рабочим основаниям p1(z), p2(z), р3(z), средняя часть равенства - получена на основании выражения (10), а правая - модулярная комбинация системы оснований p1(z), р2(z), p3(z), p4(z), p5(z) расширенного поля Галуа GF(24), поступившая на вход устройства для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов. Тогда согласно (11) имеем
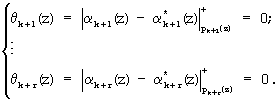
В противном случае
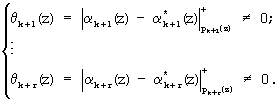
Полученный результат свидетельствует, что поступившая на вход устройства модульная комбинация A(z) содержит ошибку, которую необходимо подвергнуть коррекции. В таблице 2 представлены значения вектора ошибки (0, ..., Δαi(z), ..., 0) - модулярного кода для различных значений синдрома ошибки для ПСКВ поля GF(24).
Значения вектора ошибки модулярного кода поля GF(24)
Пусть на вход 1 устройства подается полином A(z)=z5+z4+z, значение которого в модулярном коде представляется A(z)=(1, z+1, z3+z2, 0, z2+z4+1).
Тогда согласно выражению (8) и данных, представленных в таблице 1, получаем следующие псевдоортогональные полиномы Аi(z):
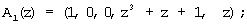
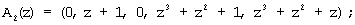
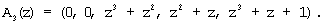
Согласно выражению (10) определяем значения остатков по контрольным основаниям:
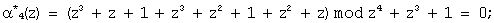
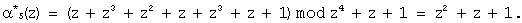
Согласно выражению (11) определяем синдром ошибки:
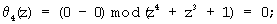
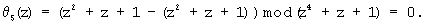
Из блока памяти 5 в соответствии с θ4(z)=0, θ5(z)=0 выбирается величина (0, 0, 0), которая складывается с A(z)=(1, z+1, z3+z2), в сумматоре 6 с образованием на выходе
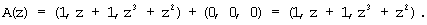
Допустим, что в принятой комбинации произошла ошибка по третьему основанию и ее глубина равна Δα3(z)=z2+z. Тогда имеем
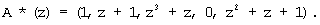
Тогда согласно выражению (8) и данных, представленных в таблице 1, получаем следующие псевдоортогональные полиномы Ai(z):
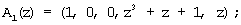
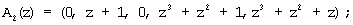
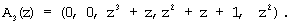
Согласно выражению (10) определяем значения остатков по контрольным основаниям:
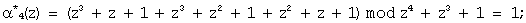
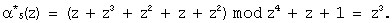
Согласно выражению (11) определяем синдром ошибки:
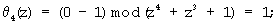
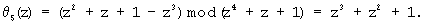
Из блока памяти 5 в соответствии с θ4(z)=1, θ5(z)=z3+z2+z+1 выбирается величина (0, 0, z2+z), которая складывается с A(z)=(1, z+1, z3+z) в сумматоре 6 с образованием на выходе
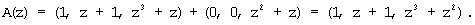
Ошибка в модулярном коде исправлена.
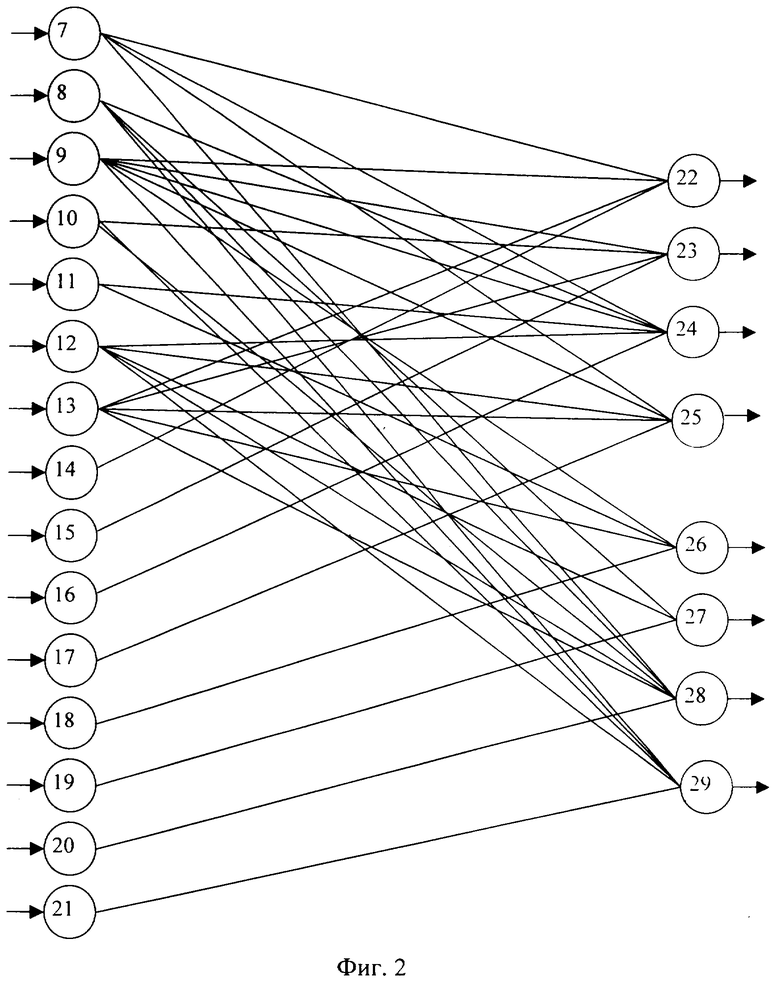
Блок вычисления синдрома ошибки представлен на фиг.2. Блок вычисления синдрома ошибки имеет 5 входов, по первым трем из которых подаются остатки α1(z), α2(2), α3(z) по рабочим основанием p1(z), p2(z), р3(z), по четвертому и пятому поступают остатки α4(z) и α5(z) по контрольным основаниям p4(z) и p5(z). Блок вычисления синдрома представляет собой двухслойную нейронную сеть. Первый слой содержит 15 нейронов. Входы нейронов 7, 8-9, 10-13 подключены соответственно к первому, второму и третьему входу блока вычисления синдрома ошибки. Входы нейронов 14-17 и 18-21 подключены соответственно к четвертому и пятому входам блока вычисления синдрома ошибок. На входы нейронов 7, 8-9, 10-13 в двоичном виде поступают остатки α1(z), α2(z), α3(z) по трем рабочим основаниям ПСКВ. На нейроны 14-17 поступает двоичный код α4(z) по первому контрольному модулю p4(z)=z4+z3+1. На нейроны 18-21 в двоичном коде поступает в двоичном коде α5(z) по второму контрольному модулю p5(z)=z4+z+1. Старшие разряды остатков полинома α1(z), α2(z), α3(z), α4(z), α5(z) записываются соответственно в нейроны 7, 8, 10, 14, 18 первого слоя. Второй слой нейронной сети содержит 8 нейронов, выполняющих базовую операцию согласно выражению (11), причем первые четыре нейрона 22-25 определяют значение θ4(z), остальные нейроны 26-29 определяют значение θ5(z). Входы нейрона 22 второго слоя соединены с выходами нейронов 7, 8, 13, 14 первого слоя. Входы нейрона 23 второго слоя соединены с выходами нейронов 9, 10, 13, 15 первого слоя. Входы нейрона 24 второго слоя соединены с выходами 7, 8, 9, 11, 12, 16 нейронов первого слоя. Входы нейрона 25 второго слоя соединены с выходами 7, 9, 12, 13, 17 нейронов первого слоя. Входы нейрона 26 второго слоя соединены с выходами 9, 11, 13, 18 нейронов первого слоя. Входы нейрона 27 второго слоя соединены с выходами 8, 12, 19 нейронов первого слоя. Входы нейрона 28 второго слоя соединены с выходами 7, 8, 10, 12, 13, 20 нейронов первого слоя. Входы нейрона 29 второго слоя соединен с выходами нейронов 8, 9, 10, 12, 21 нейронов первого слоя. Старшие значения синдрома ошибки θ4(z) и θ5(z) соответственно вычисляются в нейронах 22 и 26. Выходы нейронов второго слоя являются выход блока вычисления синдрома ошибки.
Рассмотрим процесс работы блока вычисления синдрома ошибки на примерах. Пусть на вход устройства коррекции ошибки был подан модулярный код A(z)=(1, z+1, z3+z2, 0, z2+z+1). Данный код поступает на входы нейронов первого слоя блока вычисления синдрома ошибки. Сигналы на выходе нейронов первого слоя представлены в таблице 3.
Сигналы на выходе нейронов первого слоя
Сигналы с выходов нейронов первого слоя поступают на соответствующие входы нейронов второго слоя. В таблице 4 представлены значения сигналов на входе и на выходе нейронов второго слоя. Символ «-» соответствует отсутствию связи между нейронами второго и первого слоя.
Сигналы на выходе нейронов второго слоя
Допустим, что в принятой комбинации произошла ошибка по третьему основанию и ее глубина равна Δα3(z)=z2+z. Тогда имеем
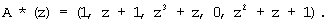
Данный код поступает на входы нейронов первого слоя блока вычисления синдрома ошибки. Сигналы на выходе нейронов первого слоя представлены в таблице 5.
Сигналы на выходе нейронов первого слоя
Сигналы с выходов нейронов первого слоя поступают на соответствующие входы нейронов второго слоя. В таблице 6 представлены значения сигналов на входе и на выходе нейронов второго слоя.
Сигналы на выходе нейронов второго слоя
Таким образом, на выходе блока вычисления синдрома ошибки определены значения θ4(z)=1, θ5(z)=z3+z2+z+1. Полученные данные совпадают с контрольными просчетами, представленными ранее.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2008 |
|
RU2393529C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2008 |
|
RU2390051C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ, ПРЕДСТАВЛЕННЫХ В РАСШИРЕННЫХ ПОЛЯХ ГАЛУА GF(2) | 2004 |
|
RU2258956C1 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ С КОРРЕКЦИЕЙ ОШИБОК | 2015 |
|
RU2584495C1 |
Устройство относится к вычислительной технике для контроля и исправления ошибки при передаче информации и для проведения арифметических операций в расширенных полях Галуа GF(2v). Техническим результатом является повышение скорости обнаружения и коррекции ошибок. Устройство содержит блок памяти, сумматор, блок вычисления синдрома ошибки, который является двухслойной нейронной сетью, содержащей нейроны, образующие первый слой, и второй слой нейронов. 6 табл., 2 ил.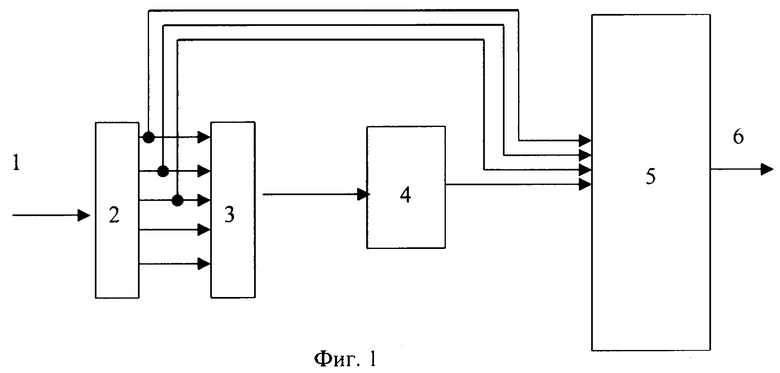
Устройство для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов содержит вход устройства, блок памяти, предназначенный для хранения весовых коэффициентов, при этом блок памяти подключен к четвертому входу сумматора, выход которого является выходом устройства, отличающееся тем, что в его состав дополнительно введен блок вычисления синдрома ошибки, входы которого подключены к входам устройства, а выходы соединены с входами блока памяти и с первыми тремя входами сумматора, при этом блок вычисления синдрома ошибки представляет собой двухслойную нейронную сеть, первый слой которой содержит пятнадцать нейронов, второй слой нейронной сети содержит восемь нейронов, при этом первый слой нейронной сети предназначен для записи контролируемого числа, представленного в полиномиальной системе классов вычетов, а второй слой предназначен для вычисления синдрома ошибки, причем входы нейронов упомянутого первого слоя являются входом блока вычисления синдрома ошибки, выходы нейронов упомянутого второго слоя являются выходами блока вычисления синдрома ошибки, при этом на входы нейронов с первого по седьмой упомянутого первого слоя поступают остатки по рабочим основаниям упомянутого контролируемого числа, на входы нейронов с восьмого по пятнадцатый упомянутого первого слоя поступают остатки по контрольным основаниям упомянутого контролируемого числа, входы первого нейрона упомянутого второго слоя соединены с выходами первого, второго, седьмого и восьмого нейронов упомянутого первого слоя, входы второго нейрона упомянутого второго слоя соединены с выходами третьего, четвертого, седьмого и девятого нейронов упомянутого первого слоя, входы третьего нейрона упомянутого второго слоя соединены с выходами первого, второго, третьего пятого, шестого и десятого нейронов упомянутого первого слоя, входы четвертого нейрона упомянутого второго слоя соединены с выходами первого, третьего, шестого, седьмого и одиннадцатого нейронов упомянутого первого слоя, входы четвертого нейрона упомянутого второго слоя соединены с выходами третьего, пятого, седьмого и двенадцатого нейронов упомянутого первого слоя, входы пятого нейрона упомянутого второго слоя соединены с выходами второго, шестого и тринадцатого нейронов упомянутого первого слоя, входы седьмого нейрона упомянутого второго слоя соединены с выходами первого, второго, четвертого, шестого, седьмого и четырнадцатого нейронов упомянутого первого слоя, входы восьмого нейрона упомянутого второго слоя соединены с выходами второго, третьего, четвертого, шестого и пятнадцатого нейронов упомянутого первого слоя.
| Устройство для обнаружения и исправления ошибок в системе остаточных классов | 1977 |
|
SU714399A1 |
| ЧЕРВЯКОВ Н.И | |||
| и др | |||
| Математическая модель нейронных сетей для исследований ортогональных преобразований сигналов в расширенных полях Галуа | |||
| Нейрокомпьютеры: разработка, применение | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 0 |
|
SU398950A1 |
| Устройство для обнаружения и исправления ошибок в системе остаточных классов | 1980 |
|
SU960823A1 |
| Устройство для декодирования линейных кодов | 1985 |
|
SU1287297A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
Авторы
Даты
2007-02-27—Публикация
2005-05-05—Подача