Изобретение относится к области измерительной техники и физики ферромагнитных материалов, магнитная восприимчивость которых зависит от температуры, и может быть использовано в качестве устройства для измерения теплопроводности ферроматериалов.
Известно, что величина, характеризующая связь намагниченности вещества с магнитным полем в веществе, называется магнитной восприимчивостью, которая определяется отношением намагниченности I вещества к напряженности поля μ0 Н и является величиной безразмерной, а ее отношение к плотности ρ вещества называется удельной магнитной восприимчивостью χ=(μr-1)/ρ, где μr - относительная магнитная проницаемость вещества. Магнитная проницаемость веществ может быть как положительной - у парамагнетиков и ферромагнетиков, так и отрицательной - у диамагнетиков. Величина магнитной восприимчивости парамагнетиков и диамагнетиков мала, и она слабо зависит от величины магнитного поля, и эти изменения начинают сказываться лишь в очень сильных магнитных полях и при низких температурах. Магнитная восприимчивость достигает особенно больших значений в ферромагнетиках от нескольких десятков до многих тысяч, причем она очень сильно и сложным образом зависит от напряженности поля Н (для чего вводят в рассмотрение дифференциальную магнитную восприимчивость, которая определяет намагниченность вещества от напряженности магнитного поля в каждой точке кривой намагничивания).
Магнитная восприимчивость, как правило, существенно зависит от температуры. У парамагнетиков она определяется законом Кюри (1885) χ=С/Т, где С - постоянная Кюри, Т - температура. Этому закону подчиняются только те парамагнетики, у которых существуют ионы или молекулы, обладающие отличным от нуля магнитным моментом. Эта формула была получена П.Ланжевеном (1905), рассмотревшим задачу о намагничивании газа, обладающего магнитным моментом. В квантовой теории парамагнетизма, развитой Д.Ван Флеком (1928-32), значение постоянной Кюри определяется величинами квантовых чисел - спинового S, орбитального - I и полного - J моментов магнитного иона и зависит от соотношения расщеплений уровней энергии иона в результате спин-орбитального взаимодействия и действия внутрикристаллического поля. При учете указанного взаимодействия закон Кюри переходит в закон Кюри-Вейсса. Связанные с этим законом отклонения от закона Кюри всегда наблюдаются при достаточно низких температурах.
Температурная зависимость магнитной восприимчивости χ парамагнетика, установленная Вейссом (1907), по закону Кюри-Вейсса имеет вид χ=С/(Т-Θ), где Θ - температура Кюри. Было показано, что у очень многих ферро- и антиферромагнетиков в парамагнитной области (при температурах соответственно выше точки Кюри Тc и выше точки Нееля tN) зависимость χ(Т) определяется законом Кюри. У ферромагнетиков Θ>0, у антиферромагнетиков Θ<0. В монокристаллах Θ анизотропна, этот эффект достигает большой величины в редкоземельных металлах. Выполнение закона Кюри-Вейсса в широком интервале температур носит приблизительный характер (Ч.Киттель, Введение в физику твердого тела, пер. с англ., М.,1978; Т.Мория, Последние достижения теории магнетизма коллективизированных электронов, пер. с англ., УФН, 1981, т.135, с.117).
В ферромагнитных веществах в областях, превышающих точку Кюри, магнитная восприимчивость сильно уменьшается с ростом температуры. Это обстоятельство положено в основу действия рассматриваемого устройства, использующего так называемый магнитотермомеханический эффект (МТМ-эффект), сущность которого рассмотрена ниже.
Другим обстоятельством, характеризующим действие заявляемого устройства, является известное положение о том, что парамагнитные вещества, и особенно ферромагнитные в присутствии неоднородного магнитного поля стремятся занять ту область этого поля, в которой оно имеет максимальное значение напряженности. Это свойство широко используется в технике, например, при работе электромагнитов, магнитных пускателей в автомашинах, реле и др.
Магнитотермомеханический эффект заключается в возникновении механической силы, приложенной к объему пара- или ферромагнитного вещества с изменяющейся от температуры магнитной восприимчивостью, помещенному в магнитное поле и находящемуся в термодинамически неравновесном состоянии, причем вектор этой силы направлен коллинеарно с вектором градиента температуры. МТМ-эффект объясняется возникновением градиента магнитной восприимчивости пара- или ферромагнитного вещества в направлении, противоположном направлению градиента температуры в нем, в результате чего «центр тяжести» намагниченности вещества смещается относительно центра притяжения действующего на него магнитного поля в направлении градиента магнитной восприимчивости.
Аналоги заявляемого технического решения отсутствуют.
Целью изобретения является измерение теплопроводности ферроматериалов с визуализацией процесса теплопередачи. Всестороннее исследование физических процессов и явлений в ферроматериалах и их взаимодействия с электрическими, магнитными и электромагнитными полями связано, в частности, с рассмотрением температурного фактора и динамики его проявления, вытекающей из скорости передачи тепловой энергии в ферроматериалах.
Указанная цель достигается в устройстве для измерения теплопроводности ферроматериалов, состоящем из ферромагнитного диска с осью вращения, постоянного магнита, в магнитном зазоре которого расположена кромка указанного ферромагнитного диска, нагреватель и холодильник, установленные с разных сторон магнитного зазора постоянного магнита с обеспечением их теплового контакта с ферромагнитным диском, причем последний выполнен из исследуемого ферроматериала.
Достижение указанной цели обеспечивается благодаря МТМ-эффекту, при этом ферромагнитный диск под действием возникающего вращательного момента вращается с линейной скоростью кромки ферромагнитного диска, находящейся постоянно в магнитном зазоре постоянного магнита, равной скорости теплопередачи в испытываемом ферроматериале и направленной коллинеарно градиенту температуры в нем. Измеряемые параметры вращения ферромагнитного диска характеризуют искомую величину теплопроводности.
На фиг.1 представлена принципиальная схема заявляемого устройства. Она включает постоянный магнит 1, в магнитном поле которого размещена краевая часть вращающегося диска 2 из ферромагнитного вещества с осью вращения 3. При этом часть диска с одной стороны от постоянного магнита, создающего однородное поле, на фиг.1 слева от магнита, связана с нагревателем 4, поддерживающим температуру T1, а другая, справа от магнита, - с холодильником 5, создающим температуру Т2 на этом крае диска. Будем полагать, что расстояние L между нагревателем и холодильником есть протяженность рассматриваемой части диска, которая целиком находится в однородном магнитном поле с напряженностью поля Н0. При этом градиент температуры в случае однородности вещества, из которого изготовлен диск, определяется как grad Т=∂Т/∂х=(T1-Т2)/L.
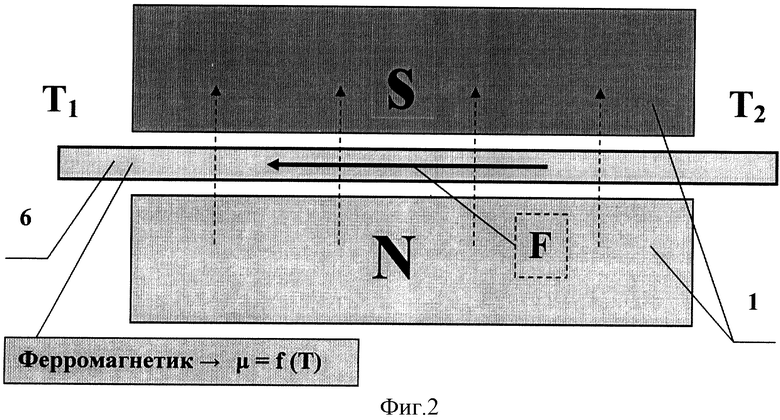
На фиг.2 представлена упрощенная схема эффекта возникновения импульса силы в ферромагнитном однородном и изотропном веществе в виде стержня 6 постоянного сечения с заданным градиентом температуры, возникающим при различных температурах T1 и Т2 на его концах. Показано действие силы, действующей на стержень 6, находящийся в магнитном поле.
Следует отметить принципиальное различие между схемами фиг.1 и фиг.2. Оно состоит в том, что ферромагнитный стержень на фиг.2 при заданном градиенте температур стремится лишь переместиться относительно его симметричного к полю положения, сдвинуться влево на некоторую величину, а затем продолжать находиться в этом положении неограниченно долго. В схеме на фиг.1 дело обстоит иначе: повернувшись на некоторый угол под действием приложенного момента силы в направлении действия градиента температуры (как показано стрелкой на фиг.1), диск вновь и вновь испытывает необходимость вращения, поскольку он непрерывен и по мере его вращения вводит в магнитное поле все новые участки диска, по которым перемещается картина температурного распределения с заданным градиентом в установившемся режиме (при постоянной угловой скорости ω диска).
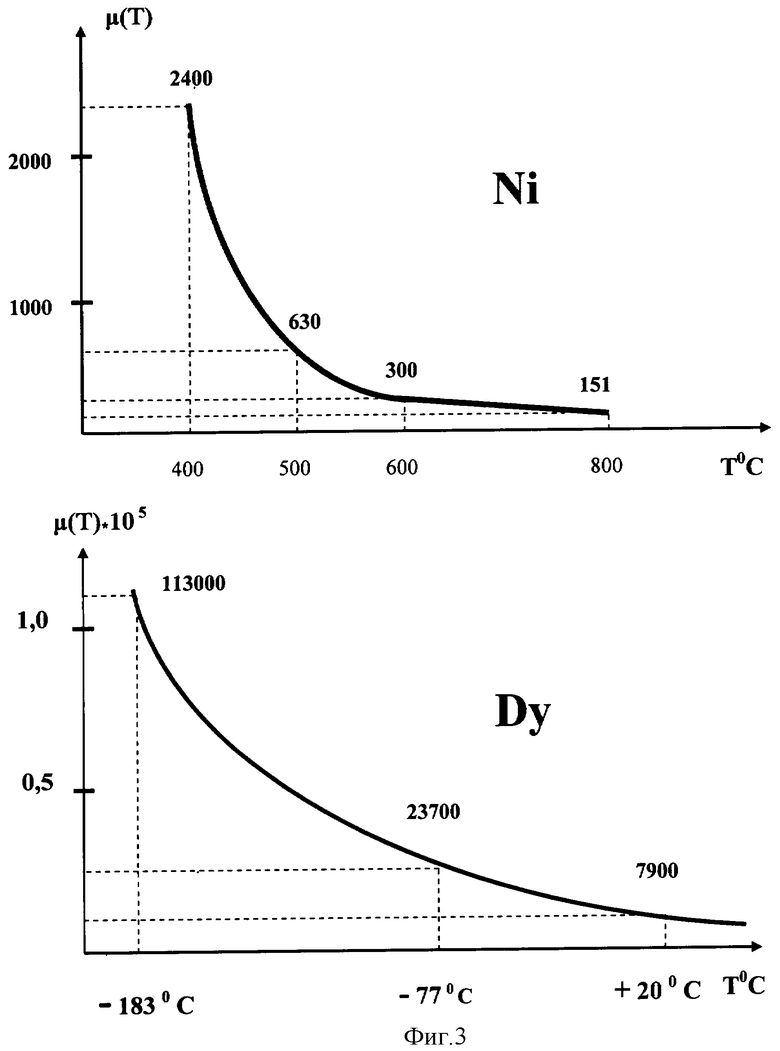
На фиг.3 изображены графики относительной магнитной проницаемости в функции температуры для двух ферроматериалов - никеля Ni (при работе на высоких температурах) и диспрозия Dy (при работе на инфранизких температурах).
Рассмотрим действие заявляемого устройства (фиг.1).
Превращение тепловой энергии в механическую основано на действии закона Фарадея, согласно которому сила притяжения магнитным полем ферромагнетика пропорциональна его относительной магнитной проницаемости (магнитной восприимчивости χ). Величина магнитной восприимчивости зависит от температурного распределения в кромке ферромагнитного диска 2, находящейся в магнитном зазоре постоянного магнита 1 (как это видно из фиг.3), при действии нагревателя 4 и холодильника 5, создающих заданный градиент температуры grad Т в материале ферромагнитного диска, связанного с магнитным зазором постоянного магнита.
Учитывая механизм образования силы, действующей на образец ферромагнетика с поперечным для магнитного поля сечением S и длиной L в однородном магнитном поле с магнитной индукцией В при разности температур ΔТ=T1-Т2 на указанной длине, для действующей на такой образец силы F можно записать выражение
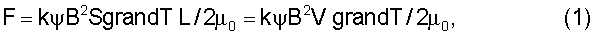
где k - некоторая константа, зависящая от эффективности преобразования тепловой энергии в механическую (вращение диска на фиг.1) и свойств материала диска, V=SL - объем рабочей части диска. Из (1) видно, что вектор силы совпадает с вектором градиента температуры и не зависит от направления магнитных силовых линий, то есть от знаков магнитных зарядов на полюсах постоянного магнита, поскольку величина вектора магнитной индукции в выражении (1) возведена в квадрат. Отметим, что выражение для энергии однородного магнитного поля имеет вид W=В2V/2μ0, откуда следует согласно (1), что сила действия на диск F=kψ×WgradT, то есть определяется энергией магнитного поля в объеме рабочей части диска и градиентом температуры в ней, а также сортом используемого вещества - величиной ψ. При этом безразмерный коэффициент k характеризует сам процесс преобразования тепловой энергии в механическую, то есть его следует рассматривать в качестве постоянной МТМ-эффекта. Так как ψ=∂χ/dT и
grad T=∂Т/∂х, то при условии однородности рабочего тела диска на всей его длине L допустимо полагать, что ψgradT=dχ/dx - градиент магнитной восприимчивости по длине рабочего тела диска, и тогда при условии такого допущения можно для силы получить простое выражение
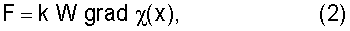
из которого видно, что искомая сила определяется энергией магнитного поля в объеме рабочей части диска и градиентом магнитной восприимчивости этой части диска, который явно учитывает вклад в процесс преобразования тепловой энергии. Указанная сила создает вращающий момент m=kWr grad χ(x), определяющий угловое ускорение диска dω/dt (ω - угловая скорость вращения диска) с учетом его момента инерции J=M r2/2, где М - масса диска в виде сплошного круга постоянной толщины, в соответствии с выражением
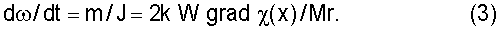
Согласно правилам механики угловое ускорение за некоторый интервал времени Δt приводит диск во вращательное движение с угловой скоростью ω, и при этом механическая энергия вращающегося диска равна Wмех=Jω2/2=Mω2r2/4, однако какой интервал времени следует брать при расчете и до какой угловой скорости будет разгоняться диск, необходимо дополнительно выяснить, учитывая процессы, связанные с разгоном диска, осложняемого конечной теплопроводностью материала диска. Важно понять, как во времени осуществляется перемещение по кромке вращающегося диска градиента температуры или, что то же, градиента магнитной восприимчивости ферромагнетика gradχ(х)=f(t), что определяется из уравнения теплопроводности и позволяет найти саму величину углового ускорения диска согласно (3), которая не является постоянной, а экспоненциально изменяется во времени с некоторой постоянной времени τ*.
Установившаяся угловая скорость вращения ω ферромагнитного диска фактически определяется скоростью перемещения по краю диска картины теплового распределения с заданным градиентом температуры. Быстрее этой скорости теплопередачи диск двигаться не в состоянии, так что процесс преобразования энергии для рассматриваемого эффекта является весьма инерционным.
Кратко рассмотрим передачу тепловой энергии по кромке диска.
Пусть дано изотропное тело: Т - температура тела, ρ - его плотность, γ - удельная теплоемкость, G - интенсивность источников тепла, то есть количество тепла, выделяемого единицей объема тела в единицу времени. Подсчитаем баланс тепла в единицу времени частиц тела, заполняющих объем V. В соответствии с гипотезой Фурье, согласующейся с опытом, количество тепла, поступающего в V через элемент поверхности ΔS тела, определяется формулой ΔQ=-λ(∂T/∂n)ΔS, где λ - положительный коэффициент пропорциональности, характеризующий свойства тела и называемый коэффициентом теплопроводности. Следовательно, количество тепла, поступающего в V через поверхность S⊥ (в нашем случае фиг.1 под величиной S⊥ надо понимать поперечное к градиенту температуры сечение кромки диска, связанной с магнитным полем постоянного магнита, обращенное к нагревателю, создающему в установившемся режиме в этом сечении температуру T1), в соответствии с формулой Остроградского будет равно
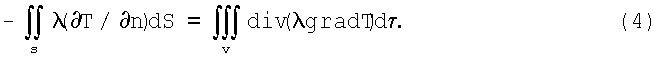
Общее количество тепла, поступающего в V, определяется равенством

где второе слагаемое в правой части (5) - тепло, поступающее за счет его источников.
Для повышения температуры элемента объема dτ на величину dT за время Δt потребуется количество тепла
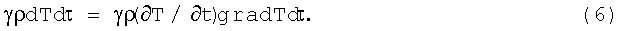
Общее количество тепла, идущего на повышение температуры частиц тела, заполняющих объем V, в единицу времени будет

Приравнивая (5) и (7), имеем
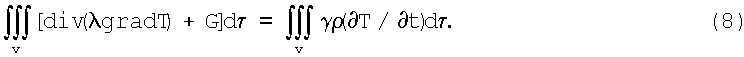
Учитывая, что область V произвольная, по теореме о среднем значении получаем

Равенство (9) представляет собой дифференциальное уравнение распространения тепла в неоднородном теле. В случае однородного тела, как в случае схемы фиг.1, это уравнение запишется в виде
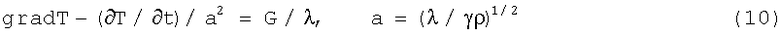
и представляет собой основное уравнение математической физики - уравнение теплопроводности. В частности, если тепловой поток является стационарным, то есть не зависит от времени, это уравнение будет уравнением Пуассона, и если при этом источники тепла отсутствуют, - уравнением Лапласа.
В нашем случае расчет осложняется тем, что диск вращается, и решение сводится к задаче с переменными параметрами. Кроме того, один конец кромки диска связан с источником тепла G, а другой - с холодильником, отнимающим запасаемую в рабочей кромке диска тепловую энергию (в установившемся режиме около G), что также должно соответственно учитываться при решении уравнения теплопроводности. При этом задача решается аналогично решению задачи о диффузии частиц среды, например жидкости, из мест большей концентрации к местам малой концентрации, понимая при этом под концентрацией функцию Т=dQ/dτ.
Решение задачи теплопередачи в случае вращающегося произвольного диска сложно, и этот частный вопрос выходит за рамки данной заявки. Важно лишь отметить, что при заданных параметрах системы (величине магнитной индукции, геометрии рабочей кромки диска, его физических свойствах - дифференциальной магнитной восприимчивости и коэффициента теплопроводности) можно в принципе строго решить задачу преобразования энергии и найти величину установившейся угловой скорости диска, то есть найти его механическую энергию согласно (2) и (3) за время Δt˜2,2τ*, величина которой равна
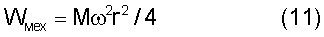
в случае использования круглого сплошного диска с постоянной толщиной. При этом скорость перемещения картины распределения температур по бесконечной длине края диска при его вращении с установившейся угловой скоростью ω должна будет совпадать с линейной скоростью края диска υ=ωr.
Мощность вращательного движения диска Nм=mω, где действующий на диск момент силы равен m=kWrgrad χ(x). Мощность теплового потока при этом равна Nт=dQ/dt, которая находится из решения уравнения (10) с учетом соотношения ΔQ=-λ(∂T/∂n)ΔS. При этом к.п.д. системы преобразования тепловой энергии в механическую при участии магнитного поля с заданной величиной магнитного потока Ф=BS (где S - сечение магнитного полюса постоянного магнита), охватывающего однородно весь рабочий участок кромки диска с градиентом температуры в нем grad Т, оказывается равным
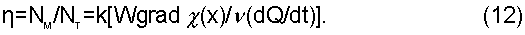
В числителе правой части дроби в выражении (12) определены параметры магнитного поля W и ферромагнитного вещества grad χ(х), а в знаменателе - скорость υ движения в диске картины теплового распределения с мощностью теплопередачи dQ/dt. Общим множителем этой дроби является постоянная k МТМ-эффекта. При этом ясно, что в силу закона сохранения энергии η<1.
В эксперименте можно определить мощность тепловой отдачи, установившуюся угловую скорость вращения диска с известными параметрами, рассчитать механическую энергию вращающегося диска, измерить величину магнитного потока, связанного с рабочей кромкой диска и таким образом найти постоянную k.
Выше был рассмотрен частный случай помещения в однородное магнитное поле ферромагнитного вещества с определенной формой, обладающей определенной симметрией к этому полю. В общем случае произвольно-неоднородного магнитного поля B(dv) и использования изотропного ферромагнитного вещества с произвольной формой его объема V решение задачи производится в два этапа. Сначала определяют центр притяжения магнитного поля, которое имеет распределение по координатам х и y, где ∂B/∂x≠0 и ∂B/∂y≠0, полагая, что вдоль магнитных силовых линий поле неизменно и ∂B/∂z=0. При этом dB(dv)=dB(x,y)=dB[(x2+y2)1/2]. Зная это распределение магнитного поля по координатам х и у, находим интегрированием координаты X0 и Y0 центра притяжения магнитного поля В(х, y) совместным решением системы интегральных уравнений при условии, что 0≤х≤Хmax и 0≤y≤Ymax:
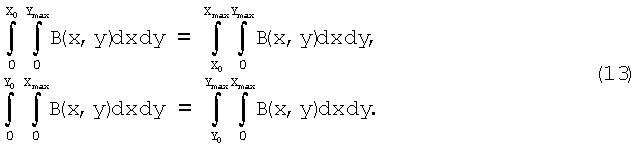
На втором этапе аналогичным образом находят координаты «центра тяжести» заданного объема ферромагнитного вещества по его трем координатам х, y и z совместным решением системы трех трехкратных интегральных уравнений, и при этом находятся координаты возмущенного тепловым потоком по объему тела координаты ХT, YT и ZT для установившейся картины распределения температур в данном объеме вещества. То же самое следует сделать для нахождения «центра тяжести» данного объема вещества для случая невозмущенного его состояния, когда T1=Т2 и, следовательно, в случае, когда gradT=∂Т/∂х=∂T/∂y=∂Т/∂z=0. Полученные значения для координат ХT=0 и YT=0 из найденного решения припишем значениям координат центра притяжения магнитного поля, сдвигая системы координат в плоскости (х, у), то есть запишем, что X0=ХT=0 и Y0=YT=0. Тогда можно вычислить отклонения координат «центра тяжести» объекта в его возмущенном состоянии относительно невозмущенного, как если бы объект своим «центром тяжести» для его невозмущенного состояния совпадал с центром притяжения магнитного поля, а именно отклонения координат ΔХ=ХT-Х0 и ΔY=YT-Y0. Если добиться того, чтобы отклонение по координате у не существовало (выбором профиля объекта) и ΔY=0, чтобы исключить поворот вектора силы F относительно вектора градиента температуры (направленного вдоль оси х), то окажется, что координата ХT «центра тяжести» возмущенного состояния объекта будет больше по величине координаты X0 центра притяжения магнитного поля на величину ΔХ>0. Это и будет создавать силу притяжения ферромагнитного объема вещества в направлении к центру притяжения магнитного поля, то есть вдоль направления градиента температуры (от более низкой температуры Т2 к более высокой T1, как показано на фиг.1 и 2). В случае стержня 6 без трения (фиг.2) такой стержень переместится на расстояние ΔХ в сторону повышения температуры в теле, а при использовании схемы на фиг.1 диск начнет непрерывное вращательное движение с постоянной угловой скоростью ω=υ/r, где υ - установившаяся скорость перемещения картины теплового поля по кромке вращающегося диска с заданным установившимся градиентом gradT.
Следует, однако, заметить, что при достаточно большом смещении центра притяжения магнитного поля в сторону градиента магнитной восприимчивости при неоднородном магнитном поле, так что ΔХ<0, вращения диска наблюдаться не будет. Поэтому для построения экспериментальной модели целесообразно выбирать режим с однородным магнитным полем в рабочем участке диска.
Интересно также отметить, что независимость направления векторов действующих сил от направления силовых линий магнитного поля позволяет использовать для вращения диска переменные поля (!), что является важной особенностью МТМ-эффекта.
На основе МТМ-эффекта могут быть созданы также различные измерительные приборы, например счетчики тепловой радиации, или измерители температуры, работающие совместно с «датчиками холода» на основе эффекта Пельтье.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ВИЗУАЛИЗАЦИИ ТЕПЛОПРОВОДНОСТИ ФЕРРОМАГНЕТИКОВ | 2007 |
|
RU2359336C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2332778C1 |
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОГЕНЕРАТОРОМ | 2010 |
|
RU2444802C1 |
| ФЕРРОМАГНИТОВЯЗКИЙ РОТАТОР | 2005 |
|
RU2309527C2 |
| МАГНИТОВЯЗКИЙ РОТАТОР | 2006 |
|
RU2325754C1 |
| СТАБИЛИЗИРОВАННЫЙ ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА | 2013 |
|
RU2542711C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2010 |
|
RU2452074C1 |
| ФЕРРОМАГНИТОВЯЗКИЙ ВРАЩАТЕЛЬ | 2013 |
|
RU2556074C1 |
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОГЕНЕРАТОРОМ | 2013 |
|
RU2537394C1 |
| ПРИБОР ДЛЯ ИЗМЕРЕНИЯ МАГНИТНОЙ ВЯЗКОСТИ ФЕРРОМАГНЕТИКОВ | 2007 |
|
RU2338216C1 |
Изобретение относится к области измерительной техники. Техническим результатом изобретения является обеспечение возможности измерения теплопроводности ферроматериалов с визуализацией процесса теплопередачи по вращению ферромагнитного диска. Этот результат обеспечивается за счет того, что устройство для измерения теплопроводности ферроматериалов состоит из ферромагнитного диска с осью вращения, постоянного магнита, в магнитном зазоре которого расположена кромка указанного ферромагнитного диска, нагреватель и холодильник, установленные с разных сторон магнитного зазора постоянного магнита с обеспечением их теплового контакта с ферромагнитным диском, причем последний выполнен из исследуемого ферроматериала. 3 ил.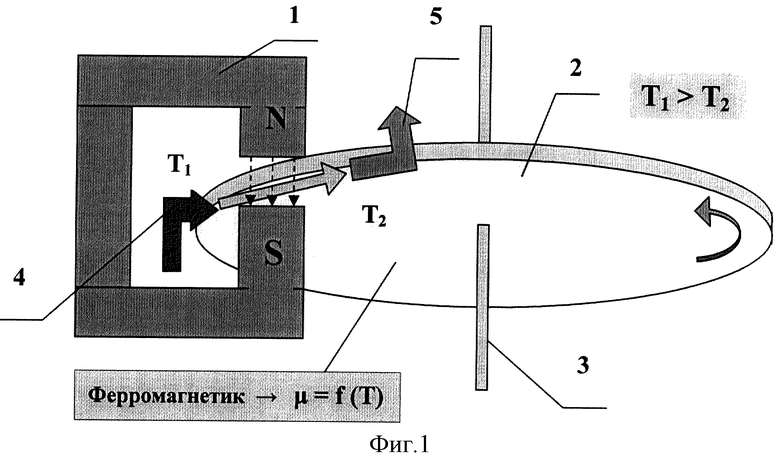
Устройство для измерения теплопроводности ферроматериалов, состоящее из ферромагнитного диска с осью вращения, постоянного магнита, в магнитном зазоре которого расположена кромка указанного ферромагнитного диска, нагреватель и холодильник, установленные с разных сторон магнитного зазора постоянного магнита с обеспечением их теплового контакта с ферромагнитным диском, причем последний выполнен из исследуемого ферроматериала.
| Способ контроля физико-механических свойств изделий из ферромагнитных материалов | 1990 |
|
SU1826051A1 |
| Устройство для определения теплопроводности | 1986 |
|
SU1603270A1 |
| US 5108191 A, 28.04.1992 | |||
| DE 4032092 A, 16.04.1992. | |||
Авторы
Даты
2008-05-20—Публикация
2006-10-05—Подача