Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах для формирования кодовых последовательностей.
Известно устройство для формирования остатка по произвольному модулю от числа, содержащее элементы ИЛИ, формирователи импульсов, счетчики, элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, блоки умножения, элемент И, группу сумматоров по модулю два (см. АС СССР №1238077, кл. G06F 11/08, 15.06.1986).
Недостатком данного устройства является низкое быстродействие.
Наиболее близким по технической сущности к заявляемому изобретению является комбинационный рекуррентный формирователь остатков, содержащий узлы формирования частичных остатков, ключи и сумматоры по произвольному модулю (см. патент РФ №2029435, кл. Н03М 7/18, 20.02.1995).
Недостатком данного устройства является его низкое быстродействие.
Цель изобретения - повышение быстродействия за счет увеличения основания преобразования числа.
Сущность изобретения заключается в реализации следующего способа формирования остатков по модулю.
Известно, что любое целое положительное число А может быть представлено в виде степеней числа 2, просуммированных в соответствии с коэффициентами при каждой степени, то есть
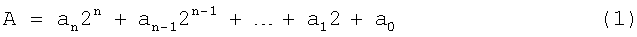
Существующие устройства формирования остатков в основном используют процедуру вычисления частичных остатков от каждой из степеней числа, представленного в двоичном виде с последующим умножением их по модулю на коэффициенты при соответствующих степенях и суммированием по модулю.
В таких устройствах число 2 в выражении (1) одновременно является и основанием системы счисления, и основанием преобразования при вычислении остатка
Предлагаемое устройство реализует процедуру приведения числа А по произвольному модулю р, используя основание преобразования М=2N, где N - целое положительное число, большее 1. В этом случае число
А=an2n+an-12n-1+...+а12+a0
для выполнения вычислений может быть приведено к виду
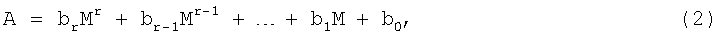
где M=2N - основание преобразования; bi (i=1, ..., r) - соответствующий коэффициент при основании преобразования. Если количество разрядов k=n+1 при представлении числа А в виде (1) кратно N, то
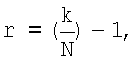
в противном случае
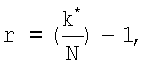
где k* - ближайшее к k целое число, большее k и кратное N. Для достижения k значений k*количество разрядов увеличивают путем добавления нулевых коэффициентов перед старшим разрядом числа А. Тогда
br={an, an-1, ..., an-N+1}, br-1={an-N, an-N-1, ..., an-2N}
и т.д.
Система счисления при изменении основания преобразования остается двоичной, то есть коэффициенты bi есть числа, которые в двоичном виде представляют собой последовательность, состоящую из коэффициентов aj, количество которых зависит от выбранного значения N.
Пример:
Пусть A=189=1·27+0·26+1·25+1·24+1·23+1·22+0·2+1·1=10111101.
Очевидно, что для формирования остатка необходимо сформировать значение частичного остатка от каждой степени числа «2» от 1 до n (т.к. увеличение степени числа 2 осуществляется сдвигом старшей степени на одну позицию в сторону возрастания, то требуется провести (n-1) операций сдвига), умножить каждое из них на коэффициент при соответствующей степени (n операций) и просуммировать, то есть выполнить 2n операций.
Пусть N=A, тогда М=2N=16. В этом случае число А можно представить в следующем виде:
A=br16r+br-116r-1+...+b116+b0.
Наивысшая степень r в данном представлении числа А определяется отношением
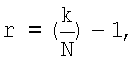
так как количество разрядов при представлении числа А в двоичном виде кратно выбранному значению N. В данном случае k=n+1=8, N=4. Следовательно, r=1. Тогда
А=b1161+b0160=b1·16+b0.
Коэффициент b1 определяется первыми N коэффициентами an, an-1, ..., an-N при представлении числа А в двоичном виде, b0 - следующими N коэффициентами, то есть, если А=10111101, то b1=1011, b0=1101.
Тогда рассматриваемое число А с измененным основанием преобразования может быть записано как
A=(1011)·16+1101=11·16+13=176+13=189
Очевидно, что для нахождения остатка от числа А с измененным основанием преобразования необходимо найти частичный остаток только от одной степени числа 16, после чего умножить его по модулю на соответствующий коэффициент и просуммировать по модулю полученные результаты.
При формировании частичных остатков от степеней числа А с измененным основанием преобразования используется следующая процедура. Известно, что любая степень числа 2, представленная в двоичной форме, может быть сформирована путем сдвига символа «1» на определенное количество разрядов в сторону возрастания. Таким образом, число 2N может быть получено при сдвиге символа «1» на N разрядов вверх. Для приведения полученного значения z степени числа А с измененным основанием преобразования по модулю данное значение сравнивается со значением модуля р. Если полученное значение z≥p, то из z вычитается значение модуля р, а полученное в результате значение z1=z-p вновь сравнивается со значением р. Если и в этом случае значение z1≥p, то из z1 вновь вычитается значение р, а полученное в результате значение z2=z1-р сравнивается со значением р. Данные операции проводятся до тех пор, пока значение zn, полученное на n-м шаге вычислений, не станет меньше значения модуля р. В этом случае значение zn является частичным остатком от степени числа А с измененным основанием преобразования по модулю р. Если уже на первом шаге входное значение z<p, значение z остается без изменений и является частичным остатком от степени числа А с измененным основанием преобразования по модулю р.
Следует отметить, что в случае представления числа А двоичной последовательностью, количество элементов которой не является кратным N, данная последовательность дополняется нулями перед старшим разрядом до достижения размеров последовательности, кратной N.
Таким образом, увеличение основания преобразования при формировании остатков с М=2 до М=2N позволяет уменьшить количество последовательных ступеней преобразования, тем самым увеличив быстродействие выполнения операции формирования остатков.
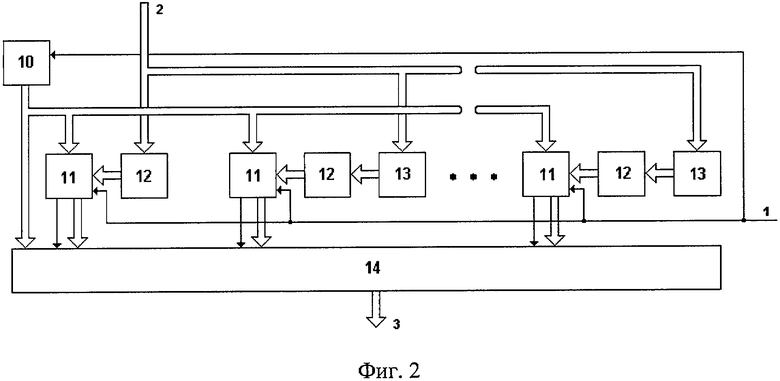
На фиг.1 представлена схема устройства для формирования остатка по произвольному модулю от числа, на фиг.2 - схема блока формирования частичных остатков.
Устройство для формирования остатка по произвольному модулю состоит из l=((k*/N)-1) блоков 1 формирования частичных остатков (где k* - количество разрядов в двоичном представлении числа, от которого формируется остаток, с учетом добавленных для достижения кратности N разрядов), (l+1) блоков 2 умножения по модулю, блока 3 распределения коэффициентов и сумматора 4 по модулю.
Блок 1 формирования частичных остатков состоит из блока 10 сдвига, t сумматоров 11 (где t равно отношению 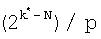 , округленному в сторону большего целого числа), t инверторов 12, (t-1) умножителей 13 на константу и мультиплексора 14.
, округленному в сторону большего целого числа), t инверторов 12, (t-1) умножителей 13 на константу и мультиплексора 14.
Первый вход каждого блока 1 формирования частичных остатков служит для записи символа «1», являющегося кодом начала операции. В блоке 1 формирования частичных остатков данный символ подается на вход блока 10 сдвига, а также на третьи входы каждого сумматора 11. Ко второму входу каждого блока 1 формирования частичных остатков подключен вход 6 записи кода модуля устройства. Выход i-го блока 1 формирования частичных остатков (где i=1, ..., l-1) подключен к первому входу i+1-го блока 2 умножения по модулю. Ко второму входу каждого блока 2 умножения по модулю подключен вход 6 записи кода модуля устройства. К третьему входу j-го блока 2 умножения по модулю (где j=1, ..., l+1) подключен j-й выход блока 3 распределения коэффициентов. Выход j-го блока 2 умножения по модулю подключен к j-му входу сумматора 4 по модулю. На (j+1)-й вход сумматора 4 по модулю подан код модуля р со входа 6 устройства. Выход сумматора 4 по модулю является выходом 8 устройства.
Устройство работает следующим образом.
В исходном состоянии на вход 6 подан двоичный код модуля р, по которому будет осуществляться формирование остатков. На вход 7 подан двоичный код числа А, от которого формируется остаток. Процесс формирования остатка начинается с подачи на вход 5 устройства символа «1», который поступает на вход каждого блока 1 формирования частичных остатков. В блоке 1 формирования частичных остатков символ «1» подается на вход блока 10 сдвига, который путем сдвига символа «1» на m×N разрядов в сторону увеличения (m=1, ..., l), на своем выходе формирует двоичный код числа z, соответствующего определенной степени числа А с измененным основанием преобразования (в m-м блоке формирования частичных остатков блок 10 сдвига формирует двоичный код m-й степени числа А). Код числа z поступает на первые входы сумматоров 11 и на первый информационный вход мультиплексора 14. Со входа 2 блока 1 формирования частичных остатков двоичный код модуля р подается на входы умножителей 13 на константу и на вход первого инвертора 12. Значение модуля в k-м умножителе 13 (где k=1, ..., t-1) умножается на величину f=(k+1). С выхода k-го умножителя на константу 13 код полученного значения поступает на вход (k+1)-го инвертора 12. В h-м (где h=1, ..., t) инверторе 12 поступающий на его вход код переводится в инверсный код, который подается на второй вход h-го сумматора 11, причем на вход первого инвертора 12 поступает непосредственно код модуля р. Очевидно, что на выходе h-го сумматора формируется инверсный код значения h×p, поступающий на второй вход h-го сумматора 11. На третий вход каждого сумматора 11 с первого входа блока 1 формирования частичных остатков поступает код числа «1», служащий для перевода инверсного кода модуля в дополнительный код.
В общем виде сумматор 11 осуществляет операцию, описываемую выражением: 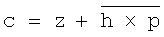 , где с - результат суммирования, z - значение степени числа А с измененным основанием преобразования, h - номер сумматора, р - модуль. Старший разряд сформированного кода значения с поступает на выход переноса сумматора 11, остальные разряды представляют разность z-h×p и поступают на информационный выход сумматора 11.
, где с - результат суммирования, z - значение степени числа А с измененным основанием преобразования, h - номер сумматора, р - модуль. Старший разряд сформированного кода значения с поступает на выход переноса сумматора 11, остальные разряды представляют разность z-h×p и поступают на информационный выход сумматора 11.
До тех пор, пока значение z превышает значение h×p, на выходе переноса h-го сумматора 11 будет формироваться символ «1», который будет поступать на h-й управляющий вход мультиплексора 14. При превышении значением h×p значения z на выходе переноса h-го сумматора 11 сформируется символ «0». При поступлении на h-й управляющий вход мультиплексора 14 символа «0» с выхода переноса h-го сумматора 11 мультиплексор 14 подключит на выход 3, являющийся выходом блока 1 формирования коэффициентов, тот свой информационный вход, на который подается значение с информационного выхода (h-1)-го сумматора 11. Данное значение представляет частичный остаток от степени числа А с по модулю р.
С выхода m-го блока 1 формирования частичных остатков полученное значение поступает на первый вход (m+1)-го блока 2 умножения по модулю. На первый вход первого блока 2 умножения по модулю подается символ «1» с входа 5 устройства.
На второй вход каждого блока 2 умножения подается код модуля со входа 6 устройства. На третий вход j-го блока 2 умножения по модулю поступает последовательность из N символов с j-го выхода блока 3 распределения коэффициентов. Данный блок представляет собой коммутатор с динамическими или жесткими связями, формирующий на выходах из поступающей на его вход последовательности длиной k символов (k*/N) последовательностей длиной N символов. Данные последовательности по сути являются коэффициентами bi при представлении числа А с помощью переменного основания преобразования. Причем на первый выход блока 3 распределения коэффициентов подаются младшие N разрядов входной последовательности, на второй выход - следующие N разрядов и т.д. В случае, если k не кратно N, последняя формируемая последовательность дополнится нулями в старших разрядах и также будет состоять из N символов.
Сформированное на выходе j-го блока 2 умножения по модулю значение, представляющее собой произведение частичного остатка от степени числа А с измененным основанием на коэффициент при данной степени, подается на сумматор 4 по модулю, где суммируется в соответствии с модулем со значениями, сформированными в других блоках 2 умножения. Полученное в результате суммирования по модулю значение, являющееся остатком от числа А по произвольному модулю р, подается на выход сумматора, который является выходом 8 устройства.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ЧИСЕЛ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2006 |
|
RU2316042C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 1992 |
|
RU2025897C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2007 |
|
RU2368942C2 |
| УМНОЖИТЕЛЬ НА ДВА ПО МОДУЛЮ | 2009 |
|
RU2445681C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2348965C1 |
| УМНОЖИТЕЛЬ НА ДВА ПО МОДУЛЮ | 2005 |
|
RU2299460C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2024 |
|
RU2829089C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2005 |
|
RU2299461C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2016 |
|
RU2626654C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2019 |
|
RU2717915C1 |
Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах для формирования кодовых последовательностей. Техническим результатом является повышение быстродействия путем сокращения количества выполняемых операций за счет увеличения основания преобразования числа. Устройство содержит блоки формирования частичных остатков, умножители по модулю, блок распределения коэффициентов, сумматор по модулю. 2 н.п. ф-лы, 2 ил.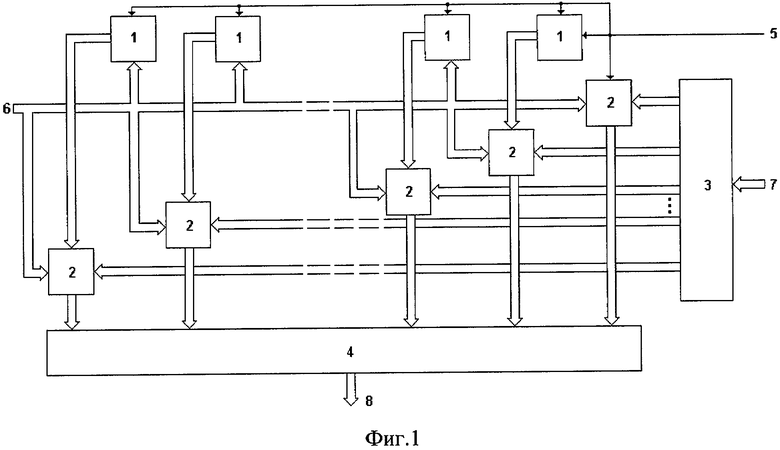
| КОМБИНАЦИОННЫЙ РЕКУРРЕНТНЫЙ ФОРМИРОВАТЕЛЬ ОСТАТКОВ | 1992 |
|
RU2029435C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ ОТ ЧИСЛА | 1991 |
|
RU2020759C1 |
| Устройство для формирования остатка по произвольному модулю от числа | 1984 |
|
SU1238077A1 |
| Устройство для формирования остатка по произвольному модулю от числа | 1990 |
|
SU1765896A1 |
| JP 11282349 А, 15.10.1999 | |||
| УСТРОЙСТВО ДЛЯ ЗАГРУЗКИ СКИПОВ | 0 |
|
SU308963A1 |
Авторы
Даты
2008-05-20—Публикация
2006-01-31—Подача