Изобретение относится к измерениям и автоматизации в области оперативной идентификации и контроля качества многокомпонентных соединений, например углеводородов в нефтепродуктах (горючесмазочных материалах) и парфюмерных изделиях, углеводородных и белковых соединений в пищевых средах и готовых продуктах по их инфракрасным спектрам поглощения в широком диапазоне длин волн.
Известно, что для идентификации и контроля качества многокомпонентных соединений, например углеводородов в нефтепродуктах (бензинах и смазочных материалах), основное значение имеет ряд специфических физико-химических показателей, определяемых соответствующими ГОСТами и/или техническими условиями (ТУ). Так, например, в бензинах в зависимости от углеводородного состава сырья и технологии получения может содержаться несколько сотен индивидуальных углеводородов различного строения.
Для идентификации и контроля качества углеводородных соединений их физико-химические показатели сравниваются с нормативными, определенными для всех марок нефтепродуктов. Если каждый из показателей соответствует своим нормативным показателям, то принимают решение о принадлежности нефтепродукта данной марке и его кондиционности (ГОСТ 4.25-83. Система показателей качества продукции. Нефтепродукты. Топлива жидкие. Номенклатура показателей) [1].
Определение значений физико-химических показателей углеводородных соединений является достаточно трудоемким и длительным процессом. Так, например, определение индукционного периода осадкообразования бензинов требует десятков часов.
Для оперативности идентификации и контроля качества углеводородных соединений в нефтепродуктах, в частности для оценки их детонационных характеристик, применяется также метод спектроскопии в инфракрасном (ИК) диапазоне, в частности в коротковолновой области (880 мкм - 1050 мкм) ближнего ИК-диапазона (БИК) (Королев В.Н., Маргулин А.В., Цареградский В.Б. Метод определения детонационных характеристик нефтепродуктов на основе регрессионного анализа спектров поглощения в ближнем инфракрасном диапазоне. ЖТФ, 2000, том 70, вып.9, с.83-88) [2].
БИК спектроскопия используется также в сельскохозяйственной индустрии для оперативного оценивания показателей качества белковых соединений растительного происхождения в зерновых культурах (Крищенко В.П. Ближняя инфракрасная спектроскопия - М.: ООО изд. Дом КРОН-ПРЕСС, 1997. - 639 с.) [3].
В (Рогов И.А., Копылов Ю.Г. и др. Электрофизические, оптические и акустические характеристики пищевых продуктов. - М.: Легкая и пищевая промышленность, 1981. - 288 с.) [4] приведены примеры использования инфракрасных спектров поглощения многочисленных пищевых сред и готовых продуктов, характеризующих состояние их белковых соединений животного происхождения.
Суть оценивания показателей качества многокомпонентных соединений на основе ИК спектроскопии заключается в совместном измерении оптической плотности известных образцов многокомпонентных соединений для нескольких выбранных длин волн и соответствующих характеристик качества, определяемых физико-химическими методами. Построение зависимостей данных характеристик от оптической плотности многокомпонентных соединений производят методом калибровки на основе линейной интерполяции, используя метод наименьших квадратов [2-4].
Основным недостатком указанного выше метода идентификации многокомпонентных соединений является ограниченность его возможностей в отношении определения ряда характеристик многокомпонентных соединений, которые не связаны простой линейной зависимостью с концентрацией светопоглощающих, светорассеивающих или флуоресцирующих веществ.
Другим недостатком этого метода является малое количество используемых длин волн или волновых чисел. Так, например, в [2] использовано 5 длин волн, хотя там же показано, что с ростом количества длин волн точность метода возрастает. В работах [3, 4] также используют узкие диапазоны длин волн, опираясь на характерные «пики» поглощения.
В то же время увеличение количества длин волн ограничено возможностью используемой линейной интерполяции при построении калибровочных зависимостей.
Наиболее близким из известных по своей технической сущности и достигаемому результату является выбранный в качестве прототипа автоматизированный способ идентификации и определения кондиционности нефтепродуктов, включающий накопление известных образцов каждой заданной марки нефтепродукта с совместной регистрацией инфракрасных спектров их оптических плотностей в диапазонах характеристических полос поглощения (ХПП) и значений показателей качества, определяемых физико-химическими методами, с последующим сравнением спектра оптической плотности нефтепродукта неизвестной марки с накопленными спектрами известных образцов (RU 2075062 С1, 10.03.97) [5].
В указанном способе используется большая информация, заключенная как в инфракрасных спектрах, так и в показателях качества нефтепродуктов.
Действительно, в [5] предлагается использовать ХПП среднего ИК-диапазона. Средний спектральный диапазон ИК-Фурье-спектрометров составляет обычно волновые числа от 200 см-1 до 8000 см-1. Именно в данном диапазоне сосредоточены все основные колебательно-вращательные тона молекул, составляющих основу нефтепродуктов, а в ближнем инфракрасном спектре находятся лишь их обертона [5].
В частности, в прототипе используется тот факт, что для каждой марки нефтепродукта характерен индивидуальный набор (количество) ХПП, обеспечивающий надежную идентификацию. Количество этих ХПП может составлять около 50 из анализируемого диапазона волновых чисел ИК-диапазона от 4000 см-1 до 400 см-1, т.е. из 3600.
Однако недостатком этого способа является сложность, а зачастую и невозможность, определения характеристических полос поглощения в углеводородных молекулярных смесях.
Другим существенным недостатком способа является сложность и неопределенность ряда используемых вероятностных характеристик, требуемых для расчета показателей качества, в частности совместных и условных плотностей распределения ХПП для каждой марки нефтепродукта.
Также неопределенной является и сама основная процедура накопления известных образцов нефтепродуктов в каждой заданной марке.
Например, по данному способу в каждую заданную марку могут попасть образцы с идентичными физико-химическими показателями и соответственно одинаковыми спектрами. Совершенно ясно, что при этом достоверность идентификации и точность контроля качества не увеличивается.
Настоящее изобретение устраняет отмеченные недостатки прототипа.
Техническим результатом заявляемого изобретения является повышение достоверности идентификации и контроля качества многокомпонентных соединений.
Технический результат достигается за счет целенаправленного накопления информации о спектрах и показателях качества известных образцов многокомпонентных соединений, повышения количества определяемых физико-химических показателей многокомпонентных соединений, а также использования методов теории статистических решений и теории нечетких множеств.
Патентуемый способ реализуется следующим образом:
- измеряют спектры оптических плотностей известных образцов при различных условиях производства, обеспечивающих равномерное заполнение диапазонов значений их показателей качества в максимальных границах, гостированных для каждой марки;
- определяют количество известных образцов, исходя из требуемой точности оценивания значений показателей качества;
- измеряют спектры оптических плотностей известных образцов для всех волновых чисел выбранного диапазона электромагнитных волн;
- оценивают нормированные значимости всех используемых длин волн или волновых чисел по дисперсиям спектральных компонентов известных образцов каждой марки;
- идентифицируют многокомпонентное соединение неизвестной марки методом «ближайшего соседа» на основе нечетких мер сходства его спектров со спектрами всех известных образцов при определенных ранее нормированных значимостях длин волн или волновых чисел каждой марки;
- оценивают значения показателей качества идентифицированного многокомпонентного соединения на основе накопленных значений спектров и показателей качества известных образцов как всех марок, так и идентифицированной марки многокомпонентного соединения;
- определяют качество многокомпонентного соединения данной марки по результатам его идентификации и оцененным значениям показателей качества.
Рассмотрим реализацию настоящего изобретения.
Показатель качества k-го известного образца многокомпонентного соединения (k=1,2,...,Кm), который определен физико-химическим методом для его заданной m-й марки или m-го состояния (m=1,2,...,М), обозначим символом pm(k), а символом Sm(ν,k) - спектр оптической плотности используемого диапазона электромагнитных волн, определенный для каждой длины волны X или каждого волнового числа ν (ν=2π/λ) этого образца.
Покажем строго необходимые условия для определения по Кm заданным значениям pm(k) показателей качества известных образцов многокомпонентного соединения m-й марки и соответствующих им спектров Sm(ν,k) показателя качества рm неизвестного образца многокомпонентного соединения той же марки с измеренным спектром Sm(ν). Для этого представим произвольный измеренный спектр Sm(ν) многокомпонентного соединения m-й марки в виде вириального ряда по степеням параметра 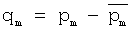
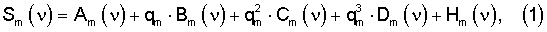
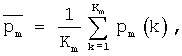
где Am(ν), Bm(ν), Сm(ν), Dm(ν) - неизвестные детерминированные спектральные функции; Hm(ν) - неизвестные случайные спектральные функции, определяемые как точностью представления (1), так и точностью измерения спектра Sm(ν).
Легко заметить частный случай (1) выражается как
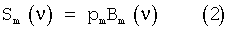
что соответствует по закону Ламберта-Бера зависимости оптической плотности образца от концентрации рm сильноразбавленного вещества, его молярной экстинкции εm(ν)=Bm(ν)/L и оптического пути L (Кунце У., Шведт Г. Основы качественного и количественного анализа: Пер. с нем. - М.: Мир, 1977. - 424 с.) [6].
Для общего случая зависимости (1) необходимо найти неизвестные детерминированные спектральные функции Am(ν), Вm(ν), Сm(ν), Dm(ν).
Для этого подставим в (1) известные значения pm(k) и соответствующие им Sm(ν,k)
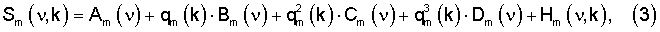
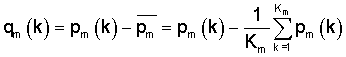 .
.
Средняя ошибка представления (1) определяется как
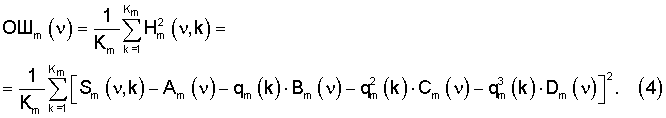
Оценки A* m(ν), B* m(ν), C* m(ν), D* m(ν) неизвестных детерминированных спектральных функций найдем путем минимизации вариации δОШm(ν) выражения (4) по вариациям δАm(ν), δBm(ν), δCm(ν), δDm(ν) детерминированных спектральных функций.
В результате получим следующие оценки
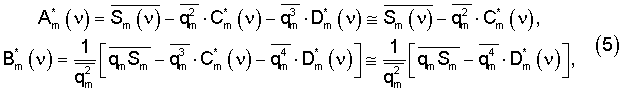
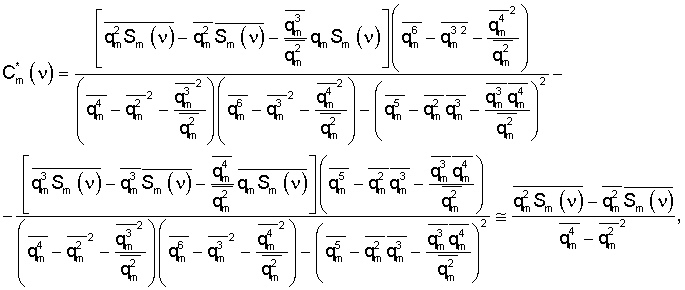

где
 ,
,
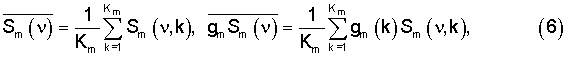
 .
.
Из (5) видно, что оценки детерминированных спектральных функций находятся лишь в том случае, когда четные моменты 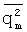 ,
, 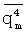 ,
, 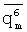 значений показателя качества известных образцов многокомпонентного соединения m-й марки не близки к нулю, а корреляции
значений показателя качества известных образцов многокомпонентного соединения m-й марки не близки к нулю, а корреляции 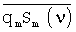 ,
, 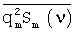 ,
, 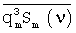 , первого и высших порядков значений показателей качества и спектров известных образцов отличны от нуля.
, первого и высших порядков значений показателей качества и спектров известных образцов отличны от нуля.
Естественно, что аналогичный вывод можно распространить на все показатели качества многокомпонентного соединения и все его выбранные марки.
Вычислим из (4) и (5) ошибку ОШm представления (1)
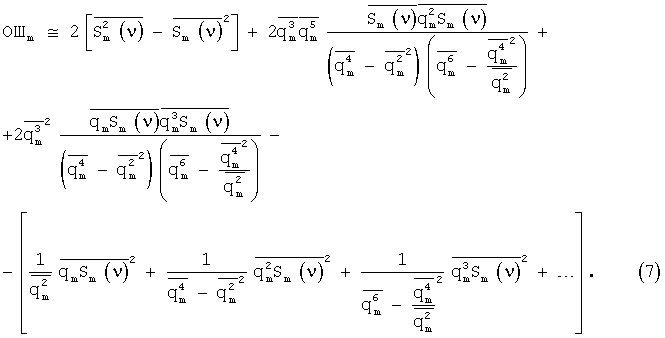
Из (7) видно, что для уменьшения ошибки представления (1) необходимо:
- уменьшать абсолютную величину нечетных моментов (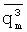 и
и 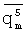 ) значений показателей качества известных образцов;
) значений показателей качества известных образцов;
- уменьшать дисперсию  значений показателей качества известных образцов.
значений показателей качества известных образцов.
Это возможно реализовать только отбором известных образцов многокомпонентных соединений, полученных при различных условиях их производства таким образом, чтобы, с одной стороны, получить наибольший разброс значений показателей качества, а с другой стороны, наиболее равномерно и тесно заполнить максимальный диапазон их значений.
Приведем пример реализации способа.
Пусть имеются различные наборы измеренных значений p95(k) октановых чисел бензина марки 95 и соответствующие им спектральные значения S95(k) оптических плотностей (k=1,2,...,7), измеренные для одного волнового числа, как показано в таблице 1.
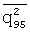

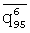
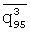
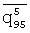
Предположим, что эталонные (истинные) значения оптических плотностей известных образцов составляют величины 0,20; 0,25; 0,32; 0,34; 0,37; 0,45; 0,70.
Вычислим абсолютные и относительные ошибки представления (1), используя эталонные значения оптических плотностей и значения, рассчитанные на основании (1) и (5).
Из таблицы 1 видно, что при равномерном заполнении диапазона значений (набор 1) абсолютные и относительные ошибки представления (1) малы и составляют 0,003 и 0,0337% соответственно. При неравномерном заполнении диапазона значений (набор 2) и тем более при уменьшении разброса значений (набор 3) абсолютные и относительные ошибки представления (1) возрастают и составляют 0,016 (2,774%) и 0,036 (16,869%) соответственно.
На чертеже показаны графики зависимости оптической плотности от октанового числа, построенные с помощью выражений (1) и (5) по данным таблицы 1.
Отчетливо видно преимущество равномерного заполнения диапазона значений показателей качества при их максимально возможном разбросе. Как следует из представления (1), при известных оценках A*m(ν), B*m(ν), С*m(ν), D*m(ν) детерминированных спектральных функций значение показателя качества неизвестного образца многокомпонентного соединения m-й марки можно оценить по его измеренному спектру Sm(ν)
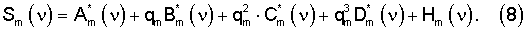
Решить стохастическое уравнение (8) относительно qm возможно методом наименьших квадратов, минимизируя среднеквадратичную ошибку (СКО)
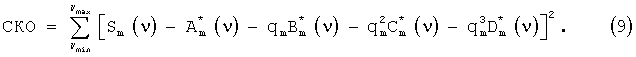
В результате получим уравнение относительно qm
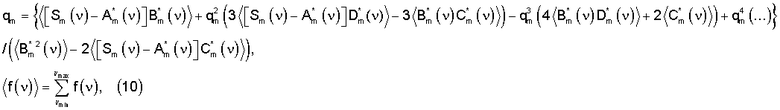
которое может быть решено численно, например, методом стохастической аппроксимации Роббинса-Монро
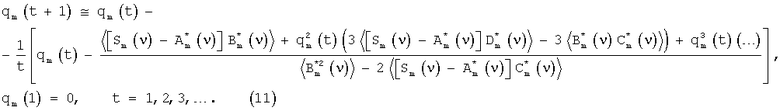
Ошибка решения hm(t)
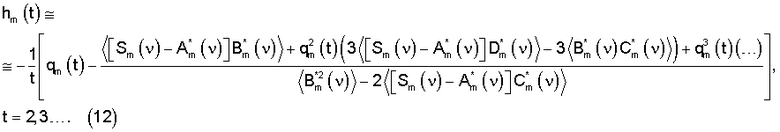
позволяет контролировать точность вычисления показателя качества qm(t) неизвестного образца многокомпонентного соединения на t-м шаге, начиная со 2-го.
Так, например, на 3-м шаге получим
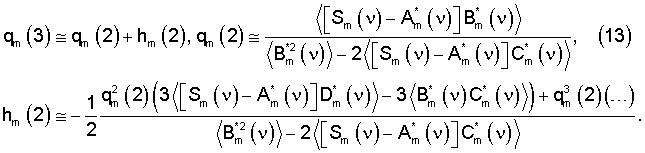
Воспользовавшись (5) и (13), получим выражение для расчета показателя качества многокомпонентного соединения и относительной ошибки (в приближении линейно-квадратичной зависимости спектров от показателя качества)

При выводе (14) использовался тот факт, что все спектры образцов многокомпонентного соединения близки 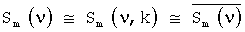 .
.
Так, например, при 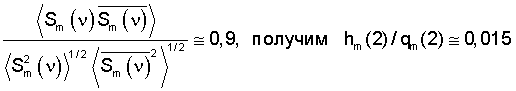
С учетом членов второго и третьего порядка в зависимости (3) (зависимости спектров от показателя качества), а также ростом количества итераций в решении (11) ошибка уменьшается. Поэтому относительная ошибка оценки показателя качества многокомпонентного соединения будет составлять не более hm/qm≅0,015 или 1,5% уже на 3-м шаге аппроксимации.
Для того чтобы воспользоваться рассмотренной технологией вычислений показателей качества, необходимо провести идентификацию (определить марку) неизвестного образца многокомпонентного соединения.
Будем считать, что наблюдаемый спектр S(ν) многокомпонентного соединения неизвестной марки описывается моделью
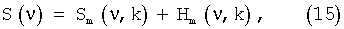
где Sm(ν, k) - спектры оптической плотности используемого диапазона электромагнитных волн, определенные для каждого волнового числа ν для k-го образца (k=1, 2,...,К) известного многокомпонентного соединения m-й марки (m=1,2,...,М); Нm(ν, k) - неизвестные случайные спектральные функции, описываемые усеченными нормальными распределениями вероятностей, с нулевыми средними 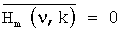 и неизвестными дисперсиями
и неизвестными дисперсиями 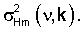
Модель (15) характерна для измерений спектров оптической плотности образцов, помещенных в толстые кюветы (L≅100 мкм ÷ 1000 мкм).
В модели (15) считается, что наблюдаемый спектр S(ν) является зашумленной версией какого-либо полностью известного спектра Sm(ν, k), измеряемого с известными дисперсиями 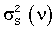 , определяемыми точностью σS(ν) используемого инструментального средства при измерении спектра поглощения для данного волнового числа ν.
, определяемыми точностью σS(ν) используемого инструментального средства при измерении спектра поглощения для данного волнового числа ν.
Тогда на основании теории статистических решений возможно идентифицировать известный спектр, а следовательно, и марку неизвестного многокомпонентного соединения, используя статистики в виде нечетких мер сходства наблюдаемого спектра S(ν) с известными спектрами Sm(ν, k)

где γm(ν) - коэффициенты значимости ν-х волновых чисел (0≤γm(ν)≤1) для m-й марки, удовлетворяющие условию нормирования 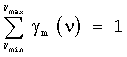 .
.
Коэффициенты значимости определим через дисперсии значений спектральных компонентов с помощью выражений
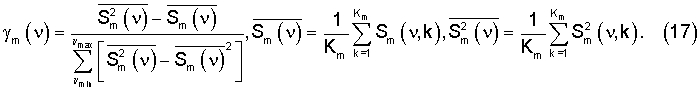
В другом случае, характерном для регистрации спектров оптической плотности многокомпонентных соединений, помещаемых в тонкие кюветы (L≅0, 5 мкм ÷ 10 мкм), наблюдаемый спектр S(ν) образца неизвестной марки описывается моделью

аналогичной модели (15) с той лишь разницей, что масштабный коэффициент ϑ неизвестен.
Тогда снова на основании теории статистических решений возможно идентифицировать известный спектр, а следовательно, и марку многокомпонентного соединения, используя статистики в виде нечетких мер сходства наблюдаемого спектра S(ν) с известными спектрами Sm(ν, k)

Идентификацию неизвестной марки многокомпонентного соединения будем производить методом «ближайшего соседа», относя испытуемый образец к той марке m*, для которой мера сходства μ[S, Sm(k)] примет наибольшее значение, т.е.  .
.
После идентификации марки многокомпонентного соединения на основании выражений (5) и (11) приступим к расчетам его показателей качества.
Как было показано ранее (см. уравнение 1), параметризация зависимости спектра оптической плотности от показателя качества приводит к обратной нелинейной задаче - нелинейной связи оцениваемого показателя качества со спектром оптической плотности (см. уравнение 10).
Поэтому для упрощения расчетов будем использовать непараметрическую интерполяцию

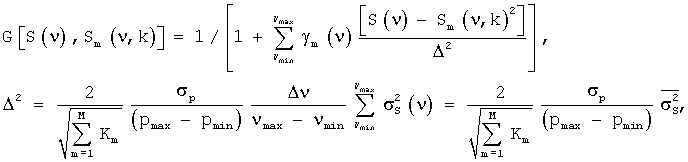
где σp - ошибка (стандартное отклонение) оценивания показателя качества p с помощью интерполяционной зависимости (20); рmin и pmax - его минимальное и максимальное значения соответственно; Δν - спектральное разрешение; 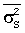 - усредненная по используемому спектральному диапазону (νmin, νmax) дисперсия спектра оптической плотности, определяемая точностью измерений оптических плотностей для различных волновых чисел ν.
- усредненная по используемому спектральному диапазону (νmin, νmax) дисперсия спектра оптической плотности, определяемая точностью измерений оптических плотностей для различных волновых чисел ν.
Зависимость (20) характерна для оценки показателей композитов - смесей, составленных из смесей.
Поэтому если показатель качества, определенный из выражения (20), не удовлетворяет условиям для m-й марки, то многокомпонентная смесь рассматривается как композит, составленный из известных образцов смесей разных марок, и признается некондиционным.
Если же показатель качества, определенный из выражения (20), удовлетворяет условиям для m-й марки, то его значение уточняется на основании решения уравнения (10).
По найденному уточненному значению показателя качества судят о качестве многокомпонентного соединения.
Равномерная вариация значений показателей качества образцов многокомпонентного соединения в максимальных границах, гостированных для каждой марки, необходима и для повышения точности непараметрической интерполяции (20).
Рассмотрим следующий пример. Пусть с помощью интерполяционной зависимости (20) необходимо оценить октановое число проверяемого бензина при наличии известных образцов четырех марок бензинов (М=4) с октановыми числами 82, 92, 95 и 98. В данной ситуации будем считать, что pmax=100, a pmin=80. Будем также считать, что количество известных образцов в каждой марке равны, т.е. К82=К92=К95=К98=К.
Определим ошибку σp оценивания октанового числа р с помощью интерполяционной зависимости (20) выражением
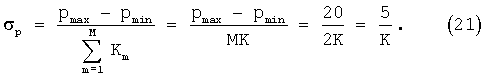
Тогда ширина окна интерполирующей функции G будет равна
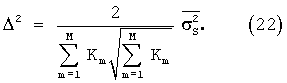
Так, например, для оценивания октанового числа p с помощью интерполяционной зависимости (20) с точностью σр=0.5, что соответствует 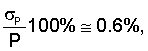 необходимо выбрать К=10 известных образцов в каждой марке бензинов.
необходимо выбрать К=10 известных образцов в каждой марке бензинов.
Для оценивания октанового числа с максимальной требуемой в промышленности точностью (≤0.1 единицы октанового числа), например σp=0.1, необходимо выбрать К=50.
Пусть мы идентифицировали неизвестный бензин, как принадлежащий 95 марке, а значение его октанового числа определили с помощью непараметрической интерполяции, как 96,5. Тем самым подтвердился факт принадлежности неизвестного бензина к 95-й марке.
После этого, решая уравнение (10) с параметрами, характерными для 95-й марки, находим уточненное значение октанового числа р*=95,5. На основании этого значения можно судить о том, что бензин, относящийся к 95-й марке, имеет высокое качество.
Если необходимо получить численное выражение степени качества,
то его можно определить, например, как Q=р* /98,0=95,5/98,0=0,97.
С помощью рассмотренного способа можно идентифицировать, например, марки бензинов и оценивать приведенные в таблице 2 показатели качества.
Приведенные выше математические расчеты, необходимые для реализации способа идентификации и контроля качества бензинов, автоматизированы, например, в «Программе расчета качественных показателей бензинов по их инфракрасным спектрам» (Федеральная служба по интеллектуальной собственности, патентам и товарным знакам. Свидетельство об официальной регистрации программы для ЭВМ №2005611834, 2005).
Патентуемый способ обеспечивает повышение достоверности идентификации и контроля качества многокомпонентных соединений и может применяться в топливной энергетике (для анализа нефтепродуктов - горюче-смазочных материалов); парфюмерной промышленности (для анализа кремов и мазей); пищевой промышленности (для анализа углеводородных и белковых соединений в пищевых средах и готовых продуктах, в частности для идентификации и контроля качества спиртосодержащих жидкостей).
| название | год | авторы | номер документа |
|---|---|---|---|
| АВТОМАТИЗИРОВАННЫЙ СПОСОБ СПЕКТРОФОТОМЕТРИЧЕСКОГО АНАЛИЗА ВЕЩЕСТВ | 2002 |
|
RU2284506C2 |
| ИК-СПЕКТРОМЕТРИЧЕСКАЯ СИСТЕМА ПАРОФАЗНОГО КОНТРОЛЯ ХИМИЧЕСКОГО СОСТАВА СМЕСЕЙ ЖИДКИХ УГЛЕВОДОРОДОВ В РЕЗЕРВУАРЕ И СПОСОБ ВЫПОЛНЕНИЯ СПЕКТРОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ С ЕЕ ИСПОЛЬЗОВАНИЕМ | 2018 |
|
RU2700331C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ И ПРОГНОЗИРОВАНИЯ Р-АЛКИЛЬНЫХ РАДИКАЛОВ ГОМОЛОГОВ О-АЛКИЛАЛКИЛФТОРФОСФОНАТОВ | 2018 |
|
RU2695039C1 |
| Способ определения суммарного содержания углеводородов в водах | 2016 |
|
RU2611413C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПОНЕНТОВ БЕНЗИНА И ОПРЕДЕЛЕНИЯ ЕГО СОСТАВА В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ | 2014 |
|
RU2568330C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОКТАНОВОГО ЧИСЛА АВТОМОБИЛЬНЫХ БЕНЗИНОВ | 2000 |
|
RU2196321C2 |
| СПОСОБ КОНТРОЛЯ КАЧЕСТВА НЕФТЕПРОДУКТОВ И ГОРЮЧЕ-СМАЗОЧНЫХ МАТЕРИАЛОВ | 2001 |
|
RU2187092C1 |
| Способ текущего контроля октанового числа товарных бензинов в процессе их производства | 2017 |
|
RU2678989C1 |
| Способ оперативной идентификации источников загрязнения водных объектов окружающей среды углеводородными топливами | 2022 |
|
RU2780842C1 |
| Способ контроля кондиционности жидких нефтепродуктов | 2020 |
|
RU2752308C1 |
Изобретение относится к измерениям и автоматизации в области оперативной идентификации и контроля качества многокомпонентных соединений, преимущественно углеводородов в нефтепродуктах и парфюмерных изделиях, углеводородных и белковых соединений в пищевых средах и готовых продуктах. Способ включает совместное измерение инфракрасных спектров оптических плотностей известных образцов каждой заданной марки многокомпонентного соединения и значений показателей их качества, определяемых физико-химическими методами. При этом известные образцы измеряют при различных условиях производства, обеспечивающих равномерное заполнение диапазонов значений их показателей качества в максимальных границах, гостированных для каждой марки. Определяют количество известных образцов, исходя из требуемой точности оценивания значений показателей качества. Измеряют спектры оптических плотностей для всех волновых чисел выбранного диапазона электромагнитных волн, оценивают нормированные значимости всех используемых волновых чисел по дисперсиям спектральных компонентов оптических плотностей известных образцов каждой марки. Идентифицируют многокомпонентное соединение неизвестной марки методом «ближайшего соседа» на основе нечетких мер сходства его спектров со спектрами всех известных образцов при определенных ранее нормированных значимостях волновых чисел каждой марки, оценивают значения показателей качества идентифицированного многокомпонентного соединения на основе непараметрической интерполяции по накопленным значениям показателей качества известных образцов всех марок, а качество многокомпонентного соединения определяют по результатам его идентификации и оцененным значениям показателей качества. Изобретение позволяет повысить достоверность идентификации и контроля качества многокомпонентных соединений. 6 з.п. ф-лы, 1 ил., 2 табл.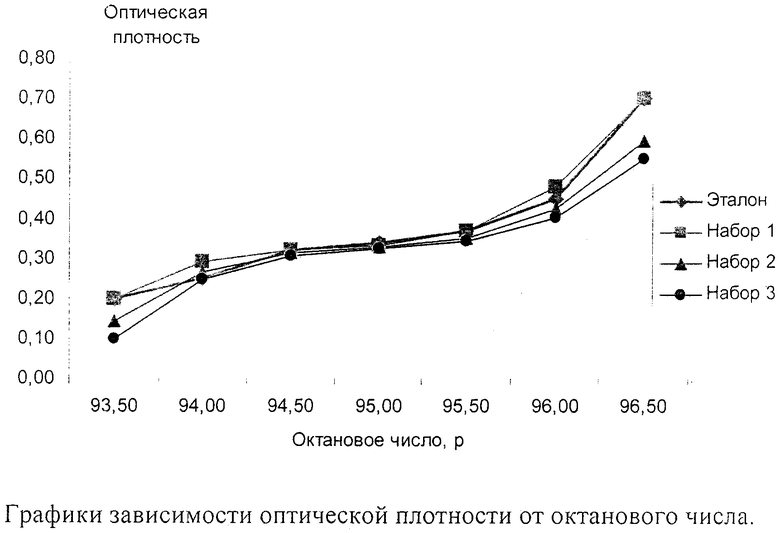

где σр - ошибка оценивания показателя качества р на основе непараметрической интерполяции; pmin и рmax - минимальное и максимальное значения показателя качества соответственно; М - количество марок многокомпонентного соединения; Кm - количество образцов в m-й марке.

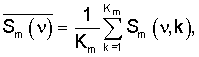
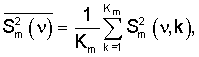

где Sm(v, k) - спектры оптической плотности используемого диапазона электромагнитных волн, определенные для каждого волнового числа ν для k-го образца известного многокомпонентного соединения m-й марки; Km - количество всех известных образцов многокомпонентного соединения m-й марки.

где 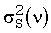 - известные дисперсии значений спектральных компонентов, определяемые точностью используемого инструментального средства при измерении спектров для данного волнового числа ν.
- известные дисперсии значений спектральных компонентов, определяемые точностью используемого инструментального средства при измерении спектров для данного волнового числа ν.
 ,
,
где 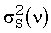 - известные дисперсии спектральных компонентов, определяемые точностью используемого инструментального средства при измерении спектров для данного волнового числа ν.
- известные дисперсии спектральных компонентов, определяемые точностью используемого инструментального средства при измерении спектров для данного волнового числа ν.

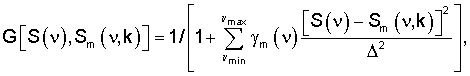
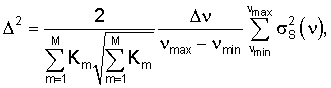
где Pm(k) - показатель качества k-го образца известного молекулярного соединения, определенный физико-химическим методом для его заданной m-й марки; Δν - спектральное разрешение в используемом спектральном диапазоне (νmin, νmax) оптической плотности.
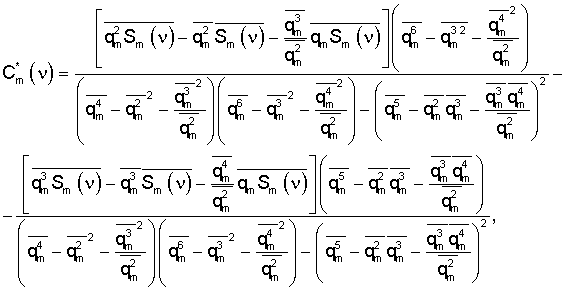
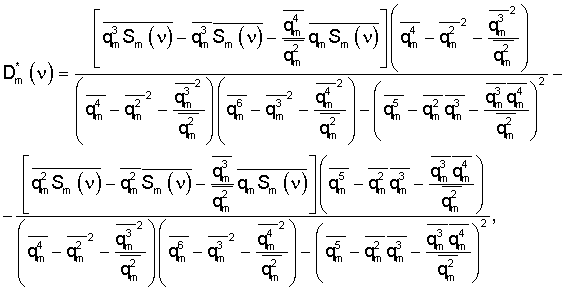
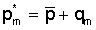 оцененного показателя качества, которое находят на основании решения уравнения
оцененного показателя качества, которое находят на основании решения уравнения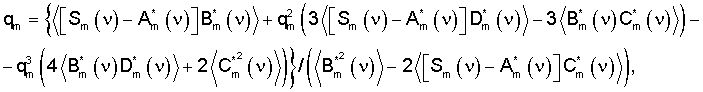

где

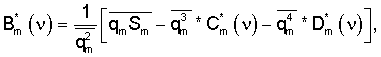
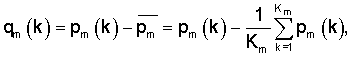
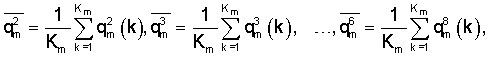
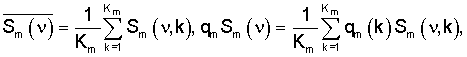

| RU 2075062 C1, 10.03.1997 | |||
| ПРИБОРЫ И МЕТОДЫ АНАЛИЗА В БЛИЖНЕЙ ИНФРАКРАСНОЙ ОБЛАСТИ | |||
| - М.: Химия, 1977, с.185-190 | |||
| Видоизменение ветряного двигателя | 1929 |
|
SU19168A1 |
| Способ Солдатова-Сагайдачного количественного определения компонентов в бинарных смесях | 1984 |
|
SU1239567A1 |
| US 5349189 A, 20.09.1994. | |||
Авторы
Даты
2008-09-27—Публикация
2006-08-09—Подача