Предпосылки создания изобретения
Настоящее изобретение относится к оптимизации последовательных (многостадийных) комбинаторных процессов.
Известно множество примеров процессов, заключающихся в осуществлении ряда стадий, при этом конечный результат таких процессов может быть оптимизирован за счет реализации этих стадий предпочтительным образом. Производственные процессы, например, могут состоять из стадий, на которых на качество производимой продукции влияют такие конкретные переменные величины, как размер, количество, длительность, давление, температура, вязкость и т.д. Поскольку промышленность, естественно, заинтересована в обеспечении высокого качества, часто желательно оптимизировать различные стадии, чтобы получить наилучший конечный результат.
Такую оптимизацию часто осуществляют путем моделирования процесса. Таким образом сравнивают различные значения параметра или группы параметров, чтобы установить, какие из них обеспечивают лучший результат. Одной из методик моделирования, которая представляет особый интерес ввиду ее высокой точности и способности справляться со сложными сценариями, является анализ методом конечных элементов. Применительно к процессу рассматриваемого типа данная модель в целом учитывает интересующие параметры как описываемые в непрерывном числовом пространстве, в котором параметры могут иметь любое значение, и ищет оптимальное значение каждого из них с учетом остальных параметров. Вместе с тем, с точки зрения необходимого для вычислений времени такое решение является дорогостоящим. Один "прогон" модели на основе метода конечных элементов для одного набора величин параметров может занять несколько часов, при этом обычно существует множество величин, требующих анализа. Это означает, что модели потребуются тысячи последовательных приближений, чтобы прийти к какому-либо оптимальному решению, в результате чего полный анализ процесса может занять неосуществимо долгое время. Связанные с ним расходы могут перевесить любые преимущества, достигнутые за счет оптимизации процесса.
Данный недостаток был преодолен за счет так называемой имитации моделирования (surrogate modelling). Идея использования имитаций моделей при оптимизации широко исследована применительно к проблемам, связанным с обширными вычислениями. Имитация является простым приближением модели на основе метода конечных элементов (или другой сложной модели) к менее длительным итерационным процессам, что ускоряет вычисления. Хорошо известной имитацией модели является криджинг, но также может использоваться любой другой метод последовательных приближений, применимый к конкретной задаче. Результаты нескольких прогонов модели анализа методом конечных элементов вводят в имитацию модели для ее "обучения". Количество таких прогонов зависит от сложности анализируемого процесса; как правило, 20-30 прогонов достаточно для обеспечения достаточного уровня точности. После завершения обучения имитации модели ее пропускают через цикл оптимизации, в ходе которого она вычисляет результат процесса при всех возможных значениях интересующего параметра или параметров и выдает значение, которое соответствует оптимальному результату процесса. Однако данное оптимальное значение основано на последовательных приближениях имитации модели и может быть неточным. В связи с этим применительно к тем же значениям параметров обычно прогоняют модель на основе метода конечных элементов и сравнивают результат с результатом, полученным при помощи имитации модели. В случае значительной разницы между ними результат такого последнего прогона модели на основе метода конечных элементов затем загружают в имитацию модели, чтобы усовершенствовать ее обучение, и снова пропускают имитации модели через цикл оптимизации и так далее до тех пор, пока не будет обеспечено приемлемое соответствие результатов двух моделей. За этот счет повышается точность имитации модели в оптимальной области, поскольку точность повышается там и тогда, когда это необходимо. Общее время на вычисления, которое требуется для получения оптимального значения, сокращается за счет переноса основной вычислительной нагрузки из медленной модели на основе метода конечных элементов в более быструю имитацию модели. Например, один прогон модели на основе метода конечных элементов занимает около 48 часов, тогда как для осуществления 50000 имитаций вычислений достаточно менее 10 минут.
Кроме того, точность может быть повышена за счет тщательного выбора начальных прогонов модели на основе метода конечных элементов с тем, чтобы охватить диапазон значений параметров, в который входят значения, считающиеся предположительно важными для определения оптимального значения. Данное решение известно как "планирование экспериментов" (DoE - сокращение от англ. "design of experiments"), которое позволяет избежать потенциальной непроизводительной траты времени на вычисления в процессе сценариев моделирования, результаты которых далеки от желаемых. Примером процесса моделирования с применением анализа методом конечных элементов в сочетании с планированием экспериментов является патент США US 6349467 [1], в котором описана методика оптимизации стадий производства отражателей для камер сгорания газотурбинных двигателей во избежание нежелательного промежуточного термического воздействия на листовой металл, из которого изготавливают отражатели.
До настоящего времени дополненное имитацией модели моделирование методом конечных элементов широко применялось для решения разнообразных задач, требующих оптимизации численного значения одного или нескольких параметров, применяемых в процессе. Круг таких задач был ограничен задачами, позволявшими решать их путем последовательного приближения с использованием функции имитации модели, зависящей от переменных величин непрерывного или дискретного характера, и выражать результат физическими или количественными параметрами. Вместе с тем, дополнительно существует множество процессов, которым может пойти на пользу оптимизация, но к которым неприменимы известные методы имитации моделирования, поскольку задача не заключается в поиске оптимального численного значения какого-либо параметра. К таким процессам относятся процессы, состоящие из нескольких стадий или действий, которые с целью достижения конечного результата процесса осуществляют или сочетают в любом порядке или последовательности. Однако качество конечного результата зависит от порядка, в котором осуществляют стадии. Иными словами, в комбинаторной области не существует доступных методик оптимизации имитации моделирования, в которых переменные величины не имеют физического смысла. Задача состоит в том, чтобы определить оптимальный порядок следования действий и получить наилучший результат. Следовательно, данную задачу можно охарактеризовать как задачу оптимизации последовательных комбинаторных процессов, которая заключается в идентификации последовательности, в которой следует сочетать действия, чтобы получить оптимальный результат. Очевидно, что данная задача отличается от задачи определения оптимального значения количественно измеримого параметра; отдельные действия и порядок их следования являются нечисловыми элементами, не имеющими физического смысла. До настоящего времени при решении задач оптимизации такого рода приходилось по большей части полагаться на данные полного анализа методом конечных элементов.
В основу настоящего изобретения положена задача обеспечения усовершенствованного способа оптимизации последовательных комбинаторных процессов, что может принести значительную пользу.
Краткое изложение сущности изобретения
Соответственно, согласно первой особенности настоящего изобретения предложен способ оптимизации последовательного комбинаторного процесса, состоящего из множества взаимозаменяемых действий (событий), осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, заключающийся в том, что используют планирование экспериментов, включающее группу последовательностей, выбранных из множества последовательностей, при этом каждая последовательность, входящая в планирование экспериментов, связана с данными, касающимися значения вклада каждого действия из каждой последовательности в достижение конечного результата, описанного рабочим параметром; используют имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений вклада, которые содержатся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения и извлекают значения вклада совпавшего действия; осуществляют прогон группы из множества последовательностей через имитацию модели и регистрируют значение конечного результата каждой последовательности; и идентифицируют оптимальную последовательность путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, является оптимальной последовательностью.
Таким образом, имитацию модели применяют в изобретении для оптимизации последовательных комбинаторных задач, решение которых в ином случае осуществимо путем сложного моделирования, такого как моделирование методом конечных элементов. В изобретении предложено быстрое и эффективное решение задачи сложного моделирования, требующей значительных затрат времени, частично благодаря тому, что изобретение позволяет извлекать полезную информацию из имеющейся в наличии информации за счет осуществления доступа к информации согласно указателю приоритетов, основанному на ее полезности. Это дает возможность использовать более точную информацию, по возможности отдавая ей предпочтение перед менее точной информацией, и при помощи имитации модели быстро получать конечный результат, который является достаточно приближенным к более точным результатам, которые не так быстро могут быть получены при помощи обычных сложных моделей.
Таким образом, значительно сокращаются расходы на вычисления без значительной потери точности. Планирование экспериментов может быть реализовано гибко, чтобы адаптировать способ к растущим объемам информации, с возможностью динамического расширения по мере появления новых доступных данных, повышающих точность.
Способ был применен в реальной инженерно-технической практике и широко продемонстрировал свои преимущества, позволив оптимизировать технологию сварки по результатам всего 27 прогонов эталонной модели анализа методом конечных элементов из возможных 46080 комбинаций.
В некоторых вариантах осуществления способа дополнительно получают данные, связанные с каждой последовательностью из планирования экспериментов, для чего осуществляют прогон каждой последовательности из планирования экспериментов через эталонную модель процесса, в которую в качестве исходных данных введена последовательность действий и которая определяет значение конечного результата и вклад в конечный результат каждого действия из введенной последовательности.
За счет такого применения эталонной модели с высокой точностью обеспечивают информацию, необходимую имитации модели, без необходимости практического осуществления процесса. Однако глобальная оптимизация все же может быть значительно быстрее, чем оптимизация с использованием только эталонной модели, поскольку процедура проверки соответствия по приоритетам позволяет наилучшим образом использовать небольшое количество информации. Так, достаточно точные результаты получают даже в случае небольшого числа прогонов сложной эталонной модели вместо требующей больших затрат времени полной серии прогонов, которая потребовалась бы в случае применения только эталонной модели. Значительная доля затрат вычислительных ресурсов может быть перенесена на имитацию модели, что значительно ускоряет оптимизацию.
Таким образом, способ дополнительно заключается в том, что эталонную модель строят перед осуществлением прогона каждой последовательности из планирования экспериментов через такую эталонную модель. Таким образом, получают и применяют специально рассчитанную на соответствующий процесс эталонную модель, которая повышает точность.
Предпочтительно, имитация модели представляет собой упрощенное приближение к эталонной модели. Чтобы лучше использовать перенос затрат вычислительных ресурсов с эталонной модели на имитацию модели, имитация модели должна быть максимально простой, насколько это позволяет точность, поскольку расчет простой модели обычно занимает меньше времени.
Способ может дополнительно включать стадию, в которой после идентификации оптимальной последовательности осуществляют прогон идентифицированной оптимальной последовательности через эталонную модель с целью определения значения конечного результата и сравнивают зарегистрированное оптимальное значение идентифицированной оптимальной последовательности, определенное при помощи имитации модели, с конечным результатом, определенным при помощи эталонной модели, с целью проверки точности идентификации оптимальной последовательности. Поскольку эталонная модель отличается более высокой точностью, чем имитация модели, при наличии времени целесообразно осуществить прогон идентифицированной оптимальной последовательности через эталонную модель, чтобы проверить согласованность двух моделей. Согласованность является хорошим показателем того, что идентифицированная последовательность действительно является оптимальной. Затем ее с высокой степенью надежности применяют для оптимизации процесса. Кроме того, при обнаружении неприемлемого расхождения между двумя результатами дополнительный прогон через эталонную модель не является лишним, поскольку это делает доступной новую точную информацию, которой может быть дополнено планирование экспериментов, чтобы повысить точность будущих прогонов имитации модели. Таким образом, в способе дополнительно при обнаружении различия между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, определенным при помощи имитации модели, и конечным результатом, определенным при помощи эталонной модели, величина которого неприемлема для процесса, дополняют планирование экспериментов идентифицированной оптимальной последовательностью, чтобы данная последовательность и значения вкладов в конечный результат каждого действия, определенные путем прогона идентифицированной оптимальной последовательности через эталонную модель, были доступны для поиска и извлечения при помощи алгоритма имитации модели; осуществляют прогон группы из множества последовательностей через имитацию модели с целью получения новых значений конечного результата каждой последовательности; и на основании новых конечных результатов идентифицируют новую оптимальную последовательность.
Описанные в предыдущем абзаце стадии могут быть осуществлены повторно применительно к новой идентифицированной оптимальной последовательности до тех пор, пока различие между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, полученным при помощи имитации модели, и конечным результатом, полученным при помощи эталонной модели, не станет приемлемым для процесса. Такое циклическое выполнение позволяет обеспечить схождение имитации модели с точным результатом за счет того, что в имитации модели используют все большие количества содержащейся в эталонной модели точной информации, о которой известно, что она способствует оптимальному осуществлению процесса, поскольку была идентифицирована имитацией модели. Таким образом, многократное повторение является эффективным и повышающим точность.
В альтернативных вариантах осуществления способа осуществляют последовательный комбинаторный процесс с использованием каждой из последовательностей из планирования экспериментов для получения данных, связанных с каждой последовательностью из планирования экспериментов, и регистрируют значения вклада в конечный результат каждого действия из каждой последовательности. Данный подход, согласно которому для получения информации, используемой имитацией модели, применяют реальные экспериментальные данные, при некоторых обстоятельствах является предпочтительным по сравнению с более абстрактными подходами. Например, в случае простого процесса быстрее и/или дешевле осуществить процесс несколько раз применительно к различным последовательностям, чем строить сложную эталонную модель или иным образом получать информацию путем вычислений. При этом обеспечивается более высокая точность, чем в случае применения других методов, таких как адаптация данных, полученных при помощи или вычисленных для родственного процесса. Точность, которую обеспечивает данный вариант осуществления, частично зависит от точности экспериментальных измерений и от того, насколько легко определить вклад различных действий в конечный результат.
Имитация модели может быть построена перед прогоном группы из множества последовательностей через названную имитацию модели. Строят точно согласованную с конкретным процессом имитацию модели, степень простоты которой соответствует требуемой точности и доступному для оптимизации процесса времени.
В некоторых вариантах осуществления указатель приоритетов содержит иерархию условий совпадения в порядке убывания уровня соответствия между действием из последовательности, введенной в имитацию модели, и действиями из последовательностей, входящих в планирование экспериментов, с точки зрения положения действия из введенной последовательности и/или действий, предшествующих действию из введенной последовательности. Это позволяет эффективно использовать доступную информацию о вкладе различных действий, поскольку во всех возможных случаях используют наиболее точные расчеты или измерения вкладов (которые соответствуют оптимальным совпадениям для последовательностей), которые только при необходимости заменяют ближайшими совпадениями.
Для облегчения достижения точного совпадения действий условия совпадения описаны таким образом, чтобы включать: порядок, определяющий число действий, предшествующих действию из последовательности, введенной в имитацию модели, которые должны совпасть с действиями, предшествующими действию из последовательностей планирования экспериментов; и тип определения совпадения положения действия из последовательности, введенной в имитацию модели, в такой последовательности, с положением действия в последовательностях из планирования экспериментов, при этом для совпадения 1-го типа положение действия во введенной последовательности должно совпадать с положением действия в последовательностях из планирования экспериментов, а для совпадения 2-го типа не требуется, чтобы положение действия во введенной последовательности совпадало с положением действия в последовательностях из планирования экспериментов.
Например, для последовательности, состоящей из n-числа действий, указатель приоритетов содержит следующие условия совпадения:
- совпадение n-го порядка 1-го типа,
- совпадение n-го порядка 2-го типа,
- совпадение (n-1)-го порядка 1-го типа,
- совпадение (n-1)-го порядка 2-го типа,
- …
- совпадение 1-го порядка 1-го типа,
- совпадение 1-го порядка 2-го типа,
- совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой в планировании экспериментов.
Таким образом, более высокий приоритет отдают совпадению предшествующих действий, для чего перед тем, как перейти к поиску усеченной подпоследовательности, в моделируемой последовательности осуществляют поиск такой же подпоследовательности действий независимо от их положения. Однако поскольку в некоторых случаях обнаруживается или возникает предположение, что абсолютное положение является более важным, чем влияние предшествующих действий, в качестве альтернативы, для последовательности, состоящей из n-числа действий, указатель приоритетов может содержать следующие условия совпадения:
- совпадение n-го порядка 1-го типа,
- совпадение (n-1)-го порядка 1-го типа,
- совпадение (n-2)-го порядка 1-го типа,
- совпадение 1-го порядка 1-го типа,
- совпадение n-го порядка 2-го типа,
- совпадение (n-1)-го порядка 2-го типа,
- совпадение (n-2)-го порядка 2-го типа,
- …
- совпадение 1-го порядка 2-го типа,
- совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой для планирования экспериментов.
Предпочтительно, планирование экспериментов включает выбор из множества последовательностей тех, которые включают действия, обеспечивающие совпадения по меньшей мере со всеми комбинациями действий, отвечающих условию совпадения выбранного порядка и типа. Это позволяет сосредоточить информацию о рабочих параметрах там, где она имеет наибольшую ценность, с целью обеспечить точный результат при наименьшем количестве информации. Применительно к различным вариантам осуществления данный подход означает, что необходимо осуществлять лишь минимальное число прогонов эталонной модели или минимальное число раз осуществлять процесс, что упрощает и ускоряет оптимизацию. Вместе с тем, дополнительные расчеты с целью определить, какие для этого необходимы последовательности, могут быть сочтены нецелесообразными. В этом случае планирование экспериментов в качестве альтернативы может включать случайный выбор последовательностей из множества последовательностей. В любом случае независимо от типа планирования экспериментов в способе можно дополнительно обуславливать планирование экспериментов. Это позволяет использовать соответствующее планирование экспериментов применительно к каждому процессу, что потенциально обеспечивает более высокую точность, чем использование, например, предыдущего или стандартного планирования, которое в принципе применимо к процессу.
Прогон группы из множества последовательностей через имитацию модели может включать прогон через имитацию модели всех из множества последовательностей. Естественно, это занимает немного больше времени, чем прогон подмножества последовательностей, но обеспечивает наиболее точный результат, несмотря на то, что во многих случаях удовлетворительно точный результат легко достижим при использовании подмножества. При выборе числа последовательностей для прогона через имитацию модели дополнительное время на вычисления компенсируется повышенной точностью.
С учетом вероятных значительных вычислений, которые необходимы, в особенности, в случае сложной эталонной модели, в предпочтительном варианте осуществления способа он по меньшей мере частично реализован при помощи компьютера. Это позволяет эффективно использовать сокращение времени на оптимизацию, которое обеспечивает настоящее изобретение.
После идентификации оптимальной последовательности ее применяют в соответствующем процессе. Таким образом, способ дополнительно заключается в том, что осуществляют последовательный комбинаторный процесс с использованием идентифицированной оптимальной последовательности действий.
В качестве примера применения изобретения последовательный комбинаторный процесс может включать приваривание лопасти к кольцу корпуса заднего подшипника газовой турбины, при этом осуществляемые действия представляют собой отдельные траектории сварки, которые осуществляют последовательно, рабочий параметр, задающий конечный результат, представляет собой деформацию кромки лопасти, а оптимальное значение рабочего параметра представляет собой минимальную величину деформации.
Согласно второй особенности настоящего изобретения предложен компьютерный программный продукт, содержащий машиночитаемые команды для реализации способа оптимизации производственного, промышленного или инженерно-технического последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, причем в соответствии с указанными командами компьютер выполняет следующие действия: запоминание планирования экспериментов, включающего группу последовательностей, выбранных из множества последовательностей; запоминание данных, связанных с каждой последовательностью из планирования экспериментов и касающихся значения вклада каждого действия из каждой последовательности из планирования экспериментов в достижение конечного результата, характеризуемого рабочим параметром; прогон группы из множества последовательностей через имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значения вклада выбирают из значений вклада, которые содержатся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, извлекают значение вклада совпавшего действия и записывают значения конечного результата каждой последовательности; и идентифицирование оптимальной последовательности путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, является оптимальной последовательностью.
Компьютерный программный продукт для реализации изобретения может представлять собой исполняемую на компьютере программу на носителе. Носитель может представлять собой среду для хранения данных, такую как твердотельная, магнитная, оптическая, магнитооптическая или иная запоминающая среда. В качестве альтернативы носитель может представлять собой среду для передачи данных, такую как вещательную, телефонную, сетевую программную, проводную, беспроводную, электрическую, электромагнитную, оптическую или практически любую иную передающую среду.
Согласно третьей особенности настоящего изобретения предложена компьютерная система для реализации способа оптимизации последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, содержащая память для запоминания планирования экспериментов, представляющего собой множество последовательностей, выбранных из множества последовательностей, и запоминания данных, связанных с каждой последовательностю из планирования экспериментов и касающихся значения вклада каждого действия из каждой последовательности в достижение конечного результата, характеризуемого рабочим параметром; и процессор, запрограммированный для прогона группы из множества последовательностей через имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений, содержащихся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, извлекают значения вклада совпавшего действия и осуществляют запись значения конечного результата каждой последовательности в памяти, и идентифицирование оптимальной последовательности путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, представляет собой оптимальную последовательность.
Другие особенности, варианты осуществления и примеры настоящего изобретения будут также раскрыты ниже.
Краткое описание чертежей
С целью облегчить понимание изобретения и показать, как оно может быть осуществлено, далее изобретение описано со ссылкой в качестве примера на приложенные чертежи, на которых:
на фиг.1 показана блок-схема последовательности стадий варианта осуществления предлагаемого в изобретении способа,
на фиг.2 - блок-схема последовательности стадий альтернативного варианта осуществления предлагаемого в изобретении способа,
на фиг.3 - вид в перспективе корпуса заднего подшипника газовой турбины, в процессе производства которого применяют один из вариантов осуществления настоящего изобретения,
на фиг.4 - вид в перспективе и вид в поперечном разрезе частей корпуса, показанного на фиг.3,
на фиг.5 - вид в поперечном разрезе лопасти, являющейся частью подшипника, показанного на фиг.3, при этом стрелками указаны траектории, по которым лопасть приваривают к внутреннему кольцу подшипника,
на фиг.6 - таблица с примерами различных последовательностей, в которых осуществляют сварку по траекториям, показанным на фиг.5,
на фиг.7 - диаграммы колебания смещения частей лопасти в процессе сварки,
на фиг.8 - диаграммы колебания смещения части лопасти при сварке в последовательностях, показанных на фиг.6,
на фиг.9 - таблица последовательностей, используемых в планировании экспериментов с целью оптимизации процесса сварки согласно одному из вариантов осуществления настоящего изобретения,
на фиг.10 - матрица событий при различных сочетаниях траекторий сварки согласно последовательностям, показанным на фиг.9,
на фиг.11 - матрица смещения части лопасти в каждом случае, показанном на фиг.10,
на фиг.12 - диаграммы колебания смещения части лопасти при сварке в некоторых из последовательностей, показанных на фиг.9, и
на фиг.13 - диаграмма колебания окончательного смещения части лопасти при сварке в каждой последовательности, показанной на фиг.9.
Подробное описание
В настоящем изобретении предложен метод применения к последовательным комбинаторным задачам подхода, основанного на имитации модели, который ранее использовался для нахождения оптимальных решений непрерывных численных задач. Имитация модели значительно сокращает расходы на вычисления, необходимые для оптимизации таких процессов, по сравнению с обычными подходами, основанными на сложных методах компьютерного моделирования, таких как анализ методом конечных элементов.
Последовательный комбинаторный процесс представляет собой процесс, состоящий из множества стадий или действий, которые являются взаимозаменяемыми в том смысле, что могут быть осуществлены в любой из нескольких или множества последовательностей, при этом одни действия, возможно, заменяют другие действия или существует возможность выбора способов осуществления каждого действия с целью получения такого же общего конечного результата, но качество такого конечного результата зависит от конкретного порядка следования действий.
Таким образом, в каждом положении последовательности осуществляют какое-либо действие, выбранное из группы действий, число которых равно числу положений в последовательности, или из более многочисленной группы действий. В последнем случае в более многочисленную группу входят некоторые действия, которые могут быть исключены из процесса или заменены другими действиями или, в качестве альтернативы, некоторыми или всеми действиями, соответствующие параметры которых могут иметь различные значения (например, осуществление конкретной стадии при одной из нескольких различных температур или в течение одного из нескольких отрезков времени), в результате чего каждое действие имеет несколько возможных вариантов, каждый из которых может сам по себе рассматриваться как действие, несмотря на то, что в любую взятую последовательность будет включен лишь один из вариантов.
Конечный результат рассматривают как описанный рабочим параметром. Природа рабочего параметра зависит от конкретного процесса, и он может, например, представлять собой размеры производимой детали или время, которое занимает осуществление процесса. Так, для каждой возможной последовательности процесса предусмотрен конечный результат, который имеет значение, описанное рабочим параметром.
В приведенном выше примере с размером конечными результатами будут являться различные значения размеров.
Что касается примера со временем, конечными результатами будут являться различные количества времени.
Поскольку каждое действие из заданной последовательности определенным образом способствует конечному результату в зависимости как от его положения в последовательности, так и природы самого действия, корректировка выбранных действий приводит к изменению значения конечного результата.
В ряду последовательностей существует последовательность, конечный результат которой имеет такое значение, которое обеспечивает оптимальное значение рабочего параметра, такое как кратчайшее время или наименьшие размеры. Поскольку не всегда очевидно, какая последовательность обеспечивает такой оптимальный результат, желательно иметь возможность определить такую последовательность, что может рассматриваться как оптимизация комбинаторного процесса. Да настоящего времени это было достижимо, как правило, при помощи сложного моделирования. Обычно моделирование одной последовательности занимает много часов, как это происходит при моделировании методом конечных элементов. Даже для процесса с относительно небольшим числом действий общее количество комбинаций действий может быть огромным, поэтому проверка каждой комбинации путем моделирования становится неосуществимой. В настоящем изобретении предложено применение более простой имитации модели, чтобы частично сократить затраты вычислительных ресурсов и, следовательно, ускорить процесс.
Таким образом, в настоящем изобретении предложен метод комбинаторной оптимизации. Оптимизация представляет собой процесс обнаружения одного или нескольких лучших или оптимальных решений в четко заданной дискретной области решения задачи. Область является дискретной, поскольку существует лишь ограниченное число действий и каждое действие входит или не входит в заданную последовательность; так, последовательная комбинаторная задача имеет отношение к эффективному распределению ограниченных ресурсов с целью достижения заданных целей, когда значения некоторых или всех переменных величин ограничены целыми числами. Ограничения на основные ресурсы, такие как время, рабочая сила, поставки или капитал, способны сузить возможные альтернативы, считающиеся осуществимыми. Такие проблемы возникают почти во всех областях менеджмента, таких как финансы, маркетинг, производство, планирование, управление товарно-материальными запасами, местоположение и планировка сооружений, управление базами данных, а также во многих инженерных отраслях. Их примерами являются оптимальное проектирование водных путей или мостов, проектирование и испытание сверхбольших интегральных схем, планировка схем с целью сведения к минимуму площади, занимаемой проводами, проектирование и анализ сетей передачи данных, управление ликвидацией твердых отходов, определение основных состояний спиновых стекол, определение минимальных энергетических уровней при составлении и разделении сплавов, модели планирования энергетических ресурсов, материально-техническое обеспечение выработки и передачи электроэнергии, планирование товаров на непрерывных производствах и задачи в области кристаллографии. Применение предложенного в изобретении техники оптимизации благоприятно сказывается на всех перечисленных процессах.
По существу, настоящее изобретение применимо в любом последовательном процессе, в котором упорядочение действий в последовательности влияет на результат процесса. Приведенные выше примеры применения служат доказательством широкой применимости изобретения. Помимо этих примеров изобретение применимо и для оптимизации процессов из числа перечисленных ниже.
а). Изготовление детали (компонента) из заготовки посредством машинной обработки. Осуществляемые действия включают различные стадии резки с целью изготовления различных частей детали, при этом желательно найти последовательность, которая наилучшим образом обеспечивает требуемую форму и/или качество детали. Данная задача может быть охарактеризована, например, такими показателями, как качество обработки поверхности, текстура и/или глубина материала поверхности, подвергаемой пластической деформации режущим инструментом. Перечисленные желаемые свойства представляют собой описанный выше рабочий параметр. В случае такого рода применение изобретения заключается в том, что материал отрезают от заготовки в такой последовательности, чтобы деталь приобрела или сохранила требуемую структурную жесткость в процессе машинной обработки и чтобы свести к минимуму дрожание или вибрацию в процессе обработки на станке. В данном случае рабочим параметром является дрожание, а его оптимальным значением является минимальный уровень.
б). Термообработка детали. Поскольку данный процесс зависит от того, как действует печь, которую используют для термообработки, возможные действия включают определение расположения и управление выходными патрубками вентилятора, определение расположения и управление направлением потоком горячего или холодного воздуха, изменение или оставление без изменения воздушного потока на любой стадии термообработки, количество выдержек и охлаждений. Задачей является достижение конечного результата, который выражен, например, в требуемой форме, жесткости или микроструктуре детали; таким образом, одна или несколько из этих характеристик является рабочим параметром, при этом требуемая форма и т.д. представляет собой оптимальное значение.
в). Формование и профилирование детали. Такой процесс представляет собой последовательность стадий формования и профилирования различных частей детали (действия) с целью придания им требуемой формы, обеспечения структурной жесткости и микроструктуры материала (конечный результат). Альтернативным конечным результатом является то, как состояние детали, изготовленной в результате заданной последовательности, влияет на последующий компонент, частью которого такая деталь должна стать.
г). Технологическая последовательность операций, представляющая собой комбинацию перечисленных производственных процессов, при этом различные процессы становятся действиями, которые с целью повлиять на качество готового изделия осуществляют в различном порядке и различными способами. Например, для придания требуемой формы, обеспечения структурной жесткости или микроструктуры материала изделия, возможно, потребуется определить, на какой стадии технологической последовательности операций следует осуществить одну или несколько термических обработок с учетом того, что такие процессы, как фрезерование, литье, машинная обработка, профилирование и сварка, придают некоторые механические свойства изделию и/или свойства материалу.
д). Поток материалов и/или деталей. Материалы и детали, используемые в производственном процессе, обычно необходимо перемещать по заводу или фабрике, при этом последовательность стадий, осуществляемых для обеспечения потока, влияет на такие параметры, как длительность и производительность процесса. Поток может представлять собой общий поток, проходящий через все предприятие или даже между предприятиями. Осуществляемые стадии или действия включают, например, транспортировку какого-либо изделия между различными станками, местами хранения и обработки. К ним также относится определение оптимальных положений станков на территории предприятия, поскольку вклад каждого действия, связанного с транспортировкой, в общий поток зависит от положения соответствующих станков, в связи с чем доступна большая группа действий, которые соответствуют различным возможностям выбора положений для станков.
е). Перекачка газа или нефти по сети трубопроводов. На схему доставки газа или нефти потребителям, например, влияют конструкции различных компонентов сети и такие рабочие параметры, как открытие и закрытие клапанов и скорость нагнетания; действия, связанные с отдельными участками сети, имеющими различные конфигурации, объединяют в последовательности, чтобы определить наилучший способ оптимальной доставки. При желании комбинаторные аспекты данной задачи дополнительно сочетают со стохастическими и нелинейными эффектами, что повышает точность процесса оптимизации и позволяет учитывать дополнительные подробности различных действий.
ж). Применение в области химии и материаловедения, такое как определение оптимальной последовательности добавления различных ингредиентов или компонентов с целью получения требуемой смеси. Таким образом, использование различных ингредиентов в различных пропорциях при различных температурах или в различных концентрациях и различных методов смешивания представляет собой возможные действия, из которых затем формируют последовательность, чтобы получить общую смесь. Качество смеси представляет собой конечный результат процесса, описанный рабочим параметром, таким как устойчивость, чистота и однородность. Он также включает оптимизацию энергетических состояний с целью составления и разделения сплавов.
з). Вычислительная биология. В данной области обычно анализируют различные задачи, используя численные методы, описывающие поведение биологических компонентов, таких как молекулы, белки и геномы. Настоящее изобретение применяют для уменьшения вычислительных затрат, связанных с исследованием большого числа возможных сочетаний последующих реакций, которые протекают, например, во время образования новых молекул и в ходе репликативных процессов в структурах ДНК. Численные методы данного типа включают ориентированные и неориентированные графы, байесовские схемы, булевы схемы, обобщенные логические цепи, обыкновенные нелинейные дифференциальные уравнения, кусочно-линейные дифференциальные уравнения, качественные дифференциальные уравнения, дифференциальные уравнения с частными производными и другие специальные модели с распределенными параметрами, стохастические основные уравнения и математическое представление, основанное на системе правил. Конкретным примером применения настоящего изобретения, в котором ожидается особый эффект, является моделирование и имитация многономенклатурных систем регулирования, для чего необходим анализ взаимодействия между ДНК, РНК, белками и малыми молекулами. Такое взаимодействие включает несколько стадий, входящих в различные последовательности, которые изучают, используя настоящее изобретение, чтобы определить, например, как возникает конкретный конечный результат какого-либо взаимодействия. Если конечный результат известен, он отображает оптимальное значение, что позволяет идентифицировать последовательность, которая обеспечивает такое значение.
и). Управление парком транспортных средств. Грузоперевозчикам и организаторам материально-технического обеспечения, использующим парк автобусов, грузовиков, самолетов, танкеров, легковых автомобилей, транспортных средств военного назначения и т.д. для доставки товаров или людей до различных мест или обратно, желательно иметь возможность оптимизировать свои расписания, чтобы максимально использовать имеющиеся ресурсы. Конкретным примером является компания грузовых перевозок, которая оптимизирует использование своих грузоперевозочных средств, определяя оптимальную последовательность транспортировки с целью выбора для множества транспортных средств парка маршрутов до десятков, сотен и тысяч мест назначения с учетом существующих для транспортных средств логических бизнес-правил и остановок, таких как объем заказов, грузоподъемность, временные окна, продолжительность обслуживания, приоритет и предварительное определение мест конкретных остановок для конкретных водителей. Путем описания различных действий, которые осуществляют по маршруту между остановками с учетом различных правил, и расположения действий в определенной последовательности, чтобы описать маршрут, определяют оптимальную последовательность, обеспечивающую достижение желаемого конечного результата. Рабочим параметром, который описывает конечный результат, могут являться, например, общие эксплуатационные расходы, общее время работы водителя в рейсе, общее пройденное расстояние (при этом обычно желательно свести к минимуму все перечисленные показатели), вероятность своевременной доставки грузов или взвешенная сумма некоторых или всех показателей. В более сложных последовательностях и группах действий учитывают оптимальный резервный парк на случай внепланового технического обслуживания транспортных средств или замены транспортных средств на длительный срок. За счет оптимизации такого рода, например, определяют количество транспортных средств, включаемых в резервный парк, и место их базирования с целью свести к минимуму перерывы в работе.
к). "Задачи о рюкзаке". К ним относятся задачи, которые можно рассматривать применительно к рюкзаку, способному выдерживать общий вес W или объем V, который заполняют сочетанием предметов из списка, включающего n-е число возможных предметов, каждый из которых имеет вес wi или объем vi и значение (va)i, чтобы предметы, упакованные в рюкзак, имели максимальное значение. Данная задача имеет ограничение (которое состоит в том, что общий вес или объем предметов в рюкзаке не должен превышать W или V), линейную или нелинейную функцию цели, которая суммирует численные значения предметов в рюкзаке, и добавочное ограничение, согласно которому каждый предмет находится либо не находится в рюкзаке (предмет не может быть поделен на части). Таким образом, каждый предмет отображен действием, а любое сочетание предметов/действий располагают в любой возможной последовательности, отображающей порядок, в котором предметы из такого сочетания помещают в рюкзак. Конечным результатом любой последовательности является суммарное численное значение предметов; любое сочетание, превышающее W и/или V, отклоняют, а для идентификации оптимальной последовательности находят неотклоненную последовательность, которая обеспечивает максимальное численное значение. Предложенный в настоящем изобретении метод имитации моделирования позволяет быстро идентифицировать оптимальную последовательность без необходимости изучения всех возможных сочетаний предметов. Задачи о рюкзаке имеют отношение, например, к управлению парком транспортных средств, если считать рюкзаком грузовую, пассажирскую или военную транспортную единицу и требуется загрузить ее до предельного значения конкретного параметра, отображенного значением предметов.
л). Объединение транспортных единиц. Данная задача представляет собой продолжение задачи о рюкзаке. Транспортные единицы, такие как железнодорожные вагоны, объединены в цепочку, при этом некоторые части цепочки впоследствии, возможно, потребуется отсоединить и удалить (например, для доставки заказчику конкретных единиц) и затем заново скомпоновать остальную цепочку, возможно, с добавлением новых единиц. Поскольку объединение, разъединение и повторное объединение единиц требует большого расхода времени и, следовательно, является дорогостоящим, желательно оптимизировать упорядочивание единиц в цепочке, чтобы свести к минимуму такие действия. Поскольку цепочку единиц рассматривают как последовательность действий, оптимальную цепочку идентифицируют, применяя настоящее изобретение.
Если речь идет о бомбардировщике, который сбрасывает свой бомбовый груз, возможно, он должен делать это в определенном порядке, а ограничениями или переменными величинами являются время, запас топлива, погода, временные окна и т.д.
м). Проведение стратегических военных игр (командно-штабных учений). Прогон имитаций на различных стратегических уровнях вплоть до оперативных уровней, когда исходы цепочек действий, например, выведение из строя мостов, электростанций, аэропортов и других стратегических целей реализуют в качестве сценариев, в которых действия могут осуществлять или не осуществляться. Моделирование дискретных действий четко описано математически. Метод применим для синхронизированного воспроизведения на кластере центральных процессоров.
н). Применение синхронизированного алгоритма, когда каждый центральный процессор осуществляет поиск всех возможных сочетаний, близких к одной переменной величине в случае установки матрицы планирования экспериментов, а компьютер воспроизводит имитацию модели, чтобы циклически пройти через все возможные сочетания переменной величины и найти требуемый результат.
Далее в общих чертах описаны варианты осуществления изобретения, применимые к любой последовательной комбинаторной задаче, такой как описанные выше задачи.
Чтобы проиллюстрировать применение изобретения, ниже приведен конкретный пример.
На фиг.1 показана блок-схема последовательности стадий с S1 no S9 способа согласно варианту осуществления настоящего изобретения.
S1 - идентификация последовательного комбинаторного процесса, нуждающегося в оптимизации
Изобретение применимо к любому процессу, который состоит из нескольких взаимозаменяемых действий, последовательность которых нуждается в оптимизации с целью достижения наилучшего результата. Процесс может рассматриваться как состоящий из n-го числа действий (включая возможность выбора такого n-го числа из более многочисленной группы действий, таких как альтернативы некоторых или всех действий), которые сочетают в виде множества или всех возможных последовательностей.
S2 - построение эталонной модели
В данном примере строят эталонную модель процесса, из которой получают данные для их использования в имитации модели. Примером модели соответствующего типа является модель анализа методом конечных элементов, но может использоваться любая, как правило, предназначенная для вычислительной машины модель, обеспечивающая соответствующую точность. Модель включает все параметры, имеющие отношение к процессу, и рассчитана на ввод в качестве исходных данных любой последовательности действий. Затем при помощи модели вычисляют значение окончательного конечного результата процесса, который был бы достигнут при осуществлении действий в порядке, заданном введенной последовательностью. Также вычисляют значение вкладов в конечный результат каждого из действий по мере их осуществления; данный вклад обычно зависит от положения действия в последовательности и от того, какое действие ему предшествовало, если оно имело место (и, возможно, следовало за ним). Вклады представлены в виде рабочего параметра моделируемого процесса.
Например, если рабочим параметром является размер изготавливаемой в ходе процесса детали, вклады также будут представлять собой значения размера, при этом вклад каждого действия представлен вкладом в обеспечение общего конечного размера в результате осуществления конкретного действия.
Если рабочим параметром является время, занимающее осуществление процесса, вклады также будут представлять собой значения времени, при этом вклад каждого действия представлен периодом времени, занимающим осуществление конкретного действия,
Без имитации модели для процесса оптимизации потребовалось бы осуществить прогон всех возможных последовательностей через эталонную модель, чтобы идентифицировать последовательность, обеспечивающую наилучший конечный результат. При наличии достаточно подробной эталонной модели это требует чрезмерно больших затрат времени даже применительно к небольшому числу действий, поскольку при большом общем числе комбинаций на прогон каждой последовательности может уйти много часов.
S3 - построение имитации модели
Имитация модели предпочтительно является упрощенным приближением к эталонной модели в том смысле, что в нее в качестве исходных данных также вводят последовательность действий и вычисляют конечный результат процесса, чтобы осуществлять действия в такой последовательности. Однако поскольку осуществляемые вычисления значительно проще, чем в эталонной модели, все сочетания действий в соответствующей последовательности могут быть вычислены достаточно быстро (обычно в течение нескольких секунд или минут, а не часов).
Имитация модели заключается в том, что суммируют вклад каждого действия в конечный результат и получают конечный результат. Значения вкладов определяют при помощи эталонной модели, что рассмотрено при описании последующих стадий. Значение каждого вклада обычно зависит от положения действия в последовательности и от любого предшествующего действия. Приближение к эталонной модели заключается в том, что информация о вкладе действия в конкретном положении из конкретной последовательности доступна не для каждого действия из заданной последовательности. Если это так, информацию согласно алгоритму заменяют информацией о конфигурации, ближайшей к рассматриваемой конфигурации.
S4 - описание планирования экспериментов (DoE)
Чтобы получить значения вкладов для использования в имитации модели, необходимо осуществить однократный или многократный прогон эталонной модели. При этом получают информацию о значениях конечных результатов выполненных последовательностей и вкладах в такие конечные результаты каждого действия из последовательности. Поскольку задачей изобретения является сокращение числа прогонов эталонной модели, связанных с трудоемкими вычислениями, чтобы получить широкий набор вкладов действий в различных положениях, для прогона через эталонную модель целесообразно выбирать применимый набор последовательностей, содержащий большой объем информации. Такая группа последовательностей, выбранных из множества возможностей, называют "планированием экспериментов" (DoE). Так, каждой последовательности DoE соответствует информация о значениях вкладов в конечный результат каждого действия из каждой последовательности, при этом, как указано выше, вклады отображены в виде рабочего параметра.
Как пояснено выше, имитация модели основана на алгоритме, который для каждого действия из последовательности определяет, какой вклад из доступных в эталонной модели (информация, которая соответствует последовательностям из планирования экспериментов) следует применить для вычисления конечного результата. Алгоритм основан на иерархическом или приоритетном наборе правил, которые определяют, какой вклад из наиболее близко доступных соответствует конфигурации вычисляемой последовательности. Близким соответствием является соответствие существующей конфигурации как с точки зрения положения действия в последовательности, так и предшествующего действия. Менее близким соответствием является меньшее число одинаковых предшествующих действий и/или иное положение, которое действие занимает в последовательности. Сопоставленные таким способом действия называют "событиями", при этом качество соответствия задано порядком и типом события, что более подробно описано далее применительно к примерному варианту осуществления. При описании DoE пользователь должен решить, какого типа событие или соответствие какого качества необходимо, чтобы обеспечить достаточный уровень точности оптимизированного конечного результата, полученного при помощи имитации модели. Например, он может решить, что требуется точное соответствие с точки зрения положения действий, которым также должны предшествовать одинаковые события, или что совпадение положений не является важным, но должны совпадать два события, предшествующие рассматриваемому действию. После того, как решение принято, выполняют вычисления с целью установить, прогон скольких и/или каких последовательностей необходимо осуществить через эталонную модель, чтобы обеспечить достаточное количество комбинаций действий для соответствия требуемому уровню подробности события. Данные последовательности представляют собой DoE.
В качестве альтернативы, в некоторых случаях достаточно просто осуществить прогон через эталонную модель случайного или псевдослучайного набора последовательностей. Тем не менее, такой набор последовательностей также рассматривают как DoE, несмотря на отсутствие описанного планирования.
S5 - прогон последовательностей DoE через эталонную модель
После описания DoE осуществляют прогон каждой последовательности DoE через эталонную модель. Результаты прогонов регистрируют и определяют вклады в конечный результат каждого действия из каждой последовательности DoE. Таким образом получают информацию о рабочем параметре, которую используют при вычислениях имитации модели.
S6 - построение указателя приоритетов имитации модели
Алгоритм имитации модели основан на указателе (перечне) приоритетов для каждого действия из последовательности, прогон которой осуществлен через модель. Он представляет собой иерархию условий совпадения между рассматриваемым действием и действиями, включенными в последовательность DoE. Указатель начинается с условия высокой степени соответствия и следует далее по нисходящей вплоть до отсутствия соответствия. Таким образом, при помощи алгоритма осуществляют поиск, начиная с верхней позиции в указателе, и ищут в DoE совпадение такого уровня с рассматриваемым действием. Если совпадение не найдено, переходят ко второму условию из указателя и так до тех пор, пока совпадение не будет найдено или не закончится указатель. После выбора условия таким способом при помощи алгоритма ранее вычисленный при помощи эталонной модели вклад рассматриваемого действия из последовательности DoE, в которой найдено совпадение, извлекают и включают в итог имитации модели, который используют для определения конечного результата.
Таким образом, для оптимизируемого процесса необходимо создать указатель приоритетов. Размер указателя влияет на время, необходимое для расчета имитации модели, поскольку время выполнения алгоритма пропорционально размеру указателя. Вместе с тем, при наличии более высокой степени соответствия из верхней части указателя повышается точность. Не следует ограничивать высшую степень соответствия той степенью совпадения, которая применялась при описании DoE, поскольку в последовательностях из DoE для некоторых подпоследовательностей событий имеются более высокие уровни соответствия, использование которых, когда они доступны, обеспечит более точный конечный результат. Таким образом, применимым указателем приоритетов общего назначения, в котором полностью использовано любое DoE, является такой указатель приоритетов, согласно которому поиск любого действия с целью определить, находится ли действие в начале и в конце последовательности, начинают в одинаковом положении при всех одинаковых предшествующих действиях. При построении указателя приоритетов выбирают, закрепить ли более высокий приоритет за совпадениями положения действия в последовательности или за совпадениями предшествующего действия. Примеры указателя приоритетов приведены далее.
S7 - прогон всех возможных последовательностей через имитацию модели
После построения имитации модели и ее указателя приоритетов и вычисления при помощи эталонной модели информации о конечном результате и вкладах в него имитацию модели используют для прогона через нее всех возможных последовательностей. Каждую последовательность вводят в имитацию модели, которая с целью определить вклад такого действия в конечный результат затем применяет алгоритм в отношении каждого действия из каждой последовательности и суммирует вклады, чтобы найти конечный результат для каждой последовательности. Поскольку алгоритм представляет собой процесс прямого поиска и извлечения, а вычисления для каждой последовательности представляют собой простое суммирование, имитация модели способна очень быстро воспроизвести каждую последовательность, и, как показывают расчеты, для изучения всех последовательностей требуется лишь несколько минут.
Однако в некоторых случаях существует возможность получить удовлетворительно оптимизированную последовательность путем прогона через имитацию модели лишь части из общего числа возможных последовательностей. Поскольку ясно, что это занимает меньше времени, чем прогон всех последовательностей, в некоторых случаях, когда ценность времени велика, это является предпочтительным, вместе с тем, при этом возможна потеря точности. Возможным решением, в особенности в случаях, когда известно требуемое оптимальное значение конечного результата, является прогон подмножества последовательностей и изучение различных конечных результатов в сравнении с требуемым значением. Если приемлемое близкое соответствие не найдено, осуществляют дальнейший прогон последовательностей до тех пор, пока не будет обнаружен удовлетворительный конечный результат.
S8 - Идентификация оптимальной последовательности из имитации модели
После получения результата прогона каждой последовательности через имитацию модели идентифицируют оптимальную последовательность путем сравнения всех конечных результатов с целью найти результат, который является оптимальным с учетом рабочего параметра, описывающего конечный результат. В зависимости от природы процесса оптимальным значением рабочего параметра может являться конечный результат с наименьшим значением, наибольшим значением или значение, наиболее близкое к требуемому значению. В некоторых случаях оптимальное значение легко идентифицировать путем сравнения конечных результатов с каким-либо требуемым значением рабочего параметра; в других случаях природа процесса такова, что рабочий параметр должен быть сведен к минимуму или доведен до максимума, например, при осуществлении процесса в течение минимального времени или получении максимального выхода. Таким образом, последовательность, обеспечивающая конечный результат, который соответствует такому оптимальному значению, идентифицируют как оптимальную последовательность.
S9 - Осуществление процесса с использованием оптимальной последовательности.
Далее с целью получения оптимального конечного результата способ осуществляют с использованием последовательности, которая была идентифицирована как оптимальная. Вместе с тем, если исследование процесса продолжается, данную стадию, возможно, не осуществляют или откладывают.
На фиг.2 показана блок-схема последовательности стадий альтернативного варианта осуществления способа, включающего некоторые дополнительные стадии, которые служат для проверки и при необходимости повышения точности выходных данных имитации модели в том, что касается оптимальной последовательности. Как и в варианте осуществления, проиллюстрированном на фиг.1, оптимальную последовательность идентифицируют по результатам применения имитации модели на стадии S8, после чего осуществляют дополнительные стадии.
S10 - прогон идентифицированной последовательности через эталонную модель
Через эталонную модель осуществляют прогон последовательности, которая по конечным результатам, вычисленным при помощи имитации модели, была идентифицирована как оптимальная последовательность. При этом получают значение конечного результата такой последовательности, находящееся в пределах точности эталонной модели, которые являются более жесткими, чем у имитации модели.
S11 - сравнение результатов
Далее конечный результат идентифицированной оптимальной последовательности, вычисленный при помощи эталонной модели, сравнивают с конечным результатом такой последовательности, который уже был вычислен при помощи имитации модели. Если сравнение является благоприятным в том смысле, что оба значения конечного результата согласуются в приемлемом диапазоне (который зависит от природы процесса и степени точности, которая необходима пользователю), последовательность принимают за оптимальную последовательность и при желании переходят к стадии S9 (осуществление процесса с использованием оптимальной последовательности). Если сравнение неблагоприятно в том смысле, что оба значения не согласуются в требуемом диапазоне, идентифицированную последовательность отбрасывают как возможно не являющуюся оптимальной последовательностью. В этом случае переходят к стадии S12 способа.
S12 - добавление последовательности к DoE
Поскольку на стадии S10 осуществили прогон идентифицированной последовательности через эталонную модель, теперь для такой последовательности доступна информация о вкладе, используемая в имитации модели для вычислений. Так, последовательность добавляют к последовательностям из DoE, просто как если бы ранее на стадии S5 осуществили ее прогон через эталонную модель. Затем снова возвращаются к стадии S7 и снова осуществляют прогон всех возможных последовательностей через имитацию модели. Однако на этот раз имитация модели располагает большим количеством доступной информации, поскольку планирование экспериментов было расширено. Следовательно, конечные результаты, вычисленные при помощи имитации модели для каждой последовательности, видимо, являются более точными, чем ранее, и более вероятно, что последовательность, идентифицированная на стадии S8, действительно является оптимальной.
Данную последовательность также пропускают через эталонную модель и сравнивают с результатом, полученным при помощи имитации модели, чтобы проверить точность. Если результаты не согласуются, на стадии S12 в DoE добавляют последовательность и снова возвращаются к стадии S7. Циклическое осуществление стадий S7, S8, S10, S11 и S12 продолжают таким способом до тех пор, пока не обнаруживают требуемый уровень согласованности между результатами имитации модели и эталонной модели, после чего переходят к стадии S9. Таким способом постепенно повышают точность оптимизации. Тем самым также обеспечивают эффективное снижение вычислительных затрат, связанных с эталонной моделью, поскольку дополнительные последовательности, пропущенные через эталонную модель при каждом осуществлении стадии S10, видимо, близки к оптимальным, так как были идентифицированы как таковые при помощи имитации модели. Таким образом, дополнительные вычисления сосредоточены на интересующей области, а повышение точности обеспечивается там, где оно более всего необходимо.
Следует отметить, что до известной степени различные описанные выше стадии могут быть осуществлены в ином порядке, чем порядок, проиллюстрированный на фиг.1 и 2. В частности, стадии с S2 по S6 могут быть осуществлены в любом порядке, удобном для пользователя. Кроме того, различные стадии могут быть сокращены в объеме или полностью исключены. Например, может отсутствовать требование построения эталонной модели, если для использования доступна ранее существовавшая модель. Такая модель может представлять собой модель, которую применяли ранее для оптимизации того же процесса, модель, которую ранее применяли для оптимизации сходного процесса, если такая модель применима к новому процессу, или модель, поступившую или иным образом полученную из отдельного источника, независимо от того, сделано ли это конкретно для реализации изобретения. Поскольку это также относится к имитации модели, изобретение может необязательно предусматривать построение имитации модели и может быть ограничено применением имитации модели без ее построения. Поскольку DoE также может быть описано для конкретного процесса оптимизации или выбрано случайным образом или может применяться планирование экспериментов, заданное ранее, предпочтительно для одинаковых или сходных процессов, не требуется описывать DoE. Использование уже существовавших элементов любым из описанных способов упрощает и, возможно, ускоряет общий процесс оптимизации.
В целях ускорения процесса и удобства эталонная модель, имитация модели, идентификация оптимальной последовательности и сравнение результатов эталонной модели и имитации модели рассчитаны на реализацию компьютерным программным обеспечением. Например, может быть создан компьютерный программный продукт, способный реализовать модели, запоминать планирование экспериментов и результаты реализации модели и идентифицировать оптимальную последовательность. Может быть предусмотрена компьютерная система, состоящая из запоминающего устройства для запоминания DoE и результатов реализации модели, считывания данных из памяти и записи данных в память и идентификации оптимальной последовательности. Вместе с тем, реализация на базе компьютера является необязательной, и в некоторых случаях предпочтительно, чтобы часть или все из перечисленных признаков были реализованы иными способами, такими как электронная аппаратура или, возможно, вручную.
Кроме того, что касается реализации изобретения на компьютерной базе, применение параллельного подхода способно дополнительно повысить скорость. Для описания DoE целесообразно использовать компьютер, при помощи которого осуществляют прогон набора последовательностей через эталонную модель (что более подробно описано далее применительно к более подробному примеру) до тех пор, пока не будет охвачен требуемый диапазон действий и вычислены соответствующие вклады. В том случае, когда действию соответствует несколько переменных величин, например, когда конкретная стадия процесса осуществима при нескольких температурах и в нескольких направлениях, для каждой переменной величины предусматривают специализированный компьютерный процессор. Для описания планирования экспериментов каждый процессор реализует последовательности применительно к одной из переменных, оставляя остальные переменные без изменения. Тем самым обеспечивают более быстрый способ описания планирования экспериментов, сохраняя при этом возможность учета всех переменных, а также использование более простых эталонных моделей, поскольку каждая из них должна учитывать только одну переменную.
Аналогичным образом параллельные процессоры могут использоваться для прогона множества последовательностей через имитацию модели, при этом каждый процессор специализирован на последовательностях, которым соответствуют различные значения одного параметра. Это также позволяет использовать более простые версии имитации модели и идентифицировать оптимальную последовательность быстрее, чем при использовании одного процессора для прогона всех последовательностей через имитацию модели.
Подробный пример I
Далее изобретение описано со ссылкой на более подробный пример.
Рассмотрим процесс, состоящий из шести стадий. Все шесть стадий могут осуществляться в любом порядке, при этом каждая стадия осуществима одним из двух способов (таким как вперед или назад или при первой или второй температуре). Порядок следования и выбор способа осуществления каждой стадии изменяет конечный результат процесса. Опишем данный конечный результат рабочим параметром X, а желательный характер конечного результата представим таким, чтобы рабочий параметр имел оптимальное значение Х=0. Иными словами, рабочий параметр должен быть сведен к минимуму.
Каждую стадию или действие снабжают обозначением, например числами с 1 по 6. Положительные и отрицательные значения таких чисел используют, чтобы обозначить два способа осуществления каждого действия. Таким образом, последовательность стадий можно представить, например, в виде [-6, 5, 3, 1, -4, 2], при этом каждое число является обозначением конкретного действия, а положение каждого числа в последовательности отображает положение, в котором осуществляют действие в последовательности.
Создают эталонную модель в виде модели конечных элементов, которая описывает последовательный процесс и которая способна учитывать каждое действие в любом положении в последовательности и при любом способе осуществления действий. В качестве исходных данных в модели используют последовательность и создают диаграмму, отображающую эволюцию рабочего параметра Х в ходе процесса. Модель позволяет вычислить конечное значение Х для любой комбинации действий, а также вклад в Х каждого отдельного действия.
Задачей процесса оптимизации является сведение к минимуму значения Х за счет изменения последовательности действий. Существует шесть переменных (по одной на каждое положение в последовательности), каждая из которых может иметь 12 нечисловых значений (6 для первого способа осуществления каждого действия и 6 для второго способа). В результате всего получают 26×6!=46080 комбинаций. В соответствии с некоторыми обычными методами оптимизации последовательных комбинаторных задач необходимо осуществить прогон всех этих комбинаций через модель на основе метода конечных элементов и выбрать последовательность с наименьшим значением X. Однако это непрактично, поскольку на вычисление одной комбинации уходит 32 часа. Другие существующие методы комбинаторной оптимизации, описанные в литературе, такие как целочисленное программирование, графы, метод ветвей и границ и двоичные деревья [2] не способны существенно сократить число комбинаций, требующих вычисления. В настоящем изобретении значительно сокращено время, необходимое для достижения результата за счет применения имитации модели, которая осуществляет вычисления значительно быстрее, чем через модель на основе метода конечных элементов, и которую применяют для сокращения числа необходимых прогонов модели на основе метода конечных элементов. Поскольку в имитации модели используют данные, полученные в результате прогонов модели на основе метода конечных элементов, необходима часть таких прогонов, но имитация модели способна обеспечить приближение к модели на основе метода конечных элементов за счет использования данных, полученных в результате гораздо меньшего числа прогонов, чем общее число возможных комбинаций.
Для разработки имитации модели суммарное значение Х можно описать просто как сумму вкладов в Х шести отдельных действий:
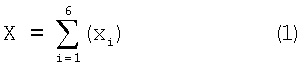
где хi является вкладом действия i из последовательности. Поскольку модель на основе метода конечных элементов способна вычислять вклад каждого действия, она обеспечивает информацию, необходимую для имитации модели.
Вклад любого отдельного действия зависит от положения действия в последовательности, от того, каким из двух возможных способов осуществляют действие, и от любых предшествующих действий. Если действие является первым действием в последовательности, его вклад не зависит от последующего действия. Назовем это главным эффектом. Главный эффект действия е обозначают как Me. В частности, приведенная выше примерная последовательность содержит информацию о М-6, поскольку -6 является первым действием в последовательности. Всего существует шесть возможных первых действий, каждое из которых осуществляют двумя способами, в результате чего всего получают двенадцать возможных значений главного эффекта. Для их определения осуществляют двенадцать прогонов модели на основе метода конечных элементов. Не требуется выполнять последовательность целиком; полную информацию обо всех возможных главных эффектах обеспечивает первое действие из двенадцати прогонов, каждый из которых в качестве первого действия последовательности содержит отличающееся действие и комбинацию характеристик.
Особо простой моделью, подходящей в качестве имитации модели, является модель, в которой конечное значение Х принимают за сумму главных эффектов:

где еi является действием е в i-м положении в последовательности. Например, согласно модели значение Х для последовательности [-6, 5, 3, 1, -4, 2] выражено как X=М-6+М5+М3+М1+М-4+М2. Данная модель основана на системе, не имеющей памяти, в которой не учитывают влияние каких-либо предшествующих действий на текущее действие. Модель исходит из протекания действий во всех положениях последовательности аналогично протеканию начального действия путем подстановки i=2, 3, 4, 5, 6 с соответствующими главными эффектами вместо всех хi. Это означает, что данные коэффициенты зависят только от действия, а не от положения в последовательности. В расчет не принимают влияние, которое могли оказать в рамках процесса предшествующие действия. Данная модель выполняет поставленную задачу сокращения числа прогонов модели на основе метода конечных элементов с целью обеспечения информации, необходимой для прогона любой возможной последовательности через имитацию модели, поскольку для этого требуется лишь двенадцать прогонов. Вместе с тем, поведение системы обычно не соответствует поведению системы без памяти; вклады в конечные результаты заданного действия меняются в зависимости от положения в последовательности. Таким образом, более точной является модель:

в которой Δ(е, i) является повышением точности за счет включения влияния положения действия в последовательности. В этом случае вклады хi=f(e, i) зависят от действия и его положения.
Чтобы способствовать участию памяти системы в оптимизации, вводят определения порядка и типа вклада любого отдельного действия в суммарный конечный результат, которые называют событиями. Чтобы описать вклад в положении i, события определяют следующим образом:
(i) члены первого порядка 1-го типа, которые игнорируют любой вклад предшествующих действий, т.е. отображают систему без памяти. Вместе с тем, они принимают во внимание влияние положения в последовательности. Ранее упомянутые главные эффекты являются членами первого порядка 1-го типа, но только в случае их применения для описания смещения в положении 1,
(ii) члены первого порядка 2-го типа также игнорируют любые предшествующие действия и влияние положения. Например, модель, основанная на уравнении (2), включает только данные члены. В X=M2+M-5+M6+M-1+M3+M-4. M2 является членом первого порядка 1-го типа, а все остальные слагаемые являются событиями 2-го типа, поскольку вклады M-5, М6, M-1, M3 и М-4 получены по результатам имитаций, когда действия -5, 6, -1, 3 и -4 происходили в положении 1 последовательностей, пропущенных через модель на основе метода конечных элементов, исключая какие-либо еще положения в данном прогоне,
(iii) члены второго порядка 1-го типа учитывают положение действия в последовательности и ближайший предшествующий характер протекания последовательности (т.е. действие, которое непосредственно предшествовало рассматриваемому действию i). События второго порядка существуют только при условии, что i≥2,
(iv) члены второго порядка 2-го типа учитывают предшествующее действие, но игнорируют значение положения пары действий в последовательности,
(v) члены третьего порядка, которые существуют только при условии, что i≥3, включают два действия, которые непосредственно предшествуют рассматриваемому действию,
(vi) и так далее по мере возрастания порядков.
В дальнейшем порядок события обозначают соответствующим цифровым подстрочным индексом, а тип события штрихами. Таким образом, события k-го порядка и первого типа обозначают как  , где v означает вектор, образованный действиями в положениях [ei-k+1, …, еi-1, еi], которые, следовательно, включают k-1 действий, предшествующих данному действию. События второго типа обозначены двойным штрихом.
, где v означает вектор, образованный действиями в положениях [ei-k+1, …, еi-1, еi], которые, следовательно, включают k-1 действий, предшествующих данному действию. События второго типа обозначены двойным штрихом.
Рассмотрим событие k=1 первого типа: последовательность 20 обеспечивает информацию о следующих событиях первого порядка (при этом первым числом в каждой паре обозначено действие, а вторым числом его положение в последовательности):
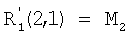 ;
;  ;
;  ;
;  ;
;  ;
; 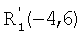 . Последовательность содержит информацию об изменении X, которое вызвано событием действия е в положении i в последовательности. Ее непосредственно используют для разработки планирования экспериментов (DoE), в котором прогон модели на основе метода конечных элементов осуществляют достаточное количество раз, чтобы заполнить матрицу, содержащую все события первого порядка первого типа
. Последовательность содержит информацию об изменении X, которое вызвано событием действия е в положении i в последовательности. Ее непосредственно используют для разработки планирования экспериментов (DoE), в котором прогон модели на основе метода конечных элементов осуществляют достаточное количество раз, чтобы заполнить матрицу, содержащую все события первого порядка первого типа 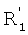 для е=-6, …, -1, 1…6; i=1, …, 6. Такое планирование требует 18 прогонов.
для е=-6, …, -1, 1…6; i=1, …, 6. Такое планирование требует 18 прогонов.
Для описания системы с памятью необходимо учесть влияния текущих и прошлых событий, а не только текущих событий, такого как 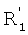 . Такие события относятся к событиям второго и более высоких порядков. Для упрощения модели целесообразно предположить, что при рассмотрении последнего действия в последовательности влияние на его смещение, оказанное, скажем, предпоследним действием, является более важным, чем на первое действие (за счет этого можно пренебречь событиями очень высоких порядков). Кроме того, можно установить, что влияние подпоследовательностей различных действий в последовательности является преимущественно одинаковым (и поэтому событий второго типа достаточно для последовательностей более высоких порядков). На основании данных предпосылок строят приближения к влиянию каждого действия, используя информацию, полученную в результате ранее осуществленных прогонов. Данная информация представляет собой DoE. Процесс осуществляют следующим образом:
. Такие события относятся к событиям второго и более высоких порядков. Для упрощения модели целесообразно предположить, что при рассмотрении последнего действия в последовательности влияние на его смещение, оказанное, скажем, предпоследним действием, является более важным, чем на первое действие (за счет этого можно пренебречь событиями очень высоких порядков). Кроме того, можно установить, что влияние подпоследовательностей различных действий в последовательности является преимущественно одинаковым (и поэтому событий второго типа достаточно для последовательностей более высоких порядков). На основании данных предпосылок строят приближения к влиянию каждого действия, используя информацию, полученную в результате ранее осуществленных прогонов. Данная информация представляет собой DoE. Процесс осуществляют следующим образом:
1. Общая задача заключается в вычислении вклада каждого действия в Х и их суммировании с целью получения общего значения X. Начальное значение Х=0.
2. Предположим, что рассматриваем последовательность zp. Например, zp=[6, 3, -5, 4, -2, 1].
3. Начинаем с i=1 (первое действие в последовательности) и затем по возрастающей.
4. Наивысшим возможным порядком события является i.
5. Создадим вектор zp1=[1:i], который содержит первые элементы i последовательности zp. В частности, для i=3; zp1=[6, 3, -5].
6. Пусть k=1.
7. Создадим вектор zp2=zp1[i-k+1:i], в котором использованы последние элементы i-k+1 вектора zp1.
8. Осуществим в планировании экспериментов поиск zp2, последний элемент которого находится в i-м положении последовательности из планирования экспериментов. В случае обнаружения используем значение соответствующего вклада xi и переходим к стадии 10, в противном случае продолжаем. Установленный вклад является событием порядка i 1-го типа.
9. Осуществим в планировании экспериментов поиск zp2 независимо от положения в последовательностях. В случае обнаружения используем значение соответствующего вклада хi и переходим к стадии 10, в противном случае продолжаем. Установленный вклад является событием порядка i 2-го типа.
10. Х=Х+хi.
11. Если i=ep, следует команда СТОП. Последовательность пройдена до конца. В рассматриваемом примере ep=6, что соответствует 6 действиям в последовательности.
12. i=i+1.
13. Переходим к стадии 4.
Вычисление данного процесса занимает гораздо меньше времени, чем прогон модели на основе метода конечных элементов. Таким образом, используя результаты относительно небольшого числа прогонов модели на основе метода конечных элементов для заполнения DoE, имитация модели осуществляет быстрый прогон всех возможных последовательностей и идентифицирует последовательность, которая обеспечивает наиболее желаемое значение X.
Чтобы проиллюстрировать идею использования данных событий, рассмотрим модель, состоящую из членов вплоть до 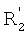 :
:
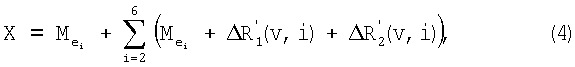
где 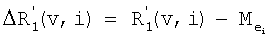 ;
;  ; i является положением в последовательности, a v=[еi-k+1, …, еi-1, еi], где k=1 и 2 соответственно.
; i является положением в последовательности, a v=[еi-k+1, …, еi-1, еi], где k=1 и 2 соответственно.
В качестве примера, последовательность [2, -5, 6, -1, 3, -4] содержит информацию о следующих событиях второго порядка:
 ;
;  ;
;  ;
; 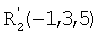 ;
;  , где последнее число в каждой группе обозначает положение в последовательности двух действий, отображенных двумя первыми числами. Для заполнения всей матрицы
, где последнее число в каждой группе обозначает положение в последовательности двух действий, отображенных двумя первыми числами. Для заполнения всей матрицы 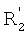 в DoE необходимо 180 прогонов модели на основе метода конечных элементов, что делает ее использование бесперспективным. Вместо этого возможно компромиссное решение за счет использования DoE, которое целиком заполняет матрицу
в DoE необходимо 180 прогонов модели на основе метода конечных элементов, что делает ее использование бесперспективным. Вместо этого возможно компромиссное решение за счет использования DoE, которое целиком заполняет матрицу  . Чтобы удостовериться в существовании всех событий второго порядка и 2-го типа, требуется осуществить 27 прогонов модели на основе метода конечных элементов. Можно доказать, что для многих процессов данное приближение, в котором игнорируется, где возникали пары подпоследовательностей, не приводит к значительной потери точности. Кроме того, некоторые пары
. Чтобы удостовериться в существовании всех событий второго порядка и 2-го типа, требуется осуществить 27 прогонов модели на основе метода конечных элементов. Можно доказать, что для многих процессов данное приближение, в котором игнорируется, где возникали пары подпоследовательностей, не приводит к значительной потери точности. Кроме того, некоторые пары 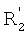 будут доступны в матрице и в этом случае могут быть использованы. Таким образом, члены
будут доступны в матрице и в этом случае могут быть использованы. Таким образом, члены 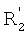 в уравнении (4) могут быть заменены
в уравнении (4) могут быть заменены

Так, по возможности используют члены второго порядка, которые заменяют членами более низкого порядка только в случае их недоступности. Такую небольшую потерю точности компенсирует сокращение числа прогонов модели на основе метода конечных элементов, необходимых для DoE.
Несмотря на то, что DoE рассчитано на включение всех событий  , для некоторых действий и положений в нем содержатся события третьего порядка и выше, применяемые для дальнейшего повышения точности. Так, уравнение 5 можно представить в следующем обобщенном виде:
, для некоторых действий и положений в нем содержатся события третьего порядка и выше, применяемые для дальнейшего повышения точности. Так, уравнение 5 можно представить в следующем обобщенном виде:
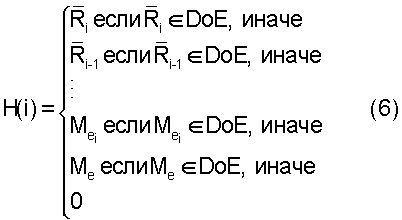
при этом суммарное значение Х вычисляют следующим образом:

где n является общим числом действий в последовательности; в данном примере n=6. Уравнение 7 представляет собой более обобщенную форму уравнения 4 и служит для получения результата сложения событий наивысшего порядка и низшего типа с целью вычисления ожидаемого значения Х для заданного действия и положения в последовательности.
Данная модель применима к любому числу переменных или действий n с учетом того, что высший порядок события равен числу переменных. Модель обладает некоторой обучаемостью в том смысле, что она всегда дает прогноз при наличии по меньшей мере одной позиции в DoE. В случае осуществления большего числа прогонов модели на основе метода конечных элементов объем DoE увеличивается, а прогнозы становятся более точными. В предельном случае, когда при помощи модели на основе метода конечных элементов проверены все возможные комбинации, модель воспроизводит точные данные испытаний. Данная особенность имитации модели позволяет применять ее при наличии любого числа позиций в DoE, благодаря чему объем DoE свободно увеличивают или перестают увеличивать в зависимости от требуемой точности модели. Как показывает опыт изучения примеров, таких как рассмотренный здесь пример с шестью действиями, существования полного набора  достаточно, чтобы обеспечить удовлетворительное соответствие существующим данным.
достаточно, чтобы обеспечить удовлетворительное соответствие существующим данным.
Ясно, что после вычисления вклада по результатам достаточного числа прогонов модели на основе метода конечных элементов, заданных в DoE, в такой модели необходимы очень незначительные вычисления, что облегчает изучение всех возможных комбинаций имитацией модели и выбор наилучшей. С целью испытания точности данный наилучший прогноз затем проверяют путем прогона соответствующей последовательности через модель на основе метода конечных элементов. Таким прогоном затем дополняют DoE, что делает последующие прогнозы имитации модели более точными. Затем имитация модели осуществляет еще один полный цикл поиска комбинации, используя все информацию DoE, включая результаты последнего прогона модели на основе метода конечных элементов, и так далее до тех пор, пока не будет получены одинаковые или достаточно сходные результаты следующих друг за другом прогонов модели.
Продолжая рассматривать пример состоящего из шести действий процесса и исходя из сделанных выше выводов, можно построить таблицу DoE, соответствующую 27 прогонам модели на основе метода конечных элементов, которая гарантирует включение всех событий  . DoE можно, построить, например, путем рассмотрения всех возможных 46080 комбинаций и выбора первого набора, обеспечивающего по меньшей мере один пример всех событий
. DoE можно, построить, например, путем рассмотрения всех возможных 46080 комбинаций и выбора первого набора, обеспечивающего по меньшей мере один пример всех событий  . Один из способов достижения этого является прогон шести вложенных циклов, в ходе каждого из которых просматривают значения -6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6 и выбирают последовательности, которые подчиняются следующему правилу |А|≠|В|≠|C|≠|D|≠|E|≠|F|, где А, В, С, D, Е и F являются переменными шести вложенных циклов. Каждую последовательность регистрируют и при обнаружении по меньшей мере одного примера каждого события
. Один из способов достижения этого является прогон шести вложенных циклов, в ходе каждого из которых просматривают значения -6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6 и выбирают последовательности, которые подчиняются следующему правилу |А|≠|В|≠|C|≠|D|≠|E|≠|F|, где А, В, С, D, Е и F являются переменными шести вложенных циклов. Каждую последовательность регистрируют и при обнаружении по меньшей мере одного примера каждого события  прекращают формирование DoE. В результате DoE содержит первый набор последовательностей, который гарантирует, что все события
прекращают формирование DoE. В результате DoE содержит первый набор последовательностей, который гарантирует, что все события  были испытаны. Данный способ формирования DoE отличается особой простотой, но следует отметить, что его результатом необязательно является оптимальное DoE или минимально возможное DoE, хотя вероятно минимально возможное DoE и не имеет намного меньший объем.
были испытаны. Данный способ формирования DoE отличается особой простотой, но следует отметить, что его результатом необязательно является оптимальное DoE или минимально возможное DoE, хотя вероятно минимально возможное DoE и не имеет намного меньший объем.
Осуществляют прогон каждой последовательности из DoE через модель на основе метода конечных элементов. По разности между накопленными значениями Х в конце и в начале последовательности, вычисленной при помощи модели на основе метода конечных элементов, вычисляют вклад в Х каждого действия последовательности из DoE.
В качестве примера рассмотрим последовательность [6, 3, -5, 4, -2, 1] и применим к ней модель:
1. Х=0.
2. i=1: для положения номер 1 высшим порядком события является 1, поэтому проверяем наличие главного эффекта 6 в позициях DoE. Предположим, что он обнаружен. Вклад главного эффекта 6 вычитают из вычисленных данных и добавляют полученное значение к X, после чего Х=М6.
3. i=2: высшим порядком события является 2, поэтому осуществляем поиск пары (6, 3) в планировании экспериментов в положении 2 (сначала осуществляем поиск события 1-го типа). В случае отсутствия совпадения далее осуществляем поиск события 2-го типа независимо от положения. Предположим, что совпадение найдено, и добавляем соответствующий вклад к X, после чего получаем 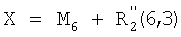 .
.
4. i=3: высшим порядком события является 3, поэтому осуществляем поиск подпоследовательности (6, 3, -5) в планировании экспериментов в положении 3 (снова сначала осуществляем поиск события 1-го типа). Если подпоследовательность не обнаружена в планировании экспериментов, проверяем ее наличие по всему планированию экспериментов. Предположим, что результат отрицательный, что говорит об отсутствии такого события третьего порядка 1-го или 2-го типа. Затем сокращаем подпоследовательность, отсекая наиболее отдаленное действие, которое предположительно имеет наименьшее влияние на отклонение в положении 3. Подпоследовательность принимает вид (3, -5). Снова сначала проверяем наличие ее события 1-го типа, т.е. такого события, когда действие -5 находится в положении 3, а действие 3 в положении 2. Предположим, что совпадение найдено, и добавляем соответствующий вклад к X, после чего получаем  .
.
5. i=4: высшим порядком события является 4, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4) в планировании экспериментов в положении 4 на предмет наличия события 1-го типа. При отсутствии совпадения осуществляем поиск событий 2-го типа, которые также не обнаруживаем. Затем усекаем подпоследовательность до (3, -5, 4) и сначала осуществляем поиск событий 1-го типа. Находим совпадение в 18-м прогоне, и добавляем соответствующий вклад члена 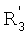 к значению X, после чего получаем
к значению X, после чего получаем 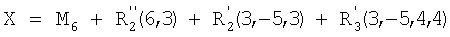 .
.
6. i=5: высшим порядком события является 5, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4, -2) в планировании экспериментов в положении 5 на предмет наличия события 1-го типа. Предположим, что событие не найдено, равно как и событие 2-го, тогда производим усечение и осуществляем поиск подпоследовательности (3, -5, 4, -2). Предположим, что результат поиска события как 1-го, так и 2-го типа снова отрицательный. Снова производим усечение подпоследовательности до (-5, 4, -2). И снова не находим совпадения ни для одного типа. Производим усечение до (4, -2). Событие 1-го типа отсутствует, но, скажем, в планировании экспериментов найдено событие 2-го типа. Добавляем вклад к X и получаем
 .
.
7. i=6: высшим порядком события является 6, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4, -2, 1) в планировании экспериментов в положении 6. Предположим, что совпадение не найдено. Повторно осуществляем такую же операцию, как на предшествующей стадии, проверяя на наличие событий 1-го и 2-го типов следующие подпоследовательности (3, -5, 4, -2, 1); (-5, 4, -2, 1); (4, -2, 1). Предположим, что результат отрицательный. Наконец, предположим, что в результате поиска (-2, 1) по всему планированию экспериментов независимо от положения найдено совпадение в 14-м прогоне. Добавляем смещение к X и получаем
 .
.
Данный алгоритм позволяет при помощи кода MATLAB менее чем за 5 минут вычислить все 46080 возможных комбинаций на компьютере с Pentium III с тактовой частотой процессора 800 МГц. Гораздо быстрее результат можно получить, если использовать код, составленный на языке Си или ФОРТРАН.
Настоящее изобретение было эффективно применено для оптимизации реального процесса, состоящего из последовательности шести действий. Для определения оптимизированного значения Х и соответствующей последовательности осуществили всего 28 прогонов модели на основе метода конечных элементов из возможных 46080 комбинаций последовательностей. Как подтвердили испытания идентифицированной последовательности с использованием модели на основе метода конечных элементов, полученное значение является точным. Таким образом, без существенной потери точности значительно снижены вычислительные затраты, связанные с процессами планирования данного типа.
Подробный пример II
Далее изобретение описано со ссылкой на конкретный пример приваривания лопасти к внутреннему кольцу корпуса заднего подшипника газовой турбины.
На фиг.3 показан вид в перспективе стандартного корпуса заднего подшипника. Он является важнейшим компонентом для установки турбореактивного двигателя на летательный аппарат. На фиг.3 проиллюстрированы его основные конструктивные элементы, которые включают внутреннее кольцо 10, наружное кольцо 12, окружающее внутреннее кольцо 10, и множество лопастей 14, проходящих в радиальном направлении между внутренним кольцом 10 и наружным кольцом 12. Лопасти 14 обычно приваривают к кольцам 10, 12 при помощи сварки вольфрамовым электродом в газовой среде, которую часто называют сваркой вольфрамовым электродом в инертном газе.
В процессе сварки внутреннее кольцо 10 и лопасти 14 фиксируют в требуемом положении. Однако вследствие внутренних напряжений, возникающих при нагревании, лопасть деформируется. Сварка вызывает сжатие, которое происходит при охлаждении расплавленного материала в сварочной ванне. Это является причиной возникновения напряжений большой амплитуды, которые распространяются по всей детали, а также вызывает деформации обрабатываемой детали. Их можно измерить по степени смещения двух вершин или кромок лопасти на ее конце, противоположном месту сварки. На фиг.4 показаны такие вершины (вершина 10 и вершина 96), обозначенные на виде в перспективе лопасти 14 и смежного участка внутреннего кольца 10, а также на виде лопасти 14 в поперечном разрезе. Вершина 10 представляет собой входную (переднюю) кромку, расположенную на передней грани лопасти 14, а вершина 96 представляет собой выходную (заднюю) кромку, расположенную на задней грани лопасти 14. Деформация является нежелательной.
Параметры сварки, такие как скорость и мощность, заданы самим процессом сварки и могут быть лишь незначительно изменены с целью уменьшения деформации. Предложенный в настоящем изобретении альтернативный подход заключается в том, что процесс сварки рассматривают в качестве последовательного комбинаторного процесса, разделяя траекторию сварки шва, соединяющего лопасть и внутреннее кольцо, на более короткие участки. Затем определяют последовательность, в которой должна осуществляться сварка на таких участках, чтобы деформация была минимальной или отсутствовала.
На фиг.5 показан вид в поперечном разрезе основания лопасти 14, которую приваривают к внутреннему кольцу 10. Сварку осуществляют по проиллюстрированному контуру, т.е. вокруг кромки лопатки. Контур поделен на шесть траекторий сварки или действий, которые показаны стрелками. Сварку одновременно осуществляют по одной траектории, а между окончанием одной стадии сварки и началом другой стадии предпочтительно предусмотрен пятисекундный интервал для изменения положения сварочного инструмента. Цифры 1-6, которыми обозначены стрелки на фиг.5, соответствуют действиям сварки, отображенным соседней стрелкой, а не порядку, в котором осуществляют сварку по траекториям. Сварку осуществляют в любом порядке. Далее в описании для описания порядка сварки использованы особые обозначения. Цифры с 1 по 6, обозначающие траектории на фиг.5, приведены в порядке, в котором осуществляют сварку по соответствующим траекториям. Сварку по каждой траектории осуществляют в любом направлении; положительное значение соответствует направлению по стрелке на фиг.5, а отрицательное значение соответствует сварке в противоположном направлении.
На фиг.6 приведена таблица с обозначениями, которые используют для описания некоторых возможных последовательностей сварки. Проиллюстрированы четыре последовательности (обозначенные в левом столбце как 1, 2, 6 и 20). В среднем столбце показаны последовательности сварки. В шапке данного столбца цифрами с 1 по 6 обозначены шесть мест или положений в последовательности сварки. В данном столбце указана каждая последовательность сварки и приведены обозначения 1-6 действий сварки, показанных на фиг.5, при этом, как было пояснено, знак минус соответствует противоположному направлению сварки. Вертикальными пунктирными линиями в среднем столбце обозначены пятисекундные интервалы для смены или изменения положения сварочного инструмента. Так, цифрами в шапках столбцов обозначен порядок, в котором осуществляют сварку согласно последовательности, а цифрами в строках под ними обозначены отдельные действия сварки. В правом столбце графически представлены направления и положения действий сварки в каждой последовательности, при этом цифрами обозначено положение каждого действия сварки (в отличие от обозначений на фиг.5, которые относятся к действию сварки, обозначенному соседней стрелкой).
Создают эталонную модель в виде модели на основе метода конечных элементов, которая описывает последовательный процесс сварки и которая способна учитывать каждое действие сварки, осуществляемое в любом положении в последовательности и в любом направлении. В качестве исходных данных в модель вводят последовательность сварки и получают диаграмму смещений в процессе сварки. Данная диаграмма служит для вычисления суммарного смещения у вершины 10 и вершины 96 при любом сочетании действий, а также смещения вклада в смещение каждого отдельного действия сварки. Данные смещения вычислены, например, для последовательности 6, показанной на фиг.6. Как показывает анализ, наиболее актуальным для оптимизации является компонент Х смещения, как наиболее значимый и меняющийся в обоих направлениях (плюс и минус). Компонент Z на порядок величины меньше компонента Х и поэтому не оказывает значительного влияния на полученное смещение. Компонент Y изменяется только в положительном направлении и не может быть компенсирован путем изменения последовательности сварки.
На фиг.7 показана кривая результатов осуществления модели, включая три компонента смещения у вершины 10 для последовательности сварки номер 6. Также проиллюстрирована кривая, обозначенная как "скорость", которая отображает скорость работы сварочного инструмента и может применяться с целью визуализации и проведения различий между шестью процессами сварки и пятью пятисекундными интервалами. Сварку завершают через 193 секунды и затем шов в течение 300 секунд охлаждают в зафиксированном положении, после чего средства фиксации удаляют и продолжают охлаждение до комнатной температуры.
На фиг.8 показаны кривые смещения компонента Х для проиллюстрированных на фиг.6 последовательностей 1, 2, 6 и 20, вычисленные при помощи модели на основе метода конечных элементов. Из них ясно, что варьирование последовательности сварки способно значительно изменить смещение и, следовательно, может применяться в целях оптимизации. Таким образом, задачей настоящего примера является оптимизация последовательности сварки с целью сведения к минимуму смещений, когда компоненты находятся в зафиксированном состоянии. Стоит задача уменьшить конечное смещение за счет изменения последовательности сварки. Существует шесть переменных (по одной на каждое положение сварки), каждая из которых может иметь 12 нечисловых значений (6 для одного направления и 6 для противоположного направления). В сумме это дает 26×6!=46080 комбинаций. Согласно некоторым обычным методам оптимизации последовательных комбинаторных задач необходимо осуществить прогон всех таких комбинаций через модель на основе метода конечных элементов и выбрать последовательность сварки с наименьшим смещением. Однако это неосуществимо, поскольку на вычисление одной комбинации уходит 32 часа. Другие существующие методы комбинаторной оптимизации, описанные в литературе, такие как целочисленное программирование, графы, метод ветвей и границ и двоичные деревья [2] не способны существенно сократить число комбинаций, требующих вычисления. В настоящем изобретении значительно сокращено время, необходимое для достижения результата за счет применения имитации модели, которая осуществляет вычисления значительно быстрее, чем через модель на основе метода конечных элементов, и которую применяют для сокращения числа необходимых прогонов модели на основе метода конечных элементов. Поскольку в имитации модели используют данные, полученные в результате прогонов модели на основе метода конечных элементов, необходима часть таких прогонов, но имитация модели способна обеспечить приближение к модели на основе метода конечных элементов за счет использования данных, полученных в результате гораздо меньшего числа прогонов, чем общее число возможных комбинаций.
Для разработки имитации модели суммарное смещение D можно описать просто как сумму смещений D, вызванных шестью отдельными сварками и сопутствующим охлаждением:

Данное уравнение отображает наложение di, смещения, вызванного сваркой i в последовательности сварки; 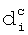 , смещения, вызванного стадией охлаждения после каждой сварки; и dc, смещения, вызванного стадией конечного охлаждения. Для простоты сначала отбросим смещение в результате охлаждения, после чего уравнение (1) приобретет следующий вид:
, смещения, вызванного стадией охлаждения после каждой сварки; и dc, смещения, вызванного стадией конечного охлаждения. Для простоты сначала отбросим смещение в результате охлаждения, после чего уравнение (1) приобретет следующий вид:

Тестовые прогоны модели на основе метода конечных элементов с охлаждением и без охлаждения показали, что данное допущение не приводит к значительной потере качества, поскольку вклады в общее смещение процесса сварки несравненно превышают вклады процессов охлаждения. Модель на основе метода конечных элементов способа позволяет вычислить смещение, вызванное каждой сваркой, и тем самым обеспечивает информацию, необходимую для имитации.
Смещение, вызванное любой отдельной сваркой, зависит от положения сварки в последовательности, направления сварки и любых предшествующих сварок. Если сварка является первой сваркой в последовательности, вызванное ею смещение не зависит от последующих сварок. Назовем данное явление главным эффектом. Обозначим главный эффект действия сварки w как Мw. В частности, описанные выше прогоны 1, 2, 6 и 20 обеспечивают информацию о М1, М-1, М-6 и М2 соответственно, поскольку 1, -1, -6 и 2 являются первыми действиями сварки в данных последовательностях. В целом, в данных последовательностях существуют шесть возможных первых действий сварки, что в сумме дает двенадцать возможных значений главного эффекта. Их определяют по результатам двенадцати прогонов модели на основе метода конечных элементов. Не требуется осуществлять последовательность сварки целиком; первая сварка из двенадцати прогонов, каждый из которых соответствует сочетанию различных положений и направлений сварки в качестве первого действия в последовательности, обеспечивает полную информацию обо всех возможных главных эффектах.
Особо простой моделью, подходящей в качестве имитации модели, является модель, в которой конечное смещение принимают за сумму главных эффектов:

где wi является действием w в i-м положении в последовательности. Например, согласно модели смещение для последовательности 20, показанной на фиг.6, выражено как D=М2+М-5+М6+M-1+M3+М-4. Данная модель основана на системе, не имеющей памяти, в которой не учитывают влияние каких-либо предшествующих сварок на текущую сварку. Модель исходит из того, что протекание действий во всех положениях последовательности аналогично протеканию начальной сварки путем подстановки i=2, 3, 4, 5, 6 с соответствующими главными эффектами вместо всех di. Это означает, что данные коэффициенты зависят только от действия сварки, а не от их положения в последовательности. В расчет не принимают влияние, которое могли оказать в рамках процесса предшествующие сварки, такое как смещение в результате внутренних напряжений и термических деформаций. Данная модель выполняет поставленную задачу сокращения числа прогонов модели на основе метода конечных элементов с целью обеспечения информации, необходимой для прогона любой возможной последовательности через имитацию модели, поскольку для этого требуется лишь двенадцать прогонов. Вместе с тем, протекание процесса сварки обычно не соответствует поведению системы без памяти; смещения результаты заданного действия сварки меняются в зависимости от его положения в последовательности сварки. Таким образом, более точной является модель:

в которой Δ(w, i) является повышением точности за счет включения влияния положения, которое занимает в последовательности действие сварки. В этом случае смещения di=f(w, i) зависят от действия сварки и его положения.
Чтобы способствовать участию памяти системы в оптимизации, вводят определения порядка и типа вклада любого отдельного действия в суммарное смещение, которые называют событиями. Чтобы описать смещение в положении i, события определяют следующим образом:
(vii) члены первого порядка типа 1, которые игнорируют любой вклад предшествующих действий сварки, т.е. отображают систему без памяти. Вместе с тем, они принимают во внимание влияние положения в последовательности. Ранее упомянутые главные эффекты являются членами первого порядка типа 1, но только в случае их применения для описания смещения в положении 1,
(viii) члены первого порядка типа 2 также игнорируют любые предшествующие действия и влияние положения. Например, модель, основанная на уравнении (3), включает только данные члены. В D=М2+М-5+М6+М-1+М3+М-4M2 является членом первого порядка типа 1, а все остальные слагаемые являются событиями типа 2, поскольку вклады M-5, М6, М-1, М3, и М-4 получены по результатам имитаций, когда действия -5, 6, -1, 3 и -4 происходили в положении 1 последовательностей сварки, пропущенных через модель на основе метода конечных элементов, исключая какие-либо еще положения в данном прогоне,
(ix) члены второго порядка типа 1 учитывают положение действия сварки в последовательности и ближайший предшествующий характер протекания последовательности (т.е. действие сварки, которое непосредственно предшествовало рассматриваемому действию сварки i). События второго порядка существуют только при условии, что i≥2,
(х) члены второго порядка типа 2 учитывают предшествующее действие сварки, но игнорируют значение положения пары действий в последовательности,
(xi) члены третьего порядка, которые существуют только при условии, что i≥3, включают два действия сварки, которые непосредственно предшествуют рассматриваемому действию,
(xii) и так далее по мере возрастания порядков.
В дальнейшем порядок события обозначают соответствующим цифровым подстрочным индексом, а тип события штрихами. Таким образом, события k-го порядка и первого типа обозначают как 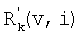 , где v означает вектор, образованный действиями в положениях [wi-k+1+, …, wi-1, wi], которые, следовательно, включают k-1 действий, предшествующих данному действию. События второго типа обозначены двойным штрихом.
, где v означает вектор, образованный действиями в положениях [wi-k+1+, …, wi-1, wi], которые, следовательно, включают k-1 действий, предшествующих данному действию. События второго типа обозначены двойным штрихом.
Рассмотрим событие k=1 первого типа: последовательность 20 обеспечивает информацию о следующих событиях первого порядка (при этом первым числом в каждой паре обозначено действие, а вторым числом его положение в последовательности):
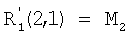 ;
;  ;
;  ;
;  ;
;  ;
; 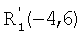 . Последовательность содержит информацию об изменении смещения, которое вызвано событием действия сварки в положении w в последовательности сварки. Ее непосредственно используют для разработки DoE, в котором прогон модели на основе метода конечных элементов осуществляют достаточное количество раз, чтобы заполнить матрицу, содержащую все события первого порядка первого типа
. Последовательность содержит информацию об изменении смещения, которое вызвано событием действия сварки в положении w в последовательности сварки. Ее непосредственно используют для разработки DoE, в котором прогон модели на основе метода конечных элементов осуществляют достаточное количество раз, чтобы заполнить матрицу, содержащую все события первого порядка первого типа  для w=-6, …, -1, 1…6; i=1, …, 6. Такое планирование требует 18 прогонов.
для w=-6, …, -1, 1…6; i=1, …, 6. Такое планирование требует 18 прогонов.
Для описания системы с памятью необходимо учесть влияния текущих и прошлых событий, а не только текущих событий, такого как 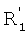 . Такие события относятся к событиям второго и более высоких порядков. Для упрощения модели целесообразно предположить, что при рассмотрении последнего действия сварки в последовательности влияние на его смещение, оказанное, скажем, предпоследним действием сварки, является более важным, чем на первое действие (за счет этого можно пренебречь событиями очень высоких порядков). Кроме того, можно установить, что влияние подпоследовательностей различных действий сварки в последовательности является преимущественно одинаковым (и поэтому событий второго типа достаточно для последовательностей более высоких порядков). На основании данных предпосылок строят приближения к влиянию любого действия сварки, используя информацию, полученную в результате ранее осуществленных прогонов. Данная информация представляет собой DoE. Процесс осуществляют следующим образом:
. Такие события относятся к событиям второго и более высоких порядков. Для упрощения модели целесообразно предположить, что при рассмотрении последнего действия сварки в последовательности влияние на его смещение, оказанное, скажем, предпоследним действием сварки, является более важным, чем на первое действие (за счет этого можно пренебречь событиями очень высоких порядков). Кроме того, можно установить, что влияние подпоследовательностей различных действий сварки в последовательности является преимущественно одинаковым (и поэтому событий второго типа достаточно для последовательностей более высоких порядков). На основании данных предпосылок строят приближения к влиянию любого действия сварки, используя информацию, полученную в результате ранее осуществленных прогонов. Данная информация представляет собой DoE. Процесс осуществляют следующим образом:
14. Общая задача заключается в вычислении отклонения в результате каждого действия и их суммировании с целью получения общего отклонения. Изначально D=0.
15. Предположим, что рассматриваем последовательность хр. Например, хр=[6, 3, -5, 4, -2, 1].
16. Начинаем с i=1 (первое действие в последовательности) и затем по возрастающей.
17. Наивысшим возможным порядком события является i.
18. Создадим вектор хр1=[1:i], который содержит первые элементы i последовательности хр. В частности, для i=3; хр1=[6, 3, -5].
19. Пусть k=1.
20. Создадим вектор хр2=хр1[i-k+1:i], в котором использован последние элементы i-k+1 вектора хр1.
21. Осуществим в DoE поиск хр2, последний элемент которого находится в i-м положении последовательности DoE. В случае обнаружения используем значение соответствующего смещения di и переходим к стадии 10, в противном случае продолжаем. Установленное смещение является событием порядка i 1-го типа.
22. Осуществим в DoE поиск хр2 независимо от положения в последовательностях. В случае обнаружения используем значение соответствующего вклада di и переходим к стадии 10, в противном случае продолжаем. Установленное смещение является событием порядка i 2-го типа.
23. D=D+di.
24. Если i=wp, команда СТОП. Последовательность пройдена до конца. В рассматриваемом примере wp=6, что соответствует 6 действиям сварки в последовательности.
25. i=i+1.
26. Переходим к стадии 4.
Вычисление данного процесса занимает гораздо меньше времени, чем прогон модели на основе метода конечных элементов. Таким образом, на основе результатов относительно небольшого числа прогонов модели на основе метода конечных элементов для заполнения DoE имитация модели осуществляет быстрый прогон всех возможных последовательностей и идентифицирует минимально возможное смещение.
Чтобы проиллюстрировать идею использования данных событий, рассмотрим модель, состоящую из членов вплоть до 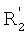 :
:

где 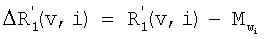 ;
; 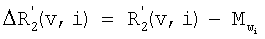 ; i является положением в последовательности, a v=[wi-k+1, …, wi-1, wi], где k=1 и 2 соответственно.
; i является положением в последовательности, a v=[wi-k+1, …, wi-1, wi], где k=1 и 2 соответственно.
Прогон 20 содержит информацию о следующих событиях второго порядка:  ;
;  ;
;  ;
; 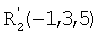 ;
;  , где последнее число в каждой группе обозначает положение в последовательности двух действий сварки, отображенных двумя первыми числами. Для заполнения всей матрицы
, где последнее число в каждой группе обозначает положение в последовательности двух действий сварки, отображенных двумя первыми числами. Для заполнения всей матрицы  DoE необходимо 180 прогонов модели на основе метода конечных элементов, что делает ее использование бесперспективным. Вместо этого возможно компромиссное решение за счет использования DoE, которое целиком заполняет матрицу
DoE необходимо 180 прогонов модели на основе метода конечных элементов, что делает ее использование бесперспективным. Вместо этого возможно компромиссное решение за счет использования DoE, которое целиком заполняет матрицу  . Чтобы удостовериться в существовании всех событий второго порядка и 2-го типа, требуется осуществить 27 прогонов модели на основе метода конечных элементов. Можно доказать, что данное приближение, в котором игнорируется, где возникали пары подпоследовательностей, не приводит к значительной потери точности. Кроме того, некоторые пары
. Чтобы удостовериться в существовании всех событий второго порядка и 2-го типа, требуется осуществить 27 прогонов модели на основе метода конечных элементов. Можно доказать, что данное приближение, в котором игнорируется, где возникали пары подпоследовательностей, не приводит к значительной потери точности. Кроме того, некоторые пары  будут доступны в матрице и в этом случае могут быть использованы. Таким образом, члены
будут доступны в матрице и в этом случае могут быть использованы. Таким образом, члены  в уравнении (5) могут быть заменены
в уравнении (5) могут быть заменены

Так, по возможности используют члены второго порядка, которые заменяют членами более низкого порядка только в случае их недоступности. Такую небольшую потерю точности компенсирует сокращение числа прогонов модели на основе метода конечных элементов, необходимых для DoE.
Несмотря на то, что DoE рассчитано на включение всех событий R^(v), для некоторых действий и положений в нем содержатся события третьего порядка и выше, применяемые для дальнейшего повышения точности. Так, уравнение (6) можно представить в следующем обобщенном виде:
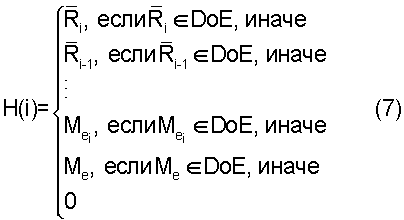
при этом общее смещение вычисляют следующим образом:
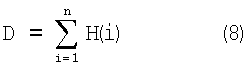
где n является общим числом действий в последовательности; в данном примере n=6. Уравнение (8) представляет собой более обобщенную форму уравнения (5) и служит для получения результата сложения событий наивысшего порядка и низшего типа с целью вычисления ожидаемого значения смещения для заданного действия сварки и его положения в последовательности.
Данная модель применима к любому числу переменных или действий n с учетом того, что высший порядок события равен числу переменных. Модель обладает некоторой обучаемостью в том смысле, что она всегда дает прогноз при наличии по меньшей мере одной позиции в DoE. В случае осуществления большего числа прогонов модели на основе метода конечных элементов объем DoE увеличивается, а прогнозы становятся более точными. В предельном случае, когда при помощи модели на основе метода конечных элементов проверены все возможные комбинации, модель воспроизводит точные данные испытаний. Данная особенность имитации модели позволяет применять ее при наличии любого числа позиций в DoE, благодаря чему объем DoE свободно увеличивают или перестают увеличивать в зависимости от требуемой точности модели. Как показывает опыт изучения примеров, таких как рассмотренный здесь пример с шестью действиями, существования полного набора 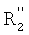 достаточно, чтобы обеспечить удовлетворительное соответствие существующим данным.
достаточно, чтобы обеспечить удовлетворительное соответствие существующим данным.
Ясно, что после вычисления вклада по результатам достаточного числа прогонов модели на основе метода конечных элементов, заданных в DoE, в такой модели необходимы очень незначительные вычисления, что облегчает изучение всех возможных комбинаций имитацией модели и выбор наилучшей. С целью испытания точности данный наилучший прогноз затем проверяют путем прогона соответствующей последовательности через модель на основе метода конечных элементов. Таким прогоном затем дополняют DoE, что делает последующие прогнозы имитации модели более точными. Затем имитация модели осуществляет еще один полный цикл поиска комбинации, используя все информацию DoE, включая результаты последнего прогона модели на основе метода конечных элементов, и так далее до тех пор, пока не будут получены одинаковые или достаточно сходные результаты следующих друг за другом прогонов модели.
Продолжая рассматривать оптимизацию последовательности сварки в качестве примера осуществления настоящего изобретения и исходя из сделанных выше выводов, обратимся к фиг.9, на которой проиллюстрирована таблица DoE, соответствующая 27 прогонам модели на основе метода конечных элементов, которая гарантирует включение всех событий  . На фиг.10 показана матрица, указывающая число событий второго порядка и 2-го типа для каждого сочетания текущего и прошлого сварочных положений, обнаруженных в DoE, проиллюстрированном на фиг.9. Первый элемент данной матрицы (1, 1) равен 0, поскольку действие сварки -6 не может быть осуществлено после действия сварки -6, следовательно, все расположенные по диагонали элементы равны 0. Элемент под ним (2, 1) равен 1, что говорит о наличии одного события, представляющего собой пару прошлого-текущего действий (-5, -6). Оно находится в шестом положении во 2-м прогоне. На строке матрицы, обозначенной 0, содержатся главные эффекты. В частности, показано, что 3 прогона обеспечивают информацию о главном эффекте -6. Это прогоны 6, 7 и 23, в которых действие сварки -6 осуществляли первым в последовательности сварки. Данная матрица подтверждает отсутствие нулевых элементов помимо элементов, расположенных по диагонали.
. На фиг.10 показана матрица, указывающая число событий второго порядка и 2-го типа для каждого сочетания текущего и прошлого сварочных положений, обнаруженных в DoE, проиллюстрированном на фиг.9. Первый элемент данной матрицы (1, 1) равен 0, поскольку действие сварки -6 не может быть осуществлено после действия сварки -6, следовательно, все расположенные по диагонали элементы равны 0. Элемент под ним (2, 1) равен 1, что говорит о наличии одного события, представляющего собой пару прошлого-текущего действий (-5, -6). Оно находится в шестом положении во 2-м прогоне. На строке матрицы, обозначенной 0, содержатся главные эффекты. В частности, показано, что 3 прогона обеспечивают информацию о главном эффекте -6. Это прогоны 6, 7 и 23, в которых действие сварки -6 осуществляли первым в последовательности сварки. Данная матрица подтверждает отсутствие нулевых элементов помимо элементов, расположенных по диагонали.
В данном примере DoE построено с учетом всех возможных 46080 комбинаций и выбора первого набора, заполнившего все не расположенные по диагонали элементы в матрице, показанной на фиг.10. Для этого осуществляют прогон шести вложенных циклов, в ходе каждого из которых просматривают значения -6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6 и выбирают последовательности, которые подчиняются следующему правилу |А|≠|В|≠|С|≠|D|≠|E|≠|F|, где А, В, С, D, Е и F являются переменными шести вложенных циклов. Каждую последовательность регистрируют в матрице, как это показано на фиг.10, и когда все не расположенные по диагонали элементы не равны нулю, формирование DoE прекращают. В результате DoE содержит первый набор последовательностей, который гарантирует, что все события  были испытаны. Данный способ формирования DoE отличается особой простотой, но следует отметить, что его результатом необязательно является оптимальное DoE или минимально возможное DoE, хотя вероятно минимально возможное DoE и не имеет намного меньший объем.
были испытаны. Данный способ формирования DoE отличается особой простотой, но следует отметить, что его результатом необязательно является оптимальное DoE или минимально возможное DoE, хотя вероятно минимально возможное DoE и не имеет намного меньший объем.
Каждую последовательность из DoE прогоняют через модель на основе метода конечных элементов. По разности между смещением в конце и начале сварки, вычисленной при помощи модели на основе метода конечных элементов, вычисляют значение смещения для каждого элемента матрицы, показанной на фиг.10. Результаты данных вычислений приведены в таблице на фиг.11, структура которой аналогична структуре матрицы на фиг.10. В частности, смещение в результате события, представляющего собой пару прошлого-текущего действий (-5, -6), равно -0,12721 мм и является значением  .
.
В качестве примера рассмотрим последовательность [6, 3, -5, 4, -2, 1] и применим к ней модель:
3. D=0.
9. i=1: для положения номер 1 высшим порядком события является 1, поэтому проверяем наличие главного эффекта 6 в позициях DoE. Предположим, что он обнаружен (в прогонах 8, 24, 25). Смещение в результате главного эффекта 6 вычитают из вычисленных данных и добавляют полученное значение к D, после чего D=М6.
10. i=2: высшим порядком события является 2, поэтому осуществляем поиск пары (6, 3) в планировании экспериментов в положении 2 (сначала осуществляем поиск события 1-го типа). В случае отсутствия совпадения далее осуществляем поиск события 2-го типа независимо от положения. Предположим, что найдено совпадение в прогоне 27. Добавляем соответствующее значение смещения из фиг.11 к значению D, после чего получаем 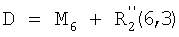 .
.
11. i=3: высшим порядком события является 3, поэтому осуществляем поиск подпоследовательности (6, 3, -5) в DoE в положении 3 (снова сначала осуществляем поиск события 1-го типа). Данная подпоследовательность не может быть обнаружена в DoE. Ее поиск по всему DoE также не дает результата, что говорит об отсутствии такого события третьего порядка 1-го или 2-го типа. Затем сокращаем подпоследовательность, отсекая наиболее отдаленное действие, которое предположительно имеет наименьшее влияние на отклонение в положении 3. Подпоследовательность принимает вид (3, -5). Снова сначала проверяем наличие ее события 1-го типа, т.е. такого события, когда действие -5 находится в положении 3, а действие 3 в положении 2. Предположим, что совпадение найдено, и добавляем соответствующее смещение к значению D, после чего получаем  .
.
12. i=4: высшим порядком события является 4, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4) в DoE в положении 4 на предмет наличия события 1-го типа. При отсутствии совпадения осуществляем поиск событий 2-го типа, которые также не обнаруживаем. Затем усекаем подпоследовательность до (3, -5, 4) и сначала осуществляем поиск событий 1-го типа. Находим совпадение в 18-м прогоне и добавляем значение смещения, соответствующее вкладу члена 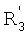 , к значению D, после чего получаем
, к значению D, после чего получаем 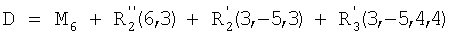 .
.
13. i=5: высшим порядком события является 5, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4, -2) в DoE в положении 5 на предмет наличия события 1-го типа. Предположим, что событие не найдено, равно как и событие 2-го, тогда производим усечение и осуществляем поиск подпоследовательности (3, -5, 4, -2). Предположим, что результат поиска события как 1-го, так и 2-го типа снова отрицательный. Снова производим усечение подпоследовательности до (-5, 4, -2). И снова не находим совпадения ни для одного типа. Производим усечение до (4, -2). Событие 1-го типа отсутствует, но, скажем, в DoE в прогоне 4 найдено событие 2-го типа. Добавляем смещение к Л и получаем
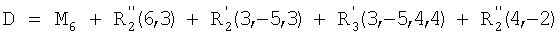 .
.
14. i=6: высшим порядком события является 6, поэтому осуществляем поиск подпоследовательности (6, 3, -5, 4, -2, 1) в DoE в положении 6. Предположим, что совпадение не найдено. Повторно осуществляем такую же операцию, как на предшествующей стадии, проверяя на наличие событий 1-го и 2-го типов следующие подпоследовательности (3, -5, 4, -2, 1); (-5, 4, -2, 1); (4, -2, 1). Предположим, что результат отрицательный. Наконец, предположим, что в результате поиска (-2, 1) по всему планированию экспериментов независимо от положения найдено совпадение в 14-м прогоне. Добавляем смещение к D и получаем 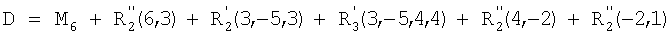 .
.
8. В суммарное смещение также следует включить смещение, вызванное стадией конечного охлаждения, которое определено методом аппроксимации кривых, для моделирования которого используют dc=0.7152*H(6)+0.0143.
Данный алгоритм позволяет при помощи кода MATLAB менее чем за 5 минут вычислить все 46080 возможных комбинаций на компьютере с Pentium III с тактовой частотой процессора 800 МГц. Гораздо быстрее результат можно получить, если использовать код, составленный на языке Си или ФОРТРАН. Было обнаружено, что следующая последовательность, обозначенная как прогон "28", обеспечивает наименьшее значение |D|: -6, -1, -5, 2, -4, 3. Значение смещения у данной последовательности задано уравнением:

Эту же последовательность вычислили при помощи модели на основе метода конечных элементов и получили очень близкий результат: D=0,000231. Данный результат считается удовлетворяющим требованиям точности при изготовлении корпусов задних подшипников, а также является вероятным абсолютным минимумом применительно к данной задаче оптимизации.
На фиг.12 показана диаграмма, на которой окончательный результат оптимизации проиллюстрирован в виде зависимости смещения от времени, и показана имитация прогона 28 модели на основе метода конечных элементов в сравнении с прогонами 1, 5, 6, 16, 24 и 24 из DoE. Кривая, отображающая прогон 28, достигает нуля непосредственно перед наступлением 300-й секунды, когда удаляют средства фиксации. Показано улучшение смещения Х по сравнению с прогоном 1, который представляет собой последовательность, широко применяемую в качестве стандартной при изготовлении корпуса заднего подшипника.
На фиг.13 приведена диаграмма окончательных смещений для всех 28 прогонов, на которой показано, что минимальное смещение вызывает оптимизированный прогон 28.
Таким образом, настоящее изобретение было эффективно применено для оптимизации процесса сварки и продемонстрировано, что для определения оптимальной послесварочной деформации достаточно лишь 28 прогонов модели на основе метода конечных элементов из возможных 46080 комбинаций последовательностей. За счет этого значительно сокращаются расходы на вычисления, необходимые для разработки технологии сварки, без значительной потери точности.
Можно отметить ряд преимуществ настоящего изобретения, многие из которых относятся к применению изобретения в других последовательных комбинаторных процессах:
- способ обеспечивает привязку дискетного пространства процесса к непрерывному пространству, позволяя преобразовать последовательную комбинаторную задачу в обычную форму преставления,
- способ применим к широкому спектру последовательных комбинаторных задач,
- поскольку имитацию модели наращивают последовательно, каждая новая представленная комбинация делает ее более точной, эффективность имитации модели заключается в том, она позволяет извлекать всю полезную информацию из представленных прогонов эталонной модели и организовать ее в виде указателя приоритетов в зависимости от ее полезности,
- способ отличается быстротой; в случае шести действий при помощи кода MATLAB менее чем за 5 минут можно вычислить все 46080 возможных комбинаций на компьютере с Pentium III с тактовой частотой процессора 800 МГц. Гораздо быстрее результат можно получить, если использовать код, составленный на языке Си или ФОРТРАН,
- применительно к примеру оптимизации описанного выше процесса сварки достаточно 27 вычислений исходной эталонной модели для получения при помощи имитации модели отличающегося высокой точностью быстрого прогноза, согласно которому значение оптимального смещения составляет 0,00023 мм, что очень близко к значению 0,000231 мм, спрогнозированному при помощи модели на основе метода конечных элементов.
Дополнительные варианты осуществления
Описанное выше изобретение является быстрым и эффективным заменителем связанных с высокими расходами на вычисления моделей на основе метода конечных элементов и других моделей, которые обычно применяют для решения последовательных комбинаторных задач. Алгоритм непрерывно обращается к существующей информации о рассматриваемой системе и тем самым привязывает дискретный нечисловой набор информации к непрерывной числовой области. Чтобы имитация модели могла действовать, используя небольшое число дорогостоящих прогонов полной эталонной модели, в ней прогнозируют следующий указатель приоритетов условий совпадения. В него, например, включены:
1. События максимально высокого порядка 1-го типа.
2. События максимально высокого порядка 2-го типа.
3. События более низкого порядка 1-го типа.
4. События более низкого порядка 2-го типа.
5. Главные эффекты.
Согласно вариантам осуществления предложенного алгоритма всегда осуществлялся поиск элемента с максимально высоким положением в указателе. Однако для некоторых задач будет более приемлемо применять альтернативный указатель приоритетов, такой как:
1. События максимально высокого порядка 1-го типа.
2. События более низкого порядка 1-го типа.
3. События максимально высокого порядка 2-го типа.
4. События более низкого порядка 2-типа.
5. Главные эффекты.
Также возможны другие указатели приоритетов для их изучения с целью уточнения прогнозов в заданной системе.
При отсутствии доступных прогонов эталонной модели алгоритм дает нулевой результат всех прогнозов. За счет обеспечения доступности по меньшей мере всех главных эффектов получают очень приблизительный прогноз, который может быть приемлем в некоторых случаях. В системах, не имеющих памяти, такой прогноз должен отличаться достаточной точностью. Для получения главных эффектов осуществляют только первые действия, не вычисляя всей последовательности. За счет этого значительно ускоряют процесс оптимизации, поскольку для этого требуются незначительные вычисления по сравнению с полными расчетами всех возможных последовательностей. Однако при необходимости более точных результатов рекомендуется включение по меньшей мере событий второго порядка и 2-го типа.
Что касается задач с большой размерностью, включающих множество действий, для повышения точности за некоторыми положениями или действиями закрепляют более высокий приоритет, чем за другими. В таких случаях возможно применение смешанного DoE, когда наиболее важным действиям присваивают более высокий порядок события, а менее значимым действиям присваивают более низкий порядок. За счет этого расходы на вычисления сосредотачивают на тех частях последовательности, которые оказывают наибольшее воздействие на конечный результат. В результате соответствующих модификаций уменьшают размеры DoE таким образом, чтобы большая часть информации относилась к наиболее важным действиям.
Несмотря на то, что в подробно описанном варианте осуществления изобретения рассмотрен пример последовательности сварки, изобретение не ограничено данным примером. Изобретение применимо к любому последовательному процессу, в котором упорядоченность последовательности влияет на исход процесса. Примеры процессов, в которых может применяться настоящее изобретение, включают:
- приваривание множества лопастей к кольцам корпуса заднего подшипника газовой турбины или аналогичной турбины или конструкции винта, т.е. последовательность, в которой лопасти приваривают к кольцам, и
- нахождение оптимальной последовательности соединения с точки зрения механических свойств одной или нескольких произвольных геометрий, которые соединяют посредством сварки, приклеивания, болтового соединения, горячей запрессовки, склеивания слоистых материалов или любым иным способом соединения, зависящим от порядка, в котором осуществляют различные операции.
Изобретение также не ограничено моделями на основе метода конечных элементов. Может применяться модель любого типа, способная обеспечивать требуемую информацию. Например, в качестве эталонной модели может применяться любая соответствующая компьютерная программа, способная имитировать отклонение или иной рабочий параметр. Однако имитация модели на компьютере не является обязательной. В частности, вместо или в сочетании с имитированными результатами могут использоваться результаты реальных испытаний процесса с целью выбора последовательностей.
Например, применительно к потоку деталей через предприятие при помощи таймера измеряют промежутки времени для различных станков/операций и используют их в качестве информации, которой пользуется имитация модели.
Аналогичным образом могут применяться результаты испытаний сходных или родственных процессов, возможно, в измененном виде, чтобы более точно моделировать рассматриваемый процесс. Реальные результаты также могут использоваться в сочетании с эталонной моделью, при этом DoE может включать некоторые последовательности, пропущенные через эталонную модель, и некоторые последовательности, для которых были получены реальные результаты, и/или эталонная модель может использоваться для проверки точности прогноза, полученного при помощи имитации модели. По существу, в качестве информации, к которой обращается имитация модели, могут использоваться любые значения вкладов в конечный результат каждого действия из последовательности независимо от того, каким образом они получены. За счет этого может применяться наиболее применимый метод получения информации.
Источники информации
1. Патент США 6349467.
2. Winston, W, 1995, "Introduction to mathematical programming", второе издание, Duxbury Press, Калифорния, США.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и система для анализа спектральных данных | 2017 |
|
RU2764200C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО СОСТАВА УГОЛЬНОЙ ШИХТЫ ДЛЯ КОКСОВАНИЯ | 2006 |
|
RU2307862C1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОИЗВОДСТВЕННЫМ ПРОЦЕССОМ | 2012 |
|
RU2580394C1 |
| СПОСОБ И СИСТЕМА МАШИННОГО ОБУЧЕНИЯ ИЕРАРХИЧЕСКИ ОРГАНИЗОВАННОМУ ЦЕЛЕНАПРАВЛЕННОМУ ПОВЕДЕНИЮ | 2019 |
|
RU2755935C2 |
| КОМПЛЕКС ТЕСТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ЭЛЕКТРОННЫХ УСТРОЙСТВ | 2020 |
|
RU2729210C1 |
| СПОСОБ ОПТИМИЗАЦИИ СОСТАВА РЕЦЕПТУРНОЙ СМЕСИ МЯСНОГО РУБЛЕНОГО ПОЛУФАБРИКАТА | 2004 |
|
RU2269910C1 |
| СПОСОБЫ, СИСТЕМЫ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ ИДЕНТИФИКАЦИИ БИОМОЛЕКУЛ СО ВЗАИМОДЕЙСТВУЮЩИМИ КОМПОНЕНТАМИ | 2014 |
|
RU2695146C2 |
| Способ моделирования двусторонних воздействий при использовании конфликтующими системами управления общего технологического ресурса | 2018 |
|
RU2692423C1 |
| СИСТЕМЫ И СПОСОБЫ ОПТИМИЗАЦИИ ОПЕРАЦИЙ ДОБЫЧИ В РЕАЛЬНОМ ВРЕМЕНИ | 2008 |
|
RU2502120C2 |
| Способ обработки результатов радиомониторинга | 2020 |
|
RU2740708C1 |
Группа изобретений относится к средствам, обеспечивающим оптимизацию комбинаторных процессов, взаимозаменяемой последовательности действий. Техническим результатом является повышение точности определения оптимальной последовательности действий. В способе для моделирования набора возможных последовательностей используют эталонную модель и информацию, полученную при помощи эталонной модели. Осуществляют имитацию модели при помощи алгоритма для выбора из информации, которая в наибольшей степени соответствует действиям из текущей последовательности, в соответствии с системой приоритетов, позволяющей всегда по возможности использовать наилучшее соответствие. Полученные результаты сравнивают, идентифицируя моделированные последовательности. Качество конечного результата зависит от порядка, в котором осуществляют действия, из которых состоит процесс, включая производственный процесс, такой как машинная обработка, резка, формование, профилирование и/или термообработка детали, направление потоков материалов через предприятие или перекачивание нефти или газа по системе трубопроводов, процессы смешивания в химии и материаловедении, моделирование в области вычислительной биологии и управление парком транспортных средств. 2 н. и 47 з.п. ф-лы, 13 ил.
1. Способ оптимизации производственного, промышленного или инженерно-технического последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, заключающийся в том, что
используют планирование экспериментов (DoE), включающее группу последовательностей, выбранных из множества последовательностей, при этом каждая последовательность, входящая в планирование экспериментов, связана с данными, касающимися значения вклада каждого действия из каждой последовательности в достижение конечного результата, характеризуемого рабочим параметром,
используют имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений, которые содержатся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, и извлекают значения вклада совпавшего действия, осуществляют прогон группы из множества последовательностей через имитацию модели и регистрируют значение конечного результата каждой последовательности, и
идентифицируют оптимальную последовательность путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, представляет собой оптимальную последовательность.
2. Способ по п.1, в котором получают данные, связанные с каждой последовательностью из планирования экспериментов, посредством прогона каждой последовательности из планирования экспериментов через эталонную модель процесса, в которую в качестве исходных данных введена последовательность действий и которая определяет значение конечного результата и значения вкладов в конечный результат каждого действия из введенной последовательности.
3. Способ по п.2, в котором эталонную модель строят перед осуществлением прогона каждой последовательности из планирования экспериментов через указанную эталонную модель.
4. Способ по п.2 или 3, в котором имитация модели представляет собой упрощенное приближение к эталонной модели.
5. Способ по п.2, в котором после идентификации оптимальной последовательности осуществляют прогон идентифицированной оптимальной последовательности через эталонную модель с целью определения значения конечного результата и сравнивают зарегистрированное оптимальное значение идентифицированной оптимальной последовательности, определенное при помощи имитации модели, с конечным результатом, определенным при помощи эталонной модели, на основе чего проверяют точность идентифицирования оптимальной последовательности.
6. Способ по п.5, в котором
при обнаружении различия между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, определенным при помощи имитации модели, и конечным результатом, определенным при помощи эталонной модели, величина которого неприемлема для процесса, дополняют планирование экспериментов идентифицированной оптимальной последовательностью так, чтобы данная последовательность и значения вкладов в конечный результат каждого действия, определенные путем прогона идентифицированной оптимальной последовательности через эталонную модель, были доступны для поиска и извлечения при помощи алгоритма имитации модели, осуществляют прогон группы из множества последовательностей через имитацию модели с целью получения новых значений конечного результата каждой последовательности и
на основании новых конечных результатов идентифицируют новую оптимальную последовательность.
7. Способ по п.6, в котором повторно осуществляют стадии по пп.5 и 6 применительно к новой идентифицированной оптимальной последовательности до тех пор, пока различие между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, полученным при помощи имитации модели, и конечным результатом, полученным при помощи эталонной модели, не станет приемлемым для процесса.
8. Способ по п.1, в котором данные, которым соответствует каждая последовательность из планирования экспериментов, получают посредством осуществления последовательного комбинаторного процесса с использованием каждой из последовательностей из планирования экспериментов и регистрируют значения вклада в конечный результат каждого действия из каждой последовательности.
9. Способ по п.1, в котором имитацию модели строят перед прогоном группы из множества последовательностей через названную имитацию модели.
10. Способ по п.1, в котором указатель приоритетов содержит иерархию условий совпадения в порядке убывания уровня соответствия между действием из последовательности, введенной в имитацию модели, и действиями из последовательностей, входящих в планирование экспериментов, с точки зрения положения действия из введенной последовательности и/или действий, предшествующих действию из введенной последовательности.
11. Способ по п.1, в котором условия совпадения включают порядок, определяющий число действий, предшествующих действию из последовательности, введенной в имитацию модели, которые должны совпасть с действиями, предшествующими действию из последовательностей планирования экспериментов, и тип определения совпадения положения действия в последовательности, введенной в имитацию модели, с положением действия в последовательностях из планирования экспериментов, при этом для совпадения 1-го типа положение действия во введенной последовательности должно совпадать с положением действия в последовательностях из планирования экспериментов, а для совпадения 2-го типа не требуется, чтобы положение действия во введенной последовательности совпадало с положением действия в последовательностях из планирования экспериментов.
12. Способ по п.11, в котором для последовательности, состоящей из n-го числа действий, указатель приоритетов содержит следующие условия совпадения:
совпадение n-го порядка 1-го типа,
совпадение n-го порядка 2-го типа,
совпадение (n-1)-го порядка 1-го типа,
совпадение (n-1)-го порядка 2-го типа,
...
совпадение 1-го порядка 1-го типа,
совпадение 1-го порядка 2-го типа,
совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой в планировании экспериментов.
13. Способ по п.11, в котором для последовательности, состоящей из n-го числа действий, указатель приоритетов содержит следующие условия совпадения:
совпадение n-го порядка 1-го типа,
совпадение (n-1)-го порядка 1-го типа,
совпадение (n-2)-го порядка 1-го типа,
совпадение 1-го порядка 1-го типа,
совпадение n-го порядка 2-го типа,
совпадение (n-1)-го порядка 2-го типа,
совпадение (n-2)-го порядка 2-го типа,
совпадение 1-го порядка 2-го типа,
совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой для планирования экспериментов.
14. Способ по п.11, в котором планирование экспериментов включает выбор из множества последовательностей тех, которые включают действия, обеспечивающие совпадения по меньшей мере со всеми комбинациями действий, отвечающих условию совпадения выбранного порядка и типа.
15. Способ по п.1, в котором планирование экспериментов включает случайный выбор последовательностей из множества последовательностей.
16. Способ по п.1, в котором обуславливают планирование экспериментов.
17. Способ по п.1, в котором прогон группы из множества последовательностей через имитацию модели включает прогон всех последовательностей из множества последовательностей.
18. Способ по п.1, который реализуют по меньшей мере частично посредством компьютера.
19. Способ по п.1, в котором осуществляют последовательный комбинаторный процесс с использованием идентифицированной оптимальной последовательности действий.
20. Способ по п.1, в котором последовательный комбинаторный процесс включает приваривание лопасти к кольцу корпуса заднего подшипника газовой турбины, при этом осуществляемые действия представляют собой проведение сварки последовательно по отдельным траекториям, рабочий параметр, характеризующий конечный результат, представляет собой деформацию кромки лопатки, а оптимальное значение рабочего параметра представляет собой минимальную величину деформации.
21. Способ по п.1, в котором последовательный комбинаторный процесс включает изготовление из заготовки детали посредством машинной обработки, при этом осуществляемые действия представляют собой образующие последовательность стадии обработки резанием, рабочим параметром, характеризующим конечный результат, является форма детали, а оптимальным значением рабочего параметра является требуемая форма детали.
22. Способ по п.1, в котором последовательный комбинаторный процесс включает изготовление из заготовки детали посредством машинной обработки, при этом осуществляемые действия представляют собой образующие последовательность стадии обработки резанием, рабочим параметром, характеризующим конечный результат, является качество детали, а оптимальным значением рабочего параметра является наивысший показатель качества детали.
23. Способ по п.1, в котором последовательный комбинаторный процесс включает изготовление из заготовки детали посредством машинной обработки, при этом осуществляемые действия представляют собой образующие последовательность стадии обработки резанием, рабочим параметром, характеризующим конечный результат, является вибрация детали в процессе обработки вследствие недостаточной структурной жесткости детали, а оптимальным значением рабочего параметра является минимальная величина вибрации.
24. Способ по п.1, в котором последовательный комбинаторный процесс включает термообработку детали, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии нагрева и/или охлаждения, рабочим параметром, характеризующим конечный результат, является форма, жесткость или микроструктура материала детали, а оптимальным значением рабочего параметра является требуемая форма, жесткость или микроструктура материала.
25. Способ по п.1, в котором последовательный комбинаторный процесс включает формование детали, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии формования, рабочим параметром, характеризующим конечный результат, является форма, жесткость или микроструктура материала детали, а оптимальным значением рабочего параметра является требуемая форма, жесткость или микроструктура материала.
26. Способ по п.1, в котором последовательный комбинаторный процесс включает изготовление детали, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии посредством машинной обработки, резки, формования и/или термообработки, рабочим параметром, характеризующим конечный результат, является форма, жесткость или микроструктура материала детали, а оптимальным значением рабочего параметра является требуемая форма, жесткость или микроструктура материала.
27. Способ по п.1, в котором последовательный комбинаторный процесс включает поток материалов и/или деталей на предприятии, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии транспортировки материалов и/или деталей между участками предприятия, рабочим параметром, характеризующим конечный результат, является продолжительность последовательности, а оптимальным значением рабочего параметра является минимальная продолжительность.
28. Способ по п.1, в котором последовательный комбинаторный процесс включает поток материалов и/или деталей на предприятии, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии транспортировки материалов и/или деталей между участками предприятия, рабочим параметром, характеризующим конечный результат, является скорость потока, а оптимальным значением рабочего параметра является максимальная скорость потока.
29. Способ по п.1, в котором последовательный комбинаторный процесс включает перекачку газа или нефти по сети трубопроводов, при этом осуществляемые действия представляют собой образующие последовательность действия на отдельных участках сети трубопроводов по управлению соответствующими элементами трубопроводов, скоростью нагнетания и клапанами, причем рабочим параметром, характеризующим конечный результат, является схема доставки нефти или газа, а оптимальным значением рабочего параметра является требуемая схема доставки нефти или газа.
30. Способ по п.1, в котором последовательный комбинаторный процесс включает смешивание компонентов или ингредиентов, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии добавления в смесь различных компонентов или ингредиентов, рабочим параметром, характеризующим конечный результат, является качество смеси, такое, как устойчивость, чистота или однородность, а оптимальным значением рабочего параметра является требуемое качество.
31. Способ по п.1, в котором последовательный комбинаторный процесс включает численный метод, характеризующий поведение биологических компонентов, при этом осуществляемые действия представляют собой отдельные образующие последовательность стадии взаимодействия между компонентами, причем рабочим параметром, характеризующим конечный результат, является конечный результат последовательности, а оптимальным значением рабочего параметра является известный конечный результат.
32. Способ по п.1, в котором последовательный комбинаторный процесс относится к "задаче о рюкзаке", при этом осуществляемые действия представляют собой образующую последовательность загрузку в "рюкзак" отдельных предметов, рабочим параметром, характеризующим конечный результат, является численное значение предметов в "рюкзаке", а оптимальным значением рабочего параметра является максимальное численное значение.
33. Способ по п.1, в котором последовательный комбинаторный процесс включает объединение транспортных единиц в цепочку, при этом осуществляемые действия представляют собой образующие последовательность действия по объединению отдельных единиц, рабочим параметром, характеризующим конечный результат, является время, необходимое для разъединения цепочки и повторного объединения в цепочку с целью удаления и/или добавления единиц, а оптимальным значением рабочего параметра является минимальное количество времени.
34. Компьютерная система для реализации способа оптимизации последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, содержащая
память для запоминания планирования экспериментов, представляющего собой группу последовательностей, выбранных из множества последовательностей, и запоминания данных, связанных с каждой последовательностью из планирования экспериментов и касающихся значения вклада каждого действия из каждой последовательности в достижение конечного результата, характеризуемого рабочим параметром, и
процессор, запрограммированный для
прогона группы из множества последовательностей через имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений, содержащихся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, извлекают значения вклада совпавшего действия и осуществляют запись значения конечного результата каждой последовательности в памяти, и
идентифицирования оптимальной последовательности путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, представляет собой оптимальную последовательностью.
35. Компьютерная система по п.34, в которой процессор дополнительно запрограммирован для вычисления данных, связанных с каждой последовательностью из планирования экспериментов, путем прогона каждой последовательности из планирования экспериментов через эталонную модель процесса, в которую в качестве исходных данных введена последовательность действий и которая определяет значение конечного результата и значения вкладов в конечный результат каждого действия из введенной последовательности.
36. Компьютерная система по п.35, в которой имитация модели представляет собой упрощенное приближение к эталонной модели.
37. Компьютерная система по п.35, в которой процессор дополнительно запрограммирован для прогона идентифицированной оптимальной последовательности через эталонную модель после идентификации оптимальной последовательности с целью определения значения конечного результата и сравнения зарегистрированного оптимального значения идентифицированной оптимальной последовательности, определенной при помощи имитации модели, с конечным результатом, определенным при помощи эталонной модели с целью проверки точности идентификации оптимальной последовательности.
38. Компьютерная система по п.37, в которой процессор дополнительно запрограммирован для
дополнения планирования экспериментов идентифицированной оптимальной последовательностью при обнаружении различия между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, определенным при помощи имитации модели, и конечным результатом, определенным при помощи эталонной модели, величина которого неприемлема для процесса, так, чтобы идентифицированная оптимальная последовательность и значения вкладов в конечный результат каждого действия, определенные путем прогона идентифицированной оптимальной последовательности через эталонную модель, были доступны для поиска и извлечения при помощи алгоритма имитации модели,
прогона группы из множества последовательностей через имитацию модели с целью получения новых значений конечного результата каждой последовательности и
идентификации новой оптимальной последовательности на основании новых конечных результатов.
39. Компьютерная система по п.38, в которой процессор дополнительно запрограммирован для повторного осуществления стадий по пп.37 и 38 применительно к новой идентифицированной оптимальной последовательности до тех пор, пока различие между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, полученным при помощи имитации модели, и конечным результатом, полученным при помощи эталонной модели, не станет приемлемым для процесса.
40. Компьютерная система по п.34, в которой данные, связанные с каждой последовательностью из планирования экспериментов, содержат значения вкладов в конечный результат каждого действия из каждой последовательности планирования экспериментов, полученные в результате осуществления последовательного комбинаторного процесса с использованием каждой последовательности из планирования экспериментов.
41. Компьютерная система по п.34, в которой указатель приоритетов представляет собой иерархию условий совпадения в порядке убывания уровня совпадения между действием из последовательности, введенной в имитацию модели, и действиями из последовательностей, входящих в планирование экспериментов, с точки зрения положения действия во введенной последовательности и/или действий, предшествующих действию из введенной последовательности.
42. Компьютерная система по п.34, в которой условия совпадения включают:
порядок, определяющий число действий, предшествующих действию в последовательности, введенной в имитацию модели, которые должны совпасть с действиями, предшествующими действию из последовательностей планирования экспериментов, и
тип определения совпадения положения действия в последовательности, введенной в имитацию модели, с положением действия в последовательностях из планирования экспериментов, при этом для совпадения 1-го типа положение действия во введенной последовательности должно совпадать с положением действия в последовательностях из планирования экспериментов, а для совпадения 2-го типа не требуется, чтобы положение действия во введенной последовательности совпадало с положением действия в последовательностях из планирования экспериментов.
43. Компьютерная система по п.42, в которой для последовательности, состоящей из n-го числа действий, указатель приоритетов содержит следующие условия совпадения:
совпадение n-го порядка 1-го типа,
совпадение n-го порядка 2-го типа,
совпадение (n-1)-го порядка 1-го типа,
совпадение (n-1)-го порядка 2-го типа,
...
совпадение 1-го порядка 1-го типа,
совпадение 1-го порядка 2-го типа,
совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой в планировании экспериментов.
44. Компьютерная система по п.42, в которой для последовательности, состоящей из n-го числа действий, указатель приоритетов содержит следующие условия совпадения:
совпадение n-го порядка 1-го типа,
совпадение (n-1)-го порядка 1-го типа,
совпадение (n-2)-го порядка 1-го типа,
...
совпадение 1-го порядка 1-го типа,
совпадение n-го порядка 2-го типа,
совпадение (n-1)-го порядка 2-го типа,
совпадение (n-2)-го порядка 2-го типа,
...
совпадение 1-го порядка 2-го типа,
совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой для планирования экспериментов.
45. Компьютерная система по п.42, в которой планирование экспериментов включает выбор из множества последовательностей тех, которые включают действия, обеспечивающие совпадения по меньшей мере со всеми комбинациями действий, отвечающих условию совпадения выбранного порядка и типа.
46. Компьютерная система по п.34, в которой планирование экспериментов включает случайный выбор последовательностей из множества последовательностей.
47. Компьютерная система по п.34, в которой процессор дополнительно запрограммирован для выбора последовательностей для планирования экспериментов.
48. Компьютерная система по п.34, в которой процессор дополнительно запрограммирован для прогона всех из множества последовательностей через имитацию модели.
49. Компьютерная система по п.34, в которой последовательный комбинаторный процесс включает приваривание лопасти к кольцу корпуса заднего подшипника газовой турбины, при этом осуществляемые действия представляют собой проведение сварки последовательно по отдельным траекториям, рабочий параметр, характеризующий конечный результат, представляет собой деформацию кромки лопатки, а оптимальное значение рабочего параметра представляет собой минимальную величину деформации.
| УСТРОЙСТВО ДЛЯ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ СЛОЖНОЙ СИСТЕМЫ РАБОТ | 1998 |
|
RU2136040C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ СУБОПТИМАЛЬНОГО РАЗМЕЩЕНИЯ И ЕГО ОЦЕНКИ | 2001 |
|
RU2193796C2 |
| VOUTCHKOV IVAN at al, COMBINATORIAL OPTIMIZATION OF WELDING SEQUENCES, 04.08.2003, pages 1-2, XP002313286 SOUTHAMPTON UK www | |||
| archive, org Retrieved from the Internet: URL:http//web | |||
| archive.org/web/20030804223 | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| US 2003037349, 20.02.2003 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
Авторы
Даты
2009-04-20—Публикация
2004-09-10—Подача