ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННЫЕ ЗАЯВКИ
По настоящей заявке испрашивается приоритет по 35 U.S.C. § 119(e) предварительной заявки на патент США № 61/759276, озаглавленной: METHODS, SYSTEMS, AND SOFTWARE FOR IDENTIFYING BIO-MOLECULES WITH INTERACTING COMPONENTS, поданной 31 января 2013, и предварительной заявки на патент США № 61/799377, озаглавленной: METHODS, SYSTEMS, AND SOFTWARE FOR IDENTIFYING BIO-MOLECULES USING MODELS OF MULTIPLICATIVE FORM, поданной 15 марта 2013, которые включены в настоящее описании посредством ссылки во всей их полноте для всех целей.
УРОВЕНЬ ТЕХНИКИ
Настоящее раскрытие относится к областям молекулярной биологии, молекулярной эволюции, биоинформатики и цифровых систем. Более конкретно, раскрытие относится к способам для вычислительного прогнозирования активности биомолекулы и/или руководства направленной эволюцией. Системы, включая цифровые системы, и системное программное обеспечение для выполнения этих способов также предоставляются. Способы по настоящему раскрытию являются целесообразными для оптимизации белков для промышленного и терапевтического применения.
Дизайн белка, как было давно известно, является трудной задачей по причине комбинаторного взрыв возможных молекул, которые составляют доступное для поиска пространство последовательностей. Пространство последовательностей белков является огромным и в нем невозможно выполнить исчерпывающий поиск с применением способов, известных в технике в настоящий момент. Вследствие данной сложности множество приближенных способов применялось для дизайна более хороших белков; главным среди них является способ направленной эволюции. Сегодня, в направленной эволюции белков доминируют форматы высокопроизводительного скрининга и рекомбинации, часто выполняемые итеративно.
Параллельно, различные вычислительные методики были предложены для исследования пространства последовательности-активности. В то время как каждая вычислительная методика имеет преимущества в определенных контекстах, новые способы эффективного поиска в пространстве последовательностей с целью идентификации функциональных белков были бы очень востребованы.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Настоящее раскрытие представляет методы для генерации и применения моделей последовательности-активности, которые используют нелинейные члены, в частности, члены, которые учитывают взаимодействия между двумя или более субъединицами в последовательности. Модели последовательности-активности описывают активности, характеристики, или свойства биологических молекул как функции различных биологических последовательностей. Эти нелинейные члены могут представлять собой члены "перекрестного произведения", которые включают перемножение двух или более переменных, каждая из которых представляет наличие (или отсутствие) субъединиц, участвующих во взаимодействии. В некоторых вариантах осуществления применяются методики для выбора нелинейных членов, которые лучше всего описывают активность последовательности. Следует отметить, что часто имеется намного больше возможных нелинейных членов взаимодействия, чем реальное число взаимодействий между субъединицами. Следовательно, для того, чтобы избежать переобучения, обычно рассматривают только ограниченное количество нелинейных членов, и используемые члены должны отражать взаимодействия, которые заметно воздействуют на активность.
Один из аспектов раскрытия предоставляет способ подготовки модели последовательности-активности, которая может помочь в идентификации биологических молекул с улучшенной требуемой активностью, при этом способ включает в себя: (a) получение данных последовательности и активности для множества биологических молекул; (b) подготовку базовой модели по данным последовательности и активности, при этом базовая модель прогнозирует активность как функцию наличия или отсутствия субъединиц последовательности; (c) подготовку по меньшей мере одной новой модели посредством добавления к базовой модели или изымания из базовой модели по меньшей мере одного нового члена взаимодействия, при этом новый член взаимодействия представляет взаимодействие между двумя или более взаимодействующими субъединицами; (d) определение способности по меньшей мере одной новой модели прогнозировать активность как функцию наличия или отсутствия субъединиц; и (e) определение того, добавлять ли к базовой модели или изымать ли из базовой модели новый член взаимодействия на основании способности по меньшей мере одной новой модели прогнозировать активность в соответствии с определенным (d) и с предубеждением против включения дополнительных членов взаимодействия. Полученная модель может затем применяться в различных приложениях, таких как направленная эволюция библиотек белка, с целью идентификации белков с требуемыми биологическими активностями и свойствами.
В некоторых вариантах осуществления, в которых способ определяет, что новый член взаимодействия должен быть добавлен к базовой модели, с тем чтобы произвести обновленную модель, способ также включает в себя дополнительные этапы для поиска дополнительных членов взаимодействия, которые могут дополнительно улучшить обновленную модель. Конкретно, способ включает в себя: (f) повторение (c) с использованием обновленной модели вместо базовой модели и добавление или изымание члена взаимодействия, отличного от добавленного/вычтенного в (c); и (g) повторение (d) и (e) с использованием обновленной модели вместо базовой модели. В некоторых вариантах осуществления способ также включает в себя (h) повторение (f) и (g) с использованием дополнительно обновленной модели. В различных вариантах осуществления последовательность может представлять собой весь геном, всю хромосому, сегмент хромосомы, совокупность последовательностей генов для взаимодействующих генов, ген, последовательность нуклеиновой кислоты, белок, полисахарид и т.д. В одном или более вариантах осуществления субъединицы последовательностей могут являться хромосомами, сегментами хромосомы, гаплотипами, генами, нуклеотидами, кодонами, мутациями, аминокислотами, углеводами (моно-, ди-, три-, или олигомерными) и т.д.
В одной или более реализациях в соответствии с указанными выше вариантами осуществления, предоставлен способ для идентификации аминокислотных остатков, которые будут модифицированы в библиотеке вариантов белка. В этих вариантах осуществления множество биологических молекул составляет обучающее множество библиотеки вариантов белка. Библиотека вариантов белка может содержать белки из различных источников. В одном из примеров элементы включают естественные белки, такие как закодированные представителями одного семейства генов. В другом примере последовательности включают белки, полученные с применением основанного на рекомбинации механизма создания разнообразия. Например, опосредованная фрагментацией ДНК рекомбинация, опосредованная синтетическими олигонуклеотидами рекомбинация, или их комбинация, могут быть выполнены на нуклеиновых кислотах, кодирующих все или часть из одного или более естественных родительских белков с этой целью. В еще одном примере представителей получают посредством реализации протокола планирования эксперимента (DOE) для идентификации систематически различающихся последовательностей.
В некоторых вариантах осуществления по меньшей мере один из членов взаимодействия представляет собой член перекрестного произведения, содержащий произведение одной переменной, представляющей наличие одного взаимодействующего остатка, и другой переменной, представляющей наличие другого взаимодействующего остатка. Форма модели последовательности-активности может представлять собой сумму по меньшей мере одного члена перекрестного произведения и одного или более линейных членов, при этом каждый из линейных членов представляет влияние переменного остатка в обучающем множестве библиотеки вариантов белка. По меньшей мере один член перекрестного произведения может быть выбран из группы потенциальных членов перекрестного произведения с помощью различных методик, включая пошаговое добавление или изымание членов без замены.
В одном или более вариантах осуществления модель, содержащая члены перекрестного произведения, приспосабливается к определенным данным с применением методик Байесовой регрессии, в которых априорные знания используются для определения апостериорных распределений вероятности для модели.
В одном или более вариантах осуществления создаются две или более новых моделей, каждая из которых содержит по меньшей мере один отличающийся член взаимодействия. В таких вариантах осуществления способ также включает в себя подготовку ансамблевой модели на основании двух или более новых моделей. Ансамблевая модель включает в себя члены взаимодействия из двух или более новых моделей. Ансамблевая модель взвешивает члены взаимодействия согласно способностям двух или более новых моделей прогнозировать интересующую активность.
Модель последовательности-активности может быть произведена из обучающего множества посредством множества различных методик. В определенных вариантах осуществления модель представляет собой регрессионную модель, такую как частичная модель наименьших квадратов, Байесова регрессионная модель или модель регрессии основного компонента. В другом варианте осуществления модель представляет собой нейронную сеть.
Применение модели последовательности-активности для идентификации остатков для фиксации или изменения может предполагать любую из множества различных возможных аналитических методик. В некоторых случаях, "опорная последовательность" используется для определения изменений. Такая последовательность может являться последовательностью, которая, как было спрогнозировано посредством модели, имеет самое высокое значение (или одно из самых высоких значений) требуемой активности. В другом случае опорная последовательность может являться последовательностью элемента исходной библиотеки вариантов белка. Из опорной последовательности способ может выбрать последовательности для осуществления изменений. Дополнительно или альтернативно, модель последовательности-активности упорядочивает положения остатков (или конкретные остатки в определенных положениях) в порядке влияния на требуемую активность.
Одна из целей способа может состоять в создании новой библиотеки вариантов белка. В качестве части этого процесса, способ может идентифицировать последовательности, которые должны использоваться для создания этой новой библиотеки. Такие последовательности содержат изменения в остатках, идентифицированных в (e), (g) или (h) выше, или являются предшественниками, используемыми для того, чтобы впоследствии осуществить такие изменения. Последовательности могут быть изменены посредством выполнения мутагенеза или основанного на рекомбинации механизма создания разнообразия с целью создания новой библиотеки вариантов белка. Это может являться частью процедуры направленной эволюции. Новая библиотека также может быть использована в разработке новой модели последовательности-активности. Новая библиотека вариантов белка анализируется с целью оценки влияния на конкретную активность, такую как стабильность, каталитическая активность, терапевтическая активность, устойчивость к патогену или токсину, токсичность и т.д.
В некоторых вариантах осуществления способ включает в себя выбор одного или более элементов новой библиотеки вариантов белка для продуцирования. Один или более из них может затем синтезироваться и/или экспрессироваться в экспрессионной системе. В конкретном варианте осуществления способ продолжается следующим способом: (i) предоставление экспрессионной системы, в которой выбранный элемент новой библиотеки вариантов белка может быть экспрессирован; и (ii) экспрессия выбранного элемента новой библиотеки вариантов белка.
В некоторых вариантах осуществления, вместо того, чтобы использовать аминокислотные последовательности, способы используют нуклеотидные последовательности для создания моделей и прогнозирования активности. Изменения в группах нуклеотидов, например, кодонах, влияют на активность пептидов, закодированных нуклеотидными последовательностями. В некоторых вариантах осуществления модель может обеспечивать систематическое отклонение для кодонов, которые являются предпочтительно экспрессируемыми (по сравнению с другими кодонами, кодирующими ту же самую аминокислоту) в зависимости от организма-хозяина, используемого для экспрессии пептида.
Другой аспект раскрытия относится к устройству и компьютерным программным продуктов, включая машиночитаемые носители информации, на которых представлены инструкции программы и/или осуществления данных для реализации способов и систем программного обеспечения, описанных выше. Часто инструкции программы предоставляются в форме кода для выполнения определенных операций способа. Данные, если они используются для реализации функций по настоящему раскрытию, могут быть предоставлены в форме структур данных, таблиц базы данных, объектах данных, или других соответствующих конструкций указанной информации. Любой из способов или систем, описанных в настоящем раскрытии, может быть представлен, полностью или частично, в форме таких инструкций программы и/или данные, предоставленных на любых соответствующих машиночитаемых носителях информации.
Эти и другие функции более подробно описаны ниже в подробном описании вместе со следующими фигурами.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фигура 1 поясняет иллюстрирует общий пошаговый способ для подготовки модели последовательности-активности.
Фигура 2 представляет собой блок-схему, изображающую последовательность операций для создания одного или более поколений библиотек вариантов белка, при этом в операциях применяется модель последовательности-активности, такая как одна из полученных на фигуре 1, для управления созданием библиотек вариантов белка. Созданные различные библиотеки могут предоставлять данные последовательности и активности для подготовки одной или более новых моделей последовательности-активности, формируя цикл исследования-моделирования для направленной эволюции.
Фигуры 3A-3H представляют собой графики, на которых производится сравнение прогнозных способностей определенных линейных и нелинейных моделей.
Фигура 4A-4B иллюстрирует блок-схемы процессов, реализующих способы пошагового добавления и изымания для подготовки модели последовательности-активности. Фигура 4A иллюстрирует конкретный пример пошагового способа сложения для подготовки модели; и Фигура 4B иллюстрирует конкретный пример пошагового способа изымания для подготовки модели.
Фигура 5 иллюстрирует блок-схемы процесса, реализующего Байесову регрессию в направленной эволюции вариантов последовательности в соответствии с вариантом осуществления.
Фигура 6 иллюстрирует блок-схемы процесса, реализующего ансамблевую регрессию в направленной эволюции вариантов последовательности в соответствии с вариантом осуществления.
Фигура 7 представляет собой блок-схему, изображающую способ бутстреп p-значения для создания библиотек вариантов белка в соответствии с вариантом осуществления.
Фигура 8 представляет собой схематическое изображение типового цифрового устройства.
ПОДРОБНОЕ ОПИСАНИЕ
I. ОПРЕДЕЛЕНИЯ
Если в настоящем раскрытии не определено другое, все технические и научные термины, используемые в настоящем раскрытии, имеют то же самое значение, которое обычно понимается специалистом в данной области техники. Различные научные словари, которые содержат термины, содержащиеся в настоящем раскрытии, известны и доступны специалистам в данной области техники. Любые способы и материалы, аналогичные или эквивалентные описанным в настоящем раскрытии, применяются при практическом применении вариантов осуществления, раскрытых в настоящем раскрытии.
Термины, определенные ниже, более полно понимаются в отношении спецификации в целом. Определения приведены только с целью описания конкретных вариантов осуществления и способствования пониманию сложных концепций, описанных в данной спецификации. Не предполагается, что они ограничивают полный объем раскрытия. Конкретно, следует понимать, что настоящее раскрытие не ограничено конкретными описанными последовательностями, композициями, алгоритмами, системами, методологией, протоколами, и реагентами, поскольку они могут меняться в зависимости от контекста, в котором они применяются специалистами в данной области техники.
При использовании в данной спецификации и прилагаемой формуле изобретения, формы единственного числа включают в себя ссылки на множественные элементы, если содержание и контекст явно не указывают противоположное. Таким образом, например, ссылка на "устройство" включает в себя комбинацию двух или более таких устройств и т.п.
Если не указано другое, предполагается, что конъюнкция "или" используется в ее корректном смысле в качестве Булева логического оператора, охватывая как выбор характеристик в виде альтернативы (A или B, где выбор A является взаимно исключающим относительно B) и выбор характеристик совместно (A или B, где выбраны и A, и B). В некоторых местах в тексте, термин "и/или" используется для той же самой цели, которая не должна рассматриваться, как подразумевающая, что "или" используется в отношении взаимно исключающих вариантов.
"Биомолекула" или "биологическая молекула" относятся к молекуле, которая обычно находится в биологическом организме. В некоторых вариантах осуществления биологические молекулы включают в себя полимерные биологические макромолекулы, имеющие множество субъединиц (то есть "биополимеры"). Типичные биомолекулы включают в себя, но не ограничиваются указанным, молекулы, которые имеют некоторые общие структурные характеристики с естественными полимерами, такими как РНК (сформированные из нуклеотидных субъединиц), ДНК (сформированные из нуклеотидных субъединиц) и пептиды или полипептиды (сформированные из аминокислотных субъединиц), включая, например, РНК, аналоги РНК, ДНК, аналоги ДНК, полипептиды, аналоги полипептидов, пептидные нуклеиновые кислоты (PNA), комбинации РНК и ДНК (например, химерапласты) и т.п. Не предполагается, что биомолекулы ограничены какой-либо конкретной молекулой, поскольку любая соответствующая биологическая молекула находит применение в настоящем изобретении, включая, но не ограничиваясь, например, липиды, углеводы или другие органические молекулы, которые сделаны из одной или более генетически кодируемых молекул (например, один или более ферментов или ферментных путей) и т.п.
Термины "полинуклеотид" и "нуклеиновая кислота" относятся к дезоксирибонуклеотидам или рибонуклеотидам и их полимерам (например, олигонуклеотиды, полинуклеотиды и т.д.), в одно- или двухцепочечной форме. Эти термины включают в себя, но не ограничиваются указанным, одно-, двух- и трехцепочечную ДНК, геномную ДНК, кДНК, РНК, гибрид ДНК-РНК, полимеры, содержащие пуриновые и пиримидиновые основания и/или другие естественные, химически или биохимически измененные, неестественные или производные нуклеотидные основания. Следующие элементы являются неограничивающими примерами полинуклеотидов: гены, фрагменты генов, фрагменты хромосом, маркер экспрессируемой последовательности (EST), экзоны, интроны, мРНК, тРНК, рРНК, рибозимы, кДНК, рекомбинантные полинуклеотиды, разветвленные полинуклеотиды, плазмиды, векторы, выделенные ДНК любой последовательности, выделенные РНК любой последовательности, зонды для нуклеиновой кислоты и праймеры. В некоторых вариантах осуществления полинуклеотиды включают в себя измененные нуклеотиды, такие как метилированные нуклеотиды и аналоги нуклеотидов, урацил, другие сахарные и связующие группы, такие как фторибоза и тиосоль, и/или ветви нуклеотидов. В некоторых альтернативных вариантах осуществления последовательность нуклеотидов прерывается ненуклеотидными компонентами.
Если конкретно не ограничено, термин охватывает нуклеиновые кислоты, содержащие известные аналоги естественных нуклеотидов, которые имеют аналогичные свойства связывания относительно опорной нуклеиновой кислоты и метаболизируются аналогично естественным нуклеотидам. Если не указано иное, конкретная последовательность нуклеиновой кислоты также неявно охватывает ее консервативно измененные варианты (например, вырожденные замены кодона), и комплементарные последовательности, так же как и последовательность, указанная явно. Конкретно, вырожденные замены кодона могут быть достигнуты посредством создания последовательностей, в которых третье положение одного или более выбранных (или всех) кодонов заменено смешанным основанием и/или остатками дезоксиинозина (Batzer et al. (1991) Nucleic Acid Res. 19:5081; Ohtsuka et al. (1985) J. Biol. Chem. 260:2605-2608; Rossolini et al. (1994) Mol. Cell. Probes 8:91-98). Термин «нуклеиновая кислота» используется взаимозаменяемо, например, с олигонуклеотидом, полинуклеотидом, кДНК и мРНК.
Термины "белок", "полипептид" и "пептид" используются взаимозаменяемо для обозначения полимера из по меньшей мере двух аминокислот, ковалентно связанных посредством амидной связи, независимо от длины или посттрансляционной модификации (например, гликозилирование, фосфорилирование, липидизация, миристиолирование, убиквитинирование и т.д.). В некоторых случаях, полимер имеет по меньшей мере около 30 аминокислотных остатков, и обычно по меньшей мере около 50 аминокислотных остатков. В большинстве случаев, они содержат по меньшей мере около 100 аминокислотных остатков. Термины включают композиции, которые, как обычно полагают, являются фрагментами полноразмерных белков или пептидов. В пределы этого определения включены D-и L-аминокислоты, и смеси D- и L-аминокислот. Полипептиды, описанные в настоящем раскрытии, не ограничены генетически закодированным аминокислотами. Действительно, в дополнение к генетически закодированным аминокислотам, полипептиды, описанные в настоящем раскрытии, могут быть составлены из, полностью или частично, естественных и/или синтетических незакодированных аминокислот. В некоторых вариантах осуществления полипептид представляет собой часть полноразмерного предкового или родительского полипептида, содержащую аминокислотные добавления или удаления (например, гэпы) или замены по сравнению с аминокислотной последовательностью полноразмерного родительского полипептида, при этом все еще сохраняя функциональную активность (например, каталитическую активность).
При использовании в настоящем раскрытии, термин "целлюлаза" относится к категории ферментов, способных к гидролизации целлюлозы (β-1,4-глюкан или β-D-гликозидные связи) до более коротких целлюлозных цепей, олигосахаридов, целлобиозы и/или глюкозы. В некоторых вариантах осуществления термин "целлюлаза" охватывает бета-глюкозидазы, эндоглюканазы, целлобиогидролазы, дегидрогеназы целлобиозы, эндоксиланазы, бета-ксилозидазы, арабинофуранозидазы, альфа-глюкуронидазы, ацетилксилан эстеразу, ферулоил эстеразу, и/или альфа-глюкуронил эстеразу. В некоторых вариантах осуществления термин "целлюлаза" охватывает гидролизующие гемицеллюлозу ферменты, включая, но не ограничивась указанным, эндоксиланазы, бета-ксилозидазы, арабинофуранозидазы, альфа-глюкуронидазы, ацетилксилан эстеразу, ферулоил эстеразу и альфа-глюкуронил эстеразу. "Продуцирующая целлюлазу грибная клетка" представляет собой грибную клетку, которая экспрессирует и секретирует по меньшей мере один гидролизующий целлюлозу фермент. В некоторых вариантах осуществления продуцирующие целлюлазу грибные клетки экспрессируют и секретируют смесь гидролизующих целлюлозу ферментов". "Целлюлолитический", "гидролизующий целлюлозу", "разлагающий целлюлозу" и аналогичные термины относятся к таким ферментам, как эндоглюканазы и целлобиогидролазы (последние также упоминаются как "экзоглюконазы"), которые действуют синергистически для расщепления целлюлозы на растворимые ди- или олигосахариды, такие как целлобиоза, которые затем далее гидролизуются до глюкозы посредством бета-глюкозидазы. В некоторых вариантах осуществления целлюлаза представляет собой рекомбинантную целлюлазу, выбранную из β-глюкозидаз (BGL), целлобиогидролаз типа 1 (CBH1), целлобиогидролаз типа 2 (CBH2), гликозидгидролазы 61s (GH61s), и/или эндоглюканаз (EG). В некоторых вариантах осуществления целлюлаза представляет собой рекомбинантную целлюлазу Myceliophthora, выбранную из β - глюкозидаз (BGL), целлобиогидролаз типа 1 (CBH1), целлобиогидролаз типа 2 (CBH2), гликозидгидролазы 61s (GH61s), и/или эндоглюканаз (EG). В некоторых дополнительных вариантах осуществления целлюлаза представляет собой рекомбинантную целлюлазу, выбранную из EG1b, EG2, EG3, EG4, EG5, EG6, CBH1a, CBH1b, CBH2a, CBH2b, GH61a и/или BGL.
Термин "последовательность" используется в настоящем раскрытии для обозначения порядка и наименования произвольных биологических последовательностей, включая, но не ограничиваясь, весь геном, целую хромосому, сегмент хромосомы, совокупность последовательностей генов для взаимодействующих генов, ген, последовательность нуклеиновой кислоты, белок, полисахарид и т.д. В некоторых контекстах «последовательность» относится к порядку и наименованию аминокислотных остатков в белке (то есть последовательности белка или символьной строке белка) или к порядку и наименованию нуклеотидов в нуклеиновой кислоте (то есть последовательности нуклеиновой кислоты или символьной строке нуклеиновой кислоты). Последовательность может быть представлена символьной строкой. "Последовательность нуклеиновой кислоты" относится к порядку и наименованию нуклеотидов, содержащих нуклеиновую кислоту. "Последовательность белка" относится к порядку и наименованию аминокислот, содержащих белок или пептид.
"Кодон" относится к конкретной последовательности трех последовательных нуклеотидов, которая является частью генетического кода, и которая определяет конкретную аминокислоту в белке или запускает или останавливает синтез белка.
"Интактная последовательность" или "последовательность дикого типа" относится к полинуклеотиду или полипептиду, выделенному из естественного источника. В пределы "интактной последовательности" включены рекомбинантные формы интактного полипептида или полинуклеотида, которые имеют последовательность, идентичную интактной форме.
Термин "ген" используется в широком смысле для обозначения произвольного сегмента ДНК или другой нуклеиновой кислоты, ассоциированного с биологической функцией. Таким образом, гены включают в себя кодирующие последовательности и, необязательно, регуляторные последовательности, требующиеся для их экспрессии. Гены также, необязательно, включают в себя неэкспрессируемые сегменты нуклеиновых кислот, которые, например, формируют последовательности распознавания для других белков. Гены могут быть получены из множества источников, включая клонирование из интересующего источника или синтезирование по известной или спрогнозированной информации о последовательности, и могут включать последовательности, спроектированные как имеющие требуемые параметры.
"Мотив" относится к структуре субъединиц в биологических молекулах или среди биологических молекул. Например, термин "мотив" может быть использован в отношении структуры субъединиц незакодированной биологической молекулы или структуры субъединиц закодированного представления биологической молекулы.
Термин "хромосома" используется в отношении организованной структуры ДНК и ассоциированных связанных с белком клеток, содержащих один элемент спиральной ДНК, содержащий множество генов, регуляторных элементов и других нуклеотидных последовательностей. Термин также используется в отношении ДНК-последовательности структуры.
"Скрининг" относится к процессу, в котором определяют одно или более свойств одной или более биомолекул. Например, типичные процессы скрининга включают процессы, в которых определяют одно или более свойств одного или более элементов одной или более библиотек. "Экспрессионная система" представляет собой систему для экспрессирования белка или пептида, закодированного геном или другой нуклеиновой кислотой.
"Клетка-хозяин" или "рекомбинантная клетка-хозяин" относятся к клетке, которая содержит по меньшей мере одну молекулу рекомбинантной нуклеиновой кислоты. Таким образом, например, в некоторых вариантах осуществления, рекомбинантные клетки-хозяева экспрессируют гены, которые не присутствуют в интактной (то есть не являющейся рекомбинантной) форме клетки.
"Направленная эволюция", "управляемая эволюция" или "искусственная эволюция" относятся к in vitro или in vivo процессам искусственного изменения одной или более последовательностей биомолекул (или строки символов, представляющей последовательность) посредством искусственного отбора, рекомбинации или другой манипуляции. В некоторых вариантах осуществления направленная эволюция происходит в репродуктивной популяции, в которой присутствуют (1) изменчивости индивидов, при этом некоторые изменчивости являются (2) наследуемыми, из которых некоторые изменчивости (3) отличаются по приспособляемости. Репродуктивный успех определяется результатом отбора для предварительно заданного свойства, такого как благоприобретенное свойство. Репродуктивная популяция может представлять собой физическую популяцию или виртуальную популяцию в компьютерной системе.
В определенных вариантах осуществления способы направленной эволюции создают библиотеки вариантов белка посредством рекомбинации генов, кодирующих библиотеку родительских вариантов белка. В способах могут использоваться олигонуклеотиды, содержащие последовательности или подпоследовательности для кодирования белков из библиотеки родительского варианта. Некоторые из олигонуклеотидов родительской библиотеки вариантов могут быть тесно взаимосвязаны, отличаясь только по выбору кодонов для альтернативных аминокислот, выбранных в качестве изменяющихся посредством рекомбинации с другими вариантами. Способ может выполняться для одного или множества циклов, пока требуемые результаты не будут достигнуты. Если применяется множество циклов, то каждый включает в себя этап скрининга для идентификации того, какие варианты, имеющие приемлемые рабочие характеристики, должны использоваться в последующем цикле рекомбинации.
"Перетасовка" и "генная перетасовка" относится к способам направленной эволюции для внесения разнообразия посредством рекомбинации совокупности фрагментов родительских полинуклеотидов через ряд циклов удлинения цепи. В определенных вариантах осуществления, один или более циклов удлинения цепи является самозаполняющимся; то есть выполняются без добавления праймеров, помимо самих фрагментов. Каждый цикл включает в себя отжиг одноцепочечных фрагментов через гибридизацию, последовательное удлинение отожженных фрагментов через удлинение цепи и денатурацию. В течение перетасовки растущая цепь нуклеиновой кислоты обычно подвергается воздействию множества различных партнеров по отжигу в процессе, иногда называемом "обменом матрицами". При использовании в настоящем раскрытии, "обмен матрицами" относится к возможности обменять один домен нуклеиновой кислоты из одной нуклеиновой кислоты на второй домен из второй нуклеиновой кислоты (то есть первые и вторые нуклеиновые кислоты служат матрицами в процедуре перетасовки).
Обмен матрицами часто приводит к образованию химерных последовательностей, которые возникают вследствие внесения перекрытий между фрагментами из различных источников. Перекрытия создаются через рекомбинации посредством обмена матрицами в течение множества циклов отжига, удлинения и денатурации. Таким образом, перетасовка обычно приводит к продуцированию вариантов полинуклеотидных последовательностей. В некоторых вариантах осуществления вариантные последовательности составляют "библиотеку" вариантов. В некоторых вариантах осуществления этих библиотек варианты содержат сегменты последовательности из двух или более из родительских полинуклеотидов.
Когда используется два или более родительских полинуклеотидов, индивидуальные родительские полинуклеотиды являются достаточно гомологичными для того, чтобы фрагменты от различных родителей гибридизировались в условиях отжига, используемых в циклах перетасовки. В некоторых вариантах осуществления перетасовка допускает рекомбинацию родительских полинуклеотидов, имеющих относительно ограниченную гомологию. Часто, индивидуальные родительские полинуклеотиды имеют отличительные и/или уникальные домены и/или другие интересующие характеристики последовательности. При использовании родительских полинуклеотидов, имеющих отличительные характеристики последовательности, перетасовка может произвести имеющие высокое разнообразие варианты полинуклеотидов.
Различные методики перетасовки известны в технике. См. например, патенты США № 6917882, 7776598, 8029988, 7024312 и 7795030, все из которых включены в настоящее раскрытие посредством ссылки во всей их полноте.
"Фрагмент" представляет собой произвольную часть последовательности нуклеотидов или аминокислот. Фрагменты могут быть произведены с применением произвольного подходящего способа, известного в технике, включая, но не ограничиваясь, расщепление полипептидной или полинуклеотидной последовательности. В некоторых вариантах осуществления фрагменты производят посредством применения нуклеаз, которые расщепляют полинуклеотиды. В некоторых дополнительных вариантах осуществления фрагменты создаются с применением методик химического и/или биологического синтеза. В некоторых вариантах осуществления фрагменты включают в себя последовательности по меньшей мере из одной родительской последовательности, созданные с применением частичного удлинения цепи комплементарной(-ых) нуклеиновой(-ых) кислоты (-т).
"Родительский полипептид", "родительский полинуклеотид," "родительская нуклеиновая кислота" и "родитель" обычно используются для обозначения полипептида дикого типа, полинуклеотида дикого типа, или варианта, используемого в качестве исходной точки в процедуре создания разнообразия, такой как направленная эволюция. В некоторых вариантах осуществления сам родитель продуцируется через перетасовку или другую процедуру создания разнообразия. В некоторых вариантах осуществления мутанты, используемые в направленной эволюции, прямо связаны с родительским полипептидом. В некоторых вариантах осуществления родительский полипептид является стабильным, когда подвергается действию экстремальных условий температуры, pH и/или растворителя, и может служить основой для создания вариантов для перетасовки. В некоторых вариантах осуществления родительский полипептид не является устойчивым к экстремальным условиям температуры, pH и/или растворителя, и родительский полипептид изменяется с целью создания устойчивых вариантов.
"Родительская нуклеиновая кислота" кодирует родительский полипептид.
"Мутант", "вариант" и "вариант последовательности" при использовании в настоящем раскрытии относится к биологической последовательности, которая отличается в некотором отношении от стандартной или опорной последовательности. Различие может называться "мутацией". В некоторых вариантах осуществления мутантом является аминокислотная (то есть полипептидная) или полинуклеотидная последовательность, которая была изменена посредством по меньшей мере одной замены, вставки, перехода, удаления и/или другой генетической операции. Для целей настоящего раскрытия мутанты и варианты не ограничиваются конкретным способом, посредством которого они были созданы. В некоторых вариантах осуществления, мутант или вариант последовательности имеет повышенные, пониженные или по существу аналогичные активности или свойства по сравнению с родительской последовательностью. В некоторых вариантах осуществления вариант полипептида содержит один или более аминокислотных остатков, которые были мутированы по сравнению с аминокислотной последовательностью полипептида дикого типа (например, материнского полипептида). В некоторых вариантах осуществления один или более аминокислотных остатков полипептида оставляются неизменными, являются инвариантными или не подвергаются мутации по сравнению с родительским полипептидом в вариантах полипептидах, составляющих множество. В некоторых вариантах осуществления родительский полипептид используется в качестве основы для создания вариантов с улучшенной устойчивостью, активностью или другим свойством.
"Мутагенез" представляет собой процесс внесения мутации в стандартную или опорную последовательность, такую как родительская нуклеиновая кислота или родительский полипептид.
"Библиотека" или "популяция" относятся к совокупности по меньшей мере из двух различных молекул, символьных строк и/или моделей, таких как последовательности нуклеиновых кислот (например, гены, олигонуклеотиды и т.д.) или их продукты экспрессии (например, ферменты или другие белки). Библиотека или популяция обычно содержит ряд различных молекул. Например, библиотека или популяция обычно содержит по меньшей мере около 10 различных молекул. Большие библиотеки обычно содержат по меньшей мере около 100 различных молекул, и, как правило, по меньшей мере около 1000 различных молекул. Для некоторых приложений библиотека содержит по меньшей мере приблизительно 10000 или более различных молекул. В определенных вариантах осуществления библиотека содержит ряд различных или фантастические нуклеиновые кислоты или белки, произведенные направленной процедурой эволюции.
Две нуклеиновых кислоты "рекомбинируются", когда последовательности от каждой из этих двух нуклеиновых кислот комбинируются в нуклеиновой кислоте-потомке. Две последовательности рекомбинируются "прямо", когда обе нуклеиновые кислоты являются субстратами для рекомбинации.
"Отбор" относится к процессу, в котором одна или более биомолекул идентифицируются как имеющие одно или более интересующих свойств. Таким образом, например, можно провести скрининг библиотеки с целью определения одного или более свойств одного или более элементов библиотеки. Если один или более элементов библиотеки идентифицированы как обладающие интересующим свойством, они отбираются. Отбор может включать в себя выделение элемента библиотеки, но это не является необходимым. Кроме того, отбор и скрининг могут выполняться, и часто выполняются, одновременно.
"Зависимая переменная" представляет результат или эффект, или тестируется на предмет определения, является ли она эффектом. "Независимые переменные" представляют входные данные или причины, или тестируется на предмет определения того, являются ли они причиной. Зависимая переменная может исследоваться с целью установления того, меняется ли она и насколько сильно при изменении независимых переменных.
В простой стохастической линейной модели
yi=a+bxi+ei
где член yi является i-м значением зависимой переменной, и xi является i-м значением независимой переменной. Член ei называется как "ошибкой" и содержит изменчивость зависимой переменной, не объясняемую независимой переменной.
Независимая переменная также называется "предикторной переменной", "независимой переменной в уравнении регрессии", "регулируемой переменной", "манипулируемой переменной", "объясняющей переменной" или "входной переменной".
"Ортогональный/ортогональность" относится к независимой переменной, которая не коррелирует с другими независимыми переменными в модели или другой функциональной зависимости.
Термин "модель последовательности-активности" относится к любым математическим моделям, которые описывают зависимость между активностями, характеристиками или свойствами биологических молекул с одной стороны, и различными биологическими последовательностями с другой стороны.
Термин "закодированная символьная строка" относится к представлению биологической молекулы, которое сохраняет информации о последовательности/структурную информацию для этой молекулы. В некоторых вариантах осуществления закодированная символьная строка содержит информацию о мутациях последовательности в библиотеке вариантов. Закодированные символьные строки биомолекул наряду с информацией об активности для биомолекул могут использоваться в качестве обучающего множества для модели последовательности-активности. Не относящиеся к последовательности свойства биомолекул могут быть сохранены или иначе ассоциированы с закодированными символьными строками для биомолекул.
"Опорная последовательность" представляет собой последовательность, относительно которой производится изменение последовательности. В некоторых случаях, "опорная последовательность" используется для задания изменений. Такая последовательность может являться последовательностью, спрогнозированной посредством модели как имеющая самое высокое значение (или одно из самых высоких значений) требуемой активности. В другом случае опорная последовательность может являться последовательностью элемента исходной библиотеки вариантов белка. В определенных вариантах осуществления опорная последовательность представляет собой последовательность родительского белка или нуклеиновой кислоты.
"Обучающее множество" относится к множеству данных или наблюдений последовательности-активности, под которое подогнаны или на основании которого построены одна или более моделей. Например, для модели последовательности-активности белка, обучающее множество содержит последовательности остатков для исходной или улучшенной библиотеки вариантов белка. Как правило, эти данные включают полную или частичную информацию о последовательности остатков вместе со значением активности для каждого белка в библиотеке. В некоторых случаях, множество типов активности (например, данные коэффициента кинетики и данные тепловой стабильности) представлены вместе в обучающем множестве. Активность иногда является выгодным свойством.
Термин "наблюдение" представляет собой информацию о белке или другом биологическом объекте, который может использоваться в обучающем множестве для создания модели, такой как модель последовательности-активности. Термин "наблюдение" может относиться к любым отсеквенированным и проанализированным биологическим молекулам, включая варианты белка. В определенных вариантах осуществления каждое наблюдение представляет собой значение активности и ассоциированную последовательность для варианта в библиотеке. Обычно, чем больше наблюдений используется для создания модели последовательности-активности, тем выше предиктивная сила этой модели последовательности-активности.
При использовании в настоящем раскрытии, термин "выгодное свойство" предназначен для обозначения фенотипической или другой идентифицируемой характеристики, которая приносит некоторую пользу белку или композиции объекта или процесса, ассоциированного с белком. Примеры выгодных свойств включают в себя увеличение или уменьшение, по сравнению с родительским белком, каталитических свойств вариантного белка, связующей способности, стабильности при подвергании воздействию экстремальных значений температуры, pH и т.д., чувствительности к стимулам, ингибированию и т.п. Другие выгодные свойства могут включать в себя измененный профиль в ответ на конкретный стимул. Дальнейшие примеры выгодных свойств сформулированы ниже. Значения выгодных свойств могут использоваться в качестве значений активности в наблюдениях, используемых в обучающем множестве для модели последовательности-активности.
"Секвенирование следующего поколения" или "высокопроизводительное секвенирование" являются методиками секвенирования, которые распараллеливают процесс секвенирования, производя тысячи или миллионы последовательностей единовременно. Примеры соответствующих методов секвенирования следующего поколения включают, но не ограничиваются указанным, одномолекулярное секвенирование в реальном времени (например, Pacific Biosciences, Менло-Парк, Калифорния), ионное полупроводниковое секвенирование (например, Ion Torrent, Южный -Сан-Франциско, Калифорния), пиросеквенирование (например, 454, Брэнфорд, Коннектикут), секвенирование посредством лигирования (например, секвенирование SOLid Life Technologies, Карлсбад, Калифорния), секвенирование посредством синтеза и обратимо присоединяемого ограничителя (например, Illumina, Сан-Диего, Калифорния), технологии формирования изображений нуклеиновой кислоты, такие как просвечивающая электронная микроскопия, и т.п. Дальнейшие описания типовых методик описаны в подробном описании данного раскрытия.
"Предиктивная сила" относится к способности модели правильно прогнозировать значения зависимой переменной для данных при различных условиях. Например, предиктивная сила модели последовательности-активности относится к способности модели прогнозировать активность по информации о последовательности.
"Перекрестная проверка" относится к способу для проверки обобщаемости способности модели прогнозировать интересующее значение (то есть значение зависимой переменной). Способ подготавливает модель с использованием одного множества данных и проверяет ошибки модели, используя другое множество данных. Первое множество данных рассматривается как обучающее множество, и второе множество данных представляет собой контрольное множество.
"Систематическое изменение" относится к различным дескрипторам элемента или множества элементов, изменяемых в различных комбинациях.
"Систематически изменяющиеся данные" относится к данным, произведенным, выведенным или следующим из различных дескрипторов элемента или множества элементов, изменяемых в различных комбинациях. Множество различных дескрипторов могут быть изменены одновременно, но в различных комбинациях. Например, данные активности, собранные для полипептидов, в которых были изменены комбинации аминокислот, являются систематически изменяющимися данными.
Термин "систематически изменяющиеся последовательности" относится к множеству последовательностей, в которых каждый остаток можно видеть во множестве контекстов. В принципе, уровень систематического изменения может быть определен количественно посредством степени, до которой последовательности являются ортогональными друг другу (то есть максимально отличаются по сравнению со средним значением).
Термин "переключение" относится к введению множества типов аминокислотных остатков в конкретную позицию в последовательностях вариантов белка в оптимизированной библиотеке.
Термины "регрессия" и "регрессионный анализ" относятся к методикам, применяемым для выяснения того, какие из независимых переменных связаны с зависимой переменной, и исследования форм таких связей. При ограниченных обстоятельствах регрессионный анализ может применяться для выведения причинно-следственных связей между независимыми и зависимыми переменными. Он представляет собой статистическую методику для оценки связей между переменными. Он включает в себя множество методик для моделирования и анализа нескольких переменных, в которых внимание сосредоточено на связи между зависимой переменной и одной или более независимых переменных. Более конкретно, регрессионный анализ помогает в понимании того, каким образом типичное значение зависимой переменной изменяется, когда изменяется любая из независимых переменных, в то время как другие независимые переменные остаются зафиксированными. Методики регрессии могут применяться для создания моделей последовательности-активности по обучающим множествам, содержащим множество наблюдений, которые могут содержать информацию о последовательность и активности.
Методы дробных наименьших квадратов, или PLS, составляют семейство методов, которые строят линейную регрессионную модель посредством отображения спрогнозированных переменных (например, активностей) и наблюдаемых переменных (например, последовательностей) в новое пространство. PLS также называют проекцией на скрытые структуры. Данные как для X (независимые переменные), так и для Y (зависимые переменные) проецируются в новые пространства. PLS применяется для нахождения фундаментальных соотношений между двумя матрицами (X и Y). Подход, основанный на скрытых переменных, применяется для моделирования структур ковариации в пространствах Y и X. PLS-модель будет пытаться найти многомерное направление в пространстве X, которое объясняет направление максимальной многомерной изменчивости в пространстве Y. Регрессия PLS является особенно подходящей, когда матрица предикторов имеет больше переменных, чем наблюдений, и когда присутствует мультиколлинеарность среди значений X.
"Дескриптор" относится к чему-либо, что служит для описания или идентификации элемента. Например, символы в символьной строке могут быть дескрипторами аминокислот в полипептиде, представленном символьной строкой.
В регрессионной модели зависимая переменная связана с независимыми переменными посредством суммы членов. Каждый член содержит произведение независимой переменной и ассоциированного коэффициента регрессии. В случае чисто линейной регрессионной модели коэффициенты регрессии задаются β в форме следующего выражения:
yi=βixi1+…+βpxip+εi=хiTβ+εi,
где yi представляет собой зависимую переменную, xi представляют собой независимые переменные, εi представляет собой переменную ошибки, и T обозначает транспонирование, то есть скалярное произведение векторов xi и β.
"Регрессия главных компонентов" (PCR) относится к регрессионному анализу, в котором применяется анализ главных компонентов при оценке коэффициентов регрессии. В PCR вместо того, чтобы регрессировать зависимую переменную по независимой переменной напрямую, используются главные компоненты независимых переменных. PCR обычно использует только подмножество главных компонентов в регрессии.
"Анализ главных компонентов" (PCA) относится к математической процедуре, в которой применяется ортогональное преобразование для преобразования множества наблюдений, возможно, скоррелированных переменных, в множество значений линейно нескоррелированных переменных, называемых главными компонентами. Число главных компонентов меньше либо равно числу исходных переменных. Это преобразование определено таким образом, что первый главный компонент имеет наибольшую возможную изменчивость (то есть учитывает столько изменчивости в данных, сколько возможно), и каждый последующий компонент, в свою очередь, имеет самую высокую изменчивость, которая возможна при условии его ортогональности (то есть отсутствии корреляции) с предшествующими компонентами.
"Нейронная сеть" представляет собой модель, содержащую взаимосвязанную группу обрабатывающих элементов, или "нейронов", которые обрабатывают информацию с применением коннекционного подхода к вычислениям. Нейронные сети применяются для моделирования сложных взаимосвязей между входными и выходными данными или для нахождения шаблонов в данных. Большинство нейронных сетей обрабатывает данные нелинейным, распределенным, параллельным образом. В большинстве случаев нейронная сеть является адаптивной системой, которая изменяет свою структуру во время фазы обучения. Функции выполняются совместно и параллельно всеми обрабатывающими элементами, вместо того, чтобы задавать четкое разделение на подзадачи, которые назначаются различным элементам.
Обычно, нейронная сеть включает в себя сеть простых обрабатывающих элементов, которые демонстрируют сложное глобальное поведение, определяемое связями между обрабатывающими элементами и параметрами элементов. Нейронные сети применяются с алгоритмами, спроектированными для изменения силы связей в сети с целью обеспечения требуемого потока сигнала. Мощность изменяется во время обучения или изучения.
"Случайный лес" относится к комбинации предикторов дерева классификации, при которой каждое дерево зависит от значений случайного вектора, отобранного независимо и с одним и тем же распределением для всех деревьев в лесу. Случайный лес представляет собой обучающий ансамбль, состоящий из инкапсуляции неотсеченных обучаемых деревьев решений с рандомизированным выбором характеристик при каждом разделении дерева решений. Случайный лес выращивает большое количество деревьев классификации, каждое из которых выбирает самый популярный класс. Случайный лес затем классифицирует переменную посредством выбора самого популярного выбранного класса из всех деревьев прогнозирования в лесу.
"Распределение априорной вероятности", или "априорное значение" неопределенной величины p является вероятностным распределением, которое выражает неопределенность в отношении p до того, как интересующие данные (например, обучающее множество последовательностей белка) будут приняты во внимание. Неизвестная величина может являться параметром, коэффициентом, переменной, скрытой переменной и т.п. (например, коэффициентом в модели множественной регрессии).
"Распределение апостериорной вероятности" или "апостериорное значение", неопределенной величины p является вероятностным распределением, которое выражает неопределенность в отношении после того, как интересующие данные были приняты во внимание.
Термин "Байесова линейная регрессия" относится к подходу к линейной регрессии, в котором статистический анализ предпринимается в контексте Байесового вывода. Исходные предположения о модели линейной регрессии, включая функцию априорного распределения вероятности параметра модели, объединяется с функцией правдоподобия данных согласно теореме Байеса с целью получения апостериорного распределения вероятности для параметров.
"Переобучение" относится к состоянию, которое возникает, когда статистическая модель описывает случайную ошибку или шум вместо базовой зависимости. Переобучение обычно происходит, когда модель является чрезмерно сложной, например, имеет слишком много параметров относительно числа наблюдений. Модель, которая была переобучена, обычно будет иметь плохие характеристики прогнозирования, поскольку при этом может произойти преувеличение незначительных флуктуаций в данных. В некоторых вариантах осуществления математическая модель применяется для описания зависимости между одной или более независимых переменных (IV) и зависимой переменной (DV). Модель может быть записана как DV = алгебраическое выражение для (IV). "Алгебраическое выражение" может включать в себя переменные, коэффициенты, константы и символы операций, такие как знаки "плюс" и знаки "минус". 4x2+3xy+7y+5 представляет собой алгебраическое выражение с двумя переменными.
В некоторых вариантах осуществления "члены" алгебраического выражения или математической модели представляют собой элементы, разделенные знаками "плюс" или знаками "минус". В этом контексте пример, приведенный выше, имеет четыре члена, 4x2, 3xy, 7y и 5. Члены могут состоять из переменных и коэффициентов (4x2, 3xy и 7y) или констант (5). В алгебраических выражениях переменные могут принимать различные значения для представления изменяющихся условий системы. Например, непрерывная переменная может представлять скорость перемещающегося автомобиля, или дискретная переменная с множеством не являющихся непрерывными значений может представлять типы аминокислот. Переменная может являться переменной с двоичным значением, представляющей наличие или отсутствие элемента, например, наличие или отсутствие остатка определенного типа в конкретном положении. В алгебраическом выражении, приведенном выше, переменными являются x и y.
В некоторых вариантах осуществления "члены" выражения могут представлять собой элементы выражения, ограниченные другими знаками, такими как знак умножения.
"Коэффициент" относится к скалярной величине, умноженной на зависимую переменную или выражение, содержащее зависимую переменную. В приведенном выше примере "коэффициентами" являются цифровые части членов в алгебраическом выражении. В 4x2+3xy+7y+5, коэффициент первого члена равен 4. Коэффициент второго члена равен 3, и коэффициент третьего члена равен 7. Если член состоит только из переменных, его коэффициент равен 1.
"Константы" представляют собой члены в алгебраическом выражении, которые содержат только цифры. Таким образом, они представляют собой члены без переменных. В выражении 4x2+3xy+7y+5 членом-константой является "5".
"Линейный член" представляет собой член со степенью 1, или одну переменную, возведенную в степень 1. В примере выше, член 7y является линейным членом, потому что его степень равна 1 (y1 или просто y). Напротив, член 4x2 является квадратичным членом, потому что x имеет степень 2, и 3xy является квадратичным членом с двумя переменными, потому что как x, так и y имеют степень 1, в результате чего произведение имеет степень 2.
В некоторых местах в тексте "линейный член" и "не относящийся к взаимодействию член" используются взаимозаменяемо в настоящем описании для обозначения члена регрессионной модели, содержащего произведение единственной независимой переменной и ассоциированного коэффициента, при этом единственная IV представляет наличие/отсутствие одного из остатков.
В некоторых вариантах осуществления, "нелинейный член", "член перекрестного произведения" и "член взаимодействия" используются взаимозаменяемо в настоящем раскрытии, когда они относятся к члену модели регрессии, содержащему произведение двух или более независимых переменных и ассоциированного коэффициента. В более общем смысле, "нелинейные члены" используются для указания членов со степенью, большей либо меньшей 1, например, степенной функции или показательной функции независимой переменной. Некоторые примеры нелинейных членов включают в себя xy, x2, x1/3 xy, и ex. Таким образом, в некоторых местах в тексте, "нелинейный член" используется в более широком смысле, чем член, содержащий произведение двух независимых переменных.
В некоторых вариантах осуществления член взаимодействия может быть реализован как член, содержащий нелинейную функцию двух или более IV, например, функцию произведения, степенную функцию или показательную функцию двух или более IV, при этом каждая IV представляет наличие остатка определенного типа в конкретном положении. Например, в y=ax1+bx2+cx1x2, переменные x1 и x2 могут представлять наличие/отсутствие двух конкретных остатков в одном конкретном положении, и член cx1x2 является членом взаимодействия, представляющим эффект взаимодействия двух конкретных остатков. В других вариантах осуществления член взаимодействия может быть реализован как член, содержащий единственную IV, представляющую взаимодействие двух или более остатков. Например, в y=ax1+bx2+cz, переменные x1 и x2 могут представлять наличие/отсутствие двух конкретных остатков в конкретном положении, и член cz является членом взаимодействия, представляющим эффект взаимодействия двух конкретных остатков. В этом последнем примере член взаимодействия cz не является членом перекрестного произведения. Хотя технически cz является линейным членом, он не называется таковым в настоящем раскрытии во избежание путаницы с линейными не относящимися к взаимодействию членами ax1 и bx2. При использовании в раскрытии, термин "линейная модель" относится к моделям, содержащим только линейные члены. Напротив, термин "нелинейная модель" относится к моделям, содержащим как линейные, так и нелинейные члены. В некоторых вариантах осуществления нелинейные модели включают в себя члены взаимодействия, реализованные как члены перекрестного произведения.
В более общем смысле, линейная модель или линейная система удовлетворяют принципу суперпозиции и гомогенности степени 1. Принцип суперпозиции утверждает, что для всех линейных систем суммарный отклик в заданном месте и в заданный момент времени, вызванный двумя или более стимулами, является суммой откликов, которые были бы вызваны каждым стимулом индивидуально. Это также известно как аддитивность. Если вход A выдает отклик X, и вход B выдает отклик Y, то вход (A+B) выдает отклик (X+Y). Гомогенность степени 1 относится к любой модели, выход или зависимая переменная (DV) которой изменяются пропорционально ее входной или независимой переменную. Наоборот, "нелинейная модель" представляет собой модель, которая не удовлетворяет принципу суперпозиции или гомогенности степени 1.
Термин "взаимодействующие субъединицы" относится к двум или более субъединицам последовательности, которые оказывают синергический эффект на моделируемую активность последовательности, при этом синергический эффект является отдельным и отличающимся от индивидуальных эффектов субъединиц на моделируемую активность.
Термин "базовая модель" используется в отношении модели последовательности-активности, предоставленной в начале процесса улучшения модели.
Термин "обновленная модель" используется в отношении модели последовательности-активности, которая выведена напрямую или косвенно из базовой модели, и которая имеет улучшенную предиктивную силу по сравнению с базовой моделью и/или другой моделью, из которой она выведена.
"Функция правдоподобия" или "правдоподобие" модели представляет собой функцию параметров статистической модели. Вероятность множества значений параметров при наличии некоторых наблюдаемых исходов равняется вероятности этих наблюдаемых исходов при этих заданных значениях параметров, то есть, L(θ|x)=Р(х|θ).
"Моделирование методом Монте-Карло" представляет собой моделирование, которое основано на использовании большого количества случайных выборок для получения численных результатов, которые моделируют реальное явление. Например, взятие большого количества псевдослучайных равномерных переменных из интервала (0,1] и обозначение значений, меньших либо равных 0,50 как «орлов» и больших 0,50 как «решек» является моделированием методом Монте-Карло поведения многократно бросаемой монеты.
"Алгоритм Метрополис" или "Алгоритм Метрополиса-Хастингса" представляет собой метод Монте-Карло с цепями Маркова (MCMC) для получения последовательности случайных выборок из вероятностного распределения, для которого непосредственное получение выборок является трудным. Эта выборочная последовательность может применяться для аппроксимации распределения (то есть генерации гистограммы), или вычисления интеграла (такого как математическое ожидание). Метрополис-Хастингс и другие алгоритмы MCMC обычно применяются для осуществления выборок из многомерных распределений, особенно в случае большого числа измерений. Цель алгоритма Метрополис-Хастингс состоит в том, чтобы асимптотически генерировать состояния x согласно требуемому распределению P (x) и применении стохастического процесса для выполнения этого. Идея алгоритма состоит в том, чтобы создать такие условия для стохастического процесса, чтобы он асимптотически сходился к единственному распределению P(x).
"Цепь Маркова" представляет собой последовательность случайных величин X1, X2, X3 … с марковским свойством. Другими словами, если задано текущее состояние, будущие и прошлые состояния являются независимыми. Формально,
Pr(Xn+1=x|X1=x1, X2=x2, … Xn=xn)=Pr(Xn+1=x|Xn=xn)
Возможные значения Xi формируют счетное множество S, называемое пространством состояний цепи. Система "цепи Маркова" представляет собой математическую систему, которая осуществляет переходы из одного состояния в другое между конечным или счетным числом возможных состояний. Это является случайным процессом, обычно характеризуемым как «не имеющим памяти»: следующее состояние зависит только от текущего состояния, а не от последовательности событий, которые предшествовали ему.
"Информационный критерий Акаике" (AIC) является мерой относительной степени согласия статистической модели, и он часто используется в качестве критерия для выбора модели из конечного множества моделей. AIC основан в понятии информационной энтропии, фактически предлагая относительную меру информации, которая теряется, когда данная модель применяется для описания действительности. Можно сказать, что он описывает компромисс между отклонением и дисперсией при создании модели, или, грубо говоря, между точностью и сложностью модели. AIC может быть вычислен как: AIC=-2logeL+2k, где L представляет собой максимальное правдоподобие функции, и k является числом свободных параметров модели, которая должна быть оценена.
"Байесов информационный критерий" представляет собой критерий для выбора модели из конечного множества моделей, и тесно связан с AIC. BIC может быть вычислен как: BIC=-2logeL+kloge(n), где n является количеством наблюдений данных. При увеличении числа наблюдений BIC часто штрафует дополнительное количество свободных параметров в большей степени, чем AIC.
"Генетический алгоритм" представляет собой процесс, который имитирует процесс эволюции. Генетические алгоритмы (GA) применяются во многих областях для решения задач, которые не являются полностью охарактеризованными или являются слишком сложными для того, чтобы обеспечить возможность полной характеризации, но для которых доступна некоторая аналитическая оценка. Таким образом, GA применяются для решения задач, которые могут быть оценены посредством некоторой количественно оцениваемой меры для относительной ценности решения (или, по меньшей мере, относительной ценности одного потенциального решения по сравнению с другим). В контексте настоящего раскрытия генетический алгоритм представляет собой процесс для отбора или манипулирования символьными строками в компьютере, при этом как правило символьная строка соответствует одной или более биологическим молекулам (например, нуклеиновым кислотам, белкам и т.п.).
Термин "генетическая операция" (или "GO") относится к биологическим и/или вычислительным генетическим операциям, в которых все изменения в любой популяции любого типа символьных строк (и, таким образом, в любых физических свойствах физических объектов, закодированных такими рядами), могут быть описаны как результат случайного и/или предварительно определенного применения конечного множества логических алгебраических функций. Примеры GO включают в себя, но не ограничиваются, размножение, перекрестное соединение, рекомбинацию, мутацию, лигирование, фрагментацию и т.д.
"Ансамблевая модель" представляет собой модель, члены которой включают в себя все члены группы моделей, при этом коэффициенты ансамблевой модели для членов основаны на взвешенных коэффициентах соответствующих членов для индивидуальных моделей группы. Взвешивание коэффициентов основано на предиктивной силе и/или приспособленности индивидуальных моделей.
II. СОЗДАНИЕ УЛУЧШЕННЫХ БИБЛИОТЕК ВАРИАНТОВ БЕЛКА
В подходе направленной эволюции к исследованию последовательностей белка модели последовательности-активности применяются для направления создания вариантов белка. Один из аспектов раскрытия предоставляет различные способы для подготовки моделей последовательности-активности, которые основаны на библиотеках белка и могут применяться для поиска новых и улучшенных библиотек белка. В данном разделе сначала представлен краткий обзор процесса для поиска новых и улучшенных белков, и затем представлена более подробная информация о проблемах, связанных с выбором стартовой библиотеки, созданием модели последовательности-активности и применением модели для направления исследования новых белков.
Настоящее раскрытие предоставляет иллюстративные примеры, включающие последовательности аминокислотных остатков и активности белка, но подразумевается, что подход, описанный в настоящем раскрытии, может также быть реализован для других биологических последовательностей и активностей. Например, в различных вариантах осуществления, последовательность может являться целым геномом, целой хромосомой, сегментом хромосомы, совокупностью последовательностей генов для взаимодействующих генов, геном, последовательностью нуклеиновой кислоты, белком, полисахаридом и т.д. В одном или более вариантах осуществления субъединицы последовательностей могут являться хромосомами, сегментами хромосомы, гаплотипами, генами, нуклеотидами, кодонами, мутациями, аминокислотами, моно-, ди-, три- или олигомерными углеводами и т.д.
Как правило, в начале конкретного цикла направленной эволюции последовательностей получают обучающее множество отсеквенированных и протестированных вариантов белка. Данный цикл направленной эволюции продуцирует множество различных белков, которые отличаются одной или более мутациями от родительского пептида или пептидов, используемых в начале цикла направленной эволюции. Варианты пептидов, продуцированные в течение цикла направленной эволюции, проверяются на активность. Пептиды, обладающие требуемой активностью и/или улучшенной активностью по сравнению с родительским(-и) пептидом(-ами), отбираются для использования по меньшей мере в одном последующем цикле направленной эволюции.
Отсеквенированные и протестированные варианты белка могут также использоваться для получения последовательности-активности. Как правило, они используются в модели последовательности-активности, если они действительно отсеквенированы. Каждый из отсеквенированных и протестированных вариантов белка называется "наблюдением". Обычно, чем больше наблюдений используется для создания модели последовательности-активности, тем лучше предиктивная сила этой модели последовательности-активности.
До появления технологии массового параллельного секвенирования следующего поколения было трудно экономно отсеквенировать более чем от 10 до 30 вариантов пептидов, продуцированных в каком-либо цикле направленной эволюции. Теперь с применением секвенирования следующего поколения, намного больше вариантов белков, продуцированных в цикле направленной эволюции, могут быть отсеквенированы. В результате намного больший пул данных обучающего множества может использоваться для получения моделей последовательности-активности. Модели последовательности-активности могут теперь быть созданы с использованием обучающего множества, которое включает в себя не только пептиды, имеющие лучшие показатели в цикле, но также и некоторые пептиды, которые не являются представляющими интерес для дальнейших циклов направленной эволюции, но информация о последовательности и активности которых может быть применена для продуцирования более гибкой модели последовательности-активности.
В некоторых вариантах осуществления обычно требуется получить модели последовательности-активности, обладающие хорошей способностью прогнозировать активность произвольной последовательности. Предиктивная сила может быть охарактеризована посредством точности прогнозирования, а также стабильности, с которой модель точно прогнозирует активность. Кроме того, модель может быть охарактеризована ее способностью точно прогнозировать активность в широких пределах пространства последовательностей. Например, предиктивная сила может быть охарактеризована с точки зрения остаточных членов между расчетными и фактическими активностями для заданного тестового и/или проверочного множества пептидов. Модель с более высокой обобщенной предиктивной силой имеет тенденцию выдавать меньшие и более согласованные остаточные члены для различных множеств проверочных данных. Модель, которая является переобученной для тестового множества данных, имеет тенденцию к выдаче больших и менее согласованных остаточных членов для проверочных данных, как показано в приведенном ниже примере. Один из аспектов раскрытия предоставляет способ для эффективного поиска модели с высокой предиктивной силой для различных множеств данных.
A. КРАТКИЙ ОБЗОР ПРОЦЕССА ПОИСКА УЛУЧШЕННЫХ ВАРИАНТОВ БЕЛКА
Модели последовательности-активности, описанные в настоящем раскрытии, могут применяться для способствования идентификации одного или более родительских "генов" в исходной библиотеке вариантов, которая будет подвергаться направленной эволюции. После того, как был выполнен цикл эволюции, идентифицируется новая библиотека вариантов, предоставляющая новое множество наблюдений, которые могут тогда быть возвращены как данные для подготовки новой или улучшенной модели последовательности-активности. Этот процесс чередования между подготовкой модели последовательности-активности, основанной на новых наблюдениях, и проведением направленной эволюции на основании модели последовательности-активности, может формировать итерационный цикл из моделирования-исследования, который может повторяться до тех пор, пока не будут получены требуемые белки и библиотеки.
Из-за контура обратной связи между моделями последовательности-активности и библиотеками вариантов, лучшие модели и лучшие библиотеки вариантов зависят друг от друга в исследовании белков с улучшенными активностями. Поэтому, «узкие места» и улучшения в доменах моделирования и/или секвенирования могут воздействовать на оба домена. В некоторых вариантах осуществления изобретения улучшение эффективности моделирования вследствие улучшенных методик моделирования обеспечивает лучшие модели для выполнения исследования последовательности. В некоторых вариантах осуществления технологии секвенирования следующего поколения применяются для улучшения скорости секвенирования in vitro, а также для предоставления данных перекрестной проверки для улучшения вычислительных моделей in silico.
В некоторых вариантах осуществления изобретения полезные модели последовательности-активности требуют робастных методик математического моделирования и большого количества "наблюдений". Эти наблюдения представляют собой данные, предоставленные в обучающем множестве для модели. Конкретно, каждое наблюдение представляет собой значение активности и ассоциированную с ним последовательность для варианта в библиотеке. Исторически, секвенирование являлось лимитирующим этапом при разработке больших обучающих множеств и, следовательно, более робастных моделей последовательности-активности. В обычно используемых в настоящий момент способах создаются библиотеки вариантов, имеющие, возможно, сотни вариантов. Однако, только небольшая часть этих вариантов реально секвенируется. В типичном цикле направленной эволюции реально секвенируется только от около 10 до 30 вариантов с самой высокой активностью. В идеальном случае была бы отсеквенирована намного большая доля вариантов в библиотеке, включая некоторые варианты с относительно низкими активностями. Средства секвенирования следующего поколения имеют значительно улучшенную скорость секвенирования, позволяя включать варианты с низкой активностью и с высокой активностью в обучающее множество. В некоторых вариантах осуществления включение вариантов, имеющих диапазон уровней активности, приводит к получению моделей, которые лучше функционируют и/или являются лучшими в прогнозировании активности в более широком диапазоне пространства активностей и последовательностей.
Некоторые регрессионные модели последовательности-активности, указанные в настоящем раскрытии, включают индивидуальные остатки в качестве независимых переменных с целью прогнозирования любой интересующей активностью. Линейные регрессионные модели последовательности-активности не включают в себя члены для учета взаимодействия между двумя или более остаточными членами. Если взаимодействие между двумя остаточными членами оказывает синергический эффект на активность, линейная модель может предоставить искусственно увеличенные значения коэффициентов, ассоциированных с двумя взаимодействующими остатками. В результате работающий с моделью может ошибочно заключить, что, в результате простого выполнения замены остатка в соответствии с предложенным относительно высоким значением коэффициента, активность полученного пептида была бы более высокой, чем ожидается. Это происходит потому, что при использовании линейной модели исследователь не понимает, что увеличенная активность, ассоциированная с заменой остатка, является прежде всего результатом взаимодействия этой замены с другой заменой. Если бы исследователь понял значимость этого взаимодействия, то он или она мог(-ла) бы выполнить обе замены одновременно и достигнуть увеличения активности, предполагаемого линейной моделью.
Если два остатка взаимодействуют для подавления активности нелинейным образом, то линейная модель приписывает более низкие значения коэффициентам, ассоциированным с этими остатками, чем было бы подходящим, если бы остатки рассматривались просто в изоляции друг от друга. Другими словами, выполнение одной, но не другой, замены для взаимодействующих остатков приведет к большему влиянию на активность, чем предполагается на основании линейной модели.
Поскольку линейная модель может быть неадекватной, когда взаимодействия между остатками оказывают сильное влияние на активность, нелинейные модели с нелинейными членами взаимодействия, учитывающими взаимодействия среди остатков, часто являются необходимыми для точных прогнозов активности. Однако, модели, которые используют нелинейные члены, создают вычислительные и эмпирические проблемы. Наиболее значимым является то, что существует очень много потенциальных членов взаимодействия, которые необходимо учесть при разработке/применении модели, что требует значительного объема вычислений. Намного большим ограничением является потенциальное число наблюдений, необходимых для получения модели со значительным количеством членов взаимодействия остаток-остаток. Дополнительно, для методики создания модели может иметься тенденция к переобучению по данным при наличии заданного числа доступных наблюдений. Для решения этой проблемы тщательный выбор и ограничение членов взаимодействия, представленных в модели последовательности-активности, является важным соображением при разработке многих моделей.
На фигуре 1 представлена блок-схема, показывающая одну из реализаций процесса подготовки модели последовательности-активности. В соответствии с изображенным, процесс 100 начинается в блоке 103, чтобы предоставить данные последовательности и активности для различных генов ("наблюдения"). Данные последовательности могут быть взяты, например, из обучающего множества, содержащего последовательности остатков для начальной или улучшенной библиотеки вариантов белка. Как правило, эти данные включают в себя полную или частичную информацию о последовательности остатков вместе со значением активности для каждого белка в библиотеке. В некоторых случаях, множество типов активностей (например, данные константы скорости реакции и данные тепловой стабильности) представлены вместе в обучающем множестве. Также могут рассматриваться другие источники данных, в соответствии с определяемыми требуемыми результатами. Некоторые соответствующие источники данных включают, но не ограничиваются указанным, литературные ссылки, которые описывают информацию о конкретных пептидах, имеющих отношение к создаваемой модели последовательности-активности. Источники дополнительной информации включают, но не ограничены указанным, более ранние или другие циклы направленной эволюции в том же самом проекте. Фактически, предполагается, что информация, полученная из предыдущих циклов направленной эволюции (с применением любого подходящего способа, включая указанные в настоящем раскрытии, но не ограничиваясь ими), будет находить применение в разработке создаваемых позднее библиотек, вариантов и т.д.
Во многих вариантах осуществления индивидуальные элементы библиотеки вариантов белка представляют широкий диапазон последовательностей и активностей. Это способствует созданию модели последовательности-активности, которая применима в широком диапазоне пространства последовательностей. Методики для создания таких разнообразных библиотек включают в себя, но не ограничиваются указанным, систематическое изменение последовательностей белка и методик направленной эволюции в соответствии с описанным в настоящем раскрытии. Однако, в некоторых альтернативных вариантах осуществления требуется создать модели по последовательностям генов в конкретном семействе генов (например, конкретная киназа, найденная во множестве видов или организмов). Поскольку многие остатки будут идентичны для всех членов семейства, модель описывает только те остатки, которые изменяются. Таким образом, в некоторых вариантах осуществления, статистические модели, основанные на таких относительно небольших обучающих множествах, по сравнению с множеством всех возможных вариантов, справедливы в локальном смысле. А именно, модели справедливы только для заданных наблюдений заданных вариантов. В некоторых вариантах осуществления цель не состоит в том, чтобы найти глобальную функцию пригодности, поскольку известно, что в некоторых моделях, это лежит за пределами емкости и/или необходимости рассматриваемой(-ых) системы(-м) моделей.
Данные для активности могут быть получены с применением любых соответствующих средств, известных в технике, включая, но не ограничиваясь указанным, анализы и/или скрининги, спроектированные соответствующим образом для измерения величины интересующей активности/активностей. Такие методики хорошо известны и не являются существенными для настоящего изобретения. Правила для проектирования соответствующих анализов или скринингов широко поняты и известны в технике. Способы для получения последовательностей белка также являются известными и не являются существенными для настоящего изобретения. Как указано выше, могут применяться технологии секвенирования следующего поколения. Активность, используемая в вариантах осуществления, описанных в настоящем раскрытии, может представлять собой стабильность белка (например, тепловая стабильность). Однако во многих важных вариантах осуществления рассматриваются другие активности, такие как каталитическая активность, устойчивость к патогенам и/или токсинам, терапевтическая активность, токсичность и т.п. Фактически, не предполагается, что настоящее изобретение ограничено какими-либо конкретными способами анализа/скрининга и/или способом(-ами) секвенирования, поскольку любой соответствующий способ, известный в технике, может быть применен в настоящем изобретении.
После того, как данные обучающего множества были сгенерированы или получены, процесс использует их для создания модели базовой последовательности-активности, которая прогнозирует активность как функцию информации о последовательности. Смотри блок 105. Данная модель представляет собой выражение, алгоритм или другой инструмент, который прогнозирует относительную активность конкретного белка при предоставлении информации о последовательности для этого белка. Другими словами, информация о последовательности белка является входными данными, и прогноз активности является выходными данными. В некоторых вариантах осуществления базовая модель не содержит члены взаимодействия. В таких случаях базовая модель может быть описана как "линейная модель". В других вариантах осуществления базовая модель содержит все доступные члены взаимодействия, и в этих случаях базовая модель может быть описана как нелинейная модель или модель взаимодействия.
Для многих вариантов осуществления базовая модель может ранжировать вклад различных остатков в активность. Методы создания таких моделей, все из которых относятся к области обучения машин (например, частичная регрессия наименьших квадратов (PLS), регрессия главных компонентов (PCR) и множественная линейная регрессия (MLR), Байесова линейная регрессия), обсуждаются ниже, наряду с форматом независимых переменных (информация о последовательности), форматом зависимой(-ых) переменной(-ых) (активности) и формой самой модели (например, линейное выражение первого порядка).
После того, как базовая модель последовательности-активности была создана, процесс итеративно добавляет к базовой модели или изымает из базовой модели члены взаимодействия из пула доступных членов взаимодействия и оценивает полученные в результате новые модели в отношении улучшения базовой модели с целью получения конечной модели. Смотри блок 107. Когда базовая модель включает в себя все доступные члены взаимодействия, процесс изымает такие члены пошаговым образом. Когда базовая модель не включает в себя члены взаимодействия, процесс добавляет такие члены пошаговым образом.
При оценке новой модели способы по настоящему раскрытию учитывают не только вариации, которые учитывает модель для рассматриваемого множества данных, но также и способность модели прогнозировать новые данные. В некоторых вариантах осуществления в таком подходе к выбору модели штрафуются модели, имеющие больше коэффициентов/параметров, чем эквивалентные модели, имеющие меньше коэффициентов/параметров, во избежание переобучения модели на заданном множестве данных. Примеры методов выбора включают в себя, но не ограничиваются указанным, информационный критерий Акаике (AIC) и Байесов информационный Критерий (BIC), и их вариации.
В ряду вложенных моделей, как в регрессионных моделях с поступательно увеличивающимся количеством членов взаимодействия (и ассоциированных коэффициентов) относительно базовой модели, более сложные модели обеспечивают одинаково хорошую или лучшую согласованность с данными, чем более простые, даже если дополнительные коэффициенты являются случайными, потому что более сложная модель обладает дополнительными степенями свободы. В определенных вариантах осуществления настоящего раскрытия применяются способы выбора модели, которые штрафуют более сложные модели до такой степени, чтобы улучшение в согласованности модели превышало отклонение за счет случайных параметров.
Типовые алгоритмы для создания моделей последовательности-активности согласно операциям в блоках 105 и 107 представлены ниже. Такие методики включают в себя, но не ограничиваются указанным, пошаговые методики, которые вводят предубеждение против включения дополнительных членов взаимодействия в модели. Однако не предполагается, что настоящее раскрытие ограничено этими конкретными примерами.
В одном из аспектов настоящее раскрытие предоставляет способы подготовки модели последовательности-активности, которая может способствовать идентификации биологических молекул, влияющих на требуемую активность. В некоторых вариантах осуществления способ включает в себя: (a) получение данных последовательности и активности для множества биологических молекул; (b) подготовку базовой модели по данным последовательности и активности, при этом базовая модель прогнозирует активность как функцию наличия или отсутствия субъединиц последовательности; (c) подготовку по меньшей мере одной новой модели посредством добавления к базовой модели или изымания из базовой модели по меньшей мере одного нового члена взаимодействия, при этом новый член взаимодействия представляет взаимодействие между двумя или более взаимодействующими субъединицами; (d) определение способности по меньшей мере одной новой модели прогнозировать активность как функцию наличия или отсутствия субъединиц; и (e) определение того, добавлять ли к базовой модели или изымать ли из базовой модели новый член взаимодействия на основании способности по меньшей мере одной новой модели прогнозировать активность в соответствии с определенным (d) и с предубеждением против включения дополнительных членов взаимодействия. Полученная модель может затем применяться в различных приложениях, таких как направленная эволюция библиотек белка, с целью идентификации белков с требуемыми биологическими активностями и свойствами.
В некоторых вариантах осуществления, в которых способ определяет, что новый член взаимодействия должен быть добавлен к базовой модели с целью получения обновленной модели, способ также включает в себя: (f) повторение (c) с использованием обновленной модели вместо базовой модели и добавление или изымание члена взаимодействия, отличного от добавленного/вычтенного в (c); и (g) повторение (d) и (e) с использованием обновленной модели вместо базовой модели. В некоторых вариантах осуществления способ также включает в себя (h) повторение (f) и (g) с использованием дополнительно обновленной модели.
После того, как были отобраны наблюдения для обучающего множества, и был выбран математический метод для получения модели последовательности-активности, создается базовая модель. Базовая модель обычно создается без принятия во внимание ее прогнозной способности. Ее получают просто в соответствии с определенной процедурой для получения базовой модели по доступным наблюдениям (то есть множеству наблюдений), как описано в настоящем раскрытии. Как указано выше, модели последовательности могут описать различные последовательности, при этом в некоторых вариантах осуществления модели описывают белки. В последнем случае базовая модель представляет собой просто линейную модель с единственным членом для каждой из мутаций, присутствующих в совокупности пептидов, использованных для создания обучающего множества. В этих вариантах осуществления базовая модель не содержит членов, представляющих взаимодействия между остатками в пептидах. В некоторых вариантах осуществления базовая модель не содержит отдельный член для каждой мутации, присутствующей во множестве наблюдений.
В альтернативных подходах базовая модель включает в себя не только члены, описывающие каждую из мутаций по отдельности, но дополнительно включает в себя члены для всех потенциально взаимодействующих остатков. В крайнем случае, каждое мыслимое взаимодействие между отмеченными мутациями используется в базовой модели. При этом включается член для каждого парного взаимодействия между мутациями, а также члены для всех возможных взаимодействий трех остатков, а также для всех возможных взаимодействий четырех остатков и т.д. Некоторые варианты осуществления включают в себя только парные взаимодействия или парные взаимодействия и трехсторонние взаимодействия. Трехстороннее взаимодействие представляет собой оказывающее влияние на активность взаимодействие между тремя различными субъединицами.
В одном или более вариантах осуществления, при использовании простой линейной модели в качестве базовой модели, последовательные попытки улучшения модели включают добавление новых членов, представляющие различные взаимодействия. В альтернативных вариантах осуществления, в которых базовая модель включает в себя все линейные и нелинейные члены, последовательные попытки улучшения модели включают выборочное удаление некоторых из нелинейных членов взаимодействия.
В одном или более вариантах осуществления изобретения процесс улучшения базовой модели включает в себя итеративное добавление или изымание членов взаимодействия из базовой модели при определении, достаточно ли полученная в результате модель улучшает качество модели. На каждой итерации предиктивная сила текущей модели определяется и сравнивается с другой моделью, например, базовой моделью или обновленной моделью.
В вариантах осуществления, в которых мера предиктивной силы уже принимает во внимание способность модели быть обобщенной на другие множества данных, только одна эта мера может определить, должна ли модель-кандидат быть выбрана. Например, мера, такая как AIC или BIC, принимает во внимание как вероятность модели (или остаточную ошибку), так и число параметров. "Функция правдоподобия" или "правдоподобие" модели является функцией параметров статистической модели. Правдоподобие множества значений параметров при условии наличия некоторых наблюдаемых исходов равняется вероятности этих наблюдаемых исходов при заданных значениях параметров, то есть L(θ|x)=Ρ(x|θ). Типовое вычисление правдоподобия модели описано в приведенном ниже разделе. Меры, такие как AIC и BIC, обладают предубеждением против модели, обладающей большим числом параметров, если модель, обладающая большим числом параметров, захватывает ту же самую величину разброса данных, что и модель, обладающая меньшим числом параметров. Если мера предиктивной силы принимает во внимание только остаточную ошибку, величина улучшения остаточной ошибки должна быть рассмотрена для определения того, включать ли или нет изменение, ассоциированное с текущей итерацией, в текущую наилучшую обновленную модель. Это может быть выполнено посредством сравнения величины улучшения с порогом. Если величина меньше, чем порог, рассматриваемое изменение на текущей итерации не принимается. Если, альтернативно, величина улучшения превышает порог, то рассматриваемое изменение включается в обновленную модель, и обновленная модель служит в качестве новой наилучшей модели, переходящей в оставшиеся итерации.
В определенных вариантах осуществления на каждой итерации рассматривается добавление или изымание единственного члена взаимодействия для текущей рассматриваемой наилучшей модели. В случае аддитивной модели, то есть в случае, когда базовая модель содержит только линейные члены, может рассматриваться пул всех доступных членов взаимодействия. Каждый из этих членов взаимодействия рассматривают последовательно, пока процесс не будет завершен и не будет получена итоговая наилучшая модель.
В некоторых случаях, после определения того, что процесс эффективно сошелся и дальнейшее улучшение маловероятно, процесс создания модели завершается до того, как будут рассмотрены все имеющиеся в пуле члены взаимодействия.
Фигура 2 иллюстрирует, каким образом модель может итеративно использоваться для направления создания новых библиотек вариантов белка с целью исследования пространства последовательностей и активности белка и активности в процессе (см. 200). После того, как была создана итоговая модель, итоговая модель применяется для идентификации множества положений остатков (например, положение 35) или конкретных значений остатков (например, глутамин в положении 35), которые, как было спрогнозировано, влияют на активность. Смотри блок 207. В дополнение к определению таких положений, модель может применяться для «ранжирования» положений остатка или значений остатков на основании их вкладов в требуемую активность (активности?). Например, модель может прогнозировать, что глутамин в положении 35 имеет наиболее выраженное положительное влияние на активность; фенилаланин в положении 208 имеет второе наиболее выраженное положительное влияние на активность; и так далее. В одном конкретном подходе, описанном ниже, коэффициенты регрессии PLS или PCR используются для ранжирования значимости конкретных остатков. В другом конкретном подходе матрица нагрузки PLS используется для ранжирования значимости конкретных положений остатков.
После того, как процесс идентифицировал остатки, которые влияют на активность, некоторые из них выбираются для изменения, как обозначено в блоке 209 (фигура 2). Это делается с целью исследования пространства последовательностей. Остатки выбираются с применением любого из множества различных протоколов выбора, некоторые из которых описаны ниже. В одном иллюстративном примере конкретные остатки, спрогнозированные, как оказывающие наибольшее влияние на активность, сохраняются (то есть не изменяются). Определенное число других остатков, спрогнозированных, как оказывающих меньшее влияние, однако, выбирается для изменения. В другом иллюстративном примере положения остатка, которые, как было обнаружено, оказывают самое большое влияние на активность, выбираются для изменения, но только если было обнаружено, что они изменяются в высокопроизводительных элементах обучающего множества. Например, если модель прогнозирует, что положение остатка 197 оказывает самое большое влияние на активность, но у всех или большинства белков с высокой активностью в этом положении находится лейцин, то положение 197 не будет выбрано для изменения в этом подходе. Другими словами, все или большинство белков в библиотеке следующего поколения будут иметь лейцин в положении 197. Однако, если бы у некоторых "хороших" белков в этом положении находился валин, и у других находился лейцин, то процесс выбрал бы изменение аминокислоты в этом положении. В некоторых случаях будет обнаружено, что комбинация двух или более взаимодействующих остатков оказывает самое большое влияние на активность. Следовательно, в некоторых стратегиях, эти остатки будут изменяться совместно.
После того, как остатки для изменения были идентифицированы, далее способ создает новую библиотеку вариантов, имеющую указанное изменение остатка. Смотри блок 211 (фигура 2). Для достижения этой цели имеются различные методологии. В одном из примеров основанный на рекомбинации механизм создания разнообразия выполняется in vitro и in vivo с целью создания новой библиотеки вариантов. В таких процедурах могут использоваться олигонуклеотиды, содержащие последовательности или подпоследовательности для кодирования белков родительской библиотеки вариантов. Некоторые из олигонуклеотидов будут тесно связаны, отличаясь только выбором кодонов для чередующихся аминокислот, выбранных для изменения в 209. Основанный на рекомбинации механизм создания разнообразия может быть выполнен в течение одного или множества циклов. Если применяется множество циклов, то каждый включает в себя этап скрининга для идентификации того, какие варианты обладают приемлемой производительностью для использования в следующем цикле рекомбинации. Это является формой направленной эволюции. Однако не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом основанного на рекомбинации способа создания разнообразия, поскольку любой соответствующий способ/методика может применяться в настоящем изобретении.
В дополнительном иллюстративном примере выбрана "опорная" последовательность белка, и остатки, выбранные в 209 c фигуры 2, "переключены" с целью идентификации индивидуальных элементов библиотеки вариантов. Новые белки, идентифицированные таким образом, синтезируются с помощью соответствующей методики с целью создания новой библиотеки. В одном из примеров опорная последовательность может являться элементом обучающего множества с наилучшими характеристиками или "лучшей" последовательностью, спрогнозированной посредством модели PLS или PCR.
В другом иллюстративном примере остатки для изменения в цикле направленной эволюции выбираются в одной родительской последовательности. Родитель может быть идентифицирован с использованием результатов моделирования из предыдущего цикла направленной эволюции или с использованием данных, которые идентифицируют элемент библиотеки, имеющий лучшие характеристики в соответствии с анализом. Олигонуклеотиды для следующего цикла направленной эволюции могут быть определены как содержащие части остова выбранного родителя с одной или более мутациями, спрогнозированными алгоритмически по модели последовательности-активности для текущего цикла. Эти олигонуклеотиды могут быть произведены с применением любых соответствующих средств, включая синтетические способы, но не ограничиваясь ими.
После того, как новая библиотека была получена, осуществляется ее скрининг относительно активности, как обозначено в блоке 213 (фигура 2). В идеальном случае новая библиотека предоставляет один или более элементов с лучшей активностью, чем наблюдалась в предыдущей библиотеке. Однако, даже без такого преимущества, новая библиотека может предоставить выгодную информацию. Ее элементы могут использоваться для создания улучшенных моделей, которые учитывают влияние изменений, выбранных в 209 (фигура 2), и, таким образом, более точно прогнозируют активность для более широких областей пространства последовательностей. Кроме того, библиотека может представлять в пространстве последовательностей путь от локального максимума к глобальному максимуму (например, для активности).
В зависимости от цели процесса 200 (фигура 2), в некоторых вариантах осуществления требуется создать ряд новых библиотек вариантов белка, каждая из которых предоставляет новые элементы для обучающего множества. Обновленное обучающее множество затем применяется для создания улучшенной модели. Для того чтобы достигнуть улучшенной модели, показан процесс 200 с операцией принятия решения в соответствии с показанным в блоке 215, который определяет, должна ли быть получена еще одна библиотека вариантов белка. Различные критерии могут применяться для принятия этого решения. Примеры критериев решения включают, но не ограничиваются указанным, число библиотек вариантов белка, сгенерированных до настоящего момента, активность лучших белков из текущей библиотеки, требуемую величину активности и уровень улучшения, наблюдаемый в недавно полученных новых библиотеках.
Если предположить, что процесс применяется для продолжения с новой библиотекой, процесс возвращается к функционированию в блоке 100 (фигура 2), где новая модель последовательности-активности генерируется по данным последовательности и активности, полученным для текущей библиотеки вариантов белка. Другими словами, данные последовательности и активности для текущей библиотеки вариантов белка служат частью обучающего множества для новой модели (или они могут служить в качестве всего обучающего множества). После этого операции, показанные в блоках 207, 209, 211, 213 и 215 (фигура 2) выполняются в соответствии с описанным выше, но с новой моделью.
Когда было определено, что достигнута конечная точка способа, цикл, проиллюстрированный на фигуре 2, заканчивается, и новая библиотека не генерируется. В этой точке процесс или просто завершается или, в некоторых вариантах осуществления, одна или более последовательностей из одной или более библиотек выбирается для разработки и/или производства. Смотри блок 217.
B. ГЕНЕРАЦИЯ НАБЛЮДЕНИЙ
Библиотеки вариантов белка представляют собой группы из множества белков, имеющих один или более остатков, которые изменяются от одного элемента к другому элементу в библиотеке. Эти библиотеки могут быть сгенерированы с применением способов, описанных в настоящем раскрытии и/или любых соответствующих средств, известных в технике. Эти библиотеки находят применение в предоставлении данных для обучающих множеств, используемых для создания моделей последовательности-активности в соответствии с различными вариантами осуществления данного изобретения. Количество белков, включенных в библиотеку вариантов белка, часто зависит от применения и стоимости, связанной с их созданием. Не предполагается, что настоящее изобретение ограничено каким-либо конкретным числом белков в библиотеках белка, применяемых в способах по настоящему изобретению. Также не предполагается, что настоящее изобретение ограничено какой-либо конкретной библиотекой или библиотеками вариантов белка.
В одном из примеров библиотека вариантов белка создается из одного или более естественных белков, которые могут быть закодированы одним семейством генов. Могут использоваться другие исходные точки включая, но не ограничиваясь, рекомбинантные варианты известных белков или новые синтетические белки. Из этих исходных или начальных белков библиотека может быть создана посредством различных методик. В одном из случаев библиотека создается посредством опосредованной фрагментацией ДНК рекомбинации, как описано в Stemmer (1994) Proceedings of The National Academy of Sciences, USA, 10747-10751 и WO 95/22625 (оба включены в настоящее раскрытие посредством ссылки), синтетической опосредованной олигонуклеотидом рекомбинации, как описано в Ness и соавт. (2002) Nature Biotechnology 20: 1251-1255 и WO 00/42561 (оба включены в настоящее раскрытие посредством ссылки), посредством нуклеиновых кислот, кодирующих часть или все из одного или более родительских белков. Также могут применяться комбинации этих способов (например, рекомбинация фрагментов ДНК и синтетические олигонуклеотиды), а также другие основанные на рекомбинации способы, описанные, например, в WO97/20078 и WO98/27230, оба из которых включены в настоящее раскрытие посредством ссылки. Любые соответствующие способы, применяемые для создания библиотек вариантов белка, находят применение в настоящем изобретении. Фактически, не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом для продуцирования библиотек вариантов.
В некоторых вариантах осуществления единственная "начальная" последовательность (которая может являться последовательностью "предка") может использоваться для целей задания группы мутаций, используемых в процессе моделирования. В некоторых вариантах осуществления по меньшей мере одна из начальной последовательности представляет собой последовательность дикого типа.
В определенных вариантах осуществления мутации (a) идентифицированы в литературе как оказывающие влияние на специфичность, селективность, стабильность или другое выгодное свойство субстрата и/или (b) спрогнозированы вычислительно как улучшающие схемы сворачивания белка (например, упаковывание внутренних остатков белка), связывание с лигандом, взаимодействие субъединицы, перетасовка семейств между множеством разнообразных гомологов и т.д. Альтернативно, мутации могут быть физически внесены в начальную последовательность и продукты экспрессии, подвергаемые скринингу в отношении выгодных свойств. Сайт-направленный мутагенез является одним из примеров полезной методики для внесения мутаций, при этом любой соответствующий способ может быть применен. Таким образом, альтернативно или в дополнении, мутанты могут быть получены посредством генного синтеза, насыщающего неспецифического мутагенеза, полусинтетических комбинаторных библиотек остатков, направленной эволюции, рекурсивной рекомбинации последовательностей ("RSR") (см. например, заявку на патент США No. 2006/0223143, включенную в настоящее раскрытие посредством ссылки во всей ее полноте), перетасовки генов, ПЦР с внесением ошибок и/или любого другого соответствующего способа. Один из примеров соответствующей процедуры насыщающего мутагенеза описан в опубликованной заявке на патент № 20100093560, которая включена в настоящее раскрытие посредством ссылки во всей ее полноте.
Начальная последовательность не обязательно должна быть идентичной последовательности аминокислот белка дикого типа. Однако, в некоторых вариантах осуществления, начальная последовательность представляет собой последовательность белка дикого типа. В некоторых вариантах осуществления начальная последовательность содержит мутации, не присутствующие в белке дикого типа. В некоторых вариантах осуществления начальная последовательность представляет собой консенсус-последовательность, полученную из группы белков, имеющих общее свойство, например, семейства белков.
Неограничивающий репрезентативный перечень семейств или классов ферментов, которые могут служить источниками родительских последовательностей, включают, но не ограничены, следующее: оксидоредуктазы (E.C. I); трансферазы (E.C.2); гидролазы (E.C.3); лиазы (E.C.4); изомеразы (E.C. 5) и лигазы (E.C. 6). Более конкретные, но неограничивающие подгруппы оксидоредуктаз включают дегидрогеназы (например, алкоголь-дегидрогеназы (карбонилредуктазы), ксилулозредуктазы, альдегидредуктазы, фарнезол-егидрогеназы, лактат-дегидрогеназы, арабинозодегидрогеназы, глюкозодегидрогеназы, фруктозодегидрогеназы, ксилозредуктазы и сукцинатдегидрогеназы), оксидазы (например, глюкозооксидазы, гексозооксидазы, галктозооксидазы и лакказы), тираминазы, липоксигеназы, пероксидазы, альдегиддегидогеназы, длинноцепочечные ацил-[ацил-носитель-белок] редуктазы, ацила-CoA-дегидрогеназы, ене-редуктазы, синтазы (например, глутамат-синтазы), нитратредуктазы, моно и ди-оксигеназы, и каталазы. Более конкретные, но неограничивающие, подгруппы трансфераз включают метил-, амидино- и карбоксил-трансферазы, транскетолазы, трансальдолазы, ацилтрансферазы, гликозилтрансферазы, трансаминазы, трансглутаминазы и полимеразы. Более конкретные, но неограничивающие, подгруппы гидролитических ферментов включают эфирные гидролитические ферменты, пептидазы, гликозилазы, амилазы, целлюлазы, гемицеллюлазы, ксиланазы, хитиназы, глюкозидазы, глюканазы, глюкоамилазы, ацилазы, галактозидазы, пуллуланазы, фитазы, лактазы, арабинозидазы, нуклеозидазы, нитрилазы, фосфатазы, липазы, фосфолипазы, протеазы, АТФазы, и дегалогеназы. Более конкретные, но неограничивающие, подгруппы лиаз включают декарбоксилазы, альдолазы, гидратазы, дегидратазы (например, карбоангидразы), синтазы (например, изопрен-, пинен- и фарнезин-синтазы), пектиназы (например, пектинлиазы) и дегидразы галоидгидрина. Более конкретные, но неограничивающие подгруппы изомераз включают рацемазы, эпимеразы, изомеразы (например, ксилозо-, арабинозо-, рибозо-, глюкозо-, галактозо- и маннозо-изомеразы), таутомеразы и мутазы (например, ацил-переносящие мутазы, фосфомутазы и аминомутазы. Более конкретные, но неограничивающие, подгруппы лигаз включают эфирсинтазы. Другие семейства или классы ферментов, которые могут использоваться в качестве источников родительских последовательностей, включают трансаминазы, протеазы, киназы и синтазы. Этот список, хотя и иллюстрирует определенные конкретные аспекты возможных ферментов по раскрытию, не считается исчерпывающим и не показывает ограничения и не ограничивает объем раскрытия.
В некоторых случаях, ферменты-кандидаты, целесообразные для способов, описанных в настоящем раскрытии, способны к катализации энантиоселективной реакции, такой как, например, энантиоселективная реакция восстановления. Такие ферменты могут применяться для того, чтобы сделать промежуточные продукты полезными, например, в синтезе фармацевтических соединений.
В некоторых вариантах осуществления ферменты-кандидаты выбирают из эндоксиланаз (EC 3.2.1.8); β-ксилозидаз (EC 3.2.1.37); альфа-L-арабинофуранозидаз (EC 3.2.1.55); альфа-глюкуронидаз (EC 3.2.1.139); ацетилксиланэстераз (EC 3.1.1.72); ферулоилэстераз (EC 3.1.1.73); кумароилэстераз (EC 3.1.1.73); альфа-галактозидаз (EC 3.2.1.22); бета-галактозидаз (EC 3.2.1.23); бета- маннаназ (EC 3.2.1.78); бета-маннозидаз (EC 3.2.1.25); эндо-полигалактуроназ (EC 3.2.1.15); эстераза метила пектина (EC 3.1.1.11); эндо-галактаназ (EC 3.2.1.89); пектинметилэстераз (EC 3.1.1.6); эндо-пектинлиаз (EC 4.2.2.10); пектат-лиаз (EC 4.2.2.2); альфа-рамнозидаз (EC 3.2.1.40); экзо-поли-альфа-галактуроназидаз (EC 3.2.1.82); 1,4-альфа- галактуроназидазы (EC 3.2.1.67); экзополигалактуронатлиаз (EC 4.2.2.9); рамногалактуронан-эндолиаз (EC 4.2.2.B3); рамногалактуронан-ацетилэстераз (EC 3.2.1.B11); рамногалактуронан-галактуроногидролаз (EC 3.2.1.B11); эндо-арабиназаз (EC 3.2.1.99); лакказ (EC 1.10.3.2); зависимых от марганца пероксидаз (EC 1.10.3.2); амилаз (EC 3.2.1.1), глюкоамилаз (EC 3.2.1.3), протеаз, липаз и лигнинпероксидаз (EC 1.11.1.14). Любая комбинация из одного, двух, трех, четырех, пяти или более пяти ферментов находит применение в композициях по настоящему изобретению.
В одном или более вариантах осуществления изобретения единственную начальную последовательность модифицируют различными способами с целью создания библиотеки. В некоторых вариантах осуществления библиотека создается посредством систематического изменения индивидуальных остатков начальной последовательности. В одном иллюстративном примере методология планирования эксперимента (DOE) применяется для идентификации систематически изменяющихся последовательностей. В другом примере процедура "классической лаборатории", такая как опосредованная олигонуклеотидом рекомбинация, применяется для внесения некоторого уровня систематических изменений. Не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом генерации систематически изменяющихся последовательностей, поскольку любой соответствующий способ находит применение.
При использовании в настоящем раскрытии, термин "систематически изменяющиеся последовательности" относится к множеству последовательностей, в которых каждый остаток можно видеть во множестве контекстов. В принципе, уровень систематического изменения может быть определен количественно по степени, в которой последовательности являются ортогональными друг относительно друга (то есть, максимально отличаются по сравнению со средним значением). В некоторых вариантах осуществления процесс не зависит от наличия максимально ортогональных последовательностей. Однако качество модели будет улучшаться прямо пропорционально ортогональности тестируемого пространства последовательностей. В простом иллюстративном примере последовательность пептида систематически изменяют посредством идентификации двух положений остатков, в каждом из которых может находиться одна из двух различных аминокислот. Максимально разнообразная библиотека содержит все четыре возможных последовательности. Такое максимальное систематическое изменение возрастает по экспоненте с увеличением числа переменных положений; например, как 2N, когда имеется 2 возможности в каждом из положений остатка N. Специалистам в данной области техники будет сразу понятно, что максимальное систематическое изменение, однако, не требуется. Систематическое изменение обеспечивает механизм для идентификации относительно небольшого множества последовательностей для тестирования, которое обеспечивает хорошую выборку из пространства последовательностей.
Варианты белка, имеющие систематически изменяющиеся последовательности, могут быть получены рядом способов с применением методик, которые хорошо известны специалистам в данной области техники. Как указано выше, соответствующие способы включают в себя, но не ограничиваются, основанные на рекомбинации способы, которые генерируют варианты на основании одной или более "родительских" полинуклеотидных последовательностей. Полинуклеотидные последовательности могут рекомбинировать с применением множества методик, включая, например, расщепление ДНКазой полинуклеотидов, которые будут рекомбинироваться, с последующим лигированием и/или повторной ПЦР-сборкой нуклеиновых кислот. Эти методы включают, но не ограничены описанными, например, в Stemmer (1994) Proceedings of The National Academy of Sciences, USA, патенте США № 5605793, "Methods for In Vitro Recombination", патенте США No. 5811238, "Methods for Generating Polynucleotides having Desired Characteristics by Iterative Selection and Recombination," патенте США No. 5830721, "DNA Mutagenesis by Random Fragmentation and Reassembly," патенте США No. 5834252, "End Complementary Polymerase Reaction," Патенте США No. 5837458, "Methods and Compositions for Cellular and Metabolic Engineering," WO 98/42832, "Recombination of Polynucleotide Sequences Using Random or Defined Primers," WO 98/27230, "Methods and Compositions for Polypeptide Engineering," WO 99/29902, "Method for Creating Polynucleotide and Polypeptide Sequences, и т.п., все из которых включены в настоящее раскрытие посредством ссылки.
Синтетические способы рекомбинации также особенно хорошо подходят для создания библиотек вариантов белка с систематическими изменениями. В синтетических способах рекомбинации синтезируется множество олигонуклеотидов, которые совместно кодируют множество генов, которые будут рекомбинировать. В некоторых вариантах осуществления олигонуклеотиды совместно кодируют последовательности, полученные из гомологичных родительских генов. Например, интересующие гомологичные гены выравниваются с применением программы выравнивания последовательностей, такой как BLAST (см. например, Atschul, и соавт., Journal of Molecular Biology, 215:403-410 (1990). Отмечают нуклеотиды, соответствующие изменениям аминокислот между гомологами. Эти изменения, необязательно, также ограничены подмножеством всех возможных изменений на основании анализа ковариации родительских последовательностей, функциональной информации для родительских последовательностей, выбора консервативных или неконсервативных изменений между родительскими последовательностями, или другими соответствующими критериями. Изменения, необязательно, дополнительно увеличивают с целью кодирования дополнительного разнообразия аминокислот в положениях, идентифицированных, например, посредством анализа ковариации родительских последовательностей, функциональной информации для родительских последовательностей, выбора консервативных или неконсервативных изменений между родительскими последовательностями или очевидным допуском положения для изменения. Результат представляет собой вырожденную последовательность гена, кодирующую консенсусную аминокислотную последовательность, полученную из родительских последовательностей генов, с вырожденными нуклеотидами в положениях, кодирующих изменения аминокислот. Спроектированы олигонуклеотиды, которые содержат нуклеотиды, требуемые для сборки разнообразия, присутствующего в вырожденном гене. Подробности относительно таких подходов могут быть найдены в, например, в работах Ness и др. (2002), Nature Biotechnology, 20: 1251-1255, WO 00/42561, "Oligonucleotide Mediated Nucleic Acid Recombination", WO 00/42560, "Methods for Making Character Strings, Polynucleotides and Polypeptides having Desired Characteristics", WO 01/75767, "In Silico Cross-Over Site Selection" и WO 01/64864, "Single-Stranded Nucleic Acid Template-Mediated Recombination and Nucleic Acid Fragment Isolation, каждая из которых включена в настоящее раскрытие посредством ссылки. Идентифицированные полинуклеотидные последовательности вариантов подвергаться транскрипции или трансляции, in vitro или in vivo, с целью создания множества или библиотеки последовательностей вариантов белка.
Множество систематически изменяющихся последовательностей может также быть спроектировано заранее с применением способа планирования экспериментов (DOE) с целью определения последовательностей в множестве данных. Описание способов DOE может быть найдено в работах Diamond, W.J. (2001) Practical Experiment Designs: for Engineers and Scientists, John Wiley & Sons and in "Practical Experimental Design for Engineers и Scientists" by William J Drummond (1981) Van Nostrand Reinhold Co New York, "Statistics for experimenters" George E.P. Box, William G Hunter and J. Stuart Hunter (1978) John Wiley and Sons, New York, или, например, во всемирной паутине по адресу itl.nist.gov/div898/handbook/. Существует несколько вычислительных пакетов, доступных для выполнения соответствующих математических операций, включая панель инструментов статистики (MATLAB®), JMP®, STATISTICA®, и STAT-EASE® DESIGN EXPERT®. Результатом является систематически изменяющееся и ортогонально рассеянное множество данных последовательностей, которое подходит для построения модели последовательности-активности по настоящему изобретению. Основанные на DOE множества данных могут также быть легко сгенерированы с применением плана Плакетта-Бермана или плана факторного эксперимента с дробными репликами, как известно в технике. Diamond, W.J. (2001).
В технических и химических науках планы факторного эксперимента с дробными репликами используются для задания меньшего количества экспериментов по сравнению с планами факторного эксперимента с полными репликами. В этих методах фактор изменяют (то есть, "переключают") между двумя или более уровнями. Методики оптимизации применяются для обеспечения того, чтобы выбранные эксперименты были максимально информативными относительно учета разброса факторного пространства. Те же самые подходы к планированию (например, факторный эксперимент с дробными репликами, D-оптимальный план) могут быть применены в белковой инженерии, чтобы создать меньше последовательностей, в которых заданное число положений переключается между двумя или более остатками. В некоторых вариантах осуществления это множество последовательностей обеспечивает оптимальное описание систематического разброса, присутствующего в рассматриваемом пространстве последовательностей белка.
Иллюстративный пример подхода DOE, примененный к белковой инженерии, включает в себя следующие операции:
1) Определение положений для переключения на основании правил, описанных в настоящем раскрытии (например, присутствие в родительских последовательностях, уровень сохранения и т.д.)
2) Создание эксперимента DOE с применением одного из общедоступных пакетов статистического программного обеспечения посредством задания ряда факторов (то есть переменных положений), числа уровней (то есть вариантов выбора в каждом положении) и числа экспериментов для выполнения с целью получения выходной матрицы. Информационное содержание выходной матрицы (обычно состоящей из 1 и 0, которые представляют варианты выбора остатка в каждом положении) зависит прямо пропорционально от числа выполняемых экспериментов (обычно, чем больше, тем лучше).
3) Применение выходной матрицы для построения выравнивания белков, которое кодирует 1 и 0 обратно в конкретные выбранные остатки в каждом положении.
4) Синтез генов, кодирующих белки, представленные в белковом выравнивании.
5) Проверка белков, закодированных синтезированными генами в соответствующем(-их) анализе(-ах).
6) Построение модели на основании проверенных генов/белков.
7) Выполнение этапов, описанных в настоящем раскрытии, для идентификации важных положений и создания одной или более последующих библиотек с улучшенной пригодностью.
В иллюстративном примере исследован белок, в котором должны быть определены функционально лучшие аминокислотные остатки в 20 положениях (например, когда имеется 2 возможных аминокислоты, доступных в каждом положении). В этом примере план факторного эксперимента разрешения IV был бы подходящим. План разрешения IV разрешающей способности определен как план, который способен объяснить влияние всех единичных переменных, при отсутствии наложения на них двухфакторных влияний. В плане затем было бы определено 40 конкретных последовательностей аминокислот, покрывающих полное разнообразие, составляющее 220 (~1 миллион) возможных последовательностей. Эти последовательности затем генерируются с применением произвольного стандартного протокола синтеза генов, и определяется функциональность и пригодность этих клонов.
Альтернатива указанным выше подходам состоит в использовании некоторых или всех доступных последовательностей (например, базы данных GENBANK® и других общедоступных источников) для предоставления библиотеки вариантов белка. Этот подход обеспечивает указание интересующих областей пространства последовательностей.
C. СПОСОБЫ СЕКВЕНИРОВАНИЯ
Исторически, секвенирование являлось ограничивающим этапом в разработке больших обучающих множеств и, следовательно, все более и более устойчивых моделей последовательности-активности. Высокая стоимость и длительное время, требуемое для секвенирования вариантов, ограничивало число наблюдений несколькими десятками вариантов. Инструментальные средства секвенирования следующего поколения значительно снизили стоимость и увеличили скорость и объем секвенирования, позволяя включать в обучающее множество варианты как с низкой, так и с высокой активностью.
Инструментальные средства секвенирования следующего поколения позволяют недорого отсеквенировать большие количества пар азотистых оснований (например, по меньшей мере приблизительно 1000000000 пар азотистых оснований) за один запуск прибора. Такой объем может использоваться при секвенировании вариантов белков, которые обычно имеют длину только несколько тысяч пар оснований, за один запуск прибора. Часто инструментальные средства секвенирования следующего поколения оптимизированы для секвенирования единственных больших геномов (например, человеческого генома), а не множества более коротких последовательностей, в одном запуске прибора. Для того чтобы реализовать потенциал инструментальных средств секвенирования следующего поколения для параллельного секвенирования множества наблюдений, источник каждого из секвенируемых в одном запуске прибора наблюдений должен быть однозначно определен. В некоторых вариантах осуществления, помеченные штрих-кодом последовательности используются в каждом фрагменте, поданном в секвенатор следующего поколения для одного запуска. В одном из примеров штрих-коды однозначно определяют конкретную лунку на конкретном планшете (например, 96-луночных планшетах). В некоторых из этих вариантов осуществления каждый источник каждого планшета содержит единственный уникальный вариант. Посредством мечения штрих-кодом каждого варианта, или, более конкретно, каждого фрагмента каждого варианта, последовательности генов множества различных вариантов могут быть отсеквенированы и идентифицированы за один запуск прибора. В процессе, все прочтения фрагмента, имеющие один и тот же штрих-код, идентифицируются и обрабатываются совместно с помощью алгоритма, идентифицирующего последовательности длины для вариантов.
В некоторых вариантах осуществления ДНК из клеток варианта в заданной лунке извлекается и затем фрагментируется. Фрагменты затем помечаются штрих-кодом с целью идентификации, по меньшей мере, лунки, и иногда лунки и планшета, ассоциированных с этим вариантом. Полученные в результате фрагменты затем отбираются по размеру с целью получения последовательностей соответствующей длины для секвенатора следующего поколения. В одном иллюстративном примере длины прочтений составляют около 200 пар азотистых оснований. В некоторых вариантах осуществления штрих-код планшета не наносится, пока фрагменты ДНК из различных лунок планшета не будут сначала объединены в пул. Объединенная в пул ДНК затем помечается штрих-кодом с целью идентификации планшета. В некоторых вариантах осуществления каждый фрагмент, независимо от того, из какой лунки он был получен, имеет один и тот же штрих-код планшета. Однако в некоторых альтернативных вариантах осуществления фрагменты имеют различные штрих-коды. Кроме того, штрих-коды лунок и планшетов могут быть нанесены для идентификации ДНК, извлеченной из заданной лунки.
В одном или более вариантах осуществления данные последовательностей могут быть получены с применением методов массового секвенирования включая, например, секвенирование по Сэнгеру или секвенирование методом Максама-Гилберта, которые считают методами секвенирования первого поколения. Секвенирование по Сэнгеру, которое включает в себя использование помеченных дидезокси-элементов обрыва цепи, известно в технике; см., например, Sanger и соавт., Proceedings of The National Academy of Sciences of the United States of America 74, 5463-5467 (1997). Секвенирование Максама-Гилберта, которое включает в себя выполнение множества частичных химических реакций разложения на частях образца нуклеиновой кислоты, после которых следует обнаружение и анализ фрагментов с целью выведения последовательности, также известно в технике; см., например, Maxam и соавт., Proceedings of The National Academy of Sciences of the United States of America 74, 560-564 (1977). Другим методом массового секвенирования является секвенирование посредством гибридизации, в котором последовательность образца выводят на основании ее свойств гибридизации с множеством последовательностей, например, на микрочипе или ДНК-чипе; см., например, Drmanac, и соавт., Nature Biotechnology 16, 54-58 (1998).
В одном или более вариантах осуществления данные последовательностей получают с применением методов секвенирования следующего поколения. Секвенирование следующего поколения также называется "высокопроизводительным секвенированием". Методики распараллеливают процесс секвенирования, выдавая тысячи или миллионы последовательностей единовременно. Примеры соответствующих методов секвенирования следующего поколения включают в себя, но не ограничиваются указанным, секвенирование единичной молекулы в реальном времени {например, Pacific Biosciences, Менло-Парк, Калифорния), ионное полупроводниковое секвенирование (например, Ion Torrent, Южный Сан-Франциско, Калифорния), пиросеквенирование (например, 454, Брэнфорд, Коннектикут), секвенирование посредством лигирования (например, секвенирование SOLid Life Technologies, Карлсбад, Калифорния), секвенирование посредством синтеза и обратимого обрывателя цепи (например, Illumina, Сан-Диего, Калифорния), технологии визуализации нуклеиновой кислоты, такие как просвечивающий электронный микроскоп, и т.п.
Как правило, методы секвенирования следующего поколения обычно применяют в качестве этапа клонирования in vitro для амплификации индивидуальных молекул ДНК. Эмульсионная ПЦР (emPCR) изолирует индивидуальные молекулы ДНК на покрытых праймером гранулах в водных каплях в пределах масляной фазы. ПЦР производит копии молекулы ДНК, которые связываются с праймерами на грануле, после чего производится фиксация для последующего секвенирования. emPCR применяется в способах, приведенных в работах Marguilis и др. (коммерциализированных 454 Life Sciences, Брэнфорд, Коннектикут), Shendure и Porreca и др. (также известных как "секвенирование молекулярных колоний") и секвенировании SOLiD, (Applied Biosystems Inc., Фостер-Сити, Калифорния). См. M. Margulies, и соавт. (2005) "Genome sequencing in microfabricated high-density picolitre reactors" Nature 437: 376-380; J. Shendure и соавт. (2005) "Accurate Multiplex Polony Sequencing of an Evolved Bacterial Genome" Science 309 (5741): 1728-1732. Амплификация клонов in vitro также может быть выполнена посредством "бридж-ПЦР", в которой фрагменты амплифицируют после прикрепления праймеров к твердой поверхности. Braslavsky и др. разработали метод единичной молекулы (коммерциализированный Helicos Biosciences Corp., Кембридж, Массачусетс), который пропускает данный этап амплификации, напрямую фиксируя молекулы ДНК на поверхности. I. Braslavsky, и соавт. (2003) "Sequence information can be obtained from single DNA molecules" Proceedings of the National Academy of Sciences of the United States of America 100: 3960-3964.
Молекулы ДНК, которые физически связаны с поверхностью, могут быть отсеквенированы параллельно. В "секвенировании посредством синтеза" комплементарная нить строится на основании последовательности матричной нити с применением ДНК-полимеразы, как в электрофоретическом секвенирование с окрашенным прерывателем. Методы обратимого прерывания (коммерциализированные Illumina, Inc., Сан-Диего, Калифорния и Helicos Biosciences Corp., Кембридж, Массачусетс) используют обратимые версии окрашенных прерывателей, добавляя один нуклеотид за один раз, и детектируют флуоресценцию в каждом положении в режиме реального времени, посредством циклического удаления блокирующей группы с целью обеспечения полимеризации другого нуклеотида. В "пиросеквенировании" также применяется полимеризация ДНК, добавление одного нуклеотида за один раз и детектирование и количественное определение числа нуклеотидов, добавленных к данному положению, через свет, излучаемый при высвобождении присоединенных пирофосфатов (коммерциализировано 454 Life Sciences, Брэнфорд, Коннектикут). См. M. Ronaghi и соавт. (1996). "Real-time DNA sequencing using detection of pyrophosphate release" Analytical Biochemistry 242: 84-89.
Конкретные примеры методов секвенирования следующего поколения подробнее описаны ниже. Одна или более реализаций настоящего изобретения могут применять один или более из приведенных ниже методов секвенирования, не отклоняясь от принципов изобретения.
Одномолекулярное секвенирование в реальном времени (также известное как SMRT) представляет собой технологию распараллеленного секвенирования одиночных молекул ДНК посредством синтеза, разработанную Pacific Biosciences. Одномолекулярное секвенирование в реальном времени использует нулевой волновод (ZMW). Единственный фермент ДНК-полимеразы прикреплен на дне ZMW к единственной молекуле ДНК в качестве матрицы. ZMW представляет собой структуру, которая создает освещенный объем наблюдения, который является достаточно малым для наблюдения только одного нуклеотида ДНК (также известного как основание), присоединяемого ДНК-полимеразой. Каждое из четырех оснований ДНК присоединено к одному из четырех различных флуоресцентных красителей. Когда нуклеотид присоединяется ДНК-полимеразой, флуоресцентная метка отщепляется и диффундирует из области наблюдения ZMW, где ее флуоресценция больше не наблюдается. Детектор обнаруживает флуоресцентный сигнал присоединения нуклеотида, и определение основания выполняется согласно соответствующей флуоресценции красителя.
Другой подходящей технологией одномолекулярного секвенирования является технология истинного одномолекулярного секвенирования Helicos (tSMS) (например, как описано в работе Harris T.D. и соавт., Sciences 320: 106-109 [2008]). В методике tSMS образец ДНК расщепляется на нити длиной около 100-200 нуклеотидов, и последовательности полиА добавляется к 3'-концам каждой нити ДНК. Каждая нить помечается посредством добавления флуоресцентно помеченного аденозинового нуклеотида. Нити ДНК затем гибридизуются в проточной ячейке, которая содержит миллионы сайтов захвата олиго-T, которые зафиксированы на поверхности проточной ячейки. В определенных вариантах осуществления матрицы могут присутствовать с плотностью около 100 миллионов матриц/см2. Проточная ячейка затем загружается в прибор, например, секвенатор HeliScope™, и лазер освещает поверхность проточной ячейки, показывая положение каждой матрицы. Камера CCD может отобразить положение матриц на поверхности клеток потока. Матричная флуоресцентная метка затем отщепляется и смывается. Реакция секвенирования начинается посредством внесения ДНК-полимеразы и флуоресцентно помеченного нуклеотида. Нуклеиновая кислота олиго-T служит праймером. Полимераза присоединяет помеченные нуклеотиды к праймеру на основании матрицы. Полимераза и неприсоединенные нуклеотиды удаляются. Матрицы, которые направляли присоединение флуоресцентно помеченного нуклеотида, различают посредством визуализации поверхности проточной ячейки. После визуализации на этапе расщепления удаляется флуоресцентная метка, и процесс повторяется с другими флуоресцентно помеченными нуклеотидами, пока требуемая длина чтения не будет достигнута. Информация последовательности собирается на каждом шаге добавления нуклеотида. Секвенирование всего генома посредством технологий одномолекулярного секвенирования исключает или обычно устраняет основанную на ПЦР амплификацию при подготовке библиотек секвенирования, и способы позволяют осуществлять прямое измерение образца, а не измерение копий этого образца.
Ионное полупроводниковое секвенирование представляет собой метод секвенирования ДНК, основанный на обнаружении ионов водорода, которые высвобождаются во время полимеризации ДНК. Данный метод является методом "секвенирования посредством синтеза", во время которого комплементарная нить строится на основании последовательности матричной нити. Микролунка, содержащая матричную нить ДНК, которая будет секвенироваться, заливаются единичными молекулами дезоксирибонуклеотидтрифосфата, (dNTP). Если внесенный dNTP является комплементарным находящемуся в начале матричному нуклеотиду, он включается в растущую комплементарную нить. Это вызывает высвобождение иона водорода, который переключает ионный датчик ISFET, который показывает, что реакция произошла. Если гомополимерные повторы будут присутствовать в матричной последовательности, то множество молекул dNTP будут включены в одном цикле. Это приводит к соответствующему количеству высвобожденных водородов и пропорционально более высокому электронному сигналу. Эта технология отличается от других технологий секвенирования, в том, что в ней не используются какие-либо измененные нуклеотиды или оптика. Ионное полупроводниковое секвенирование может также называться как поточным ионным секвенированием, pH-опосредованным секвенированием, кремниевым секвенированием или полупроводниковым секвенирование.
В пиросеквенировании пирофосфат-ион, высвобожденный в результате реакции полимеризации, реагирует с 5'-фосфосульфатом аденозина посредством АТФ-сульфурилазы с образованием АТФ; АТФ затем управляет преобразованием люциферина в оксилюциферин плюс свет от люциферазы. Поскольку флуоресценция является временной, то в данном методе отсутствует необходимость в отдельном шаге удаления флуоресценции. Один тип дезоксирибонуклеотитрифосфата (dNTP) добавляется за один раз, и информацию о последовательности различают по тому, какой dNTP генерирует значительный сигнал в месте реакции. Имеющийся в продаже прибор Roche GS FLX получает последовательность с применением данного метода. Эта методика и ее применения подробно обсуждаются, например, в Ronaghi и соавт., Analytical Biochemistry 242, 84-89 (1996) и Margulies и соавт., Nature 437, 376-380 (2005) (поправки в Nature 441, 120 (2006)). Коммерчески доступной технологией пиросеквенирования является 454-секвенирование (Roche) (например, как описано в Margulies и соавт., Nature 437:376-380 [2005]).
В секвенировании посредством лигирования фермент лигаза применяется для соединения являющего частично двухцепочечным олигонуклеотида с «липким» концом с секвенируемоей нуклеиновой кислотой, которая имеет «липкий» конец; для того, чтобы происходило лигирование, липкие концы должны быть комплементарными. Основания в липком конце являющего частично двухцепочечным олигонуклеотида могут быть идентифицированы согласно флуорофору, конъюгированному с частично двухцепочечным олигонуклеотидом и/или для вторичным олигонуклеотидом, который гибридизуется с другой частью частично двухцепочечного олигонуклеотида. После получения флуоресцентных данных лигированный комплекс расщепляется в точке, находящейся ближе к 5'-концу, чем сайт лигирования, например, рестрикционным ферментом типа II, например, Bbvl, который разрезает в сайте, находящемся на фиксированном расстоянии от сайта распознавания (который был включен в частично двухцепочечный олигонуклеотид). Данная реакция расщепления открывает новый липкий конец, находящийся в 5'-направлении непосредственно рядом с предыдущим липким концом, и процесс повторяется. Эта методика и ее применения подробно обсуждаются, например, в работе Brenner и соавт., Nature Biotechnology 18, 630-634 (2000). В некоторых вариантах осуществления секвенирование посредством лигирования адаптировано для способов по изобретению посредством получения продукта амплификации по типу катящегося кольца круговой молекулы нуклеиновой кислоты и использования данного продукта амплификации по типу катящегося кольца в качестве матрицы для секвенирования посредством лигирования.
Коммерчески доступным примером технологии секвенирования посредством лигирования является технология SOLiD™ (Applied Biosystems). В секвенировании посредством лигирования SOLiD™ геномная ДНК разрезается на фрагменты, и адаптеры присоединяются к 5'- и 3'-концам фрагментов с целью создания библиотеки фрагментов. Альтернативно, внутренние адаптеры могут быть введены посредством лигирования адаптеров с 5'- и 3'-концами фрагментов, расщепления скругленного фрагмента с целью создания внутреннего адаптера и присоединения адаптеров к 5'- и 3'-концам следующих фрагментов с целью создания парно сопряженной (mate-paired) библиотеки. Затем, популяции клональных гранул подготавливаются в микрореакторах, содержащих гранулы, праймеры, матрицу и компоненты ПЦР. После ПЦР матрицы денатурируются, и гранулы обогащают с целью выделения гранул с удлиненными матрицами. Матрицы на отобранных гранулах подвергаются 3'- модификациям, которые позволяют связываться со стеклянной пластинкой. Последовательность может быть определена посредством последовательной гибридизации и лигирования частично случайных олигонуклеотидов с центральным определенным основанием (или парой оснований), которое идентифицируют по конкретному флуорофору. После того, как цвет был записан, лигированный олигонуклеотид расщепляется и удаляется, и процесс затем повторяют.
В секвенировании с применением обратимого обрывателя цепи флуоресцентный помеченный красителем аналог нуклеотида, который является обратимым обрывателем цепи вследствие наличия блокирующей группы, вносят в реакцию удлинения на одно основание. Наименование основания определяют согласно флуорофору; другими словами, каждое основание связано с различным флуорофором. После того, как данные флуоресценции/последовательности были получены, флуорофор и блокирующую группу химически удаляют, и цикл повторяют для получения информации о следующем основании из последовательности. Прибор Illumina GA функционирует в соответствии с данным методом. Данная методика и ее применения подробно обсуждены, например, в Ruparel и соавт., Proceedings of The National Academy of Sciences of the United States of America 102, 5932-5937 (2005), и Harris и соавт., Science 320, 106-109 (2008).
Коммерчески доступным примером секвенирования с применением обратимого обрывателя цепи является секвенирование посредством синтеза и основанное на обратимом обрывателе цепи секвенирование Illumina (например, как описано в Bentley и соавт., Nature 6:53-59 [2009]). Технология секвенирования Illumina основана на прикреплении фрагментированной геномной ДНК к плоской оптически прозрачной поверхности, на которой связаны фиксаторы олигонуклеотидов. Матричная ДНК подвергается восстановлению конца с целью получения 5'-фосфорилированных тупых концов, и полимеразная активность фрагмента Кленова используется для добавления единичного основания A к 3'-концу тупых фосфорилированных фрагментов ДНК. Это добавление подготавливает фрагменты ДНК к лигированию с олигонуклеотидными адаптерами, которые имеют липкий конец из одного основания T на своих 3'- концах, с целью повышения эффективности лигирования. Олигонуклеотиды адаптера являются комплементарными к фиксаторам проточной ячейки. В условиях предельного разведения модифицированная адаптером одноцепочечная матричная ДНК добавляется к проточной ячейке и фиксируется посредством гибридизации с фиксаторами. Присоединенные фрагменты ДНК удлиняются и бридж-амплифицируются с целью создания проточной ячейки секвенирования со сверхвысокой плотностью с сотнями миллионов кластеров, каждый из которых содержит ~1000 копий одной и той же матрицы. Матрицы секвенируют с применением гибкой четырехцветной технологии секвенирования ДНК посредством синтеза, в которой используют обратимые обрыватели цепи с удаляемыми флуоресцентными красителями. Обнаружение флуоресценции с высокой чувствительностью достигается с применением возбуждения лазером и оптики полного внутреннего отражения. Короткие прочтения последовательности около 20-40 н.п. например, 36 н.п., выравнивают с опорным геномом с маскированными повторами, и уникальное отображение коротких прочтений последовательности на опорный геном идентифицируют с применением специально разработанного конвейерного программного обеспечения анализа данных. Также могут использоваться опорные геномы без маскирования повторов. Независимо от того, используются ли опорные геномы с маскированными повторами или без маскирования повторов, подсчитывают только прочтения, которые уникально отображаются на опорный геном. После завершения первого прочтения матрицы могут быть восстановлены на месте с целью обеспечения второго прочтения с противоположного конца фрагментов. Таким образом, может быть применено или одностороннее секвенирование, или секвенирование парных концов фрагментов ДНК. Выполняется частичное секвенирование фрагментов ДНК, присутствующих в образце, и маркерные последовательности, содержащие прочтения с предварительно заданной длиной, например, 36 н.п., отображают на известный опорный геном и подсчитывают.
В нанопорном секвенировании одноцепочечная молекула нуклеиновой кислоты продевается через пору, например, с применением электрофоретической движущей силы, и последовательность выводят посредством анализа данных, полученных при прохождении одноцепочечной молекулы нуклеиновой кислоты через пору. Данные могут быть данными ионного тока, при этом каждое основание изменяет ток, например, посредством частичного блокирования тока, проходящего через пору, в различной различимой степени.
В другом иллюстративном, но неограничивающем, варианте осуществления способы, описанные в настоящем раскрытии, включают в себя получение информации о последовательности с применением просвечивающей электронной микроскопии (TEM). Способ включает в себя применение визуализации посредством трансмиссионного электронного микроскопа с разрешением в один атом имеющей высокий молекулярный вес ДНК (150 т.п.н. или более), выборочно помеченной маркерами из тяжелых атомов, и размещение этих молекул на ультратонких пленках в сверхплотных (3 нм между цепочками) параллельных множествах с согласованным интервалом между основаниями. Электронный микроскоп применяется для визуализации молекул на пленках с целью определения положения маркеров из тяжелых атомов и извлечения информации о последовательности оснований из ДНК. Способ подробнее описан в патентной публикации PCT WO 2009/046445.
В другом иллюстративном, но неограничивающем, варианте осуществления способы, описанные в настоящем раскрытии, включают в себя получение информации о последовательности с применением секвенирования третьего поколения. В секвенировании третьего поколения пластинка с алюминиевым покрытием с множеством маленьких отверстий (~50 нм) используется в качестве нулевого волновода (см., например, Leven и соавт., Science 299, 682-686 (2003)). Алюминиевая поверхность предохраняется от прикрепления ДНК-полимеразы посредством полифосфонатной химии, например, поливинилфосфонатной химии (см., например, Korlach и соавт., Proceedings of The National Academy of Sciences of the United States of America 105, 1176-1181 (2008)). Это приводит к преимущественному прикреплению молекул ДНК-полимеразы к открытому кремнию в отверстиях алюминиевого покрытия. Такая конструкция позволяет использовать явление нераспространяющейся волны для снижения фонового уровня флуоресценции, что позволяет использовать более высокие концентрации флуоресцентно помеченных dNTP. Флуорофор присоединен к концевому фосфату dNTP таким образом, что флуоресценция высвобождается после внесения dNTP, но флуорофор не остается присоединенным к недавно внесенному нуклеотиду, что означает, что комплекс сразу готов к еще одному циклу включения. Посредством этого метода, включение dNTP в индивидуальные комплексы праймер-матрица, присутствующие в отверстиях алюминиевого покрытия, может быть обнаружено. См., например, Eid и соавт., Science 323, 133-138 (2009).
D. СОЗДАНИЕ МОДЕЛИ ПОСЛЕДОВАТЕЛЬНОСТИ-АКТИВНОСТИ
Как указано выше, модель последовательности-активности, применяемая с вариантами осуществления настоящего раскрытия, связывает информацию о последовательности белка с активностью белка. Информация о последовательности белка, используемая моделью, может принимать множество форм. В некоторых вариантах осуществления она представляет собой полную последовательность аминокислотных остатков в белке (например, HGPVFSTGGA...). Однако, в некоторых вариантах осуществления, полная аминокислотная последовательность является ненужной. Например, в некоторых вариантах осуществления, достаточно предоставить только те остатки, которые должны изменяться в конкретной программе исследований. В некоторых вариантах осуществления, включающих в себя более поздние стадии исследования, множество остатков являются фиксированными, и только ограниченные области пространства последовательностей остаются для исследования. В некоторых из таких ситуаций удобно предоставить модели последовательности-активности, которые требуют, в качестве входных данных, идентификацию только тех остатков в областях белка, для которых продолжается исследование. В некоторых дополнительных вариантах осуществления модели не требуется, чтобы были известны точные наименования остатков в положениях остатков. В некоторых таких вариантах осуществления идентифицированы одно или более физических или химических свойств, которые характеризуют аминокислоту в конкретном положении остатка. В одном иллюстративном примере модель требует задания положений остатков по объему, гидрофобности, кислотности и т.д. Кроме того, в некоторых моделях используются комбинации таких свойств. Фактически, не предполагается, что настоящее изобретение ограничено каким-либо конкретным подходом, поскольку модели находят применение в различных конфигурациях информации о последовательности, информации об активности и/или других физических свойств (например, гидрофобности и т.д.).
Таким образом, форма модели последовательности-активности может значительно изменяться, пока она обеспечивает средство для правильной аппроксимации относительной активности белков на основании информации о последовательности, в соответствии с требованиями. В некоторых вариантах осуществления модели обычно обрабатывают активность как зависимую переменную, и значения последовательности/остатка как независимые переменные. Примеры математической/логической формы моделей включают линейные и нелинейные математические выражения различных порядков, нейронные сети, классификационные и регрессионные деревья/графы, методы кластеризации, рекурсивное разделение, метод опорных векторов и т.п. В одном из вариантов осуществления формой модели является линейная аддитивная модель, в которой суммированы произведения коэффициентов и значений остатков. В другом варианте осуществления форма модели представляет нелинейное произведение различных членов последовательности/остатка, включая определенные перекрестные произведения остатков (которые представляют члены взаимодействия между остатками). Фактически, не предполагается, что раскрытые варианты осуществления ограничены каким-либо конкретным форматом, поскольку любой соответствующий формат находит применение, как проиллюстрировано в настоящем раскрытии.
В некоторых вариантах осуществления модели разрабатывают по обучающим множествам активности в зависимости информации о последовательности, чтобы обеспечить математическую/логическую зависимость между активностью и последовательностью. Эта зависимость обычно проверяется до применения для прогнозирования активности новых последовательностей или воздействия остатков на интересующую активность.
Различные методики для создания моделей доступны и находят применение в настоящем изобретении. В некоторых вариантах осуществления методики включают в себя оптимизацию моделей или минимизацию ошибок модели. Конкретные примеры включают частичные наименьшие квадраты, ансамблевую регрессию, случайный лес, различные другие методы регрессии, а также методики нейронных сетей, рекурсивное разделение, методики опорных векторов, CART (деревья классификации и регрессии), и/или т.п. Обычно, методика должна произвести модель, которая может отличить остатки, которые оказывают значительное влияние на активность от тех, которые не оказывают. В некоторых вариантах осуществления модели также упорядочивают индивидуальные остатки или положения остатков на основании их воздействия на активность. Не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом для создания модели, поскольку любой соответствующий способ, известный в технике, находит применение в настоящем изобретении.
В некоторых вариантах осуществления модели создаются посредством методики регрессии, которая идентифицирует ковариацию независимых и зависимых переменных в обучающем множестве. Различные методики регрессии известны и широко применяются. Примеры включают множественную линейную регрессию (MLR), регрессию главных компонент (PCR) и регрессия частичных наименьших квадратов (PLS). В некоторых вариантах осуществления модели создаются с применением методик, которые включают в себя множество составных частей, включая, ансамблевую регрессию и случайный лес, но не ограничиваясь указанным. Эти и любые другие соответствующие методики находят применение в настоящем изобретении. Не предполагается, что настоящее изобретение ограничено какой-либо конкретной методикой.
MLR является самой простой из этих методик. Она применяется просто для решения множества уравнений относительно коэффициентов обучающего множества. Каждое уравнение относится к активности элемента обучающего множества (то есть зависимым переменным) при наличии или отсутствии конкретного остатка в конкретном положении (то есть независимые переменные). В зависимости от количества возможных вариантов остатка в обучающем множестве число этих уравнений может быть довольно большим.
Как и MLR, PLS и PCR создают модели по уравнениям, связывающим активность последовательности со значениями остатков. Однако данные методики делают это другим образом. Они сначала выполняют преобразование координат с целью сокращения числа независимых переменных. Затем они выполняют регрессию на преобразованных переменных. В MLR имеется потенциально очень большое количество независимых переменных: две или более для каждого положения остатка, которое изменяется в пределах обучающего множества. С учетом того, что белки и интересующие пептиды часто являются достаточно большими, и обучающее множество может предоставлять множество различных последовательностей, количество независимых переменных может быстро стать очень большим. В результате сокращения количества с целью сосредоточения на тех, которые обеспечивают большую часть изменчивости во множестве данных, PLS и PCR обычно требуют меньшего количества выборок и упрощают этапы, включенные в создание моделей.
PCR аналогична регрессии PLS в том, что фактическая регрессия выполняется на относительно небольшом количестве скрытых переменных, полученных посредством преобразования координат необработанных независимых переменных (то есть значений остатков). Различие между PLS и PCR заключается в том, что скрытые переменные в PCR создаются посредством максимизации ковариации между независимыми переменными (то есть значениями остатка). В регрессии PLS скрытые переменные создаются таким образом, чтобы максимизировать ковариацию между независимыми переменными и зависимыми переменными (то есть значениями активности). Частичная регрессия наименьших квадратов описана в Hand, D.J., и соавт. (2001) Principles of Data Mining (Adaptive computation and Machine Learning), Бостон, Массачусетс, MIT Press, и в Geladi, и соавт. (1986) "Partial List-Squares Regression: a Tutorial", Analytica Chimica Acta, 198: 1-17. Обе эти ссылки включены в настоящее раскрытие посредством ссылки для всех целей.
В PCR и PLS непосредственным результатом регрессионного анализа является выражение для активности, которое представляет собой функцию взвешенных скрытых переменных. Это выражение может быть преобразовано к выражению для активности как функции исходных независимых переменных посредством выполнения преобразования координат, которое преобразует скрытые переменные обратно в исходные независимые переменные.
По существу, и PCR, и PLS сначала понижают размерность информации, содержавшейся в обучающем множестве, и затем выполняют регрессионный анализ преобразованного множества данных, которое было преобразовано с целью создания новых независимых переменных, но при этом сохраняет исходные значения зависимой переменной. Преобразованные версии множеств данных могут давать в результате только относительно немного выражений для выполнения регрессионного анализа. В протоколах, в которых какое-либо снижение размерности не выполнялось, необходимо рассмотреть каждый отдельный остаток, который может быть изменен. В результате может быть получено очень большое множество коэффициентов (например, 2N коэффициентов для двусторонних взаимодействий, где N представляет собой количество положений остатка, которые могут измениться в обучающем множестве). В типичном анализе главных компонентов используется только 3, 4, 5, 6 главных компонентов.
Способность методов машинного обучения подгонять обучающие данные часто называют "подгонкой модели" и в методиках регрессии, таких как MLR, PCR и PLS, подгонку модели обычно измеряют по сумме квадратов разностей между измеренными и спрогнозированными значениями. Для данного обучающего множества оптимальная подгонка модели будет достигнута с применением MLR, при этом PCR и PLS часто дают худшую подгонку модели (выше сумма квадратичной ошибки между измерениями и прогнозированиями). Однако, главное преимущество использования методик регрессии скрытой переменной, таких как PCR и PLS, заключается в прогнозирующей способности таких моделей. Получение подгонки модели с очень небольшой суммой квадратичной ошибки никоим образом не гарантирует, что модель будет в состоянии точно прогнозировать новые образцы, не присутствующие в обучающем множестве - фактически, часто происходит противоположное, особенно когда имеется много переменных и только несколько наблюдений (то есть образцов). Таким образом, методики регрессии скрытой переменной (например, PCR, PLS), хотя и часто имеют худшую подгонку модели на обучающих данных, обычно являются более гибкими и способными прогнозировать новые образцы вне обучающего множества более точно.
Другим классом инструментов, которые могут применяться для создания моделей в соответствии с настоящим раскрытием, являются методы опорных векторов (SVM). Эти математические инструменты берут множества данных обучения для последовательностей, которые были классифицированы по двум или более группам на основании активностей в качестве входных данных. Методы опорных векторов функционируют посредством взвешивания элементов обучающего множества по-разному в зависимости от того, насколько они близко к границе гиперплоскости, разделяющей "активные" и "неактивные" элементы обучающего множества. В данной методике требуется, чтобы ученый сначала решил, какие элементы обучающего множества поместить в "активную" группу и какие элементы обучающего множества поместить в "неактивную" группу. В некоторых вариантах осуществления это выполняется посредством выбора соответствующего числового значения для уровня активности, которое служит границей между "активными" и "неактивными" элементами обучающего множества. По этой классификации метод опорных векторов генерирует вектор, W, который может предоставить значения коэффициентов для индивидуальных независимых переменных, определяющих последовательности для членов активных и неактивных групп в обучающем множестве. Эти коэффициенты могут использоваться, чтобы "упорядочить" индивидуальные остатки, как описано в другом месте настоящего раскрытия. Методика применяется для идентификации гиперплоскости, которая максимизирует интервал между самыми близкими элементами обучающего множества на противоположных сторонах этой плоскости. В другом варианте осуществления выполняется регрессионное моделирование на основе опорных векторов. В этом случае, зависимая переменная представляет собой вектор непрерывных значений активности. Регрессионная модель на основе опорных векторов генерирует вектор коэффициентов, W, который может применяться для ранжирования индивидуальных остатков.
SVM применялись для изучения больших множеств данных во многих исследованиях и нашли широкое применение в микропанелях ДНК. Их потенциальные преимущества включают в себя возможность точного различения (посредством взвешивания) факторов, которые отделяют выборки друг от друга. До той степени, в которой SVM могут точно отделить, какие остатки вносят вклад в функции, данный метод может являться особенно полезным инструментом для ранжирования остатков. SVM описаны в работе S. Gunn (1998) "Support Vector Machines for Classification and Regression", Технический отчет, факультет инженерии и прикладных наук, отдел электроники и информатики, университет Саутгемптона, которая включена в настоящее раскрытие посредством ссылки для всех целей.
В некоторых вариантах осуществления изобретения другой класс инструментов, которые могут применяться для создания моделей, представляет собой классификацию и регрессию, основанные на ансамбле деревьев классификации с использованием случайных входных данных, примером которых является случайный лес. См. Breiman (2001). "Random Forests", Machine Learning 45 (1): 5-32. Случайные леса представляют собой такую комбинацию прогнозных деревьев, в которой каждое дерево зависит от значений случайного вектора, выборка которых получена независимо и с одним и тем же распределением для всех деревьев в лесу. Случайный лес представляет собой обучающий ансамбль, состоящий из изолирования неподрезанных обучающих деревьев решений со случайным выбором характеристик при каждом разделении дерева решений. Ошибка обобщения для лесов сходится к пределу, когда число деревьев в лесу становится большим.
Случайные леса могут быть созданы следующим образом:
1) Если число случаев в обучающем множестве равно N, осуществляется случайная выборка N случаев, но с возвращением, из исходных данных. Эта выборка являться обучающим множество для выращивания дерева.
2) Если имеется М входных независимых переменных, число m<<М задают таким образом, чтобы в каждой вершине в дереве случайным образом выбиралось m из M переменных, и лучшее разделение по этим m применялось для разделения вершины. Значение m считается постоянным во время выращивания леса.
3) В некоторых реализациях каждое дерево выращивают до самой большой возможной степени. Подрезание отсутствует.
4) Затем создается большое количество деревьев, k=1, …, K (обычно K>=100).
5) После того, как было создано большое количество деревьев, все они «голосуют» за классификацию интересующих переменных. Например, каждое из них может внести вклад в итоговый прогноз активности или внести вклад в конкретные мутации.
6) Случайный лес затем классифицирует x (например, последовательность мутаций или другую независимую переменную) посредством выбора получившего наибольшее количество голосов класса из всех прогнозных деревьев в лесу.
Величина ошибки леса зависит от корреляции между произвольными двумя деревьями в лесу. Увеличение корреляции увеличивает величину ошибки леса. Величина ошибки леса зависит от мощности каждого индивидуального дерева в лесу. Дерево с низкой величиной ошибки является хорошим классификатором. Увеличение мощности индивидуальных деревьев уменьшает величину ошибки леса. Уменьшение m приводит к снижению и корреляции, и мощности. Его увеличение увеличивает и то, и другое. Где-то между этими значениями находится промежуточный "оптимальный" диапазон m - обычно достаточно широкий.
Методики случайного леса могут применяться для качественных переменных, а также для непрерывных переменных в регрессионных моделях. В некоторых вариантах осуществления изобретения, модели случайного леса обладают предиктивной силой, сопоставимой с SVM и моделями нейронной сети, но имеют тенденцию к обладанию более высокой вычислительной эффективностью вследствие, среди других причин, того, что перекрестная проверка встроена в процесс моделирования, и отдельный процесс для перекрестной проверки не является необходимым.
i) Линейные модели
В то время как настоящее раскрытие направлено на нелинейные модели, они могут быть более легко поняты в контексте линейных моделей активности в зависимости от последовательности. Дополнительно, в некоторых вариантах осуществления, линейная модель используется в качестве "базовой" модели в пошаговом процессе для создания нелинейной модели. В общем случае модель линейной регрессии активности в зависимости от последовательности имеет следующую форму:
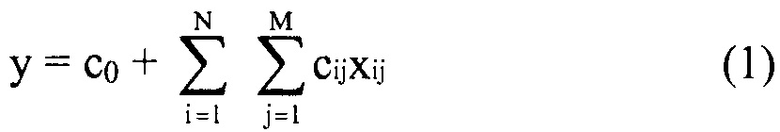
В этом линейном выражении y представляет собой вычисленное решение, тогда как cij и xij представляют собой коэффициент регрессии и битовое значение, или фиктивную переменную, используемую для представления выбора остатка, соответственно, в положении i в последовательности. В последовательностях библиотеки вариантов белка имеется N положений, и каждое из них может быть занято одним или более остатками. В любом заданном положении может находиться от j=1 до М различных типов остатков. Эта модель предполагает линейную (аддитивную) зависимость между остатками в каждом положении. Расширенная версия уравнения 1 приведена ниже:
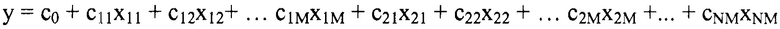
Как указано, данные в форме активности и информации о последовательности получены из начальной библиотеки вариантов белка и используются для определения регрессионных коэффициентов модели. Фиктивные переменные сначала идентифицируются по выравниванию последовательностей вариантов белка. Положения аминокислотных остатков определяют среди последовательностей вариантов белка, в которых аминокислотные остатки в этих положениях отличаются между последовательностями. Информация об аминокислотном остатке в некоторых или всех этих положениях изменяющихся остатков может быть включена в модель последовательности-активности.
Таблица I содержит информацию о последовательности в форме положений изменяющихся остатков и типов остатков для 10 иллюстративных вариантов белков, наряду со значениями активности, соответствующими каждому варианту белка. Они являются репрезентативными элементами большего множества, которое обязано генерировать достаточное количество уравнений для решения относительно всех коэффициентов. Таким образом, например, для иллюстративных последовательностей вариантов белка в таблице I, положения 10, 166, 175 и 340 являются положениями изменяющихся остатков, и все остальные положения, то есть не обозначенные в таблице, содержат остатки, которые идентичны в вариантах 1-10.
В этом примере эти 10 вариантов могут содержать или не содержать последовательность остова дикого типа. В некоторых вариантах осуществления модель, разработанная с учетом данных всех вариантов, включая последовательность остова дикого типа, создавать проблему точной мультиколлинеарности, или ловушку фиктивных переменных. Эта проблема может быть решена посредством различных методик. Некоторые варианты осуществления могут исключить данные остова дикого типа из разработки модели. Некоторые варианты осуществления могут отбрасывать коэффициенты, представляющие остов дикого типа. Некоторые варианты осуществления могут применять такие методики, как PLS-регрессия, чтобы решить проблему мультиколлинеарности.
Иллюстративные данные последовательности и активности
Таким образом, на основании уравнения 1, регрессионная модель может быть получена из систематически изменяемой библиотеки в таблице I, то есть:
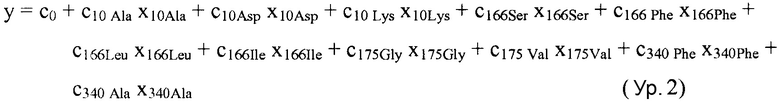
Битовые значения (фиктивные переменные x) могут быть представлены как 1 или как 0, что отражает наличие или отсутствие обозначенного аминокислотного остатка, или, альтернативно, как 1 или -1, или некоторое другое суррогатное представление. Например, с использованием обозначений 1 или 0, x10Ala был бы "1" для варианта 1 и "0" для варианта 2. При использовании обозначений 1 или -1, x10Ala был бы "1" для варианта 1 и "-1" для варианта 2. Коэффициенты регрессии могут, таким образом, быть получены из уравнений регрессии на основании информации об активности последовательности для всех вариантов в библиотеке. Примеры таких уравнений для вариантов 1-10 (с использованием обозначений 1 или 0 для x) приведены ниже:
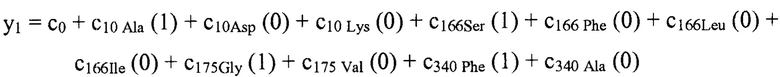
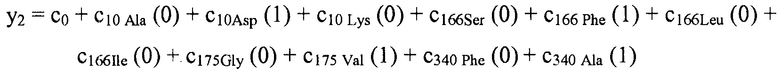
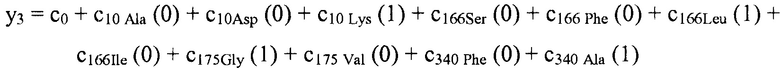
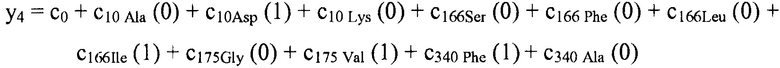
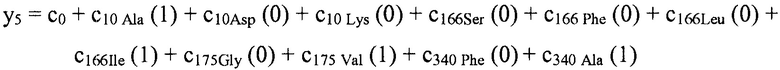
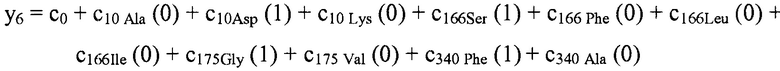
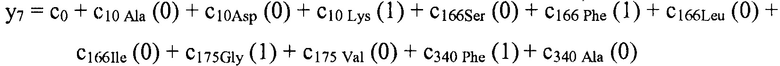
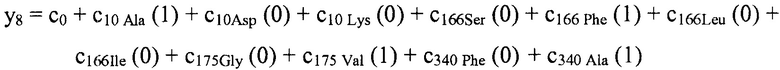
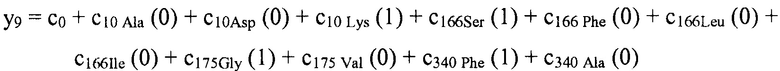
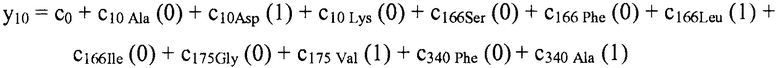
Полная система уравнений может быть легко решена с применением любой соответствующей методики регрессии (например, PCR, PLS, или MLR) с целью определения значений для коэффициентов регрессии, соответствующих каждому остатку и интересующему положению. В этом примере относительная величина коэффициента регрессии коррелирует с относительной величиной вклада в активность конкретного остатка в конкретном положении. Коэффициенты регрессии могут затем быть проранжированы или категоризированы иным способом с целью определения того, какие остатки имеют большую вероятность внести позитивный вклад в требуемую активность. В таблице II представлены иллюстративные значения коэффициентов регрессии, соответствующие систематически изменяемой библиотеке, иллюстрируемой в таблице I:
Иллюстративный ранговый порядок коэффициентов регрессии
Упорядоченный по рангу список коэффициентов регрессии может использоваться для создания новой библиотеки вариантов белка, которая оптимизирована относительно требуемой активности (то есть имеет улучшенную пригодность). Это может быть сделано различными способами. В одном из вариантов осуществления это выполняется посредством сохранения аминокислотных остатков, имеющих коэффициенты с самыми высокими наблюдаемыми значениями. Такие остатки представляют собой остатки, обозначенные моделью регрессии, как вносящие наибольший вклад в требуемую активность. Если отрицательные дескрипторы используются для идентификации остатков (например, 1 для лейцина и -1 для глицина), становится необходимым упорядочивать положения остатка на основании абсолютного значения коэффициента. Следует отметить, что в таких ситуациях обычно имеется только один коэффициент для каждого остатка. Абсолютное значение величины коэффициента дает ранжирование соответствующего положения остатка. Затем, становится необходимым рассмотрение знаков индивидуальных остатков для определения того, является ли каждый из них вредным или выгодным с точки зрения требуемой активности.
ii) Нелинейные Модели
Нелинейное моделирование применяется для учета взаимодействий между остатками, которые вносят вклад в активность в белках. Среда N-K описывает эту задачу. Параметр N относится к числу изменяющихся остатков в совокупности связанных последовательностей полипептидов. Параметр K представляет взаимодействие между индивидуальными остатками в пределах любого из этих полипептидов. Взаимодействие обычно является результатом близкого физического положения между различными остатками в первичной, вторичной, или третичной структуре полипептида. Взаимодействие может возникать вследствие прямых взаимодействий, косвенных взаимодействий, физико-химических взаимодействий, взаимодействий вследствие промежуточных состояний укладки, эффектов трансляции и т.п. См. Kaufman, S. и Levin, S. (1987), "Towards a general theory of abstractive walks in rugged landscapes", Journal of Theoretical Biology 128 (1) 11-45.
Параметр K определяют таким образом, что для значения K=1 каждый изменяющийся остаток (например, имеется 20 остатков) взаимодействует ровно с одним другим остатком в своей последовательности. В случае, где все остатки физически и химически отделены от влияния всех других остатков, значение K равно нулю. Очевидно, в зависимости от структуры полипептида, K может иметь широкий диапазон различных значений. На основании строго решенной структуры рассматриваемого полипептида может быть оценено значение для K. Часто, однако, дело обстоит не так.
Чисто линейная аддитивная модель активности полипептида (как описано выше) может быть улучшена посредством включения одного или более нелинейных членов взаимодействия, представляющих конкретные взаимодействия между 2 или более остатками. В контексте формы модели, представленной выше, эти члены обозначены как "перекрестные произведения", содержащие две или более фиктивных переменных, представляющих два или более конкретных остатков (каждый ассоциирован с конкретным положением в последовательности), которые взаимодействуют и оказывают существенное значительное положительное или отрицательное воздействие на активность. Например, член перекрестного произведения может иметь форму cabXaXb, где xa представляет собой фиктивную переменную, представляющую наличие конкретного остатка в конкретном положении в последовательности, и переменная Xb представляет наличие конкретного остатка в другом положении (которое взаимодействует с первым положением) в последовательности полипептида. Детальный пример формы модели показан ниже.
Наличие всех остатков, представленных в члене перекрестного произведения (то есть каждого из двух или более конкретных типов остатков в конкретно идентифицированных положениях), оказывает влияние на суммарную активность полипептида. Воздействие может быть проявлено разными способами. Например, каждый из индивидуальных взаимодействующих остатков, если он присутствует в полипептиде один, может оказывать отрицательное влияние на активность, но когда они присутствуют в полипептиде, общий эффект будет положительным. Обратное может иметь место в других случаях. Кроме того, может возникать синергический эффект, при котором каждый из индивидуальных остатков оказывает относительно ограниченное влияние на активность, но когда все они присутствуют, влияние на активность будет больше, чем кумулятивные активности всех индивидуальных остатков.
В некоторых вариантах осуществления нелинейные модели содержат член перекрестного произведения для каждой возможной комбинации взаимодействующих переменных остатков в последовательности. Однако это не представляет физическую реальность, поскольку только подмножество переменных остатков фактически взаимодействует друг с другом. Кроме того, это привело бы к "переобучению", в результате чего была бы получена модель, которая дает ложные результаты, которые являются проявлениями конкретных полипептидов, использованных для создания модели, и не представляют фактические взаимодействия в пределах полипептида. Корректное число членов перекрестного произведения для модели, которая представляет физическую реальность и избегает переобучения, определяется значением K. Например, если K=1, число членов взаимодействия перекрестного произведения равно N.
При построении нелинейной модели в некоторых вариантах осуществления важно идентифицировать те члены взаимодействия перекрестного произведения, которые представляют реальные структурные взаимодействия, которые оказывают значительное влияние на активность. Это может быть выполнено различными способами, включая, но не ограничиваясь, прямое добавление, при котором члены-кандидаты перекрестного произведения добавляют к исходному линейному члену модели только по одному, пока добавление членов не перестанет быть статистически значимым, и обратное изымание, при котором все возможные члены перекрестного произведения представлены в начальной модели и удаляются по одному. Иллюстративные примеры, представленные ниже, включают в себя применение методик пошагового добавления и изымания с целью идентификации полезных нелинейных членов взаимодействия.
В некоторых вариантах осуществления подход к созданию нелинейной модели, содержащей такие члены взаимодействия, является тем же самым как подходом, описанным выше для создания линейной модели. Другими словами, обучающее множество используется для того, чтобы "подогнать" данные к модели. Однако, один или более нелинейных членов, предпочтительно, члены перекрестного произведения, обсужденные выше, добавлены к модели. Далее, полученная в результате нелинейная модель, как и линейные модели, описанные выше, может применяться для ранжирования значимости различных остатков для общей активности полипептида. Различные методики могут применяться для идентификации наилучшей комбинации переменных остатков в соответствии со спрогнозированным нелинейным уравнением. Подходы к ранжированию остатков описаны ниже. В некоторых вариантах осуществления используются очень большие количества возможных членов перекрестного произведения для переменных остатков, даже когда они ограничены взаимодействиями, вызванными только двумя остатками. С увеличением числа взаимодействий количество потенциальных взаимодействий для рассмотрения в нелинейной модели возрастает экспоненциальным образом. Если модель включает возможность взаимодействий, которые включают три или более остатков, число потенциальных членов возрастает еще быстрее.
В простом иллюстративном примере, в котором имеется 20 переменных остатков и K=1 (это предполагает, что каждый переменный остаток взаимодействует с одним другим переменным остатком), в модели должно быть 20 членов взаимодействия (перекрестные произведения). Если будет иметься некоторое меньшее число членов взаимодействия, то модель не будет полностью описывать взаимодействия (хотя некоторые из взаимодействий, возможно, не оказывают значительного влияния на активность). Напротив, если имеется больше членов взаимодействия, модель может быть переобученной на множестве данных. В этом примере имеется N*(N-l)/2, или 190, возможных пар взаимодействий. Нахождение комбинации 20 уникальных пар, которые описывают эти 20 взаимодействий в последовательности, является значительной вычислительной задачей, поскольку существует приблизительно 5,48×1026 возможных комбинаций.
Многочисленные методики могут применяться для идентификации соответствующих членов перекрестного произведения. В зависимости от размера задачи и доступной вычислительной мощности, возможно исследовать все возможные комбинации и таким образом идентифицировать одну модель, которая наилучшим образом подогнана под данные. Однако часто задача является трудоемкой в вычислительном отношении. Таким образом, в некоторых вариантах осуществления применяется эффективный алгоритм поиска или аппроксимация. Как указано в настоящем раскрытии, одной из подходящих методик поиска является пошаговая методика. Однако не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом идентификации соответствующих членов перекрестного произведения.
Иллюстративный пример представлен ниже в таблице III, чтобы показать значение включения нелинейных членов перекрестного произведения в модель, прогнозирующую активность по информации о последовательности. Этот пример представляет собой нелинейную модель, в которой предполагается, что имеется только два варианта остатков в каждом переменном положении в последовательности. В этом примере последовательность белка преобразуется в закодированную последовательность с использованием фиктивных переменных, которые соответствуют выбору A или выбору B, с использованием +1 и -1, соответственно. Модель устойчива к произвольному выбору того, какое числовое значение используется для назначения выбора каждого остатка. Положения изменений, показанные в первой строке таблицы III, не указывают фактические положения последовательности в последовательности белка. Вместо этого они представляют собой произвольные обозначения, представляющие любые 10 гипотетических положений в последовательности белка, в которые могут изменяться в зависимости от одного из двух вариантов, показанных во второй и третьей строках таблицы III для выбора остатка A и выбора остатка B.
Пример кодирования остатков в положениях, каждое из которых имеет два варианта
При этой схеме кодирования линейная модель, использованная для ассоциирования последовательностей белка с активностью, может быть записана следующим образом:
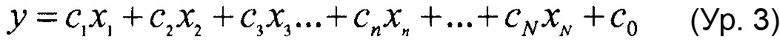
где y представляет собой отклик (активность), cn представляет собой регрессионный коэффициент для выбора остатка в положении n, x представляет собой фиктивную переменную, кодирующую выбор остатка (+1/-1) в положении n, и c0 обозначает среднее значение отклика. Эта форма модели предполагает отсутствие взаимодействий между изменяющимися остатками (то есть каждый выбор остатка независимо вносит вклад в суммарную пригодность белка).
Нелинейная модель включает в себя определенное число (пока еще неопределенное) членов перекрестного произведения, чтобы учесть взаимодействия между остатками:
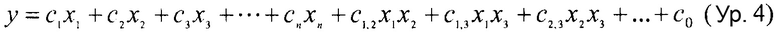
где переменные являются такими же, как в уравнении (3), но теперь присутствуют нелинейные члены, например, c1,2 представляет собой регрессионный коэффициент для взаимодействия между переменными положениями 1 и 2.
Для того чтобы оценить производительность линейных и нелинейных моделей, был использован синтетический источник данных, известный как NK среда (Kauffman и Levin, 1987). Как упомянуто выше, N представляет собой число переменных положений в моделируемом белке, и K является эпистатическим соединением между остатками. Кроме того, множество синтетических данных было сгенерировано in silico.
Это множество данных использовалось для генерации исходного обучающего множества с S=40 синтетическими образцами, с переменными положениями N=20 и K=1 (еще раз, для K=1, каждое переменное положение функционально соединено с одним другим переменным положением). При генерации рандомизированных белков каждое переменное положение имело равную вероятность содержания фиктивных переменных +1 или -1. Взаимодействия между остатками (представленные перекрестными произведениями) и фактические активности были известны для каждого элемента синтетического обучающего множества. Другие V=100 образцов был сгенерированы для использования в проверке. Снова, взаимодействия между остатками и активности были известны для каждого элемента проверочного множества.
Обучающие множества использовались для создания и линейных, и нелинейных моделей. Некоторые нелинейные модели были сгенерированы с выбором членов перекрестного произведения, и другие нелинейные модели были сгенерированы без выбора таких членов. Модели для фигуры 3A-F были сгенерированы с применением способа моделирования на основе генетического алгоритма, в то время как модели для фигуры G-H были сгенерированы с применением способа пошагового моделирования. Хотя количественное преимущество моделей, имеющих и линейные, и нелинейные члены, относительно моделей, имеющих только линейные члены, отличается между способом моделирования, основанном на генетическом алгоритме, и способом пошагового моделирования, результаты показывают обобщаемое преимущество моделей с нелинейными членами, независимо от способов моделирования. Фактически, не предполагается, что настоящее изобретение ограничено какими-либо конкретными способами, поскольку любые соответствующие способы моделирования находят применение в настоящем изобретении.
Для размера обучающего множества S=40, описанного выше, линейная модель была способна к достаточно хорошему сопоставлению измеренных и спрогнозированных значений, но демонстрировала более слабую корреляцию при проверке на данных, не присутствовавших в обучающем множестве (см. фигуру 3A). Как показано, темные точки данных представляют наблюдаемую активность 40 точек обучающих данных по сравнению с прогнозами, сделанными линейной моделью. Легкие точки данных представляют прогнозы, сделанные той же самой моделью, созданной из 40 учебных образцов, и используемые для прогнозирования проверочных образцов V, ни один из которых не присутствовал в исходном обучающем множестве. Проверочное множество предоставляет хорошую меру истинной прогнозирующей способности модели, в противоположность обучающему множеству, которое может пострадать от проблемы переобучения модели, особенно для нелинейных случаев, описанных ниже.
Этот результат для обучающего множества S=40, описанного выше, является значимым, с учетом того, что линейная модель применялась для моделирования нелинейной среды пригодности. В этом случае, линейная модель могла бы, в лучшем случае, описать средний вклад в пригодность для выбора заданного остатка. При условии наличия достаточного количества средних вкладов, рассматриваемых в комбинации, линейная модель примерно прогнозирует фактический измеренный отклик. Результаты проверки для линейной модели были несколько лучше, когда размер обучающего множества был увеличен до S=100 (см. фигуру 3B). Тенденция относительно простых моделей к недообучению по данным известна как "систематическая ошибка" (предубеждение).
Когда нелинейная модель обучалась с использованием только S=40 образцов, корреляция с элементами обучающего множества была отличной (см. фигуру 3C). К сожалению, в этом иллюстративном примере, модель обеспечивала ограниченную предиктивную силу вне обучающего множества, что доказывается его ограниченной корреляцией с измеренными значениями в проверочном множестве. Эта нелинейная модель, с множеством потенциальных переменных (210 возможных), и ограниченными учебными данными для способствования идентификации соответствующих членов перекрестного произведения, была способна, по существу, только запомнить множество данных, на котором она обучалась. Эта тенденция моделей высокой сложности к переобучению на основе данных известна как "изменчивость". Компромисс между систематической ошибкой и изменчивостью представляет собой фундаментальную проблему в машинном обучении, и некоторая форма проверки практически всегда требуется для ее решения при работе с новыми неохарактеризованными задачами машинного обучения.
Однако когда нелинейная модель была обучена с использованием большего обучающего множества (S=100), как показано на фигуре 3D, нелинейная модель работала крайне хорошо и для учебного прогнозирования, и, что более важно, для проверочного прогнозирования. Проверочные прогнозы были достаточно точными, и большинство точек данных затемнено темными кругами, используемыми для изображения обучающего множества.
Для сравнения, фигуры 3E и 3F демонстрируют производительность нелинейных моделей, подготовленных без тщательного отбора членов перекрестного произведения. В отличие от моделей, на фигурах 3C и 3D, был выбран каждый возможный член перекрестного произведения (то есть 190 членов перекрестного произведения для N=20). Как показано на этих фигурах, способность прогнозировать активность проверочного множества сравнительно плохая по сравнению со способностью нелинейных моделей, сгенерированных с тщательным отбором членов перекрестного произведения. Эта плохая способность прогнозировать проверочные данные является проявлением переобучения.
На фигурах 3G и 3H, соответственно, показана предиктивная сила, указываемая остаточными членами линейной модели и пошаговой нелинейной модели для данных, моделируемых in silico. Ступенчатая нелинейная модель была реализована в соответствии с общим описанием, приведенным выше, и более конкретным описанием, приведенным ниже.
Для того чтобы проверить эти модели, были сгенерированы модельные данные. Генератор случайных чисел R создавался на основании нормального распределения со средним MN и стандартным отклонением SD. Затем было определено множество из 10 мутаций. Они были названы М1, M2 … M10 (эта схема именования была произвольной). Этот шаг моделирует создание разнообразия.
Каждая мутация представляла изменение аминокислоты в заданном положении в пределах последовательности белка, и каждое положение было независимым от других положений. Каждая мутация, указанная выше, имела случайное значение активности, присвоенное на основании R (MN=0, SD=0,2). Шесть мутаций, приведенных выше, были выбраны и объединены в три пары P. Эти пары представляли эпистатические взаимодействия между мутациями.
Значение активности AP было присвоено каждой паре P на основании R (MN=0, SD=0,2). Была создана библиотека из L=50 вариантов, в которой каждый вариант содержал случайное число мутаций М, определенное выше - случайное число мутаций было задано округленным абсолютным значением R (MN=4, С=0,25). Этот шаг моделирует создание библиотеки и секвенирование.
Активность каждого варианта в L была вычислена посредством, сначала, добавления 1,0 (заданная активность дикого типа, последовательность без мутаций) к значению активности для каждой попарной мутации PA (если присутствовали обе мутации), сопровождаемый, после чего следовало добавление оставшихся одиночных мутаций (A). Погрешность анализа моделировалась посредством добавления к конечному значению для каждого варианта случайной величины R (MN=0, SD=0,005). Этот шаг моделирует скрининг вариантов.
Линейная модель LM была создана на основании данных с последнего шага. Эта модель содержала десять независимых переменных/коэффициентов, каждый из которых представлял одну мутацию М. Линейная модель затем подгонялась с применением обыкновенной регрессии наименьших квадратов и данных, полученных выше.
Способ пошагового добавления затем применялся для выбора модели MM на основании данных, полученных выше, с основной моделью LM, с применением AIC в качестве критерия выбора, и выбора моделей, которые содержали только коэффициенты, представляющие одиночные мутации и парные взаимодействия. См. описание выбора модели ниже для получения дальнейшей информации о способе выбора модели. Наилучшая модель, выбранная AIC, была подогнана с применением обыкновенной регрессии наименьших квадратов.
Для того чтобы оценить прогнозирующую способность линейной модели и нелинейной модели, процедуры, описанные выше, были повторены 20 раз. Прогнозы моделей были изображены на графике в сравнении со смоделированными данными, при этом на фигуре 3G показана линейная модель и на фигуре 3H показана пошаговая нелинейная модель. Модели применялись для прогнозирования значения одиночных мутаций, описанных выше. Это прогнозирование выполнялось с применением моделей для прогнозирования варианта, содержащего только одну интересующую мутацию, и изымания 1,0 (дикий тип). Как очевидно из фигур 3G и 3H, нелинейная модель более точно прогнозирует значения, имеющие более линейный тренд и меньшие остаточные члены.
iii) Выбор модели
В некоторых вариантах осуществления способы пошагового добавления или изымания применяют для подготовки моделей с нелинейными членами взаимодействия. Путем реализации операции, показанной в блоке 107 с фигуры 1, конечная модель с высокой предиктивной силой, содержащая члены взаимодействия, предоставляется посредством пошагового добавления или изымания членов взаимодействия из базовой модели. На фигуре 4A представлена блок-схема реализации операции блока 107 с фигуры 1 посредством добавления членов взаимодействия к базовой модели и оценки новых моделей с целью создания наилучшей конечной модели.
В этом примере модель последовательности оснований не содержит членов взаимодействия. Способ сначала устанавливает текущую модель последовательности и лучшую модель последовательности как базовую модель последовательности оснований в блоке 409. Способ определяет пул членов взаимодействия для вариантов последовательности. Эти члены взаимодействия могут включать в себя любое число парных взаимодействий или взаимодействий более высокого порядка двух или более аминокислотных остатков. Смотри блок 411. Хотя блок 409 проиллюстрирован как происходящий до блока 411, порядок этих двух шагов неважен. В некоторых вариантах осуществления пул членов взаимодействия включает факториальные комбинации всех интересующих аминокислотных остатков. В некоторых дополнительных вариантах осуществления включены, по меньшей мере, все члены парного взаимодействия. В некоторых дальнейших вариантах осуществления включены члены парного и трехстороннего взаимодействия.
После создания базовой модели способ выбирает член взаимодействия, который еще не был проверен, из пула. Способ затем создает новую модель последовательности путем добавления выбранного члена взаимодействия к текущей модели последовательности. Смотри блок 413. Способ затем оценивает предиктивную силу новой модели последовательности с применением способа выбора модели, имеющего предубеждение против включения дополнительных членов взаимодействия. Смотри блок 415. Способ определяет, больше ли предиктивная сила новой модели последовательности, чем предиктивная сила наилучшей модели последовательности. Смотри блок решения 417. Например, способ может применять методику, использующую определение "правдоподобия" (например, AIC) в качестве критерия выбора модели. В таких случаях только модель, имеющая значение AIC, меньшее, чем ранее проверенная модель, считается имеющей более высокую предиктивную силу.
В некоторых вариантах осуществления способ выбора смещается против моделей с большим количеством параметров. Примеры таких способов выбора включают в себя, но не ограничены, информационный критерий Акаике (AIC) и Байесов информационный критерий (BIC), и их вариации. Например, AIC может быть вычислен как:
AIC =-2logeL+2k
где L представляет собой правдоподобие модели при наличии множества данных, и k является числом свободных параметров в модели.
В некоторых вариантах осуществления вероятность модели при наличии множества данных, может быть вычислена различными способами, включая, но не ограничиваясь, метод максимального правдоподобия. Например, для бинарной зависимой переменной, где активность или присутствует, или отсутствует для одного наблюдения, вероятность модели может быть вычислена как:
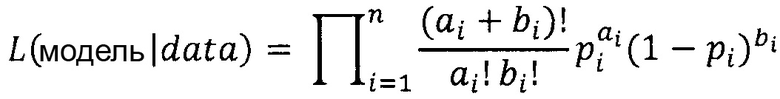
где n представляет собой общее количество точек данных в множестве данных; ai и bi представляют собой количество наблюдаемых испытаний, содержащих i-е условие; p представляет собой вероятность того, что зависимая переменная будет наблюдаться в соответствии с прогнозом от модели.
В некоторых вариантах осуществления, включающих ряд вложенных моделей, как в регрессионных моделях с прогрессивно увеличивающимся количеством членов взаимодействия (и ассоциированных коэффициентов) по сравнению с базовой моделью, более сложные модели обеспечивают одинаково хорошие или лучшие подгонки, чем более простые, даже если дополнительные коэффициенты являются фиктивными, потому что более сложная модель обладает дополнительными степенями свободы. В некоторых вариантах осуществления AIC штрафует более сложную модель до такой степени, что повышение степени согласия больше, чем смещение за счет фиктивных параметров. При выборе модели меньшее значение AIC показывает лучшую модель.
В примере, показанном на фигуре 4A, если предиктивная сила новой модели последовательности больше, чем предиктивная сила лучшей модели последовательности, то способ устанавливает новую модель в качестве наилучшей модели. Смотри блок 419. Затем способ проверяет, остались ли в пуле какие-либо дополнительные члены взаимодействия, которые не были проверены. Смотри блок решения 421. Если так, процесс идет в обратную сторону к блоку 413, таким образом, формируя внутренний цикл для проверки всех доступных членов взаимодействия, доступных в пуле взаимодействия. Через итерации внутреннего цикла единственный наилучший член взаимодействия может быть найден и добавлен к модели.
После того, как все члены взаимодействия были проверены, и внутренний цикл завершился, идентифицируется наилучшая модель, имеющая один дополнительный член взаимодействия, при условии фактического наличия модели, имеющей большую предиктивную силу по сравнению с предыдущей лучшей моделью. Смотри блок решения 423. В таких вариантах осуществления способ устанавливает текущую модель в качестве наилучшей модели, и исключает члены взаимодействия лучшей модели из пула доступных членов взаимодействия. Смотри блок 425. Затем способ возвращается к блоку 413. Этот внешний цикл ищет следующий лучший член взаимодействия, который может улучшить предиктивную силу модели. Если такой член взаимодействия найден, поиск следующего лучшего члена взаимодействия продолжается во внешнем цикле до тех пор, пока нельзя будет идентифицировать модель, имеющую предиктивную силу, превышающую предиктивную силу предыдущей наилучшей модели последовательности.
Когда больше не может быть найдено членов взаимодействия, улучшающих модель, способ устанавливает наилучшую модель в качестве конечной модели. Смотри блок 427. Поиск наилучшей модели для заданных данных последовательности и активности завершается. Модель затем применяется для прогнозирования активности новых последовательностей. Такие прогнозы могут направлять отбор последовательностей для дальнейшего изменения и проверки.
В определенных вариантах осуществления каждый из доступных членов взаимодействия в пуле членов взаимодействия обрабатывают как оказывающий потенциально равное влияние на качество или предиктивную силу модели. Другими словами, в реализации, каждый из доступных членов взаимодействия в пуле имеет одинаковую вероятность выбора для рассмотрения во время конкретной итерации. В некоторых вариантах осуществления доступные члены взаимодействия выбирают случайным образом или в некоторых произвольных порядках. В некоторых других вариантах осуществления члены взаимодействия смещены или взвешены таким образом, что некоторые члены имеют большую вероятность быть выбранными для рассмотрения, чем другие, во время данной итерации. Смещение или взвешивание, в определенных вариантах осуществления, могут быть применены на основании физической или теоретической информации о взаимодействиях. Например, может быть известно, что мутации в двух конкретных областях белка, вероятно, будут физически близкими друг к другу и, следовательно, будут взаимодействовать. Члены взаимодействия, имеющие отношение к остаткам в этих двух общих областях, могут иметь смещения для выбора во время итеративного процесса улучшения модели.
Псевдокод, иллюстрирующий процессы, аналогичные процессам с фигуры 4A, приведен ниже:
УСТАНОВИТЬ Coeff = Члены Взаимодействия для тестирования
Best = Базовая модель
count = 1
ПОКА count > 0
count = 0
BestFromRound = Best
BestCoefficient = NULL
ЦИКЛ каждого члена взаимодействия в Coeff
TestModel = (best + Член Взаимодействия)1
ЕСЛИ TestModel ЛУЧШЕ ЧЕМ BestFromRound ТО2
BestFromRound = TestModel
Count ++
BestCoefficient = Член Взаимодействия
КОНЕЦ ЕСЛИ
КОНЕЦ ЦИКЛА
ЕСЛИ count > 0 ТО
Best = BestFromRound
Удалить BestCoefficient ИЗ Coeff3
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
Элемент 1 добавляет тестовый член взаимодействия к регрессионной модели
Элемент 2 представляет сравнение модели, один или более информационного критерия Акаике (AIC), Байесова информационного критерия (BIC), перекрестной валидации (ошибки среднего), дисперсионного анализа или вклада коэффициентов.
Элемент 3 представлен во избежание повторного тестирования члена взаимодействия
Фигура 4B представляет блок-схему, показывающую вариант осуществления операции, показанной в блоке 107 с фигуры 1. В этом процессе члены взаимодействия изымают из базовой модели, которая содержит все возможные члены взаимодействия из пула таких членов, с целью создания конечной наилучшей модели.
В этом варианте осуществления модель последовательности оснований содержит все члены взаимодействия в пределах заданного пула. Способ сначала устанавливает текущую модель последовательности и наилучшую модель последовательности равными базовой модели последовательности в начале процесса, блок 439. Этот вариант осуществления аналогичен конечной модели, описанной выше, в том, что весь пул членов взаимодействия может содержать любое число взаимодействий парного или более высокого порядка двух или более аминокислотных остатков. В некоторых вариантах осуществления пул членов взаимодействия содержит факториальные комбинации всех аминокислотных остатков, которые представляют интерес.
После создания базовой модели способ выбирает член взаимодействия, который еще не был проверен, из пула членов, уже включенных в базовую модель. Способ затем создает новую модель последовательности посредством изымания выбранного члена взаимодействия из текущей модели последовательности. Смотри блок 441. Способ затем оценивает предиктивную силу новой модели последовательности с применением способа выбора модели, имеющего предубеждение против дополнительных членов взаимодействия. Смотри блок 443. Способ оценивает, является ли предиктивная сила новой модели последовательности выше, чем предиктивная сила наилучшей модели последовательности. См. операцию принятия решения, показанную в блоке 445. В некоторых вариантах осуществления AIC применяется в качестве критерия выбора модели, в результате чего модель, имеющая значение AIC, меньшее, чем у ранее проверенной модели, считается имеющей более высокую предиктивную силу.
В этом иллюстративном примере, если предиктивная сила новой модели последовательности больше чем предиктивная сила наилучшей модели последовательности, то способ устанавливает новую модель в качестве наилучшей модели. Смотри блок 447. Затем способ проверяет, остались ли в пуле какие-либо дополнительные члены взаимодействия, которые не были проверены (то есть вычтены из текущей модели последовательности). Смотри блок решения 449. Если имеются какие-либо непротестированные члены, способ переходит обратно к блоку 441, таким образом, формируя внутренний цикл, для проверки всех доступных членов взаимодействия, доступных в пуле взаимодействия. Через итерации внутреннего цикла идентифицируется единственный член взаимодействия. Его исключение из модели улучшает модель в наибольшей степени (и понижает AIC до наибольшего предела, если AIC применяется для измерения предиктивной силы модели).
После того, как все члены взаимодействия были проверены, и внутренний цикл завершился, идентифицируют наилучшую модель, имеющую меньшее на единицу количество членов взаимодействия, при условии, что модель, имеющая большую предиктивную силу, чем предыдущая наилучшая модель, действительно существует. Смотри блок решения 451. В этом случае способ устанавливает текущую модель в качестве наилучшей модели. Смотри блок 453. Затем, способ возвращается обратно к блоку 441. Этот внешний цикл ищет следующий член взаимодействия, который может улучшить предиктивную силу модели в наибольшей степени. Если такой член взаимодействия найден, поиск следующего члена взаимодействия, который будет вычтен, продолжается во внешнем цикле, пока больше нельзя будет идентифицировать новую модель, имеющую предиктивную силу, большую, чем предиктивная сила предыдущей наилучшей модели последовательности.
Когда внутренний цикл завершен, и больше не может быть найдено членов взаимодействия, которые могут быть вычтены для улучшения модели (то есть ответ на операцию решения, показанную в блоке 451, является отрицательным), способ устанавливает последнюю наилучшую модель в качестве конечной модели. Смотри блок 455. Поиск наилучшей модели для заданных данных последовательности и активности завершается.
iv) Альтернативные возможности моделирования
Множественные дополнительные изменений приведенного выше подхода находятся в пределах объема раскрытия. Фактически, не предполагается, что настоящее изобретение ограничено какой-либо конкретной моделью, поскольку любая соответствующая модель находит применение в настоящем изобретении. В качестве одного иллюстративного примера, переменные xij являются представлениями физических или химических свойств аминокислот - а не точными наименованиями самих аминокислот (лейцин в сравнении с валином в сравнении с пролином…). Примеры таких свойств включают липофильность, объемные и электронные свойства (например, формальный заряд, площадь поверхности Ван-дер-Ваальса, ассоциированная с частичным зарядом и т.д.). Для того чтобы реализовать этот подход, значения xij, представляющие аминокислотные остатки, могут быть представлены с точки зрения их свойств или главных компонентов, созданных из этих свойств. Не предполагается, что настоящее изобретение ограничено каким-либо конкретным свойством аминокислот, пептидов, и/или полипептидов, поскольку любое соответствующее свойство находит применение в способах по настоящему изобретению.
В некоторых дополнительных вариантах осуществления xij переменные представляют нуклеотиды, а не аминокислотные остатки. В этих вариантах осуществления цель состоит в том, чтобы идентифицировать последовательности нуклеиновой кислоты, которые кодируют белки для библиотеки вариантов белка. При использовании нуклеотидов, а не аминокислот, параметры помимо активности (например, конкретная активность) могут быть оптимизированы при необходимости. Например, экспрессия белка в конкретном хозяине или векторе может являться функцией нуклеотидной последовательности. Две различных нуклеотидных последовательности могут кодировать белок, имеющий одну и ту же аминокислотную последовательность, но одна из нуклеотидных последовательностей может приводить к продуцированию больших количеств белка, и/или белок является более активным. При использовании нуклеотидных последовательностей, а не аминокислотных последовательностей, способы, описанные в настоящем раскрытии, могут применяться для оптимизации штаммов микроорганизмов, которые демонстрируют улучшенные свойства экспрессии гена и/или улучшенные свойства (например, конкретную активность, стабильность и т.д.).
В некоторых вариантах осуществления нуклеотидная последовательность представлена как последовательность кодонов. В некоторых вариантах осуществления модели используют кодоны в качестве атомарного элемента нуклеотидной последовательности, в результате чего спрогнозированные активности являются функцией различных кодонов, присутствующих в нуклеотидной последовательности. Каждый кодон, вместе с его положением в полной нуклеотидной последовательности, служит независимой переменной для создания моделей последовательности-активности. Было замечено, что в некоторых случаях различные кодоны для данной аминокислоты имеют различную экспрессию в заданном организме. В некоторых вариантах осуществления каждый организм имеет предпочтительный кодон, или распределение частот кодонов, для заданной аминокислоты. При использовании кодонов в качестве независимых переменных вариант осуществления учитывает это предпочтение. Таким образом, вариант осуществления может применяться для создания библиотеки вариантов экспрессии (например, где "активность" включает уровень экспрессии гена конкретного организма-хозяина).
В некоторых вариантах осуществления способы включают в себя следующие операции: (a) получение данных, характеризующих обучающее множество библиотеки вариантов белка; (b) разработку нелинейной модели последовательности-активности, которая прогнозирует активность как функцию типов нуклеотидов и соответствующих положений в нуклеотидной последовательности, на основании данных, полученных в (a); (c) применение модели последовательности-активности для ранжирования положений в нуклеотидной последовательности и/или типов нуклеотиде в конкретных положениях в нуклеотидной последовательности по порядку влияния на требуемую активность; и (d) применение ранжирования для идентификации одного или более нуклеотидов в нуклеотидной последовательности, которые должны быть изменены или зафиксированы для улучшения требуемой активности. Как указано, в некоторых вариантах осуществления нуклеотиды, которые будут изменяться, кодируют конкретные аминокислоты.
В некоторых других вариантах осуществления способы включают в себя применение различных методик для ранжирования или другой характеризации остатков с точки зрения их значимости, связанной с определенным свойством. Как описано выше для линейных моделей, величины коэффициентов регрессии использовались для упорядочивания остатков. Остатки, имеющие коэффициенты с большими величинами (например, 166 Ile) считались имеющими высокий ранг остатками. Эта характеризация применялась для принятия решения о том, изменить ли или нет конкретный остаток при создании новой оптимизированной библиотеки вариантов белка. Для нелинейных моделей анализ чувствительности является более сложным, как описано в настоящем раскрытии.
PLS и другие методики предоставляют дополнительную информацию, помимо величины коэффициентов регрессии, которая может использоваться для упорядочивания конкретных остатков или положений остатков. Такие методики, как PLS и анализ главных компонентов (PCA) или PCR предоставляют информацию в форме главных компонентов или характеристических векторов. Они представляют направления или векторы максимального изменения в множествах многомерных данных, таких как пространство последовательности-активности белка, используемое в вариантах осуществления настоящего изобретения, раскрытых в настоящем раскрытии. Эти характеристические векторы являются функциями различных измерений последовательности; то есть индивидуальные остатки или положения остатков, которые содержатся в последовательностях белка, содержащихся в различных библиотеках, используемых для создания обучающего множества. Характеристические векторы, следовательно, содержат сумму вкладов каждого из положений остатка в обучающем множестве. Некоторые положения вносят больший вклад в направление вектора. Они проявляются относительно большими "нагрузками", то есть коэффициентами, используемыми для описания вектора. В качестве простого иллюстративного примера, обучающее множество может состоять из трипептидов. В этом примере первый характеристический вектор содержит вклады от всех трех остатков.
вектор 1 = a1 (положение остатка 1) + a2 (положение остатка 2) + a3 (положение остатка 3)
Коэффициенты, a1, a2 и a3 являются нагрузками. Поскольку они отражают значимость соответствующих положений остатка для изменения во множестве данных, они могут использоваться для упорядочивания значимости индивидуальных положений остатков для целей решений по "переключению", как описано выше. Нагрузки, как и регрессионные коэффициенты, могут использоваться для упорядочивания остатков в каждом переключаемом положении. Различные параметры описывают значимость этих нагрузок. Некоторые варианты осуществления используют такие методы, как значимость переменных в проекции (VIP), для применения матрицы нагрузок. Эта матрица нагрузок состоит из нагрузок для множества характеристических векторов, взятых из обучающего множества. В методах важности переменных для проекции PLS значимость переменной (например, положения остатка) вычисляют посредством вычисления VIP. Для заданной размерности PLS (VIN)ak2 равен квадрату веса PLS (wak)2 переменной, умноженной на процент объясняемой изменчивости в y (зависимая переменная, например, определенная функция) этим измерением PLS. (VIN)ak2 суммируют по всем измерениям PLS (компонентам). VIP затем вычисляют посредством деления суммы на суммарный процент изменчивости в y, объясняемый моделью PLS, и умножением на число переменных в модели. Переменные с VIP, превышающим 1, являются самыми важными для корреляции с определенной функцией (y), и, следовательно, имеют самый высокий ранг для целей принятия решений о переключении.
Во многих вариантах осуществления настоящее изобретение применяет общие методы линейной регрессии для идентификации влияний мутаций в комбинаторной библиотеке на интересующую активность последовательности. Альтернативные возможности и методики моделирования, например, Байесова регрессия, ансамблевая регрессия, бутстреппинг, могут применяться в комбинации с методами, указанными выше, или вместо них. Фактически, не предполагается, что настоящее изобретение ограничено какими-либо конкретными возможностями и/или методиками моделирования, поскольку любой(-ые) соответствующий(-е) метод(-ы) находят применение в настоящем изобретении.
Байесова линейная регрессия
В некоторых вариантах осуществления настоящего изобретения находит применение Байесова линейная регрессия. Данный метод представляет собой подход к линейной регрессии, в котором статистический анализ выполняется в рамках контекста Байесового вывода. Когда регрессионная модель имеет ошибки, которые распределены нормально, и если предполагается конкретная форма априорного распределения, то апостериорные распределения вероятности параметров модели могут быть определены с применением методик Байесова вывода.
Решение обычным методом наименьших квадратов линейной регрессионной модели оценивает вектор коэффициентов и ошибку модели на основании функции правдоподобия данных с применением аналитического метода вычисления, такого как псевдо-обратный метод Мур-Пенроуз. Данный подход является частотным подходом, который предполагает, что имеется достаточно наблюдений за данными для того, чтобы представить соотношение последовательности-активности для всех последовательностей. Однако фактические наблюдения выборки практически никогда не являются достаточными для представления всех элементов совокупности. Это особенно проблематично, когда размер выборки (или обучающего множества) ограничен. В Байесовском подходе данные выборки дополняют дополнительной информацией в форме априорного распределения вероятности. Исходные убеждения о параметрах комбинируют с функцией правдоподобия данных согласно теореме Байеса, в результате чего получают апостериорные убеждения о параметрах. Априорные убеждения могут принимать различные функциональные формы в зависимости от области и информации, которая доступна априорно.
Например, в некоторых вариантах осуществления, Байесова регрессия может использовать априорную информацию для взвешивания коэффициентов перед подгонкой модели. В некоторых вариантах осуществления, данные последовательности/активности, взятые из предыдущего цикла направленной эволюции, например, цикла, выполненного с использованием родительского или опорного остова, и по меньшей мере некоторые из мутаций, используемых в предыдущих циклах, могут применяться для взвешивания линейных коэффициентов. Кроме того, прогнозы эпистатической зависимости между двумя или более мутациями могут использоваться для взвешивания нелинейных коэффициентов взаимодействия. Одно из главных преимуществ для этого подхода состоит во включении априорной информации в непосредственные прогнозы модели.
Одним иллюстративным примером источника априорной информации является модель с независимыми членами взаимодействия для каждой из множества мутаций в опорном остове. В некоторых вариантах осуществления данные получают из совокупности вариантов, которая содержит одну мутацию на вариант.
Дополнительные примеры априорной информации, которые находят применение в настоящем изобретении, включают, но не ограничиваются, интуитивную или физическую информацию о роли определенных мутаций или типов мутаций. Независимо от источника априорная информация служит в качестве заранее сложившегося убеждения о зависимости между последовательностью и активностью.
В некоторых вариантах осуществления для того, чтобы оценить параметры модели, Байесова линейная регрессия применяет моделирование Монте-Карло, такое как выборки Гиббса или алгоритмы Метрополис, чтобы подогнать модель под заданные данные. Выборка Гиббса представляет собой основанный на цепи Маркова алгоритм Монте-Карло для получения последовательности наблюдений, которые приблизительно относятся к указанному многомерному распределению вероятностей (то есть к совместному вероятностному распределению двух или более случайных величин), когда непосредственное получение выборок представляет трудности.
Фигура 5 представляет собой блок-схему, иллюстрирующую применение Байесовой регрессии в направленной эволюции библиотек вариантов. Каждый цикл эволюции последовательности включает мутации, основанные на последовательностях из предыдущего цикла, которые могут направляться такой информацией, как модель последовательности-активности. В n-ом цикле эволюции, как в блоке 501, например, имеется одна мутация на вариант. Следующий, или (n+1)-й цикл эволюции является текущим циклом, как показано в блоке 503. Имеется по меньшей мере одна новая мутация для каждого варианта, что составляет две или более мутаций на вариант. Байесова регрессия реализуется в данном цикле в этом иллюстративном примере.
Варианта последовательностей для цикла n+1 предоставляют обучающее множество данных для новых моделей. Эти новые модели могут включать в себя базовую модель, которая включает в себя только линейные члены для индивидуальных остатков, или полную модель, которая содержит все возможные члены/коэффициенты взаимодействия, как показано в блоке 507. Новые модели могут также включать в себя модель, выбранную посредством различных методик, включая методики пошагового добавления или изымания, объясненные выше, Смотри блок 505. Альтернативно, модель может быть выбрана с применением генетического алгоритма или методики бутстреппинга, как обсуждается ниже. Все эти модели основаны на текущих/новых данных из обучающего множества данных цикла n+1. Методика Байесова вывода может быть применена к этим моделям, в результате чего модель основывается и на вероятностной функции текущих данных, и на распределении априорной информации. Априорная информация может быть получена из данных предыдущего цикла вариантов последовательности, как в цикле n, обозначенном блоком 501. Информация может также быть получена из данных последовательности-активности для любого предыдущего цикла эволюции, или другой предшествующей интуитивной информации или знания, как показано в блоке 513. Байесова регрессионная модель, обозначенная блоком 509, прогнозирует активность на основании информации, предоставленной текущими данными и априорной информацией, смотри блок 511. Хотя фигура 5 иллюстрирует применение методики Байесовой регрессии только для цикла n+1, она может быть применена на различных стадиях. Также не предполагается, что настоящее изобретение ограничено конкретными шагами, представленными на фигуре 5, поскольку любые соответствующие методики находят применение в настоящем изобретении.
Ансамблевая регрессия
В некоторых вариантах осуществления настоящее изобретение применяет методику ансамблевой регрессии для подготовки модели последовательности-активности. Модель ансамблевой регрессии основана на нескольких моделях регрессии. Прогноз каждой модели взвешивается на основании конкретного информационного критерия (IC), и прогноз ансамбля представляет собой взвешенную сумму прогнозов всех моделей, которые он содержит. В некоторых вариантах осуществления разработка модели начинается с базовой модели, содержащей все линейные члены. Последующие модели создаются посредством добавления коэффициентов взаимодействия в некоторых или всех возможных комбинациях. В некоторых вариантах осуществления коэффициенты взаимодействия добавляют в пошаговом процессе. Каждая модель подгоняется под данные и генерируется IC. Вес для каждой модели основан на IC, который может представлять собой непосредственно IC, или его преобразованную версию, например, значение логарифма, отрицание значения и т.д. Прогнозы могут быть сделаны для наблюдения посредством генерации прогноза каждой модели в ансамбле и определения прогноза ансамбля путем взятия взвешенного среднего прогноза от каждой модели. Полный ансамбль содержит все возможные модели, но может быть усечен с целью удаления плохо работающих моделей посредством установки порога для числа моделей, которое он содержит, или для IC.
Модели, составляющие ансамбль, могут быть созданы с применением различных методик. Например, в некоторых вариантах осуществления, генетический алгоритм применяется для создания составляющих ансамбль моделей. Данные последовательности/активности используются для получения множества регрессионных моделей, каждая из которых имеет свое собственное множество коэффициентов. Лучшие модели выбирают в соответствии с критерием пригодности (например, AIC или BIC). Эти модели "сопрягаются" с получением новых гибридных моделей, которые затем оценивают в отношении их пригодности и выбирают соответственно. В некоторых вариантах осуществления этот процесс повторяют для множества циклов "вычислительной эволюции" с целью получения ансамбля лучших моделей. Альтернативно, в некоторых вариантах осуществления, составляющие ансамбль модели создаются посредством пошаговой регрессии, как описано выше, и лучшие n моделей отбирают для формирования ансамбля.
На фигуре 6 представлена блок-схема для процесса, который реализует ансамблевую регрессию в направленной эволюции вариантов последовательности в соответствии с вариантом осуществления настоящего изобретения. В этом варианте осуществления методика ансамблевой регрессии может быть применена на любой стадии множества циклов эволюции последовательности. Например, в n-м цикле варианты последовательности, показанные в блоке 601, обеспечивают обучающее множество данных для различных моделей с формированием пула моделей как указано в блоке 603. Модели в пуле моделей могут являться моделями, сгенерированными посредством генетического алгоритма и/или пошагового отбора. В других вариантах осуществления пул моделей содержит n-кратные модели перекрестной проверки и/или бутстреппинга. В некоторых вариантах осуществления только модели с наилучшей предиктивной силой выбираются для введения в пул на основании различных критериев отбора моделей, таких как AIC или BIC.
Альтернативно или дополнительно, в некоторых вариантах осуществления, модели, которые не были отобраны отбором моделей, также вводят в пул моделей. В одном варианте осуществления все модели со всеми линейными и нелинейными членами вводятся в пул моделей. Для большого количества остатков и намного большего количества факториальных взаимодействий между остатками этот вариант осуществления может требовать очень большого объема вычислений. В некоторых альтернативных вариантах осуществления только модели, содержащие линейные члены и члены парного взаимодействия, вводятся в пул моделей. Независимо от способа включения моделей в пул, ансамблевая модель включает в себя все члены составляющих ее моделей. Пул моделей может содержать любое число моделей, включая, но не ограничиваясь, Байесовы модели, и в этом случае априорная информация может быть включена в ансамбль.
В некоторых вариантах осуществления ансамбль прогнозирует активность последовательности на основании взвешенной средней величины коэффициентов каждой модели в пуле, при этом веса определяются предиктивной силой соответствующих моделей, как указано в блоке 605.
В некоторых вариантах осуществления ансамблевая регрессия использует следующий поток операций: (1) предоставляет пустой ансамбль; (2) выбирает размер группы n, составляющий 1 или более; (3) классифицирует точки данных в группы размера n, при этом точки данных группируют без замены; и (4) подготавливает ансамблевую модель для прогнозирования индивидуальных коэффициентов и коэффициентов взаимодействия. В некоторых вариантах осуществления шаг (4) для подготовки ансамблевой модели также включает в себя: a) удаление точек данных из каждой группы, при этом оставшиеся данные формируют обучающее множество и удаленные данные формируют проверочное множество; b) подготовку модели посредством подгонки под обучающее множество с применением пошаговой регрессии; c) проверку модели с использованием проверочного множества, которое обеспечивает указание относительно прогнозной способности модели; d) добавление модели к пулу моделей, которые используются для создания ансамблевой модели, как описано выше.
Подход бутстреппинга
Другие методики для того, чтобы охарактеризовать предиктивную силу модели, рассматриваемой на заданной итерации, находят применение в настоящем изобретении. В некоторых вариантах осуществления эти методики включают в себя методики перекрестной проверки или бутстреппинга. В некоторых вариантах осуществления перекрестная проверка использует множество наблюдений, использованных для создания модели, но пропускает некоторые из наблюдений, чтобы оценить прогнозную способность модели. В некоторых вариантах осуществления методика бустреппинга включает использование множества выборок, которые проверяются с возвращением. В некоторых вариантах осуществления модели, сгенерированные посредством перекрестной проверки или бутстреппинга, могут быть скомбинированы в ансамблевую модель, как описано выше.
В некоторых дополнительных вариантах осуществления методы ранжируют остатки не только по величине их спрогнозированных вкладов в активность, но также по достоверности этих спрогнозированных вкладов. В некоторых случаях, исследователя беспокоит обобщаемость модели от одного множества данных к другому множеству. Другими словами, исследователь хочет знать, являются ли значения коэффициентов или главных компонентов фиктивными. Методики перекрестной проверки и бутстреппинга предоставляют меры для указания уровня достоверности того, что модели являются обобщаемыми на различные данные.
В некоторых вариантах осуществления применяется более статистически строгий подход, в котором ранжирование основано на комбинации величины и распределения. В некоторых из этих вариантов осуществления коэффициенты как с высокими величинами, так и с плотными распределениями, дают наибольший ранг. В некоторых случаях, одному коэффициенту с более низкой величиной, чем у другого, может быть дан более высокий ранг на основании наличия меньшей изменчивости. Таким образом, некоторые варианты осуществления упорядочивают аминокислотные остатки или нуклеотиды на основании как величины, так и стандартного отклонения или дисперсии. Различные методики могут применяться для достижения этого. Фактически, не предполагается, что настоящее изобретение ограничено каким-либо конкретным способом для ранжирования. Один вариант осуществления, использующий подход бустреппинга с p-значением, описан ниже.
Иллюстративный пример способа, который использует метод бутстреппинга, изображен на фигуре 7. Как показано на фигуре 7, способ 725 начинается в блоке 727, где предоставляется исходное множество данных S. В некоторых вариантах осуществления оно представляет собой обучающее множество в соответствии с описанным выше. Например, в некоторых вариантах осуществления, его генерируют посредством систематического изменения индивидуальных остатков начальной последовательности любым способом (например, как описано выше). В случае, иллюстрируемом посредством способа 725, множество данных S имеет М различных точек данных (информация активности и последовательности, собранная из аминокислотных или нуклеотидных последовательностей) для использования в анализе.
Из множества данных S создаются различные множества бутстреппинга B. Каждое из этих множеств получают посредством осуществления выборки с возвращением из множества S с целью создания нового множества из М элементов - все взятые из исходного множества S. Смотри блок 729. Условие "с заменой" создает вариации исходного множества S. Новое множество бутстреппинга, B, будет иногда содержать повторяющиеся выборки из S. В некоторых случаях, множество бутстреппинга B также не содержит определенные выборки, исходно содержавшиеся в S.
В качестве иллюстративного примера, представлено множество S из 100 последовательностей. Множество бутстреппинга B создается посредством случайного выбора 100 последовательностей-элементов из этих 100 последовательностей в исходном множестве S. Каждое множество бутстреппинга B, используемое в способе, содержит 100 последовательностей. Таким образом, возможно, что некоторые последовательности будут выбраны более одного раза, и другие не будут выбраны вообще. С использованием множества бутстреппинга B, полученного из множества S из 100 последовательностей, способ затем строит модель. Смотри блок 731. Модель может быть создана как описано выше, с применением PLS, PCR, SVM, пошаговой регрессии и т.д. Фактически, предполагается, что любой подходящий способ найдет применение в создании модели. Эта модель предоставляет коэффициенты или другие индексы ранжирования для остатков или нуклеотидов, найденных в различных выборках из множества B. Как показано в блоке 733, эти коэффициенты или другие индексы записываются для последующего использования.
Затем, в блоке решения 735, способ определяет, должно ли быть создано другое множество бутстреппинга. Если да, то способ возвращается к блоку 729, где новое множество B бутстреппинга создается как описано выше. Если нет, способ переходит к блоку 737, обсуждаемому ниже. Решение в блоке 735 зависит от того, сколько различных множеств значений коэффициентов должно использоваться в оценке распределений этих значений. Число множеств B должно быть достаточным, чтобы генерировать точную статистику. В некоторых вариантах осуществления от 100 до 1000 множеств бутстреппинга подготавливается и анализируется. Это представлено посредством от около 100 до 1000 прохождений через блоки 729, 731, и 733 способа 725. Однако не предполагается, что настоящее изобретение ограничено каким-либо конкретным количеством множеств бутстреппинга, поскольку любое количество, соответствующее требуемому анализу, находит применение.
После того, как было подготовлено и проанализировано достаточное количество множеств бутстреппинга B, решение 735 дает отрицательный ответ. Как указано, способ затем переходит к блоку 737. В нем среднее значение и стандартное отклонение коэффициента (или другого индикатора, сгенерированного моделью) вычисляется для каждого остатка или нуклеотида (включая кодоны) с использованием значений коэффициентов (например, от 100 до 1000 значений, одно из каждого множества бутстреппинга). По этой информации способ может вычислить t-статистику и определить доверительный интервал для того, что измеренное значение является отличным от ноля. По t-статистике он вычисляет p-значение для доверительного интервала. В этом иллюстративном случае, чем меньше p-значение, тем больше достоверность того, что измеренный коэффициент регрессии отличается от ноля.
Отмечено, что p-значение является всего лишь одни из многих различных типов характеризаций, которые могут учитывать статистическую вариацию коэффициента или другого показателя значимости остатка. Примеры включают, но не ограничиваются, вычисление 95-процентных доверительных интервалов для коэффициентов регрессии и исключение из рассмотрения всех коэффициентов регрессии, для которых 95-процентный доверительный интервал пересекает нулевую линию. В основном, в некоторых вариантах осуществления находит применение любая характеризация, которая учитывает стандартное отклонение, дисперсию, или другую относящуюся к статистике меру распределения данных. В некоторых вариантах осуществления этот шаг характеризации также учитывает величину коэффициентов.
В некоторых вариантах осуществления следует большое стандартное отклонение. Это большое стандартное отклонение может быть сбором к различным причинам, включая, но не ограниченное недостаточными измерениями в наборе данных, и/или ограниченным представлением конкретного остатка или нуклеотида в исходном наборе данных. В этом последнем случае некоторые множества бутстреппинга не будут содержать местонахождений конкретного остатка или нуклеотида. В таких случаях значение коэффициента для того остатка будет нолем. Другие множества бутстреппинга будут содержать, по меньшей мере, некоторые положения остатка или нуклеотида и будут давать ненулевое значение соответствующего коэффициента. Но множества, дающие нулевое значение, приведут к тому, что стандартное отклонение коэффициента станет относительно большим. Это снижает достоверность значения коэффициента и приводит к более низкому рангу. Но этого следовало ожидать при условии наличия относительно небольшого объема данных для вовлеченного остатка или нуклеотида.
Затем в блоке 739 способ ранжирует коэффициенты регрессии (или другие показатели) от самого низкого (наилучшего) p-значения до самого высокого (наихудшего)/p-значения. Это ранжирование сильно коррелирует с абсолютным значением самих коэффициентов регрессии вследствие того факта, что чем больше абсолютное значение, тем больше стандартные отклонения удалены от ноля. Таким образом, для заданного стандартного отклонения, p-значение становится меньше, когда коэффициент регрессии становится больше. Однако, абсолютное ранжирование не всегда будет одни и тем же как со способами, основанными на p-значении, так и со способами, основанном на чистом значении величины, особенно когда относительно немного точек данных доступны в начале во множестве S.
Наконец, как показано в блоке 741, способ фиксирует и переключает определенные остатки на основании ранжирований, наблюдаемых в операции блока 739. По существу, это то же самое применение ранжирования, как описано выше для других вариантов осуществления. В одном из подходов способ фиксирует наилучшие остатки (теперь остатки с самыми низкими p-значениями) и переключает другие (остатки с самыми высокими p-значениями).
Было показано, что данный способ 725 хорошо функционирует in silico. Кроме того, в некоторых вариантах осуществления, подход ранжирования по p-значению в норме работает с одним или несколькими экземплярами остатков: p-значения обычно будут выше (хуже), потому что в процессе бутстреппинга те остатки, которые не появлялись часто в исходном множестве данных, будут иметь меньшую вероятность быть выбранными при случайном выборе. Даже если их коэффициенты будут большими, то их изменчивость (измеренная в стандартных отклонениях) будет также довольно высока. В некоторых вариантах осуществления это является желаемым результатом, поскольку те остатки, которые не представлены хорошо (то есть не наблюдаются с достаточной частотой или имеют более низкие коэффициенты регрессии), могут быть хорошими кандидатами на переключение в следующем цикле конструирования библиотеки.
E. СОЗДАНИЕ ОПТИМИЗИРОВАННОЙ БИБЛИОТЕКИ ВАРИАНТОВ БЕЛКА ПОСРЕДСТВОМ ИЗМЕНЕНИЯ СПРОГНОЗИРОВАННЫХ МОДЕЛЬЮ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Одна из целей изобретения состоит в создании оптимизированной библиотеки вариантов белка через направленную эволюцию. Некоторые варианты осуществления изобретения предоставляют способы для ведения направленной эволюции вариантов белка с применением созданных моделей последовательности-активности. Различные модели последовательности-активности, подготовленные и настроенные в соответствии со способами, описанными выше, являются подходящими для ведения направленной эволюции белков или биологических молекул. В качестве части процесса, способы могут идентифицировать последовательности, которые должны быть использованы для создания новой библиотеки вариантов белка. Такие последовательности содержат изменения в определенных остатках, идентифицированных выше, или являются предшественниками, используемыми для последующего внесения таких изменений. Последовательности могут быть модифицированы посредством выполнения мутагенеза или основанного на рекомбинации механизма создания разнообразия для создания новой библиотеки вариантов белка. Новая библиотека также может использоваться в разработке новой модели последовательности-активности.
В некоторых вариантах осуществления подготовка олигонуклеотидов или последовательностей нуклеиновых кислот достигается посредством синтеза олигонуклеотидов или последовательностей нуклеиновых кислот с применением синтезатора нуклеиновой кислоты. Некоторые варианты осуществления изобретения включают выполнение цикла направленной эволюции с использованием готовых олигонуклеотидов или последовательности белка в качестве элементарных звеньев для направленной эволюции. Различные варианты осуществления изобретения могут применять рекомбинацию и/или мутагенез к этим элементарным звеньям с целью создания разнообразия.
В качестве одного конкретного примера, некоторые варианты осуществления применяют методики рекомбинации к олигонуклеотидам. В этих вариантах осуществления способ включают в себя выбор одной или более мутаций для цикла направленной эволюции посредством оценки коэффициентов членов модели последовательности-активности. Мутации выбирают из комбинаций заданных аминокислот или нуклеотидов определенных типов в определенных положениях на основании их вклада в активность белков в соответствии с прогнозами от моделей. В некоторых вариантах осуществления выбор мутаций включает в себя идентификацию одного или более коэффициентов, которые, как было определено, являются большими, чем другие коэффициенты, и выбор определенной аминокислоты или нуклеотида в определенном положении, представленном одним или более коэффициентов, идентифицированных указанным образом. В некоторых вариантах осуществления после выбора мутаций согласно моделям последовательности-активности, способы включают в себя подготовку множества олигонуклеотидов, содержащих или кодирующих одну или более мутаций, и выполнение цикла направленной эволюции с использованием подготовленных олигонуклеотидов. В некоторых вариантах осуществления методики направленной эволюции включают в себя объединение и/или повторное объединение олигонуклеотидов.
В других вариантах осуществления изобретения методики рекомбинации применяются к последовательностям белков. В некоторых вариантах осуществления способы включают в себя идентификацию нового белка или новой последовательности нуклеиновой кислоты, и подготовку и исследование нового белка или белка, закодированного новой последовательностью нуклеиновой кислоты. В некоторых вариантах осуществления способы также включают в себя использование нового белка или белка, закодированного новой последовательностью нуклеиновой кислоты, в качестве исходной точки для дальнейшей направленной эволюции. В некоторых вариантах осуществления процесс направленной эволюции включает в себя фрагментацию и повторное объединение последовательности белка, которая имеет требуемый уровень активности в соответствии с прогнозом модели.
В некоторых вариантах осуществления способы идентифицируют и/или подготавливают новый белок или новую последовательность нуклеиновой кислоты на основании индивидуальных мутаций, которые, как было спрогнозировано моделью, являются важными. Эти способы включают в себя: выбор одной или более мутаций посредством оценки коэффициентов членов модели последовательности-активности с целью идентификации одной или более определенных аминокислот или нуклеотидов в определенных положениях, которые вносят вклад в активность; идентификацию нового белка или новой последовательности нуклеиновой кислоты, содержащей одну или более мутаций, выбранных выше, и подготовку и исследование нового белка или белка, закодированного новой последовательностью нуклеиновой кислоты.
В других вариантах осуществления способы идентифицируют и/или подготавливают новый белок или новую последовательность нуклеиновой кислоты на основании спрогнозированной активности всей последовательности вместо индивидуальных мутаций. В некоторых из этих вариантов осуществления способы включают в себя применение множественных последовательностей белка или множественных последовательностей аминокислот к модели последовательности-активности и определение значений активности, спрогнозированных моделью последовательности-активности, для каждой из множества последовательностей белка или последовательностей нуклеиновых кислот. Способы также включают в себя выбор новой последовательности белка или новой последовательности нуклеиновой кислоты из числа множества последовательностей белка или множества последовательностей аминокислот, примененных выше, посредством оценки значений активности, спрогнозированных моделью последовательности-активности для множества последовательностей. Способы также включают в себя подготовку и исследование белка, имеющего новую последовательность белка, или белка, закодированного новой последовательностью нуклеиновой кислоты.
В некоторых вариантах осуществления, вместо того, чтобы просто синтезировать единственный спрогнозированный как лучший белок, комбинаторная библиотека белков создается на основании анализа чувствительности лучших изменений в выборе остатка в каждом положении в белке. В этом варианте осуществления, чем более чувствительным является заданный выбор остатка для спрогнозированного белка, тем больше будет прогнозное изменение пригодности. В некоторых вариантах осуществления эти чувствительности сортируются от самой высокой до самой низкой, и показатели чувствительности используются для создания комбинаторных библиотек белка в последующих циклах (то есть посредством включения этих остатков на основании чувствительности). В некотором варианте осуществления, в котором применяется линейная модель, чувствительность идентифицируют путем простого рассмотрения размера коэффициента, ассоциированного с членом данного остатка в модели. Однако, это невозможно для нелинейных моделей. Вместо этого в вариантах осуществления, применяющих нелинейные модели, чувствительность остатка определяют посредством применения модели для вычисления изменений в активности, когда единственный остаток изменяют в "лучшей" спрогнозированной последовательности.
Некоторые варианты осуществления изобретения включают в себя выбор одного или более положений в последовательности белка или последовательности нуклеиновой кислоты и проведение насыщающего мутагенеза в одном или более положений, идентифицированных таким образом. В некоторых вариантах осуществления положения выбирают посредством оценки коэффициентов членов модели последовательности-активности с целью идентификации одной или более определенных аминокислот или нуклеотидов в определенных положениях, которые вносят вклад в активность. Соответственно, в некоторых вариантах осуществления, цикл направленной эволюции включает в себя выполнение насыщающего мутагенеза на последовательности белка в положениях, выбранных с применением моделей последовательности-активности. В некоторых вариантах осуществления, включающих модели, содержащие один или более членов взаимодействия, способы включают в себя применение мутагенеза одновременно в двух или более взаимодействующих остатках.
В некоторых вариантах осуществления остатки рассматривают в порядке их ранжирования. В некоторых вариантах осуществления для каждого рассматриваемого остатка процесс определяет, переключить ли этот остаток. Термин "переключение" относится к введению множества типов аминокислотных остатков в конкретное положение в последовательностях вариантов белка в оптимизированной библиотеке. Например, серин может появляться в положении 166 в одном из вариантов белка, тогда как фенилаланин может появляться в положении 166 в другом варианте белка в той же самой библиотеке. Аминокислотные остатки, которые не изменяются между последовательностями вариантов белка в обучающем множестве, обычно остаются фиксированными в оптимизированной библиотеке. Однако это происходит не всегда, поскольку может присутствовать изменчивость в оптимизированных библиотеках.
В некоторых вариантах осуществления оптимизированная библиотека вариантов белка спроектирована таким образом, что все идентифицированные остатки, имеющие "высокий" ранг коэффициента регрессии, фиксируются, и остальные остатки, имеющие более низкий ранг коэффициента регрессии, переключаются. Объяснение для данного варианта осуществления состоит в том, что поиск должен осуществляться в локальном пространстве, окружающем 'наилучший' спрогнозированный белок. Отмечено, что исходный "остов", в который вносятся переключения, может являться лучшим белком, спрогнозированным моделью, и/или уже проверенным 'наилучшим' белком из подвергнутой скринингу библиотеки. Фактически, не предполагается, что исходный остов ограничен каким-либо конкретным белком.
В альтернативном варианте осуществления по меньшей мере один или более, но не все, идентифицированные остатки с высоким рангом коэффициента регрессии фиксируют в оптимизированной библиотеке, и другие переключают. Этот подход является рекомендуемым в некоторых вариантах осуществления, если имеется требование не изменять сильно контекст других аминокислотных остатков путем единовременного внесения слишком большого числа изменений. Снова, исходная точка для переключения может являться наилучшим множеством остатков в соответствии со спрогнозированным моделью, наилучшим проверенным белком из существующей библиотеки, или "средним" клоном, который хорошо моделируется. В последнем случае может требоваться переключение остатков, которые были спрогнозированы как имеющие более высокую важность, поскольку большее пространство должно исследоваться при поиске пиков активности, ранее пропущенных при осуществлении выборки. Этот тип библиотеки обычно является более подходящим на ранних циклах продуцирования библиотеки, поскольку он создает более усовершенствованную картину последующих циклов. Также не предполагается, что исходный остров ограничен каким-либо конкретным белком.
Некоторые альтернативы для вышеупомянутых вариантов осуществления включают в себя различные процедуры для использования значимости остатков (ранжирования) в определении того, какие остатки будут переключаться. В одном таком альтернативном варианте осуществления имеющие более высокий ранг положения остатков более активно предпочитаются для переключения. Информация, необходимая в данном подходе, включает в себя последовательность наилучшего белка из обучающего множества, спрогнозированную PLS или PCR наилучшую последовательность и ранжирование остатков из модели PLS или PCR. "Наилучший" белок представляет собой проверенный в практической лаборатории "наилучший" клон во множестве данных (то есть, клон с самым высоким значением взвешенной функцией, который все еще хорошо моделируется, то есть попадает относительно близко к заранее определенному значению при перекрестной проверке). Способ сравнивает каждый остаток из этого белка с соответствующим остатком из "наилучшей спрогнозированной" последовательности, имеющей самое высокое значение требуемой активности. Если остаток с самым высоким коэффициентом нагрузки или регрессии не присутствует в 'наилучшем' клоне, способ вносит это положение в качестве положения переключения для последующей библиотеки. Если остаток присутствует в наилучшем клоне аналоге, способ не обрабатывает положение как положение переключения, и он будет последовательно переходить в следующее положение. Процесс повторяется для различных остатков с перемещением через последовательно уменьшающиеся значения нагрузки, пока не будет создана библиотека достаточного размера.
В некоторых вариантах осуществления, число остатков коэффициента регрессии, которые должны быть сохранены, и число остатков коэффициента регрессии, которые должны быть переключены, изменяется. Определение того, какие остатки переключить и какие сохранить, основано на различных факторах, включая, но не ограничиваясь, требуемый размер библиотеки, величину разности между коэффициентами регрессии и степень, до которой, как полагают, присутствует нелинейность. Сохранение остатков с небольшими (нейтральными) коэффициентами может раскрыть важные нелинейности в последующих циклах эволюции. В некоторых вариантах осуществления оптимизированные библиотеки вариантов белка содержат около 2N вариантов белка, где N представляет число положений, которые переключаются между двумя остатками. Другими словами, разнообразие, добавляемое каждым дополнительным переключением, удваивает размер библиотеки таким образом, что, 10 положений переключения производят ~1000 клонов (1024), 13 положений ~10000 клонов (8192) и 20 положений ~1000000 клонов (1048576). Подходящий размер библиотеки зависит от коэффициентов, таких как стоимость скрининга, надежность среды, предпочтительный процент выборки в пространстве и т.д. В некоторых случаях было обнаружено, что относительно большое количество измененных остатков производит библиотеку, в которой чрезмерно большой процент клонов являются нефункциональными. Поэтому, в некоторых вариантах осуществления, число остатков для переключения находится в диапазоне от около 2 до около 30; то есть размер библиотеки находится в диапазоне между около 4 и 230 ~109 клонов.
Кроме того, предполагается одновременное применение различных стратегий проведения последующих циклов для библиотек, при этом некоторые стратегии являются более агрессивными (фиксация более "выгодных" остатков) и другие стратегии являются более консервативными (фиксируют меньше "выгодных" остатков с целью более тщательного исследования пространства).
В некоторых вариантах осуществления группы, или остатки, или "мотивы", которые имеются в большинстве естественных или других успешных пептидах, идентифицируют и/или сохраняют, поскольку они могут быть важными для функциональности белка (например, активности, стабильности и т.д.). Например, можно обнаружить, что Ile в переменном положении 3 всегда связан с Val в переменном положении 11 в природных пептидах. Следовательно, в одном из вариантов осуществления, сохранение таких групп требуется в любой стратегии переключения. Другими словами, единственными приемлемыми переключателями являются те, которые сохраняют конкретную группировку в базовом белке, или те, которые создают другую группировку, которая также может быть найдена в активных белках. В последнем случае необходимо переключить два или более остатков.
В некоторых дополнительных вариантах осуществления проверенный в практической лаборатории 'наилучший' (или один из нескольких лучших) белок в текущей оптимизированной библиотеке (то есть белок с самым высоким значением, или одним из нескольких самых высоких значений, взвешенной функции, который все еще хорошо моделируется, то есть попадает относительно близко к заранее определенному значению при перекрестной проверке) служит остовом, в который вносят различные изменения. В другом подходе практическая лаборатория проверила 'наилучший' (или один из нескольких лучших) белок в текущей библиотеке, который может плохо моделироваться, и который служит остовом, в который вносятся различные изменения. В некоторых других подходах последовательность, спрогнозированная моделью последовательности-активности как имеющая самое высокое значение (или одно из самых высоких значений) требуемой активности, служит остовом. В этих подходах множество данных для библиотеки "следующего поколения" (и, возможно, соответствующую модель) получают посредством изменения остатков в одном или нескольких из лучших белков. В одном из вариантов осуществления эти изменения включают в себя систематическое изменение остатков в остове. В некоторых случаях, изменения включают в себя различные методики мутагенеза, рекомбинации и/или выбора последовательности. Каждый из них может быть выполнен в in vitro, in vivo и/или in silico. Фактически, не предполагается, что настоящее изобретение ограничено каким-либо конкретным форматом, поскольку любой соответствующий формат находит применение.
В некоторых вариантах осуществления, в то время как оптимальная последовательность, спрогнозированная линейной моделью, может быть идентифицирована посредством исследования, как описано выше, это нельзя сделать для нелинейных моделей. Определенные остатки появляются и в линейных членах, и в членах перекрестного произведения, и их суммарное влияние на активность в контексте многих возможных комбинаций других остатков может быть проблематичным. Таким образом, как и с выбором членов перекрестного произведения для нелинейной модели, оптимальная последовательность, спрогнозированная нелинейной моделью, может быть идентифицирована посредством проверки всех возможных последовательностей с помощью модели (что предполагает достаточные вычислительные ресурсы) или с применением алгоритма поиска, такого как пошаговый алгоритм.
В некоторых вариантах осуществления информация, содержащаяся в построенных компьютером белках, идентифицированных, как описано выше, используется для синтезирования новых белков и их проверки в физических анализах. Точное in silico представление фактической определенной в практической лаборатории функции пригодности позволяет исследователям сократить число циклов эволюции, и/или число варианта, которое должно подвергаться скринингу в лаборатории. В некоторых вариантах осуществления оптимизированные библиотеки вариантов белка создаются с применением способов рекомбинации, описанных в настоящем раскрытии, или, альтернативно, посредством способов генного синтеза с последующей экспрессией in vivo или in vitro. В некоторых вариантах осуществления, после того, как был проведен скрининг оптимизированных библиотек вариантов белка относительно требуемой активности, их секвенируют. Как указано выше в обсуждении фигур 1 и 2, информация об активности и последовательности из оптимизированной библиотеки вариантов белка может применяться для создания другой модели последовательности-активности, из которой может быть спроектирована последующая оптимизированная библиотека с применением способов, описанных в настоящем раскрытии. В одном из вариантов осуществления все белки из этой новой библиотеки используются в качестве части множества данных.
III. ЦИФРОВОЕ УСТРОЙСТВО И СИСТЕМЫ
Как должно быть очевидным, в вариантах осуществления, описанных в настоящем раскрытии, применяются процессы, выполняемые под управлением инструкций и/или данных, хранящихся или передаваемых через одну или более вычислительных систем. Варианты осуществления, раскрытые в настоящем раскрытии, также относятся к устройству для выполнения этих операций. В некоторых вариантах осуществления устройство специально спроектировано и/или сконструировано для заданных целей, или оно может представлять собой универсальный компьютер, выборочно активированный или реконфигурированный посредством компьютерной программы и/или структуры данных, хранящейся в компьютере. Процессы, предоставленные настоящим изобретением, по своей сути не связаны с каким-либо конкретным компьютером или другим конкретным устройством. В частности, различные универсальные машины находят применение с программами, написанными в соответствии с изложенным в настоящем раскрытии. Однако, в некоторых вариантах осуществления, специализированное устройство конструируется для выполнения требуемых операций способа. Один из вариантов осуществления конкретной структуры для множества таких машин описан ниже.
Кроме того, определенные варианты осуществления настоящего изобретения относятся к машиночитаемым носителями или компьютерным программным продуктам, которые содержат инструкции программы и/или данные (включая структуры данных) для выполнения различных реализованных компьютером операций. Примеры машиночитаемых носителей включают в себя, но не ограничиваются указанным, магнитные носители, такие как жесткие диски, гибкие диски, магнитная лента; оптические носители, такие как устройства CD-ROM и голографические устройства; магнитооптические носители; полупроводниковые запоминающие устройства; и устройства, которые специально сконфигурированы для хранения и выполнения инструкций программ, такие как постоянные запоминающие устройства (ROM) и запоминающее устройство с произвольной выборкой (RAM), специализированные интегральные схемы (ASIC) и программируемые логические устройства (PLD). Данные и инструкции программы могут также быть воплощены в несущей волне или другой транспортной среде (например, оптические линии, электрические линии, и/или радиоволны). Фактически, не предполагается, что настоящее изобретение ограничено какими-либо конкретными машиночитаемыми носителями или любыми другими компьютерными программными продуктами, которые содержат инструкции и/или данные для выполнения реализуемых компьютером операций.
Примеры инструкций программы включают, но не ограничены, код низкого уровня, такой как выдаваемый компилятором код, и файлы, содержащие код более высокого уровня, которые могут быть выполнены компьютером с применением интерпретатора. Кроме того, инструкции программы включают, но не ограничены, машинный код, исходный кодом и любой другой код, который прямо или косвенно управляет работой вычислительной машины в соответствии с настоящим изобретением. Код может определять входные данные, выходные данные, вычисления, условные выражения, ветвления, итерационные циклы и т.д.
В одном иллюстративном примере воплощающие код способы, изложенные в настоящем раскрытии, воплощены в фиксированных носителях или передаваемом программном компоненте, содержащем логические инструкции и/или данных, которые при загрузке в соответствующим образом сконфигурированное вычислительное устройство вызывает выполнение устройством моделирования генетической операции (GO) на одной или более символьных строках. На фигуре 8 показан пример цифрового устройства 800, которое представляет собой логическое устройство, которое может считывать инструкции с носителя 817, сетевого порта 819, клавиатуры 809 для ввода данных пользователем, пользовательского ввода 811, или других средств ввода. Устройство 800 может затем применять эти инструкции для направления статистических операций в пространстве данных, например, создания одного или более множеств данных (например, определения множества репрезентативных элементов пространства данных). Одним из типов логического устройства, которое может воплотить раскрытые варианты осуществления, является вычислительная система, такая как вычислительная система 800, содержащая CPU 807, необязательную клавиатуру - устройство ввода данных пользователем 809, и манипулятор GUI 811, а также периферийные компоненты, такие как дисковые накопители 815 и монитор 805 (какие отображает модифицированные посредством GO символьные строки и обеспечивает упрощенный выбор подмножеств таких символьных строк пользователем). Несъемные носители 817, необязательно, применяются для программирования системы в целом и могут включать, например, оптические или магнитные носители данных дискового типа или другие электронные запоминающие элементы памяти. Порт 819 связи может использоваться для программирования системы и может представлять любой тип соединения связи.
В некоторых вариантах осуществления раскрытие предоставляет вычислительную систему, содержащую один или более процессоров; системную память; и один или более читаемых компьютером носителей, на которых хранятся исполнимые компьютером инструкции, которые, при их выполнении одним или более процессорами, вызывают выполнение вычислительной системой реализации способа для проведения направленной эволюции биологических молекул. В некоторых вариантах осуществления способ включает в себя: (a) получение данных последовательности и активности для множества биологических молекул; (b) подготовку базовой модели по данным последовательности и активности, при этом базовая модель прогнозирует активность как функцию наличия или отсутствия субъединиц последовательности; (c) подготовку по меньшей мере одной новой модели посредством добавления к базовой модели или изымания из базовой модели по меньшей мере одного нового члена взаимодействия, при этом новый член взаимодействия представляет взаимодействие между двумя или более взаимодействующими субъединицами; (d) определение способности по меньшей мере одной новой модели прогнозировать активность как функцию наличия или отсутствия субъединиц; и (e) определение того, добавлять ли к базовой модели или изымать ли из базовой модели новый член взаимодействия на основании способности по меньшей мере одной новой модели прогнозировать активность в соответствии с определенным в (d) и с предубеждением против включения дополнительных членов взаимодействия.
Определенные варианты осуществления могут также быть воплощены в пределах электрической схемы специализированной интегральной схемы (ASIC) или программируемого логического устройства (PLD). В таком случае варианты осуществления реализуют на читаемом компьютером дескрипторном языке, который может применяться для создания ASIC или PLD. Некоторые варианты осуществления настоящего изобретения реализованы в пределах электрической схемы или логических процессоров множества других цифровых устройств, таких как PDA, системы ноутбука, дисплеи, оборудование для редактирования изображений и т.д.
В некоторых вариантах осуществления настоящее изобретение относится к компьютерному программному продукту, содержащему один или более читаемых компьютером носителей, которые, при их выполнении одним или более процессорами вычислительной системы, вызывают выполнение вычислительной системой реализации способа для идентификации биологических молекул, которые оказывают влияние на требуемую активность. Такой способ может представлять собой любой способ, описанный в настоящем раскрытии, такой как способы, охваченные фигурами и псевдокодом. В некоторых вариантах осуществления способ получает данные последовательности и активности для множества биологических молекул, и подготавливает базовую модель и улучшенную модель по данным последовательности и активности. В некоторых вариантах осуществления модель прогнозирует активность как функцию наличия или отсутствия субъединиц последовательности.
В некоторых вариантах осуществления настоящего изобретения способ, реализованный посредством компьютерного программного продукта, подготавливает по меньшей мере одну новую модель посредством добавления к базовой модели или изымания из базовой модели по меньшей мере одного нового члена взаимодействия, при этом новый член взаимодействия представляет взаимодействие между двумя или более взаимодействующими субъединицами. В некоторых вариантах осуществления способ определяет способность по меньшей мере одной новой модели прогнозировать активность как функцию наличия или отсутствия субъединиц. Способ также определяет, добавлять ли к базовой модели или изымать ли из базовой модели новый член взаимодействия на основании способности по меньшей мере одной новой модели прогнозировать активность в соответствии с определенным выше и с предубеждением против включения дополнительных членов взаимодействия.
Несмотря на то, что приведенное выше было описано с некоторыми подробностями для целей ясности и понимания, специалисту в данной области техники после прочтения настоящего раскрытия будет ясно, что различные изменения в форме и деталях могут быть произведены без отклонения от фактического объема изобретения. Например, все методики и устройство, описанные выше, могут применяться в различных комбинациях. Все публикации, патенты, заявки на патент или другие документы, процитированные в настоящей заявке, включены посредством ссылки во всей их полноте для всех целей до той же самой степени, как если бы каждая индивидуальная публикация, патент, заявка на патент или другой документ были бы индивидуально указаны как включенные посредством ссылки для всех целей.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБЫ, СИСТЕМЫ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ ИДЕНТИФИКАЦИИ БИОМОЛЕКУЛ С ПОМОЩЬЮ МОДЕЛЕЙ МУЛЬТИПЛИКАТИВНОЙ ФОРМЫ | 2014 |
|
RU2664695C2 |
| ОСНОВАННОЕ НА СТРУКТУРЕ ПРОГНОЗНОЕ МОДЕЛИРОВАНИЕ | 2014 |
|
RU2694321C2 |
| КОМПОЗИЦИИ И СПОСОБЫ С УЧАСТИЕМ НУКЛЕИНОВЫХ КИСЛОТ, НАЦЕЛЕННЫХ НА НУКЛЕИНОВЫЕ КИСЛОТЫ | 2014 |
|
RU2662932C2 |
| ВЫСОКОПРОИЗВОДИТЕЛЬНЫЕ БИБЛИОТЕКИ ОДИНОЧНЫХ КЛЕТОК И СПОСОБЫ ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ | 2020 |
|
RU2838946C2 |
| НОВАЯ КОМПОЗИЦИЯ И СПОСОБЫ ЛЕЧЕНИЯ СВЯЗАННЫХ С ИММУНИТЕТОМ ЗАБОЛЕВАНИЙ | 2004 |
|
RU2375078C2 |
| ИДЕНТИФИКАЦИЯ, ПРОИЗВОДСТВО И ПРИМЕНЕНИЕ НЕОАНТИГЕНОВ | 2016 |
|
RU2729116C2 |
| МУТАГЕНЕЗ ДНК ЗА СЧЕТ НЕУПОРЯДОЧЕННОЙ ФРАГМЕНТАЦИИ И ВТОРИЧНОЙ СБОРКИ | 1995 |
|
RU2157851C2 |
| ПЛАТФОРМА ДЛЯ ОБНАРУЖЕНИЯ И АНАЛИЗА ТЕРАПЕВТИЧЕСКИХ АГЕНТОВ | 2016 |
|
RU2724998C2 |
| КОНЪЮГАТЫ АФФИННАЯ МОЛЕКУЛА-ОЛИГОНУКЛЕОТИД И ИХ ПРИМЕНЕНИЯ | 2017 |
|
RU2763554C2 |
| ВАРИАНТЫ ИЗОПРЕНСИНТАЗЫ, ПРИМЕНЯЕМЫЕ ДЛЯ УЛУЧШЕНИЯ ПРОДУЦИРОВАНИЯ ИЗОПРЕНА МИКРООРГАНИЗМАМИ | 2009 |
|
RU2516343C2 |





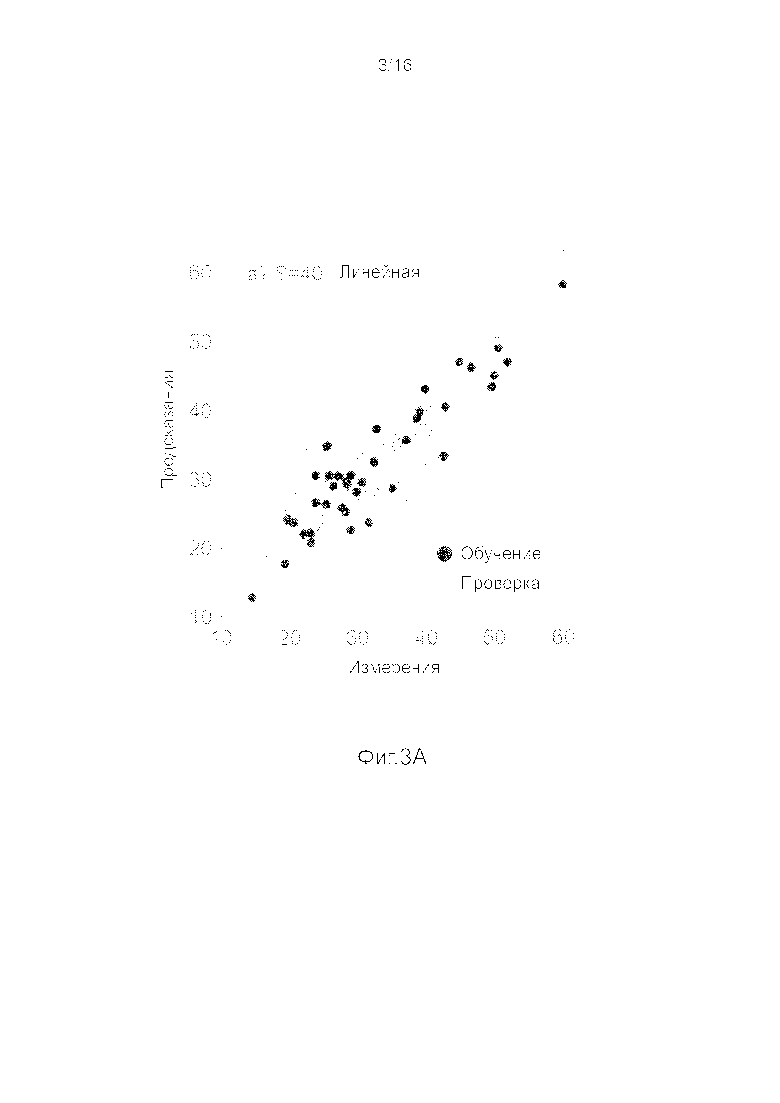
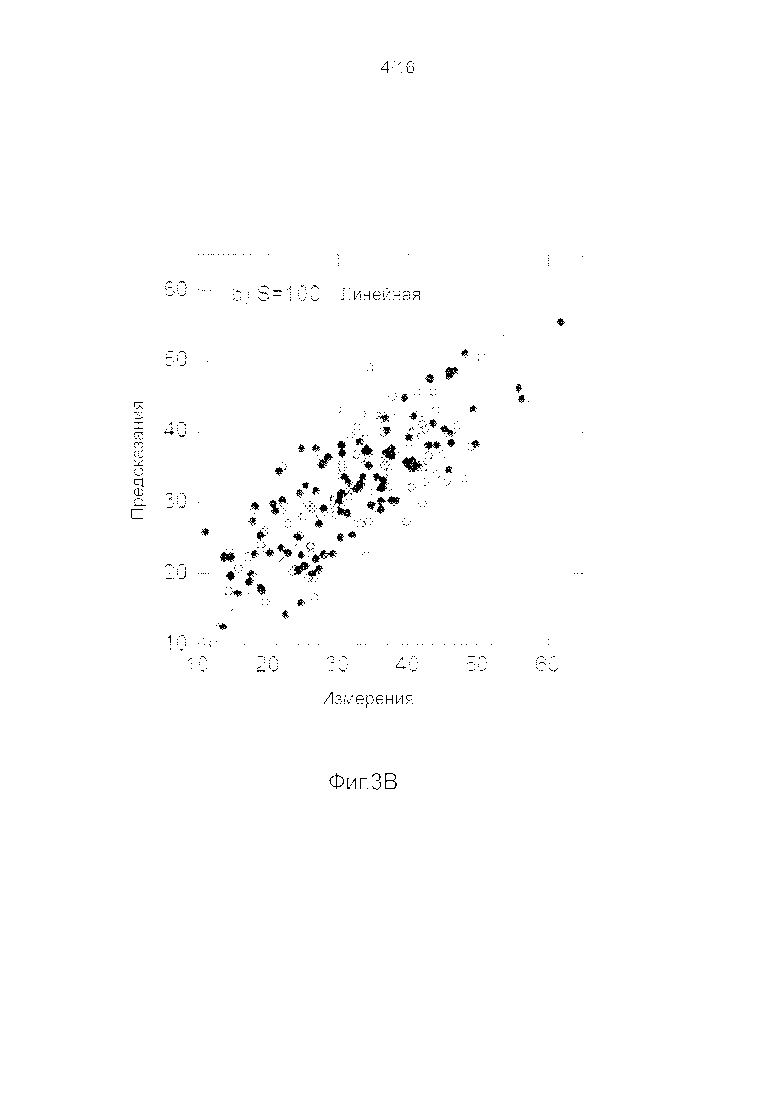
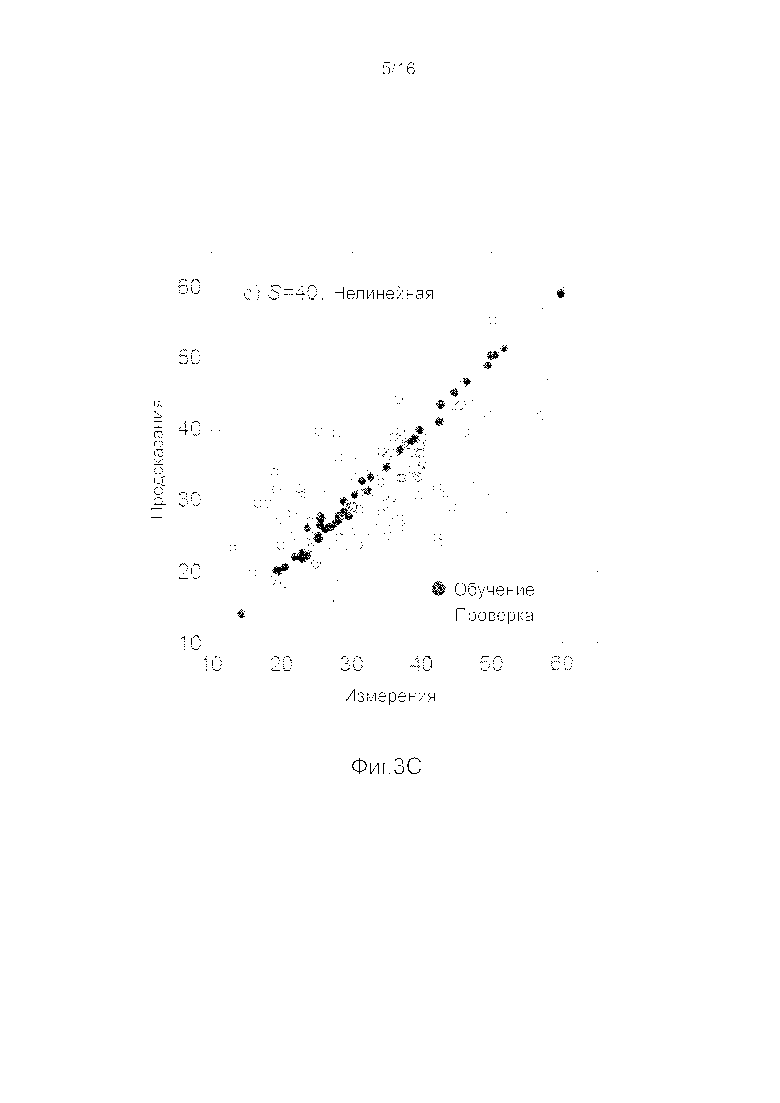
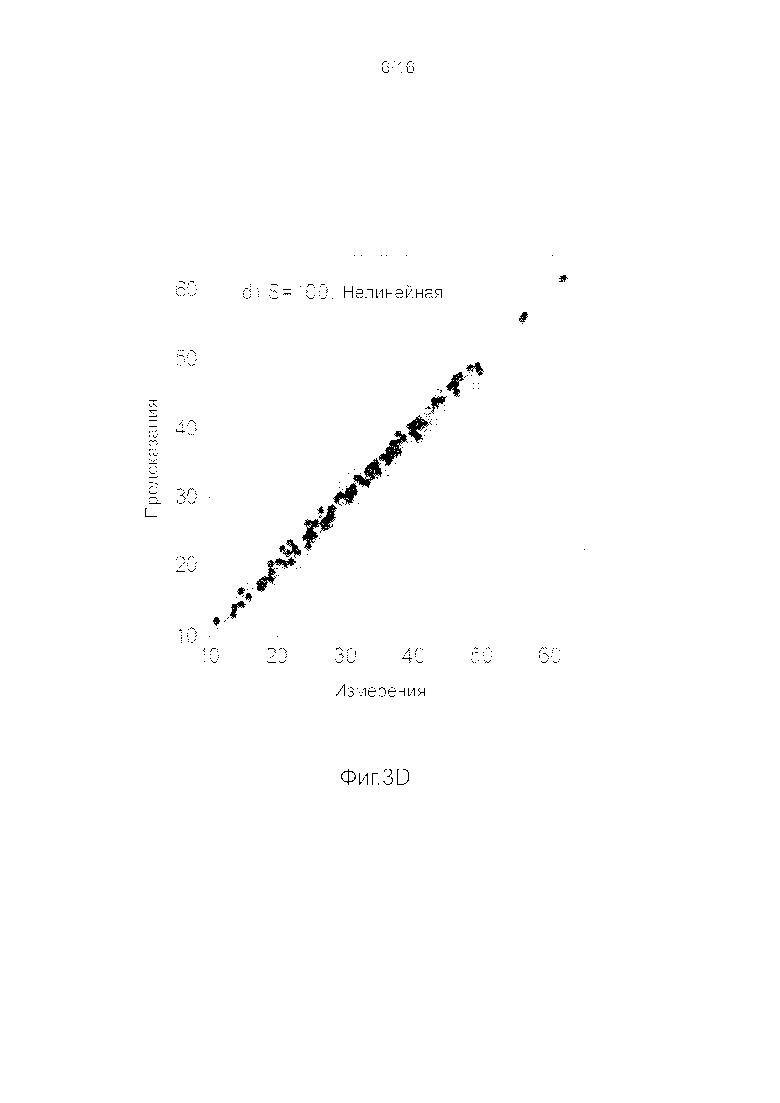
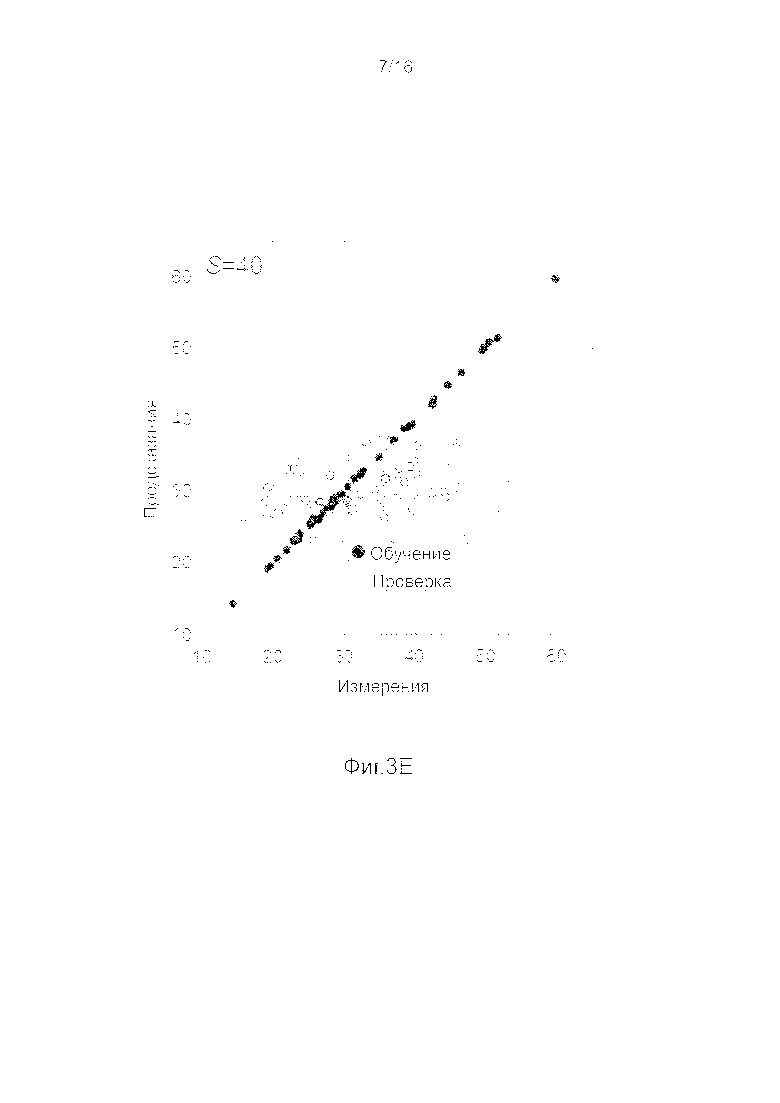
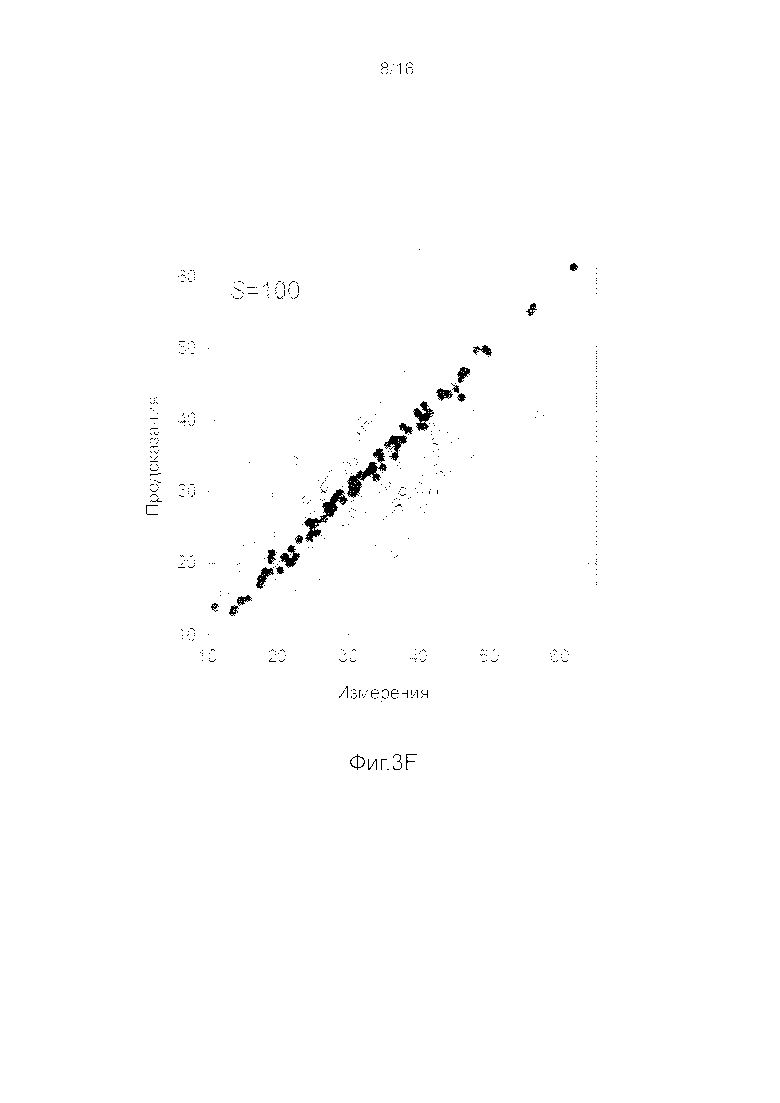
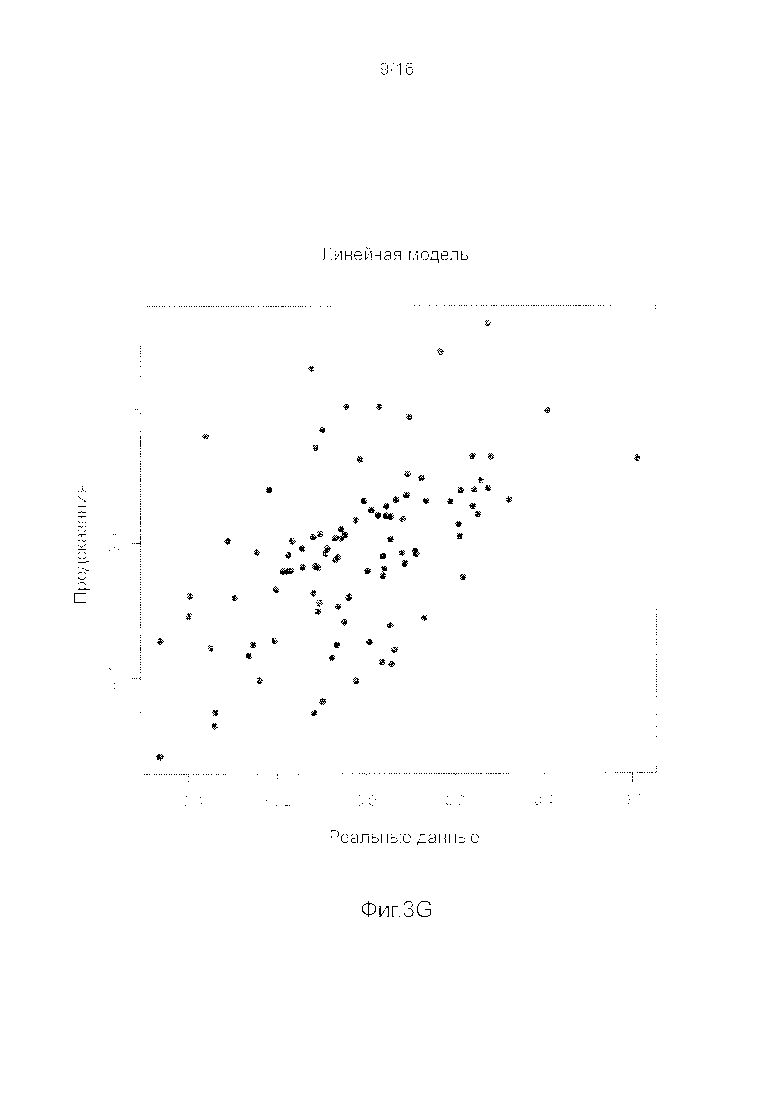
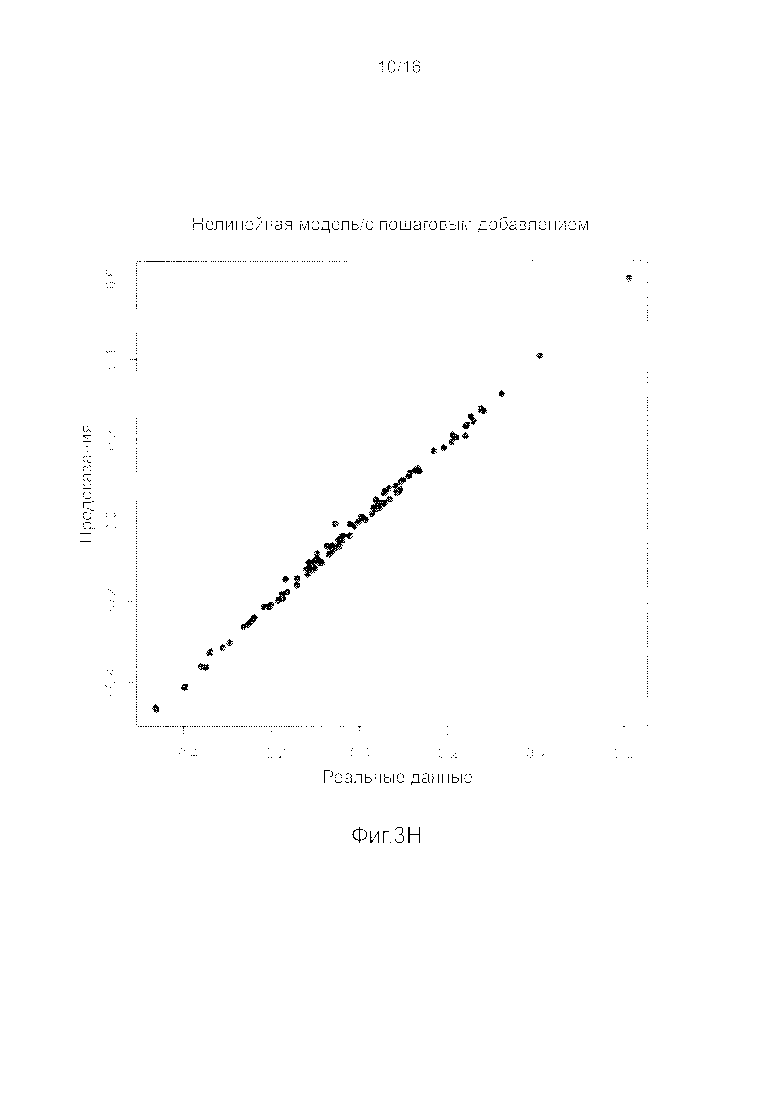






Настоящее изобретение относится к биоинформатике. Предложены способы проведения направленной эволюции одной или более молекул полипептидов или полинуклеотидов и системы для их осуществления. Данное изобретение обеспечивает получение молекул полипептидов и полинуклеотидов, имеющих желаемую активность. 4 н. и 14 з.п. ф-лы, 8 ил., 3 табл.
1. Способ проведения направленной эволюции одной или более молекул полипептидов или полинуклеотидов, при этом способ включает в себя:
(a) получение данных последовательности множества молекул полипептидов или множества молекул полинуклеотидов, кодирующих упомянутое множество молекул полипептидов, при этом данные последовательности содержат наименования и положения множества аминокислот для каждой молекулы из множества молекул полипептидов или множества нуклеотидов для каждой молекулы из множества молекул полинуклеотидов;
(b) получение данных активности множества молекул полипептидов;
(c) подготовку базовой модели из полученных данных последовательности и полученных данных активности,
при этом
базовая модель получает в качестве одного или более вводов одну или более аминокислот молекулы полипептида или один или более нуклеотидов молекулы полинуклеотида, кодирующей молекулу полипептида, и обеспечивает в качестве вывода активность молекулы полипептида,
базовая модель включает в себя множество линейных членов, но никаких членов взаимодействия,
каждый линейный член содержит коэффициент и независимую переменную, представляющую аминокислоту или нуклеотид в некотором положении в последовательности, и
каждый член взаимодействия содержит коэффициент и две или более независимые переменные, представляющие две или более взаимодействующие аминокислоты в двух или более положениях в последовательности или нуклеотиды, кодирующие упомянутые две или более взаимодействующие аминокислоты;
(d) подготовку множества новых моделей, при этом каждую новую модель получают путем добавления к базовой модели одного другого члена взаимодействия из определенного пула членов взаимодействия;
(e) вычисление статистического значения для каждой модели из упомянутого множества новых моделей, при этом статистическое значение (i) указывает способность модели прогнозировать активность как функцию наличия или отсутствия аминокислот или нуклеотидов, (ii) зависит от того, сколько свободных параметров имеет эта модель, и (iii) имеет предубеждение против включения дополнительных членов взаимодействия;
(f) идентификацию по меньшей мере одной наилучшей модели из числа упомянутого множества новых моделей на основе статистического значения каждой модели из упомянутого множества новых моделей;
(g) повтор одной или более итераций (d)-(f), используя упомянутую по меньшей мере одну наилучшую модель в одной итерации в качестве базовой модели в следующей итерации;
(h) определение одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, используя упомянутую по меньшей мере одну наилучшую модель; и
(i) синтез или экспрессию упомянутой одной или более молекул полипептидов или полинуклеотидов на основе одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, при этом упомянутая одна или более молекул полипептидов или полинуклеотидов связаны с активностью, которая является более желательной, чем у упомянутого множества молекул полипептидов.
2. Способ проведения направленной эволюции одной или более молекул полипептидов или полинуклеотидов, при этом способ включает в себя:
(a) получение данных последовательности множества молекул полипептидов или множества молекул полинуклеотидов, кодирующих упомянутое множество молекул полипептидов, при этом данные последовательности содержат наименования и положения множества аминокислот для каждой молекулы из множества молекул полипептидов или множества нуклеотидов для каждой молекулы из множества молекул полинуклеотидов;
(b) получение данных активности множества молекул полипептидов;
(c) подготовку базовой модели из полученных данных последовательности и полученных данных активности,
при этом
базовая модель получает в качестве одного или более вводов одну или более аминокислот молекулы полипептида или один или более нуклеотидов молекулы полинуклеотида, кодирующей молекулу полипептида, и обеспечивает в качестве вывода активность молекулы полипептида,
базовая модель включает в себя множество линейных членов и определенный пул членов взаимодействия,
каждый линейный член содержит коэффициент и независимую переменную, представляющую аминокислоту или нуклеотид в некотором положении в последовательности, и
каждый член взаимодействия содержит коэффициент и две или более независимые переменные, представляющие две или более взаимодействующие аминокислоты в двух или более положениях в последовательности или нуклеотиды, кодирующие упомянутые две или более взаимодействующие аминокислоты;
(d) подготовку множества новых моделей, при этом каждую новую модель получают путем изъятия из базовой модели одного другого члена взаимодействия из упомянутого пула членов взаимодействия;
(e) вычисление статистического значения для каждой модели из упомянутого множества новых моделей, при этом статистическое значение (i) указывает способность модели прогнозировать активность как функцию наличия или отсутствия аминокислот или нуклеотидов, (ii) зависит от того, сколько свободных параметров имеет эта модель, и (iii) имеет предубеждение против включения дополнительных членов взаимодействия;
(f) идентификацию по меньшей мере одной наилучшей модели из числа упомянутого множества новых моделей на основе статистического значения каждой модели из упомянутого множества новых моделей;
(g) повтор одной или более итераций (d)-(f), используя упомянутую по меньшей мере одну наилучшую модель в одной итерации в качестве базовой модели в следующей итерации;
(h) определение одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, используя упомянутую по меньшей мере одну наилучшую модель; и
(i) синтез или экспрессию упомянутой одной или более молекул полипептидов или полинуклеотидов на основе одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, при этом упомянутая одна или более молекул полипептидов или полинуклеотидов связаны с активностью, которая является более желательной, чем у упомянутого множества молекул полипептидов.
3. Способ по п.1 или 2, в котором подготовка множества новых моделей на этапе (d) содержит использование априорной информации для определения апостериорных распределений вероятности новой модели.
4. Способ по п.3, в котором подготовка множества новых моделей содержит использование выборки Гиббса для подгонки модели к данным последовательности и активности.
5. Способ по п.1 или 2, в котором по меньшей мере одна наилучшая модель содержит две или более наилучшие модели, каждая из которых включает в себя различные члены взаимодействия.
6. Способ по п.5, дополнительно содержащий подготовку ансамблевой модели, основанной на двух или более наилучших моделях, при этом
ансамблевая модель включает в себя члены взаимодействия из двух или более наилучших моделей, и
члены взаимодействия взвешивают посредством статистического значения.
7. Способ по п.1 или 2, в котором статистическое значение содержит информационный критерий Акаике или Байесов информационный критерий.
8. Способ по п.1 или 2, в котором множество молекул полипептидов составляет обучающее множество библиотеки вариантов белка.
9. Способ по п.1 или 2, в котором определенный пул членов взаимодействия содержит один или более членов взаимодействия для некоторого определенного набора из одной или более комбинаций двух или более взаимодействующих аминокислот или один или более членов взаимодействия для некоторого определенного набора из одной или более комбинаций нуклеотидов, кодирующих упомянутые две или более взаимодействующие аминокислоты.
10. Способ по п.1 или 2, в котором этап (h) содержит:
выбор одной или более мутаций для цикла направленной эволюции посредством оценки коэффициентов двух или более из множества членов выбранной модели для идентификации одной или более определенных аминокислот или нуклеотидов в определенных положениях в последовательности, которые вносят свой вклад в эту активность; и
определение множества олигонуклеотидов, содержащих или кодирующих упомянутую одну или более мутаций, при этом множество олигонуклеотидов содержит по меньшей мере участки одной или более последовательностей нуклеиновых кислот.
11. Способ по п.10, в котором выбор мутаций для цикла направленной эволюции содержит идентификацию одного или более коэффициентов, которые определяются как коэффициенты, которые больше других коэффициентов, и выбор определенной аминокислоты или нуклеотида в некотором определенном положении, представленном упомянутым одним или более коэффициентами, идентифицированными таким образом.
12. Способ по п.10, дополнительно содержащий синтез множества олигонуклеотидов с использованием синтезатора нуклеиновой кислоты.
13. Способ по п.1 или 2, в котором этап (i) содержит фрагментацию и рекомбинацию молекулы полинуклеотида, кодирующей молекулу полипептида, которая спрогнозирована выбранной моделью как имеющая некоторый желаемый уровень активности.
14. Способ по п.1 или 2, в котором этап (i) содержит выполнение насыщающего мутагенеза в отношении молекулы полипептида, которая спрогнозирована выбранной моделью как имеющая некоторый желаемый уровень активности.
15. Способ по п.1 или 2, в котором этап (h) содержит:
выбор одной или более мутаций посредством оценки коэффициентов выбранной модели для идентификации одной или более определенных аминокислот или нуклеотидов в определенных положениях в последовательности, которые вносят свой вклад в активность; и
идентификацию нового белка или новой последовательности нуклеиновых кислот, которые содержат упомянутую одну или более мутаций.
16. Способ по п.1 или 2, в котором этап (h) содержит:
выбор одного или более положений в последовательности аминокислот или последовательности нуклеиновых кислот посредством оценки коэффициентов выбранной модели для идентификации одной или более определенных аминокислот или нуклеотидов в одном или более положениях, которые вносят свой вклад в активность; и
выполнение насыщающего мутагенеза в упомянутом одном или более положениях.
17. Вычислительная система для проведения направленной эволюции одной или более молекул полинуклеотидов, содержащая:
один или более процессоров;
системную память; и
один или более считываемых компьютером носителей, хранящих исполняемые компьютером инструкции, которые, при их исполнении одним или более процессорами, вызывают выполнение вычислительной системой реализации способа для проведения направленной эволюции одной или более молекул полинуклеотидов, при этом способ содержит:
(a) получение данных последовательности множества молекул полипептидов или множества молекул полинуклеотидов, кодирующих упомянутое множество молекул полипептидов, при этом данные последовательности содержат наименования и положения множества аминокислот для каждой молекулы из множества молекул полипептидов или множества нуклеотидов для каждой молекулы из множества молекул полинуклеотидов;
(b) получение данных активности множества молекул полипептидов;
(c) подготовку базовой модели из полученных данных последовательности и полученных данных активности,
при этом
базовая модель получает в качестве одного или более вводов одну или более аминокислот молекулы полипептида или один или более нуклеотидов молекулы полинуклеотида, кодирующей молекулу полипептида, и обеспечивает в качестве вывода активность молекулы полипептида,
базовая модель включает в себя множество линейных членов, но никаких членов взаимодействия,
каждый линейный член содержит коэффициент и независимую переменную, представляющую аминокислоту или нуклеотид в некотором положении в последовательности, и
каждый член взаимодействия содержит коэффициент и две или более независимые переменные, представляющие две или более взаимодействующие аминокислоты в двух или более положениях в последовательности или нуклеотиды, кодирующие упомянутые две или более взаимодействующие аминокислоты;
(d) подготовку множества новых моделей, при этом каждую новую модель получают путем добавления к базовой модели одного другого члена взаимодействия из определенного пула членов взаимодействия;
(e) вычисление статистического значения для каждой модели из упомянутого множества новых моделей, при этом статистическое значение (i) указывает способность модели прогнозировать активность как функцию наличия или отсутствия аминокислот или нуклеотидов, (ii) зависит от того, сколько свободных параметров имеет эта модель, и (iii) имеет предубеждение против включения дополнительных членов взаимодействия;
(f) идентификацию по меньшей мере одной наилучшей модели из числа упомянутого множества новых моделей на основе статистического значения каждой модели из упомянутого множества новых моделей;
(g) повтор одной или более итераций (d)-(f), используя упомянутую по меньшей мере одну наилучшую модель в одной итерации в качестве базовой модели в следующей итерации;
(h) определение одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, используя упомянутую по меньшей мере одну наилучшую модель;
(i) управление синтезатором нуклеиновой кислоты для синтеза упомянутой одной или более молекул полинуклеотидов,
при этом упомянутая одна или более молекул полинуклеотидов (1) кодирует одну или более молекул полипептидов, имеющую упомянутую одну или более последовательностей аминокислот, или (2) имеет упомянутую одну или более последовательностей нуклеиновых кислот,
и при этом упомянутая одна или более молекул полинуклеотидов или упомянутая одна или более молекул полипептидов связаны с активностью, которая является более желательной, чем у упомянутого множества молекул полипептидов.
18. Вычислительная система для проведения направленной эволюции одной или более молекул полинуклеотидов, содержащая:
один или более процессоров;
системную память; и
один или более считываемых компьютером носителей, хранящих исполняемые компьютером инструкции, которые, при их исполнении одним или более процессорами, вызывают выполнение вычислительной системой реализации способа для проведения направленной эволюции одной или более молекул полинуклеотидов, при этом способ содержит:
(a) получение данных последовательности множества молекул полипептидов или множества молекул полинуклеотидов, кодирующих упомянутое множество молекул полипептидов, при этом данные последовательности содержат наименования и положения множества аминокислот для каждой молекулы из множества молекул полипептидов или множества нуклеотидов для каждой молекулы из множества молекул полинуклеотидов;
(b) получение данных активности множества молекул полипептидов;
(c) подготовку базовой модели из полученных данных последовательности и полученных данных активности,
при этом
базовая модель получает в качестве одного или более вводов одну или более аминокислот молекулы полипептида или один или более нуклеотидов молекулы полинуклеотида, кодирующей молекулу полипептида, и обеспечивает в качестве вывода активность молекулы полипептида,
базовая модель включает в себя множество линейных членов и определенный пул членов взаимодействия,
каждый линейный член содержит коэффициент и независимую переменную, представляющую аминокислоту или нуклеотид в некотором положении в последовательности, и
каждый член взаимодействия содержит коэффициент и две или более независимые переменные, представляющие две или более взаимодействующие аминокислоты в двух или более положениях в последовательности или нуклеотиды, кодирующие упомянутые две или более взаимодействующие аминокислоты;
(d) подготовку множества новых моделей, при этом каждую новую модель получают путем изъятия из базовой модели одного другого члена взаимодействия из упомянутого пула членов взаимодействия;
(e) вычисление статистического значения для каждой модели из упомянутого множества новых моделей, при этом статистическое значение (i) указывает способность модели прогнозировать активность как функцию наличия или отсутствия аминокислот или нуклеотидов, (ii) зависит от того, сколько свободных параметров имеет эта модель, и (iii) имеет предубеждение против включения дополнительных членов взаимодействия;
(f) идентификацию по меньшей мере одной наилучшей модели из числа упомянутого множества новых моделей на основе статистического значения каждой модели из упомянутого множества новых моделей;
(g) повтор одной или более итераций (d)-(f), используя упомянутую по меньшей мере одну наилучшую модель в одной итерации в качестве базовой модели в следующей итерации;
(h) определение одной или более последовательностей аминокислот или одной или более последовательностей нуклеиновых кислот, используя упомянутую по меньшей мере одну наилучшую модель;
(i) управление синтезатором нуклеиновой кислоты для синтеза упомянутой одной или более молекул полинуклеотидов,
при этом упомянутая одна или более молекул полинуклеотидов (1) кодирует одну или более молекул полипептидов, имеющую упомянутую одну или более последовательностей аминокислот, или (2) имеет упомянутую одну или более последовательностей нуклеиновых кислот,
и при этом упомянутая одна или более молекул полинуклеотидов или упомянутая одна или более молекул полипептидов связаны с активностью, которая является более желательной, чем у упомянутого множества молекул полипептидов.
| EP 1266337 A2, 18.12.2002 | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| LUO ARONG et al | |||
| "Performance of criteria for selecting evolutionary models in phylogenetics: a comprehensive study based on simulated datasets." BMC Evolutionary Biology, 2010, 10(1): 242 | |||
| FROMER MENACHEM, YANOVER CHEN, "A Computational Framework to Empower Probabilistic Protein Design." Bioinformatics, 2008, 24(13): i214-i222. | |||
Авторы
Даты
2019-07-22—Публикация
2014-01-29—Подача