Изобретение относится к электротехнике и, в частности, заявленные объекты могут быть использованы в устройствах согласования выходов (входов) радиопередатчиков (радиоприемников) с импедансными нагрузками (антеннами), в трактах диаграммобразующих схем антенных решеток или в регулируемых линиях задержки электромагнитных сигналов.
Известны дискретные реактивные цепи (ДРЦ). ДРЦ, описанная в книге Маркова Г.М., Сазонова Д.М. Антенны. Учебник для студентов радиотехнических специальностей. Изд. 2-е, переработанное и дополненное. - М.: Энергия, 1975. - с.327, 464-470, состоит из N дискретных реактивных элементов (ДРЭ), выполненных из отрезков фидерных линий. Указанная ДРЦ входит в систему фазирования антенной решетки. С помощью управляемых переключателей (УП) обеспечивается формирование необходимой совокупности ДРЭ для достижения требуемого фазового сдвига. В качестве УП могут использоваться pin-диоды или ферриты с прямоугольной петлей гистерезиса. Число фазовых сдвигов М выбирают равным двум в целой степени М=2p, где p=1, 2,… и т.д.
Недостатком известной ДРЦ является ее низкая структурная надежность. Структурная надежность ДРЦ характеризуется коэффициентом структурной надежности Кн, определяемым отношением числа Пi сохранившихся позиций номинальных значений на выходе ДРЦ при выходе из строя i-го ДРЭ, к суммарному числу Пс позиций исправной ДРЦ, т.е. Кн=Пi/Пс. Относительно низкая структурная надежность известной ДРЦ обусловлена тем, что при выходе из строя одного из ДРЭ с помощью оставшихся ДРЭ можно обеспечить не более половины фазовых состояний ДРЦ. При этом антенная решетка фактически будет неработоспособна.
Известна также ДРЦ, описанная в книге: Бабков В.Ю., Муравьев Ю.К. Основы построения устройств согласования антенн. - Л.: ВАС, 1980, с.82, 83, рис.218.
Известная ДРЦ состоит из N ДРЭ, в качестве которых могут использоваться емкостные элементы (конденсаторы), индуктивные элементы (катушки индуктивности) или отрезки длинных линий, например, отрезки коаксиального кабеля. С помощью УП в ДРЦ предусмотрена возможность формирования совокупности из Р≤N ДРЭ, подключенных к выходам ДРЦ. Номинальное значение аi i-го ДРЭ, где i=1, 2, …, N выбрано из условия a1=aminki, где amin - минимальный шаг дискретного изменения номинального значения совокупности из Р ДРЭ; ki=F(i) - весовой коэффициент номинального значения i-го ДРЭ, вычисленный с помощью расчетной функции F(i)=2i-1.
Недостатком известной ДРЦ является ее относительно низкая структурная надежность в силу того, что при выходе из строя одного из ДРЭ структура ДРЦ разрушается до пределов, существенно ограничивающих диапазон ее использования.
Наиболее близкой по своей технической сущности - прототипом к заявленной является ДРЦ по патенту РФ №2276454, по заявке №2004137201 от 20.12.2004 г, МПК Н03Н 7/38, опубл. 10.05.2006 г. Бюл. №13.
ДРЦ - прототип состоит из N ДРЭ с возможностью формирования из них с помощью УП совокупности из Р≤N ДРЭ, подключенной к выходам ДРЦ. Номинальное значение аi i-го ДРЭ выбрано из условия аi=аminki, где amin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из Р ДРЭ, ki=F(i) - весовой коэффициент номинального значения i-го ДРЭ, вычисленный с помощью функции F(i) рекуррентного ряда.
В зависимости от выбранного типа ДРЭ: емкостей или индуктивностей они включены соответственно параллельно или последовательно. В качестве расчетной функции F(i) в известной ДРЦ используют рекуррентную формулу последовательности чисел Фибоначчи или Люка. Для повышения структурной надежности в состав ДРЦ введен дополнительный ДРЭ.
Недостатком ближайшего аналога является относительно низкая кратность резервирования каждого из номинальных значений на выходе ДРЦ. Попытка резервирования путем включения в схему нескольких однотипных ДРЦ приводит к неоправданному увеличению массогабаритных показателей устройства и увеличению его стоимости.
Целью заявленных изобретений является разработка вариантов построения ДРЦ, обеспечивающих повышение кратности резервирования каждого дискретного номинального значения реактивности на выходе ДРЦ в пределах заданного диапазона за счет оптимизации структуры ДРЦ.
Заявленные варианты ДРЦ расширяют арсенал средств данного назначения.
В первом варианте поставленная цель достигается тем, что в известной ДРЦ, содержащей первую группу из N ДРЭ с возможностью формирования из них с помощью УП совокупности из Р ДРЭ, подключенной к выходам ДРЦ, в которой номинальное значение аi i-го ДРЭ, где i=1, 2, …, N, выбрано из условия ai=aminki, где amin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из ДРЭ, ki=F(i) - весовой коэффициент номинального значения i-го ДРЭ, вычисленный с помощью функции F(i) рекуррентного ряда, в структуру ДРЦ введена вторая группа из М ДРЭ. Номинальное значение aj j-го ДРЭ второй группы из М ДРЭ, где j=1, 2, …, М, выбрано из условия aj=aminkj, где kj=F(j) - весовой коэффициент номинального значения j-го ДРЭ, вычисленный с помощью функции F(j) рекуррентного ряда, идентичного рекуррентному ряду, с помощью которого вычислены номинальные значения ДРЭ первой группы из N ДРЭ, т.е. F(i)=F(j). Причем к выходу ДРЦ с помощью УП обеспечивается подключение совокупности Р≤(N+М) ДРЭ. В качестве расчетной функции рекуррентного ряда F(i)=F(j) выбрана рекуррентная формула последовательности чисел Фибоначчи
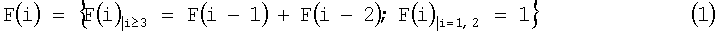
или рекуррентная формула последовательности чисел Люка
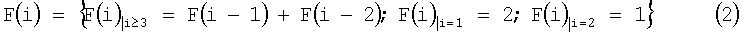
Во втором варианте в отличие от первого варианта дополнительно в структуру ДРЦ введены В вспомогательных ДРЭ. При этом к выходам ДРЦ обеспечивается подключение совокупности из Р≤(N+М+В) ДРЭ. Причем при выборе в качестве расчетной функции рекуррентного ряда F(i)=F(j) рекуррентной формулы последовательности чисел Фибоначчи (1) число В вспомогательных ДРЭ выбрано в интервале 1≤В≤2, а номинальное значение каждого из вспомогательных ДРЭ выбрано равным номинальному значению первого ДРЭ a1 рекуррентного ряда чисел Фибоначчи. При выборе в качестве расчетной функции рекуррентного ряда F(i)=F(j) рекуррентной формулы последовательности чисел Люка (2) число вспомогательных ДРЭ выбрано в интервале 2≤В≤5, а номинальное значение каждого из вспомогательных ДРЭ выбрано равным номинальному значению второго ДРЭ а2 рекуррентного ряда чисел Люка.
В третьем варианте в отличие от первого варианта номинальные значения аi и aj из первой и второй групп ДРЭ вычислены с помощью отличающихся соответственно первой F1(i) и второй F2(j) функций рекуррентного ряда. В качестве функций F1(i) и F2(j) выбраны рекуррентные формулы последовательности чисел соответственно Фибоначчи и Люка.
В четвертом варианте в отличие от третьего варианта в структуру ДРЦ введены В вспомогательных ДРЭ. При этом к выходу ДРЦ с помощью УП обеспечивается подключение совокупности из Р≤(N+М+В) ДРЭ. Число В вспомогательных ДРЭ выбрано в интервале 1≤В≤4, а номинальные значения каждого из ДРЭ выбрано равным номинальному значению первого ДРЭ а1 первой группы из N ДРЭ или равным номинальному значению второго ДРЭ а2 второй группы из М ДРЭ.
Благодаря новой совокупности существенных признаков в каждом из вариантов формируемая структура ДРЦ обеспечивает увеличение кратности резервирования каждого из номинальных значений ДРЦ минимум в 5 раз при ограниченном, не более чем двухкратном увеличении общего числа ДРЭ.
Заявленные технические решения поясняются чертежами, на которых показаны:
на фиг.1 - структурная схема ДРЦ первого и третьего вариантов при использовании емкостных ДРЭ;
на фиг.2 - структурная схема ДРЦ первого и третьего вариантов при использовании индуктивных ДРЭ;
на фиг.3 - структурная схема второго и четвертого вариантов при использовании индуктивных ДРЭ;
на фиг.4 - структурная схема второго и четвертого вариантов при использовании емкостных ДРЭ.
В первом и третьем вариантах структурные схемы одинаковы. ДРЦ состоит из N+М ДРЭ 11-112 и N+М УП 21-212. На фиг.1, 2 принято число N=М=6, т.е. М+N=12. Общее число N+М ДРЭ 1 выбирают исходя из требуемого диапазона изменения параметров на выходе ДРЦ. Соотношение числа ДРЭ 1 в первой N и во второй М группах ДРЭ может быть произвольным: N=М или N>М или N<М. Выбор конкретного соотношения определяется как требованием по диапазону изменения параметров на выходе ДРЦ, так и требованием по достижению минимально допустимой кратности резервирования ДРЭ 1 в данной ДРЦ.
Формирование необходимой совокупности Р ДРЭ 1, обеспечивающей на выходных клеммах 5, 6 ДРЦ требуемое номинальное значение реактивности ДРЦ, обеспечивается УП 2. Положение первых 3 и вторых 4 контактов каждого УП 2 с помощью соответствующих токовых обмоток 7 определяется сигналами от блока управления 8.
В качестве УП 2 могут быть использованы механические реле, pin-диоды, ферриты и т.п. Блок управления может быть реализован на ПЭВМ или в виде специально изготовленного микропроцессора, но предварительно заданной программе, формирующего управляющего сигнала на подключение соответствующей совокупности Р ДРЭ к выходам 5, 6 ДРЦ.
При использовании емкостных ДРЭ 1 их первые выводы объединены и являются первым выходом 5 ДРЦ (фиг.1, 3). Второй вывод i-го ДРЭ 1 подключен к первому контакту 3 i-го УП 2. Вторые контакты 4 всех УП 2 объединены и являются вторым выходом 6 ДРЦ.
В первом варианте структуру ДРЦ формируют из двух групп ДРЭ 1. Первая группа состоит из N ДРЭ 1, вторая - из М ДРЭ 1. Номинальные значения ДРЭ 1 в первой и второй группах вычисляют с помощью рекуррентной формулы последовательности чисел Фибоначчи (1) или Люка (2). В Таблице 1 приведены два примера А и Б структур ДРЦ первого варианта, включающих две группы ДРЭ 1 (при N=М=6), номинальные значения которых вычислены в первом примере (А) с помощью рекуррентной формулы чисел Фибоначчи (1), во втором (Б) - с помощью рекуррентной формулы чисел Люка (2).
Последовательность расстановки ДРЭ 1 в общей структуре ДРЦ принципиального значения не имеет. В Таблице 1 порядковые номера ДРЭ 1, относящиеся к первой группе из N ДРЭ 1, обозначены одним штрихом, к второй группе из МДРЭ 1 - двумя штрихами.
При использовании индуктивных ДРЭ 1 (фиг.2) все ДРЭ 1 включены последовательно. Первый вывод первого ДРЭ 1' и второй вывод (N+М)-го ДРЭ 12" (на фиг.2 (N+М)=12) являются соответственно первым 5 и вторым 6 выходами ДРЦ. К первому и второму выводам каждого и ДРЭ подключены соответственно первый 3 и второй 4 контакты соответствующего УП 2. Второй контакт 4 m-го УП 2 подключен к первому контакту 3 (m+1)-го УП 2, где m=1, 2, …, [(N+М)-1].
Во втором и четвертом вариантах ДРЦ их структурные схемы одинаковы и показаны на фиг.3 (при использовании емкостных ДРЭ 1) и на фиг.4 (при использовании индуктивных ДРЭ 1). Отличие структурных схем второго и четвертого вариантов (фиг.3, 4) от структурных схем первого и третьего вариантов (фиг.1, 2) заключается в том, что в их состав введены по В вспомогательных ДРЭ, обозначенных в Таблице 1 индексом «о». В частности в Таблице 1 и на фиг.3, 4 В=2, т.е. введено по два вспомогательных ДРЭ, а их номинальные значения равны аmin, что для ряда чисел Фибоначчи соответствует amin=a1, а для ряда чисел Люка аmin=a2.
Структура ДРЦ всех заявленных вариантов при условии M=N=6 приведена в Таблице 1.
Заявленные устройства работают следующим образом. В качестве примера рассмотрим схемы ДРЦ, в которых N=М=6; В=2; аmin=1; а1=1 (для ряда Фибоначчи) и
а2=1 (для ряда Люка).
В этих условиях номинальные значения ДРЭ 1, соответствующих ряду чисел Фибоначчи, вычисляют по формуле (1), а соответствующих ряду Люка - по формуле (2).
Указанные формулы известны и приведены соответственно в книгах: Математическая энциклопедия. - М.: Советская энциклопедия, 1985, Т.5. - с.911; Грехем Р., Кнут Д., Пташник О. Конкретная математика. Основание информатики, пер с англ. - М.: Мир, 1988. - с.344.
Номинальные значения ДРЭ 1 в соответствующих вариантах ДРЦ будут характеризоваться числовыми последовательностями, отраженными в Таблице 1.
В любом из вариантов для функционирования ДРЦ с возможностью ее дискретной перестройки с минимальным шагом amin (в рассматриваемом примере amin=1) с помощью соответствующей коммутации должна формироваться совокупность из Р ДРЭ 1, одновременно подключенных к выходам 5, 6 ДРЦ, номинальное суммарное значение которой без разрывов изменяется от amin до amax. В приведенных ниже примерах аmax=20. В Таблицах 2, 3, 4, 5, 6, 7 приведены всевозможные комбинации каждого из номинальных значений на выходе с ДРЦ соответственно для вариантов: I-A, I-Б, II-А, II-Б, III, IV.
Каждое из промежуточных значений в интервале аmin÷amax=1÷20 может быть сформировано несколькими совокупностями Р ДРЭ 1. Например, необходимое номинальное значение, равное 10, на выходах 5, 6 ДРЦ может быть сформировано различными комбинациями ДРЭ:
в I-A варианте: 8+2=8+2=5+5=5+3+2=3+3+2+2=3+2+2+1+1+1;
в 1-Б варианте: 7+3=7+3=4+4+2=4+3+3=3+3+2+2;
в II-A варианте: 8+2=8+2=5+5=5+3+2=3+3+2+2=3+2+2+1+1+1=2+2+2+1+1+1+1;
в II-Б варианте: 7+3=7+3=4+4+2=4+3+3=3+3+2+2=3+2+2+1+1+1;
в III варианте: 8+2=7+3=5+4+1=4+3+3=3+3+2+2=3+2+2+1+1+1;
в IV варианте: 8+2=7+3=5+4+1=4+3+3=3+3+2+2=3+2+2+1+1+1.
Таким образом, в каждом из вариантов при выходе из строя любого из ДРЭ 1, образующих структуру ДРЦ, обеспечивается многократное резервирование каждого из номинальных значений в интервале аmin÷amax. В частности, номинальное значение а=10 резервируется:
в I-A варианте 6 - кратно; в I-Б варианте 5-кратно; во II-A варианте 7-кратно; во II-Б варианте 6-кратно; в III варианте 6-кратно; в IV варианте 6-кратно.
На фиг.1, 2, 3, 4 в качестве примера отражены положения контактов УП 2 при необходимости получения на выходе ДРЦ номинального значения, равного 15.
На фиг.1 положения контактов соответствуют варианту I-A, а для достижения на выходе ДРЦ номинального значения 15 использованы следующие ДРЭ1: a5=2; а7=3; a9=5; a10=5, т.е. Р=4.
Аналогично на фиг.2 для варианта I-Б использованы ДРЭ 1: а3=1; a5=3; а6=3; а7=4, a8=4, т.е. Р=5.
На фиг.3 для варианта II-A имеем:
a5=2; a6=2; a7=3, a8=3, a10=5, т.е. Р=5.
На фиг.4 для варианта IV имеем:
а1 o=1; а2=2; a5=2; а6=3, а7=3, а8=4, т.е. Р=6.
Указанные пределы выбора числа В вспомогательных ДРЭ выбраны из следующих соображений:
нижний предел указывает на минимально допустимое число 5, при котором будет иметь место положительный эффект (увеличение краткости резервирования);
верхний предел указывает на то, что при дальнейшем его увеличении положительный эффект уже не возрастает.
Приведенные данные дают основание для вычисления среднеарифметического значения кратности резервирования 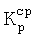 для каждого из вариантов ДРЦ.
для каждого из вариантов ДРЦ.
С учетом кратности резервирования каждого из дискретных номинальных значений среднеарифметическое значение кратности резервирования 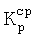 , вычисленное для каждого варианта ДРЦ по формуле:
, вычисленное для каждого варианта ДРЦ по формуле:
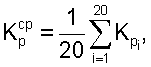
где 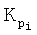 - кратность резервирования i-го номинального значения на выходе ДРЦ, i=1, 2, …, 20, принимает значение (см. также таблицы 2, 3, 4, 5, 6, 7):
- кратность резервирования i-го номинального значения на выходе ДРЦ, i=1, 2, …, 20, принимает значение (см. также таблицы 2, 3, 4, 5, 6, 7):
для I-А варианта - 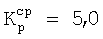 ;
;
для I-Б варианта - 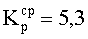 ;
;
для II-A варианта - 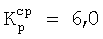 ;
;
для II-Б варианта - 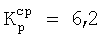 ;
;
для III варианта - 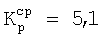 ;
;
для IV варианта - 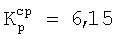 .
.
При использовании даже двух комплексов ДРЦ, принятой за прототип, или двухкратном увеличении общего числа ее ДРЭ их суммарное значение 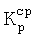 не будет превышать 2,5.
не будет превышать 2,5.
Таким образом, в заявленных вариантах ДРЦ даже при двухкратном увеличении числа ДРЭ 1 достигается неожиданный эффект - увеличение коэффициента резервирования до (5-6)-кратного, что обеспечит высокую надежность работы ДРЦ. Полученные данные подтверждают возможность достижения сформулированного технического результата - повышение кратности резервирования каждого номинального дискретного значения реактивности на выходе ДРЦ в пределах заданного диапазона.
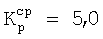
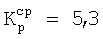
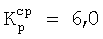
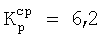
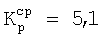
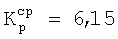
| название | год | авторы | номер документа |
|---|---|---|---|
| ДИСКРЕТНАЯ РЕАКТИВНАЯ ЦЕПЬ | 2010 |
|
RU2414809C1 |
| ДИСКРЕТНАЯ РЕАКТИВНАЯ ЦЕПЬ (ВАРИАНТЫ) | 2004 |
|
RU2276454C1 |
| Генератор последовательности р-чисел Фибоначчи | 1986 |
|
SU1324019A2 |
| Устройство для развертки кодов Фибоначчи | 1986 |
|
SU1417194A1 |
| Генератор последовательности @ -чисел Фибоначчи | 1983 |
|
SU1091146A1 |
| Сервопривод с цифровым управлением | 1980 |
|
SU962952A1 |
| Генератор последовательности @ -чисел Фибоначчи | 1987 |
|
SU1411725A1 |
| Генератор последовательности @ -чисел Фибоначчи | 1983 |
|
SU1112356A2 |
| Генератор последовательности @ -чисел Фибоначчи | 1984 |
|
SU1233132A2 |
| Генератор последовательности обобщенных @ -чисел фибоначчи с произвольными начальными условиями | 1986 |
|
SU1474627A2 |
Изобретение относится к электротехнике и может использоваться в устройствах согласования выходов радиопередатчиков (радиоприемников) с импедансными нагрузками (антеннами), в диаграммообразующих схемах антенных решеток, регулируемых линиях задержек и т.п. Техническим результатом является повышение кратности резервирования каждого номинального дискретного значения реактивности на выходе дискретной реактивной цепи (ДРЦ). ДРЦ содержит первую из N и вторую из М группы дискретных реактивных элементов (ДРЭ) с возможностью их подключения к выходам ДРЦ с помощью управляемых переключателей (УП). Номинальные значения ДРЭ в первой и второй группах выбраны из условия аi=аminki, где amin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из ДРЭ, ki=F(i) - весовой коэффициент i-го ДРЭ, вычисленный с помощью функции F(i) рекурентного ряда. В первом варианте ДРЭ первой и второй групп вычислены по идентичным функциям F(i): ряда Фибоначчи или Люка. В третьем варианте - по отличающимся функциям F(i). Во втором и четвертом в ДРЦ введены вспомогательные ДРЭ. 4 н. и 6 з.п. ф-лы, 4 ил., 7 табл.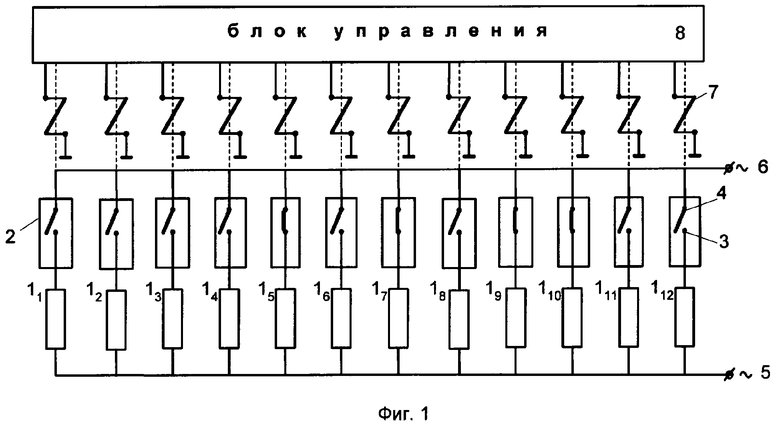
1. Дискретная реактивная цепь, содержащая первую группу из N дискретных реактивных элементов с возможностью формирования из них с помощью управляемых переключателей совокупности из Р дискретных реактивных элементов, подключенной к выходам дискретной реактивной цепи, в которой номинальное значение аi i-го дискретного реактивного элемента, где i=1, 2,…, N, выбрано из условия аi=аminki, где amin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из Р дискретных реактивных элементов, ki=F(i) - весовой коэффициент номинального значения i-го дискретного реактивного элемента, вычисленный с помощью функции F(i) рекуррентного ряда, отличающаяся тем, что в дискретную реактивную цепь введена вторая группа из М дискретных реактивных элементов, номинальное значение аj j-го дискретного реактивного элемента второй группы, где j=1, 2,…, М, выбрано из условия aj=aminkj, где kj=F(j) - весовой коэффициент номинального значения j-го дискретного реактивного элемента, вычисленный с помощью функции F(j) рекуррентного ряда, идентичного рекуррентному ряду, с помощью которого вычислены номинальные значения дискретных реактивных элементов первой группы из N дискретных реактивных элементов, причем к выходу дискретной реактивной цепи обеспечивается подключение совокупности из P≤(N+M) дискретных реактивных элементов.
2. Дискретная реактивная цепь по п.1, отличающаяся тем, что в качестве расчетной функции рекуррентного ряда F(i)=F(j) выбрана рекуррентная формула последовательности чисел Фибоначчи
F(i)={F(i)|i≥3=F(i-1)+F(i-2); F(i)|i=1,2=1}
3. Дискретная реактивная цепь по п.1, отличающаяся тем, что в качестве расчетной функции рекуррентного ряда F(i)=F(j) выбрана рекуррентная формула последовательности чисел Люка
F(i)={F(i)|i≥3=F(i-1)+F(i-2); F(i)|i=1=2; F(i)|i=2=1}
4. Дискретная реактивная цепь, содержащая первую группу из N дискретных реактивных элементов с возможностью формирования из них с помощью управляемых переключателей совокупности из Р дискретных реактивных элементов, подключенной к выходам дискретной реактивной цепи, в которой номинальное значение аi i-го дискретного реактивного элемента, где i=1, 2,…, N, выбрано из условия ai=aminki, где аmin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из Р дискретных реактивных элементов, ki=F(i) - весовой коэффициент номинального значения i-го дискретного реактивного элемента, вычисленный с помощью функции F(i) рекуррентного ряда, отличающаяся тем, что в дискретную реактивную цепь введены дополнительно В вспомогательных дискретных реактивных элементов и вторая группа из М дискретных реактивных элементов, номинальное значение aj j-го дискретного реактивного элемента вычислено с помощью функции F(j) рекуррентного ряда, идентичного рекуррентному ряду, с помощью которого вычислены номинальные значения дискретных реактивных элементов первой группы из N дискретных элементов, причем к выходу дискретной реактивной цепи обеспечивается подключение совокупности из P≤(N+M+B) дискретных реактивных элементов.
5. Дискретная реактивная цепь по п.4, отличающаяся тем, что в качестве расчетной функции рекуррентного ряда F(i)=F(j) выбрана рекуррентная формула последовательности чисел Фибоначчи
F(i)-{F(i)|i≥3=F(i-1)+F(i-2);F(i)|i=2=1},
причем число В вспомогательных дискретных реактивных элементов выбрано в интервале 1≤В≤2, а номинальное значение каждого из вспомогательных дискретных реактивных элементов выбрано равным номинальному значению первого дискретного реактивного элемента а1.
6. Дискретная реактивная цепь по п.4, отличающаяся тем, что в качестве расчетной функции рекуррентного ряда F(i)=F(j) выбрана рекуррентная формула последовательности чисел Люка
F(i)={F(i)|i≥3=F(i-1)+F(i-2); F(i)|i=1=2; F(i)|i=2=1}
причем число В вспомогательных дискретных реактивных элементов выбрано в интервале 2≤В≤5, а номинальное значение каждого из вспомогательных дискретных реактивных элементов выбрано равным номинальному значению второго дискретного элемента а2.
7. Дискретная реактивная цепь, содержащая первую группу из N дискретных реактивных элементов с возможностью формирования из них с помощью управляемых переключателей совокупности из Р дискретных реактивных элементов, подключенной к выходам дискретной реактивной цепи, в которой номинальное значение аi i-го дискретного реактивного элемента, где i=1, 2,…, N выбрано из условия ai=aminki, где аmin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из Р дискретных реактивных элементов, ki=F1(i) - весовой коэффициент номинального значения i-го дискретного реактивного элемента, вычисленный с помощью первой функции F1(i) рекуррентного ряда, отличающаяся тем, что в дискретную реактивную цепь введена вторая группа из М дискретных реактивных элементов, номинальное значение aj j-го дискретного реактивного элемента, j=l, 2,…, М, выбрано из условия aj=aminkj, где kj=F2(j) - весовой коэффициент номинального значения j-го дискретного реактивного элемента, вычисленный с помощью второй функции F2(j) рекуррентного ряда, отличающегося от ряда, с помощью которого вычислены номинальные значения дискретных реактивных элементов первой группы из N дискретных реактивных элементов, причем к выходу дискретной реактивной цепи обеспечивается подключение совокупности из P≤(N+M) дискретных реактивных элементов.
8. Дискретная реактивная цепь по п.7, отличающаяся тем, что в качестве первой расчетной функции F1(i) выбрана рекуррентная формула последовательности чисел Фибоначчи
F(i)={F(i)|i≥3=F(i-1)+F(i-2); F(i)|i=1,2=1},
а в качестве второй расчетной функции F2(j) выбрана рекуррентная формула последовательности чисел Люка
F(j)={F(j)|j≥3=F(j-1)+F(j-2); F(j)|j=1=2; F(j)|j=2=1}.
9. Дискретная реактивная цепь, содержащая группу из N дискретных реактивных элементов с возможностью формирования из них с помощью управляемых переключателей совокупности из Р дискретных реактивных элементов, подключенной к выходам дискретной реактивной цепи, в которой номинальное значение аi i-го дискретного реактивного элемента, где i=1, 2,…, N, выбрано из условия ai=aminki, где аmin - минимальный шаг дискретного изменения суммарного номинального значения совокупности из Р дискретных реактивных элементов, ki=F1(i) - весовой коэффициент номинального значения i-го дискретного реактивного элемента, вычисленный с помощью первой функции F1(i) рекуррентного ряда, отличающаяся тем, что в дискретную реактивную цепь введены дополнительно В вспомогательных дискретных реактивных элементов и вторая группа из М дискретных реактивных элементов, номинальное значение aj j-го дискретного реактивного элемента, где j=1, 2,…, М, выбрано из условия aj=amimkj, где kj=F(j) - весовой коэффициент номинального значения j-го дискретного реактивного элемента, вычисленный с помощью второй функции F2(j) рекуррентного ряда, отличающегося от ряда, с помощью которого вычислены номинальные значения дискретных реактивных элементов первой группы из N дискретных реактивных элементов, причем к выходу дискретной реактивной цепи обеспечивается подключение совокупности из P≤(N+M+B) дискретных реактивных элементов.
10. Дискретная реактивная цепь по п.9, отличающаяся тем, что в качестве первой расчетной функции F1(i) выбрана рекуррентная формула последовательности чисел Фибоначчи
F(i)={F(i)|i≥3=F(i-1)+F(i-2); F(i)|i=1,2=1},
в качестве второй расчетной функции F2(j) выбрана рекуррентная формула последовательности чисел Люка
F(j)={F(j)|i≥3=F(j-1)+F(j-2); F(f)|j=1=2; F(j)|j=2=1}.
причем число В вспомогательных дискретных реактивных элементов выбрано в интервале 1≤В≤4, а номинальное значение каждого из вспомогательных дискретных реактивных элементов выбрано равным номинальному значению первого дискретного реактивного элемента a1 из первой группы из N дискретных реактивных элементов, или равным номинальному значению второго дискретного реактивного элемента а2 из второй группы из М дискретных реактивных элементов.
| ДИСКРЕТНАЯ РЕАКТИВНАЯ ЦЕПЬ (ВАРИАНТЫ) | 2004 |
|
RU2276454C1 |
| Способ последовательного согласования импедансов в диапазоне дискретных частот | 1989 |
|
SU1778827A1 |
| ВСЕСОЮЗНАП f ОАТ?йПШ-Т[ХЩ:ЧН:НАЙ | 0 |
|
SU342284A1 |
| US 5276411 A, 04.01.1994 | |||
| Центробежный классификатор | 1980 |
|
SU940878A1 |
Авторы
Даты
2009-05-10—Публикация
2007-11-06—Подача