СПОСОБ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ТУРБОКОДОВ Российский патент 2015 года по МПК H03M13/33 H03M13/25 H04L7/08 

Изобретение относится к электросвязи и может быть использовано для цикловой синхронизации при приеме передач, использующих блоковые турбокоды (ТКБ) [Pyndiah R.M. and others, Near-Optimum Decoding of Product Codes: Block Turbo Codes - IEEE Transaction on Communications, Vol. 46, №8, p. 1003, Aug. 1998.], в которых компонентными кодами являются расширенные двоичные циклические коды и коды с проверкой на четность [Product Specification АНА4501: 36 Mbits/sec Turbo Product Code Encoder/Decoder, Product Specification AHA4540: 155 Mbits/sec Turbo Product Code Encoder/Decoder], в условиях параметрической неопределенности относительно структуры блокового турбо кодера.

Известен способ кодовой цикловой синхронизации при передаче информации помехоустойчивыми блоковыми кодами (фазирование по словам), основанный на методе последовательных сдвигов, заключающийся в том, что принимаемая дискретная последовательность элементов поступает на вход приемника дискретной информации, после чего производится анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, когда информация о начале кодовых слов в принимаемой последовательности не известна. В качестве признака синхронного состояния используется равенство нулю синдрома. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один элемент по принимаемой последовательности в одну и ту же сторону. Сдвиги производятся до тех пор, пока не будут обнаруживаться только кодовые слова. В этом случае принимается решение о наличии синхронного состояния и процесс вхождения в синхронизм заканчивается [Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и декодирование сложных дискретных сигналов / Под ред. В.И. Коржика. - М.: Радио и связь, 1988, с 132-137].

Однако этот способ невозможно использовать в условиях параметрической неопределенности структуры кодера помехоустойчивого кода, поскольку вычисление синдрома требует знания проверочной матрицы кода или порождающего полинома [Кларк Дж., мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. - М.: Радио и связь, 1986, с 81; Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш. Зигангирова. - М.: Мир, 1986, с 62-71, 116-121].

Известен способ кодовой цикловой синхронизации ТКБ, в котором компонентными кодами являются циклические коды, с порождающими многочленами, имеющими общий делитель, расширенные за счет добавления проверки на четность, заключающийся в том, что принимаемая дискретная последовательность элементов поступает на вход приемника дискретной информации, после чего производится анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, когда информация о начале кодовых слов в принимаемой последовательности не известна. Анализ состояния приемника основан на расчете дискретного преобразования Фурье-Галуа (ДПФГ) принимаемой дискретной последовательности на длине N-1, то есть меньшей длины кодового слова на один элемент. Признаком синхронного состояния приемника дискретной информации является равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один элемент по принимаемой последовательности в одну и ту же сторону. После выявления признака синхронного состояния дополнительно производят проверку истинности установления синхронного состояния по наличию признака истинности фазирования. Для этого выделяют не менее четырех фрагментов той же длины, последовательно расположенных за фрагментом, выбранным на этапе определения синхронного состояния, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один элемент последовательности, выполняют ДПФГ выделенных фрагментов и определяют наличие признака истинности фазирования, а в случае отсутствия признака истинности фазирования поиск синхронного состояния возобновляют с момента выявления признака синхронного состояния [Способ кодовой цикловой синхронизации: пат. 2359414 Рос. Федерация: МПК H04L 7/08 / Тамп В.Л., Балунин Е.И., Ратушин А.П.; заявитель и патентообладатель Череповецкий военный инженерный институт радиоэлектроники. - №2007140294/09; заявл. 30.10.2007; опубл. 10.03.09].

Однако недостатком данного способа является ограниченность синхронизацией ТКБ, в которых компонентными кодами являются двоичные циклические коды с порождающими многочленами имеющими общий делитель, расширенными за счет проверки на четность. Следовательно, данный способ не может синхронизировать ТКБ, в которых компонентными кодами являются разные двоичные циклические коды Хэмминга, расширенные за счет проверки на четность. Вызвано это тем, что порождающие полиномы циклических кодов Хэмминга являются неприводимыми [М. Вернер Основы кодирования: Пер. с нем. Д.К. Зигангирова. - М.: Техносфера, 2006, с. 196], следовательно, не могут иметь общий делитель. Также, в результате имитационного моделирования работы данного способа на ЭВМ для кодовой цикловой синхронизации ТКБ, состоящих из компонентных расширенных циклических кодов и используемых со спиральным перемежителем [White paper, «Helical Interleaving for Burst Error Correction with Turbo Product Codes», Efficient Channel Coding, Inc., June 1998], установлено, что данный способ теряет работоспособность.

Наиболее близким к предлагаемому способу является способ цикловой синхронизации циклического помехоустойчивого кода при декодировании циклического помехоустойчивого кода, заключающийся в том, что входную дискретную последовательность элементов кодовых слов циклического кода принимают с использованием приемника дискретной информации, после чего производят анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, когда информация о начале кодовых слов в принимаемой последовательности не известна. Анализ приемника производят по признаку синхронного состояния путем выделения из принятой дискретной последовательности кодовых слов предполагаемых длин [N_min-N_max] и задания предполагаемой фазы начала кодового слова, из принятой кодовой последовательности с фазы φ₀ выделяют несколько предполагаемых кодовых слов f_i и формируют из выделенных кодовых слов пары согласно условию f≠f_k, вычисляют N наибольших общих делителей (НОД), представленных многочленами, для различных пар кодовых слов и выбирают среди вычисленных многочленов многочлен наименьшей степени, который отождествляют с порождающим многочленом g(x) циклического помехоустойчивого кода, если НОД равен «1», то увеличивают длину предполагаемого кодового слова на единицу, изменяют фазу предполагаемого начала кодового слова на единицу, если НОД, отличный от «1», не найден при всех [N_min-N_max], определяют комбинации ошибок в кодовом слове и декодируют выделенные кодовые слова [Способ декодирования циклического помехоустойчивого кода: пат. 2284085 Рос. Федерация: МПК Н03М 13/15, G06F 11/00 Егурнов В.О., Наукович А.Н., Химии C.B., Циленко Д.В. заявитель и патентообладатель Военная академия связи. - №2005106284/09; заявл. 10.03.05; опубл. 20.09.06]. Принят за прототип.

Однако в ходе имитационного моделирования данного способа на ЭВМ для синхронизации ТКБ, в которых компонентными кодами являются расширенные циклические коды и коды с проверкой на четность, установлено, что данный способ не применим для синхронизации ТКБ, поскольку имеет высокую вероятность ложной синхронизации. Во-первых, в связи тем, что длина кодового слова ТКБ N не известна и находится путем перебора [N_min-N_max], возможна синхронизация по одному из компонентных кодов ТКБ или фрагменту кодового слова ТКБ. Во-вторых, даже если длина кодового слова ТКБ N выбрана верно, начальная фаза определяется из условия, что НОД нескольких (в способе рекомендуется выбирать три) фрагментов длины N отличен от единицы. Однако возможен случай нахождения НОД, отличного от единицы, короткой длины до 17 элементов и, следовательно, ошибочной синхронизации. Например, каждый фрагмент последовательности четного веса делится на многочлен x+1 (в двоичном представлении «11») без остатка, вероятность выделения фрагмента последовательности четного веса приближенно равна 0,5 и тогда НОД трех подряд фрагментов равняется «11» с вероятностью возникновения такого события приблизительно 0,5×0,5×0,5=0,125. В-третьих, возможно ошибочное нахождение начальной фазы вблизи истинной начальной фазы. Например, двоичный фрагмент, смещенный на один элемент относительно истинной начальной фазы, будет кодовым словом с вероятностью 0,5, следовательно, вероятность наступления события, когда каждый из трех выделенных смещенных на один элемент относительно истинной начальной фазы фрагментов является кодовым словом, приблизительно равна 0,125.

Технический результат - устранение возможности ложной цикловой синхронизации и расширение арсенала средств аналогичного назначения.

Для достижения указанного технического результата в способе цикловой синхронизации входную дискретную последовательность элементов кодовых слов ТКБ принимают с использованием приемника дискретной информации, после чего производят анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, когда информация о начале кодовых слов в принимаемой последовательности не известна. Перед анализом на приемной стороне задают предполагаемые длины кодовых слов ТКБ: 256, 512, 1024, 2048, 4096, 8192, 16384. Устанавливают N_min=256, N_max=16384, N=N_min, φ₀=0, порог длины наибольшего общего делителя L=17, вспомогательный параметр Μ=1. Анализ состояния приемника производят по признаку синхронного состояния путем выделения из принятой дискретной последовательности с фазы φ₀ двух фрагментов f длины N. 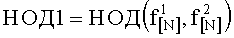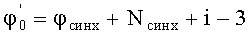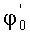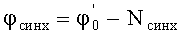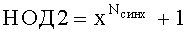Вычисляют наибольший общий делитель (НОД) выделенных фрагментов $$НОД1=НОД\left(f_{\left[N\right]}^1,f_{\left[N\right]}^2\right)$$ . Признаком синхронного состояния приемника дискретной информации является нахождение НОД длины не менее порогового значения L. В случае отсутствия признака синхронного состояния увеличивают длину выделяемых фрагментов N вдвое и повторяют процесс поиска признака синхронного состояния. Если при переборе фрагментов длин N≤N_max признак синхронного состояния не обнаружен, до его установления сдвигаются по принимаемой последовательности на один элемент вправо с последующим выделением новых фрагментов длин N_min, 2N_min, 4N_min, …, N_max и определением признака синхронного состояния. После выявления данного признака производят проверку наличия признака истинности синхронного состояния. Выделяют M фрагментов длины N, последовательно расположенных за первым фрагментом, выбранным на этапе определения синхронного состояния. Из двучленов x^l+1 двоичного вида «10…01» длин 17, 33, 65, 129, 257, 513, 1025, 2049, 4097, 8193 отбирают те, длины которых не превышают длину L(НОД1). Вычисляют остатки от деления НОДХ на каждый из двучленов x^l+1 (где l=16, 32, 64, 128, 256, 512, 1024) двоичного вида «10…01», начиная с наибольшего двучлена x^l+1. Как только остаток от деления НОДХ на двучлен будет равен нулю, вычисление остатков заканчивают и считают признак истинности синхронного состояния выявленным с N_синх, φ_синх, НОД2. В случае отсутствия признака истинности синхронного состояния, возвращаются к моменту установления отсутствия признака синхронного состояния. После установления признака истинности синхронного состояния, повышают вероятность истинного фазирования. Для этого выполняют цикл в течение пяти раз для i=1…5, т.е. сдвигаются по последовательности к начальной фазе $${\varphi }_0^{\text{'}}={\varphi }_{синх}+N_{синх}+i-3$$ , выделяют M фрагментов длины N_синх, вычисляют остатки от деления M фрагментов на НОД2. Производят подсчет фаз, для которых все M фрагментов делятся на НОД2 без остатка. Если таких фаз больше одной, то увеличивают M на единицу и повторяют проверку истинности фазирования, иначе, если только одна фаза $${\varphi }_0^{\text{'}}$$ , $${\varphi }_{синх}={\varphi }_0^{\text{'}}-N_{синх}$$ считают истинной начальной фазой и синхронизируют по двухмерному ТКБ с N_синх, φ_синх. Если 4N_синх>N_max=16384 трехмерный ТКБ отсутствует, иначе, если 4N_синх≤N_max=16384, проверяют возможность наличия трехмерного ТКБ и синхронизации по нему. Корректируют параметры, вводят N_min=4N_синх, N=N_min, $$НОД2=x^{N_{синх}}+1$$ (в двоичном виде «10…01» длины N_синх+1), φ₀=φ_синх. Выделяют из принятой дискретной последовательности с фазы φ₀ фрагмент f длины Ν, вычисляют остаток от деления выделенного фрагмента на НОД2. Проверяют наличие признака синхронного состояния по трехмерному ТКБ, которым является нулевой остаток от деления выделенного фрагмента на НОД2. В случае отсутствия признака синхронного состояния по трехмерному ТКБ для всех выделенных фрагментов длин N_min, 2N_min, …, N_max ,до его установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на φ_синх вправо с последующим выделением нового фрагмента длины N и определением наличия признака синхронного состояния приемника по признаку синхронного состояния трехмерного ТКБ, после выявления данного признака осуществляют синхронизацию по трехмерному ТКБ с параметрами N_тсинх и φ_тсинх.

Общим с прототипом является то, что с использованием приемника дискретной информации принимают входную последовательность, представляющую собой последовательно передаваемые элементы кодовых слов, выделяют фрагменты дискретной последовательности и определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. При отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один элемент в одну и ту же сторону с последующим выделением новых фрагментов и определением наличия синхронного состояния приемника по признаку синхронного состояния приемника.

Отличием от прототипа является то, что поиск длины кодового слова производят среди степеней двойки N: 256, 512, 1024, 2048, 4096, 8192, 16384 N_min=2⁸=256, N_max=2¹⁴=16384 и выделяют фрагменты дискретной последовательности длины N. В качестве признака синхронного состояния приемника используют ненулевой 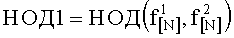$$НОД1=НОД\left(f_{\left[N\right]}^1,f_{\left[N\right]}^2\right)$$ ) длины не меньше порога 17. После выявления данного признака дополнительно производят проверку установления синхронного состояния по наличию признака истинности синхронного состояния. В качестве признака истинности синхронного состояния используют нулевые остатки от деления M фрагментов на НОД2=(x^l+1). Повышают вероятность истинного фазирования и синхронизируются по двухмерному ТКБ. В зависимости от найденных параметров синхронизации N_синх, φ_синх корректируют параметры способа и проверяют возможность синхронизации по трехмерному ТКБ с N_синх, φ_тсинх.

Благодаря новой совокупности существенных признаков технический результат проявляется в возможности цикловой синхронизации всех ТКБ, в которых компонентными кодами являются расширенные двоичные циклические коды и коды с проверкой на четность.

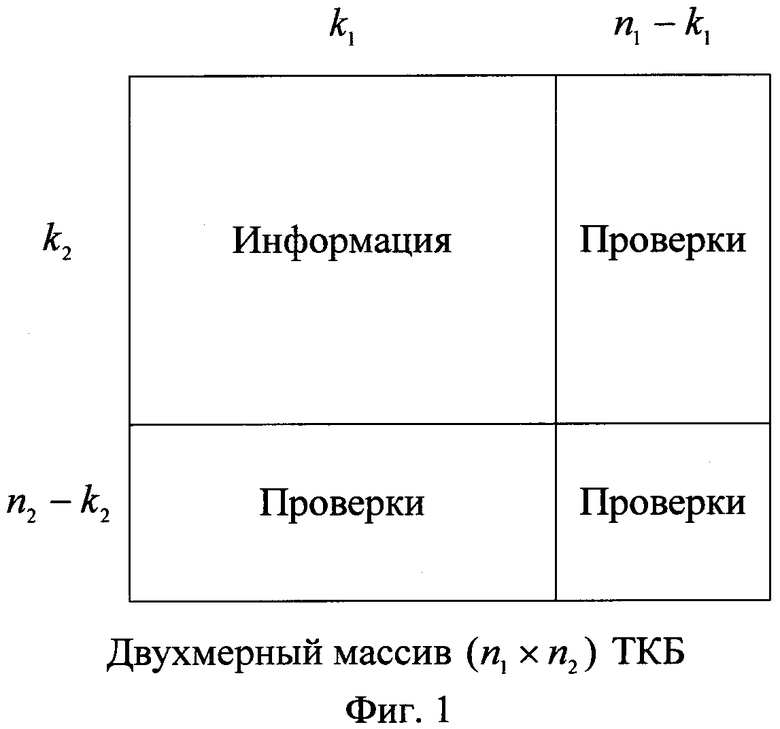
Известно, что ТКБ представляют собой коды-произведения [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш. Зигангирова. - М.: Мир, 1986, с 326], кодовыми словами которых являются все двухмерные таблицы со строками, являющимися словами кода (n₁, k₁), и столбцами, являющимися словами кода (n₂, k₂). Кодовое слово двухмерного ТКБ изображено на фигуре 1.

Имеется также трехмерная конструкция ТКБ, тогда к двухмерной матрице добавляется третье измерение в виде третьего компонентного кода [Product Specification AHA4501: 36 Mbits/sec Turbo Product Code Encoder/Decoder, Product Specification АНА4540: 155 Mbits/sec Turbo Product Code Encoder/Decoder].

В существующих ТКБ считывание элементов массива в канал (формирование выходной дискретной последовательности) осуществляется по строкам в измерении по оси x.

Если исходные компонентные линейные блоковые коды расширены проверкой на четность, то кодовые слова таких кодов имеют четный вес и могут быть записаны в виде c′(x)=c(x)(x+1). Тогда кодовое слово ТКБ, получаемое путем считывания по строкам двухмерной таблицы, изображенной на фиг. 1, в измерении по оси x, может быть представлено как 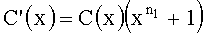$$C\text{'}\left(x\right)=C\left(x\right)\left(x^{n_1}+1\right)$$ . Чтобы установить это, напомним, что все столбцы двухмерной таблицы являются кодовыми словами (n₂, k₂) кода, а передача данных таблицы в канал по строкам эквивалентна прямоугольному перемежению {n₂, k₂) кода глубиной n₁.

Пусть

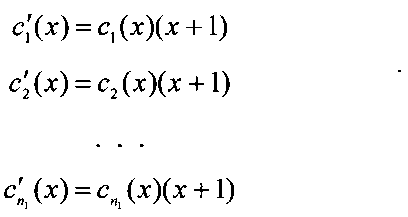
представляют собой кодовые слова (n₂, k₂) линейного блокового кода с проверкой на четность. Для формирования кодового слова ТКБ каждое из (n₂, k₂) кодовых слов растягивается вставкой между элементами слова n₁-1 нулей. Кодовое слово ТКБ получается затем задержкой и сложением этих слов:

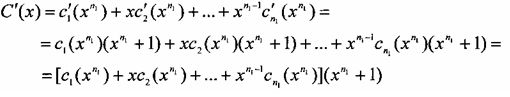
Следовательно:

Из (1) видно, что кодовые слова (n₁×n₂) ТКБ, в которых компонентными кодами являются расширенные двоичные циклические коды и коды с проверкой на четность, содержат постоянный сомножитель (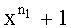 $$x^{n_1}+1$$ ).

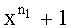
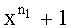
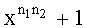
Данный сомножитель может быть найден как НОД двух и более кодовых слов ТКБ. В двоичном представлении НОД эквивалентный двучлену ( $$x^{n_1}+1$$ ), имеет вид «10…01» длины (n₁+1) элементов, что используется в способе в качестве признака синхронизации. Признаком установления синхронизации является наличие НОД у двух предполагаемых кодовых слов ТКБ длины N, причем НОД должен или совпадать с двучленом $$x^{n_1}+1$$ вида «10…01» или делится на него с нулевым остатком. Проведенные исследования показали, что рассуждения для двухмерного (n₁×n₂) ТКБ применимы к трехмерному (n₁×n₂×n₃) ТКБ, отличие в том, что постоянный сомножитель будет иметь вид ( $$x^{n_1{n}_2}+1$$ ), то есть удлинится на n₂ нулей по сравнению с постоянным сомножителем двухмерного ТКБ и кодовые слова трехмерного ТКБ можно представить как

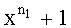
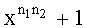
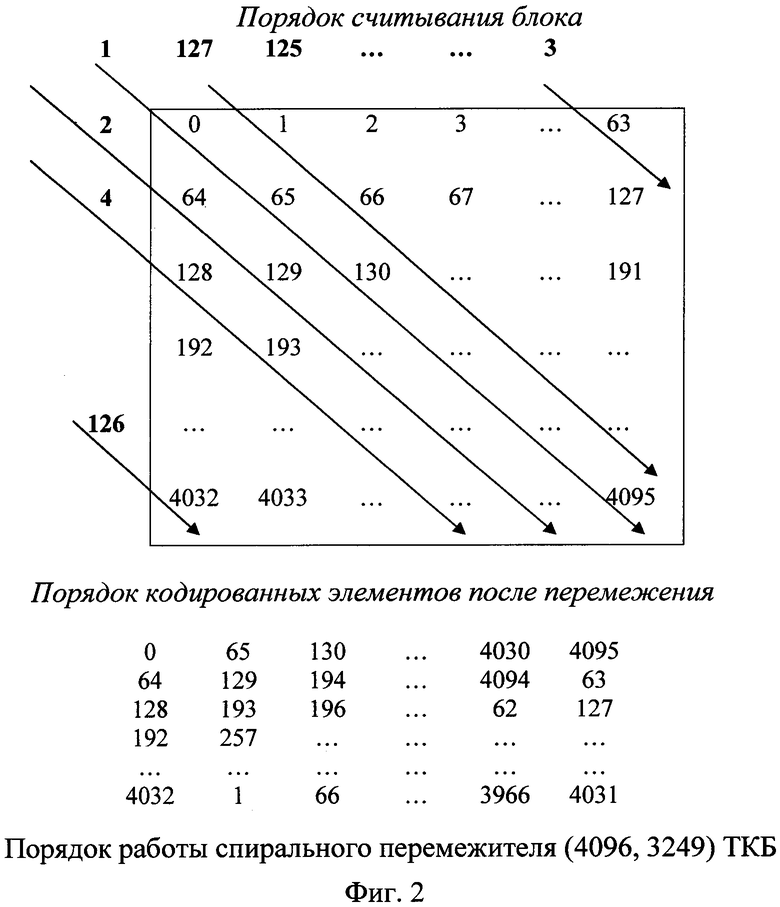
Для удобства будем называть НОД двух предполагаемых кодовых слов НОД1, а двучлен вида x^l+1 (общий вид двучлена для $$x^{n_1}+1$$ и $$x^{n_1{n}_2}+1$$ ) НОД2. Выражения (1) и (2) подразумевает возможность использования НОД1 кодовых слов в качестве признака синхронизации, а делимость НОД1 на НОД2=(x^l+1) без остатка в качестве признака истинности синхронизации по ТКБ.

Применение спирального перемежения значительно повышает способность ТКБ противостоять пакетам ошибок [White paper, «Helical Interleaving for Burst Error Correction with Turbo Product Codes», Efficient Channel Coding, Inc., June 1998]. Порядок работы спирального перемежителя на примере двухмерного (4096, 3249) ТКБ показан на фигуре 2.

Спиральный перемежитель трехмерного ТКБ работает подобным образом, за исключением того, что вместо чтения по диагоналям двухмерного массива перемежитель считывает данные по диагоналям кубического массива.

Математически спиральный перемежитель для двухмерного (n₁×n₂) ТКБ может быть представлен следующим образом. Если оригинальные элементы в массиве проиндексированы через строки и столбцы, то индексы для спирального считывания элементов вычисляются как

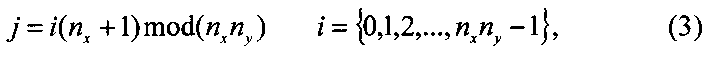
где i - оригинальный индекс, j - индекс спирального перемежителя, n_x - число элементов в измерении по оси x, n_y - число элементов в измерении по оси y.

Подобным образом, спиральное считывание для трехмерного ТКБ вычисляется как

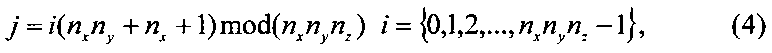
где n_z - код в измерении по оси 2.

Теперь рассмотрим процедуру спирального перемежения двухмерного ТКБ, для упрощения возьмем длину кодового слова N=64 элемента и в качестве компонентных кодов семиэлементные расширенные (n+1=8) двоичные линейные блоковые коды. Двухмерный массив кодового слова (8×8) ТКБ представлен на фигуре 3:

После спирального перемежения кодовое слово ТКБ примет вид, изображенный на фигуре 4.

Согласно фигуре 1 столбцы двухмерного массива, изображенного на фигуре 3, являются кодовыми словами (n₂, k₂) компонентного кода. Заметим, что столбцы спирально-перемеженного кодового слова ТКБ, представленного на фигуре 4, совпадают со столбцами неперемеженного ТКБ (см. фигуру 3) с точностью до циклического сдвига. Очевидно, что свойство четности (n₂, k₂) кодовых слов инвариантно к любым перестановкам, в том числе к циклическим сдвигам. Следовательно, каждый столбец спирально-перемеженного ТКБ имеет четный вес Хэмминга и поэтому содержит двучлен (x+1) в качестве постоянного сомножителя. 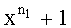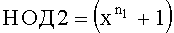С учетом предыдущих рассуждений, можем заключить, что кодовое слово спирально-перемеженного ТКБ, в котором компонентными кодами являются коды с проверкой на четность, содержит двучлен ( $$x^{n_1}+1$$ ) в качестве сомножителя. Данное свойство спирально-перемеженного ТКБ подразумевает возможность использования НОД1 кодовых слов в качестве признака синхронизации, а делимость НОД1 на $$НОД2=\left(x^{n_1}+1\right)$$ без остатка в качестве признака истинности синхронизации.

Проведенные исследования для спирально-перемеженного трехмерного ТКБ показали, что рассуждения для двухмерного спирально-перемеженного (n₁×n₂) ТКБ применимы к трехмерному (n₁×n₂×n₃) ТКБ, отличие в том, что постоянный сомножитель будет иметь вид (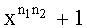 $$x^{n_1{n}_2}+1$$ ), то есть удлинится еще на n₂ нулей по сравнению с постоянным сомножителем двухмерного ТКБ.

Таким образом, вычисление НОД1 двух предполагаемых кодовых слов длины N и делимость найденного НОД1 на двучлен НОД2 вида x^l+1 с нулевым остатком положены в основу способа синхронизации всех ТКБ, в которых компонентными кодами являются расширенные двоичные циклические коды и коды с проверкой на четность. НОД1 предлагается вычислять с помощью бинарного алгоритма нахождения НОД. Данный алгоритм разработан Джозефом Стейном и ориентирован на двоичную арифметику [Дональд Э. Кнут. Искусство программирования. Том 2. Получисленные алгоритмы: Пер. с англ. В. Тертышный. - М.: Вильямс, 2001, с. 371].

В связи с тем, что длина кодовых слов практически используемых ТКБ n≥256 (для эффективности системы турбокодирования произведение длин кодовых слов компонентных кодов должно превышать данную величину) и учитывая то, что в качестве компонентных используются расширенные циклические коды и коды с проверкой на четность, поиск предполагаемой длины кодового слова ТКБ производят среди степеней двойки: 256, 512, 1024, 2048, 4096, 8192, 16384. В ходе исследований применяемых ТКБ [Product Specification АНА4501: 36 Mbits/sec Turbo Product Code Encoder/Decoder, Product Specification AHA4540: 155 Mbits/sec Turbo Product Code Encoder/Decoder] установлено, что компонентными кодами ТКБ могут быть расширенные коды Хэмминга или коды с проверкой на четность с длинами кодовых слов 4, 8, 16, 32, 64, 128, причем коды длин 4 и 8 используются в качестве кодов третьего измерения трехмерных ТКБ и в двухмерных ТКБ не применяются. Следовательно, минимальным двучленом 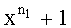$$x^{n_1}+1$$ , который в качестве сомножителя содержит двухмерный ТКБ, будет x¹⁶+1, а максимальным x¹⁰²⁴+1. Данная особенность взята за основу выбора минимальной длины L двучлена x^l+1 в двоичных элементах, для двухмерных ТКБ - x¹⁶+1 эквивалентно 10000000000000001, поэтому L=17 и позволяет не рассматривать возможные делители короткой длины меньшей 17 элементов, возникающие при поиске НОД1.

Возможны случаи ошибочной синхронизации по начальной фазе (ошибочного фазирования). Например, двоичный фрагмент, смещенный на один элемент относительно истинной начальной фазы, будет кодовым словом с вероятностью 0,5, следовательно, вероятность наступления события, когда каждый из трех выделенных смещенных на один элемент относительно истинной начальной фазы фрагментов, является кодовым словом, приблизительно равна 0,125.

Для исключения ошибок, возникающих при синхронизации вблизи истинной начальной фазы (когда найденная начальная фаза смещена от истинной не более чем на 2 элемента), повышают вероятность истинного фазирования. Вероятность истинного фазирования повышается за счет проверки делимости без остатка на НОД2 M=1 выделенных фрагментов, которые смещены относительно найденной начальной фазы φ_синх не более чем на 2 элемента. Если признак делимости M фрагментов на НОД2 без остатка выявляется больше чем для одной фазы, то увеличивают количество M фрагментов, на единицу до тех пор, пока данный признак выявится не более одного раза. Начальная фаза, соответствующая единственному выявленному разу, и будет уточненной истинной начальной фазой.

Из-за того, что кодовые слова трехмерного ТКБ представляют собой последовательность кодовых слов двухмерного ТКБ, то при наличии трехмерного ТКБ возможна ошибочная синхронизация по кодовым словам двухмерного ТКБ. Для исключения данной ошибки предлагается проводить проверку на наличие третьего измерения ТКБ. После выполнения синхронизации по двухмерному ТКБ с параметрами N_синх, φ_синх проверяется условие 4N_синх≤N_max. Если условие выполняется, то изменяют входные параметры N_min=4N_синх, φ₀=φ_сних, 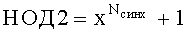$$НОД2=x^{N_{синх}}+1$$ и осуществляют поиск синхронного состояния возможного трехмерного ТКБ. Признаком синхронного состояния трехмерного ТКБ считают наличие нулевого остатка от деления выделенного фрагмента на НОД2. Цифра 4 в условии и в измененных входных параметрах используется вследствие того, что минимальный код, который может быть в третьем измерении трехмерного ТКБ - (4, 3), т.е. минимальная длина кода n₃=4.

Проведенный анализ уровня существующей техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, которые тождественны всем признакам заявленного технического решения, отсутствует, что указывает на соответствие заявленного способа условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».

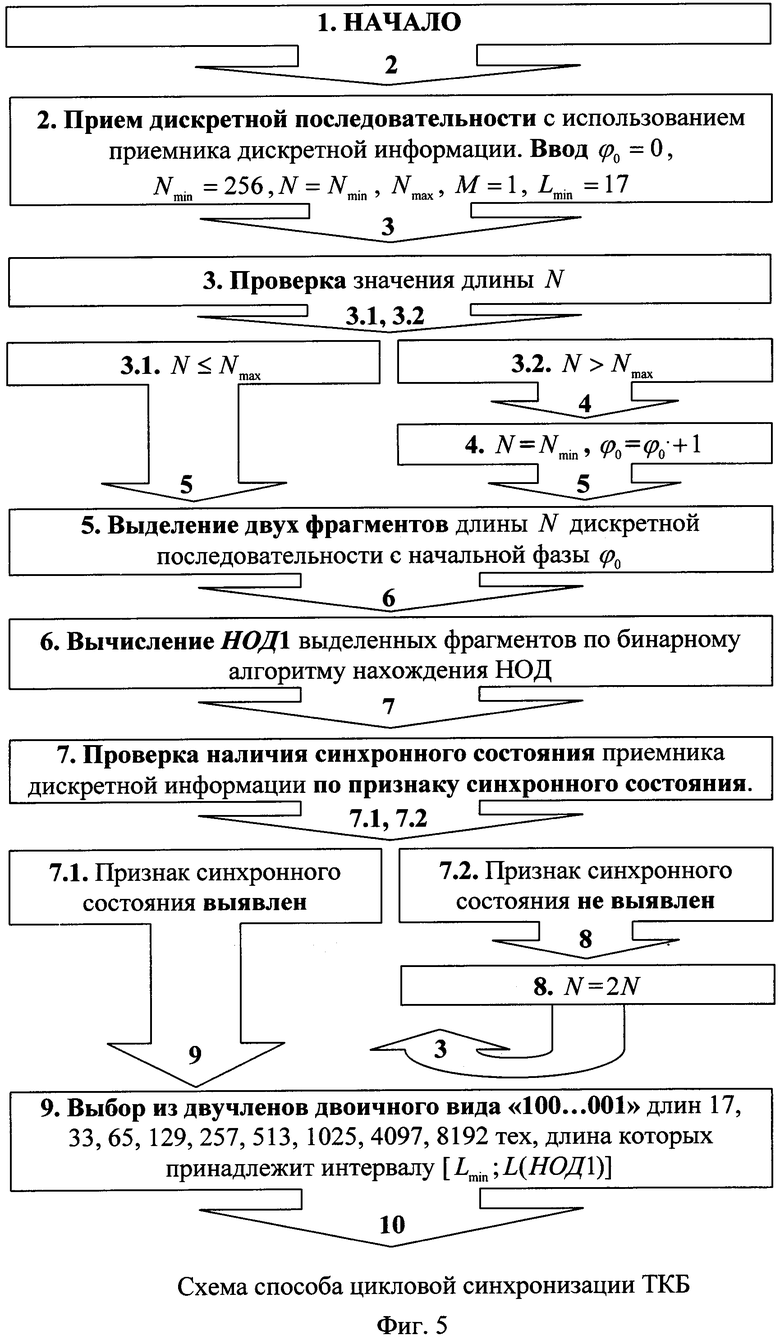
Заявленный способ поясняется иллюстрацией (см. фигуру 5), на которой изображена структурная схема способа цикловой синхронизации ТКБ и повышения вероятности правильного фазирования.

Цикловая синхронизация ТКБ в условиях параметрической неопределенности осуществляется следующим образом:

Этап 1. Начало. Дискретную последовательность элементов кодовых слов ТКБ принимают с использованием приемника дискретной информации.

Этап 2. Задают N_min=256, N_max=16384, длину фрагментов N=N_min, начальную фазу φ₀=0, значение количества фрагментов М=1, К=0.

Далее производят анализ состояния приемника дискретной информации.

Этап 3. Проверяют значение N. Если N≤N_max выполняется, то переход к этапу 5, иначе переход к этапу 4.

Этап 4. N присваивают значение N_min, φ₀ присваивают значение φ₀+1.

Этап 5. Выделяют из принятой дискретной последовательности друг за другом два фрагмента длины N с начальной фазы φ₀:

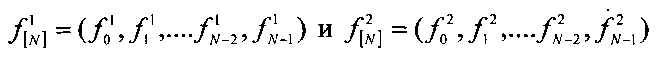
Этап 6. Вычисляют НОД1 двух выделенных фрагментов с помощью бинарного алгоритма нахождения НОД:

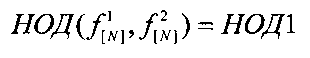
Этап 7. Проверяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. В качестве признака используют наличие НОД двух выделенных фрагментов, при этом длина НОД не меньше 17. Если L[НОД1]≥17, то синхронное состояние выявлено, запоминают НОД1 и переходят к этапу 9, иначе переходят к этапу 8.

Этап 8. N присваивают значение 2N и возвращаются к этапу 3.

Этап 9. Производят выбор из двучленов x^l+1 двоичного вида «100…001» длин 17, 33, 65, 129, 257, 513, 1025, 4097, 8192 тех двучленов, длина которых принадлежит интервалу [17; L(НОД1)]

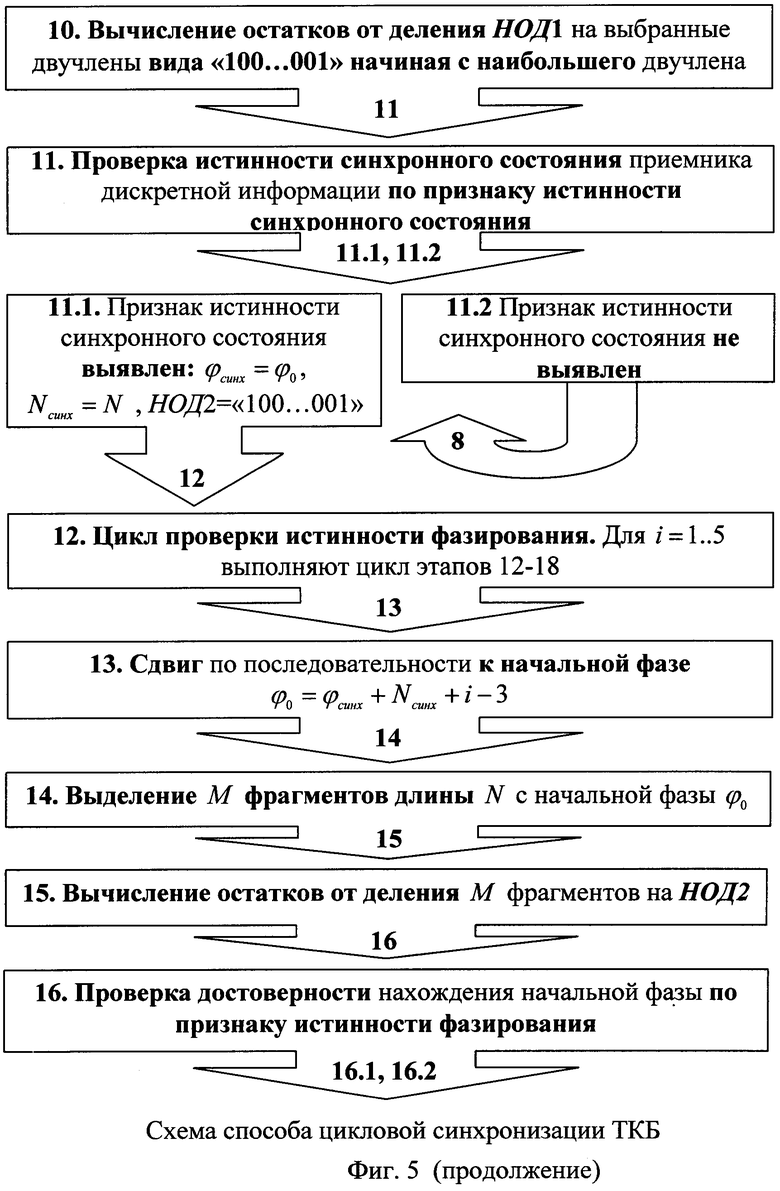
Этап 10. Вычисляют остатки от деления НОД1 на двучлены x^l+1, выбранные на этапе 9, начиная с наибольшего двучлена, как только получен нулевой остаток, вычисление прерывают и досрочно переходят к этапу 11.

(НОД1)mod(x^l+1)

Этап 11. Проверяют наличие синхронного состояния приемника дискретной информации по признаку истинности синхронного состояния.

В качестве признака истинности синхронного состояния используют наличие нулевого остатка при делении НОД1 на двучлен x^l+1. Если

(НОД1)mod(x^l+1)=0,

то считают, что истинность синхронного состояния выявлена N_синх=N, φ_синх=φ₀, НОД2=x^l+1 и переходят к этапу 12, иначе переходят к этапу 8.

Этап 12. Повышают вероятность нахождения начальной фазы. Для i-1…5 выполняют цикл: этапы 12-18.

Этап 13. Сдвигаются по последовательности к начальной фазе φ₀=φ_синх+N_синх-3+i.

Этап 14. Выделяют М фрагментов длины N_синх с начальной фазы φ₀.

Этап 15. Вычисляют остатки от деления выделенных М фрагментов на НОД2

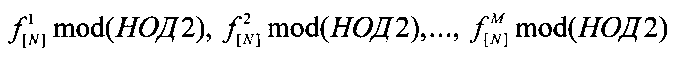
Этап 16. Проверяют точность нахождения начальной фазы по признаку истинности фазирования. Если все остатки от деления выделенных М фрагментов на НОД2 равны нулю

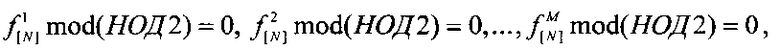
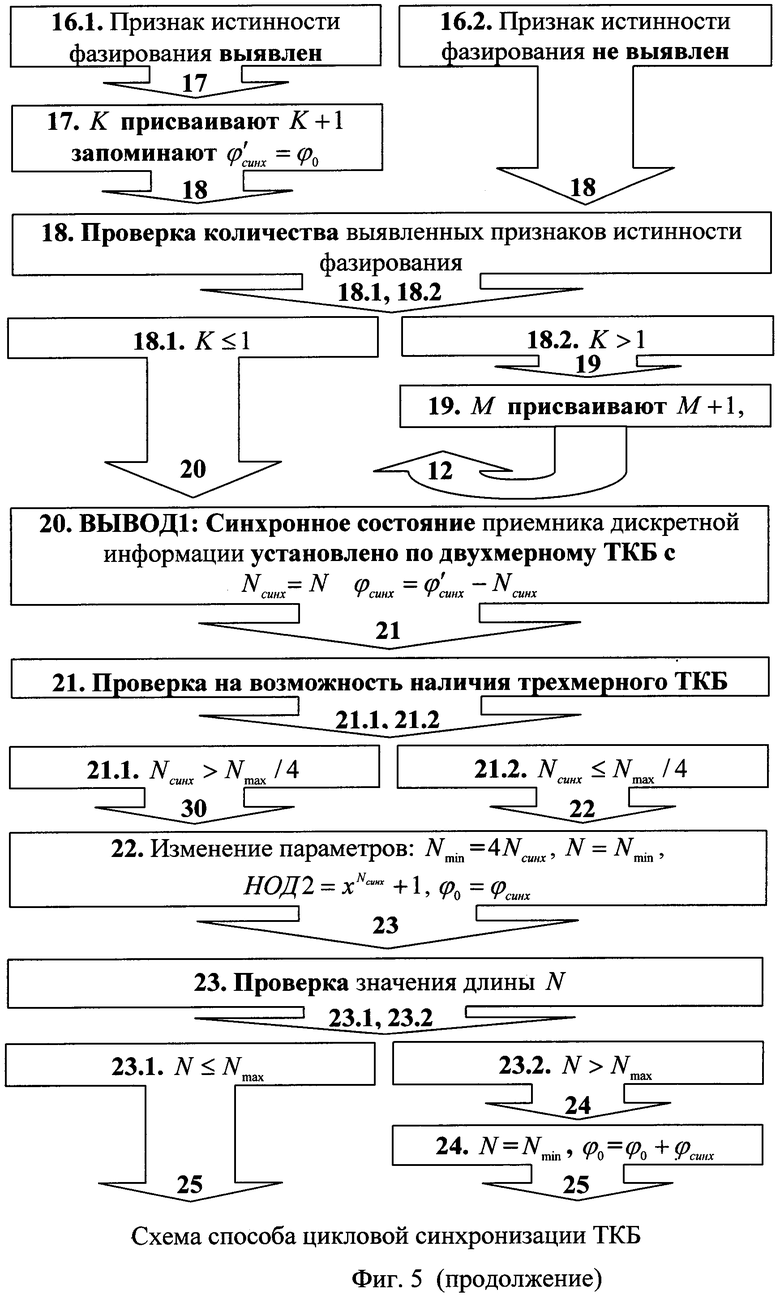
то переходят к этапу 17, иначе переходят к этапу 18.

Этап 17. К присваивают значение К+1. Запоминают 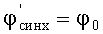$${\varphi }_{синх}^{\text{'}}={\varphi }_0$$ .

Этап 18. Проверяют количество выявленных признаков истинности синхронизации К. Если К≤1, то считают синхронное состояние приемника установлено с 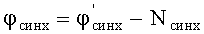$${\varphi }_{синх}={\varphi }_{синх}^{\text{'}}-N_{синх}$$ , и переходят к этапу 20, иначе переход к этапу 19.

Этап 19. М присваивают значение М+1 и переходят к этапу 12.

Этап 20. Выводят данные о том, что синхронное состояние приемника дискретной информации установлено

Этап 21. Проверяют возможность наличия трехмерного ТКБ. Если N_синх≤N_max /4, то переход к этапу 22, иначе, если N_синх>N^max /4, то переход к этапу 30.

Этап 22. Корректируют параметры: N_min=4N_синх, 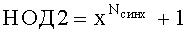$$НОД2=x^{N_{синх}}+1$$ (т.е. «100…001» длины L=N_синх+1), φ₀=φ_синх, М=1, К=0.

Этап 23. Проверяют значение N. Если N≤N_max выполняется, то переход к этапу 25, иначе переход к этапу 24.

Этап 24. N присваивают значение N_min, φ₀ присваивают значение φ₀+φ_синх.

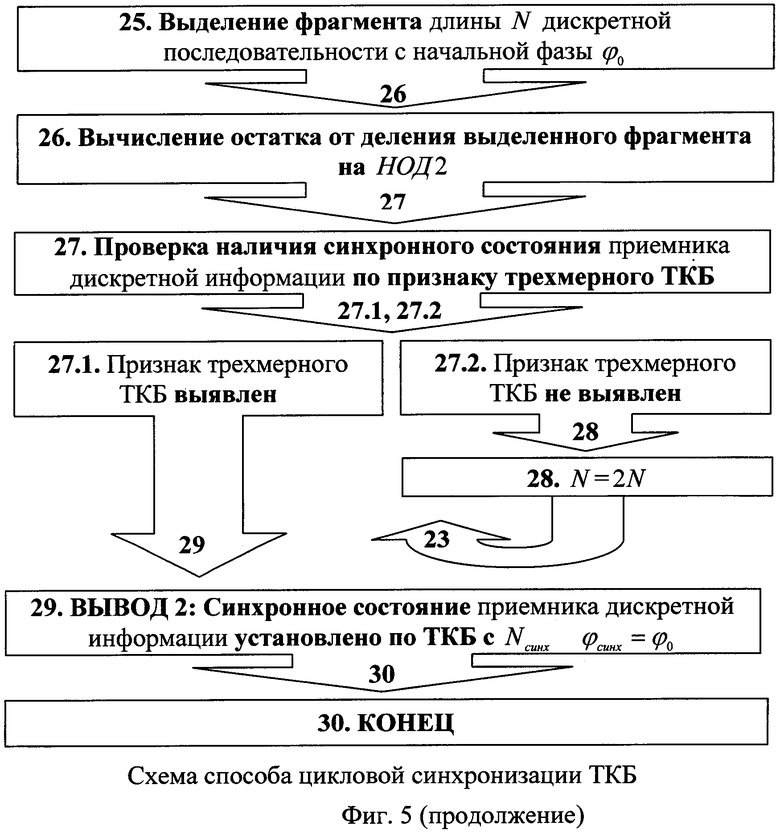
Этап 25. Выделяют из принятой дискретной последовательности фрагмент длины N с начальной фазы φ₀

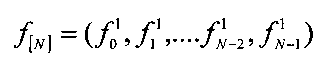
Этап 26. Вычисляют остаток от деления выделенного фрагмента на НОД2:

f_[N]mod(НОД2)

Этап 27. Проверяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния трехмерного ТКБ. В качестве признака используют наличие нулевого остатка от деления выделенного фрагмента на НОД2. Если f_[N]mod(НОД2)=0, то синхронное состояние выявлено, и переходят к этапу 29, иначе переходят к этапу 28.

Этап 28. N присваивают значение 2N и возвращаются к этапу 23.

Этап 29. Выводят данные о том, что синхронное состояние приемника дискретной информации установлено по трехмерному ТКБ с N_тсинх=N и φ_тсинх=φ₀.

Этап 30. Конец.

Данную последовательность этапов можно условно разделить на три стадии:

1 стадия. Осуществление синхронизации по ТКБ по признаку синхронизации и признаку истинности синхронизации: этапы 2-11.

2 стадия: Повышение вероятности истинного фазирования и синхронизация по ТКБ с уточненной начальной фазой: этапы 12-20.

3 стадия: Проверка на возможность наличия трехмерного ТКБ и принятие решения на завершение способа или возврат к началу с измененными параметрами и повторение способа: этапы 21-29.

Для исследования возможности осуществления предложенного способа проведено имитационное моделирование его работы. Моделирование выполнено в инструментальной среде МАТLАВ 7.

Например, приемник дискретной информации принимает двоичную дискретную последовательность спирально-перемеженного (32,26)×(32,26)×(4,3) ТКБ, длина кодового слова которого N=4096 элементов и в качестве компонентных кодов в кодере которого используются два тридцатидвухэлементных расширенных (п+1=32) двоичных (q=2)

кода Хэмминга и четырехэлементный двоичный код с проверкой на четность.

Входными данными является непосредственно последовательность ТКБ, N_min=256, N_max=16384, φ₀=0, M=1, K=0.

На первой стадии работы способа синхронизация выполнилась и успешно определены параметры N_синх=1024, φ_синх=120 и НОД2=100000000000000000000000000000001, L(НОД2)=33.

На второй стадии алгоритм повышения вероятности правильной синхронизации подтвердил φ_синх=120. На третьей стадии работы способа проводилась проверка ТКБ на трехмерность, для этого входные параметры были изменены: N_min=4096, N_max=16384, φ₀=120, M=1, L=16×L(НОД2)=16×32=512. В результате синхронизация успешно выполнена с параметрами N_тсинх=4096, φ_тсинх=1144, и вычисленный НОД имеет вид «10×10» длиной 1025 элементов. Алгоритм повышения вероятности истинного фазирования подтвердил φ_тсинх=1144.

Изобретение относится к вычислительной технике. Технический результат заключается в устранении возможности ложной цикловой синхронизации. Способ цикловой синхронизации турбокодов, в котором поиск длины кодового слова производят среди степеней двойки N: N_min=2⁸=256, N_max=2¹⁴=16384 и выделяют фрагменты дискретной последовательности длины N. В качестве признака синхронного состояния приемника используют ненулевой наибольший общий делитель выделенных фрагментов (НОД1) длины не меньше порога 17. После выявления данного признака дополнительно производят проверку установления синхронного состояния по наличию признака истинности синхронного состояния. В качестве признака истинности синхронного состояния используют нулевые остатки от деления фрагментов на НОД2=(x^l+1). После установления истинности синхронного состояния проверяют истинность фазирования и синхронизируют по двухмерному блоковому турбокоду (ТКБ). В зависимости от найденных параметров синхронизации N_синх, φ_синх, корректируют параметры способа и осуществляют поиск синхронного состояния для трехмерного ТКБ. 5 ил.

Способ цикловой синхронизации турбокодов, заключающийся в том, что с использованием приемника дискретной информации принимают входную последовательность, представляющую собой последовательно передаваемые элементы кодовых слов, задают диапазон предполагаемых длин кодовых слов [N_min-N_max], выбирают предполагаемую фазу начала кодового слова φ₀, выделяют из принятой закодированной информационной последовательности несколько Z предполагаемых кодовых слов длины N, для выделенных Z кодовых слов вычисляют наибольший общий делитель и в зависимости от его отличия от единицы определяют наличие синхронного состояния приемника, при отсутствии синхронизации до ее установления производят поиск синхронного состояния путем выделения и вычисления наибольшего общего делителя Z кодовых слов новых длин из [N_min-N_max], если при переборе всех длин кодовых слов из [N_min-N_max] наличие признака синхронного состояния не обнаружено, увеличивают предполагаемую фазу начала кодового слова на единицу и продолжают поиск синхронного состояния, отличающийся тем, что задают N_min=256, N_max=16384, осуществляют поиск синхронного состояния, для этого из дискретной последовательности блокового турбокода (ТКБ) выделяют два фрагмента длины N из набора N_min, 2N_min, 4N_min, …, N_max с начальной фазы φ₀ и вычисляют наибольший общий делитель выделенных фрагментов НОД1, как только будет найден НОД1 длины 17 и больше, считают синхронное состояние установленным, при отсутствии синхронного состояния для всех длин набора N_min, 2N_min, 4N_min, …, N_max увеличивают предполагаемую фазу начала кодового слова на единицу и продолжают поиск синхронного состояния, после установления синхронного состояния проверяют его истинность, для этого проверяют наличие нулевого остатка при делении НОД1 на двучлен вида x^l+1, где l=16, 32, 64, 128, 256, 512, 1024, начиная с наибольшего, как только нулевой остаток найден, то истинность синхронного состояния считается установленной φ_синх, а двучлен, делящий НОД1 без остатка, отождествляется с НОД2, при отсутствии истинности синхронного состояния увеличивают N вдвое и возвращаются к поиску синхронного состояния, после установления истинности синхронного состояния проверяют истинность фазирования посредством выделения фрагментов длины N_синх с начальных фаз из [φ_синх+N_синх-2, φ_синх+N_синх+2] и сравнения с нулем остатков от деления этих фрагментов на НОД2, после синхронизации по двухмерному ТКБ, если 4N_синх>N_max, то завершают способ, иначе, если 4N_синх≤N_max, корректируют параметры N_min=4N_синх, N=N_min, 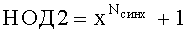, φ₀=φ_синх, осуществляют поиск синхронного состояния для трехмерного ТКБ.