Предлагаемый способ относится к области техники связи и может быть использован в системах передачи данных, а также в системах телеизмерения, телеуправления, в радиопередающей аппаратуре малых космических аппаратов и телеметрии дальнего космоса без использования синхрокомбинаций и дополнительного канала управления.
Известен способ декодирования циклического помехоустойчивого кода (Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и декодирование сложных дискретных сигналов / Под ред. В.И.Коржика. - М.: Радио и связь, 1988, стр.136), при котором на приемной стороне вычисляют синдром помехоустойчивого кода. При обнаружении неискаженного помехоустойчивого кода, что определяется по нулевому синдрому, принимают решение о приеме помехоустойчивого кода и затем выделяют информационную часть помехоустойчивого кода.
Этот способ имеет невысокую помехоустойчивость, обусловленную низкой вероятностью правильной синхронизации и тем, что декодирование помехоустойчивого кода выполняют только с обнаружением ошибок без их исправления.
Известен также способ декодирования циклического помехоустойчивого кода (Болховитин Л.М., Журкин С.П., Квашенников В.В., Сосин П.А. Передача формализованных сообщений самосинхронизирующимся кодом с переменными параметрами. Техника средств связи, сер. ТПС, вып.8, 1990, стр.39), при котором на передающей стороне формируют выходную последовательность, представляющую собой сумму по модулю два циклического помехоустойчивого кода и синхронизирующей последовательности, на приемной стороне последовательность умножают на проверочный полином помехоустойчивого кода и в результате вычисляют синхронизирующую последовательность. При обнаружении определенной комбинации синхронизирующей последовательности принимают решение о наличии цикловой синхронизации и затем выделяют информационную часть помехоустойчивого кода.
Однако и этот способ имеет низкую помехоустойчивость в связи с тем, что декодирование помехоустойчивого кода выполняют только с обнаружением ошибок без их исправления.
Известен также способ декодирования циклического помехоустойчивого кода (Бек Г.В., Богданович В.Н., Киреев О.П. Метод синхронизации сообщений. Сб.: Построение и анализ систем передачи информации. М.: Наука, 1980, стр.84), заключающийся в том, что на передающей стороне формируют выходную последовательность, представляющую собой сумму по модулю два циклического помехоустойчивого кода и синхронизирующей последовательности. На приемной стороне принятую последовательность сначала умножают на проверочный полином помехоустойчивого кода и в результате вычисляют синхронизирующую последовательность. Далее осуществляют обнаружение определенной комбинации синхронизирующей последовательности с учетом ошибок, наложенных на принятую последовательность в канале связи. При обнаружении синхронизирующей последовательности принимают решение о наличии цикловой синхронизации и выделяют помехоустойчивый код. Затем определяют комбинацию ошибок и осуществляют исправление ошибок в информационной части помехоустойчивого кода.
Недостатком этого способа также является невысокая помехоустойчивость, поскольку прием сообщения возможен лишь при наличии в кодовом слове ошибок, кратность которых не выше исправляющей способности кода.
Известны способы декодирования циклических кодов (патенты РФ №№2231216 С2, 2109407 С1, 2024053 С1).
Из известных способов наиболее близким к предлагаемому является Способ декодирования циклического помехоустойчивого кода (патент РФ №2231216 С2), который и выбран в качестве прототипа. Данный способ обеспечивает повышение помехоустойчивости приема за счет того, что на передающей стороне выходная последовательность рекуррентно продолжена с использованием проверочного соотношения циклического помехоустойчивого кода и на приемной стороне дополнительно осуществляют декодирование циклических продолжений принятой последовательности. При этом декодирование осуществляют в скользящем окне приема и за пределами скользящего окна допускают возникновение произвольного количества ошибок в принятой последовательности, в том числе превышающее корректирующую способность помехоустойчивого кода, но не приводящее к трансформации кода.
Однако при использовании данного способа необходимо присутствие символов синхронизации, а параметры корректирующего кода остаются постоянными вне зависимости от помеховой обстановки, что приводит к уменьшению скорости передачи и увеличению энергопотребления радиопередающей аппаратурой. Снижение электропотребления является актуальной задачей при использовании малых космических аппаратов и космических аппаратов дальнего космоса.
Технической задачей изобретения является увеличение скорости передачи информации при одновременном снижении энергопотребления радиопередающей аппаратурой в каналах связи с помехами.
Поставленная задача решается согласно способу декодирования циклического помехоустойчивого кода, заключающемуся в том, что на передающей стороне формируют выходную последовательность, представляющую собой сумму по модулю два циклического помехоустойчивого кода и синхронизирующей последовательности, рекуррентно продолжают с использованием проверочного соотношения циклического помехоустойчивого кода, на приемной стороне дополнительно осуществляют декодирование циклических продолжений принятой последовательности, отличающемуся тем, что на передающей стороне формируют кодовые слова путем кодирования информационных символов с помощью циклического кода без использования синхрокомбинаций, изменяют параметры циклического кода в зависимости от уровня помех, на приемной стороне осуществляют накопление передаваемой информации, формируют тем самым выборку, затем для фазирования по кодовым словам определяют границы кодового слова, задаются предполагаемой длиной кодового слова и заданным окном осуществляют "скользящее" посимвольное дискретное преобразование Фурье в поле Галуа по всему объему анализируемой выборки, при этом на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа осуществляют выделение нулевых спектральных компонент и определение их количества с построением функции количества нулевых спектральных компонент на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа, затем осуществляют децимацию данной функции с шагом, равным предполагаемой длине кодового слова, с построением функции оценки математического ожидания числа нулевых спектральных компонент, моменты фазирования достигают максимума функции оценки математического ожидания числа нулевых спектральных компонент, с учетом полученного максимума выделяют кодовые слова, затем определяют оценку математического ожидания элементов спектров кодовых слов и оценивают параметры циклического кода по полученным кодовым словам, далее определяют циклотомические классы, восстанавливают порождающий полином циклического кода и осуществляют декодирование кодовых слов.
Рассмотрим осуществление предлагаемого способа декодирования циклического помехоустойчивого кода.
На передающей стороне формируют выходную последовательность. Для этого исходное сообщение объемом k символов вначале кодируют циклическим помехоустойчивым кодом. В результате кодирования информации получают слово циклического кода C(n,k)=x0, x1, ..., xn-1, где k - число информационных символов, n - длина кодового слова циклического кода. Поскольку код является циклическим, существует рекуррентное соотношение, с помощью которого получают все контрольные символы кода xk+i=f(xi, x1+i, ..., xk-1+i) где i=0...n-k-1. При этом перед началом передачи данных осуществляют оценку помеховой обстановки и в соответствии с ней определяют параметры помехоустойчивого кода. Полученные кодовые слова передаются далее в канал связи.
На приемной стороне осуществляют накопление передаваемой информации, формируют тем самым выборку объемом L. Для фазирования по кодовым словам, т.е. определения границ и длины кодового слова, задаются предполагаемой длиной кодового слова n и заданным окном осуществляют "скользящее" посимвольное ДПФГ по всему объему анализируемой выборки:
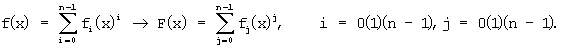
При этом на каждом шаге "скользящего" ДПФГ осуществляют выделение нулевых спектральных компонент и определяют их количество 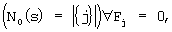 где N0(s) - значение функции количества нулевых элементов на s-м-шаге. График функции N0(s) при "скользящем" ДПФГ для циклического кода (63,57) изображен на фиг.1 (дальнейший графический материал представлен для циклического кода (63,57)).
где N0(s) - значение функции количества нулевых элементов на s-м-шаге. График функции N0(s) при "скользящем" ДПФГ для циклического кода (63,57) изображен на фиг.1 (дальнейший графический материал представлен для циклического кода (63,57)).
Далее осуществляют анализ функции N0 количества нулевых элементов спектра. Задаются размером анализируемого окна, равным предполагаемой длине кодового слова n либо большим. Осуществляют оценку математического ожидания числа нулевых элементов данной функции, используя выражение 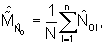 где N
где N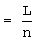 - количество анализируемых выборок (длина "окна" предполагаемого кодового слова).
- количество анализируемых выборок (длина "окна" предполагаемого кодового слова).
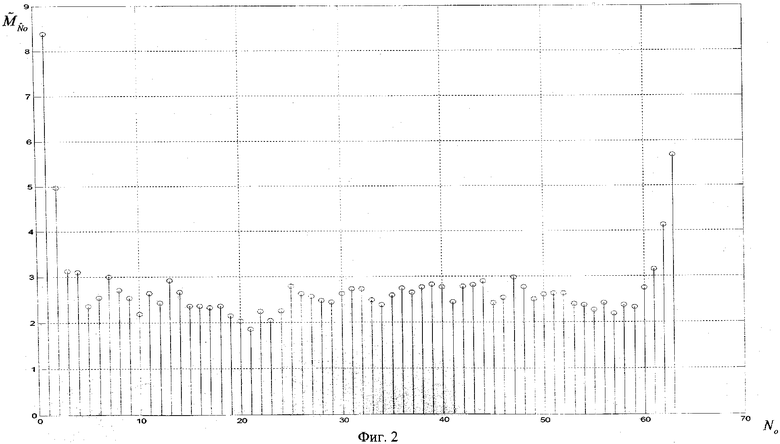
При адекватной синхронизации функция 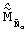 оценки математического ожидания количества нулевых спектральных элементов будет иметь вид, представленный на фиг.2.
оценки математического ожидания количества нулевых спектральных элементов будет иметь вид, представленный на фиг.2.
В моменты правильного фазирования будут иметь место максимумы функции 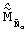 . Если при анализе функции N0 количества нулевых элементов спектра было взято окно размером, равным предполагаемой длине кодового слова, n, то график функция
. Если при анализе функции N0 количества нулевых элементов спектра было взято окно размером, равным предполагаемой длине кодового слова, n, то график функция 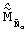 оценки математического ожидания количества нулевых спектральных элементов будет иметь один максимум. Если максимум данной функции не наблюдается, то необходимо осуществить изменение длины предполагаемого кодового слова и провести построение функции N0, а затем и функции
оценки математического ожидания количества нулевых спектральных элементов будет иметь один максимум. Если максимум данной функции не наблюдается, то необходимо осуществить изменение длины предполагаемого кодового слова и провести построение функции N0, а затем и функции 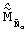 .
.
В случае если анализируемый цифровой поток сфазирован, т.е. начинается с кодового слова, то график функции 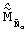 будет иметь вид, представленный на фиг.2. Если же поток не сфазирован, то график функции
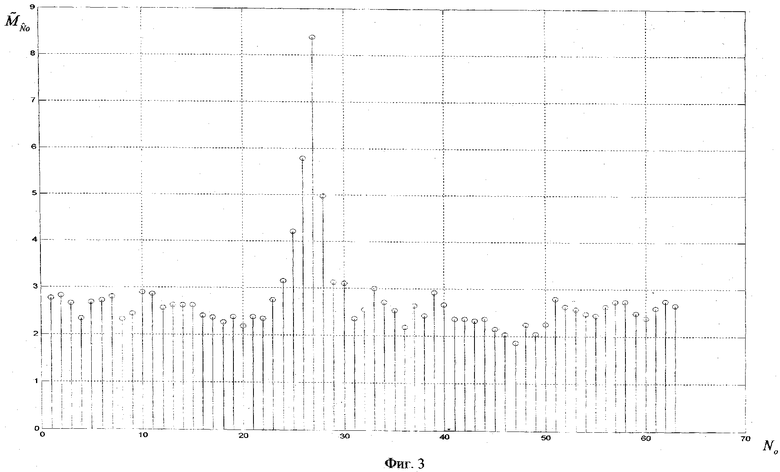
будет иметь вид, представленный на фиг.2. Если же поток не сфазирован, то график функции 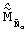 будет иметь вид, представленный на фиг.3.
будет иметь вид, представленный на фиг.3.
Если при анализе N0 количества нулевых элементов спектра было взято окно размером, в два и более раз превышающим длину кодового слова n, то на графике функции 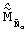 оценки математического ожидания количества нулевых спектральных элементов будет иметься соответственно два или более максимумов функции, причем период их повторения будет равен длине кодового слова n.
оценки математического ожидания количества нулевых спектральных элементов будет иметься соответственно два или более максимумов функции, причем период их повторения будет равен длине кодового слова n.
В случае, если функция 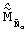 будет иметь максимум, больший либо равный пороговому значению, то принимают решение о том, что обнаружен сигнал, кодированный циклическим кодом. Величина порога определяется длиной анализируемого при дискретном преобразовании Фурье в поле Галуа окна. Таким образом, осуществляется фазирование методом последовательных сдвигов, основанное на отличии синхронного состояния приемника от асинхронного, где под синхронным понимается такое состояние, в котором принимаются только кодовые слова (без учета влияния ошибок в линии связи).
будет иметь максимум, больший либо равный пороговому значению, то принимают решение о том, что обнаружен сигнал, кодированный циклическим кодом. Величина порога определяется длиной анализируемого при дискретном преобразовании Фурье в поле Галуа окна. Таким образом, осуществляется фазирование методом последовательных сдвигов, основанное на отличии синхронного состояния приемника от асинхронного, где под синхронным понимается такое состояние, в котором принимаются только кодовые слова (без учета влияния ошибок в линии связи).
После осуществления обнаружения наличия кодирования, а следовательно, определения длины кодового слова и фазирования возникает задача по определению структуры и параметров кодера. Для этого над кодовыми словами осуществляют ДПФГ.
Определяют оценку математического ожидания 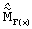 элементов спектра F(x)
элементов спектра F(x)
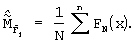
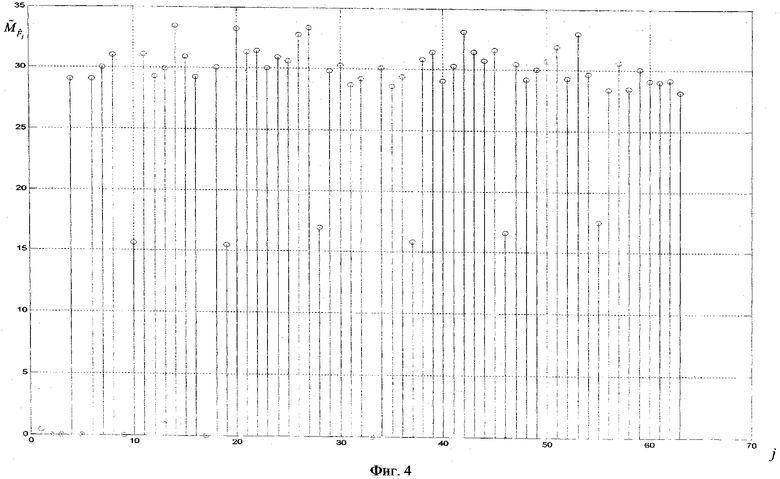
График распределения оценки математического ожидания 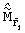 элементов спектра представлен на фиг.4.
элементов спектра представлен на фиг.4.
Как видно из графиков, в случае если сигнал принят без помех, оценка математического ожидания 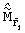 элементов спектра, характеризующих порождающие полиномы кодеров, равна 0. В случае наличия помех в канале связи значения спектральных компонентов, характеризующих корни порождающего полинома, которые должны быть равными 0, будут отличны от 0. Проведенный анализ показал, что использование статистических оценок математического ожидания значений спектральных компонентов позволяет обеспечить вероятность идентификации 0,99 при ошибке в канале связи до 10-3. Затем осуществляют определение циклотомических классов
элементов спектра, характеризующих порождающие полиномы кодеров, равна 0. В случае наличия помех в канале связи значения спектральных компонентов, характеризующих корни порождающего полинома, которые должны быть равными 0, будут отличны от 0. Проведенный анализ показал, что использование статистических оценок математического ожидания значений спектральных компонентов позволяет обеспечить вероятность идентификации 0,99 при ошибке в канале связи до 10-3. Затем осуществляют определение циклотомических классов 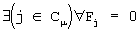 с последующим восстановлением порождающего полинома кодера
с последующим восстановлением порождающего полинома кодера 
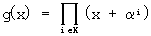 , где αi - примитивный элемент поля GF(n)(q) в степени i, где
, где αi - примитивный элемент поля GF(n)(q) в степени i, где 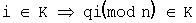 . Множество К равно объединению циклотомических классов.
. Множество К равно объединению циклотомических классов.
В зависимости от параметров кодера кодовое слово будет иметь характеризующий структуру кодера циклотомический класс по модулю n=pm-1 нулевых спектральных компонентов.
Таким образом, предлагаемый способ по сравнению с прототипом обеспечивает не только повышение помехоустойчивости приема кодового слова циклического кода, но и позволяет ускорить процесс фазирования при передаче кодовых слов без использования символов синхронизации. Используемый признак для фазирования кодовых слов является единым для различных классов кодов. Ввиду того что исчезает необходимость в символах синхрокомбинаций, появляется возможность повысить скорость передачи информации. Таким образом, появляется возможность динамического изменения характеристик и параметров кодера передающей аппаратуры МКА и КА дальнего космоса без использования отдельного канала управления при увеличении скорости и уменьшении энергетических затрат при передаче информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2006 |
|
RU2319308C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2359414C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2011 |
|
RU2455773C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ С МЯГКИМИ РЕШЕНИЯМИ | 2012 |
|
RU2500074C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2231216C2 |
| СПОСОБ СОВМЕСТНОЙ ТАКТОВОЙ И КОДОВОЙ СИНХРОНИЗАЦИИ | 2010 |
|
RU2460219C2 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ МНОГОБЛОЧНЫХ СООБЩЕНИЙ | 2023 |
|
RU2819177C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2342796C1 |
| СПОСОБ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ТУРБОКОДОВ | 2014 |
|
RU2566945C1 |
| Способ кодовой цикловой синхронизации с мягкими решениями | 2017 |
|
RU2664409C1 |
Изобретение относится к области техники связи и может быть использовано в системах передачи данных, системах телеизмерения, телеуправления, в радиопередающей аппаратуре малых космических аппаратов и телеметрии дальнего космоса. Технический результат - повышение помехоустойчивости приема циклического кода, автоматической адаптации характеристик передаваемого сигнала к интенсивности помех, увеличение скорости передачи информации и ускорение процесса фазирования при передаче кодовых слов без синхрокомбинаций. Для этого на передающей стороне формируют кодовые слова путем кодирования информационных символов с помощью циклического кода без использования синхрокомбинаций, изменяют параметры циклического кода в зависимости от уровня помех, на приемной стороне осуществляют накопление передаваемой информации, формируют тем самым выборку, затем для фазирования по кодовым словам определяют границы кодового слова, задаются предполагаемой длиной кодового слова и заданным окном осуществляют "скользящее" посимвольное дискретное преобразование Фурье в поле Галуа по всему объему анализируемой выборки, при этом на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа осуществляют выделение нулевых спектральных компонент и определение их количества с построением функции количества нулевых спектральных компонент на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа, затем осуществляют децимацию данной функции с шагом, равным предполагаемой длине кодового слова, с построением функции оценки математического ожидания числа нулевых спектральных компонент, моменты фазирования достигают максимума функции оценки математического ожидания числа нулевых спектральных компонент, с учетом полученного максимума выделяют кодовые слова, затем определяют оценку математического ожидания элементов спектров кодовых слов и оценивают параметры циклического кода по полученным кодовым словам, далее определяют циклотомические классы, восстанавливают порождающий полином циклического кода и осуществляют декодирование кодовых слов. 4 ил.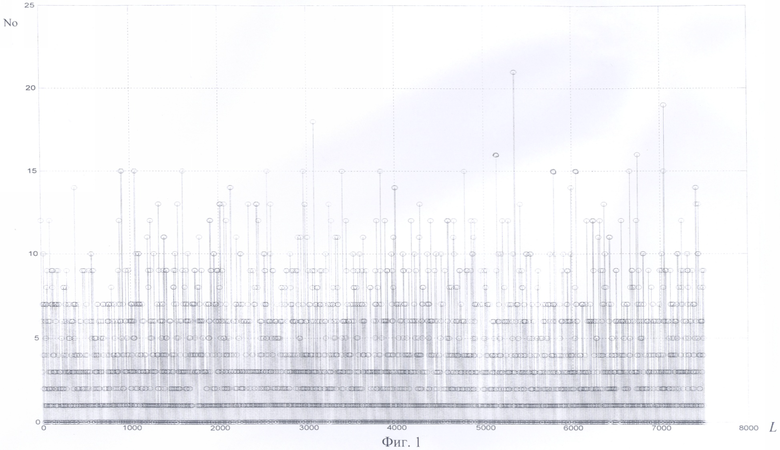
Способ декодирования циклического помехоустойчивого кода, заключающийся в том, что на передающей стороне формируют выходную последовательность, представляющую собой сумму по модулю два циклического помехоустойчивого кода и синхронизирующей последовательности, рекуррентно продолжают с использованием проверочного соотношения циклического помехоустойчивого кода, на приемной стороне дополнительно осуществляют декодирование циклических продолжений принятой последовательности, отличающийся тем, что на передающей стороне формируют кодовые слова путем кодирования информационных символов с помощью циклического кода без использования синхрокомбинаций, изменяют параметры циклического кода в зависимости от уровня помех, на приемной стороне осуществляют накопление передаваемой информации, формируют тем самым выборку, затем для фазирования по кодовым словам определяют границы кодового слова, задаются предполагаемой длиной кодового слова и заданным окном осуществляют "скользящее" посимвольное дискретное преобразование Фурье в поле Галуа по всему объему анализируемой выборки, при этом на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа осуществляют выделение нулевых спектральных компонент и определение их количества с построением функции количества нулевых спектральных компонент на каждом шаге "скользящего" дискретного преобразования Фурье в поле Галуа, затем осуществляют децимацию данной функции с шагом, равным предполагаемой длине кодового слова, с построением функции оценки математического ожидания числа нулевых спектральных компонент, в моменты фазирования достигают максимума функции оценки математического ожидания числа нулевых спектральных компонент, с учетом полученного максимума выделяют кодовые слова, затем определяют оценку математического ожидания элементов спектров кодовых слов и оценивают параметры циклического кода по полученным кодовым словам, далее определяют циклотомические классы, восстанавливают порождающий полином циклического кода и осуществляют декодирование кодовых слов.
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2231216C2 |
| КОДЕК ПОМЕХОУСТОЙЧИВОГО ЦИКЛИЧЕСКОГО КОДА | 2003 |
|
RU2254676C2 |
| КОДЕК ПОМЕХОУСТОЙЧИВОГО ЦИКЛИЧЕСКОГО КОДА | 2003 |
|
RU2251210C1 |
| КОДЕК ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2212101C1 |
| US 6049903 А, 11.04.2000 | |||
| Пенообразователь для тушения пожаров | 1984 |
|
SU1353446A1 |
| СПОСОБ ПРЕДОСТАВЛЕНИЯ РЕСУРСОВ С ОГРАНИЧЕННЫМ ДОСТУПОМ | 2005 |
|
RU2387089C2 |
Авторы
Даты
2007-10-27—Публикация
2006-04-07—Подача