Изобретение относится к электросвязи и может быть использовано для цикловой синхронизации при приеме передач, использующих систематические линейные блоковые низкоплотностные коды большой длины (n>10000 бит) [R.G. Gallager, Low Density Parity Check Codes, Monograph, M.I.T. Press, Cambridge, MA, 1963, pp.7-20; R. M. Tanner, A recursive approach to low complexity codes, IEEE Trans. Inform. Theory, vol. 27, Sept. 1981, pp. 533-547], в условиях параметрической неопределенности относительно структуры кодера.
Известен способ кодовой цикловой синхронизации при передаче информации помехоустойчивыми блоковыми кодами (фазирование по словам), основанный на выполнении последовательных сдвигов, заключающийся в том, что принимаемая дискретная последовательность символов поступает на вход приемника дискретной информации, после чего производится анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых комбинаций и асинхронное, - когда информация о начале кодовых комбинаций в принимаемой последовательности неизвестна. В качестве признака синхронного состояния используется равенство нулю синдрома. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один символ по принимаемой последовательности в одну и ту же сторону. Сдвиги производятся до тех пор, пока не будут обнаруживаться только кодовые комбинации. В этом случае принимается решение о наличии синхронного состояния и процесс вхождения в синхронизм заканчивается [Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и декодирование сложных дискретных сигналов / Под ред. В.И. Коржика. - М.: Радио и связь, 1988, с. 132-137].
Однако этот способ невозможно использовать в условиях параметрической неопределенности структуры кодера помехоустойчивого кода, поскольку вычисление синдрома требует знания проверочной матрицы кода или порождающего полинома [Кларк Дж., мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. - М.: Радио и связь, 1986, с. 81; Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш. Зигангирова. - М.: Мир, 1986, с. 62-71, 116-121].
Известен способ кодовой цикловой синхронизации кодов Рида-Соломона, заключающийся в том, что принимаемая дискретная последовательность символов поступает на вход приемника дискретной информации, после чего производится анализ его состояния [Зайцев И.Е. Формирование признаков для фазирования кодов Рида-Соломона в условиях параметрической неопределенности структуры кодера - Известия вузов. Приборостроение. 1998. Т. 41, №8, с. 13]. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов и асинхронное, - когда информация о начале кодовых слов в принимаемой последовательности неизвестна. Анализ состояния приемника основан на расчете дискретного преобразования Фурье Галуа (ДПФГ) принимаемой дискретной последовательности на длине кодового слова. В качестве признака синхронного состояния используется превышение числа нулевых компонентов в спектрах над пороговым значением. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один символ по принимаемой последовательности в одну и ту же сторону. Сдвиги производятся до установления синхронного состояния.
Однако данный способ применим только для многоосновных кодов Рида-Соломона, что не позволяет использовать данный способ применительно к линейным блоковым низкоплотностным кодам большой длины (n>10000 бит).
Наиболее близким к предлагаемому способу является способ кодовой цикловой синхронизации, заключающийся в том, что входную дискретную последовательность символов кодовых слов линейного блокового кода произвольной длины п принимают с использованием приемника дискретной информации, после чего производят анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, - когда информация о начале кодовых слов в принимаемой последовательности неизвестна. Анализ состояния приемника производят по признаку синхронного состояния. Для этого 2⋅n последовательно выделенных из принятой дискретной последовательности фрагментов длиной 2⋅n записывают в строки матрицы Y[2⋅n,2⋅n], приводят ее элементарными операциями над строками к матрице Y'[2⋅n,2⋅n] в канонической ступенчатой форме [Питерсон У., Уэлдон Э. Коды,
исправляющие ошибки. - М: Мир, 1976, с. 43-45; Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с. 52-53], перестановкой строк матрицы Y'[2⋅n,2⋅n] получают матрицу Y''[2⋅,2⋅], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца, и разбивают матрицу Y''[2⋅n,2⋅n] на четыре подматрицы A[n,n], B[n,n],C[n,n], D[n,n].
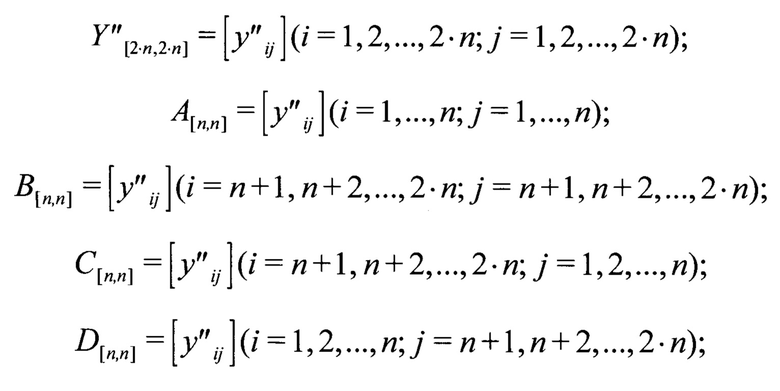
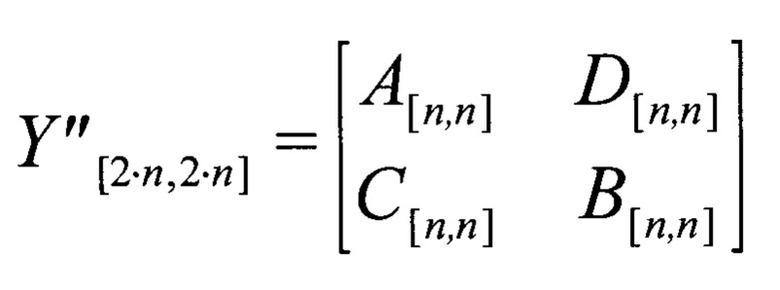
Признаком синхронного состояния приемника дискретной информации является равенство подматриц A[n,n] и B[n,n] между собой, а также равенство С[n,n] и D[n,n] нулю. После выявления данного признака дополнительных операций не производят.
При отсутствии синхронизации (асинхронном состоянии приемника) до ее установления производят поиск синхронного состояния. Для этого производят последовательный сдвиг по принимаемой последовательности на один символ в одну и ту же сторону, построение новой матрицы, проведение с ней необходимых преобразований и определением наличия синхронного состояния приемника по признаку синхронного состояния. [Способ кодовой цикловой синхронизации: пат. 2455773 С Рос.Федерация: МПК7 H04L 7/08 / Балунин Е.И., Дианов С.В., Ратушин А.П.; автор(ы) и патентообладатель(и): Балунин Е.И., Дианов С.В., Ратушин А.П. - №2011136314/08; заявл. 31.08.11; опубл. 10.07.12, Бюл. №19. - 1 с: ил.]. Принят за прототип.
Однако в результате имитационного моделирования работы данного способа на ЭВМ для цикловой синхронизации систематических линейных блоковых низкоплотностных кодов установлено, что данный способ применим только в случае приема последовательности неискаженных символов объемом выборки, равным (2⋅n)×(2⋅n).
Таким образом, недостатком прототипа (способа кодовой цикловой синхронизации на основе признака синхронного состояния приемника дискретной информации соответствия матрицы виду
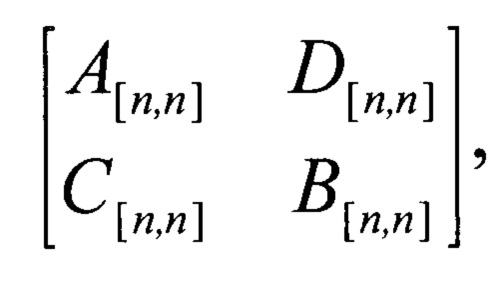
при этом подматрицы A[n,n] и В[n,n] равны между собой, а С[n,n] и D[n,n] равны нулевой матрице O[n,n]), является то, что при кодовой цикловой синхронизации систематических линейных блоковых низкоплотностных кодов большой длины (n>10000 бит) он применим только в случае приема последовательности неискаженных символов объемом выборки, равным (2⋅n)×(2⋅n), что затруднительно обеспечить для синхронизации блоковых низкоплотностных кодов большой длины в реальных каналах связи.
Достигаемым техническим результатом изобретения является уменьшение объема выборки символов принимаемой дискретной последовательности, требуемого для кодовой цикловой синхронизации, увеличение количества синхронизируемых кодов по отношению к прототипу (кодовая цикловая синхронизация линейных блоковых кодов произвольной длины) в условиях параметрической неопределенности (известны только длина кодового слова n и скорость кода R) и расширение арсенала средств аналогичного назначения.
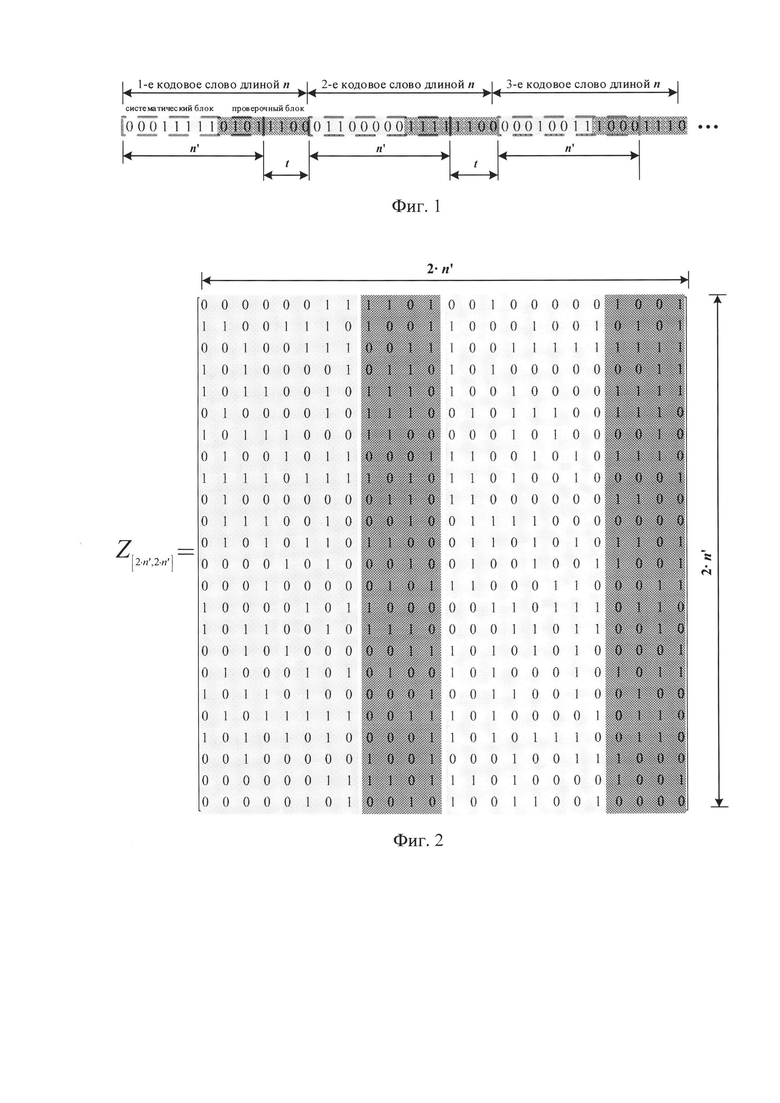
Для достижения указанного технического результата в способе кодовой цикловой синхронизации блоковых низкоплотностных кодов входную дискретную последовательность символов кодовых слов длины n принимают с использованием приемника дискретной информации, после чего производят анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, - когда информация о начале кодовых слов в принимаемой последовательности неизвестна. Анализ состояния приемника производят по признаку синхронного состояния. Для этого из входной дискретной последовательности символов кодовых слов длины п выделяют фрагменты длины n' (фиг. 1) с интервалом t, которые рассчитываются в соответствии с выражениями:


Далее 2⋅n' фрагментов длиной 2⋅n' записывают в строки матрицы Z[2⋅n',2⋅n'] (фиг. 2), приводят ее элементарными операциями над строками к матрице Z'[2⋅n',2⋅n'] в канонической ступенчатой форме [Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. - М.: Мир, 1976, с. 43-45; Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш. Зигангирова. - М.: Мир, 1986, с. 52-53], перестановкой строк матрицы Z'[2⋅n',2⋅n'] получают матрицу Z''[2⋅n',2⋅n'], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца, и разбивают матрицу Z''[2⋅n',2⋅n'] на четыре подматрицы A[n',n'], B[n',n'], C[n',n'], D[n',n'].
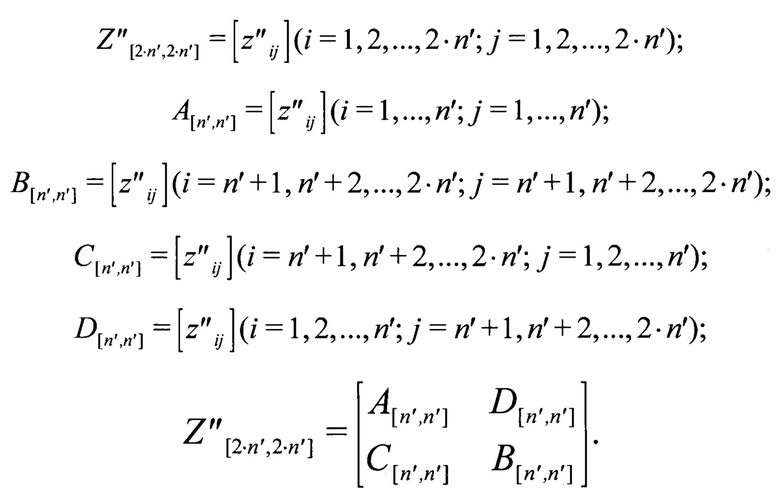
Признаком синхронного состояния приемника дискретной информации является равенство подматриц A[n',n'] и B[n',n'] между собой, а также равенство C[n',n'] и D[n',n'] нулевой матрице O[n',n']. После выявления данного признака дополнительных операций не производят.
При отсутствии синхронизации (асинхронном состоянии приемника) до ее установления производят поиск синхронного состояния. Для этого производят последовательный сдвиг принимаемой последовательности на один символ в одну и ту же сторону, выделяют фрагменты длины n' с интервалом t, формируют новую матрицу Z[2⋅n',2⋅n'], приводят ее элементарными операциями над строками к матрице Z'[2⋅n',2⋅n'] в канонической ступенчатой форме, получают из матрицы Z'[2⋅n',2⋅n'] перестановкой ее строк матрицу Z''[2⋅n',2⋅n'], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца, формирование четырех подматриц A[n',n'], B[n',n'], C[n',n'], D[n',n'] и определяют наличие синхронного состояния приемника по признаку синхронного состояния.
Общим с прототипом является то, что с использованием приемника дискретной информации принимают входную последовательность, представляющую собой последовательно передаваемые символы кодовых слов, выделяют фрагменты дискретной последовательности и определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. При отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением новых фрагментов и определением наличия синхронного состояния приемника по признаку синхронного состояния приемника дискретной информации при соответствии матрицы виду
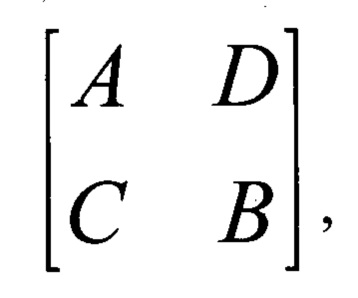
где подматрицы А и В равны между собой, а С и D равны нулевой матрице.
Отличием от прототипа является то, что для принятия решения о наличии признака синхронного состояния приемника дискретной информации из входной дискретной последовательности символов кодовых слов длины n выделяют фрагменты длины n' с интервалом t, формируют квадратную матрицу с числом строк и столбцов, равных двойной длине n', строками которой являются фрагменты длиной 2⋅n' (фиг. 2). В качестве признака синхронного состояния используют равенство подматриц A[n',n'] и Bn',n'] между собой, а также равенство С[n',n'] и D[n',n'] нулевой матрице O[n',n'].
Путем непосредственных вычислений установлено, что при выделении из входной дискретной последовательности символов кодовых слов длины n фрагментов длины n' с интервалом t приемник будет находится в синхронном состоянии, когда все к - число информационных символов в кодовом слове укладываются на длине n' (фиг. 1). Сокращение длины с n до n' позволяет сохранить линейные зависимости систематических и проверочных блоков низкоплотностного кода, при этом сократить объем выборки, необходимой для поиска синхронного состояния, и уменьшить вычислительную сложность всей процедуры.
Благодаря новой совокупности существенных признаков технический результат проявляется в возможности цикловой синхронизации систематических линейных блоковых низкоплотностных кодов большой длины (n>10000 бит).
Результаты сравнительного анализа объемов выборки прототипа и изобретения, требуемых для кодовой цикловой синхронизации, представлены в таблице 1. Для примера расчеты проводились при количестве информационных символов в кодовом слове k=12600.
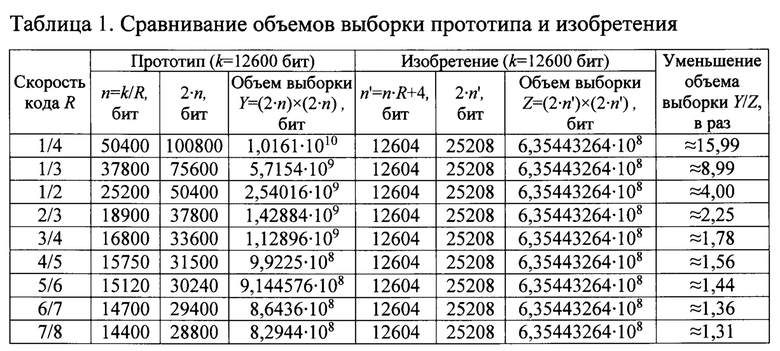
Проведенный анализ уровня существующей техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, которые тождественны всем признакам заявленного технического решения, отсутствует, что указывает на соответствие заявленного способа условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличными от прототипа признаками заявленного объекта показали, что они не следуют явным образом из уровня техники. Из уровня техники так же не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
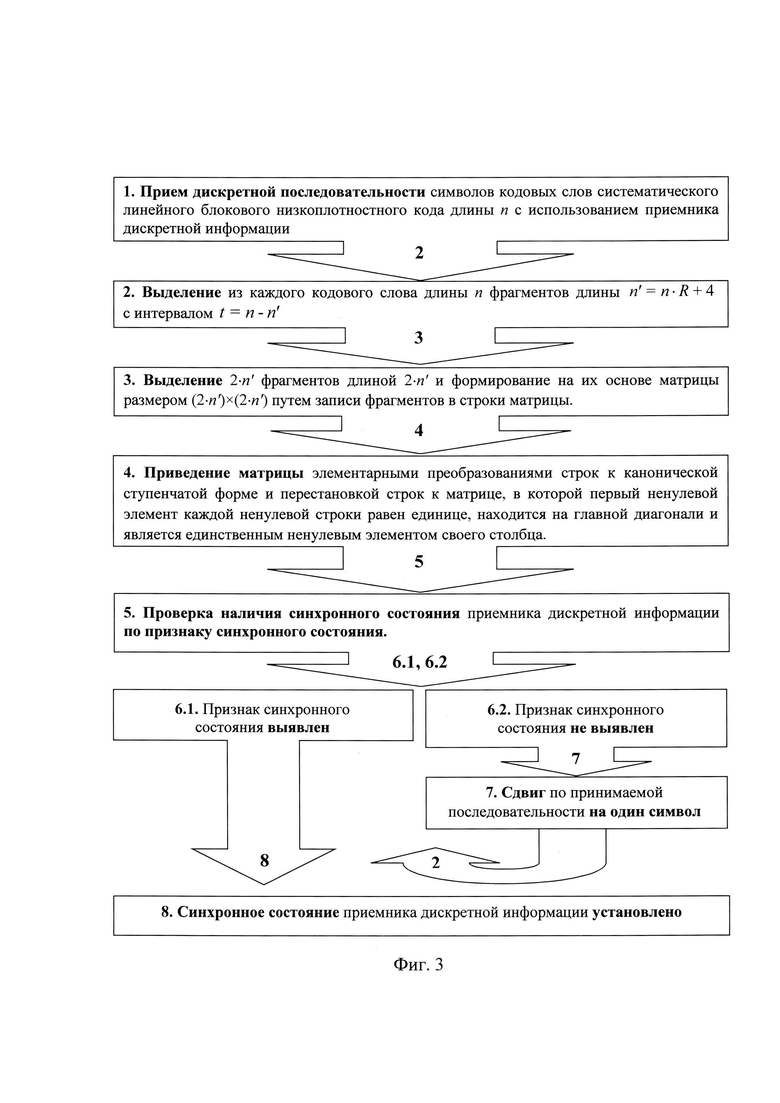
Заявленный способ поясняется иллюстрацией (фиг. 3), на которой изображена структурная схема способа кодовой цикловой синхронизации.
Способ цикловой синхронизации систематических линейных блоковых низкоплотностных кодов большой длины (n>10000 бит) в условиях параметрической неопределенности (известна длина кодового слова п и скорость кода R) осуществляется следующим образом:
Этап 1. Дискретную последовательность символов кодовых слов линейного блокового низкоплотностного кода принимают с использованием приемника дискретной информации.
Данный этап может быть реализован с помощью специализированных средств цифровой обработки сигналов или программно на ЭВМ.
Далее производят анализ состояния приемника дискретной информации (этапы 2-6).
Этап 2. Из входной дискретной последовательности символов кодовых слов длины n выделяют фрагменты длины n' с интервалом t, рассчитанные в соответствии с выражениями (1) и (2).
Этап 3. Записывают 2⋅n' фрагментов длиной 2.n' в строки матрицы вида:
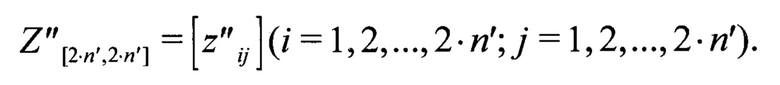
Этап 4. Приводят сформированную матрицу Z[2⋅n',2⋅n'] элементарными преобразованиями строк к матрице Z'[2⋅n',2⋅n'] в канонической ступенчатой форме. Перестановкой строк матрицы Z'[2⋅n',2⋅n'] получают матрицу Z''[2⋅.n',2⋅n'], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца.
Этап 5. Определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. В качестве признака используют равенство подматриц A[n',n'] и B[n',n'] между собой, а также равенство C[n',n'] и D[n',n'] нулевой матрице O[n',n'], где
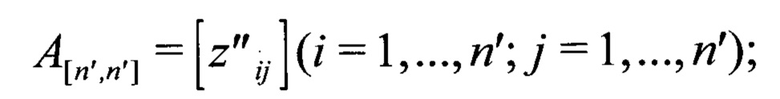
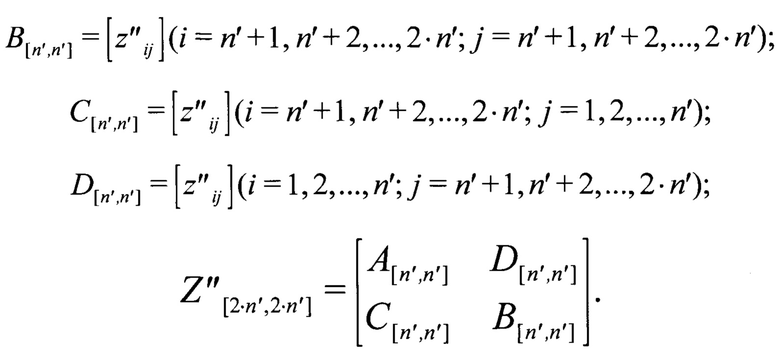
Этап 6. Если признак синхронного состояния выявлен, то считают, что приемник синхронизирован с началом кодовой комбинации, в противном случае продолжают поиск синхронного состояния (переход на этап 7).
Этап 7. Если признак синхронного состояния не выявлен, то осуществляют последовательный сдвиг принимаемой последовательности на один символ в одну и ту же сторону, выделяют фрагменты длины n' с интервалом t, и заново анализируют состояние приемника (возвращаются на этап 3).
Этапы 2-7 могут быть реализованы с помощью специализированных вычислителей или программно на ЭВМ.
Для исследования возможности осуществления предложенного способа на ПЭВМ проведено имитационное моделирования его работы. Программа написана на языке MATLAB.
Результат решения контрольного примера с помощью имитационной модели выглядят следующим образом.
Например, приемник дискретной информации принимает двоичную дискретную последовательность символов кодовых слов систематического линейного блокового низкоплотностного кода с длиной кодового слова n=16, k=8 и скоростью кодирования R=1/2:
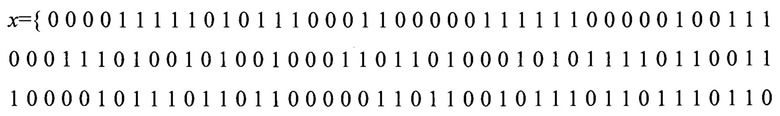

Синхронизируем приемник по границам кодовых слов (найдем ƒ).
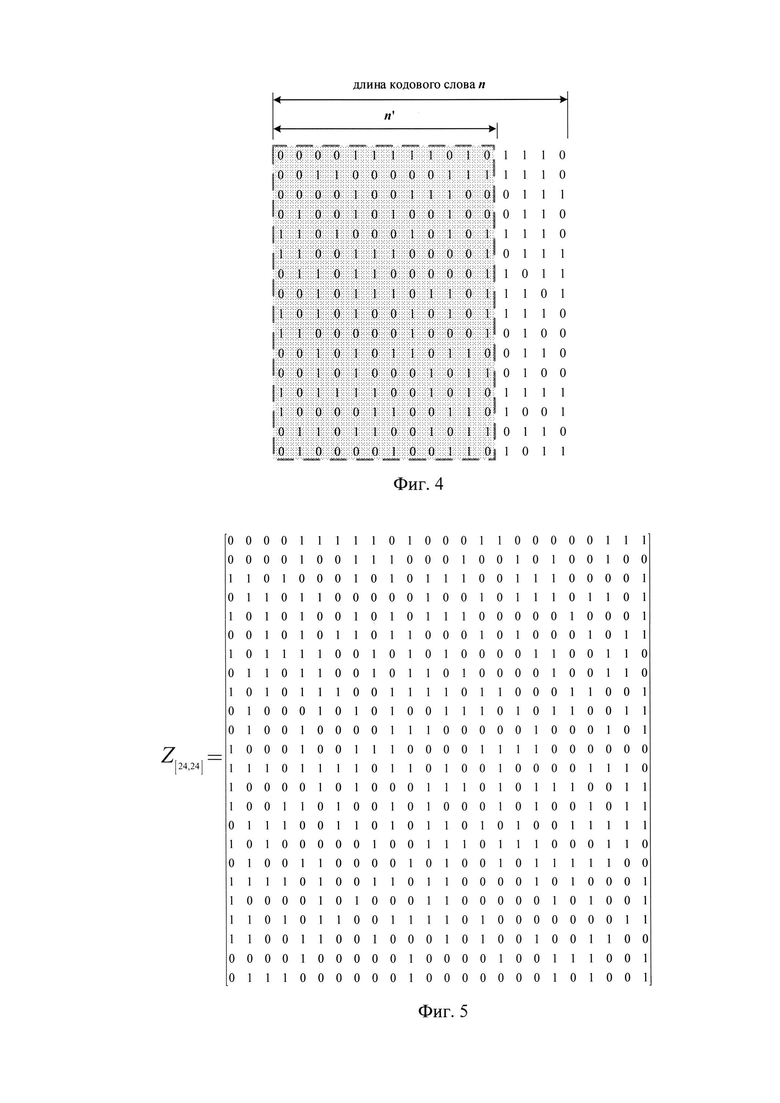
Проанализируем состояние приемника дискретной информации, начиная с первого (ƒ=1). Выделим из каждого кодового слова фрагменты длины n'=12 с интервалом t=4 (фиг. 4).
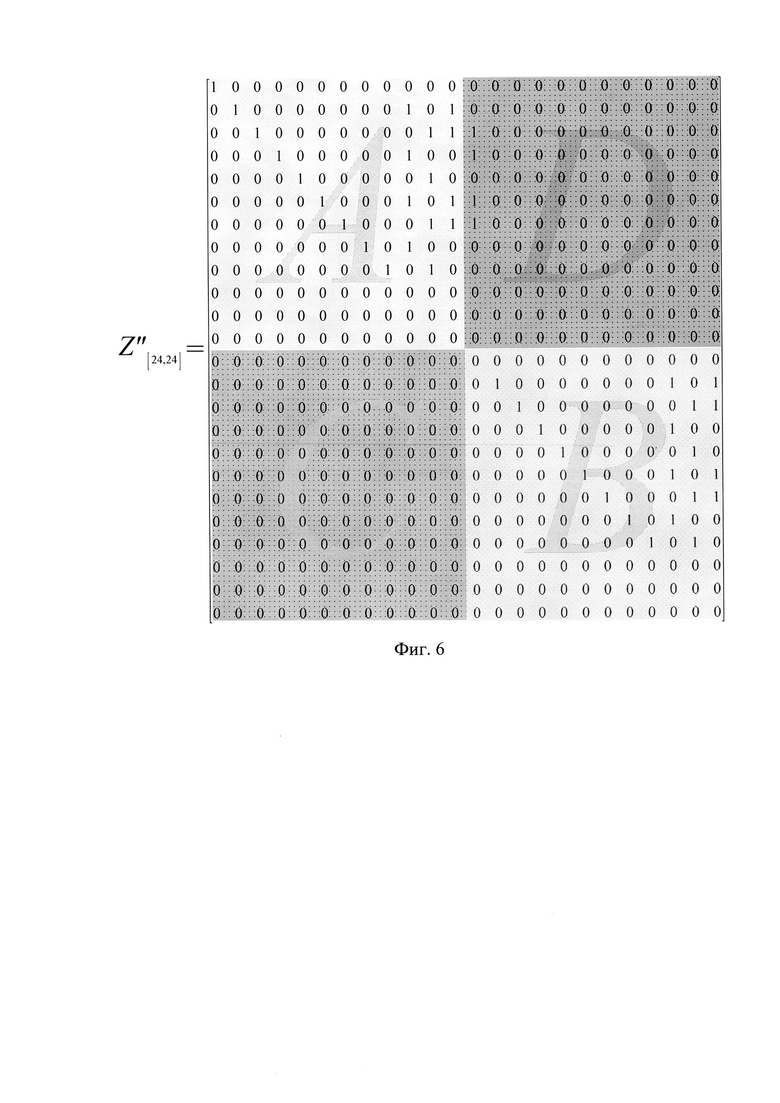
Выделяем 2⋅n'=24 фрагмента длины 2⋅n'=24, записываем их в строки матрицы Z[24,24] (фиг. 5).
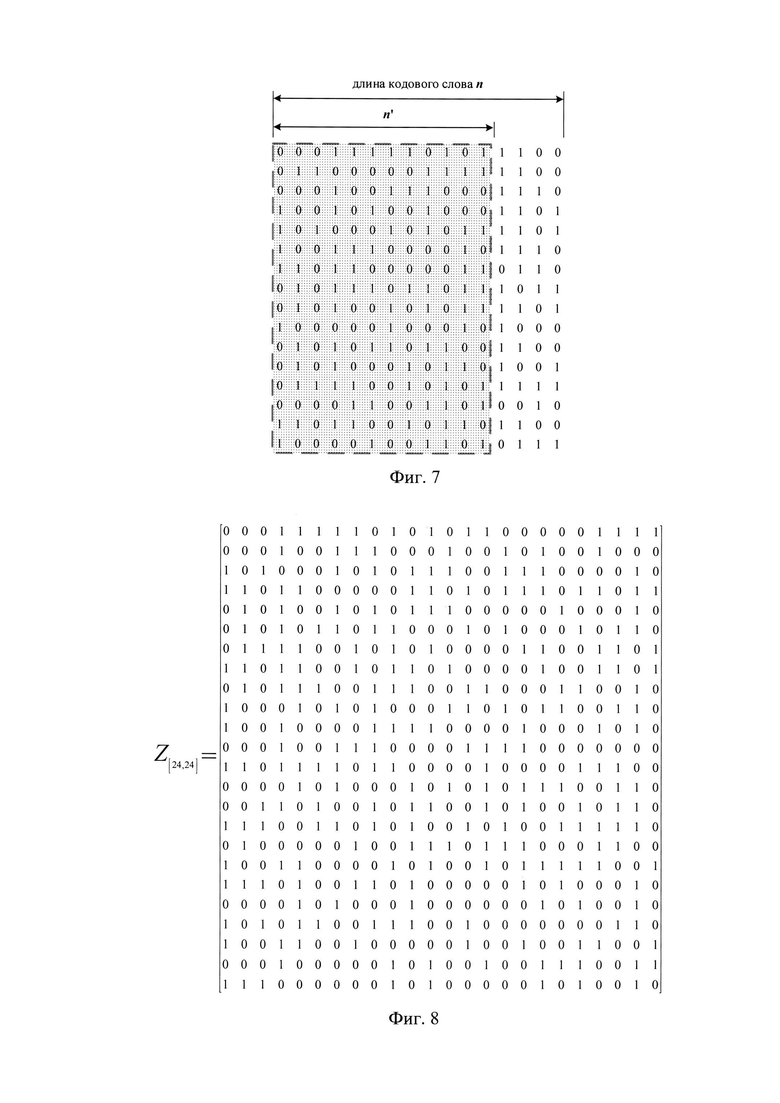
Элементарными преобразованиями строк матрицы Z[24,24] приводим ее к матрице в канонической ступенчатой форме Z'[24,24]. Перестановкой строк матрицы Z'[24,24] получаем матрицу Z''[24,24], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца. Затем проверяем наличие признака синхронного состояния (фиг. 6).
Подматрицы А[12,12] и B[12,12] равны между собой, однако подматрица D[12,12] не равна нулевой матрице O[12,12], то признак синхронного состояния приемника отсутствует, поэтому осуществляем сдвиг по дискретной последовательности х на один символ (ƒ=2) (фиг. 7) и формируем новую матрицу Z[24,24] (фиг. 8).
Элементарными преобразованиями строк матрицы Z[24,24] приводим ее к матрице к канонической ступенчатой форме Z'[24,24]. Перестановкой строк матрицы Z'[24,24] получаем матрицу Z''[24,24], в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца. Затем проверяем наличие признака синхронного состояния (фиг. 9).
Поскольку подматрицы А[12,12] и B[12,12] равны между собой, а С[12,12] и D[12,12] равна нулевой матрице O[12,12], то считаем, что приемник дискретной информации синхронизирован по границам кодовых слов (ƒ=2).
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. R.G. Gallager, Low Density Parity Check Codes, Monograph, M.I.T. Press, Cambridge, MA, 1963, pp. 7-20.
2. R.M. Tanner, A recursive approach to low complexity codes, IEEE Trans. Inform. Theory, vol. 27, Sept. 1981, pp. 533-547.
3. Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и декодирование сложных дискретных сигналов / Под ред. В.И. Коржика. - М.: Радио и связь, 1988, с. 132-137.
4. Кларк Дж., мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. - М.: Радио и связь, 1986, с. 81.
5. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш. Зигангирова. - М.: Мир, 1986, с. 62-71, 116-121.
6. Зайцев И.Е. Формирование признаков для фазирования кодов Рида-Соломона в условиях параметрической неопределенности структуры кодера - Известия вузов. Приборостроение. 1998. Т. 41, №8, с. 13.
7. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. - М.: Мир, 1976, с. 43-45.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2011 |
|
RU2455773C1 |
| СПОСОБ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ТУРБОКОДОВ | 2014 |
|
RU2566945C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2359414C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2006 |
|
RU2319308C1 |
| СПОСОБ УСТОЙЧИВОЙ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ПРИ ПРИМЕНЕНИИ ЖЕСТКИХ И МЯГКИХ РЕШЕНИЙ И МОДУЛЯЦИИ ПО ТИПУ СТЫКА С1-ФЛ | 2023 |
|
RU2812964C1 |
| СПОСОБ СИНХРОНИЗАЦИИ ПЕРЕДАВАЕМЫХ СООБЩЕНИЙ И СИСТЕМА МОНИТОРИНГА ЕЁ ЭФФЕКТИВНОСТИ | 2024 |
|
RU2840714C1 |
| Способ устойчивой кодовой цикловой синхронизации при применении жестких и мягких решений | 2022 |
|
RU2797444C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С ЖЕСТКИМИ И МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА И МОДУЛЯЦИИ ПО ТИПУ СТЫКА С1-ФЛ | 2024 |
|
RU2834891C1 |
| Способ кодовой цикловой синхронизации для каскадного кода Рида-Соломона и Боуза-Чоудхури-Хоквингема [РС(32,16,17), БЧХ(31,16,7)] при одновременном применении жестких и мягких решений | 2020 |
|
RU2747623C1 |
| СПОСОБ АДАПТИВНОЙ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2001 |
|
RU2210870C2 |

Изобретение относится к способу цикловой синхронизации при приеме передач, использующих систематические линейные блоковые низкоплотностные коды большой длины. Технический результат - уменьшение объема выборки символов принимаемой дискретной последовательности, требуемого для кодовой цикловой синхронизации. Входную дискретную последовательность символов кодовых слов длины n принимают с использованием приемника дискретной информации, проводят выделение из каждого кодового слова длиной n фрагментов длины n'=n⋅R+4 с интервалом t=n-n'. Далее 2⋅n' последовательно выделенных из получившейся дискретной последовательности фрагментов длиной 2⋅n' записывают в строки матрицы, элементарными преобразованиями строк приводят сформированную матрицу к канонической ступенчатой форме, перестановкой строк получают матрицу, в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца, в качестве признака синхронного состояния приемника дискретной информации используют соответствие полученной матрицы. После выявления данного признака считают, что синхронное состояние достигнуто, а в случае отсутствия признака синхронного состояния осуществляют последовательный сдвиг принимаемой последовательности на один символ в одну и ту же сторону, выделяют фрагменты длины n' с интервалом t и заново анализируют состояние приемника по признаку синхронного состояния. После выявления признака синхронного состояния считают, что синхронное состояние достигнуто. 9 ил., 1 табл.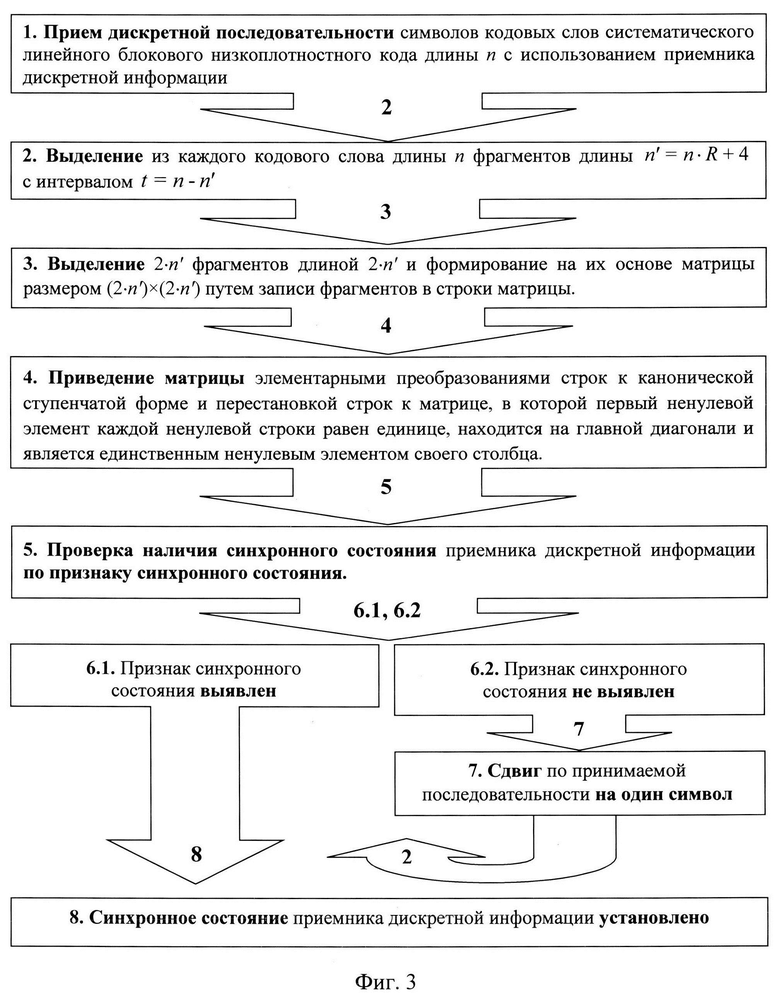
Способ цикловой синхронизации блоковых низкоплотностных кодов в условиях параметрической неопределенности (известны только длина кодового слова n и скорость кода R), заключающийся в том, что с использованием приемника дискретной информации принимают входную последовательность, представляющую собой последовательно передаваемые символы кодовых слов длиной n, выделяют из получившейся дискретной последовательности фрагменты и определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния, а при отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением новых фрагментов и определением наличия синхронного состояния приемника по признаку синхронного состояния, отличающийся тем, что при поиске синхронного состояния проводят выделение из каждого кодового слова длиной n фрагментов длины n'=n⋅R+4 с интервалом t=n-n', выделяют из получившейся дискретной последовательности 2⋅n' фрагменты длиной 2⋅n', формируют на их основе матрицу путем записи этих фрагментов в строки матрицы и элементарными преобразованиями строк приводят сформированную матрицу к канонической ступенчатой форме, перестановкой строк получают матрицу, в которой первый ненулевой элемент каждой ненулевой строки равен единице, находится на главной диагонали и является единственным ненулевым элементом своего столбца, в качестве признака синхронного состояния приемника дискретной информации используют соответствие полученной матрицы виду
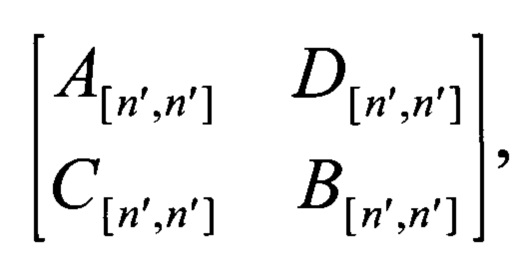
где подматрицы A[n',n'] и B[n',n'] равны между собой, а подматрицы С[n',n'] и D[n',n'] равны нулевой матрице размерности n'×n', после выявления данного признака считают, что синхронное состояние достигнуто, а в случае отсутствия признака синхронного состояния осуществляют последовательный сдвиг принимаемой последовательности на один символ в одну и ту же сторону, выделяют фрагменты длины n' с интервалом t и заново анализируют состояние приемника по признаку синхронного состояния.
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2006 |
|
RU2319308C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2295198C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКИХ КОДОВ С "ЖЕСТКИМ" РЕШЕНИЕМ ПО ВЕКТОРУ-УКАЗАТЕЛЮ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2575394C1 |
| US 8151165 B2, 03.04.2012. | |||
Авторы
Даты
2024-09-30—Публикация
2024-04-01—Подача