Изобретение относится к способам вибрационной диагностики объектов и может быть использовано для оценки технического состояния машин и механизмов.
Известен способ вибродиагностики, использующий кепстральный анализ [1], позволяющий разделить во времени информацию о сигнале, полученную в результате многократных отражений, при нелинейных преобразованиях и модуляции. Данный способ может быть использован, например, для оценки технического состояния зубчатого зацепления, подшипников качения, для которых характерно присутствие иногда десятков гармоник основных частот возбуждения. В этих условиях трудно найти информативный диагностический признак, используя традиционное спектрально-корреляционное представление сигнала. При кепстральном представлении энергия виброакустического сигнала, рассеянная по множеству гармоник в спектральном представлении, локализуется в одной составляющей в кепстральной функции сигнала.
В качестве диагностических признаков используют значения функций кепстра: амплитуда кепстральных компонент - квефренция, соответствующих частотам дефектов объекта диагностики (квефренси или квефренция - величина, имеющая размерность времени и соответствующая обратной величине частоты компонент).
Недостатком данного метода является то, что в традиционных для кепстра координатах «амплитуда-время» сложно распознавать кепстральные компоненты составляющих, соответствующие частотам дефектов, так как при проведении диагностики обычно рассчитывают частоты дефектов и их комбинационные составляющие, являющиеся результатом перемножения и суперпозиции частотных составляющих дефектов. При оценке соответствия временного параметра кепстральной компоненты частотной составляющей дефекта приходится каждый раз производить преобразование значения величины времени в значение частоты.
Известен способ вибродиагностики машины [2], заключающийся в том, что измеряют сигнал с вибродатчика, получают спектр сигнала, логарифмируют спектр, получают спектр логарифмированного спектра, т.е. кепстр, выделяют амплитуды дискретных составляющих кепстра, сравнивают полученные амплитуды с пороговыми значениями.
Недостатком известного способа является то, что по полученному в известных координатах «амплитуда кепстральной компоненты - время» кепстру сложно выделить дискретные составляющие кепстра, соответствующие частоте дефекта, поскольку для оценки дефекта необходимо, во-первых, проводить преобразование значений времени в значение частоты, а во-вторых, сравнивать серии дискретных амплитуд кепстра с весьма малой разницей между значениями по оси времени в диапазоне, соответствующем основным частотам дефектов, располагающихся, как правило, в области временной шкалы, соответствующей высокочастотной части спектра.
Указанный в [2] способ требует вычислений с весьма малой дискретностью по оси времени, что существенно затрудняет распознавание указанного дефекта при наличии других дефектов, например дисбаланса и несоосности. Так, при частоте сети f=50 Гц (на оси времени τ=20 мс) и частоте вращения асинхронного двигателя n=2940 об/мин, что соответствует f=49 Гц (τ=20.408 мс), разность между частотой дефекта f=49 Гц типа «дисбаланс» и частотой сети составляет Δf=1 Гц. Во временной же области эта разность будет составлять Δτ=0.408 мс. Для выявления такого различия составляющих на шкале времени полоса частот исходного спектра должна быть не менее
fMAX=4900 Гц. Для того чтобы отличить статический эксцентриситет (f=100 Гц, τ=10 мс) от частоты дефекта при несоосности (f=98 Гц, τ=10.204 мс), необходимо обеспечить шаг по оси времени не менее Δτ=0.204 мс, что соответствует полосе частот исходного спектра fMAX=9800 Гц. Таким образом, дискретные составляющие дефектов различаются на 2% от минимальной частоты дефекта и визуально на графике их различить очень сложно.
При частоте вращения n≈3000 мин-1 основные частоты дефектов, в частности подшипников качения, заключены в огибающей виброускорения в диапазоне от 20 до 500 Гц. Общая длина выборки сигнала для построения кепстра с приемлемой точностью составляет не менее τ=200 мс (0,2 сек), т.е. длина оси абсцисс - шкалы времени - равна τ=200 мс. Тогда компонента, содержащая гармоники частоты дефекта f=500 Гц, соответствует периоду τ=2 мс, т.е. занимает 1% оси абсцисс, что существенно затрудняет анализ значений шкалы времени и амплитуд компонент.
Преимущество кепстрального метода заключается в том, что энергия виброакустического сигнала, рассеянная по множеству гармоник в спектральном представлении, локализуется в одной составляющей в кепстральном представлении сигнала. При этом кепстры относительно не чувствительны к изменениям пути передачи механических колебаний (пути между вибродатчиком и источником механических колебаний).
Целью заявляемого изобретения является повышение достоверности диагностики состояния объекта.
Поставленная цель в способе вибродиагностики технического состояния объекта, включающем измерение вибрации в информативной точке диагностируемого объекта, получение кепстра вибрации, оценку амплитуды и квефренции информативных компонент кепстра, соответствующих дефектам объекта диагностики, достигается тем, что кепстр вибрации строят в частотной области, линеаризуют шаг расположения информативных составляющих путем нелинейного преобразования масштаба частот, определяют частоты существенных дефектов по величине существенных кепстральных компонент, по которым оценивают состояние объекта, при этом кепстр строят по следующей формуле:
CSNL(fNL)=CS(τ),
где 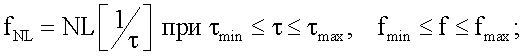
СS(τ) - кепстральная компонента вибросигнала s(t), где аргументом служит квефренция (время);
CSNL(fNL) - модифицированная кепстральная компонента вибросигнала s(t), где аргументом служит fNL - частота кепстральной компоненты в нелинейном масштабе
fNL=NL[1/τ], NL[] - оператор нелинейного преобразования;
τ - квефренция кепстральной компоненты;
τmin - минимальные значение квефренции, определяемое максимальной частотой диагностируемого дефекта;
τmax - максимальное значение квефренции, определяемое минимальной частотой диагностируемого дефекта;
fmin - минимальное значение частоты, определяемое минимальной частотой диагностируемого дефекта;
fmax - максимальное значение частоты, определяемое максимальной частотой диагностируемого дефекта.
Поставленная цель в способе вибродиагностики технического состояния объекта решается также тем, что логарифмирование шкалы частот производят по формуле:
CSLF(flog)=CS(τ),
где 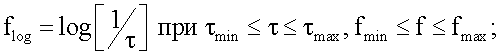
СS(τ) - кепстральная компонента вибросигнала s(t), где аргументом служит квефренция (время);
CSLF(flog) - модифицированная кепстральная компонента вибросигнала s(t), где аргументом служит flog - частота в логарифмическом масштабе flog=log[1/τ]=-log[τ].
Анализ отличительных признаков предлагаемого способа вибродиагностики объектов и обеспечиваемых ими технических результатов показал, что:
- трансформация кепстра из координат «амплитуда кепстральных компонент - квефренция» в координаты «амплитуда кепстральных компонент - частота» значительно упрощает анализ составляющих кепстра, так как основной проблемой при анализе кепстра является соотнесение составляющих кепстра со значениями основных частот и их гармоник;
- перевод кепстра из временной области в частотную позволяет «растянуть» «сжатую» на временной шкале информацию о высокочастотных дефектах и более точно определить дефект (формулы для расчета частот дефектов различных узлов оборудования приведены в [1]), поскольку кепстр используется при анализе высокочастотных составляющих, когда спектр имеет полигармонический характер, то и полученный кепстр также может иметь громоздкую структуру в области малых значений квефренции, что затрудняет распознавание характера дефектов;
- логарифмирование шкалы частот приводит к линеаризации отображаемых данных. Это связано с тем, что при преобразовании кепстра из координат «амплитуда кепстральных компонент - квефренция» в кепстр в координатах «амплитуда кепстральных компонент - частота» происходит переход линейного шага квефренции в нелинейный шаг частоты. Соответственно, высокочастотные составляющие кепстра оказываются расположенными на графике очень плотно друг к другу, что в свою очередь затрудняет визуальное различение составляющих. Расчеты показывают, что линейность аппроксимации нелинейного масштаба шкалы частот значительно выше линейности линейного масштаба шкалы частот.
Сущность изобретения поясняется чертежами, на которых изображено:
фиг.1 - кепстр виброакустического сигнала подшипника качения, представленный в координатах «амплитуда кепстральных компонент - квефренция». Амплитуды кепстральных компонент, соответствующие квефренциям дефектов, обозначены следующим образом:
1 - CS(1/2BPFI) - амплитуда, квефренция которой соответствует второй гармонике частоты дефекта внутреннего кольца (BPFI);
2 - CS(1/(3BSF-FTF)) - амплитуда, квефренция которой соответствует разностной частоте между третьей гармоникой частоты дефекта тел качения (BSF) и частотой дефекта сепаратора (FTF);
3 - CS(1/2BPFO) - амплитуда, квефренция которой соответствует второй гармонике частоты дефекта внешнего кольца подшипника (BPFO);
4 - CS (1/BPFI) - амплитуда, квефренция которой соответствует частоте дефекта внутреннего кольца (BPFI);
5 - CS(1/(BPFI-Fo)) - амплитуда, квефренция которой соответствует разностной частоте между частотой дефекта внутреннего кольца (BPFI) и частотой вращения вала (Fo);
6 - CS(1/(BSF+Fo)) - амплитуда, квефренция которой соответствует сумме частоты дефекта тел качения (BSF) и частоты вращения (Fo);
7 - CS(1/4Fo) - амплитуда, квефренция которой соответствует четвертой гармонике частоты вращения (Fo);
8 - CS(1/BPFO) - амплитуда, квефренция которой соответствует частоте дефекта внешнего кольца подшипника (BPFO);
9 - CS(1/BSF) - амплитуда, квефренция которой соответствует частоте дефекта тел качения (BSF);
10 - CS(1/2Fo) - амплитуда, квефренция которой соответствует второй гармонике частоты вращения (Fo);
11 - CS(1/Fo) - амплитуда, квефренция которой соответствует частоте вращения (Fo);
12 - CS(1/(Fo-FTF)) - амплитуда, квефренция которой оответствует разностной частоте между частотой вращения (Fo) и частотой дефекта сепаратора (FTF);
13 - CS(1/FTF) - амплитуда, квефренция которой соответствует частоте дефекта сепаратора (FTF);
фиг.2 - кепстр виброакустического сигнала подшипника качения, представленный в координатах «амплитуда кепстральных компонент - частота»; амплитуды кепстральных компонент, соответствующие частотам дефектов, обозначены следующим образом:
1 - CSF(2BPFI) - компонента соответствует второй гармонике частоты дефекта внутреннего кольца (BPFI);
2 - CSF(3BSF-FTF) - соответствует разностной частоте между третьей гармоникой частоты дефекта тел качения (BSF) и частотой дефекта сепаратора (FTF);
3 - CSF(2BPFO) - соответствует второй гармонике частоты дефекта внешнего кольца подшипника (BPFO);
4 - CSF(BPFI) - соответствует частоте дефекта внутреннего кольца (BPFI);
5 - CSF(BPFI-Fo) - соответствует разностной частоте между частотой дефекта внутреннего кольца (BPFI) и частотой вращения вала (Fo);
6 - CSF(BSF+Fo) - соответствует сумме частоты дефекта тел качения (BSF) и частоты вращения (Fo);
7 - CSF(4Fo) - соответствует четвертой гармонике частоты вращения (Fo);
8 - CSF(BPFO) - соответствует частоте дефекта внешнего кольца подшипника (BPFO);
9 - CSF(BSF) - соответствует частоте дефекта тел качения (BSF);
10 - CSF(2Fo) - соответствует второй гармонике частоты вращения (Fo);
11 - CSF(Fo) - соответствует частоте вращения (Fo);
12 - CSF(Fo-FTF) - соответствует разностной частоте между частотой вращения (Fo) и частотой дефекта сепаратора (FTF);
13 - CSF (FTF) - соответствует частоте дефекта сепаратора (FTF);
14 - CSF(3BSF) - соответствует третьей гармонике частоты дефекта тел качения (BSF);
фиг.3 - кепстр виброакустического сигнала подшипника качения, представленный в координатах «амплитуда кепстральных компонент - частота в логарифмическом масштабе». Амплитуды кепстральных компонент, соответствующие частотам дефектов, обозначены в соответствие с обозначениями фиг.2.
фиг.4 - графики функций аппроксимации шкалы частот, где
15 - зависимость квефренции компонент от порядкового номера;
16 - зависимость частоты компонент от порядкового номера;
фиг.5 - графики функций аппроксимации шкалы частот, где
17 - зависимость квефренции компонент от порядкового номера;
18 - зависимость логарифма частоты компонент от порядкового номера;
фиг.6 - графики функций аппроксимации шкалы частот, где
19 - аппроксимация зависимости десятичного логарифма частоты компонент от порядкового номера линейной функцией;
20 - зависимость логарифма частоты компонент от порядкового номера;
фиг.7 - графики функций аппроксимации шкалы частот, где
21 - аппроксимация зависимости двоичного логарифма частоты компонент от порядкового номера линейной функцией;
22 - зависимость логарифма частоты компонент от порядкового номера;
фиг.8 - графики функций аппроксимации шкалы частот, где
23 - аппроксимация зависимости частоты компонент от порядкового номера степенной функцией;
24 - зависимость частоты компонент от порядкового номера;
фиг.9 - графики функций аппроксимации шкалы частот, где
25 - зависимость частоты компонент аппроксимированной степенной функции от порядкового номера;
26 - аппроксимация частоты компонент от порядкового номера линейной функцией;
фиг.10 - кепстр виброакустического сигнала подшипника качения, представленный в координатах «амплитуда кепстральных компонент - частота в нелинейном масштабе». Амплитуды кепстральных компонент, соответствующие частотам дефектов, обозначены в соответствие с обозначениями фиг.2.
Реализуемость способа проверялась путем анализа кепстра виброакустического сигнала, полученного с датчика, установленного на подшипник качения.
На фиг.1 приведен кепстр виброакустического сигнала подшипника качения, представленный во временной области на шкале 3-110 мс. Как видно, на данном кепстре присутствует часть составляющих, очень близко расположенных друг к другу в интервале 9-13 мс (фиг.1, поз.1-9), и для того, чтобы точно определить природу дефекта, необходимо определить значение каждой составляющей по времени, вычислить для них соответствующие значения частоты, произвести сопоставление полученных частот с возможными частотами дефектов данного механизма и их комбинационными составляющими (суммарными и разностными комбинациями различных частот дефектов), что является весьма трудоемкой задачей.
При построении функции кепстра в координатах «амплитуда кепстральных компонент - квефренция» значения СS(τ) строят от τmin до τmax, а в координатах «амплитуда кепстральных компонент - частота» значения кепстральных компонент СS(f) располагают от fmin до fmax. Таким образом, функция вида СS(τ) преобразуется в функцию вида СSF(f).
Например, если значение кепстральной компоненты при τ=10 мс равно 5 (C(10×10-3c)=5), то при преобразовании: CSτ(1/(10×103c))=CSF(100 Гц)=5. Если
СS(20×10-3c)=7, то CSτ(1/(20×103c)=CSF(50 Гц)=7. Естественно, что при таком преобразовании и изменяется порядок распознавания составляющих по оси абсцисс.
На фиг.2 приведен этот же кепстр, представленный в частотной области. Как видно, множество составляющих, расположенных в интервале 9-13 мс (фиг.1, 2, поз.1-9), разделены и распределены в диапазоне от 75 до 300 Гц на шкале 10-350 Гц, что значительно облегчает определение дефекта. При этом на кепстре в частотной области можно обнаружить еще одну составляющую (фиг.2, поз.14) - третью гармонику частоты дефекта тел качения (CSF(3BSF)), которую в кепстре во временной области обнаружить практически невозможно. В данном случае присутствует дефект и перекос внутреннего кольца, а также нарушение внутренних зазоров и несоосность подшипника.
Использование частотной шкалы связано с расчетом частот дефектов, обусловленных периодическим взаимодействием деталей и элементов узлов объекта, имеющих дефекты. Именно на этом физическом принципе - выявлении амплитуд колебаний на определенных частотах - и построена диагностика по параметрам вибрации. Пересчет отдельных существенных значений квефренции в значения частоты с целью выявления присутствия частот дефектов может вносить ошибки и дополнительные погрешности в определение частот дефектов, особенно, при «ручном» пересчете с ограниченной точностью, что и приводит к снижению достоверности диагностики. Систематизированное преобразование шкал позволяет исключить ошибки и снизить погрешности определения частот дефектов.
Математически преобразование может быть записано следующим образом:

где 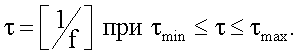
Равномерные интервалы времени кепстра во временной области приводят к неравномерной шкале частот кепстра в частотной области. При визуальной оценке кепстральных составляющих в частотной области низкочастотные составляющие оказываются сжатыми, что затрудняет идентификацию кепстральных составляющих дефектов. Для линеаризации шага по частоте кепстральных составляющих производят нелинейное преобразование значений частотной шкалы:
CSNL(fNL)=CS(τ),
где 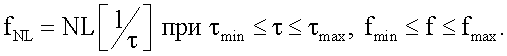
Например, можно использовать логарифмирование
CSF(f)=CSLF(flog)
где flog=log[f]=log[1/τ]=-log[τ].
Тогда алгоритм получения кепстра выглядит следующим образом [3]:
1. Исходный сигнал - спектр:
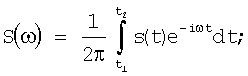
2. Спектр - кепстр в координатах «амплитуда кепстральных компонент - квефренция (время)»:
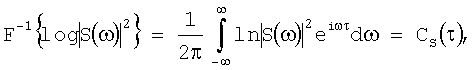
вводим следующий алгоритм преобразования, соответствующий предлагаемому способу;
3. Кепстр в координатах «амплитуда кепстральных компонент-квефренция (время)» преобразуем в кепстр в координатах «амплитуда кепстральных компонент - частота»:
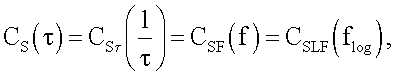
где Cs(τ) - кепстральная компонента s(t), где аргументом служит время;
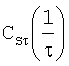 - кепстральная компонента s(t), где аргументом служит величина, обратная времени;
- кепстральная компонента s(t), где аргументом служит величина, обратная времени;
CSF(f) - модифицированная кепстральная компонента s(t), где аргументом служит f - частота;
CSLF(flog) - модифицированная кепстральная компонента s(t), где аргументом служит flog - частота в логарифмическом масштабе flog=log[f]=log[1/τ]=-log[τ];
f - частота кепстральной компоненты;
τ - квефренция кепстральной компоненты;
τmin - минимальные значение квефренции, определяемое минимальной частотой диагностируемого дефекта;
τmах - максимальное значение квефренции, определяемое максимальной частотой диагностируемого дефекта;
fmin - минимальные значение частоты, определяемое минимальной частотой диагностируемого дефекта;
fmах - максимальное значение частоты, определяемое максимальной частотой диагностируемого дефекта.
Таким образом, для повышения достоверности распознавания кепстральных компонент в низкочастотной области функции кепстра целесообразно отображать ось частот в нелинейном, например логарифмическом, масштабе (фиг.3). Это позволяет более равномерно отображать составляющие на графике.
Использование нелинейного масштаба оси частот кепстра можно иллюстрировать следующим образом.
На фиг.4 приведена зависимость квефренции (поз.15) и частоты (поз.16) от порядкового номера компоненты при эквидистантном расположении величины квефренции компонент. Данные графики построены исходя из следующих параметров квефренции кепстра: Δτ=0.61 мс; полная длина реализации кепстра - 16384 отсчета; диапазон квефренции: от 1.221 до 244.141 мс, что соответствует изменению частоты от 819.2 до 4.096 Гц. Из графиков фиг.4 видно, насколько нелинейна зависимость 16 величины частоты от порядкового номера компоненты. В то же время при линейной зависимости квефренции от порядкового номера (фиг.5 поз.17) после логарифмирования значений частоты нелинейность шкалы частот уменьшается (фиг.5 поз.18). При аппроксимации прямой линией (фиг.6 поз.19) зависимости десятичного логарифма значений частот от порядкового номера (фиг.6 поз.20) в заданном диапазоне частот (10-150 Гц) величина достоверности аппроксимации (мера Линдера или квадрат смешанной корреляции) R2 составляет 0.905.
При аппроксимации прямой линией (фиг.7 поз.22) зависимости двоичного логарифма значений частот от порядкового номера (фиг.6 поз.21) в заданном диапазоне частот (10-150 Гц) величина достоверности аппроксимации R2 также составляет 0.905.
Большей степени линеаризации можно достичь путем аппроксимирования функции зависимости частоты от порядкового номера кепстральной компоненты нелинейной функцией подходящего вида. Так, величина достоверности аппроксимации R2=0.9999 достигается при аппроксимации функции зависимости частоты в диапазоне 10-150 Гц от порядкового номера кепстральной компоненты (фиг.8 поз.23) степенной функцией (фиг.8 поз.24) вида у=1459.5·x-0.9772.
Построенная аппроксимированная степенной функцией зависимость частоты от порядкового номера кепстральной компоненты (фиг.9 поз.25) аппроксимируется прямой линией (фиг.9 поз.26) с величиной достоверности аппроксимации R2=0.9903, что свидетельствует о высокой степени линеаризации. Это подтверждает и кепстр (фиг.10), построенный с осью частот в нелинейном масштабе по фиг.8.
Таким образом, предлагаемый способ вибродиагностики технического состояния объекта позволяет повысить достоверность диагностики путем измерения вибрации в информативной точке диагностируемого объекта, получения кепстра вибрации в частотной области, линеаризации шага расположения информативных составляющих путем нелинейного преобразования масштаба частот и определения частот существенных дефектов по величине существенных кепстральных компонент, по которым и оценивают состояние объекта.
Источники информации
1. Вибрации в технике: Справочник. В 6-ти т. / Ред.совет: В.Н.Челомей (пред.) - М.: Машиностроение, 1981. - Т.5, Измерения и испытания./ Под ред. М.Д.Генкина. 1981. - С.389-396.
2. Авторское свидетельство СССР №1065789 A, кл. G01R 31/34. Способ косвенного определения эксцентриситета воздушного зазора электрической машины. БИ №1 07.01.84.
3. Генкин М.Д., Соколова А.Г. Виброакустическая диагностика машин и механизмов. - М.: Машиностроение, 1987. - С.162-164.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ вибрационной диагностики подшипников качения | 2019 |
|
RU2720328C1 |
| СПОСОБ ДИАГНОСТИКИ ЭЛЕКТРОМЕХАНИЧЕСКОГО ОБОРУДОВАНИЯ | 2014 |
|
RU2574315C1 |
| СИСТЕМА ДИАГНОСТИКИ ПРОЦЕССОВ ГИДРОРАЗРЫВА ПЛАСТА И СПОСОБ ЕЁ РАБОТЫ | 2022 |
|
RU2792427C1 |
| Способ обнаружения дефектов подшипников турбокомпрессора | 1990 |
|
SU1784851A1 |
| СПОСОБ ВИБРАЦИОННОЙ ДИАГНОСТИКИ РОТОРНЫХ СИСТЕМ | 2007 |
|
RU2356021C2 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ ЦИКЛИЧЕСКИХ МАШИН - МЕТАЛЛОРЕЖУЩИХ СТАНКОВ ФАЗОХРОНОМЕТРИЧЕСКИМ МЕТОДОМ | 2013 |
|
RU2561236C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ ОБЪЕКТОВ ПРИ ВИБРОДИАГНОСТИКЕ | 1999 |
|
RU2187086C2 |
| АСИНХРОННЫЙ ВЕЙВЛЕТ-КЕПСТРАЛЬНЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ ПАЧЕК СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2011 |
|
RU2464704C1 |
| ПОМЕХОУСТОЙЧИВЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ ПАЧЕК СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2010 |
|
RU2422991C1 |
| Способ вибродиагностики зарождающихся дефектов механизмов | 2018 |
|
RU2680640C1 |
Изобретение относится к области диагностики технического состояния машин и механизмов и может быть использовано, например, для оценки технического состояния зубчатого зацепления, подшипников качения. При реализации способа кепстр вибрации строят в частотной области, линеаризуют шаг расположения информативных составляющих путем нелинейного преобразования масштаба частот, выделяют существенные компоненты, определяют частоты существенных дефектов, по которым оценивают состояние объекта. Технический результат заключается в повышении достоверности диагностики состояния объекта. 1 з.п. ф-лы, 10 ил.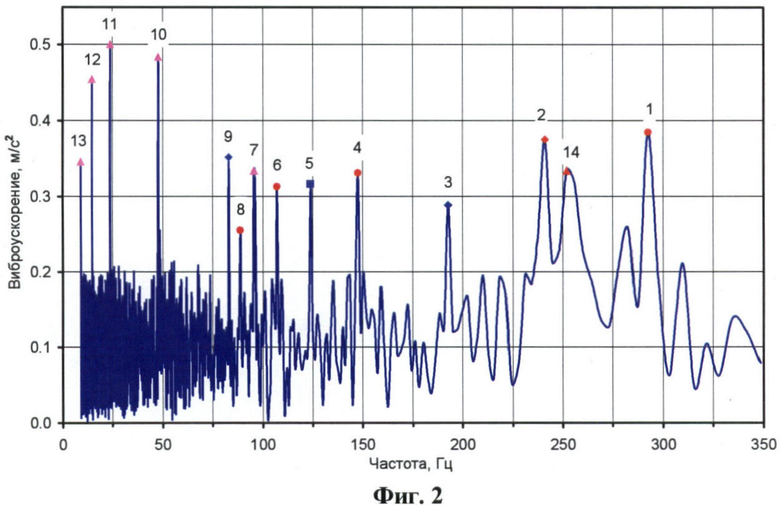
1. Способ вибродиагностики технического состояния объекта, заключающийся в том, что в информативной точке измеряют вибрацию диагностируемого объекта, получают кепстр вибрации во временной области, оценивают амплитуды и квефренции информативных компонент кепстра, соответствующих дефектам объекта, отличающийся тем, что кепстр вибрации строят в частотной области, линеаризуют шаг расположения информативных составляющих путем нелинейного преобразования масштаба частот, определяют частоты существенных дефектов по величине существенных кепстральных компонент, по которым оценивают состояние объекта, при этом кепстр строят по следующей формуле:
CSNL(fNL)=CS(τ), где
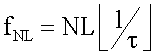 при τmin≤τ≤τmax, fmin≤f≤fmax;
при τmin≤τ≤τmax, fmin≤f≤fmax;
СS(τ) - кепстральная компонента вибросигнала s(t), где аргументом служит квефренция (время);
CSNL(fNL) - модифицированная кепстральная компонента вибросигнала s(t), где аргументом служит fNL - частота кепстральной компоненты в нелинейном масштабе
fNL=NL[1/τ], NL[] - оператор нелинейного преобразования;
τ - квефренция кепстральной компоненты;
τmin - минимальное значение квефренции, определяемое максимальной частотой диагностируемого дефекта;
τmax - максимальное значение квефренции, определяемое минимальной частотой диагностируемого дефекта;
fmin - минимальное значение частоты, определяемое минимальной частотой диагностируемого дефекта;
fmax - максимальное значение частоты, определяемое максимальной частотой диагностируемого дефекта.
2. Способ по п.1, отличающийся тем, что кепстр строят по следующей формуле:
CSNL(flog)=CS(t), где
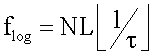 при τmin≤τ≤τmax, fmin≤f≤fmax;
при τmin≤τ≤τmax, fmin≤f≤fmax;
СS(τ) - кепстральная компонента вибросигнала s(t), где аргументом служит квефренция (время);
CSLF(flog) - модифицированная кепстральная компонента вибросигнала s(t), где аргументом служит flog - частота в логарифмическом масштабе flog=log[1/τ]=-log[τ].
| Способ косвенного определения эксцентриситета воздушного зазора электрической машины | 1982 |
|
SU1065789A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ГАЗОЖИДКОСТНОЙ СИСТЕМЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1996 |
|
RU2089860C1 |
| Способ виброакустического контроля износа зубчатых колес | 1986 |
|
SU1379669A1 |
| Способ обнаружения дефектов подшипников турбокомпрессора | 1990 |
|
SU1784851A1 |
Авторы
Даты
2009-08-10—Публикация
2008-05-27—Подача