Изобретение относится к области вибрационной диагностики роторного оборудования с использованием систем и способов обработки сигналов вибрации и может использоваться при изготовлении и эксплуатации механизмов, содержащих подшипники качения.
Известен способ вибрационной диагностики подшипника качения, включающий получение сигнала вибрации с помощью установленного на диагностируемом подшипнике акселерометра, полосовую фильтрацию сигнала и получение его огибающей, расчет спектра Фурье огибающей сигнала, расчет или выбор из справочной литературы основных подшипниковых частот, формирование заключения о наличии дефектов подшипника на основе анализа спектра огибающей сигнала вибрации и табличных или расчетных подшипниковых частот [1].
Недостатком указанного способа вибрационной диагностики подшипника качения является снижение достоверности результата диагностики по следующим причинам:
1) использование для построения диагностической модели табличных габаритных параметров подшипника качения или табличных значений подшипниковых частот, которые могут быть указаны с погрешностями и могут отличаться от их действительных значений на 1% и более;
2) значения основных подшипниковых частот в процессе эксплуатации подшипника качения могут изменяться относительно номинальных величин в пределах ±5% и более [3, 4] по причине технической деградации составных частей подшипника, ухудшения состояния смазки, изменения величины нагрузки и т.д.
В качестве прототипа способа вибрационной диагностики подшипника качения выбран способ [1].
Задачей, решаемой изобретением, является повышение достоверности вибрационной диагностики подшипника качения.
Технический результат, достигаемый заявляемым способом, заключается в повышении достоверности выявления дефектов подшипника качения и степени их выраженности.
В соответствии с изобретением описывается способ вибрационной диагностики подшипника качения, заключающийся в том, что с помощью установленного на диагностируемом подшипнике акселерометра получают сигнал вибрации, производят полосовую фильтрацию сигнала вибрации и получают его огибающую, рассчитывают спектр Фурье огибающей сигнала вибрации, из спектра огибающей сигнала вибрации выделяют все частотные компоненты, амплитуда которых превышает спектральный уровень шума по меньшей мере на 1 дБ, рассчитывают или выбирают из справочной литературы значения основных подшипниковых частот. При этом из набора основных габаритных параметров подшипника [p1, р2, …] выбирают первый габаритный параметр p1 и варьируют его значение относительно номинальной величины 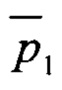 в диапазоне
в диапазоне 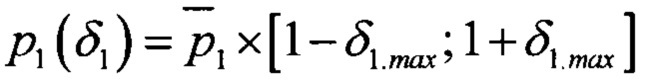 при фиксированных номинальных значениях оставшихся габаритных параметров
при фиксированных номинальных значениях оставшихся габаритных параметров 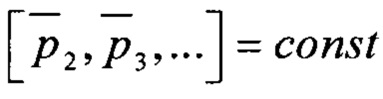 и для каждой величины отклонения δ1 ∈[-δ1.max; + δ1.max] варьируемого габаритного параметра р1 рассчитывают значения основных подшипниковых частот. На основе значений основных подшипниковых частот формируют спектральные шаблоны для всех возможных дефектов подшипника как определенные конфигурации гармоник и субгармоник подшипниковых частот и формируют общую диагностическую модель подшипника D(δ1) как совокупность полученных шаблонов. Вычисляют количество N(δ1) и суммарную амплитуду А(δ1) частотных компонент в спектре огибающей вибрации, соответствующих модели D(δ1), на их основе рассчитывают величину достоверности η(δ1) диагностической модели. Аналогичным образом варьируют значение габаритного параметра р1 для отличных от номинального значений второго габаритного параметра
и для каждой величины отклонения δ1 ∈[-δ1.max; + δ1.max] варьируемого габаритного параметра р1 рассчитывают значения основных подшипниковых частот. На основе значений основных подшипниковых частот формируют спектральные шаблоны для всех возможных дефектов подшипника как определенные конфигурации гармоник и субгармоник подшипниковых частот и формируют общую диагностическую модель подшипника D(δ1) как совокупность полученных шаблонов. Вычисляют количество N(δ1) и суммарную амплитуду А(δ1) частотных компонент в спектре огибающей вибрации, соответствующих модели D(δ1), на их основе рассчитывают величину достоверности η(δ1) диагностической модели. Аналогичным образом варьируют значение габаритного параметра р1 для отличных от номинального значений второго габаритного параметра 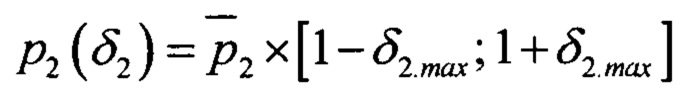 и фиксированных номинальных значениях оставшихся габаритных параметров
и фиксированных номинальных значениях оставшихся габаритных параметров 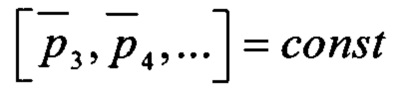 и формируют двумерную величину достоверности η(δ1, δ2) диагностической модели D(δ1, δ2). Аналогичную процедуру циклически повторяют для всех варьируемых габаритных параметров подшипника, в результате чего формируют многомерную величину достоверности η(δ1, δ2, …) диагностической модели D(δ1, δ2, …), по максимуму которой находят оптимальные значения отклонений варьируемых габаритных параметров подшипника [δ1.max, δ2.opt, …], корректируют значения основных подшипниковых частот и формируют уточненную диагностическую модель Dopt=D(δ1.opt, δ2.opt, …). Заключение о наличии дефектов подшипника и их выраженности делают на основе сходства набора найденных в спектре огибающей сигнала частотных компонент со спектральными шаблонами дефектов уточненной диагностической модели Dopt.
и формируют двумерную величину достоверности η(δ1, δ2) диагностической модели D(δ1, δ2). Аналогичную процедуру циклически повторяют для всех варьируемых габаритных параметров подшипника, в результате чего формируют многомерную величину достоверности η(δ1, δ2, …) диагностической модели D(δ1, δ2, …), по максимуму которой находят оптимальные значения отклонений варьируемых габаритных параметров подшипника [δ1.max, δ2.opt, …], корректируют значения основных подшипниковых частот и формируют уточненную диагностическую модель Dopt=D(δ1.opt, δ2.opt, …). Заключение о наличии дефектов подшипника и их выраженности делают на основе сходства набора найденных в спектре огибающей сигнала частотных компонент со спектральными шаблонами дефектов уточненной диагностической модели Dopt.
Для радиального подшипника качения в качестве габаритного варьируемого габаритного параметра р1 выбирают диаметр тел качения Bd или диаметр делительной окружности Pd. Для радиально-упорного, упорного и упорно-радиального подшипника качения, а также для самоустанавливающегося радиального подшипника качения в качестве варьируемого габаритного параметра р1 выбирают диаметр тел качения Bd или диаметр делительной окружности Pd, а в качестве варьируемого габаритного параметра р2 - угол контакта Ф.
По сравнению с известным способом заявленный способ позволяет подстраивать диагностическую модель по сигналу вибрации, тем самым компенсируя погрешность расчета основных подшипниковых частот, вызванную погрешностями указанных в справочной литературе значений габаритных параметров подшипника, деградацией технического состояния подшипника, ухудшением состояния смазки, изменением величины нагрузки и т.д. Заявленный способ вибрационной диагностики подшипника качения имеет на 10-50% большую достоверность результатов работы АСС(%), чем известный способ [1]:
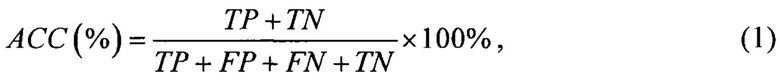
где TP - количество верно обнаруженных частотных компонент в спектре огибающей сигнала вибрации; FP - количество ложно обнаруженных частотных компонент; TN - количество верно пропущенных компонент, FN - количество ложно пропущенных компонент.
Для специалиста очевидно, что заявленный способ может использовать различные критерии выбора полосы частот для фильтрации сигнала вибрации или же использовать широкополосную фильтрацию в линейном диапазоне частот датчика вибрации.
Заявленный способ поясняется подробнее при помощи следующих фигур:
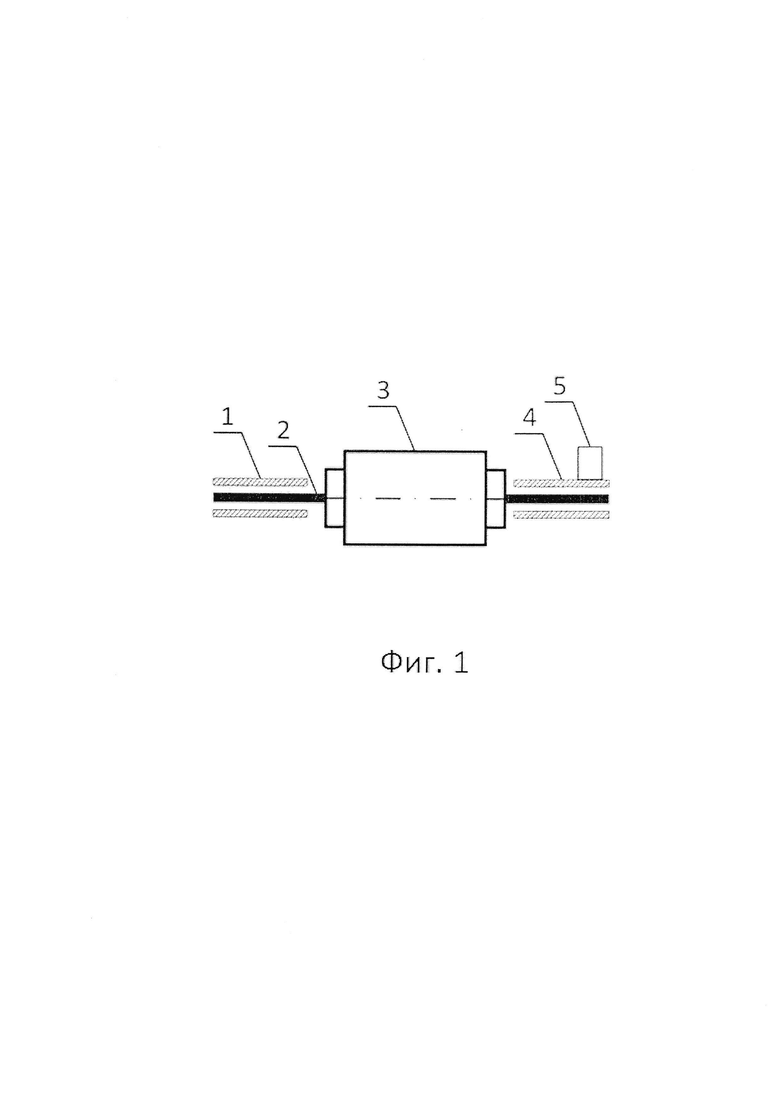
Фиг. 1 - Схема диагностируемого оборудования с установленным датчиком вибрации;
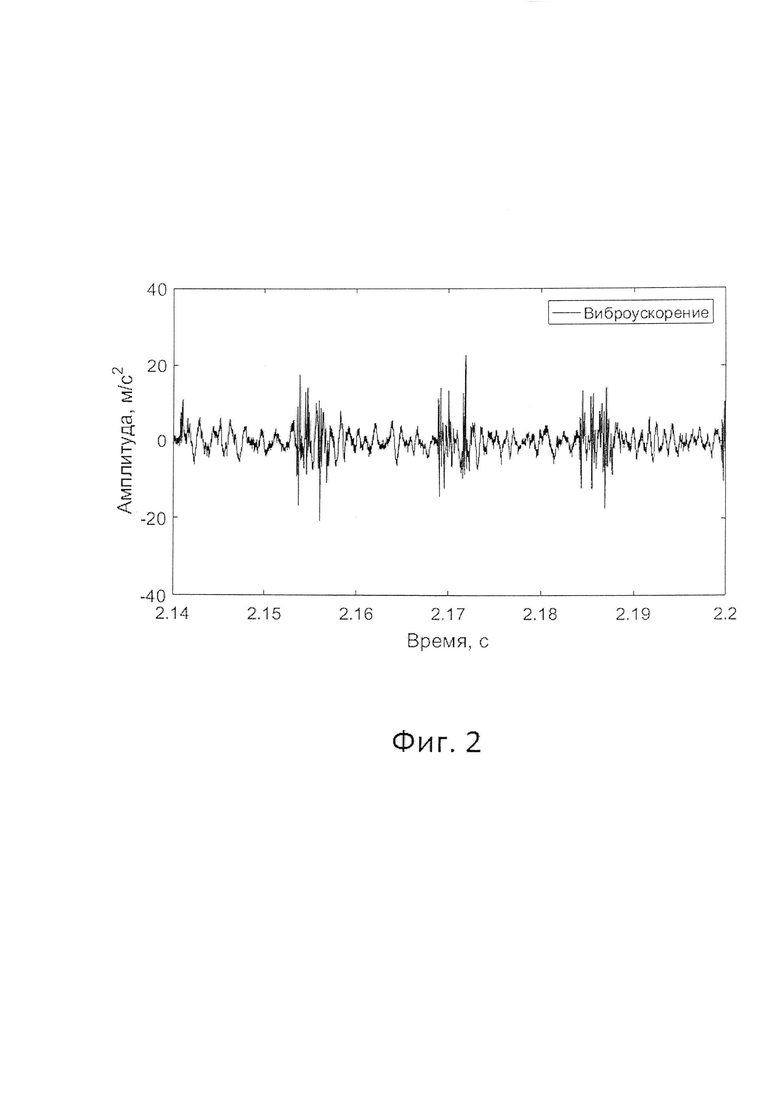
Фиг. 2 - Сигнал вибрации, полученный с радиального шарикового подшипника качения 6213 с дефектом наружного кольца;
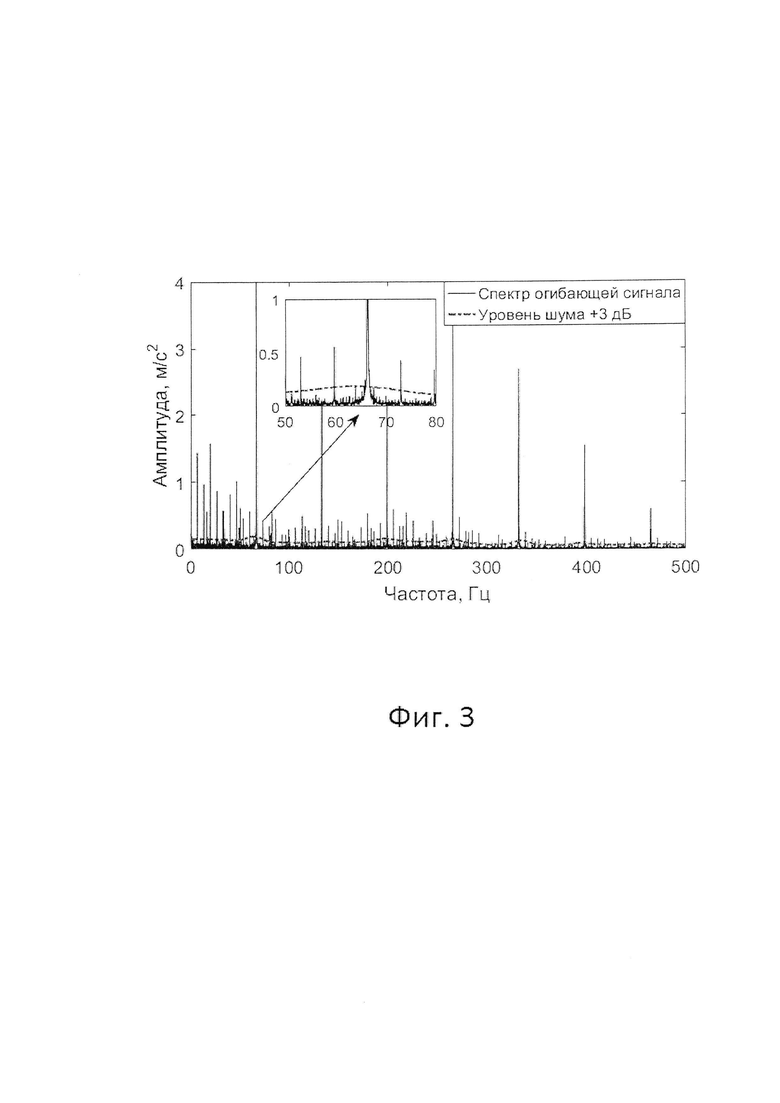
Фиг. 3 - Спектр Фурье огибающей сигнала вибрации радиального шарикового подшипника качения 6213;
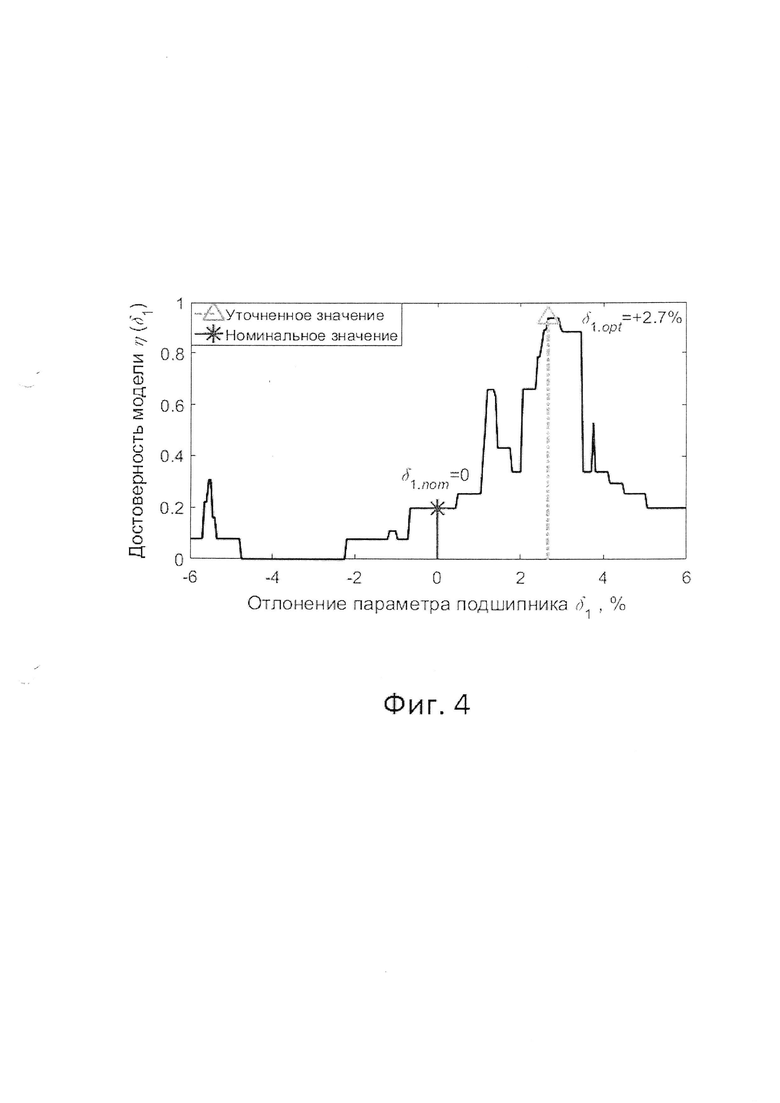
Фиг. 4 - Результат уточнения габаритных параметров диагностической модели радиального шарикового радиального шарикового подшипника качения 6213;
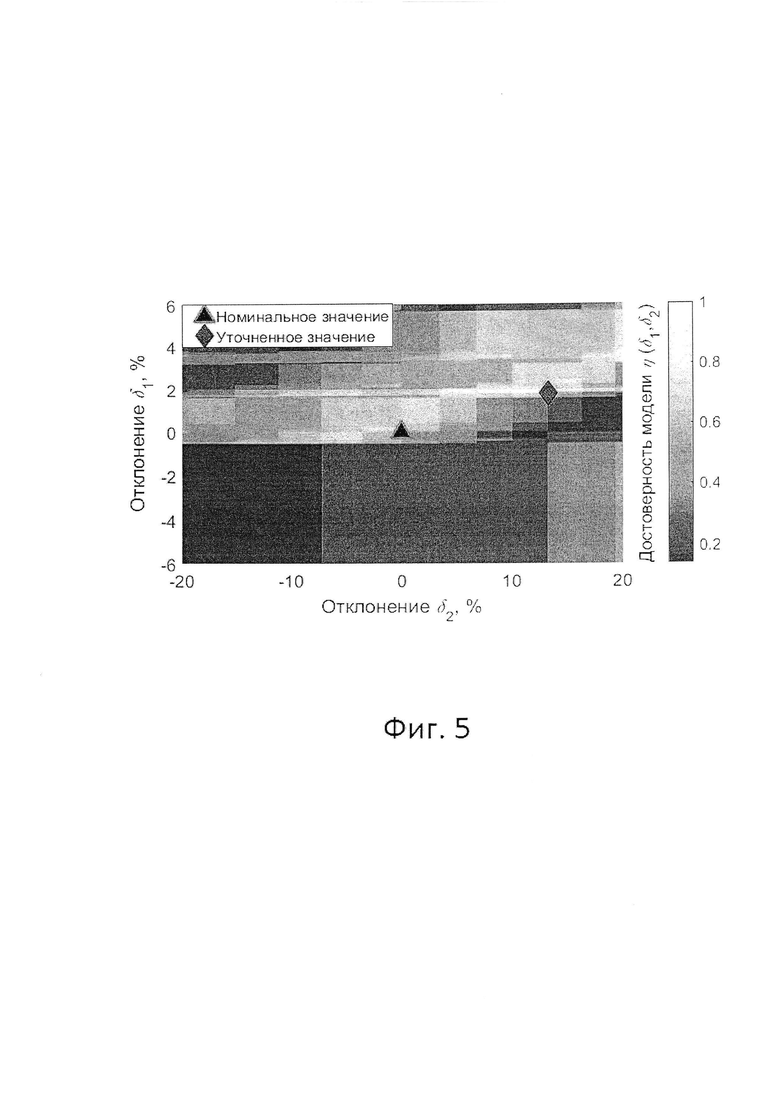
Фиг. 5 - Результат уточнения габаритных параметров диагностической модели радиального самоустанавливающегося радиального шарикового подшипника качения 2302;
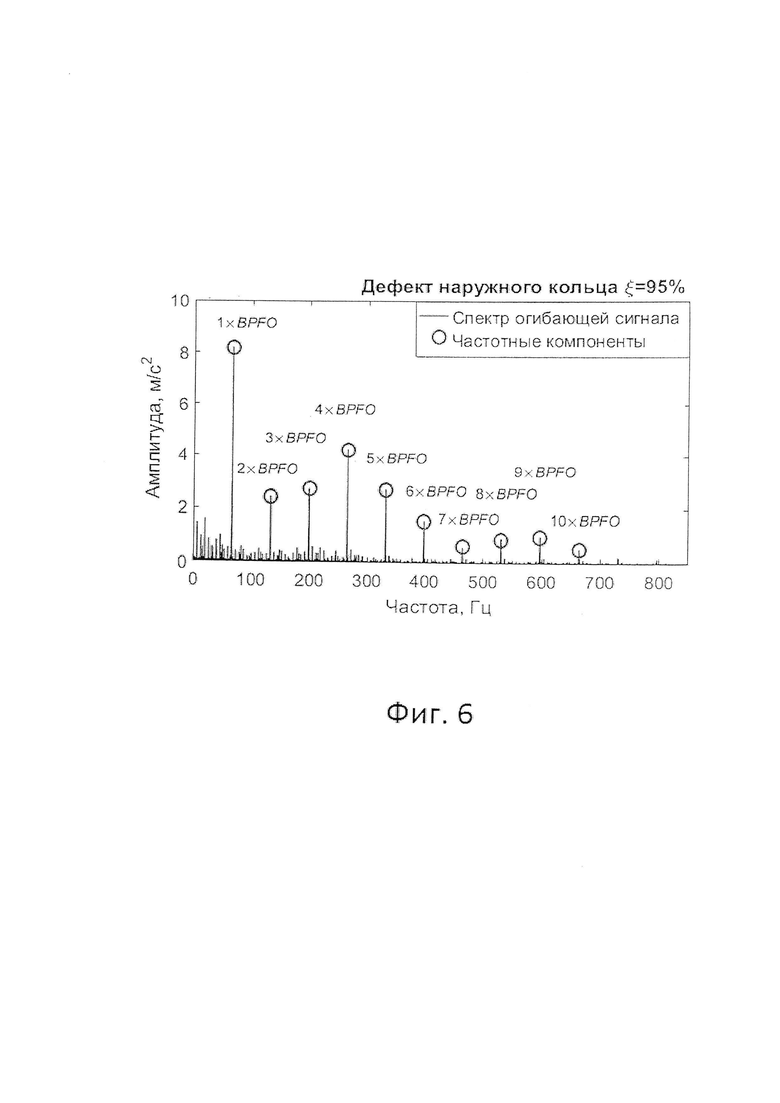
Фиг. 6 - Спектр Фурье огибающей сигнала вибрации радиального шарикового подшипника качения 6213 с обозначенными диагностическими признаками дефекта наружного кольца при уточнении габаритных параметров диагностической модели.
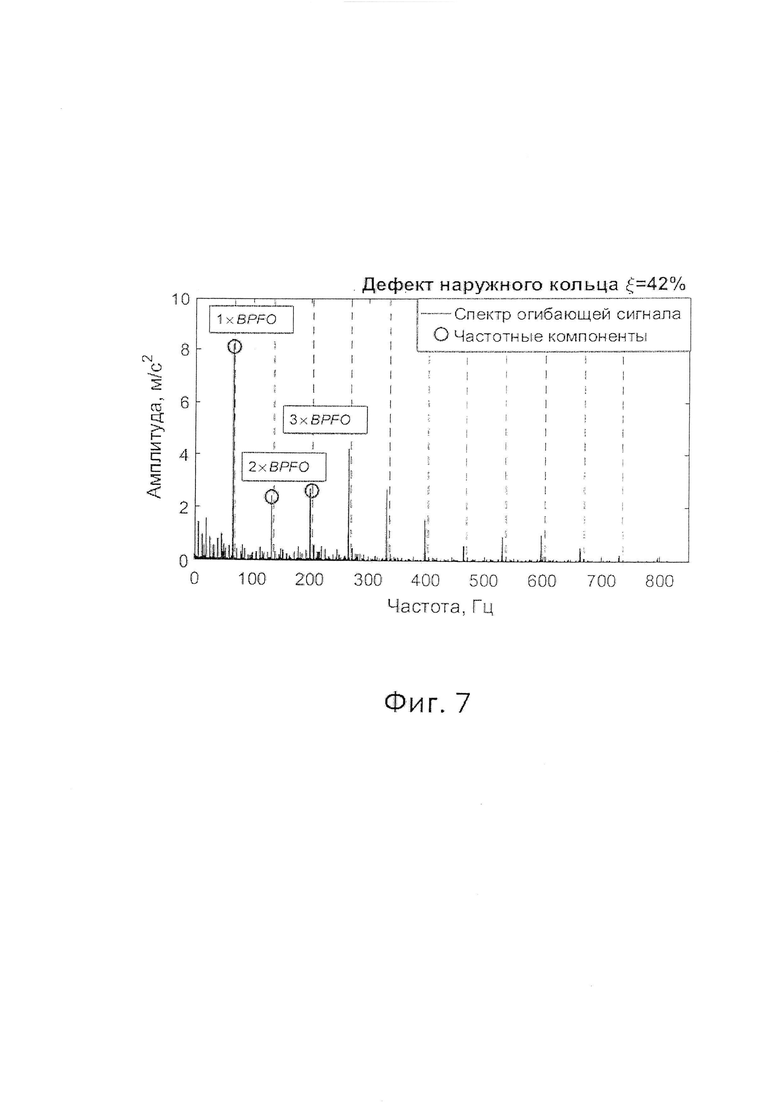
Фиг. 7 - Спектр Фурье огибающей сигнала вибрации радиального шарикового подшипника качения 6213 с обозначенными диагностическими признаками дефекта наружного кольца без уточнения габаритных параметров диагностической модели.
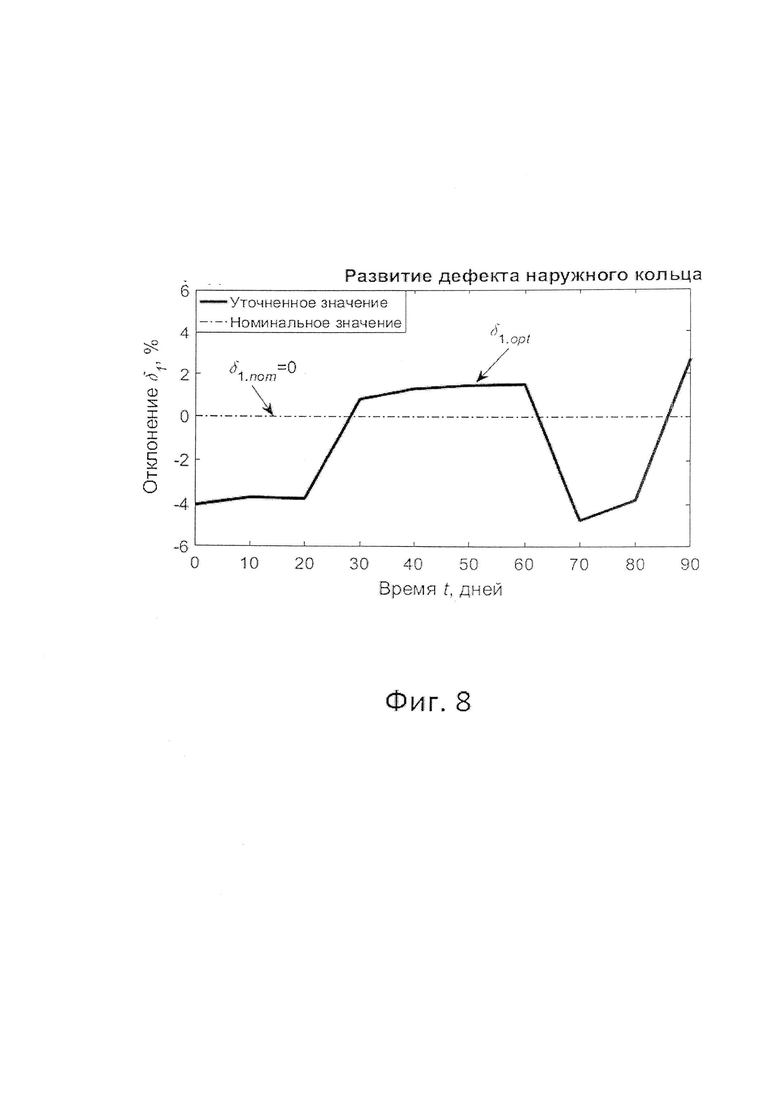
Фиг. 8 - График изменения величины отклонения габаритных параметров диагностической модели от номинальных значений по мере развития дефекта наружного кольца радиального шарикового подшипника качения 6213.
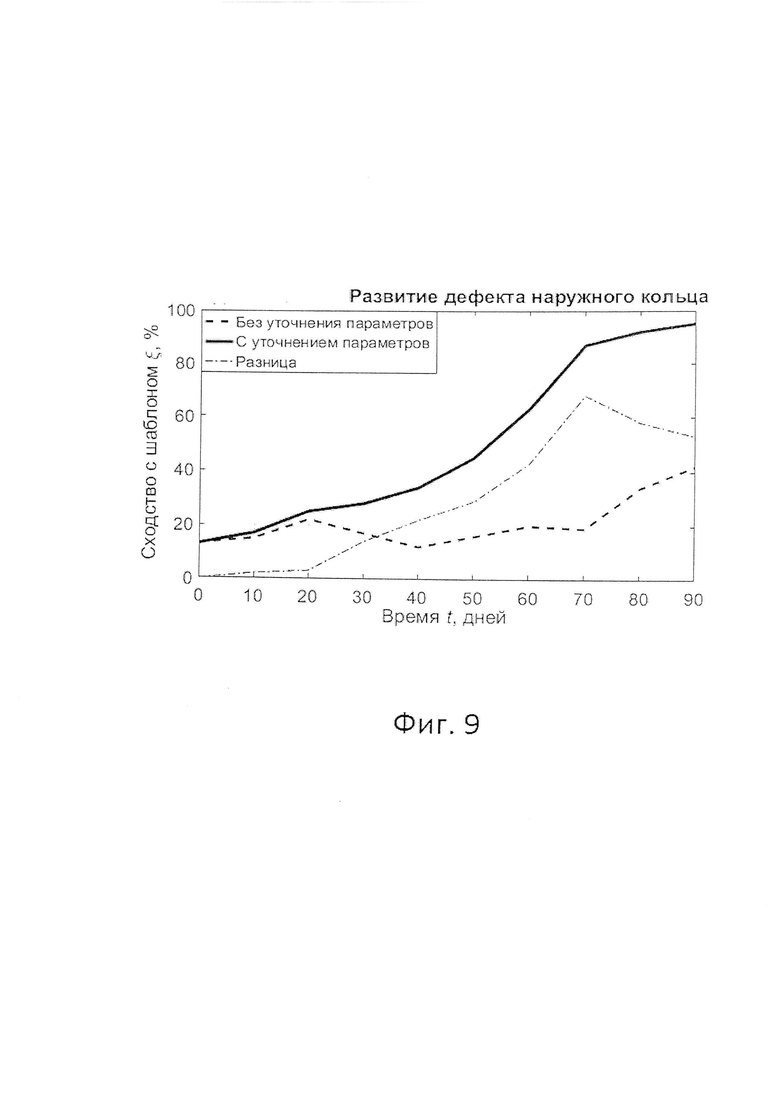
Фиг. 9 - Результаты вибрационной диагностики радиального шарикового подшипника качения 6213 при развитии дефекта наружного кольца с использованием заявленного способа и без него.
Заявляемый способ иллюстрируется примером вибрационной диагностики радиального шарикового подшипника качения 6213, установленного на испытательном стенде, схематично изображенном на фиг. 1, где 1, 4 - радиальный шариковый подшипник качения 6213; 2 - вал; 3 - электродвигатель AИP160S4, 5 - датчик вибрации, установленный на подшипнике 4 в радиальном направлении.
На первом шаге от датчика вибрации, установленного на диагностируемом элементе оборудования (фиг. 1), получают сигнал вибрации x(t), временная реализация которого представлена на фиг. 2.
На втором шаге полученный сигнал вибрации фильтруют в выбранном тем или иным способом диапазоне частот и рассчитывают его огибающую. Вычисляют спектр Фурье огибающей сигнала вибрации Х(ƒ) (фиг. 3). В приведенном примере для фильтрации сигнала и расчета спектра огибающей сигнала вибрации X(ƒ) была выбрана полоса частот 0,5-3,0 кГц.
На третьем шаге в спектре огибающей сигнала вибрации X(ƒ) находят все частотные компоненты, амплитуда которых превышает спектральный уровень шума на 3 дБ и более (фиг. 3, штрихпунктирная линия). Спектральный уровень шума может быть вычислен, например, на основе анализа логарифмического спектра вибрации [5].
На четвертом шаге на основе табличных значений габаритных параметров подшипника качения Nb, Bd, Pd и Ф [2] и значения частоты вращения вала F1 рассчитывают основные подшипниковые частоты:

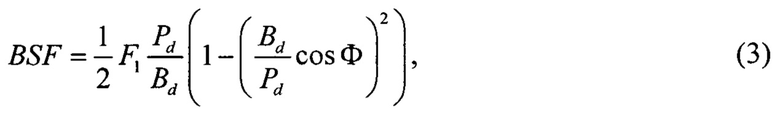
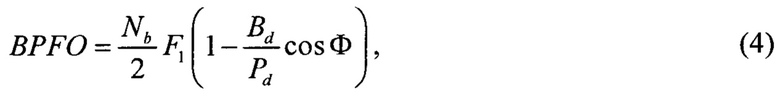

где Nb - количество тел качения, Bd - диаметр тела качения, Pd - диаметр делительной окружности, Ф - угол контакта, FTF - сепараторная частота; BSF - частота вращения тел качения; BPFO - частота перекатывания тел качения по наружному кольцу; BPFI - частота перекатывания тел качения по внутреннему кольцу.
В представленном примере частота вращения вала F1 составила F1=16,28 Гц, на ее основе в соответствии с [2] были получены следующие значения основных подшипниковых частот: FTF=6,67 Гц, BSF=43,79 Гц, BPFO=66,75 Гц и BPFI - 96,05 Гц. На базе полученных подшипниковых частот формируют диагностическую модель D подшипника качения 6213, описывающую все возможные дефекты указанного элемента: износ сепаратора; раковины и трещины на наружном кольце; износ наружного кольца и т.д. [1]. Диагностическая модель представляет собой совокупность спектральных шаблонов для всех возможных дефектов подшипника. Под спектральным шаблоном понимается определенная конфигурация гармоник и субгармоник частотных компонент (например, гармоник подшипниковых частот).
На пятом шаге один из габаритных параметров р подшипника качения варьируют относительно номинального значения 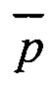 в диапазоне
в диапазоне 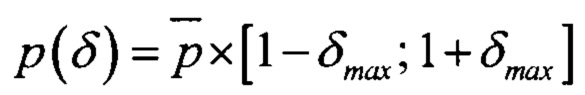 при фиксированных значениях оставшихся габаритных параметров. Значение частоты вращения вала F1 и количество тел качения подшипника Nb принимаются постоянными, поэтому основное влияние на значения подшипниковых частот (2-5) оказывает косинус угла контакта cosФ и отношение
при фиксированных значениях оставшихся габаритных параметров. Значение частоты вращения вала F1 и количество тел качения подшипника Nb принимаются постоянными, поэтому основное влияние на значения подшипниковых частот (2-5) оказывает косинус угла контакта cosФ и отношение 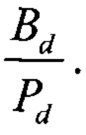
Для радиального подшипника качения номинальное значение угла контакта стремится к нулю Ф → 0 и его малые отклонения не оказывают значительного влияния на косинус соsФ → 1. По этой причине в качестве варьируемого габаритного параметра р1 в данном случае выбирают диаметр тел качения Bd или диаметр делительной окружности Pd.
Для радиально-упорного, упорного и упорно-радиального подшипника качения, а также для самоустанавливающегося радиального подшипника качения угол контакта Ф отличен от нуля, поэтому его отклонение от номинальной величины может оказывать влияние на значения подшипниковых частот (2-5). По этой причине для указанных подшипников в качестве первого варьируемого габаритного параметра р1 выбирают диаметр тел качения Bd или диаметр делительной окружности Pd, а в качестве второго варьируемого габаритного параметра р2 выбирают угол контакта Ф.
Рассматриваемый в примере шариковый подшипник качения 6213 является радиальным (Ф=0), поэтому для подстройки диагностической модели был использован только первый варьируемый габаритный параметр р1, в качестве которого был выбран диаметр тел качения Bd. Максимально возможное отклонение габаритного параметра р1 от номинала было выставлено на уровне |δ1.max(%)|=6%. Для каждой величины отклонения варьируемого габаритного параметра δ1 ∈[-δ1.max; + δ1.max] была сформирована диагностическая модель подшипника D(δ1).
На шестом шаге вычисляют величину достоверности η(δ1) полученных диагностических моделей D(δ1). Величина достоверности может быть рассчитана по-разному. В приведенном примере для ее расчета были предварительно определены следующие параметры: общее количество частотных компонент N(δ1) в спектре огибающей сигнала (количество гармоник подшипниковых частоты и гармоник оборотной частоты F1), соответствующих диагностическим моделям D(δ1), суммарная амплитуда найденных частотных компонент А(δ1), а также общее количество только подшипниковых частотных компонент NB(δ1) (только гармоник подшипниковых частот).
В приведенном примере величина достоверности η(δ1) была рассчитана как среднее арифметическое полученных зависимостей N(δ1), А(δ1) и NB(δ1):
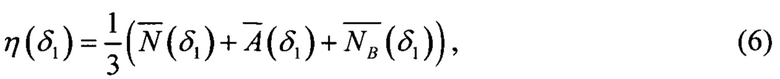
где 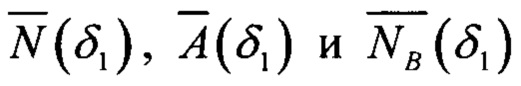 - зависимости, нормированные по максимальному значению в диапазоне δ1 ∈[-δ1.max; + δ1.max].
- зависимости, нормированные по максимальному значению в диапазоне δ1 ∈[-δ1.max; + δ1.max].
На седьмом шаге по максимуму кривой достоверности η(δ1) определяют оптимальное значение отклонения δ1.opt варьируемого габаритного параметра подшипника p1:

Кривая достоверности η(δ1) диагностических моделей для рассматриваемого примера изображена на фиг. 4. Оптимальное значение отклонения δ1.opt(%) габаритного параметра р1 (диаметр тел качения Bd) от номинала составило δ1.opt(%)=+2,70%.
В качестве примера на фиг. 5 приведен случай определения оптимальных отклонений габаритных параметров диагностической модели для радиального самоустанавливающегося подшипника качения 2302 с табличным значением угла контакта Ф=19°. В качестве первого варьируемого габаритного параметра р1 был выбран диаметр тел качения Bd, а в качестве второго варьируемого габаритного параметра р2 - угол контакта Ф. В данном случае оптимальные значения отклонений габаритных параметров р1 и р2 было определено по максимуму двумерной достоверности η(δ1, δ2). В соответствии с фиг. 5 оптимальное отклонение габаритного параметра р1 составило δ1.opt (%)=1.8%, а габаритного параметра р2 составило δ2.opt (%)=13.25%.
На восьмом шаге при помощи найденной величины отклонения δ1.opt были рассчитаны новые значения основных подшипниковых частот FTF=6,64 Гц, BSF=42,51 Гц, BPFO=66,35 Гц и BPFI=96,46 Гц и сформирована уточненная диагностическая модель подшипника качения Dopt=D(δ1.opt). На основе полученной диагностической модели Dopt у анализируемого подшипника качения 6213 был выявлен выраженный дефект наружного кольца. При этом сходство информативных признаков дефекта с его шаблоном в диагностической модели Dopt составило ξ=95%. Величина сходства ξ рассчитывается как сумма весовых коэффициентов wi найденных в спектре огибающей X(ƒ) частотных компонент 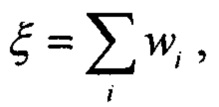 соответствующих рассматриваемому дефекту (фиг. 6).
соответствующих рассматриваемому дефекту (фиг. 6).
В тоже время, при использовании способа [1] не все частотные компоненты в спектре огибающей сигнала (гармоники BPFO) были верно идентифицированы из-за погрешности расчет подшипниковых частот. Как результат, сходство с шаблоном дефекта составило ξ=42% (фиг. 7). Вертикальными пунктирными линиями на фиг. 7 обозначены номинальные положения гармоник BPFO.
На фиг. 8 представлен график изменения значения отклонения δ1.opt варьируемого габаритного параметра р1 по мере развития дефекта наружного кольца подшипника качения 6213. В соответствии с фиг. 8 за период наблюдения величина отклонения δ1.opt изменялась в диапазоне δ1.opt (%) ∈ [-4,75;+2,7] %.
На фиг. 9 приведены графики величины сходства ξ наборов найденных частотных компонент с шаблоном дефекта наружного кольца для заявленного способа диагностики подшипника качения и способа [1]. Сплошная линия на фиг. 9 соответствует случаю оценки технического состояния подшипника 6213 с использованием заявленного способа, а пунктирная линия - с использованием способа [1]. Видно, что в приведенном примере использование заявленного способа позволило повысить достоверность вибрационной диагностики подшипника качения за период наблюдения по сравнению со способом [1] на величину до 68% (фигура 9, штрихпунктирная линия). При этом наличие неисправности подшипника качения 6213 с использованием заявленного способа может быть определено на более ранней стадии, чем с использованием способа [1] (фиг. 9).
Источники информации:
[1] Барков, А.В. Мониторинг и диагностика роторных машин по вибрации. / А.В. Барков, Н.А. Баркова, А.Ю. Азовцев. - СПб.: Изд. центр СПбГМТУ, 2000. - 169 с.
[2] Bearing Frequencies [Электронный ресурс]. - Режим доступа: http://www.ntnamericas.com/en/website/documents/brochures-and-literature/tech-sheets-and-supplements/frequencies.pdf.
[3] An experimental based assessment of the deviation of the bearing characteristic frequencies / P. Pennacchi [et al.] // 6th International Conference Acoustic and Vibratory Surveillance Methods and Diagnostic Techniques: Science & Engineering Faculty. - Compiegne, France, 2011. - 8 p.
[4] Костюков, B.H. Основы виброакустической диагностики и мониторинга машин: учеб. пособие / В.Н. Костюков, А.П. Науменко. - Омск: Изд-во ОмГТУ, 2011. - 360 с.
[5] Yeh, С. Adaptive noise level estimation / С. Yeh, 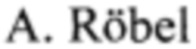 // 9th International Conference of Digital Audio Effects (DAFx-06). - Montreal, Canada, 2006. - P. 145-148.
// 9th International Conference of Digital Audio Effects (DAFx-06). - Montreal, Canada, 2006. - P. 145-148.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ диагностирования технического состояния подшипников качения по анализу сигналов вибрации | 2024 |
|
RU2831926C1 |
| Способ диагностирования технического состояния подшипников качения в режиме реального времени | 2024 |
|
RU2826382C1 |
| УСТРОЙСТВО И СПОСОБ ОЦЕНКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ АСИНХРОННЫХ ДВИГАТЕЛЕЙ | 2019 |
|
RU2711647C1 |
| Способ контроля технического состояния подшипников качения | 2015 |
|
RU2623177C2 |
| Способ вибродиагностики зарождающихся дефектов механизмов | 2018 |
|
RU2680640C1 |
| Способ контроля технического состояния подшипников качения | 1989 |
|
SU1691702A1 |
| СПОСОБ ДИАГНОСТИКИ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ | 2005 |
|
RU2297613C2 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ ОБОБЩЁННОГО ТЕХНИЧЕСКОГО СОСТОЯНИЯ ЭЛЕКТРОДВИГАТЕЛЯ | 2016 |
|
RU2641318C1 |
| Способ диагностики технического состояния трансмиссий горных машин с приводным двигателем | 1985 |
|
SU1271970A1 |
| Способ вибрационной диагностики подшипниковых опор в составе газотурбинных двигателей с применением технического микрофона | 2015 |
|
RU2613047C1 |
Изобретение относится к области метрологии. Способ вибрационной диагностики подшипника качения заключается в том, что с помощью установленного на диагностируемом подшипнике акселерометра получают сигнал вибрации, производят полосовую фильтрацию сигнала вибрации и получают его огибающую, рассчитывают спектр Фурье огибающей сигнала вибрации, из спектра огибающей сигнала вибрации выделяют все частотные компоненты, амплитуда которых превышает спектральный уровень шума по меньшей мере на 1 дБ, рассчитывают или выбирают из справочной литературы значения основных подшипниковых частот. При этом из набора основных габаритных параметров подшипника выбирают первый габаритный параметр и варьируют его значение относительно номинальной величины в диапазоне при фиксированных номинальных значениях оставшихся габаритных параметров и для каждой величины отклонения варьируемого габаритного параметра р1 рассчитывают значения основных подшипниковых частот. На основе значений основных подшипниковых частот формируют спектральные шаблоны для всех возможных дефектов подшипника как определенные конфигурации гармоник и субгармоник подшипниковых частот и формируют общую диагностическую модель подшипника как совокупность полученных шаблонов. Вычисляют количество и суммарную амплитуду частотных компонент в спектре огибающей вибрации, соответствующих модели, на их основе рассчитывают величину достоверности диагностической модели. Аналогичным образом варьируют значение габаритного параметра р1 для отличных от номинального значений второго габаритного параметра и фиксированных номинальных значений оставшихся габаритных параметров и формируют двумерную величину достоверности диагностической модели. Аналогичную процедуру циклически повторяют для всех варьируемых габаритных параметров подшипника, в результате чего формируют многомерную величину достоверности диагностической модели, по максимуму которой находят оптимальные значения отклонений варьируемых габаритных параметров подшипника, корректируют значения основных подшипниковых частот и формируют уточненную диагностическую модель. Заключение о наличии дефектов подшипника и их выраженности делают на основе сходства набора найденных в спектре огибающей сигнала частотных компонент со спектральными шаблонами дефектов уточненной диагностической модели. Технический результат – повышение точности диагностики. 2 з.п. ф-лы, 9 ил.
1. Способ вибрационной диагностики подшипника качения, включающий получение сигнала вибрации с помощью установленного на диагностируемом подшипнике акселерометра, полосовую фильтрацию сигнала и получение его огибающей, расчет спектра Фурье огибающей сигнала, расчет или выбор из справочной литературы основных подшипниковых частот, формирование вывода о наличии дефектов подшипника на основе анализа спектра огибающей сигнала вибрации и табличных или расчетных подшипниковых частот, отличающийся тем, что из спектра огибающей сигнала вибрации выделяют все частотные компоненты, амплитуда которых превышает спектральный уровень шума по меньшей мере на 1 дБ, из набора основных габаритных параметров подшипника [p1, p2, …] выбирают первый габаритный параметр р1 и варьируют его значение относительно номинальной величины 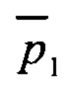 в диапазоне
в диапазоне 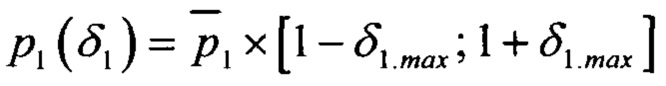 при фиксированных номинальных значениях оставшихся габаритных параметров
при фиксированных номинальных значениях оставшихся габаритных параметров 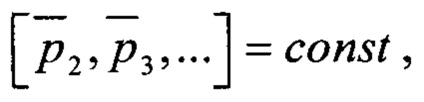 для каждой величины отклонения δ1 ∈ [-δ1.max; + δ1.max] варьируемого габаритного параметра р1 рассчитывают значения основных подшипниковых частот, на их основе формируют спектральные шаблоны для всех возможных дефектов подшипника как определенную конфигурацию гармоник и субгармоник подшипниковых частот, формируют общую диагностическую модель подшипника D(δ1) как совокупность полученных шаблонов, вычисляют количество N(δ1) и суммарную амплитуду А(δ1) частотных компонент в спектре огибающей сигнала вибрации, соответствующих модели D(δ1), на их основе рассчитывают величину достоверности η(δ1) диагностической модели, аналогичным образом варьируют значение габаритного параметра р1 для отличных от номинального значений второго габаритного параметра
для каждой величины отклонения δ1 ∈ [-δ1.max; + δ1.max] варьируемого габаритного параметра р1 рассчитывают значения основных подшипниковых частот, на их основе формируют спектральные шаблоны для всех возможных дефектов подшипника как определенную конфигурацию гармоник и субгармоник подшипниковых частот, формируют общую диагностическую модель подшипника D(δ1) как совокупность полученных шаблонов, вычисляют количество N(δ1) и суммарную амплитуду А(δ1) частотных компонент в спектре огибающей сигнала вибрации, соответствующих модели D(δ1), на их основе рассчитывают величину достоверности η(δ1) диагностической модели, аналогичным образом варьируют значение габаритного параметра р1 для отличных от номинального значений второго габаритного параметра 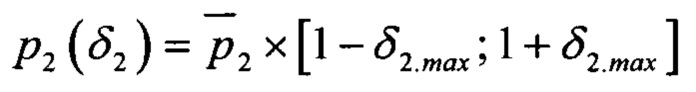 и фиксированных номинальных значений оставшихся габаритных параметров
и фиксированных номинальных значений оставшихся габаритных параметров 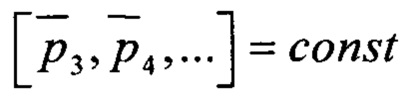 и формируют двумерную величину достоверности η(δ1, δ2) диагностической модели D(δ1, δ2), аналогичную процедуру циклически повторяют для всех варьируемых габаритных параметров подшипника, в результате чего формируют многомерную величину достоверности η(δ1, δ2, …) диагностической модели D(δ1, δ2, …), по максимуму которой находят оптимальные значения отклонений варьируемых габаритных параметров подшипника (δ1.opt, δ2.opt, …), корректируют значения основных подшипниковых частот и формируют уточненную диагностическую модель Dopt=D(δ1.opt, δ2.opt, …), на основе сходства набора найденных в спектре огибающей сигнала вибрации частотных компонент со спектральными шаблонами дефектов уточненной диагностической модели Dopt делают заключение о наличии дефектов подшипника и их выраженности.
и формируют двумерную величину достоверности η(δ1, δ2) диагностической модели D(δ1, δ2), аналогичную процедуру циклически повторяют для всех варьируемых габаритных параметров подшипника, в результате чего формируют многомерную величину достоверности η(δ1, δ2, …) диагностической модели D(δ1, δ2, …), по максимуму которой находят оптимальные значения отклонений варьируемых габаритных параметров подшипника (δ1.opt, δ2.opt, …), корректируют значения основных подшипниковых частот и формируют уточненную диагностическую модель Dopt=D(δ1.opt, δ2.opt, …), на основе сходства набора найденных в спектре огибающей сигнала вибрации частотных компонент со спектральными шаблонами дефектов уточненной диагностической модели Dopt делают заключение о наличии дефектов подшипника и их выраженности.
2. Способ по п. 1, отличающийся тем, что для радиального подшипника качения в качестве варьируемого габаритного параметра р1 выбирают либо диаметр тел качения Bd, либо диаметр делительной окружности Pd.
3. Способ по п. 1, отличающийся тем, что для радиально-упорного, упорного и упорно-радиального подшипника качения, а также для самоустанавливающегося радиального подшипника качения в качестве первого варьируемого габаритного параметра р1 выбирают либо диаметр тел качения Bd, либо диаметр делительной окружности Pd, а в качестве второго варьируемого габаритного параметра р2 - угол контакта Ф.
| Космач, Н | |||
| В | |||
| Спектр огибающей вибрационного сигнала для оценки технического состояния промышленного оборудования / Н | |||
| В | |||
| Веникодробильный станок | 1921 |
|
SU53A1 |
| - Минск: БГУИР, 2017 | |||
| - С | |||
| Механический грохот | 1922 |
|
SU41A1 |
| МЕХАТРОННОЕ УСТРОЙСТВО | 2013 |
|
RU2543522C2 |
| JP 58193425 A, 11.11.1983 | |||
| JP | |||
Авторы
Даты
2020-04-28—Публикация
2019-04-22—Подача