Изобретение относится к теории информации и предназначено для выделения последовательностей логических нулей либо единиц в процессе декодирования информации из последовательности сверхширокополосных (СШП) импульсов без синхронизации приемника и передатчика.
Известен асинхронно-кепстральный способ выделения закодированной информации, передаваемой потребителю с помощью сверхширокополосных импульсов [1]. Способ заключается в том, что с помощью источника передачи сообщений (объект X) из первой точки пространства излучают в свободное пространство кодовую последовательность сверхширокополосных импульсов (КПСШПИ). Параметры КПСШПИ известны во второй точке пространства на пункте приема сообщений (объект Y).
Правило кодирования информации заключается в использовании в качестве основных носителей информации пачек импульсов, состоящих из импульсов, длительность которых не менее 2 нс, описываемых первой производной гауссовой функции [2]. Эти импульсы имеют следующее аналитическое описание
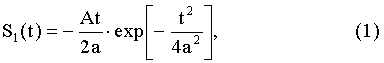
где А - амплитуда импульса; а - величина, характеризующая половину длительности импульса на уровне 0,707.
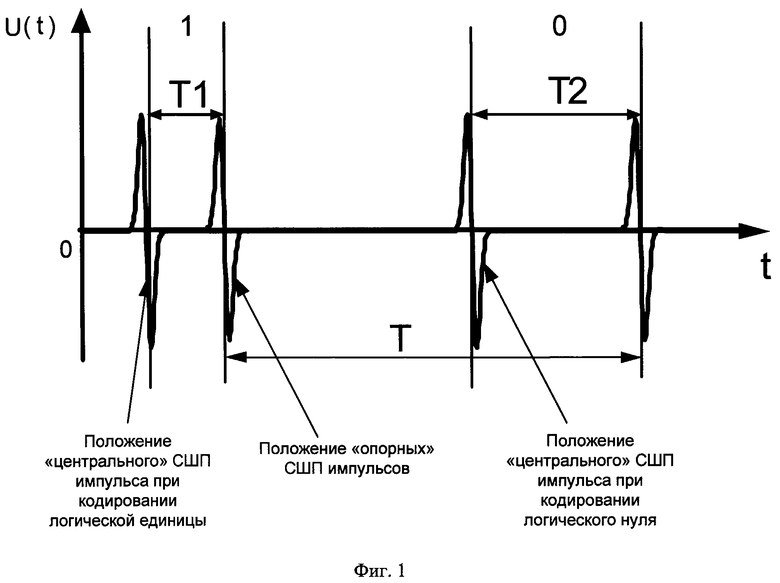
Для кодирования информации в каждом канале передачи данных предлагается использовать периодическую последовательность пачек СШП гауссовых импульсов, состоящую из расположенных в определенном порядке «опорных» и «центральных» пачек импульсов. Импульсы в каждой пачке задержаны друг относительно друга на временные задержки по определенному пин-коду. При этом пин-код для каждого последующего канала передачи данных не повторяется. Опорные пачки импульсов в каждом канале передачи данных отличаются от «центральных» тем, что их период следования Т постоянен, а период следования «центральных» пачек импульсов может изменяться. Вся информация о кодировании будет заключаться во временном положении «центральных» пачек СШП импульсов относительно «опорных». При временном положении «центральной» пачки СШП импульса с опережением «опорной» пачки на 0,2Т результат кодирования соответствует логической «единице», а при положении «центральной» пачки СШП импульсов с опережением «опорной» пачки на 0,4Т результат кодирования соответствует логическому «нулю» (фиг.1). Таким образом, всю информацию о кодировании логического «нуля» или «единицы» предлагается заключить в задержках между импульсами. При данном способе кодирования информации необходимо соблюдать условие: Т1<Т2<Т, где Т1=0,2Т, Т2=0,4Т - задержки между «опорными» и «центральными» пачками СШП импульсов; Т - период следования «опорных» пачек СШП импульсов, составляющий порядка десятков наносекунд.
Из данного условия следует, что каждый бит информации в каждом канале передачи данных кодируется одной «опорной» и одной «центральной» пачкой СШП импульсов. При этом набор нескольких бит информации в каждом канале передачи данных (ПД) будет представлять собой некоторое сообщение, именуемое кодограммой, которое излучается одновременно с другими кодограммами каналов ПД в пространство из первой точки объектом Х и принимается во второй точке пространства объектом Y.
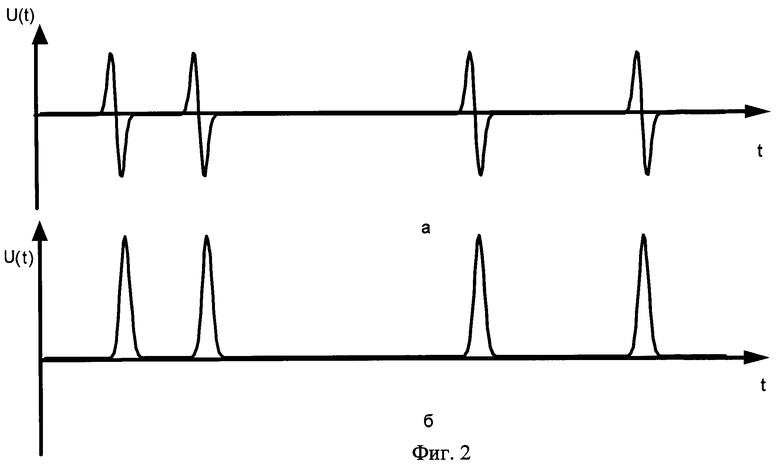
После приема всех кодограмм объектом Y и усиления КПСШПИ каждый импульс предлагается растянуть. Растяжение импульсов необходимо для обеспечения процесса оцифровки сигнала аналого-цифровым преобразователем (АЦП), так как при подаче на вход АЦП импульсов двухнаносекундной длительности для достоверного восстановления их формы квантованными значениями на выходе АЦП необходимо иметь в пределах длительности импульса достаточное количество отсчетов. Это количество определяется частотой дискретизации самого АЦП. К примеру, при подаче на вход АЦП (с частотой дискретизации 2 ГГц) импульса длительностью 2 нс количество оцифрованных в нем отсчетов будет равно 4, чего явно недостаточно для качественного описания двухполярной формы импульса. При увеличении длительности импульса, например, в 10 раз число оцифрованных отсчетов в пределах импульса будет равно уже 20. Для достоверного восстановления формы сигнала, описываемого выражением (1), количество оцифрованных отчетов должно быть не менее 6.
Для растяжения СШП сигнал после интегрирования (фиг.2) с помощью делителя с К выходами разделяется по мощности на К частей (фиг.3). Затем каждая из частей задерживается на время tзk, вычисляемое по формуле
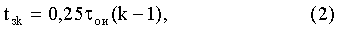
где 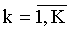 ; τои - длительность одиночного СШП импульса после интегрирования.
; τои - длительность одиночного СШП импульса после интегрирования.
При этом количество линий задержки Н будет равно Н=К-1. После задержки все сигналы складываются по мощности в сумматоре.
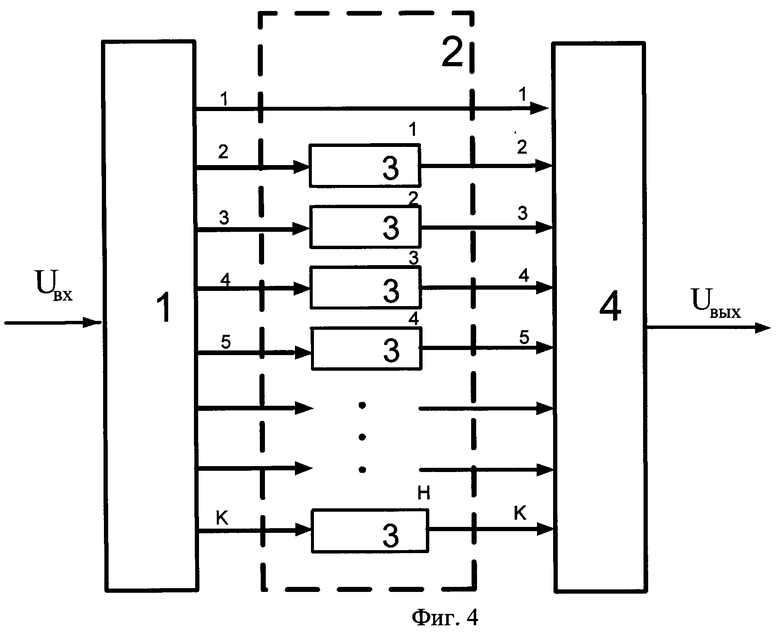
Схема, реализующая процесс растяжения, представлена на фиг.4, где использованы следующие обозначения: блок 1 - делитель, блок 2 - блок линий задержки, блок 3 - линия задержки, блок 4 - сумматор. Под Uвx подразумевается СШП сигнал после интегрирования, под Uвых - выходной сигнал сумматора, поступающий на вход АЦП. Первая линия задержки 3 задерживает сигнал второго выхода делителя 1 на tз1=0,25τои. Вторая линия задержки 3 задерживает сигнал с третьего выхода делителя 1 на tз2=0,5τои, а h-я линия задержки 3, где  , задерживает сигнал (h+1)-го выхода делителя 1 на tзh=0,25τоиh. Линия задержки 3 под номером Н задерживает сигнал с выхода делителя 1 под номером К=Н+1 на tзh=0,25τоиH.
, задерживает сигнал (h+1)-го выхода делителя 1 на tзh=0,25τоиh. Линия задержки 3 под номером Н задерживает сигнал с выхода делителя 1 под номером К=Н+1 на tзh=0,25τоиH.
Величина К будет определяться длительностью СШП импульсов после интегрирования и необходимой длительностью СШП импульсов для АЦП. Значение К должно быть целым, в связи с чем для правильного выбора К целесообразно использовать неравенство
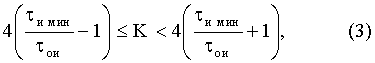
где 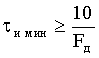 - минимальная длительность СШП импульса, которую необходимо иметь для получения нужного числа отсчетов после аналого-цифрового преобразования данного импульса; Fд - частота дискретизации АЦП.
- минимальная длительность СШП импульса, которую необходимо иметь для получения нужного числа отсчетов после аналого-цифрового преобразования данного импульса; Fд - частота дискретизации АЦП.
В последующем растянутые СШП импульсы оцифровывают при помощи АЦП. Сверхширокополосные импульсы, становясь шире по длительности, не требуют повышения частоты дискретизации АЦП и сохраняют информацию о кодировании во временных задержках между собой (фиг.5).
Получившийся в результате набор данных, описывающий оцифрованный сигнал, поступает в ЭВМ, где по мере поступления данных с АЦП осуществляют формирование генерального массива данных D, из элементов которого формируют Z пробных массивов  Каждый вновь сформированный пробный z-й массив записывается в память ЭВМ и включает в себя значения оцифрованной растянутой последовательности сверхширокополосных импульсов, ограниченной временным интервалом длительностью Δ. Причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т.
Каждый вновь сформированный пробный z-й массив записывается в память ЭВМ и включает в себя значения оцифрованной растянутой последовательности сверхширокополосных импульсов, ограниченной временным интервалом длительностью Δ. Причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т.
В результате каждый z-й пробный массив включает по N отсчетов, извлекаемых из генерального массива D, начиная с z-го элемента массива D и заканчивая (z+N-1)-м элементом массива D, где число элементов N в пробном массиве определяется по формуле

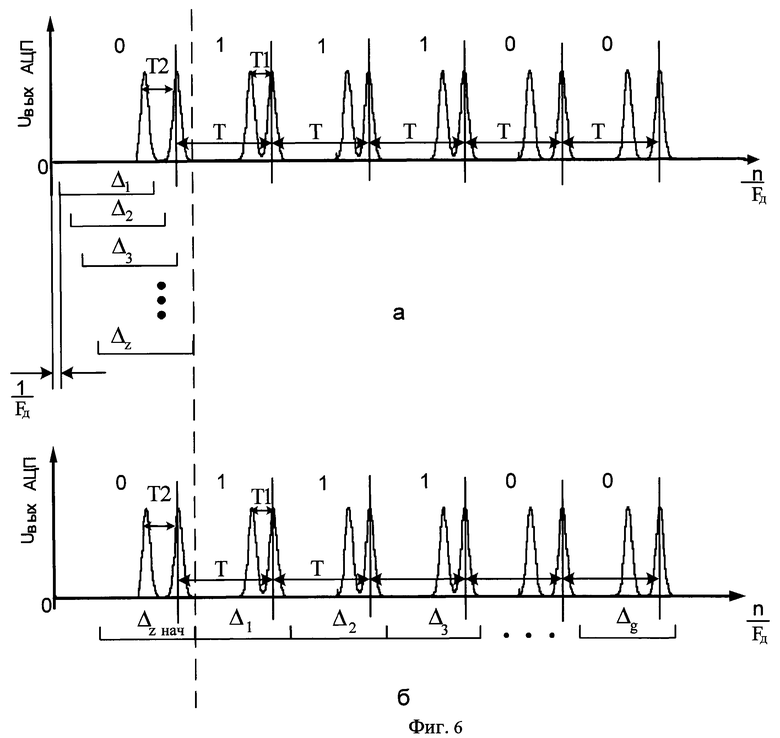
Таким образом, первый пробный массив формируют из элементов массива D с номерами с 1-го по N-й, второй пробный массив формируют из элементов массива D с номерами со 2-го по (N+1)-й, третий пробный массив формируют из элементов массива D с номерами с 3-го по (N+2)-й, a Z-й пробный массив формируют из элементов массива D с номерами с Z-го по (Z+N-1)-й (эпюра а, фиг 6). К примеру, если генеральный массив D содержит 128 элементов, а N равно 48, тогда первый пробный массив будет включать в себя элементы генерального массива D с первого по 48-й, второй пробный массив будет включать в себя элементы генерального массива D со второго по 49-й, третий пробный массив будет включать в себя элементы генерального массива D с третьего по 50-й и т.д.
После этого элементы каждого z-го пробного массива последовательно подвергают кепстральной обработке [4] по схеме, представленной на фиг.7. В начале элементы каждого z-го пробного массива подвергаются дискретному прямому преобразованию Фурье [5] с использованием формулы
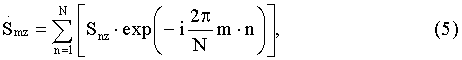
где n - номер отсчета во временной области, m - номер отсчета в частотной области; 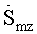 - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го пробного массива, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м пробном массиве.
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го пробного массива, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м пробном массиве.
В последующем для каждого z-го пробного массива вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле

Затем для каждого вектора, составленного из величин Umz z-го интервала Δz, вычисляют дискретное обратное преобразование Фурье [5] по формуле
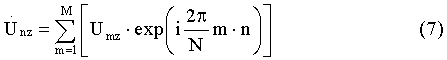
где М - число элементов в векторе Umz, количественно равное N.
В результате трех описанных операций для каждого z-го пробного массива получают соответствующий z-й основной массив, состоящий из элементов 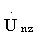 .
.
После этого вычисляют значение модуля для каждого n-го отсчета соответствующего z-го основного массива. В результате получают z-й кепстральный массив, состоящий из элементов 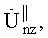 который представляет собой кепстр z-го пробного массива. Для декодирования информации каждый кепстральный массив разбивают на два массива V1z, V2z. При этом массив V1z z-го кепстрального массива включает в себя значения кепстра с номерами от m0 до m1, где m0=f(T1·Fд-1); m1=f(T1·Fд+1); f(*) - функция округления в сторону меньшего целого числа. Массив V2z z-го кепстрального массива включает в себя значения кепстра с номерами от m2 до m3, где m2=f(Т2·Fд-1); m3=f(Т2·Fд+1).
который представляет собой кепстр z-го пробного массива. Для декодирования информации каждый кепстральный массив разбивают на два массива V1z, V2z. При этом массив V1z z-го кепстрального массива включает в себя значения кепстра с номерами от m0 до m1, где m0=f(T1·Fд-1); m1=f(T1·Fд+1); f(*) - функция округления в сторону меньшего целого числа. Массив V2z z-го кепстрального массива включает в себя значения кепстра с номерами от m2 до m3, где m2=f(Т2·Fд-1); m3=f(Т2·Fд+1).
В последующем используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанного в ЭВМ, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор z для z-го кепстрального массива. Сравнивают величину θпор z с каждым значением соответствующего z-го кепстрального массива. При превышении порога θпор z значениями кепстра в массиве V1z и отсутствии превышения порога θпор z в массиве V2z или при превышении порога θпор z значениями кепстра в массиве V2z и отсутствии превышения порога θпор z в массиве V1z принимают решение о наличии в z-м интервале Δz ровно двух импульсов. Затем формируют G новых рабочих массивов данных из генерального массива данных D.
Номер кепстрального массива, которому соответствует наличие двух импульсов в соответствующем z-м интервале Δz, фиксируют как начальный Zнач, а соответствующий z-й интервал Δz принимают за начальный Δz нач. Рабочие массивы формируют размерностью N, причем первый элемент первого рабочего массива имеет в массиве D номер Zнач, второй рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+N-1]-го элемента массива D и заканчивая [Zнач+2N-2]-M элементом массива D. Каждый последующий g-й рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+(g-1)(N-1)]-го элемента массива D и заканчивая [Zнач+g(N-1)]-м элементом массива D (эпюра б, фиг.6). Если генеральный массив D содержит 512 элементов, N равно 48, а для шестидесятого интервала Δ60, включающего элементы генерального массива с шестидесятого по 107-й, в результате кепстральной обработки принято решение о наличии ровно двух импульсов, то интервал Δ60 фиксируют как начальный Δ60 нач, а шестидесятый пробный массив принимают за первый рабочий массив. Второй рабочий массив будет включать в себя элементы генерального массива D с [60+47]-го (107-го) по [60+2(47)]-й (154-й). Третий рабочий массив будет включать в себя элементы генерального массива D с [60+2(47)]-го (154-го) по [60+3(47)]-й (201-й). Четвертый рабочий массив будет включать в себя элементы указанного выше генерального массива D с 201-го по 248-й и т.д.
Элементы каждого g-го рабочего массива подвергают последовательно кепстральной обработке. В начале дискретному прямому преобразованию Фурье подвергаются элементы g-го рабочего массива по формуле

где 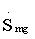 - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для g-го рабочего массива, Sng - значение амплитуды n-го по номеру отсчета, находящегося в g-м рабочем массиве оцифрованного сигнала. После чего для каждого g-го рабочего массива вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для g-го рабочего массива, Sng - значение амплитуды n-го по номеру отсчета, находящегося в g-м рабочем массиве оцифрованного сигнала. После чего для каждого g-го рабочего массива вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
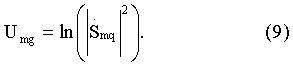
Затем для каждого вектора, составленного из величин Umg g-го интервала Δg вычисляют дискретное обратное преобразование Фурье по формуле

В результате трех описанных операций, для каждого g-го рабочего массива получают соответствующий g-й основной массив, состоящий из элементов  . После этого вычисляют значение модуля для каждого m-го отсчета соответствующего g-го основного массива. В результате получают g-й кепстральный массив, состоящий из элементов
. После этого вычисляют значение модуля для каждого m-го отсчета соответствующего g-го основного массива. В результате получают g-й кепстральный массив, состоящий из элементов 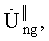 который представляет собой кепстр g-го рабочего массива. Для декодирования информации каждый кепстральный массив разбивают на два массива V1g, V2g. При этом массив V1g g-го кепстрального массива включает в себя значения кепстра от m0 до m1. Массив V2g g-го кепстрального массива включает в себя значения кепстра от m2 до m3
который представляет собой кепстр g-го рабочего массива. Для декодирования информации каждый кепстральный массив разбивают на два массива V1g, V2g. При этом массив V1g g-го кепстрального массива включает в себя значения кепстра от m0 до m1. Массив V2g g-го кепстрального массива включает в себя значения кепстра от m2 до m3
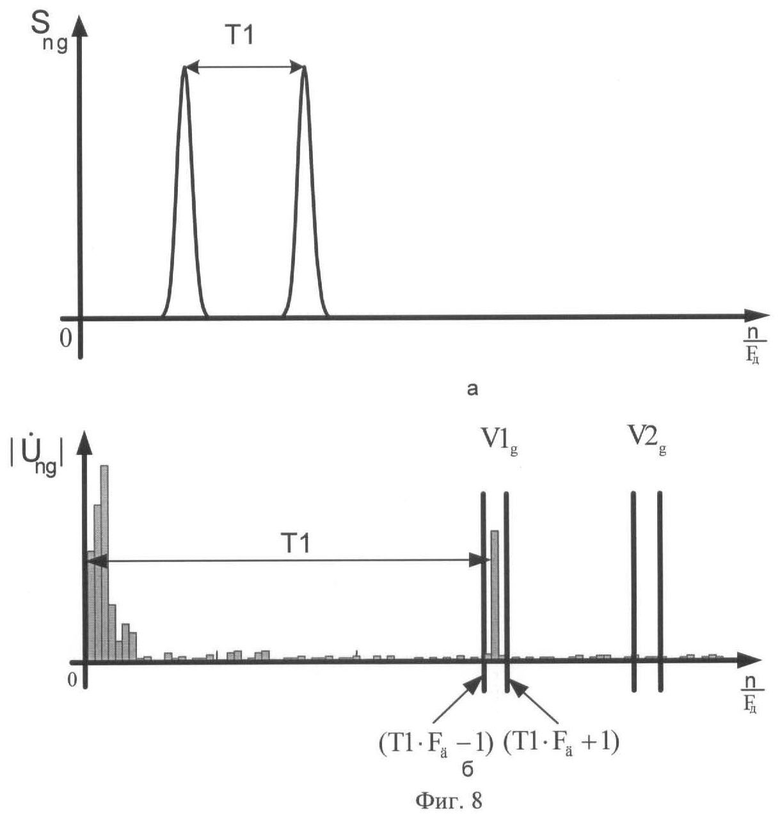
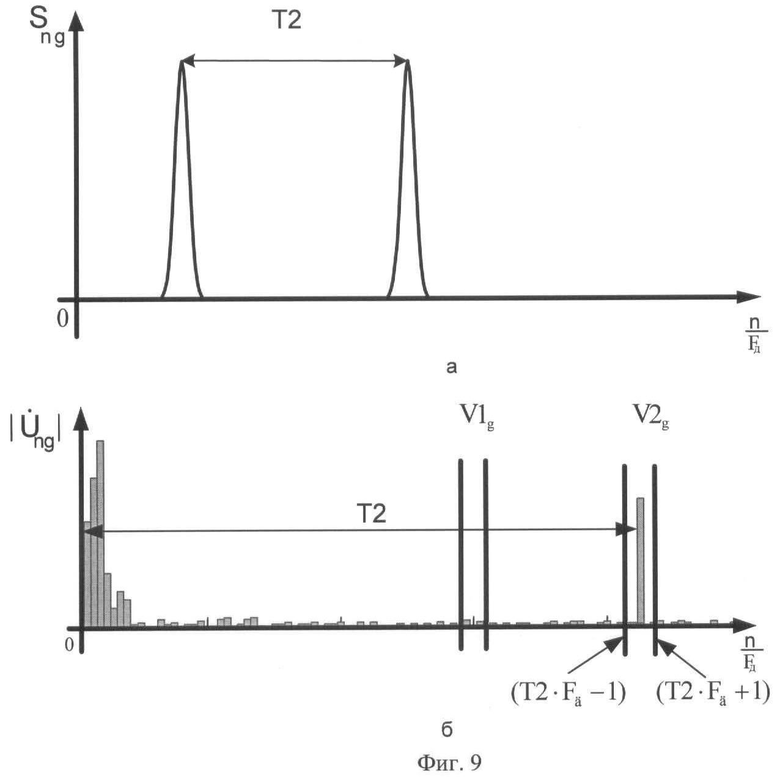
В последующем используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанного в ЭВМ. Умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор g для g-го кепстрального массива. Сравнивают величину θпор g с каждым значением соответствующего g-го кепстрального массива. При превышении порога θпор g значениями кепстра в массиве V1g и отсутствии превышения в массиве V2g принимают решение о наличии в данном g-м интервале Δg закодированной логической единицы (фиг.8). При превышении порога θпор g значениями кепстра в массиве V2g и отсутствии превышения в массиве V1g принимают решение о наличии в данном g-м интервале Δg закодированного логического нуля (фиг.9). После этого принимают решение о том, что выделенная информация из первого кепстрального массива соответствует первому биту информации принятой кодограммы, информация из второго кепстрального массива соответствует второму биту информации принятой кодограммы, а информация из g-го кепстрального массива - g-му биту информации принятой кодограммы. В последующем создают результирующий массив, представляющий собой расшифрованную кодограмму. В его элементы записывают последовательно, начиная с первого кепстрального массива и заканчивая G-м кепстральным массивом, выделенную информацию из каждого g-го кепстрального массива. При отсутствии превышения порога θпор g значениями кепстра в установленных массивах V1g и V2g принимают решение об окончании приема кодограммы, после чего с объекта Y на объект Х посылают запросный сигнал, свидетельствующий о готовности объекта Y к приему следующей кодограммы.
Сущность способа заключается в том, что для выделения информации без синхронизации моментов передачи и приема сообщения предлагается изменить способ кодирования информации, при котором информация будет заключена во взаимном временном положении дополнительно введенного СШП импульса, называемого «центральным», между периодически следующими друг за другом СШП импульсами такой же формы, называемыми «опорными». А выделение информации предлагается производить в ЭВМ, анализируя принимаемое сообщение в цифровом виде. Соответственно, при кодировании информации таким образом вся информация будет заключена во временном положении центрального «импульса» относительно задержанного «опорного» импульса (фиг.1) и будет определяться соответствующими временными задержками Т1, Т2.
Недостатком данного способа выделения информации является:
- низкая помехоустойчивость (невозможность выделения информации при отношении сигнал/шум менее 10 дБ);
- возможность использования только СШП импульсов, имеющих форму, определяемую первой производной гауссовой функции, в сочетании с интегратором и устройством растяжения импульсов;
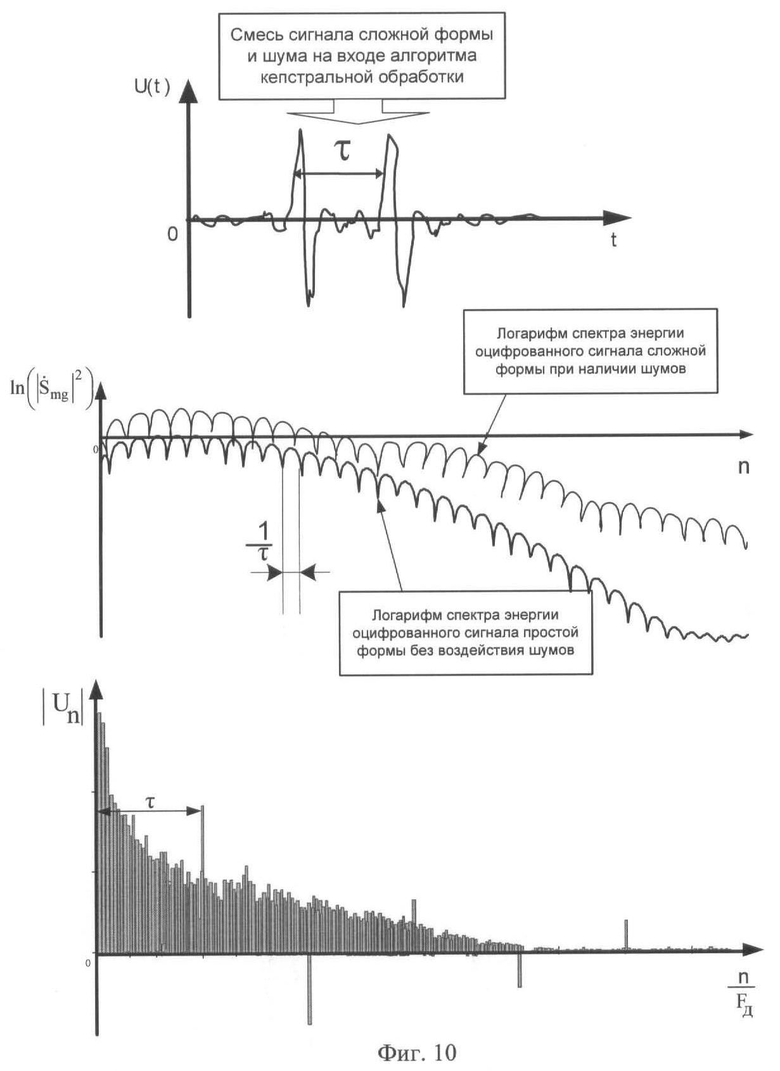
- наличие логарифмической нелинейности в алгоритме кепстральной обработки, что при использовании СШП импульсов сложной формы в шумах различной интенсивности приводит к непредсказуемому изменению огибающей логарифма квадрата модуля амплитуды спектра оцифрованного сигнала (массивы Umz, Umg на фиг.10).
В результате возможны ситуации, когда принятие решения о наличии логического «нуля» или «единицы» может быть ошибочным за счет появления «ложных» кепстральных откликов в массивах, 
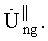
Известен также помехоустойчивый способ выделения закодированной информации, передаваемой потребителю с помощью пачек сверхширокополосных импульсов [3]. Способ заключается в том, что с помощью источника передачи сообщений (объект X) из первой точки пространства излучают в свободное пространство кодовую последовательность пачек сверхширокополосных импульсов (КППСШПИ). Параметры КППСШПИ известны во второй точке пространства на пункте приема сообщений (объект Y). Правило кодирования информации заключается в использовании в качестве основных носителей информации пачек СШП импульсов. При этом длительность каждого импульса в пачке должна составлять не менее двух наносекунд и описываться первой производной гауссовой функции [2]. Эти импульсы имеют следующее аналитическое описание

где А - амплитуда импульса; а - величина, характеризующая половину длительности импульса на уровне 0,707.
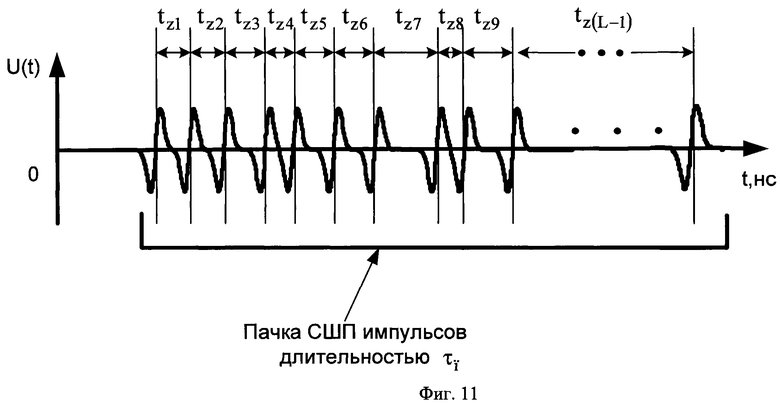
Каждая пачка СШП импульсов будет включать в себя L импульсов, при этом величина L может принимать значения от 10 до 100. Расположение импульсов внутри каждой пачки одинаково. При этом сами импульсы в пачке предполагается располагать друг относительно друга на различных временных задержках t, а величина каждой задержки должна быть не меньше половины длительности импульса τи и не больше длительности пачки (фиг.11). Длительность пачки определяется выражением

где i - порядковый номер задержки между импульсами в пачке; ti - задержка i-го импульса относительно (i-1)-го.
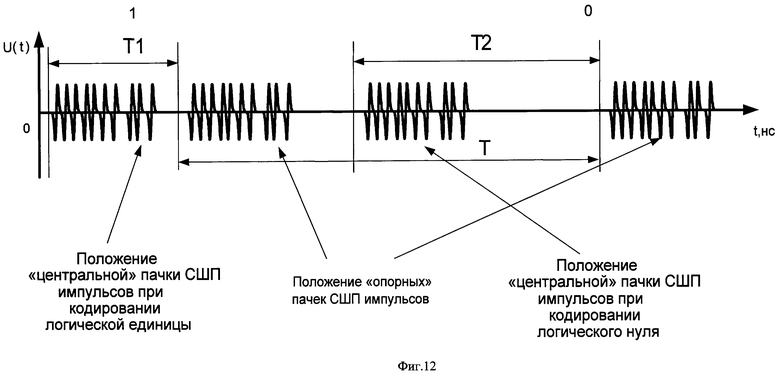
Для кодирования предлагается использовать периодическую последовательность пачек СШП импульсов, состоящую из расположенных в определенном порядке «опорных» и «центральных» пачек. Опорные пачки отличаются от «центральных» тем, что их период следования Т≥4·τп постоянен, а период следования «центральных» пачек может изменяться. Вся информация о кодировании будет заключаться во временном положении «центральной» пачки СШП импульсов относительно «опорной». При временном положении «центральной» пачки с опережением «опорной» на 0,2Т результат кодирования соответствует логической «единице», а при положении «центральной» пачки с опережением «опорной» на 0,4Т результат кодирования соответствует логическому «нулю» (фиг.12).
Таким образом, всю информацию о кодировании логического «нуля» или «единицы» предлагается заключить в задержках Т1 и Т2 между пачками СШП импульсов, при этом Т1=0,2Т, а Т2=0,4Т.
В результате каждый бит информации кодируется одной «опорной» и одной «центральной» пачкой СШП импульсов. При этом набор нескольких бит информации будет представлять собой некоторое сообщение, именуемое кодограммой (фиг.13), которое излучается в пространство из первой точки объектом Х и принимается во второй точке пространства объектом Y.
После приема кодограммы объектом Y и усиления КППСШПИ ее предлагается оцифровать при помощи АЦП с частотой дискретизации не менее 2 ГГц. К примеру, возможно использование такого АЦП, как ADS10×2G/1, с частотой дискретизации 2000 МГц.
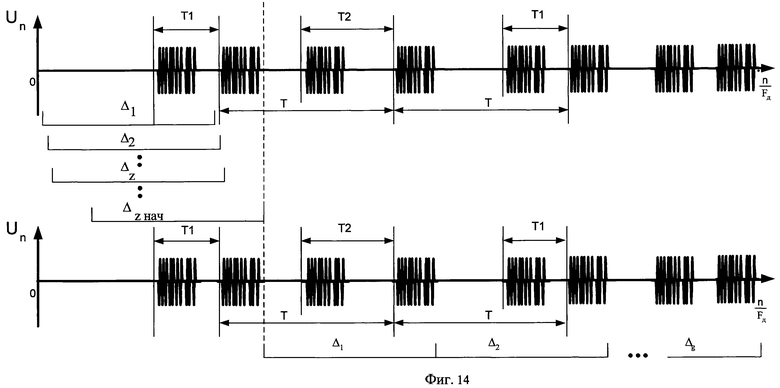
Получившийся в результате набор данных, описывающий оцифрованный сигнал, поступает в ЭВМ, где по мере поступления данных с АЦП осуществляют формирование генерального массива данных D, из элементов которого формируют Z пробных массивов  . Каждый вновь сформированный пробный z-й массив записывается в память ЭВМ и включает в себя значения оцифрованной последовательности пачек сверхширокополосных импульсов, ограниченной временным интервалом длительностью Δ. Причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т (эпюра а, фиг.14).
. Каждый вновь сформированный пробный z-й массив записывается в память ЭВМ и включает в себя значения оцифрованной последовательности пачек сверхширокополосных импульсов, ограниченной временным интервалом длительностью Δ. Причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т (эпюра а, фиг.14).
В результате каждый z-й пробный массив включает по N отсчетов, извлекаемых из генерального массива D, начиная с z-го элемента массива D и заканчивая (z+N-1)-м элементом массива D, причем число элементов N в пробном массиве определяется по формуле

где Fд - частота дискретизации АЦП.
Таким образом, первый пробный массив формируют из элементов массива D с номерами с 1-го по N-й, второй пробный массив формируют из элементов массива D с номерами со 2-го по (N+1)-й, третий пробный массив формируют из элементов массива D с номерами с 3-го по (N+2)-й, a Z-й пробный массив формируют из элементов массива D с номерами с Z-го по (Z+N-1)-й (эпюра а, фиг.14). К примеру, если генеральный массив D содержит 128 элементов, а N равно 48, тогда первый пробный массив будет включать в себя элементы генерального массива D с первого по 48-й, второй пробный массив будет включать в себя элементы генерального массива D со второго по 49-й, третий пробный массив будет включать в себя элементы генерального массива D с третьего по 50-й и т.д.
Правило накопления импульсов заключается в следующем: от каждого z-го пробного массива создается (L-1) копий: Uz1n, Uz2n…Uz(L-1)n. Каждая копия представляет собой массив данных величиной N и записывается в память ЭВМ. После этого каждый элемент первой копии z-го пробного массива, начиная с первого элемента, сдвигают на величину (Nz1+τи·Fд), где Nz1=t1·Fд, a элементы с 1-го по [Nz1+τи·Fд-1)-й и с [(Nz1+τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. Каждый элемент второй копии z-го пробного массива, начиная с первого элемента, сдвигают на величину [Nz1+Nz2+2·τи·Fд], где Nz2=t2·Fд, а элементы с 1-го по [Nz1+Nz2+2·τи·Fд-1]-й и с [(Nz1+Nz2+2·τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. Каждый элемент (L-1) копии z-го пробного массива, начиная с первого элемента, сдвигают на величину [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд], а элементы с 1-го по [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд-1]-й и с [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. После этого исходный пробный z-й массив увеличивают на [(τп-τи)·Fд] элементов. При этом элементы с [N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. В результате будет получено всего L массивов, каждый из которых включает в себя N+(τп-τи)·Fд элементов. Полученные массивы одинаковой размерностью складывают друг с другом и получают суммарный z-й пробный массив Uzsn. На фиг.15 схематично изображен процесс накопления сверхширокополосных импульсов. При этом а обозначает временную задержку t(L-1); б - временную задержку t8; в - временную задержку t7; г - временную задержку t6; д - временную задержку t5; е - временную задержку t4; ж - временную задержку t3; з - временную задержку t2; и - временную задержку t1.
От полученного суммарного z-го пробного массива Uzsn длительностью N+(τп-τи)·Fд создаются две копии Uzs1n, Uzs2n.
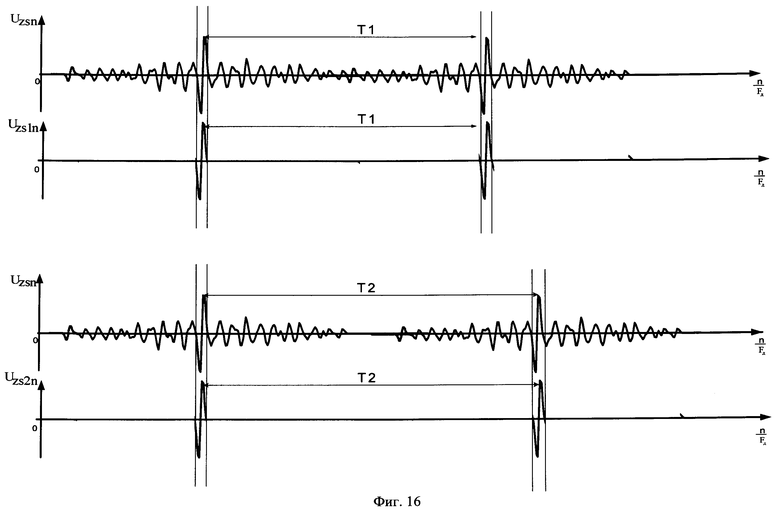
В массиве Uzs1n обнуляются все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τп·Fд)]-го по [N-(Т1)·Fд]-й, с [N-(Т1-τи)·Fд]-го по 1-й. В массиве Ugs2n обнуляются все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т2)·Fд]-й, с [N-(Т2-τи)·Fд]-го по 1-й. Полученные обнуленные массивы данных Uzs1n, Uzs2n (фиг.16) подвергают кепстральной обработке [4] по схеме, представленной на фиг.7. Вначале элементы каждого обнуленного массива подвергаются дискретному прямому преобразованию Фурье [5] с использованием формулы
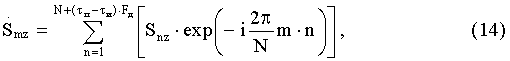
где n - номер отсчета во временной области, m - номер отсчета в частотной области;  - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го обнуленного пробного массива Uzs1n или Uzs2n, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном пробном массиве Uzs1n или Uzs2n.
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го обнуленного пробного массива Uzs1n или Uzs2n, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном пробном массиве Uzs1n или Uzs2n.
В последующем для каждого z-го обнуленного пробного массива Uzs1n и Uzs2n вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
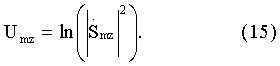
Затем для каждого вектора, составленного из величин Umz z-го интервала Δz, вычисляют дискретное обратное преобразование Фурье [5] по формуле
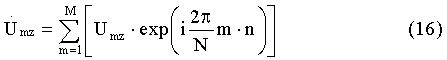
где М - число элементов в векторе Umz, количественно равное N+(τп-τи)·Fд.
В результате трех описанных операций (14), (15), (16) для каждого z-го обнуленного пробного массива Uzs1n и Uzs2n получают соответствующий z-й основной массив 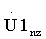 и
и  .
.
После этого вычисляют значение модуля для каждого n-го элемента массивов  и
и 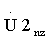 , соответствующих z-м обнуленным пробным массивам Uzs1n и Uzs2n. В результате получают два z-x кепстральных массива
, соответствующих z-м обнуленным пробным массивам Uzs1n и Uzs2n. В результате получают два z-x кепстральных массива  и
и 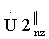 , каждый из которых представляет собой кепстр z-го обнуленного пробного массива. Для декодирования информации в кепстральном массиве
, каждый из которых представляет собой кепстр z-го обнуленного пробного массива. Для декодирования информации в кепстральном массиве  выделяют массив V1z, в кепстральном массиве
выделяют массив V1z, в кепстральном массиве 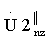 выделяют массив V2z. При этом массив V1z включает в себя значения кепстра
выделяют массив V2z. При этом массив V1z включает в себя значения кепстра 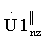 с номерами от m0 до m1, где m0=f(T1·Fд-1); m1=f(T1·Fд+1); f(*)- функция округления в сторону меньшего целого числа. Массив V2z включает в себя значения кепстра
с номерами от m0 до m1, где m0=f(T1·Fд-1); m1=f(T1·Fд+1); f(*)- функция округления в сторону меньшего целого числа. Массив V2z включает в себя значения кепстра 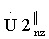 с номерами от m2 до m3, где m2=f(T2·Fд-1); m3=f(Т2·Fд+1).
с номерами от m2 до m3, где m2=f(T2·Fд-1); m3=f(Т2·Fд+1).
В последующем используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанного в ЭВМ, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор z для соответствующего обнуленного z-го кепстрального массива.
Сравнивают величину θпор z с каждым значением соответствующего обнуленного z-го кепстрального массива. При превышении порога θпор z значениями кепстра в массиве V1z и отсутствии превышения порога θпор z в массиве V2z или при превышении порога θпор z значениями кепстра в массиве V2z и отсутствии превышения порога θпор z в массиве V1z принимают решение о наличии в z-м интервале Δz ровно двух импульсов. Затем формируют G новых рабочих массивов данных из генерального массива данных D.
Номер кепстрального обнуленного массива, которому соответствует наличие двух импульсов в соответствующем z-м интервале Δz, фиксируют как начальный Zнач, а соответствующий z-й интервал Δz принимают за начальный Δz нач. Рабочие массивы формируют размерностью N, причем первый элемент первого рабочего массива имеет в массиве D номер Zнач, второй рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+N-1]-го элемента массива D и заканчивая [Zнач+2N-2]-м элементом массива D. Каждый последующий g-й рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+(g-1)(N-1)]-го элемента массива D и заканчивая [Zнач+g(N-1)]-м элементом массива D (эпюра б, фиг.14). Если генеральный массив D содержит 512 элементов, N равно 48, а для шестидесятого интервала Δ60, включающего элементы генерального массива с шестидесятого по 107-й, в результате кепстральной обработки принято решение о наличии ровно двух импульсов, то интервал Δ60 фиксируют как начальный A60 нач, а шестидесятый пробный массив принимают за первый рабочий массив. Второй рабочий массив будет включать в себя элементы генерального массива D с [60+47]-го (107-го) по [60+2(47)]-й (154-й). Третий рабочий массив будет включать в себя элементы генерального массива D с [60+2(47)]-го (154-го) по [60+3(47)]-й (201-й). Четвертый рабочий массив будет включать в себя элементы генерального массива D с 201-го по 248-й и т.д.
От каждого g-го рабочего массива создается (L-1) копий, Ug1n, Ug2n…Ug(L-1)n, значения каждой копии записываются в память ЭВМ. Каждая копия представляет собой массив данных величиной N и записывается в память ЭВМ.
После этого каждый элемент первой копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину (Ng1+τи·Fд), где Ng1=t1·Fд, а элементы с 1-го по [Ng1+τи·Fд-1]-й и с [(Ng1+τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. Каждый элемент второй копии z-го пробного массива, начиная с первого элемента, сдвигают на величину [Ng1+Ng2+2·τи·Fд], где Ng2=t2·Fд, а элементы с 1-го по [Ng1+Ng2+2·τи·Fд-1]-й и с [(Ng1+Ng2+2·τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. Каждый элемент (L-1) копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину [(Ng1+Ng2+…+Ng(L-1))+(L-1)·τи·Fд], а элементы с 1-го по [(Ng1+Ng2+…+Ng(L-1))+(L-1)·τи·Fд-1]-й и с [(Ng1+Ng2+…+Ng(L-1))+(L-1)·τи·Fд+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. После этого исходный рабочий g-й массив увеличивают на [τп-τи)·Fд] элементов. При этом элементы с [N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями. В результате будет получено всего L массивов, каждый из которых включает в себя N+(τп-τи)·Fд элементов. Полученные массивы одинаковой размерности складывают друг с другом и получают суммарный g-й рабочий массив. В массиве Ugs1n обнуляются все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(T1)·Fд]-й, с [N-(Т1-τи)·Fд]-го по 1-й. В массиве Ugs2n обнуляются все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т2)·Fд]-й, с [N-(Т2-τи)·Fд]-го по 1-й. Полученные обнуленные массивы данных Uqs1n, Ugs2n (фиг.6) подвергают кепстральной обработке. Вначале дискретному прямому преобразованию Фурье подвергаются элементы g-го рабочего массива по формуле
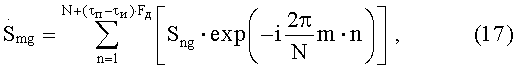
где 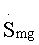 - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для g-го рабочего массива, Sng - значение амплитуды n-го по номеру отсчета, находящегося в g-м, обнуленном рабочем массиве оцифрованного сигнала. После этого для каждого g-го обнуленного рабочего массива вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для g-го рабочего массива, Sng - значение амплитуды n-го по номеру отсчета, находящегося в g-м, обнуленном рабочем массиве оцифрованного сигнала. После этого для каждого g-го обнуленного рабочего массива вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
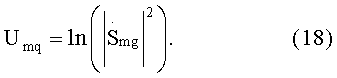
Затем для каждого вектора, составленного из величин Umg g-го интервала Δg, вычисляют дискретное обратное преобразование Фурье по формуле
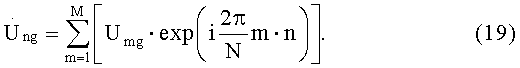
В результате трех описанных операций, для каждого g-го обнуленного рабочего массива Ugs1n, Ugs2n получают соответствующий g-й основной массив, состоящий из элементов  и
и  После этого вычисляют значение модуля для каждого m-го отсчета соответствующего g-го обнуленного основного массива. В результате получают два g-x кепстральных массива
После этого вычисляют значение модуля для каждого m-го отсчета соответствующего g-го обнуленного основного массива. В результате получают два g-x кепстральных массива  и
и 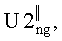 состоящих из модулей элементов основных массивов
состоящих из модулей элементов основных массивов 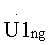 и
и 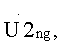 каждый из которых представляет собой кепстр g-го обнуленного рабочего массива. Для декодирования информации в каждом кепстральном массиве выделяют массив V1g или V2g. При этом массив V1g g-го обнуленного кепстрального массива включает в себя значения кепстра
каждый из которых представляет собой кепстр g-го обнуленного рабочего массива. Для декодирования информации в каждом кепстральном массиве выделяют массив V1g или V2g. При этом массив V1g g-го обнуленного кепстрального массива включает в себя значения кепстра 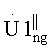 от m0 до m1. Массив V2g g-го обнуленного кепстрального массива включает в себя значения кепстра
от m0 до m1. Массив V2g g-го обнуленного кепстрального массива включает в себя значения кепстра  от m2 до m3.
от m2 до m3.
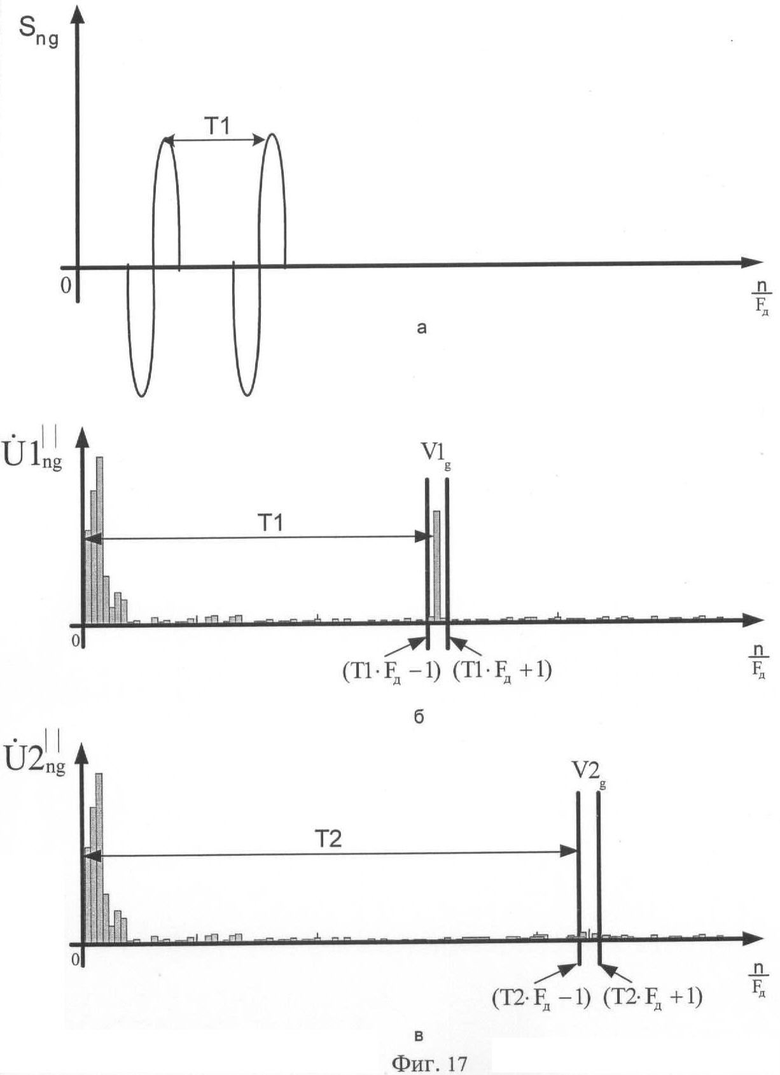
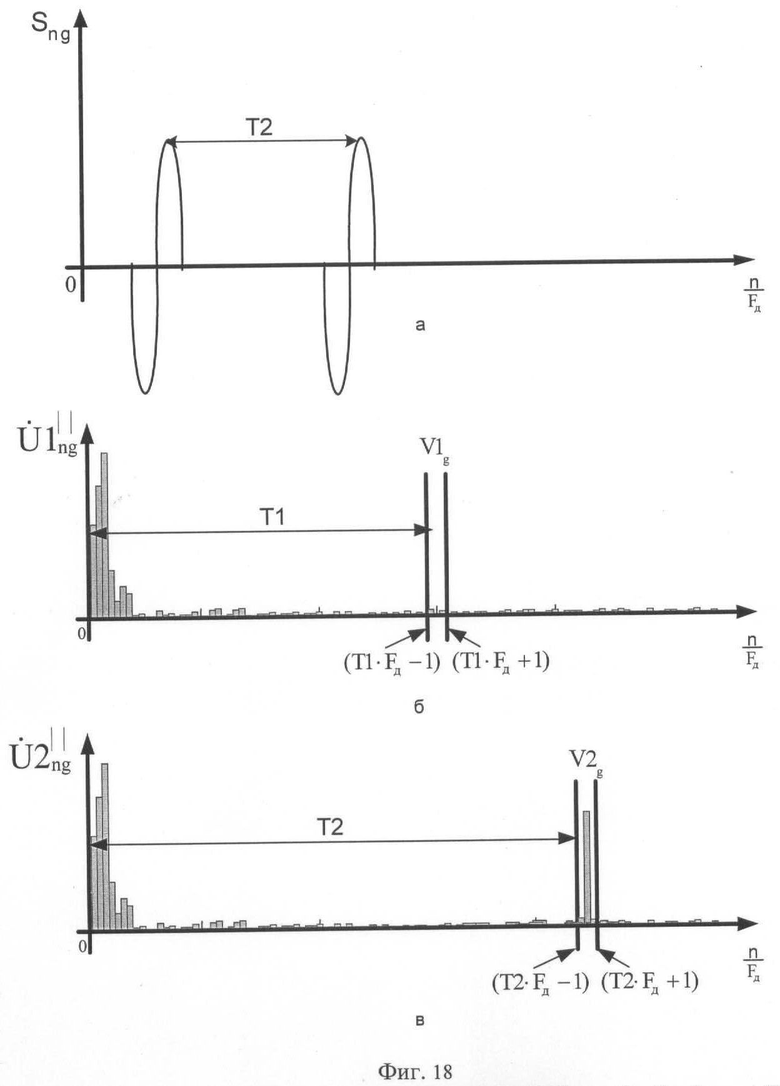
В последующем используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанное в ЭВМ. Умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор g для каждого g-го обнуленного кепстрального массива. Сравнивают величину θпор g с каждым значением соответствующего обнуленного g-го кепстрального массива. При превышении порога θпор g значениями кепстра в массиве V1g и отсутствии превышения в массиве V2g принимают решение о наличии в данном g-м интервале Δg закодированной логической единицы (фиг.17). При превышении порога θпор g значениями кепстра в массиве V2g и отсутствии превышения в массиве V1g принимают решение о наличии в данном g-м интервале Δg закодированного логического нуля (фиг.18).
Считают, что выделенная информация из первого кепстрального массива соответствует первому биту информации принятой кодограммы, информация из второго кепстрального массива соответствует второму биту информации принятой кодограммы, а информация из g-го кепстрального массива - g-му биту информации принятой кодограммы. В последующем создают результирующий массив, представляющий собой расшифрованную кодограмму. В его элементы записывают последовательно, начиная с первого кепстрального массива и заканчивая G-м кепстральным массивом, выделенную информацию из каждого g-го кепстрального массива. При отсутствии превышения порога θпор g значениями кепстра в установленных массивах V1g и V2g принимают решение об окончании приема кодограммы, после чего с объекта Y на объект Х посылают запросный сигнал, свидетельствующий о готовности объекта Y к приему следующей кодограммы.
Сущность способа, а именно сущность процесса выделения информации, позволяющая исключить режим синхронизации из общего процесса передачи и приема информации, заключается в том, что для выделения информации без синхронизации моментов передачи и приема сообщения предлагается изменить способ кодирования информации, при котором информация будет заключена во взаимном временном положении дополнительно введенной пачки СШП импульсов, называемой «центральной», между периодически следующими друг за другом пачками СШП импульсов такой же формы, называемыми «опорными». А выделение информации предлагается производить в ЭВМ, анализируя принимаемое сообщение в цифровом виде. Соответственно, при кодировании информации таким образом вся информация будет заключена во временном положении центральной пачки относительно задержанной «опорной» пачки (фиг.11) и будет определяться соответствующими временными задержками Т1, Т2. Данный способ поддерживает свою работоспособность при отношении сигнал/шум 2 дБ.
Недостатком данного способа выделения информации является:
- отсутствие учета логарифмической нелинейности в алгоритме кепстральной обработки при использовании СШП импульсов сложной формы, что в сочетании с шумами различной интенсивности приводит к непредсказуемому изменению огибающей логарифма квадрата модуля амплитуды спектра оцифрованного сигнала (массивы Umz, Umg на фиг.10). В результате возможны ситуации, когда принятие решения о наличии логического «нуля» или «единицы» может оказаться ошибочным за счет появления «ложных» кепстральных откликов в массивах  ,
,  ,
, 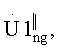
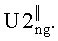
Задачей изобретения является:
- обеспечение достоверного выделения информации в виде логических «нулей» и «единиц» при передаче сообщений с помощью СШП импульсов в режиме, не требующем их синхронизации и при отношении сигнал/шум не меньше 2 дБ;
- обеспечение возможности использования СШП импульсов произвольной формы в КППСШПИ за счет снижения влияния логарифмической нелинейности в алгоритме кепстральной обработки.
Под источником передачи сообщений подразумевается первый приемопередатчик, называемый в дальнейшем объектом X. Под пунктом приема сообщений подразумевается второй приемопередатчик, называемый в дальнейшем объектом Y.
Для решения поставленной задачи предлагается применить способ выделения информации [3], при котором синхронизирующий сигнал и сама синхронизация становятся излишними, а влияние логарифмической нелинейности на результат работы алгоритма кепстральной обработки снижается за счет совместного использования процедуры вейвлет-преобразования.
Операции, выражающие существо предлагаемого способа выделения информации, по аналогии со способом [3] могут быть описаны следующей совокупностью последовательных действий:
1) кодирование информации при помощи пачек СШП импульсов, любым аналитическим выражением обеспечивающим их излучение в свободное пространство, по специальному правилу для получения кодограммы;
2) излучение кодограммы из первой точки пространства объектом X;
3) прием во второй точке пространства кодограммы объектом Y;
4) усиление каждого из импульсов принятой кодограммы;
5) оцифровка аналого-цифровым преобразователем каждого импульса кодограммы;
6) передача информации с АЦП в ЭВМ;
7) разделение при помощи ЭВМ принятой цифровой информации на массивы данных, каждый из которых соответствует временному интервалу Δ, включающему две смежные оцифрованные пачки импульсов одинаковой формы, причем смежные интервалы Δ не пересекаются;
8) накопление СШП импульсов по мощности, заключающееся в создании (L-1) копии массива данных и их последовательном сложении с исходным массивом по специальному правилу;
9) проверка общего числа элементов в массиве, полученного после накопления СШП импульсов по мощности (пункт 8), на кратность двум, при невыполнении проверки дополнение нулевыми отсчетами до величины, кратной двум (данное условие необходимо для получения двух одинаковых по числу наборов коэффициентов детализации и аппроксимации);
10) выделение информации на основе вейвлет-кепстральной обработки из каждого временного интервала Δ (вейвлеты могут быть использованы произвольной формы, однако должны быть идентичны друг другу при прямом и обратном вейвлет-преобразованиях);
11) составление из совокупности выделенных логических нулей и единиц цифровой последовательности, которую используют в качестве выделенной информации;
12) передача объектом Y объекту Х запросного сигнала, свидетельствующего о готовности объекта Y к приему следующей кодограммы. Последняя операция востребована тем, что передача каждой из кодограмм, состоящих из логических «нулей» и «единиц», будет вестись с периодом, равным длительности кодограммы. Передачу предполагается вести до тех пор, пока от объекта Y не поступит запросный сигнал, известный объекту X, сигнализирующий об установлении факта приема всей совокупности кодограмм.
В предлагаемом способе обработку принимаемого сигнала по аналогии со способом [3] предложено оставить неизменной до процедуры получения обнуленных массивов данных Uzs1n, Uzs2n включительно. После чего предложено проверять кратность двум общего числа элементов каждого обнуленного массива Uzs1n, Uzs2n, используя при этом равенство
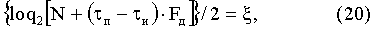
где ξ - целое число, полученное при выполнении равенства. В случае невыполнения равенства предложено считать общее число элементов в массиве Uzs1n, Uzs2n, не кратным двум, и увеличивать последовательно каждый обнуленный массив Uzs1n, Uzs2n нулевыми элементами. Для этого необходимо прибавлять по одному нулевому элементу к концу массива Uzs1n и Uzs2n до выполнения следующего равенства
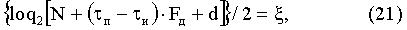
где d - общее число нулевых элементов, прибавленное к массивам Uzs1n, Uzs2n в момент выполнения равенства.
После выполнения этого равенства будут получены обнуленные дополненные массивы Uzs1n, Uzs2n, в которых общее число элементов кратно двум. Полученные массивы Uzs1n, Uzs2n c числом элементов, кратным двум, в последующем предложено подвергнуть вейвлет-кепстральной обработке по схеме, указанной на фиг.19. По данной схеме последовательно для каждого элемента обнуленного дополненного массива Uzs1n или Uzs2n предложено вычислить дискретное прямое преобразование Фурье с использованием формулы
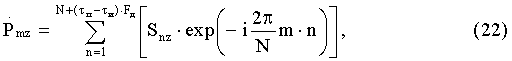
где n - номер отсчета во временной области, m - номер отсчета в частотной области; 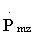 - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го массива Uzs1n или Uzs2n, число элементов в котором кратно двум, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном массиве Uzs1n или Uzs2n, число элементов в котором кратно двум. После этого необходимо найти значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го массива Uzs1n или Uzs2n, число элементов в котором кратно двум, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном массиве Uzs1n или Uzs2n, число элементов в котором кратно двум. После этого необходимо найти значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
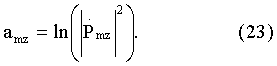
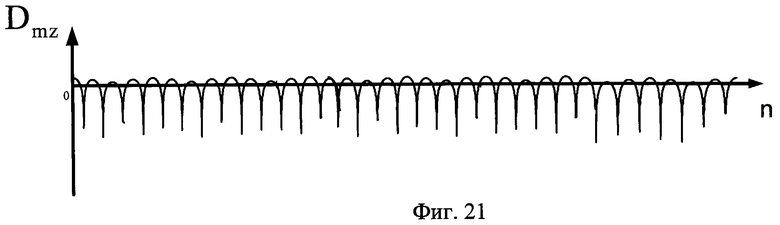
Затем для каждого вектора Аmz (фиг.20), составленного из элементов аmz z-го интервала Δz, последовательно вычисляют дискретное прямое вейвлет-преобразование по формуле
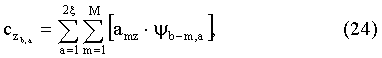
где Ψb-m,a - известный тип вейвлета [5], b - число, характеризующее сдвиги вейвлета и изменяющееся от 1 до М с шагом 1, а - число, характеризующее сжатие вейвлета и изменяющееся от 2ξ до 1, М - число элементов в векторе Amz, количественно равное N+(τп-τи)·Fд+d. После этого в полученной матрице Сz размером b×а, состоящей из коэффициентов  необходимо удалить столбцы с 1 по ξ, а затем от матрицы Сz размером b×а/2 вычислить обратное вейвлет-преобразование по формуле
необходимо удалить столбцы с 1 по ξ, а затем от матрицы Сz размером b×а/2 вычислить обратное вейвлет-преобразование по формуле

В последующем для каждого вектора, составленного из величин Dmz z-го интервала Δz, необходимо вычислить дискретное обратное преобразование Фурье по формуле
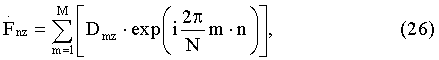
где М - число элементов в векторе Dmz, количественно равное N+(τп-τи)·Fд+d. Стандартную процедуру обработки полученного массива 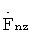 необходимо оставить аналогичной способу [3] для массива
необходимо оставить аналогичной способу [3] для массива 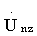 до получения обнуленных массивов данных Ugs1n, Ugs2n включительно. После этого массивы данных Ugs1n, Ugs2n подвергаются такой же обработке, как и обнуленные массивы Uzs1n, Uzs2n в предлагаемом способе, до получения массива
до получения обнуленных массивов данных Ugs1n, Ugs2n включительно. После этого массивы данных Ugs1n, Ugs2n подвергаются такой же обработке, как и обнуленные массивы Uzs1n, Uzs2n в предлагаемом способе, до получения массива 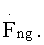 Процедуру обработки полученного массива
Процедуру обработки полученного массива 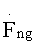 необходимо оставить такой же, как в способе [3] для массива
необходимо оставить такой же, как в способе [3] для массива 
Сущность способа, а именно сущность процесса подавления влияния логарифмической нелинейности на результат работы алгоритма кепстральной обработки заключается в использовании свойства алгоритма вейвлет-преобразования, основанного на том, что при разложении любого дискретного сигнала будет всегда получено два одинаковых набора коэффициентов. Причем первый набор отличается от второго тем, что несет в себе информацию о высокочастотной составляющей сигнала, а второй - о низкочастотной. Применительно к алгоритму кепстральной обработки выявлено, что сложность формы сигнала и наличие шумов различной интенсивности приводят к случайным изменениям низкочастотной части логарифма спектра энергии принимаемого сигнала, из-за чего достоверность выделения логического «нуля» и «единицы» резко понижается. В результате этого обратное вейвлет-восстановление сигнала без коэффициентов, несущих информацию о низкочастотных изменениях логарифма спектра энергии исходного сигнала, позволит повысить достоверность выделения логического «нуля» и «единицы».
Из описания способа следует, что в предлагаемом варианте нет необходимости оценивать временное положение каждого импульса относительно момента времени, заданного системой синхронизации приемника. В результате этого определение момента времени начала выделения информации из последовательности принимаемых пачек СШП импульсов осуществляется на основе поиска наличия во временном интервале Δ заданной длительности двух первых пачек СШП импульсов принимаемой кодограммы. Появляется возможность использования сигналов произвольной формы, повышая скрытность и конфиденциальность передаваемого сообщения.
Предложенный способ легко реализуем и не требует синхронизации моментов передачи и приема сообщения, а также сохраняет свою работоспособность при отношении сигнал/шум не менее 2 дБ. Положительный технический эффект изобретения заключается в том, что отсутствует необходимость использования дополнительного гармонического сигнала для синхронизации моментов передачи и приема сообщения. Значит, постановка помехи в области частот гармонического сигнала не влияет на совместную работу источника и приемника сообщений. Отсутствует система синхронизации, а следовательно, отсутствует необходимость использования дорогостоящих генераторов с высокой стабильностью частоты, усложняющих построение приемопередатчиков. Использование нового алгоритма вейвлет-кепстральной обработки позволяет использовать, для передачи сообщений, сигналы любой формы.
Источники информации
1. Заявка на изобретение №2010109172 от 11.03.2010. Жбанов И.Л., Силаев Н.В., Митрофанов Д.Г., Жбанова В.Л., Сеньков М.А., Васильченко О.В., Степанова Л.В., Ткаченко В.П. Асинхронно-кепстральный способ выделения закодированной информации, передаваемой потребителю с помощью сверхширокополосных импульсов. Бюллетень изобретений №10 от 10.04.2011 (аналог).
2. Иммореев И.Я. Сверхширокополосные радары: новые возможности, необычные проблемы, системные особенности. М.: Вестник МГТУ, 1998, №4, с.25-56.
3. Патент РФ №2422991 от 27.06.2011. Жбанов И.Л., Силаев Н.В., Митрофанов Д.Г., Сеньков М.А., Степанова Л.В., Ткаченко В.П., Иванушкин С.В., Тулузаков В.Г., Мартыненко Г.В. Заявка №2010117472 от 30.04.2010. Помехоустойчивый способ выделения закодированной информации, передаваемой потребителю с помощью пачек сверхширокополосных импульсов. БИ №18. 2011 г. (прототип).
4. Гоноровский И.С. Радиотехнические цепи и сигналы. Издание четвертое: Учебник для вузов. М.: Радио и связь, 1986, с.477.
5. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB: Издание третье. М.: Прикладная математика, 2008, с.39.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПОМЕХОУСТОЙЧИВЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ ПАЧЕК СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2010 |
|
RU2422991C1 |
| АСИНХРОННО-КЕПСТРАЛЬНЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2010 |
|
RU2427075C2 |
| АСИНХРОННЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2009 |
|
RU2416162C2 |
| Способ мультипараметрического кодирования информации, передаваемой с помощью сверхширокополосных импульсов | 2020 |
|
RU2733628C1 |
| Способ формирования дальностного портрета, получаемого на основе использования сигналов с перестройкой частоты, от импульса к импульсу, за счет построения характеристики изменения радиальной скорости воздушного объекта | 2023 |
|
RU2815730C1 |
| СПОСОБ ОДНОЗНАЧНОГО ИЗМЕРЕНИЯ РАДИАЛЬНОЙ СКОРОСТИ ЦЕЛИ В КОГЕРЕНТНО-ИМПУЛЬСНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2014 |
|
RU2574079C1 |
| Способ формирования дальностного портрета повышенной информативности на основе использования сигналов с перестройкой частоты от импульса к импульсу | 2023 |
|
RU2808449C1 |
| Способ адаптивного обеспечения высокой разрешающей способности радиолокатора по дальности за счет оценивания информационного диапазона параметра регуляризации инверсного фильтра | 2021 |
|
RU2785383C1 |
| Способ обеспечения высокой разрешающей способности радиолокатора по дальности за счет выбора оптимального параметра регуляризации инверсного фильтра | 2021 |
|
RU2756291C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАДИАЛЬНОЙ СКОРОСТИ ВОЗДУШНОЙ ЦЕЛИ В РЕЖИМЕ ПЕРЕСТРОЙКИ НЕСУЩЕЙ ЧАСТОТЫ ОТ ИМПУЛЬСА К ИМПУЛЬСУ ПО СЛУЧАЙНОМУ ЗАКОНУ ПРИ ПОНИЖЕННОМ ОТНОШЕНИИ СИГНАЛ-ШУМ | 2008 |
|
RU2389039C1 |







Изобретение относится к теории информации и предназначено для выделения последовательностей логических нулей либо единиц в процессе декодирования информации из последовательности сверхширокополосных импульсов без синхронизации приемника и передатчика. Предложен асинхронный вейвлет-кепстральный способ выделения закодированной информации, передаваемой потребителю с помощью пачек сверхширокополосных импульсов. Задачей изобретения является: а) обеспечение достоверного выделения информации в виде логических «нулей» и «единиц» при передаче сообщений с помощью сверхширокополосных импульсов в режиме, не требующем их синхронизации, при отношении сигнал/шум не меньше 2 дБ; б) обеспечение возможности использования сверхширокополосных импульсов произвольной формы в кодовой последовательности пачек сверхширокополосных импульсов за счет снижения влияния логарифмической нелинейности в алгоритме кепстральной обработки. Технический результат - повышение достоверности выделения принятой информации путем обратного вейвлет-восстановления сигнала без коэффициентов, несущих информацию о низкочастотных изменениях логарифма спектра энергии принимаемого сигнала. 21 ил.
Асинхронный вейвлет-кепстральный способ выделения закодированной информации, передаваемой потребителю с помощью пачек сверхширокополосных импульсов, заключающийся в том, что с помощью источника передачи сообщений, называемого объектом X, из первой точки пространства приемопередатчиком излучают в свободное пространство последовательность сверхширокополосных импульсов, на пункте приема сообщений, называемом объектом Y, расположенном во второй точке пространства, осуществляют прием и усиление передаваемых сверхширокополосных импульсов, для кодирования каждого бита информации используют по две пачки сверхширокополосных импульсов, причем длительность каждого импульса в пачке не меньше 2 нс, а форма каждого из импульсов описывается выражением
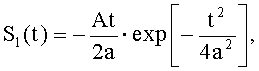
где А - амплитуда импульса; а - величина, характеризующая половину длительности импульса на уровне 0,707; t - текущее время, в каждую пачку сверхширокополосных импульсов включают L импульсов, при этом величина L составляет от 4 до 100 импульсов, импульсы внутри каждой пачки имеют одинаковое расположение, а сами импульсы в пачке располагают друг относительно друга на различных временных задержках t, каждая из которых не меньше половины длительности импульса τи и не больше длительности пачки импульсов, длительность каждой пачки сверхширокополосных импульсов определяют по формуле
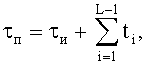
где i - порядковый номер задержки между импульсами в пачке; ti - i-я задержка между импульсами в пачке, одна пачка сверхширокополосных импульсов из двух, используемых для передачи одного бита информации, называемая опорной, повторяется с периодом следования Т, где Т≥4·τп, и составляет порядка десятков наносекунд, а вторую пачку сверхширокополосных импульсов, называемую центральной, располагают между опорными пачками сверхширокополосных импульсов, при этом центральную пачку импульсов при кодировании логического нуля располагают на временной оси с опережением опорной пачки импульсов на Т2=0,4Т, а при кодировании логической единицы центральную пачку импульсов располагают на временной оси с опережением опорной пачки импульсов на Т1=0,2Т, при этом передаваемое закодированное сообщение, именуемое кодограммой, составляют на объекте Х из конечной последовательности логических нулей и единиц, закодированных в виде совокупности опорных пачек сверхширокополосных импульсов с периодом следования Т и центральных пачек сверхширокополосных импульсов, расположенных между опорными, принятую объектом Y кодограмму усиливают по мощности и оцифровывают, оцифрованные импульсы подают на вход электронно-вычислительной машины, в электронно-вычислительной машине по мере поступления данных с аналого-цифрового преобразователя осуществляют формирование генерального массива данных D, из элементов которого формируют z-e пробные массивы, где  по мере формирования каждый вновь сформированный z-й пробный массив записывают в память электронно-вычислительной машины, в каждый z-й пробный массив включают значения оцифрованной последовательности сверхширокополосных пачек импульсов, ограниченной временным интервалом длительностью Δ, причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т, в каждый z-й пробный массив включают по N отсчетов, извлекаемых из генерального массива D, начиная с z-го элемента массива D и заканчивая (z+N-1)-м элементом массива D, где число элементов N в пробном массиве определяют по формуле
по мере формирования каждый вновь сформированный z-й пробный массив записывают в память электронно-вычислительной машины, в каждый z-й пробный массив включают значения оцифрованной последовательности сверхширокополосных пачек импульсов, ограниченной временным интервалом длительностью Δ, причем величина Δ, соответствующая z-му пробному интервалу Δz, равна Т, в каждый z-й пробный массив включают по N отсчетов, извлекаемых из генерального массива D, начиная с z-го элемента массива D и заканчивая (z+N-1)-м элементом массива D, где число элементов N в пробном массиве определяют по формуле
N=Δ·Fд,
где Fд - частота дискретизации аналого-цифрового преобразователя, первый пробный массив формируют из элементов массива D с номерами с 1-го по N-й, второй пробный массив формируют из элементов массива D с номерами со 2-го по (N+1)-й, третий пробный массив формируют из элементов массива D с номерами с 3-го по (N+2)-й, и т.д. до Z-го пробного массива, причем Z-й пробный массив формируют из элементов массива D с номерами с Z-го по (Z+N-1)-й, от каждого z-го пробного массива создают L-1 копий: Uz1n, Uz2n…Uz(L-1)n, каждую копию, представляющую массив данных, где число элементов N, записывают в память электронно-вычислительной машины, после этого каждый элемент первой копии z-го пробного массива, начиная с первого элемента, сдвигают на величину (Nz1+τи·Fд), где Nz1=t1·Fд, а элементы с 1-го по [Nz1+τи·Fд-1]-й и с [(Nz1+τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, при этом каждый элемент второй копии z-го пробного массива, начиная с первого элемента, сдвигают на величину [Nz1+Nz2+2·τи·Fд], где Nz2=t2·Fд, а элементы с 1-го по [Nz1+Nz2+2·τи·Fд-1]-й и с [Nz1+Nz2+2·τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, каждый элемент L-1 копий z-го пробного массива, начиная с первого элемента, сдвигают на величину [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд], а элементы с 1-го по [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд-1]-й и с [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд+N+1]-гo по [N+(τп-τи)·Fд]-й заполняют нулями, после этого исходный пробный z-й массив увеличивают на [(τп-τи)·Fд] элементов, при этом элементы с [N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, полученные массивы складывают друг с другом и получают суммарный z-й пробный массив Uzsn, от полученного суммарного z-го пробного массива Uzsn длительностью [N+(τп-τи)·Fд] создают для массива Uzsn две копии Uzs1n, Uzs2n, в массиве Uzs1n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т1)·Fд]-й, с [N-(Т1-τи)·Fд]-го по 1-й, в массиве Uzs2n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т2)-Fд]-й, с [N-(T2-τи]-го по 1-й, в результате дискретного обратного преобразования Фурье для каждого z-го пробного обнуленного массива получают соответствующий z-й основной массив, состоящий из элементов 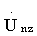 , после чего вычисляют значение модуля для каждого m-го отсчета соответствующего z-го основного массива, в результате получают два z-x кепстральных массива
, после чего вычисляют значение модуля для каждого m-го отсчета соответствующего z-го основного массива, в результате получают два z-x кепстральных массива 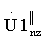 и
и  каждый из массивов в отдельности представляет собой кепстр z-го пробного обнуленного массива, для декодирования информации в кепстральном массиве
каждый из массивов в отдельности представляет собой кепстр z-го пробного обнуленного массива, для декодирования информации в кепстральном массиве 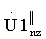 выделяют массив V1z, а в кепстральном массиве
выделяют массив V1z, а в кепстральном массиве 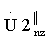 выделяют массив V2z, при этом массив V1z включает в себя значения кепстра
выделяют массив V2z, при этом массив V1z включает в себя значения кепстра 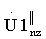 с номерами от m0 до m1, где m0=f(Т1·Fд-1); m1=f(Т1·Fд+1); f(*) - функция округления в сторону наименьшего целого числа, массив V2z включает в себя значения кепстра
с номерами от m0 до m1, где m0=f(Т1·Fд-1); m1=f(Т1·Fд+1); f(*) - функция округления в сторону наименьшего целого числа, массив V2z включает в себя значения кепстра 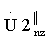 с номерами от m2 до m3, где m2=f(Т2·Fд-1); m3=f(Т2·Fд+1), используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанного в память электронно-вычислительной машины, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор z для z-го кепстрального массива, сравнивают величину θпор z с каждым значением соответствующего z-го кепстрального массива
с номерами от m2 до m3, где m2=f(Т2·Fд-1); m3=f(Т2·Fд+1), используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанного в память электронно-вычислительной машины, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор z для z-го кепстрального массива, сравнивают величину θпор z с каждым значением соответствующего z-го кепстрального массива 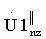 и
и 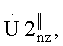 при превышении порога θпор z значениями кепстра в массиве V1z и отсутствии превышения порога θпор z в массиве V2z или при превышении порога θпор z значениями кепстра в массиве V2z и отсутствии превышения порога θпор z в массиве V1z принимают решение о наличии в z-м интервале Δz двух импульсов, после чего формируют G новых рабочих массивов данных из генерального массива данных D, номер кепстрального массива, которому соответствует наличие двух импульсов в соответствующем z-м интервале Δz, фиксируют как начальный Zнач, а соответствующий z-й интервал Δz обозначают как начальный Δz нач, рабочие массивы формируют размерностью N, причем первый элемент первого рабочего массива имеет в массиве D номер Zнач, второй рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+N-1]-го элемента массива D и заканчивая [Zнач+2N-2]-м элементом массива D, а каждый последующий g-й рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+(g-1)(N-1)]-го элемента массива D и заканчивая [Zнач+g(N-1)]-м элементом массива D, от каждого g-го рабочего массива, создают L-1 копий: Uq1n, Ug2n…Ug(L-1)n, каждую копию, представляющую массив данных, где число элементов N, записывают в память электронно-вычислительной машины, после этого каждый элемент первой копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину (Nz1+τи·Fд), где Nz1=t1·Fд, а элементы с 1-го по [Nz1+τи·Fд-1]-й и с [(Nz1+τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, каждый элемент второй копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину [Nz1+Nz2+2·τи·Fд], где Nz2=t2·Fд, a элементы с 1-го по [Nz1+Nz2+2·τи·Fд-1]-й и с [(Nz1+Nz2+2·τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, каждый элемент (L-1) копии, g-го рабочего массива, начиная с первого элемента, сдвигают на величину [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд], а элементы с 1-го по [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд-1]-й, и с [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, после этого исходный рабочий g-й массив увеличивают на [(τп-τи)·Fд] элементов, при этом элементы с [N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, полученные массивы одинаковой размерностью складывают друг с другом и получают суммарный g-й рабочий массив Ugsn, от полученного суммарного g-го рабочего массива Ugsn длительностью [N+(τп-τи)·Fд], создают две копии Ugs1n и Ugs2n, в массиве Uqs1n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т1)·Fд]-й, с [N-(Т1-τи)·Fд]-го по 1-й, в массиве Ugs2n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи-Fд)]-го по [N-(Т2)·Fд]-й, с [N-(Т2-τи)·Fд]-го по 1-й,
при превышении порога θпор z значениями кепстра в массиве V1z и отсутствии превышения порога θпор z в массиве V2z или при превышении порога θпор z значениями кепстра в массиве V2z и отсутствии превышения порога θпор z в массиве V1z принимают решение о наличии в z-м интервале Δz двух импульсов, после чего формируют G новых рабочих массивов данных из генерального массива данных D, номер кепстрального массива, которому соответствует наличие двух импульсов в соответствующем z-м интервале Δz, фиксируют как начальный Zнач, а соответствующий z-й интервал Δz обозначают как начальный Δz нач, рабочие массивы формируют размерностью N, причем первый элемент первого рабочего массива имеет в массиве D номер Zнач, второй рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+N-1]-го элемента массива D и заканчивая [Zнач+2N-2]-м элементом массива D, а каждый последующий g-й рабочий массив составляют из последовательности элементов массива D, начиная с [Zнач+(g-1)(N-1)]-го элемента массива D и заканчивая [Zнач+g(N-1)]-м элементом массива D, от каждого g-го рабочего массива, создают L-1 копий: Uq1n, Ug2n…Ug(L-1)n, каждую копию, представляющую массив данных, где число элементов N, записывают в память электронно-вычислительной машины, после этого каждый элемент первой копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину (Nz1+τи·Fд), где Nz1=t1·Fд, а элементы с 1-го по [Nz1+τи·Fд-1]-й и с [(Nz1+τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, каждый элемент второй копии g-го рабочего массива, начиная с первого элемента, сдвигают на величину [Nz1+Nz2+2·τи·Fд], где Nz2=t2·Fд, a элементы с 1-го по [Nz1+Nz2+2·τи·Fд-1]-й и с [(Nz1+Nz2+2·τи·Fд)+N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, каждый элемент (L-1) копии, g-го рабочего массива, начиная с первого элемента, сдвигают на величину [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд], а элементы с 1-го по [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд-1]-й, и с [(Nz1+Nz2+…+Nz(L-1))+(L-1)·τи·Fд+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, после этого исходный рабочий g-й массив увеличивают на [(τп-τи)·Fд] элементов, при этом элементы с [N+1]-го по [N+(τп-τи)·Fд]-й заполняют нулями, полученные массивы одинаковой размерностью складывают друг с другом и получают суммарный g-й рабочий массив Ugsn, от полученного суммарного g-го рабочего массива Ugsn длительностью [N+(τп-τи)·Fд], создают две копии Ugs1n и Ugs2n, в массиве Uqs1n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи·Fд)]-го по [N-(Т1)·Fд]-й, с [N-(Т1-τи)·Fд]-го по 1-й, в массиве Ugs2n обнуляют все элементы с [N+(τп-τи)·Fд]-го по N-й, с [N-(τи-Fд)]-го по [N-(Т2)·Fд]-й, с [N-(Т2-τи)·Fд]-го по 1-й,
в результате дискретного обратного преобразования Фурье для каждого g-го рабочего обнуленного массива получают соответствующий g-й основной массив, состоящий из элементов 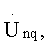 после чего вычисляют значение модуля для каждого m-го отсчета соответствующего g-го основного массива, в результате получают два g-x кепстральных массива
после чего вычисляют значение модуля для каждого m-го отсчета соответствующего g-го основного массива, в результате получают два g-x кепстральных массива  и
и 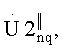 каждый из массивов представляет собой кепстр g-го рабочего массива, для декодирования информации в кепстральном массиве
каждый из массивов представляет собой кепстр g-го рабочего массива, для декодирования информации в кепстральном массиве  выделяют массив V1g, в кепстральном массиве
выделяют массив V1g, в кепстральном массиве  выделяют массив V2g, при этом массив V1g g-го кепстрального массива включает в себя значения кепстра
выделяют массив V2g, при этом массив V1g g-го кепстрального массива включает в себя значения кепстра  от m0 до m1, массив V2g g-го кепстрального массива включает в себя значения кепстра
от m0 до m1, массив V2g g-го кепстрального массива включает в себя значения кепстра  от m2 до m3, используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанное в память электронно-вычислительной машины, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор g для g-го кепстрального массива, сравнивают величину θпор g с каждым значением соответствующего g-го кепстрального массива, при превышении порога θпор g значениями кепстра в массиве V1g и отсутствии превышения в массиве V2g принимают решение о наличии в данном g-м интервале Δg закодированной логической единицы, при превышении порога θпор g значениями кепстра в массиве V2q и отсутствии превышения в массиве V1g принимают решение о наличии в данном g-м интервале Δg закодированного логического нуля, принимают, что выделенная информация из первого кепстрального массива соответствует первому биту информации принятой кодограммы, из второго кепстрального массива второму биту информации принятой кодограммы, а из g-го кепстрального массива - g-му биту информации принятой кодограммы, создают результирующий массив, представляющий собой расшифрованную кодограмму, в его элементы записывают последовательно, начиная с первого кепстрального массива и заканчивая G-м кепстральным массивом, выделенную информацию из каждого g-го кепстрального массива, при отсутствии превышения порога θпор g значениями кепстра в установленных массивах V1g или V2q принимают решение об окончании приема кодограммы, после чего с объекта Y на объект Х посылают запросный сигнал, свидетельствующий о готовности объекта Y к приему следующей кодограммы, отличающийся тем, что после обнуления элементов массивов Uzs1n, Uzs2n проверяют кратность двум общего числа элементов каждого обнуленного массива Uzs1n, Uzs2n, для этого используют равенство
от m2 до m3, используют заранее полученное максимальное значение амплитуды кепстрального отклика в массиве V1z или V2z при отсутствии помех, записанное в память электронно-вычислительной машины, умножают полученное максимальное значение кепстра на 0,7 и принимают результат в качестве порогового значения θпор g для g-го кепстрального массива, сравнивают величину θпор g с каждым значением соответствующего g-го кепстрального массива, при превышении порога θпор g значениями кепстра в массиве V1g и отсутствии превышения в массиве V2g принимают решение о наличии в данном g-м интервале Δg закодированной логической единицы, при превышении порога θпор g значениями кепстра в массиве V2q и отсутствии превышения в массиве V1g принимают решение о наличии в данном g-м интервале Δg закодированного логического нуля, принимают, что выделенная информация из первого кепстрального массива соответствует первому биту информации принятой кодограммы, из второго кепстрального массива второму биту информации принятой кодограммы, а из g-го кепстрального массива - g-му биту информации принятой кодограммы, создают результирующий массив, представляющий собой расшифрованную кодограмму, в его элементы записывают последовательно, начиная с первого кепстрального массива и заканчивая G-м кепстральным массивом, выделенную информацию из каждого g-го кепстрального массива, при отсутствии превышения порога θпор g значениями кепстра в установленных массивах V1g или V2q принимают решение об окончании приема кодограммы, после чего с объекта Y на объект Х посылают запросный сигнал, свидетельствующий о готовности объекта Y к приему следующей кодограммы, отличающийся тем, что после обнуления элементов массивов Uzs1n, Uzs2n проверяют кратность двум общего числа элементов каждого обнуленного массива Uzs1n, Uzs2n, для этого используют равенство
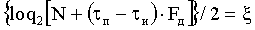 ,
,
где ξ - целое число, полученное при выполнении равенства, при невыполнении равенства принимают общее число элементов в каждом обнуленном массиве Uzs1n, Uzs2n некратным двум и увеличивают последовательно каждый обнуленный массив Uzs1n, Uzs2n нулевыми элементами, для этого последовательно прибавляют по одному нулевому элементу к концу массивов Uzs1n, Uzs2n до выполнения равенства
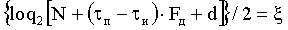 ,
,
где d - общее число нулевых элементов, добавленных к массиву Uzs1n и Uzs2n в момент выполнения равенства, после чего получают обнуленные дополненные массивы Uzs1n, Uzs2n, в которых принимают общее число элементов кратным двум и в последующем подвергают их вейвлет-кепстральной обработке, при которой последовательно для каждого элемента обнуленного дополненного массива вычисляют дискретное прямое преобразование Фурье с использованием формулы
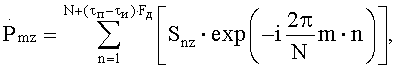
где n - номер отчета во временной области, m - номер отчета в частотной области; 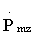 - значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го массива Uzs1n или Uzs2n, число элементов в котором кратно двум, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном массиве Uzs1n или Uzs2n, число элементов в котором кратно двум, в последующем для каждого z-го массива Uzs1n и Uzs2n, число элементов в котором кратно двум, вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
- значение комплексной амплитуды m-го отсчета спектра оцифрованного сигнала для z-го массива Uzs1n или Uzs2n, число элементов в котором кратно двум, Snz - значение амплитуды n-го по номеру отсчета, находящегося в z-м обнуленном массиве Uzs1n или Uzs2n, число элементов в котором кратно двум, в последующем для каждого z-го массива Uzs1n и Uzs2n, число элементов в котором кратно двум, вычисляют значение логарифма квадрата модуля каждого m-го отсчета, то есть m-го значения амплитуды спектра оцифрованного сигнала по формуле
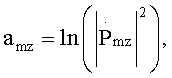
затем для каждого вектора Amz, составленного из элементов amz z-го интервала Δz, вычисляют дискретное прямое вейвлет-преобразование по формуле

где Ψb-m,a - известный тип вейвлета, b - число, характеризующее сдвиги вейвлета и изменяющееся от 1 до М с шагом 1, а - число, характеризующее сжатие вейвлета и изменяющееся от 2ξ до 1, М - число элементов в векторе Amz, количественно равное N+(τп-τи)·Fд+d, после чего в полученной матрице Cz размером b×a, состоящей из коэффициентов 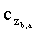 , удаляют столбцы с 1 го по ξ, а от результата вычисляют обратное вейвлет-преобразование по формуле
, удаляют столбцы с 1 го по ξ, а от результата вычисляют обратное вейвлет-преобразование по формуле

после чего для каждого вектора, составленного из величин Dmz z-го интервала Δz, вычисляют дискретное обратное преобразование Фурье по формуле
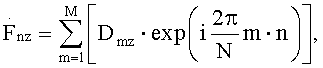
где М - число элементов в векторе Dmz, количественно равное N+(τп-τи)·Fд+d, в последующем элементы массива 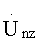 заменяют элементами массива
заменяют элементами массива  после обнуления элементов массивов Ugs1n, Ugs2n проверяют кратность двум общего числа элементов каждого обнуленного массива Ugs1n, Ugs2n, для этого с каждым обнуленным массивам Ugs1n, Ugs2n проделывают операции, аналогичные тем, которые осуществлялись ранее с обнуленными массивами Ugs1n, Ugs2n до получения массива
после обнуления элементов массивов Ugs1n, Ugs2n проверяют кратность двум общего числа элементов каждого обнуленного массива Ugs1n, Ugs2n, для этого с каждым обнуленным массивам Ugs1n, Ugs2n проделывают операции, аналогичные тем, которые осуществлялись ранее с обнуленными массивами Ugs1n, Ugs2n до получения массива 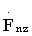 включительно, за исключением того, что результатом вейвлет-кепстральной обработки в данном случае будет являться массив
включительно, за исключением того, что результатом вейвлет-кепстральной обработки в данном случае будет являться массив 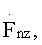 в последующем элементы массива
в последующем элементы массива 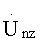 заменяют полученными элементами массива
заменяют полученными элементами массива 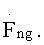
| АСИНХРОННО-КЕПСТРАЛЬНЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2010 |
|
RU2427075C2 |
| ПОМЕХОУСТОЙЧИВЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ ПАЧЕК СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2010 |
|
RU2422991C1 |
| АСИНХРОННЫЙ СПОСОБ ВЫДЕЛЕНИЯ ЗАКОДИРОВАННОЙ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПОТРЕБИТЕЛЮ С ПОМОЩЬЮ СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ | 2009 |
|
RU2416162C2 |
| WO 2008070067 A2, 12.06.2008 | |||
| US 6989782 B2, 24.01.2006 | |||
| Композиция для очистки оптических изделий | 1987 |
|
SU1475916A1 |
Авторы
Даты
2012-10-20—Публикация
2011-08-23—Подача