Изобретение относится к способам неразрушающего контроля параметров полупроводников и низкоразмерных полупроводниковых наноструктур, содержащих вырожденный электронный газ, и может быть использовано для определения квантованного холловского сопротивления полупроводников и двумерных полупроводниковых наноструктур и для контроля качества материалов, применяемых в полупроводниковом приборостроении.
Известен бесконтактный способ определения холловского сопротивления полупроводников [Авторское свидетельство СССР №1694018, кл H01L 21/66, 1994], основанный на эффекте Шубникова-де Гааза, заключающийся в том, что полупроводник охлаждают до гелиевых температур, одновременно воздействуют на него изменяющимся постоянным магнитным полем 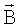 , переменным магнитным полем с амплитудой b, много меньшей В, и направленным перпендикулярно магнитному полю
, переменным магнитным полем с амплитудой b, много меньшей В, и направленным перпендикулярно магнитному полю 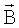 излучением, поляризованным так, что вектор напряженности электрического поля перпендикулярен постоянному магнитному полю
излучением, поляризованным так, что вектор напряженности электрического поля перпендикулярен постоянному магнитному полю 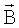 , регистрируют интенсивность прошедшего через полупроводник излучения, по соседним максимумам производной интенсивности в зависимости от магнитного поля определяют концентрацию n носителей заряда расчетным путем и по следующей расчетной формуле определяют холловское сопротивление
, регистрируют интенсивность прошедшего через полупроводник излучения, по соседним максимумам производной интенсивности в зависимости от магнитного поля определяют концентрацию n носителей заряда расчетным путем и по следующей расчетной формуле определяют холловское сопротивление 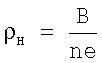 , где е - заряд электрона.
, где е - заряд электрона.
Недостатком этого способа является невозможность определения квантованного холловского сопротивления ρ12 в очень тонких слоях полупроводника, содержащих вырожденный электронный газ пониженной размерности. Это ограничение обусловлено тем, что частота падающего на полупроводник излучения во много раз больше частоты столкновения электронов с атомами. При этом передача энергии излучения свободным электронам происходит неэффективно. В результате чувствительность способа при диагностике двумерного электронного газа является недостаточной. Вторым недостатком способа является невозможность определения концентрации носителей заряда и квантованного холловского сопротивления в двумерных нанослоях полупроводника, обусловленная тем, что направление излучения выбрано перпендикулярно направлению магнитного поля, поэтому этот способ не применим, когда толщина исследуемого двумерного слоя меньше диаметров электронных орбит, составляющих десятки нанометров.
Наиболее близким к предлагаемому способу является взятый за прототип бесконтактный способ определения холловского сопротивления полупроводников [Патент РФ №2037911. Способ бесконтактного определения концентрации свободных носителей заряда в вырожденных полупроводниках. Корнилович А.А., Студеникин С.А., Булдыгин А.Ф., опубл. 19.06.95. Бюл. №17, кл. H01L 21/66. 1995 г. Приоритет изобретения 4 апреля 1991 г.], основанный на СВЧ эффекте Шубникова-де Гааза, заключающийся в том, что полупроводник охлаждают до гелиевых температур, воздействуют на него СВЧ-излучением и постоянным магнитным полем В, вектор индукции которого В направлен перпендикулярно поверхности полупроводника, дополнительно воздействуют на полупроводник переменным магнитным полем с амплитудой b<<В, изменяющимся со звуковой частотой ω, направленным параллельно постоянному магнитному полю и падающему на полупроводник СВЧ-излучению, частоту которого выбирают меньше частоты столкновений свободных носителей заряда с атомами полупроводника, регистрируют сигнал, пропорциональный первой производной интенсивности отраженного от полупроводника СВЧ-излучения по магнитному полю и по значениям магнитного поля В, соответствующим максимумам осцилляции Шубникова-де Гааза, определяют период осцилляции Δ(B-1), концентрацию носителей заряда n и холловское сопротивление 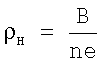 расчетным путем.
расчетным путем.
Недостатком этого способа является ограниченная область применения. Это ограничение, главным образом, обусловлено недостаточной чувствительностью способа при регистрации первой производной сигнала и невозможностью определить значение магнитного поля, соответствующее минимуму магнитосопротивления. Экстремальные значения регистрируемого сигнала не соответствуют значениям магнитного поля в минимуме магнитосопротивления, поэтому этот способ имеет ограниченную область применения для бесконтактного определения холловского сопротивления.
Задачей предложенного способа является расширение области применения.
Указанная задача достигается тем, что в способе бесконтактного определения квантованного холловского сопротивления в полупроводниках, заключающемся в том, что исследуемый образец охлаждают до гелиевых температур, воздействуют на него изменяющимся постоянным магнитным полем, вектор В индукции которого перпендикулярен поверхности образца, и дополнительно переменным магнитным полем, изменяющимся со звуковой частотой, имеющим амплитуду, во много меньшую В, и вектор индукции, направленный параллельно вектору В, облучают образец СВЧ-излучением заданной частоты в направлении, параллельном вектору индукции В постоянного магнитного поля, выбирают частоту излучения меньше частоты столкновений носителей заряда с атомами полупроводника, дополнительно охлаждают полупроводник до температуры ниже 2К, регистрируют сигнал, пропорциональный второй производной мощности СВЧ-излучения в зависимости от магнитного поля В, измеряют значение магнитного поля, соответствующее минимуму отраженного сигнала, и определяют квантованное холловское сопротивление в широком диапазоне квантующих магнитных полей расчетным путем по формуле:
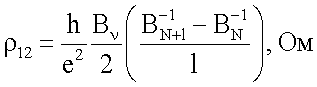
где l - число периодов осцилляции Шубникова-де Гааза,
e - заряд электрона, h - постоянная Планка,
BN+l и BN - значения магнитного поля, соответствующие N+l и N максимумам отраженного от полупроводника сигнала в области постоянного 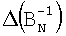 периода осцилляции Шубникова-де Гааза, Тл,
периода осцилляции Шубникова-де Гааза, Тл,
N - число уровней Ландау, лежавших ниже уровня Ферми, заполненных электронами,
Bν - значение магнитного поля, соответствующее минимуму отраженного от полупроводника сигнала,
ν - фактор заполнения уровней Ландау.
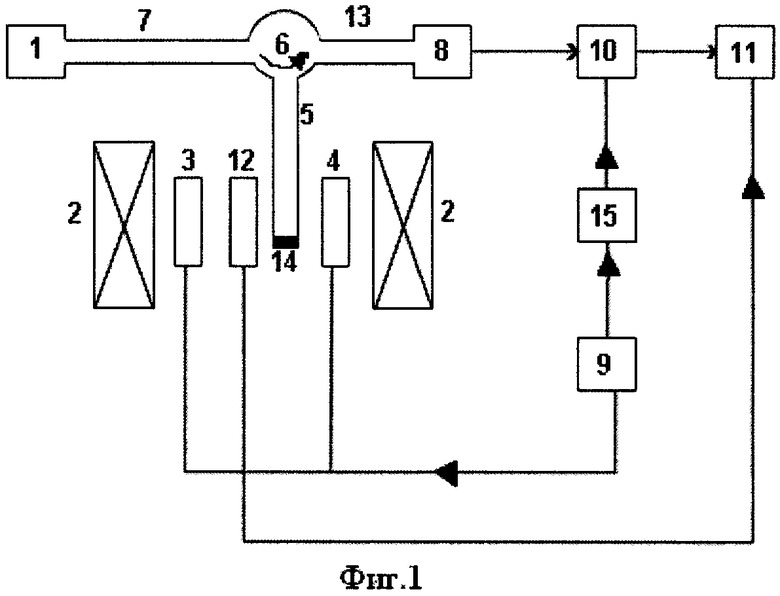
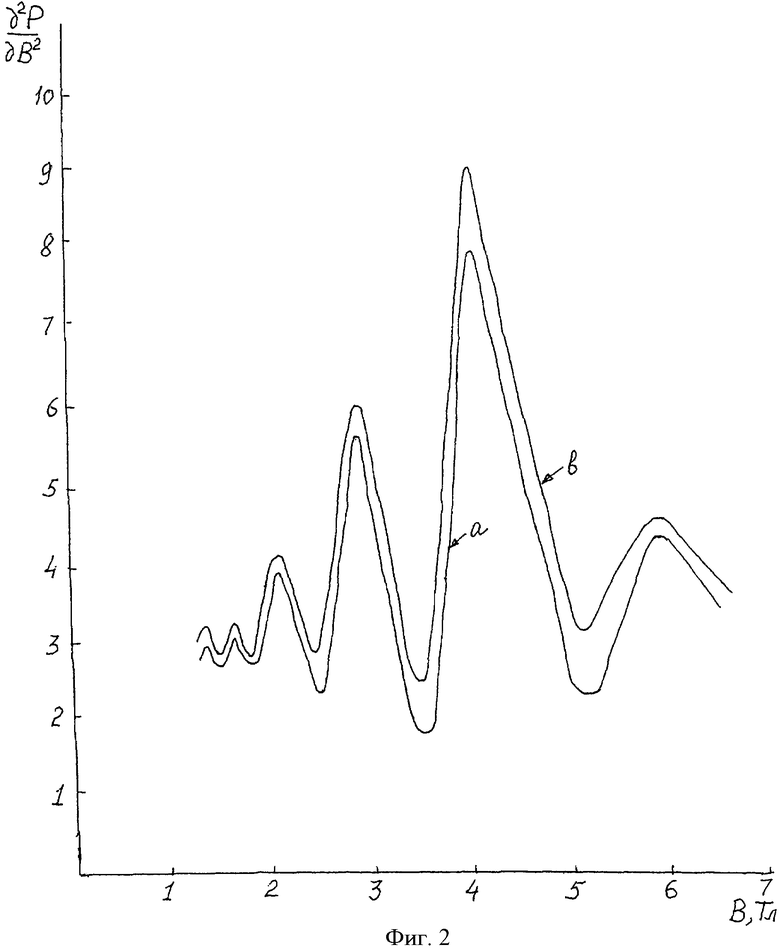
На фиг.1 приведена функциональная схема устройства, реализующего предлагаемый способ; на фиг.2 приведены графики зависимости второй производной мощности отраженного СВЧ-излучения по магнитному полю  от индукции постоянного магнитного поля В для полупроводникового образца GaAS при различных температурах (кривая а при T1=2,2K, кривая б при Т2=4,2К).
от индукции постоянного магнитного поля В для полупроводникового образца GaAS при различных температурах (кривая а при T1=2,2K, кривая б при Т2=4,2К).
Устройство (фиг.1) содержит источник 1 зондирующего СВЧ-излучения, источник 2 постоянного магнитного поля, модуляционные катушки 3 и 4, создающие переменное магнитное поле, цилиндрический диэлектрический резонатор 5, циркулятор 6, прямоугольные волноводы 7, 13, СВЧ-детектор 8, генератор 9 звуковой частоты, усилитель-детектор 10, самописец 11, датчик 12 магнитного поля, образец 14 полупроводника, удвоитель 15.
Источник 1 СВЧ-излучения может, например, представлять собой генератор на серийном диоде Ганна типа АА728Б. Источник 2 постоянного магнитного поля может представлять собой сверхпроводящий соленоид. В качестве СВЧ-детектора 8 может быть использован, например, прибор на основе диода Шоттки типа АА123А.
Прямоугольные волноводы 7,13 могут, например, представлять собой серийные волноводы размерами 3,4×7,2 мм, соединенные серийным циркулятором 6. Цилиндрический диэлектрический резонатор 5 может, например, иметь внутренний диаметр 1 мм. Усилитель-детектор 10 содержит селективный усилитель и синхронный детектор (не показаны) и может быть выполнен, например, на основе универсального прибора типа UNIPAN-232B. В качестве генератора 9 звуковой частоты может быть использован, например, прибор типа Г3-33. В качестве удвоителя 15 может быть использован, например, серийный умножитель частоты. Самописец 11 представляет собой двухкоординатный самописец, например, ENDIM 002. В качестве датчика 12 магнитного поля может быть использован, например, датчик Холла, калиброванный прибором Ш1-1, работающим на основе ядерного магнитного резонанса. Модуляционные катушки 3,4 могут, например, иметь внутренний диаметр 10 мм и содержать 960 витков провода ПЭЛ 0,2 мм.
Источник 1 зондирующего СВЧ-излучения связан с прямоугольным волноводом 7, который связан с циркулятором 6. Последний связан с цилиндрическим диэлектрическим резонатором 5 и с помощью прямоугольного волновода 13 с СВЧ-детектором 8. Исследуемый образец 14 закреплен в конце цилиндрического диэлектрического резонатора 5 в рабочем объеме источника 2 постоянного магнитного поля и вместе с цилиндрическим диэлектрическим резонатором 5, источником 2 постоянного магнитного поля, модуляционными катушками 3 и 4 и датчиком 12 магнитного поля помещен в гелиевый криостат (не показан). Модуляционные катушки 3 и 4 подключены к первому выходу генератора 9 звуковой частоты, второй выход которого соединен с входом удвоителя 15, второй выход которого соединен с опорным входом усилителя-детектора 10, являющимся опорным входом синхронного детектора, информационный вход которого соединен с выходом селективного усилителя.
Выход СВЧ-детектора 8 подключен к информационному входу усилителя-детектора 10, являющемуся входом селективного усилителя.
Выход усилителя-детектора 10, являющийся выходом синхронного детектора, соединен с входом Y самописца 11, вход X которого соединен с выходом датчика 12 магнитного поля, размещенного в рабочем объеме источника 2 постоянного магнитного поля.
Сущность предлагаемого способа заключается в следующем.
Известно, что в полупроводниковых наноструктурах со сверхрешетками либо в двумерных гетероструктурах, например, типа GaAs - AlxGa1-xAs происходит изгиб энергетических зон. Это приводит к размерному квантованию энергии носителей заряда, т.е. к образованию дискретных энергетических уровней E0, E1,…Ei,… в двумерном вырожденном нанослое GaAs. При толщине двумерного слоя меньше длины свободного пробега либо длины волны де Бройля электрона движение носителей заряда происходит в плоскости слоя. Двумерный слой GaAs имеет толщину несколько нанометров, является вырожденным, отделенным с обеих сторон слаболегированными объемными слоями AlGaAs и GaAs. При исследовании свойств двумерного электронного газа контактными методами объемные слои вносят большую погрешность.
Известно, что сильное магнитное поле перестраивает плотность состояний вырожденного полупроводника по уровням Ландау
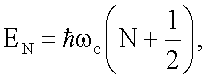
где N - номер уровня Ландау, ωc - циклотронная частота вращения электрона в магнитном поле, равная 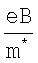 , m* - эффективная масса электрона в полупроводнике.
, m* - эффективная масса электрона в полупроводнике.
Плотность электронных состояний имеет резонансный характер с максимумами вблизи уровней Ландау. Рассеяние электронов, случайный потенциал, создаваемый неоднородностями, и температурное размытие кТ вызывают уширение уровней Ландау.
При возрастании магнитного поля энергетические интервалы между уровнями Ландау возрастают и, когда уровень Ландау EN пересекает уровень Ферми EF, который также подвергается температурному размытию кТ, электроны с уровня Ферми интенсивно переходят на свободные состояния уровней EN, EN-1, EN-2,… Это вызывает резонансное изменение высокочастотной проводимости, возбуждаемой в вырожденном полупроводнике зондирующим СВЧ-излучением, и возникновение СВЧ-осцилляций Шубникова-де Гааза.
Для наблюдения осцилляции Шубникова-де Гааза в полупроводниках необходимо выполнение следующих условий.
1. Исследуемый полупроводник должен быть вырожденным.
2. Время релаксаций свободных носителей заряда τ должно превышать период их обращения в магнитном поле.
3. Энергетические интервалы между уровнями Ландау должны превышать их уширение Г и тепловое размытие уровня Ферми и уровня Ландау.
4. Уровень Ферми должен быть больше интервалов между уровнями Ландау.
5. Электрическое поле 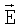 СВЧ-волны следует выбирать перпендикулярным квантующему магнитному полю
СВЧ-волны следует выбирать перпендикулярным квантующему магнитному полю 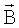 .
.
Осцилляционное условие имеет вид:
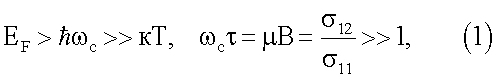
где µ - подвижность носителей заряда,
σ11 - диагональный компонент тензора проводимости,
σ12 - холловская проводимость.
Холловская проводимость в поперечном магнитном поле в основном определяется концентрацией свободных носителей заряда n и величиной магнитного поля В.

В сильных магнитных полях 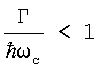
При 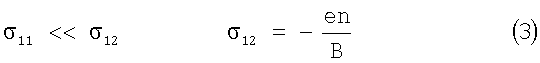
Квантованное холловское сопротивление

Магнитосопротивление является диссипативным диагональным компонентом тензора сопротивления
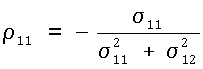
При выполнении условия (1)
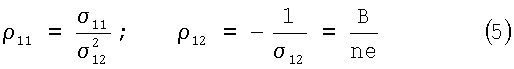
Минимумы осцилляции ρ11 и σ11 совпадают и соответствуют центру плато квантованного холловского сопротивления ρ12.
В поле СВЧ-волны высокочастотный ток свободных носителей заряда имеет компонент, изменяющийся в фазе с электрическим полем СВЧ-волны. Именно синфазный компонент дает вклад в высокочастотную проводимость σ11. При этом электроны поглощают энергию волны, поляризованной по левому кругу. В то время как направление орбитального движения электронов противоположно, т.е. является правовращающим относительно направления магнитного поля. Поскольку в первом приближении можно считать, что коэффициент отражения СВЧ-волны линейно зависит от действительной части высокочастотной проводимости, наблюдаются резонансные изменения мощности отраженной от образца СВЧ-волны - СВЧ-осцилляций Шубникова-де Гааза.
Амплитуда A отраженного СВЧ-сигнала зависит от индукции магнитного поля Bo. Индукция магнитного поля В с помощью модуляционных катушек изменялась на величину

Разлагая амплитуду сигнала А (В) в ряд Тейлора и ограничиваясь членами второго порядка, получаем
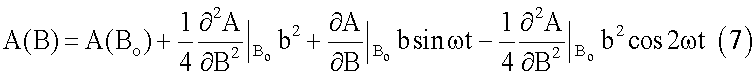
Амплитуда сигнала второй гармоники связана со второй производной функции соотношением
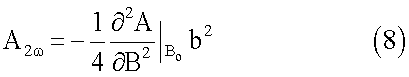
и квадратично зависит от амплитуды модулирующего магнитного поля b.
Использование модуляционной методики двойного дифференцирования с синхронным детектированием для измерения резонансных явлений позволяет выделить с помощью селективного детектора изменения амплитуды сигнала второй гармоники 2ω и регистрировать с помощью самописца изменение отраженного СВЧ-излучения 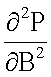 в зависимости от индукции магнитного поля В. При этом значительно увеличивается чувствительность предлагаемого способа.
в зависимости от индукции магнитного поля В. При этом значительно увеличивается чувствительность предлагаемого способа.
В условиях, когда период СВЧ-волны больше времени релаксации импульса электрона τ, происходит увеличение времени передачи энергии электрону. Когда уровень Ферми лежит в области подвижных (разрешенных) состояний вблизи N-го уровня Ландау, протекание тока сопровождается максимальной диссипацией. Концентрация носителей заряда на N-ом уровне изменяется от 0 до 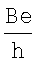 по мере прохождения уровнем Ландау EN уровня Ферми EF в области энергий кТ. Кроме этого неоднородности в двумерном слое полупроводника создают случайный потенциал, который снимает вырожденные уровни Ландау и уширяет их в энергетические подзоны. Флуктуации случайного потенциала подчиняются гауссовскому распределению случайных величин. Максимальное значение потенциала соответствует уровню Ландау EN. Масштаб неоднородностей определяется полушириной Г гауссовского распределения и характеризует область подвижных состояний, которой соответствует переходный участок (ступень) между соседними плато квантованного холловского сопротивления ρ12 и значениями N и N+1. При BN, соответствующем максимуму осцилляции Шубникова-де Гааза, концентрация носителей заряда
по мере прохождения уровнем Ландау EN уровня Ферми EF в области энергий кТ. Кроме этого неоднородности в двумерном слое полупроводника создают случайный потенциал, который снимает вырожденные уровни Ландау и уширяет их в энергетические подзоны. Флуктуации случайного потенциала подчиняются гауссовскому распределению случайных величин. Максимальное значение потенциала соответствует уровню Ландау EN. Масштаб неоднородностей определяется полушириной Г гауссовского распределения и характеризует область подвижных состояний, которой соответствует переходный участок (ступень) между соседними плато квантованного холловского сопротивления ρ12 и значениями N и N+1. При BN, соответствующем максимуму осцилляции Шубникова-де Гааза, концентрация носителей заряда

Локализованные состояния соответствуют хвостам уширенных уровней Ландау. При этом, когда уровень Ферми попадает в щель подвижности между уровнями Ландау, концентрация носителей заряда

здесь BN -значение магнитного поля, соответствующее минимуму осцилляции Шубникова-де Гааза, N - число уровней Ландау, лежащих ниже уровня Ферми ЕF, заполненных электронами. В общем случае, когда один из уровней Ландау заполнен частично, между соседними плато проявляется дробный квантовый эффект Холла. Тогда вводится фактор заполнения уровней Ландау
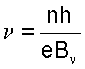
где Bν - значение магнитного поля, соответствующее центру плато ρ12 и минимумам ρ11, σ11, 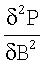 . Фактор заполнения ν принимает дробные значения и включает полное число подуровней под уровнем Ферми. Квантованное значение холловского сопротивления определяется выражением:
. Фактор заполнения ν принимает дробные значения и включает полное число подуровней под уровнем Ферми. Квантованное значение холловского сопротивления определяется выражением:

Концентрация свободных носителей заряда определяется бесконтактным способом в области постоянного периода осцилляции Шубникова-де Гааза 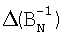 по формуле
по формуле
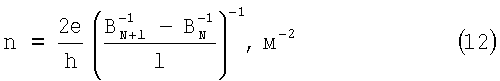
где l - число периодов осцилляции Шубникова-де Гааза.
Фактор заполнения уровней Ландау определяется по формуле
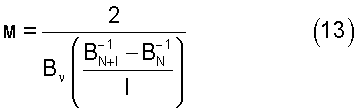
где Bν - значение магнитного поля в минимуме осцилляции Шубникова-де Гааза. Квантованное холловское сопротивление определяется по формуле:
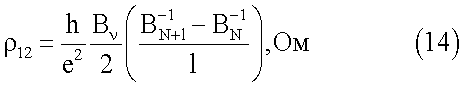
Магнитное поле Bν соответствует минимуму отраженного от образца СВЧ-сигнала, пропорционального второй производной мощности СВЧ-излучения. Отраженный сигнал имеет ярко выраженный минимум в случаях, когда плато квантованного холловского сопротивления имеет малые размеры. Размеры плато ρ12 малы в неоднородных образцах, характеризуемых пониженным значением подвижности, а также в высококачественных образцах в области дробного квантового эффекта Холла. С понижением температуры пики максимумов осцилляции сужаются, размеры плато увеличиваются ρ11→0 и минимумы осцилляции ρ11 исчезают. С повышением температуры размеры плато ρ12 уменьшаются, тогда минимум осцилляции ρ12 ярко выражен и соответствует центру плато ρ12.
Погрешность определения квантованного холловского сопротивления зависит от точности определения положения минимума отраженного сигнала, погрешности измерения индукции магнитного поля Bν и не превышает 0,5%.
Новым по отношению к прототипу в предлагаемом способе является применение СВЧ-эффекта Шубникова-де Гааза в широком диапазоне сильных квантующих магнитных полей при дополнительном охлаждении образца до температур < 2К, применение цилиндрического диэлектрического волновода меньшего сечения, регистрация отраженного от образца сигнала, пропорционального второй производной мощности СВЧ-излучения, определение квантованного холловского сопротивления расчетным путем.
Способ осуществляется следующим образом.
От источника 1 зондирующего СВЧ-излучения на образец 14 через прямоугольный волновод 7, циркулятор 6 и цилиндрический диэлектрический резонатор 5 направляют параллельно вектору индукции постоянного магнитного поля В СВЧ-волну типа E01n (n=80), частота которой 38,6 ГГц, период которой больше времени релаксации импульса свободных носителей заряда и периода обращения носителей заряда по циклотронной орбите. Для увеличения значения сигнал/шум с помощью генератора 9 звуковой частоты и модуляционных катушек 3 и 4 создают слабое переменное магнитное поле, частота которого составляет 30-389 Гц. Для снижения шума, регистрируемого СВЧ-детектором, создается вакуум над жидким гелием. Этим уменьшают температуру жидкого гелия и образца 14, например, ниже 2К. Величина индукции В магнитного поля, создаваемого источником 2, непрерывно изменяется от 0 до 7 Тл, при этом сигнал с выхода датчика 12 магнитного поля, размещенного в рабочем объеме источника 2, поступает на вход X самописца 11. Точность измерения значения индукции В магнитного поля определяется используемым датчиком магнитного поля и в данном случае составляет 0,02%. На вход Y самописца 11 поступает выходной сигнал с СВЧ-детектора 8, пропорциональный изменению проводимости образца 14, предварительно прошедший через цилиндрический диэлектрический резонатор 5, циркулятор 6, прямоугольный волновод 13 и детектируемый СВЧ-детектором 8, усиленный и выпрямленный усилителем-детектором 10. При этом на опорный вход усилителя-детектора поступает сигнал удвоенной звуковой частоты удвоителя 15. В результате самописец 11 выдает график зависимости второй производной мощности отраженного от образца 14 СВЧ-излучения от индукции В магнитного поля, в данном случае для образца GaAs-AlxGa1-xAs (фиг.2). По графикам фиг.2 определяют период осцилляции ΔB-1 мощности отраженного СВЧ-излучения и по расчетным формулам определяют квантованное холловское сопротивление в исследуемом образце, в данном случае при В4=4,17 Тл, ρ4=6,46·103Ом, при B5=3,33 Тл, ρ5=5,17·103 Ом. Точность измерений квантованного холловского сопротивления в исследуемых образцах составляет 0,5%.
Предлагаемый способ в отличие от прототипа, во-первых, выполняется при дополнительном охлаждении жидкого гелия и полупроводника до температуры ниже 2К, во-вторых, позволяет повысить чувствительность в результате регистрации сигнала, пропорционального второй производной мощности отраженного от полупроводника СВЧ-излучения по магнитному полю, определять значение магнитного поля, соответствующего минимуму отраженного сигнала, позволяет определять квантованное холловское сопротивление в широком диапазоне квантующих магнитных полей в двумерных слоях полупроводников, что позволяет расширить область применения и эффективно осуществлять неразрушающий контроль качества полупроводниковых наноструктур.
Изобретение относится к способам неразрушающего контроля параметров полупроводников и низкоразмерных полупроводниковых наноструктур. Сущность изобретения: в способе бесконтактного определения квантованного холловского сопротивления полупроводников, включающем охлаждение полупроводника до гелиевых температур, воздействие на него изменяющимся постоянным магнитным полем, вектор В индукции которого перпендикулярен поверхности образца, и дополнительно переменным магнитным полем, изменяющимся со звуковой частотой, имеющим амплитуду, во много меньшую В, и вектор индукции, направленный параллельно вектору В, облучение образца СВЧ-излучением заданной частоты в направлении, параллельном вектору индукции В постоянного магнитного поля, выбор частоты излучения меньше частоты столкновений носителей заряда с атомами полупроводника, дополнительное охлаждение полупроводника до температуры ниже 2К, регистрацию сигнала, пропорционального второй производной мощности СВЧ-излучения в зависимости от магнитного поля В, измерение значения магнитного поля, соответствующего минимуму отраженного сигнала, и определение квантованного холловского сопротивления в широком диапазоне квантующих магнитных полей расчетным путем по представленной формуле. Способ позволяет расширить область применения. 2 ил.
Способ бесконтактного определения квантованного холловского сопротивления полупроводников, включающий охлаждение полупроводника до гелиевых температур, воздействие на него изменяющимся постоянным магнитным полем, вектор В индукции которого перпендикулярен поверхности образца и дополнительно переменным магнитным полем, изменяющимся со звуковой частотой, имеющим амплитуду во много меньшую В и вектор индукции, направленный параллельно вектору В, облучение образца СВЧ-излучением заданной частоты в направлении, параллельном вектору индукции В постоянного магнитного поля, выбор частоты излучения меньше частоты столкновений носителей заряда с атомами полупроводника, дополнительное охлаждение полупроводника до температуры ниже 2К, регистрацию сигнала, пропорционального второй производной мощности СВЧ-излучения в зависимости от магнитного поля В, измерение значения магнитного поля, соответствующего минимуму отраженного сигнала, и определение квантованного холловского сопротивления в широком диапазоне квантующих магнитных полей расчетным путем по формуле
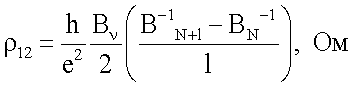 ,
,
где l - число периодов осцилляции Шубникова-де Гааза;
е - заряд электрона;
h - постоянная Планка;
BN+l и BN - значения магнитного поля, соответствующие N+l и N максимумам отраженного от полупроводника сигнала в области постоянного Δ(BN -1) периода осцилляции Шубникова-де Гааза, Тл;
N - число уровней Ландау, лежавших ниже уровня Ферми, заполненных электронами;
Bν - значение магнитного поля, соответствующее минимуму отраженного от полупроводника сигнала;
ν - фактор заполнения уровней Ландау.
| СПОСОБ БЕСКОНТАКТНОГО ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ СВОБОДНЫХ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ | 1991 |
|
RU2037911C1 |
| Способ определения квантового сопротивления Холла | 1987 |
|
SU1515115A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ НОСИТЕЛЕЙ ЗАРЯДА В ВЫРОЖДЕННЫХ ПОЛУПРОВОДНИКАХ | 1989 |
|
SU1694018A1 |
| Способ бесконтактного определения удельного электрического сопротивления полупроводников | 1990 |
|
SU1744736A1 |
| US 5789931 A, 04.08.1998. | |||
Авторы
Даты
2009-09-27—Публикация
2007-11-13—Подача