Изобретение относится к дифрактометрическим методам исследования монокристаллов и может использоваться для измерения мозаичности кристаллов.
Известен ряд способов определения параметров мозаичности кристаллов, основанных на анализе характеристик рассеянного кристаллом квазимонохроматического рентгеновского излучения. Например, измеряются и сравниваются полуширины дифракционных пиков для изучаемого и совершенного кристаллов в простом двухволновом случае [1] или сравниваются отражательные способности в многоволновом и двухволновом случаях [2].
В качестве прототипа выбран хорошо известный и проверенный экспериментально способ определения полуширины распределения мозаичности кристаллических образцов, основанный на измерении полуширины дифракционного пика [1].
Данный способ осуществляется следующим образом: исследуемый образец облучают потоком квазимонохроматического остронаправленного рентгеновского излучения и измеряют полуширину углового распределения дифракционного пика. Wm, которую затем сравнивают с полушириной эталонного образца Wi, близкого к идеальному. При этом средний угол мозаичности η0 следует из формулы 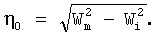
Недостатком описываемого способа, так же как и всех применяемых в настоящее время способов определения мозаичности кристаллов является принципиальная невозможность получения с его помощью полной информации о распределении микроблоков кристалла по углам ориентации. Фактически, в рамках данного способа постулируется гауссово распределение и задача способа заключается в нахождении единственного параметра этого распределения η0.
Задача предлагаемого способа состоит в расширении арсенала способов определения мозаичности кристаллов.
Технический результат - возможность определения двумерной функции распределения микроблоков мозаичного кристалла по углам мозаичности.
Предлагаемый способ направлен на устранение указанного принципиального недостатка прототипа путем нахождения функций распределения Ф||(η||), Ф⊥(η⊥) микроблоков мозаичного кристалла по углам мозаичности η⊥, η// в двух взаимно перпендикулярных направлениях и основывается на использовании установленной аналитической зависимости функции распределения Ф||(η||), Ф⊥(η⊥) микроблоков мозаичного кристалла по углам ориентации от измеряемой в эксперименте ориентационной кривой выхода рассеянного исследуемым образцом остронаправленного широкополосного рентгеновского излучения.
Технический результат изобретения достигается за счет того, что исследуемый образец, так же как и в прототипе, помещенный в вакуумную камеру, облучают потоком остронаправленного рентгеновского излучения, измеряют количество коллимированного под заданным углом потока рассеянных фотонов, оценивают характерную величину среднего угла мозаичности исследуемого образца η0 по характерной ширине дифракционного пика, но в отличие от прототипа вводят следующие новые признаки:
- для исследования образца используют вакуумную мишенную камеру, снабженную гониометрическим устройством;
- образец облучают потоком остронаправленного широкополосного рентгеновского излучения;
- определяют оптимальное значение угла рассеяния излучения χ так, чтобы характерная брэгговская частота ωg=g/2sin(χ/2), в окрестности которой сконцентрирован спектр излучения, рассеянного кристаллографической плоскостью, фиксируемой вектором обратной решетки g, попадала на наиболее пологий участок спектра первичного излучения;
- после оценки характерной величины среднего угла мозаичности исследуемого образца η0 устанавливают детектор излучения с угловым размером Δϑ, равным отношению размера детектора к расстоянию между детектором и мишенью, на расстоянии, соответствующем равенству Δϑ=η0;
- измеряют с помощью гониометра ориентационную зависимость числа рассеянных в заданном направлении квантов Ng(φ'), где φ' - угол отклонения кристалла от положения брэгговского резонанса;
- определяют функцию распределения микроблоков мозаичного кристалла в фиксированной плоскости Ф||(η||) по формуле
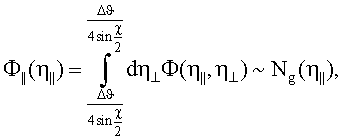
где Φ(η⊥,η||) - двухмерное дифференциальное распределение микроблоков по углам мозаичности,
Ng(η||) и Ng(η⊥) - измеренные при двух различных положениях кристалла ориентационные зависимости выхода рассеянного излучения, в которых аргумент φ' заменен на соответствующие углы мозаичности;
- поворачивают кристалл на 90 градусов вокруг среднего направления вектора обратной решетки (оси e1 на Фиг.1) и вновь измеряют ориентационную зависимость,
позволяющую определить функцию распределения в перпендикулярной плоскости по формуле:
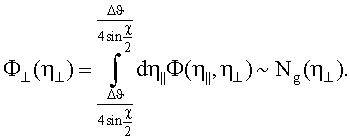
Таким образом, предлагаемый способ позволяет построить двумерную функцию распределения микроблоков мозаичного кристалла.
Для обоснования принципиальных положений предлагаемого способа ниже приводится краткое изложение теоретических основ описания обсуждаемого процесса рассеяния рентгеновского излучения в мозаичном кристалле.
Физической основой предлагаемого метода является детально изученный к настоящему времени процесс когерентного рассеяния рентгеновских лучей в упорядоченных кристаллических средах [1, 3]. Конечное выражение для спектрально-углового распределения количества квантов рассеянного излучения в виде суммы слагаемых, соответствующих различным отражающим плоскостям микроблока, задаваемых векторами обратной решетки g:
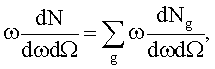
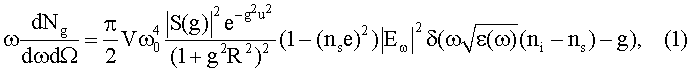
где V - объем кристалла, S(g) - структурный фактор ячейки, атомный формфактор которой рассчитан для статистической модели с экспоненциальной экранировкой, R -радиус электронного экранирования в модели атома, 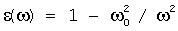 - обычная диэлектрическая проницаемость в рентгеновском диапазоне,
- обычная диэлектрическая проницаемость в рентгеновском диапазоне, 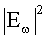 - спектр падающей немонохроматической волны, распространяющейся в направлении ni, e - вектор поляризации падающей волны, (eni)=0, ns - единичный вектор в направлении распространения рассеянной волны. Поскольку слагаемые в (1), отвечающие различным векторам обратной решетки g, вносят независимый вклад в выход рассеянного излучения, достаточно проанализировать одно слагаемое, соответствующее фиксированному g.
- спектр падающей немонохроматической волны, распространяющейся в направлении ni, e - вектор поляризации падающей волны, (eni)=0, ns - единичный вектор в направлении распространения рассеянной волны. Поскольку слагаемые в (1), отвечающие различным векторам обратной решетки g, вносят независимый вклад в выход рассеянного излучения, достаточно проанализировать одно слагаемое, соответствующее фиксированному g.
Для дальнейшего анализа необходимо выразить входящие в (1) векторные величины через угловые переменные в соответствии с Фиг.1 «Геометрия эксперимента» и формулами
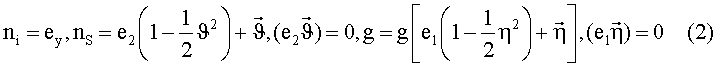
Согласно (2) угловая переменная 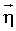 описывает искомую мозаичность кристалла. Для нахождении функции распределения Φ(η⊥,η||) микроблоков мозаичного кристалла по углам мозаичности η⊥,η||, при взаимной ориентации векторов е1, е2 и еy, близкой к брэгговскому резонансу
описывает искомую мозаичность кристалла. Для нахождении функции распределения Φ(η⊥,η||) микроблоков мозаичного кристалла по углам мозаичности η⊥,η||, при взаимной ориентации векторов е1, е2 и еy, близкой к брэгговскому резонансу
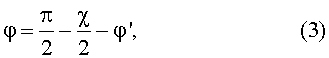
где φ'<<1 - угол отклонения системы «кристалл - падающее излучение» от положения, соответствующего брэгговскому резонансу. Найдем полное число N рассеянных фотонов в рефлексе, соответствующем вектору g, как функцию ориентационного угла φ', проинтегрировав (1) по углам излучения ϑ⊥,ϑ|| энергии фотонов ω и усреднив результат по мозаичности. Соответствующая формула имеет вид
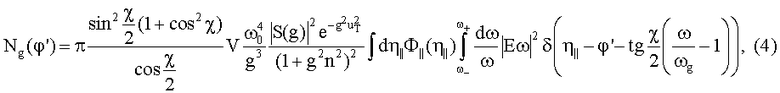
где проведено усреднение по поляризациям исходного неполяризованного излучения (при этом среднее <1-(nSe)2> приблизительно равно
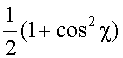
и введены следующие обозначения:
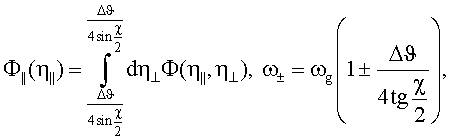
где Ф(η⊥,η||) - двумерное дифференциальное распределение микроблоков по углам мозаичности, Δϑ<<1 - угловой размер фотонного коллиматора с квадратным поперечным сечением (величина Δϑ определяется как отношение размера детектора излучения к расстоянию между детектором и мишенью).
Для дальнейшего решения необходимо совершить преобразование Фурье по переменной φ' в правой и левой частях полученного уравнения
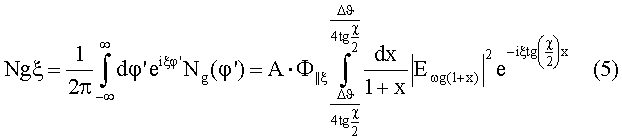
В случае широкополосного излучения (условие широкополосности является принципиальным !), спектр которого мало меняется в пределах ω-<ω<ω+ в окрестности брэгговской частоты ωg=g/2sin(χ/2), (синхротронное излучение идеально подходит для реализации рассматриваемого метода), интеграл по dx в (5) легко берется. При этом с помощью обратного преобразования Фурье из (5) можно получить точную формулу для функции распределения по углу мозаичности η||
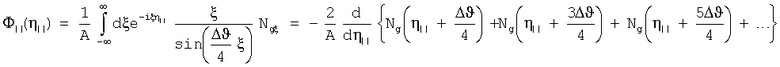
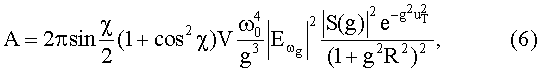
где 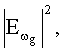
- спектральная плотность первичного излучения в окрестности брэгговской частоты. Важно отметить, что искомая функция Ф||(η||), описывающая распределение микроблоков мозаичного кристалла по ориентационному углу η|| непосредственно выражается через экспериментально измеряемую ориентационную зависимость выхода рассеянного излучения Ng(φ'). Поворотом мишени на 90 градусов вокруг среднего направления вектора обратной решетки (оси е1) с помощью гониометра снимают ориентационную зависимость выхода в перпендикулярной плоскости. Тем самым определяется функция распределения 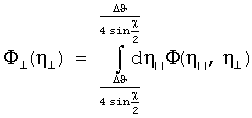
Таким образом, предлагаемый метод позволяет определять двумерную функцию распределения микроблоков мозаичного кристалла по углам мозаичности.
Остановимся на анализе чрезвычайно важного вопроса о влиянии углового размера фотонного коллиматора Δϑ на результаты измерения искомых функций распределения Ф||(η||), Ф⊥(η⊥). Обсуждаемый вопрос имеет принципиальное значение, поскольку при выводе главного результата (6) широко использовалось приближение малости углов ϑ,η,φ'.
Укажем, прежде всего, на важное свойство распределения Ф||(η||), следующее из (6) в пределе Δϑ→0 (в реальности достаточно, чтобы угловой размер коллиматора Δϑ был малым по сравнению с полушириной функции зависимости числа фотонов в рефлексе от ориентационного угла Ng(φ') измеряемой в эксперименте). Замечаем, что в обсуждаемых условиях сумма функций со сдвинутыми значениями аргумента в (6) сводится приближенно к интегральной сумме, поэтому результат (6) в рассматриваемых условиях существенно упрощается и принимает вид рабочей для предлагаемого способа формулы
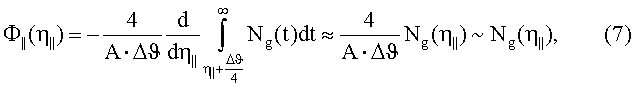
показывающий, что в рассматриваемых условиях искомая функция распределения оказывается пропорциональной измеряемой ориентационной зависимости Ng(η||). Более того, пропорциональность искомой функции распределения Ф||(η||), измеряемой в эксперименте зависимости Ng(φ'), позволяет совершенно не интересоваться величиной коэффициента пропорциональности в (7), не меняющего формы кривой Ng(φ').
С уменьшением коллиматора растет время набора статистики в эксперименте, поэтому проблема выбора оптимального значения величины Δϑ должна быть решена количественно. Пусть, например, ориентационная зависимость имеет гауссову форму
Ng(φ')~exp(-φ'2/η2 0). При этом степень отличия формы искомой функции распределения от формы ориентационной зависимости будет описываться различием двух функций exp(-x2) и
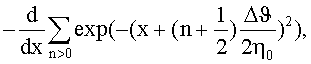
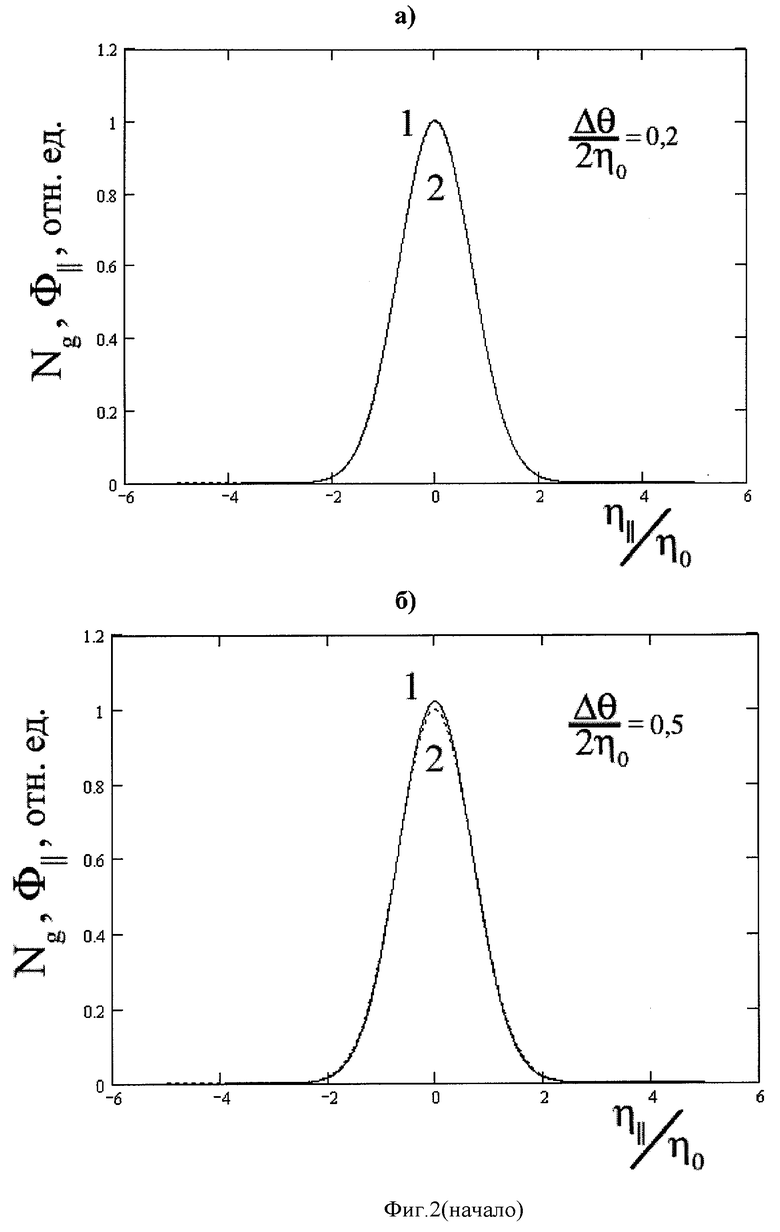
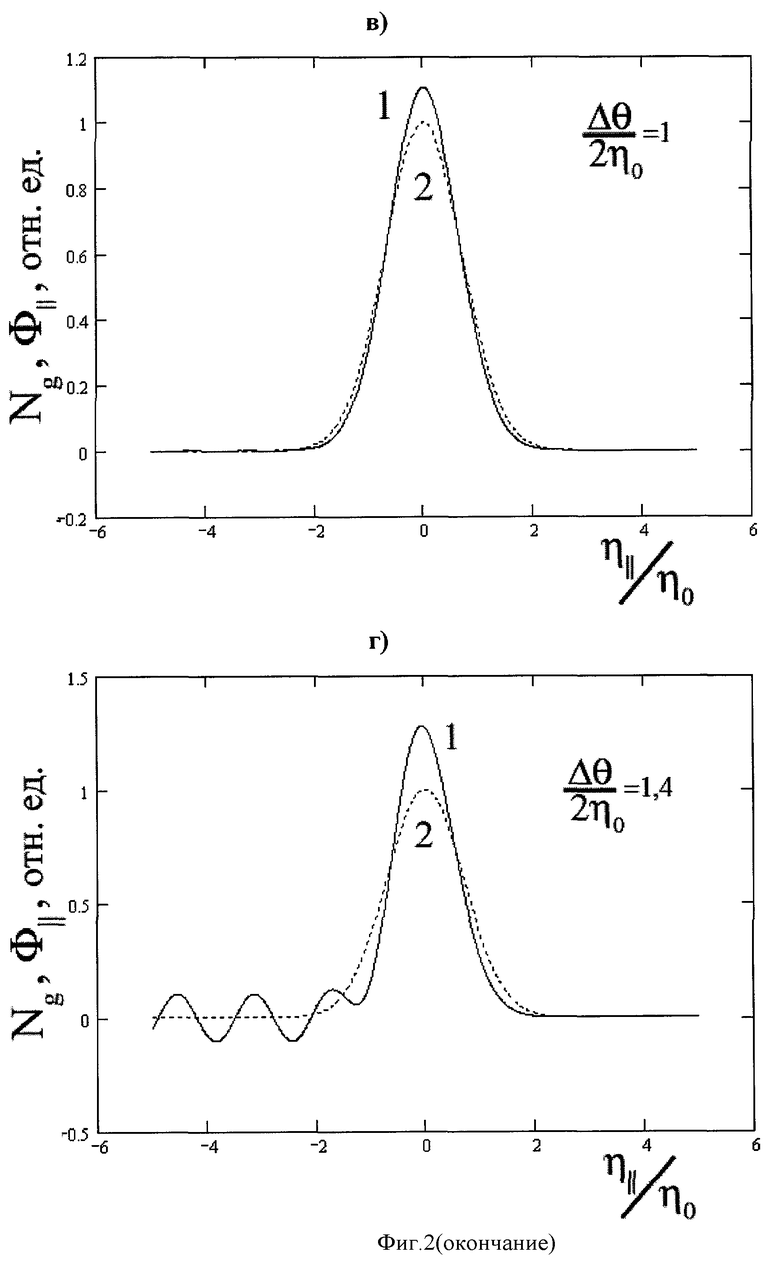
первая из которых соответствует измеряемой ориентационной зависимости, а другая - искомой функции распределения. На Фиг.2 приведены кривые, показывающие влияние конечности размера фотонного коллиматора на искажение формы функции распределения микроблоков кристалла по углу мозаичности по сравнению с формой исходной ориентационной зависимости выхода рассеянного излучения. Непосредственно из Фиг.2 следует, что оптимальное значение Δϑ равно η0.
Для реализации способа необходимо иметь источник широкополосного рентгеновского излучения в области энергий фотонов порядка 10 кэВ (в качестве такого источника может быть использован синхротрон), вакуумную мишенную камеру с гониометром, рентгеновский детектор, работающий в области 10 кэВ с энергетическим разрешением порядка нескольких процентов.
Изобретение подтверждается изображениями, представленными на Фиг.1 и Фиг.2. Фиг.1 - «Геометрия эксперимента», где показано взаимное расположение значений векторов е1, е2 и еy, описывающих соответственно орт среднего направления вектора обратной решетки, ось фотонного коллиматора и направление распространения потока первичного излучения. На чертеже показаны направления изменения составляющих угла мозаичности 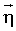 и угла наблюдения излучения
и угла наблюдения излучения 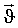 , лежащих в плоскости рисунка, а также угол рассеяния фотонов χ, и ориентационный угол φ, связанный с углом χ соотношением
, лежащих в плоскости рисунка, а также угол рассеяния фотонов χ, и ориентационный угол φ, связанный с углом χ соотношением
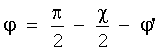
(φ'<<1), означающим, что положение кристалла соответствует резонансному брэгговскому условию отражения для среднего направления вектора обратной решетки е1, направления распространения первичного излучения еy, оси фотонного канала е2.
Фиг.2 - «Связь функции распределения микроблоков по углу мозаичности с ориентационной зависимостью числа рассеянных квантов», где приведены кривые, представляющие нормированные зависимости функции распределения микроблоков от угла мозаичности (кривые 1) и соответствующие ориентационные зависимости (кривые 2). Аргумент х определен формулой х=η///η0. Кривые построены для случая гауссовой формы ориентационной зависимости при различных значениях параметра Δϑ/2η0. Из Фиг.2а) и Фиг.2б) непосредственно следует, что в области значений параметра Δϑ/2η0<1/2 искажения практически отсутствуют. С другой стороны, в области значений Δϑ/2η0>l/2 на Фиг.2 в) и Фиг.2 г) искажения нарастают по мере роста указанного параметра и в области Δϑ/2η0>1 использование предлагаемого метода становится проблематичным.
Пример осуществления способа.
Исследуемый образец помещают в вакуумную мишенную камеру с гониометром и облучают потоком остронаправленного широкополосного рентгеновского излучения. Затем измеряют ориентационную зависимость количества квантов, рассеянных на заданный угол, который подбирают из расчета попадания брэгговской частоты ωg=g/2sin(χ/2), в окрестности которой сосредоточен спектр рассеянного излучения, в область частот, в которой спектр первичного излучения приблизительно постоянен. Оценивают средний угол мозаичности исследуемого кристалла η0 по характерной ширине дифракционного пика и устанавливают детектор излучения на расстоянии, соответствующем равенству Δϑ=η0. Измеряют с помощью гониометра ориентационную зависимость выхода количества рассеянных квантов, при этом ориентационный угол отсчитывается от положения кристалла, соответствующего точному условию брэгговского резонанса. Поворачивают кристалл на 90 градусов вокруг среднего направления вектора обратной решетки (оси e1 на Фиг.1) и вновь снимают ориентационную зависимость, позволяющую определить функцию распределения в перпендикулярной плоскости. Перестраивают кривые ориентационной зависимости в терминах углов мозаичности, нормируя для удобства кривые на единицу в максимуме, либо на единичную площадь под кривой, поскольку согласно конкретному примеру, приведенному на Фиг.2б) «Связь функции распределения микроблоков по углу мозаичности с ориентационной зависимостью числа рассеянных квантов», форма искомой функции распределения идентична форме измеряемой ориентационной зависимости.
Основное преимущество предлагаемого способа по сравнению с традиционными рентгеноструктурными способами измерения мозаичности кристаллов заключается в возможности определять двумерную функцию распределения микроблоков по углам мозаичности, а не усредненные параметры функции распределения с постулируемой формой. Следует также иметь в виду, что для определения функции распределения отсутствует необходимость проводить абсолютные измерения выхода рассеянного излучения.
Источники информации
1. Р.Джеймс. Оптические принципы дифракции рентгеновских лучей, М.: ИЛ, 1950.
2. S. Caticha-Ellis. Acta Crystallogr., A25, (1969) 666.
3. З.Г.Пинскер. Рентгеновская кристаллооптика, М.: Наука, 1982.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЗЕРЕН В УЛЬТРАМЕЛКОДИСПЕРСНОЙ СРЕДЕ | 2008 |
|
RU2386582C2 |
| Устройство для определения кристаллографических направлений монокристаллов | 1983 |
|
SU1176457A1 |
| СПОСОБ РЕНТГЕНОСПЕКТРАЛЬНОГО ОПРЕДЕЛЕНИЯ РАЗМЕРОВ НАНОЧАСТИЦ В ОБРАЗЦЕ | 2013 |
|
RU2548601C1 |
| Способ юстировки коллиматора пучка тормозного @ -излучения | 1984 |
|
SU1202490A1 |
| Способ генерации монохроматического направленного рентгеновского излучения | 1987 |
|
SU1513528A1 |
| Способ ориентирования монокристаллической мишени | 1981 |
|
SU976509A1 |
| Способ рентгеновского дифрактометрического анализа поликристаллических объектов с аксиальной текстурой | 1982 |
|
SU1062579A1 |
| СПОСОБ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА | 1998 |
|
RU2142623C1 |
| Рентгеновский спектрометр | 1983 |
|
SU1141321A1 |
| СПОСОБ СОЗДАНИЯ СИГНАТУРЫ ДЛЯ ДРАГОЦЕННОГО КАМНЯ С ИСПОЛЬЗОВАНИЕМ РЕНТГЕНОВСКОЙ ВИЗУАЛИЗАЦИИ | 2015 |
|
RU2690707C2 |
Использование: для определения мозаичности кристалла. Сущность заключается в том, что помещают образец в вакуумную камеру, облучают образец потоком остронаправленного рентгеновского излучения и оценивают характерную величину среднего угла мозаичности исследуемого образца no по характерной ширине дифракционного пика, при этом мозаичность кристалла определяют по функциям распределения микроблоков мозаичного кристалла по углам мозаичности η⊥, η// в двух взаимно перпендикулярных направлениях, для чего образец помещают в вакуумную мишенную камеру, снабженную гониометром, облучают потоком широкополосного рентгеновского излучения, определяют значение угла рассеяния излучения χ, так, чтобы брэгговская частота ωg=g/2sin(χ/2), в окрестности которой сконцентрирован спектр излучения, рассеянного кристаллографической плоскостью, фиксируемой вектором обратной решетки g, попадала на наиболее пологий участок спектра первичного излучения, после оценки величины среднего угла мозаичности η0 устанавливают детектор излучения с угловым размером Δϑ, равным отношению размера детектора к расстоянию между детектором и мишенью, на расстоянии, соответствующем равенству Δϑ=η0, измеряют с помощью гониометра ориентационную зависимость числа рассеянных квантов Ng(φ'), где φ' - угол отклонения кристалла от положения брэгговского резонанса, и определяют функцию распределения микроблоков мозаичного кристалла в фиксированной плоскости, затем поворачивают кристалл на 90 градусов вокруг среднего направления вектора обратной решетки и вновь измеряют с помощью гониометра ориентационную зависимость, позволяющую определить функцию распределения микроблоков мозаичного кристалла в перпендикулярной плоскости. Технический результат - обеспечение возможности определения двумерной функции распределения микроблоков мозаичного кристалла по углам мозаичности. 2 ил.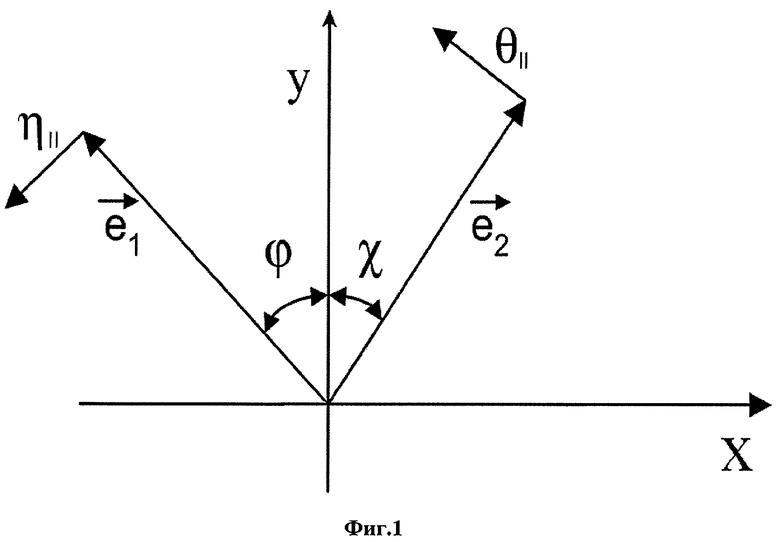
Способ определения мозаичности кристалла, заключающийся в помещении образца в вакуумную камеру, облучении образца потоком' остронаправленного рентгеновского излучения и оценке характерной величины среднего угла мозаичности исследуемого образца η0 по характерной ширине дифракционного пика, отличающийся тем, что мозаичность кристалла определяют по функциям распределения микроблоков мозаичного кристалла по углам мозаичности η⊥, η//, для чего образец помещают в вакуумную мишенную камеру, снабженную гониометром, облучают потоком широкополосного рентгеновского излучения, определяют значение угла рассеяния излучения χ так, чтобы брэгговская частота ωg=g/2sin(χ/2), в окрестности которой сконцентрирован спектр излучения, рассеянного кристаллографической плоскостью, фиксируемой вектором обратной решетки g, попадала на наиболее пологий участок спектра первичного излучения, после оценки величины среднего угла мозаичности η0 устанавливают детектор излучения с угловым размером Δϑ, равным отношению размера детектора к расстоянию между детектором и мишенью, на расстоянии, соответствующем равенству Δϑ=η0, измеряют с помощью гониометра ориентационную зависимость числа рассеянных квантов Ng(φ'), где φ' - угол отклонения кристалла от положения брэгговского резонанса, и определяют функцию распределения микроблоков мозаичного кристалла в фиксированной плоскости Ф||(η||) по формуле
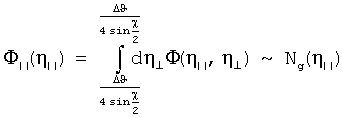 ,
,
затем поворачивают кристалл на 90° вокруг среднего направления вектора обратной решетки и вновь измеряют с помощью гониометра ориентационную зависимость, позволяющую определить функцию распределения микроблоков мозаичного кристалла в перпендикулярной плоскости Φ⊥(η⊥) по формуле
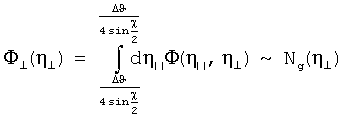 ,
,
причем в указанных формулах Φ(η⊥, η||) - двумерное дифференциальное распределение микроблоков по углам мозаичности, N(η||) и N(η⊥) - ориентационные зависимости выхода рассеянного излучения, измеренные при двух положениях кристалла, повернутых на угол 90° относительно друг друга вокруг среднего направления вектора обратной решетки g, в которых аргумент φ' заменен на соответствующие углы мозаичности.
| Р.ДЖЕЙМС | |||
| ОПТИЧЕСКИЕ ПРИНЦИПЫ ДИФРАКЦИИ РЕНТГЕНОВСКИХ ЛУЧЕЙ | |||
| - М.: ИЛ, 1950 | |||
| Рентгенографический способ исследования структурного совершенства монокристаллов (его варианты) | 1983 |
|
SU1133520A1 |
| Способ определения мозаичности монокристаллов | 1986 |
|
SU1413492A1 |
| Способ контроля степени мозаично-СТи изОгНуТОгО МОНОКРиСТАллА | 1979 |
|
SU819653A1 |
| Устройство динамической фокусировки | 1984 |
|
SU1246410A1 |
| US 6498829 B1, 24.12.2002. | |||
Авторы
Даты
2009-12-20—Публикация
2008-08-25—Подача