Предпосылки создания изобретения
Область техники, к которой относится изобретение
Это изобретение относится к способам и к устройству для определения характеристик пластовых флюидов. Более конкретно изобретение относится к определению характеристик пластовых флюидов путем использования скважинного пробоотборника флюидов, снабженного модулем ядерного магнитного резонанса.
Уровень техники
В нефтегазодобывающей отрасли имеются разнообразные разработанные приборы, посредством которых можно определять характеристики пластовых флюидов. Например, посредством скважинных приборов для отбора проб и исследования флюидов, таких как модульный динамический опробователь пластов (MDT™) фирмы Schlumberger, можно получать важную информацию о типе и характеристиках пластовых флюидов в дополнение к получению измерений пластового давления, проницаемости и подвижности. Посредством этих приборов можно выполнять измерения характеристик флюидов в скважине, используя модули датчиков, расположенные в приборах. В качестве альтернативы посредством этих приборов пробы флюидов могут извлекаться из пласта, собираться в сосуды и доставляться на поверхность для анализа. Собранные пробы в рабочем порядке отправляют в лаборатории по исследованию характеристик флюидов для анализа физических характеристик, которые включают в себя, помимо всего прочего, вязкость нефти, соотношение газ/нефть, массовую плотность, плотность в градусах Американского нефтяного института (API), молекулярный состав, концентрацию H2S, асфальтенов, смол и других разнообразных примесей. Однако лабораторные данные могут не быть полезными или соответствующими характеристикам пластового флюида, поскольку характеристики проб могут изменяться при доставке на поверхность.
Например, пластовый флюид может содержать растворенный газ, который выделяется из жидкостей, когда внешнее давление падает. Точно так же пластовый флюид может включать в себя вещества, которые могут выпадать в осадок при снижении окружающей температуры. И в том, и в другом случае измеренные лабораторные данные могут не соответствовать реальным характеристикам пластовых флюидов в естественном залегании. Поэтому желательно, чтобы анализ пластовых флюидов выполнялся в скважинных условиях.
В нескольких патентах США раскрыты способы и устройства для выполнения ядерно-магнитных резонансных измерений в стволе скважины на пробах флюида, извлекаемого из подземного пласта. Например, в патенте США №6346813 В1 (в патенте '813), выданном Kleinberg, раскрыт модуль ядерного магнитного резонанса на отводной линии модульного динамического опробователя пластов MDT™, предназначенный для определения различных характеристик пластового флюида по сигналам магнитного резонанса. Патент '813 переуступлен правопреемнику настоящего изобретения и полностью включен в настоящую заявку посредством ссылки. В патенте США №6107796, выданном Prammer M., раскрыты устройства и способы для определения степени загрязнения пробы пластовой сырой нефти, которая может быть загрязнена фильтратом бурового раствора на углеводородной основе. Способом, раскрытым в этом патенте, контролируются изменения ядерно-магнитных резонансных характеристик проб флюида в зависимости от времени, когда пробы флюида закачиваются из пласта в пробоотборник.
Пластовые флюиды часто содержат несколько компонентов, каждый из которых с большой вероятностью имеет особую диффузионную характеристику. Поэтому измерение коэффициентов диффузии может дать ценную информацию о характеристиках пластовых флюидов. В некоторых ядерно-магнитных резонансных способах для измерения диффузионных характеристик пластовых флюидов используют градиенты магнитного поля. Например, в патенте США №6737864, выданном Prammer et al., раскрыто устройство для выполнения измерений Т1 на флюидах, протекающих в отводной линии пробоотборника флюида. В нем также раскрыт статический градиентный способ для выполнения диффузионных измерений на неподвижных пробах. В способе получения данных о диффузии на основании ядерно-магнитных резонансных измерений предполагается единственная диффузионная постоянная. Однако хорошо известно, что сырые нефти имеют распределение коэффициентов диффузии. Поэтому желательно иметь способы, посредством которых можно получать коэффициенты диффузии пластовых флюидов, не предполагая, что они имеют одинаковые диффузионные постоянные.
В патенте США №6111408 (в патенте '408), выданном Blades et al., раскрыты способы и устройства для измерения времен (Т1 и Т2) релаксации и коэффициентов (D) диффузии флюидов в модуле ядерно-магнитного резонанса пробоотборника флюидов. В способе, раскрытом в этом патенте, используют электромагнит для создания градиента осциллирующего импульсного поля между рефокусирующими импульсами последовательности импульсов Карра-Парселла-Мейбума-Гилла. Градиент осциллирующего импульсного поля подстраивается по фазе (синхронизируется) к импульсам последовательности Карра-Парселла-Мейбума-Гилла (см. фиг.5 в патенте '408). Градиентом импульсного поля дефазируют спины, а затем градиент выключают на период времени, в течение которого спины диффундируют. После периода диффузии включают градиент осциллирующего импульсного поля для рефазирования спинов, за которым следует спиновое эхо. Затем первое спиновое эхо рефокусируют посредством серии радиочастотных 180-градусных импульсов, чтобы получить дополнительные спиновые эхо. Хотя с помощью синхронизированных по фазе импульсов градиентов осциллирующего импульсного поля можно обеспечить кодирование диффузии, желательно иметь лучшие способы и устройства для осуществления кодирования диффузии.
В патенте США №6346813 В1, выданном Kleinberg, раскрыт модуль ядерного магнитного резонанса, предназначенный для оценивания характеристик флюидов в приборе для отбора и исследования флюидов, таком как модульный динамический опробователь пластов (MDT™). В этом патенте раскрыты способы, предназначенные для нахождения связи времен релаксации и коэффициентов диффузии флюидов с вязкостью, соотношением газ/нефть и с другими характеристиками флюидов, представляющими интерес. В родственном патенте США №5796252, выданном Kleinberg et al. (в патенте '252), раскрыто применение последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла для кодирования информации о диффузии. В таком случае для получения коэффициента диффузии по данным на основе последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла - используют простой приближенный способ. Затем коэффициент диффузии используют для корректировки амплитуд спиновых эхо, чтобы получить более точные объемы нефти в пластах. В способах, раскрытых в патенте '252, для сырых нефтей также принимается единый коэффициент диффузии.
В патенте США №6462542 В1, выданном Venkataramanan L. et al. (в патенте '542) раскрыты последовательности импульсов, «редактируемые диффузией». Информацию о диффузии кодируют, используя статический градиент приложенного магнитного поля, используя ядерно-магнитный каротажный прибор, спускаемый на тросе или применяемый для каротажа в процессе бурения. Эти последовательности импульсов представляют собой модификации последовательностей Карра-Парселла-Мейбума-Гилла. Последовательность импульсов отличается от последовательности Карра-Парселла-Мейбума-Гилла тем, что один или несколько ранних эхо-сигналов регистрируют вместе с эхо-сигналом, отнесенным на большой промежуток времени, чтобы получить диффузионное затухание эхо-сигналов. Остальные эхо-сигналы регистрируют при небольшом разнесении, чтобы минимизировать диффузионные эффекты (D). В патенте '542 также раскрыта инверсия физической модели путем использования набора последовательностей импульсов, редактируемых диффузией, что позволяет получать двумерные функции распределения D-T2, T1-T2 и Т1/Т2-Т2.
В патенте США №6570382 (Hűrlimann et al.) также раскрыты последовательности импульсов, «редактируемые диффузией», которые могут включать в себя последовательность градиентов импульсного поля.
Хотя имеются разнообразные ядерно-магнитные устройства и способы, предназначенные для определения характеристик пластовых флюидов, все же необходимы лучшие способы и устройства для определения характеристик пластовых флюидов.
Сущность изобретения
Один объект изобретения относится к способам для определения характеристики пластового флюида. Способ согласно одному варианту осуществления изобретения включает в себя регистрацию набора ядерно-магнитных резонансных измерений пробы флюида путем использования последовательности импульсов, которая включает в себя градиентные импульсы импульсного поля для кодирования информации о диффузии, при этом каждое магнитно-ядерное резонансное измерение в наборе регистрируют при особом значении параметра в градиентных импульсах импульсного поля для получения особого диффузионного эффекта, в котором регистрацию выполняют в пробоотборнике пластового флюида в стволе скважины; инвертирование набора ядерно-магнитных резонансных измерений для получения функции распределения, которая связывает диффузионные характеристики пробы флюида с характеристикой ядерного магнитного резонанса пробы флюида; и определение характеристики пластового флюида на основании функции распределения.
Другой объект изобретения относится к датчику ядерно-магнитного резонанса. Датчик ядерно-магнитного резонанса согласно одному варианту осуществления изобретения включает в себя постоянный магнит, способный создавать по существу однородное магнитное поле на отборной камере; радиочастотную антенну, окружающую отборную камеру, при этом радиочастотная антенна выполнена с возможностью создания осциллирующих магнитных полей, которые имеют магнитные моменты, по существу ортогональные к направлению по существу однородного магнитного поля, создаваемого постоянным магнитом, и по меньшей мере одну катушку, подключенную к блоку управления, при этом по меньшей мере одна катушка и блок управления выполнены с возможностью создания градиента импульсного магнитного поля на отборной камере управляемым образом, так что градиент импульсного магнитного поля имеет выбранную величину и заранее определенную длительность.
Другие объекты изобретения станут очевидными из нижеследующего описания, чертежей и формулы изобретения.
Краткое описание чертежей
На фиг.1 приведен вид прибора для исследования (отбора проб) пластового флюида из предшествующего уровня техники, имеющего модуль ядерно-магнитного резонанса;
фиг.2 - вид датчика ядерно-магнитного резонанса согласно одному варианту осуществления изобретения;
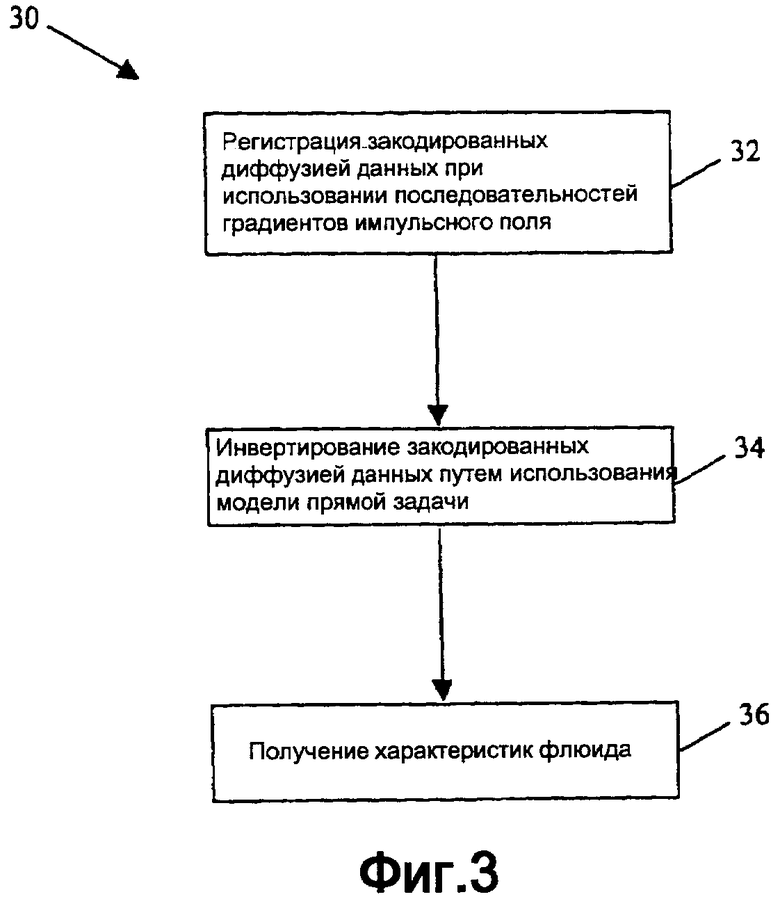
фиг.3 - иллюстрация способа определения характеристик пластового флюида согласно одному варианту осуществления изобретения;
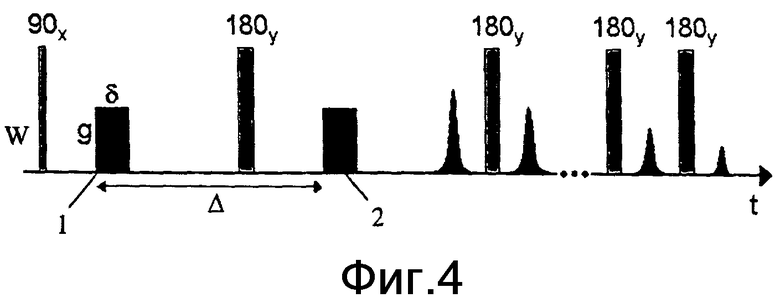
фиг.4 - иллюстрация последовательности импульсов градиентов импульсного поля - Карра-Парселла-Мейбума-Гилла согласно одному варианту осуществления изобретения;
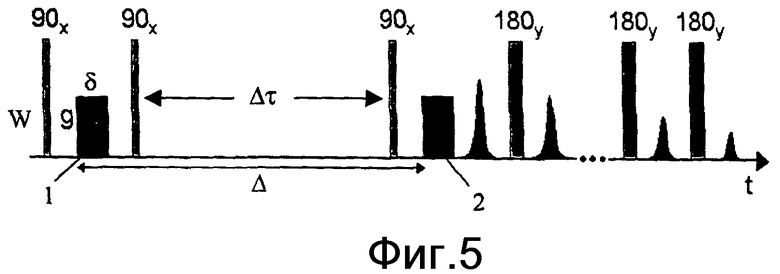
фиг.5 - иллюстрация последовательности импульсов градиентов импульсного поля со стимулированным эхо - последовательности Карра-Парселла-Мейбума-Гилла согласно одному варианту осуществления изобретения;
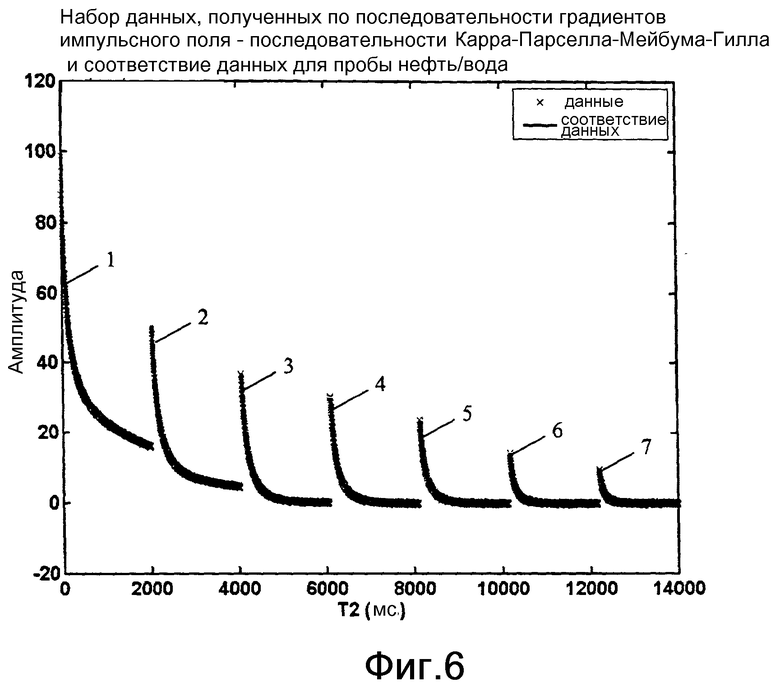
фиг.6 - иллюстрация набора кодированных данных о диффузии, полученных по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла, которые могут быть использованы для определения характеристики пластового флюида путем использования способа, согласно одному варианту осуществления изобретения;
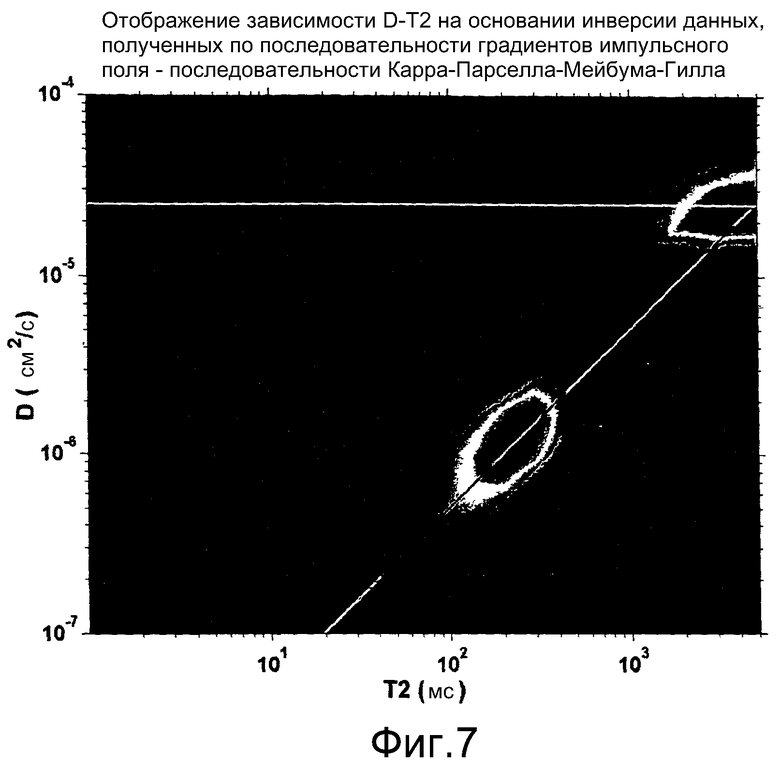
фиг.7 - график двумерной функции распределения, вычисленной на основании набора данных, показанных на фиг.6, согласно одному варианту осуществления изобретения; и
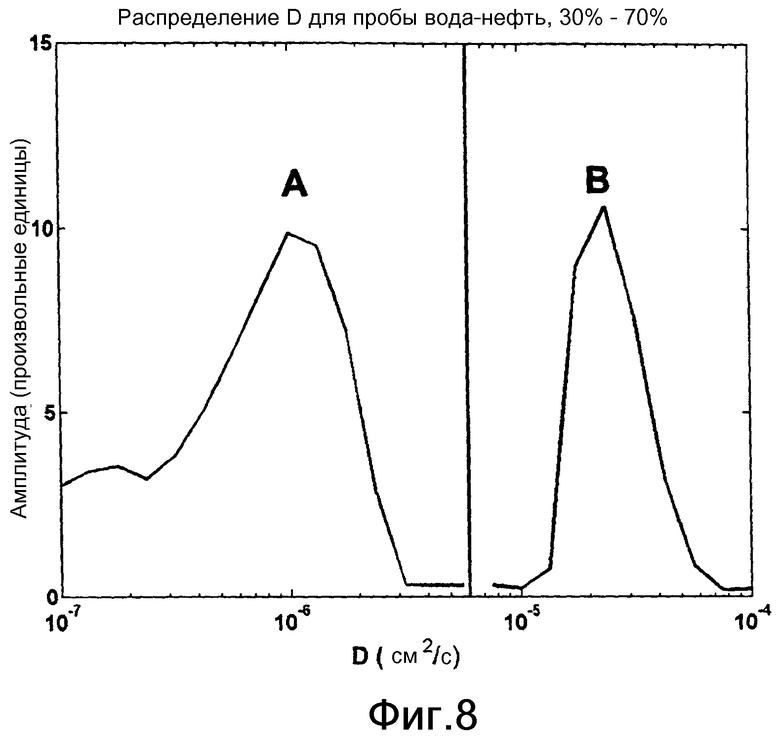
фиг.8 - графики одномерной функции распределения, полученной на основании двумерной функции распределения, показанной на фиг.7, согласно одному варианту осуществления изобретения.
Подробное описание изобретения
Варианты осуществления изобретения относятся к устройству и к способам для определения свойств пластового флюида посредством использования модуля ядерно-магнитного резонанса в скважинном приборе, таком, как пробоотборник флюидов, раскрытый в патенте США №6346813 В1, выданном Kleinberg. Примером прибора для исследования пластового флюида является модульный динамический опробователь пластов, поставляемый под торговым названием MDTТМ фирмой Schlumberger Technology Corp. (Хьюстон, Техас).
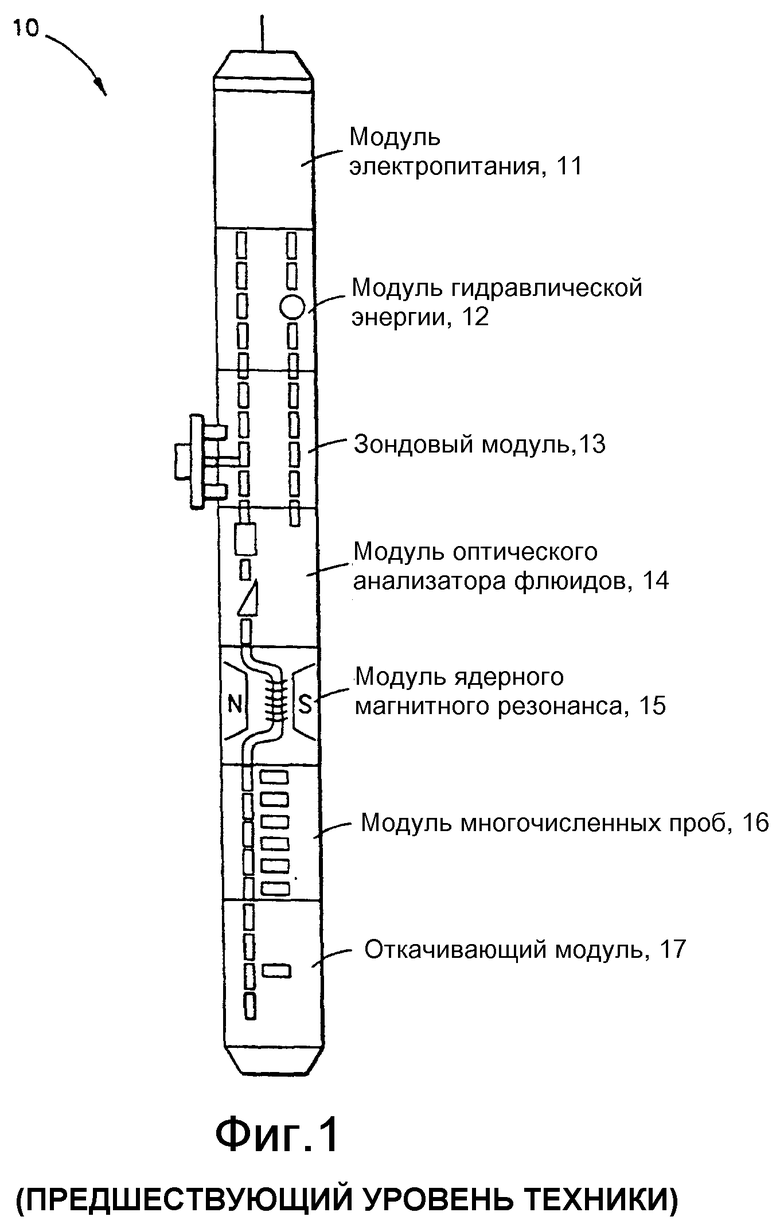
На фиг.1 показан типовой прибор 10 для исследования (или отбора проб) пластовых флюидов (например, прибор MDT™), который включает в себя следующие модули: модуль 11 электроники, который может включать в себя процессор и запоминающее устройство; модуль 12 гидравлической энергии; зондовый модуль 13, который может быть размещен с обеспечением гидравлического уплотнения относительно пласта; откачивающий модуль 17; оптический анализатор 14 флюидов; и модуль 16 многочисленных проб. Кроме того, пробоотборник 10 пластовых флюидов включает в себя модуль 15 ядерно-магнитного резонанса. Модуль 15 ядерно-магнитного резонанса может включать в себя датчик магнитного ядерно-резонанса согласно изобретению.
Датчик ядерно-магнитного резонанса согласно вариантам осуществления изобретения включает в себя постоянный магнит, который может создавать по существу однородное статическое магнитное поле по объему пробы флюида. В дополнение к этому датчик ядерно-магнитного резонанса включает в себя по меньшей мере одну катушку, которая может создавать на объеме пробы градиенты импульсного поля с определенной магнитной индукцией и длительностью. При однородном статическом магнитном поле в сочетании с градиентом импульсного магнитного поля можно получать измерения с более высокими отношениями сигнала к шуму, поскольку резонирует больший объем пробы по сравнению с объемом в случае статического магнитного поля, имеющего градиент статического поля, который может вызвать резонанс только в небольшой части пробы (в «слое пробы»). Датчик ядерно-магнитного резонанса согласно изобретению также включает в себя катушку (радиочастотную антенну) для возбуждения импульсов радиочастотного магнитного поля. Магнитный момент радиочастотной антенны является по существу перпендикулярным к магнитному моменту статического магнитного поля.
На фиг.2 показан датчик ядерно-магнитного резонанса согласно одному варианту осуществления изобретения. Как показано на фиг.2, датчик 20 ядерно-магнитного резонанса включает в себя магнит 21 (например, постоянный магнит), который предназначен для возбуждения по существу однородного магнитного поля
(В0) в объеме 22 пробы. Постоянный магнит 21 может быть изготовлен из кобальто-самариевого сплава или из любого другого подходящего материала. Постоянный магнит 21, который может быть выполнен в виде одной детали или в виде нескольких деталей, которые окружают объем 22 пробы, также может содержать несколько проницаемых полюсных деталей, прикрепленных к его поверхностям, для профилирования магнитного поля и для снижения градиента магнитного поля в области пробы, чтобы статическое поле было по существу однородным в объеме (в отборной камере) 22 пробы.
В некоторых вариантах осуществления объем 22 пробы может быть выполнен с возможностью соединения с отводной линией пластового флюида, так что датчик 20 может быть использован для измерения или контроля характеристик флюида, протекающего через объем (отборную камеру) 22 пробы. Радиочастотная антенна (катушка) 23 окружает объем 22 пробы. Радиочастотная антенна 23 предназначена для излучения осциллирующего радиочастотного магнитного поля (В1), имеющего магнитный момент, по существу перпендикулярный (ортогональный) к магнитному моменту статического магнитного поля, создаваемого постоянным магнитом 21. Радиочастотная антенна 23 может содержать соленоидную катушку, седлообразную катушку или любую другую подходящую катушку. Обычному специалисту в области техники, к которой относится изобретение, должно быть понятно, что та же самая радиочастотная антенна 23 может действовать как излучатель для возбуждения осциллирующего магнитного поля и как приемник для приема сигналов, как раскрыто в патенте США №6346813 В1, выданном Kleinberg. В качестве альтернативы могут быть использованы отдельные излучающая и приемная антенны.
Датчик 20 ядерно-магнитного резонанса, показанный на фиг.2, также включает в себя две градиентные катушки 25а и 25b, которые выполнены с возможностью создания градиентов магнитного поля на объеме 22 пробы. Градиентные катушки 25а и 25b подключены к блоку 27 управления, который может возбуждать градиентные катушки 25а и 25b с выбранной мощностью в течение заданного отрезка времени. Хотя показаны две градиентные катушки 25а и 25b, обычному специалисту в области техники, к которой относится изобретение, должно быть понятно, что без отступления от объема изобретения можно использовать одну или несколько градиентных катушек. Во время действия градиентного импульса могут быть образованы противоположные магнитные поля bg для создания градиента g магнитного поля в объеме пробы. Градиент g магнитного поля обычно измеряют в единицах Гс/см. Датчик 20 может быть защищен и может поддерживаться корпусом 24. Корпус 24 может быть изготовлен из магнитной стали с высокой магнитной проницаемостью для удержания магнитного поля В0 и для придания прочности узлу.
В дополнение к этому некоторые варианты осуществления изобретения могут включать в себя экран 26, который разделяет радиочастотную антенну 23 и постоянный магнит 21. Экран может быть изготовлен из материала (например, из меди), который может предотвращать взаимодействие осциллирующего радиочастотного магнитного поля, создаваемого радиочастотной антенной 23, с постоянным магнитом 21, так что магнитоакустические колебания в магните могут быть минимизированы.
Датчик ядерно-магнитного резонанса согласно вариантам осуществления изобретения может быть использован для выполнения измерений, имеющих отношение к диффузионным и релаксационным характеристикам проб флюидов. Поскольку эти характеристики обычно различаются для нефти и воды, то эти измерения могут иметь значение для определения относительной пропорции воды и нефти в пробе флюида. Кроме того, на основании этих измерений можно получать информацию о характеристиках нефти, включая состав, вязкость и соотношение газ/нефть (количество растворенного газа, содержащегося в нефти). Аналогичным образом для пробы флюида, которая может содержать (1) газ и воду, (2) газ, нефть и воду, (3) нефть и газ или (4) нефть и воду, измерения могут иметь значения для определения относительных пропорций различных компонентов, которые имеются в ней. Кроме того, на основании этих измерений можно получать информацию относительно характеристик углеводородов, которые являются важными для определения денежной стоимости продуктивного пласта и также являются ценными для принятия решения о заканчивании скважины.
На фиг.3 показан способ согласно одному варианту осуществления изобретения. Как показано на фиг.3, способ 30 включает в себя этап (этап 32) регистрации набора данных ядерно-магнитного резонанса с кодированной диффузией. Кодирование диффузии достигается путем использования при каждой регистрации градиентных импульсов импульсного поля. Один из параметров в градиентных импульсах импульсного поля изменяется при каждом измерении в наборе данных, так что каждое измерение включает в себя особый диффузионный эффект. Затем данные с кодированной диффузией инвертируют (этап 34) в соответствии с моделью прямой задачи, то есть в соответствии с физической моделью, описывающей спад сигналов спинового эха. Инверсия дает функцию распределения, связанную со свойствами флюида, например двумерную функцию f(D,T2) распределения, которая связывает коэффициенты (D) диффузии с временами (Т2) спин-спиновой релаксации. В заключение требуемые характеристики флюидов (например, коэффициенты диффузии, вязкости, молекулярные составы и т.д.) могут быть извлечены (этап 36) из функции распределения. Эти этапы более подробно описаны в нижеследующих частях описания.
Измерение ЯМР с градиентом импульсного поля представляет собой общепринятую процедуру, предназначенную для измерения коэффициентов диффузии молекул в жидкостях и в твердых телах. Способ, наиболее широко используемый для жидкостей, представляет собой способ Стейскала и Таннера (The Journal of Chemical Physics, v.42, №1, 288-292, 1965), который известен как способ градиента импульсного поля. Способ градиента импульсного поля может быть использован для точного измерения коэффициентов диффузии до ≈10-8 см2/с. Для вязких жидкостей и твердых тел с более медленной диффузией и/или с быстрой поперечной релаксацией широко используют способ градиента импульсного поля со стимулированным эхо, разработанный Таннером (The Journal of Chemical Physics, vol. 52, №5, pp.2523-2526, 1970). Способы градиента импульсного поля со стимулированным эхо обеспечивают лучшие результаты по сравнению со способами градиента импульсного поля только в случае, если времена (Т1) спин-решеточной релаксации заметно больше времен (Т2) поперечной или спин-спиновой релаксации. В последовательностях градиентов импульсного поля и градиентов импульсного поля со стимулированным эхо используют градиенты импульсного поля для кодирования информации о диффузии в изменениях спинового эха.
В способе изобретения можно использовать последовательность импульсов градиентов импульсного поля или градиентов импульсного поля со стимулированным эхо. Физический принцип, лежащий в основе обоих способов, заключается в том, что броуновское движение молекул вызывает ослабление интенсивностей сигналов ядерно-магнитного резонанса, которое может быть связано с коэффициентами диффузии молекулярных составляющих в пробе. Дополнительные 180° импульсы используют для рефокусировки первого эха и их добавляют с целью регистрации информации, касающейся другого механизма спада сигнала, то есть спада Т2 спиновых эхо. При последующем описании эти последовательности будут именоваться как последовательность градиентов импульсного поля - последовательность Карра-Парселла-Мейбума-Гилла (то есть последовательность градиентов импульсного поля Стейскала и Таннера, за которой следует серия 180° импульсов) и последовательность градиентов импульсного поля со стимулированным эхо - последовательность Карра-Парселла-Мейбума-Гилла (то есть последовательность Таннера градиентов импульсного поля со стимулированным эхо, за которой следует серия 180° импульсов).
На фиг.4 показана диаграмма, иллюстрирующая последовательность градиентов импульсного поля - последовательность Карра-Парселла-Мейбума-Гилла согласно одному варианту осуществления изобретения. Как видно, в типичную последовательность импульсов градиентов импульсного поля после первого 90° импульса и первого 180° импульса введены соответственно два градиентных импульса 1 и 2 импульсного поля. Затем первое эхо рефокусируют путем использования серии 180° импульсов. Импульсы градиентов импульсного поля отделены временем Δ задержки, и каждый из них имеет магнитную индукцию g градиента поля и длительность δ. Для получения другого диффузионного эффекта время Δ задержки, магнитную индукцию g градиента поля и длительность δ можно изменять.
Способ согласно вариантам осуществления изобретения, предназначенный для определения свойств пластового флюида, включает в себя регистрацию набора измерений по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла или по последовательности градиентов импульсного поля со стимулированным эхо - последовательности Карра-Парселла-Мейбума-Гилла. Число измерений в каждом наборе зависит от многих факторов. В общем случае в наборе достаточно иметь около 10 или меньше измерений. Каждое измерение в наборе отличается от каждого другого иной степенью диффузионного затухания эхо-сигналов вследствие изменения одного или нескольких параметров импульсов в последовательностях градиентов импульсного поля - последовательностях Карра-Парселла-Мейбума-Гилла или в последовательностях градиентов импульсного поля со стимулированным эхо - последовательностях Карра-Парселла-Мейбума-Гилла. Как отмечено выше и как показано на фиг.4, эти параметры включают в себя длительность (δ) импульсного градиента, магнитную индукцию (g) импульсного градиента, разнесение (задержку) Δ градиентных импульсов в последовательности градиентов импульсного поля.
Таким образом, ядерно-магнитные резонансные измерения получают «диффузионно-кодированными» и их можно инвертировать для образования функции распределения, связанной с характеристиками флюида. Например, функция распределения может быть двумерной функцией f(D, T2) распределения, связывающей коэффициенты (D) диффузии с временами (Т2) спин-спиновой релаксации пробы. Для пробы нефти с водой двумерное распределение f(D, T2) может быть использовано для оценивания, среди прочего, относительных объемов нефти и воды, вязкости нефти, молекулярного состава нефти и соотношения нефть/газ.
Кроме того, на основании двумерного распределения можно раздельно вычислять одномерные распределения диффузии и времен релаксации для нефти и воды. В дополнение к этому наборы частично поляризованных последовательностей градиентов импульсного поля - Карра-Парселла-Мейбума-Гилла могут быть зарегистрированы и инвертированы для получения трехмерной функции f(D, T2, T1) распределения, которая включает в себя время (Т1) спин-решеточной релаксации или отношение Т1/Т2.
Набор данных градиентов импульсного поля может быть инвертирован на основе физической модели (модели прямой задачи), которая описывает спад сигналов спиновых эхо, для получения (в общем виде) трехмерной функции f(D, T2, T1) распределения диффузии и времен релаксации для пробы флюида. Если в наборе данных для каждого измерения имеется достаточное время восстановления или ожидания, то не будет зависимости от Т1, и в результате инверсии образуется двумерная функция f(D, T2) распределения. Эти функции распределения дают ценную информацию относительно свойств проб флюидов.
Описание последовательностей импульсов, датчика и модели прямой задачи
Снова обратимся к фиг.4, где последовательность импульсов градиентов импульсного поля - Карра-Парселла-Мейбума-Гилла включает в себя 90° импульс возбуждения, создаваемый радиочастотным магнитным полем (B1) вдоль оси x в системе координат, вращающейся вокруг В0 со средней частотой (ωL) Лармора. 90° импульс поворачивает вектор намагниченности в поперечной (то есть x-y) плоскости. Затем создают градиент (g) магнитного поля длительностью (δ), который вызывает дефазировку спинов, зависящую от положения. После небольшой задержки используют 180° импульс для изменения знаков фаз спинов (или направления вращения спинов в поперечной плоскости). После другой небольшой задержки используют второй градиентный импульс для рефазировки спинов, которые были дефазированы первым градиентным импульсов. Рефазировка является эффективной только в случае, если спины не диффундировали из своих исходных мест. Для тех спинов, которые диффундировали на новые места в продолжение (Δ) диффузии, рефазировка не будет идеальной. Неидеальная рефазировка, обусловленная диффузией спинов, приводит к диффузионному ослаблению эхо. Информация относительно времени (Т2) спин-спиновой релаксации обеспечивается дальнейшим использованием ряда 180° импульсов, которые создают серию спиновых эхо. В случае однородного статического магнитного поля общее выражение для поперечной намагниченности (M(t)), измеряемой с помощью последовательности импульсов, показанной на фиг.4, дается следующим уравнением:
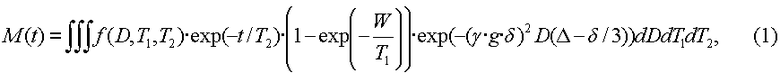
при этом M(t) оценивают в моменты t времени, в которые на фиг.4 наблюдаются спиновые эхо.
Уравнение (1) представляет собой интегральное уравнение Фредгольма первого рода, которому удовлетворяет трехмерная функция f(D, T1, T2) распределения коэффициентов диффузии и времен релаксации. Показательным множителем в подынтегральном выражении, который включает в себя Т2, учитывается спин-спиновая релаксация намагниченности, тогда как множителем, который включает в себя Т1, учитывается неполная поляризация намагниченности при условии, что она начинается от первоначального состояния нулевой намагниченности. Время W восстановления предшествует первому 90° импульсу, показанному на фиг.4. Если время W ожидания достаточно продолжительное (например, допустим в 5 раз больше самого продолжительного Т1 в пробе), то коэффициент неполной поляризации равен единице. В этом случае трехмерная функция распределения приводится к двумерной функции f(D, T2) распределения.
Показательным множителем, который включает в себя параметры градиентов импульсного поля, полученные Стейскалом и Таннером (1965), учитывается затухание эхо-сигналов, обусловленное диффузией. Коэффициент затухания градиентов импульсного поля в уравнении (1) будет более сложным при наличии статического градиента (gs) в дополнение к градиенту импульсного поля. Для этого случая Стейскал и Таннер показали, что коэффициент затухания, обусловленный диффузией, в уравнении (1) должен включать в себя два дополнительных члена: перекрестный член g·gs и второй член, который пропорционален квадрату статического градиента, то есть gs·gs. В предпочтительных вариантах осуществления этого изобретения используют статическое магнитное поле, которое является по существу однородным в объеме пробы, так что можно избежать усложнения, обусловленного градиентами статического поля. Однако специалистам в области техники, к которой относится изобретение, необходимо принять во внимание, что имеются модификации последовательностей градиентов импульсного поля Стейскала и Таннера, с помощью которых можно ослабить действие статического градиента. Используя такие модифицированные последовательности градиентов импульсного поля, варианты осуществления изобретения можно применять на практике при наличии статических градиентов. Подходящие последовательности могут включать в себя, но без ограничения ими, последовательности градиентов импульсного поля, которые раскрыли Karlicek и Lowe (“A modified pulsed gradient technique for measuring diffusion in the presence of large background gradients” в: J. of Mag. Res., v.37, p.75-91, 1980) и Cotts и др. (“Pulsed field gradient simulated echo methods for improved NMR diffusion measurements in heterogeneous systems” в: J. of Mag. Res., v.83, p.252-266, 1989).
Для измерения диффузии в вязких жидкостях и в твердых телах Таннер (J. of Chemical Physics, v.52, №5, 2523-2526) разработал последовательность, альтернативную последовательности Стейскала и Таннера, известную как последовательность «градиентов импульсного поля со стимулированным эхо». Эта последовательность может обеспечить более надежные измерения, посредством которых можно найти очень небольшие коэффициенты диффузии, и является оптимальной в системах, для которых Т1>>Т2. Как показано на фиг.5, последовательность Таннера со стимулированным эхо связана с последовательностью Карра-Парселла-Мейбума-Гилла.
Как показано на фиг.5, пара 90° импульсов введена между двумя импульсами градиентов импульсного поля. При такой последовательности второй 90° импульс поворачивает намагниченность в направлении z (по направлению статического поля), где оно испытывает продольную (Т1) релаксацию в течение временного интервала (Δτ) между вторым и третьим 90° импульсами. Однако на практике только примерно половина случайно ориентированных спинов, то есть тех, которые проецируются вдоль оси y во вращающейся системе координат, поворачиваются в направлении z посредством второго 90° импульса. В результате в способе со стимулированным эхо утрачиваются примерно 50% сигналов. Сохранение намагниченности в направлении z в течение интервала между вторым и третьим 90° импульсами позволяет иметь более продолжительное время (Δ) диффузии, чтобы измерять небольшие коэффициенты диффузии. При использовании последовательности Таннера и Стейскала этим способом можно обойти сильное затухание сигналов, которое в противном случае будет следствием быстрой релаксации Т2, например, в очень вязких жидкостях или в твердых телах.
В пренебрежении статическими градиентами для намагниченности в случае импульсной последовательности градиентов импульсного поля со стимулированным эхо - последовательности Карра-Парселла-Мейбума-Гилла справедливо уравнение:
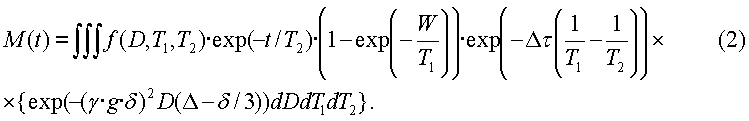
Уравнение (2) отличается от уравнения (1) тем, что оно имеет дополнительный показательный множитель в подынтегральном выражении. Этим множителем, который включает в себя разность обратных величин Т1 и Т2, учитывается то, что имеется продольная релаксация, но нет поперечной релаксации на интервале (Δτ) между вторым и третьим 90° импульсами на фиг.5. Параметр Δτ представляет собой продолжительность сохранения намагниченности в продольном направлении, то есть временной интервал между третьим и вторым 90° импульсами.
Аналогично случаю последовательности Стейскала и Таннера (градиентов импульсного поля) наличие градиента (gs) статического магнитного поля будет усложнять диффузионное затухание последовательности градиентов импульсного поля со стимулированным эхо. При наличии градиента (gs) статического магнитного поля будут иметься перекрестный член g·gs и второй член, пропорциональный квадрату gs·gs статического градиента. Коэффициенты дополнительных членов описаны Таннером (1970, уравнение (7)), который также показал, что наведенное градиентом импульсного поля затухание, обусловленное диффузией, имеет вид, идентичный показанному в уравнении (1). Так, намагниченностью в последовательности градиентов импульсного поля со стимулированным эхо - последовательности Карра-Парселла-Мейбума-Гилла, показанной на фиг.5, диффузионные эффекты кодируются таким же образом, как и в последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла. Таким образом, в отсутствие статических градиентов член диффузионного затухания в уравнении (2) будет идентичным члену в уравнении (1). Чтобы упростить анализ данных, в предпочтительных вариантах осуществления изобретения используется магнит, который возбуждает по существу однородное поле. Однако специалистам в области техники, к которой относится изобретение, следует принять во внимание, что в случае, если существует градиент статического поля, влияние членов статического градиента можно уменьшить или исключить путем использования модифицированной последовательности градиентов стимулированного импульсного поля (см., например, Cotts, et al., “Pulsed field gradient simulated echo methods for improved NMR diffusion measurements in heterogenous systems”, в: J. of Mag. Res., v.83, p.252-266, 1989).
Нижеследующий пример иллюстрирует полезность способа согласно изобретению. На фиг.6 показан набор данных ядерно-магнитного резонанса, которые получены при параметрах импульсов, указанных в таблице.
Набор данных, показанных на фиг.6, состоит из обычной последовательности Карра-Парселла-Мейбума-Гилла, содержащей 5000 эхо-сигналов с интервалом 0,2 мс между эхо-сигналами (трасса 1), и 6 последовательностей градиентов импульсного поля Стейскала и Таннера - последовательностей Карра-Парселла-Мейбума-Гилла, каждая из которых имеет 5000 эхо-сигналов (трассы 2-7). Вторые и последующие эхо-сигналы (трассы 2-7) в последовательностях градиентов импульсного поля - последовательностях Карра-Парселла-Мейбума-Гилла также имеют интервалы 0,2 мс. Для этих данных отсутствует зависимость от Т1, поскольку все последовательности были полностью поляризованными. В этом случае, как показано на фиг.7, трехмерная функция распределения приводится к двумерной функции диффузии (D) и времен (Т2) спин-спиновой релаксации.
Как отмечалось выше, информация о диффузии в наборе последовательностей градиентов импульсного поля может быть закодирована в данные путем изменения одного или нескольких из трех параметров импульсов в члене диффузионного затухания в уравнениях (1-2). Для набора данных, показанных на фиг.6, которые использовались для вычисления двумерной функции распределения на фиг.7, параметр δ изменяли для каждой из шести последовательностей градиентов импульсного поля - последовательностей Карра-Парселла-Мейбума-Гилла (трассы 2-7). Два других параметра диффузионного затухания импульсов, Δ и g, сохраняли постоянными.
В этом примере первое измерение получали при использовании обычной последовательности Карра-Парселла-Мейбума-Гилла (то есть без последовательности градиентов импульсного поля). Заметим, что нет необходимости включать результаты измерений, полученные по последовательности Карра-Парселла-Мейбума-Гилла, в набор данных, полученных по последовательности градиентов импульсного поля. В самом деле, включение результатов измерений, полученных по обычной последовательности Карра-Парселла-Мейбума-Гилла, может привести к артефактам в двумерной функции распределения, поскольку измерениями при обычной последовательности Карра-Парселла-Мейбума-Гилла не обеспечивается получение какой-либо информации о диффузии.
Для вычисления функций распределения на основании набора данных необходима инверсия модели прямой задачи, определенной уравнением (1) для набора данных, полученных по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла, или уравнением (2) в случае набора данных, полученных по последовательности Карра-Парселла-Мейбума-Гилла. Эти уравнения известны как интегральные уравнения Фредгольма первого рода, инверсию которых можно осуществить различными способами, подробно рассмотренными в публикациях, патентах и книгах. Например, в патенте США №5291137, выданном Freedman, раскрыт способ инверсии путем «оконной обработки», который может быть использован для этой цели. Этот патент полностью включен в настоящую заявку посредством ссылки.
Ниже описан процесс вычисления функции распределения (см., например, фиг.7) по набору данных, показанных на фиг.6. Модель прямой задачи в уравнении (1) для намагниченности, измеряемой с помощью последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла, может быть упрощена без потери общности путем использования набора результатов измерений при полной поляризации, то есть W<<T1, для которых поляризационная функция может быть задана равной 1. Затем интегрированием по Т1 приводят трехмерную функцию распределения к двумерной функции диффузии (D) и времен (Т2) спин-спиновой релаксации.
Использование набора полностью поляризованных данных позволяет более просто проиллюстрировать принцип способа изобретения. Однако способы изобретения не ограничены наборами полностью поляризованных данных. В самом деле, вычисление трехмерной функции распределения путем использования набора частично поляризованных данных представляется не намного более трудным и может быть осуществлено так, как описано ниже. Точно так же решение уравнения (2) путем использования наборов данных, полученных по последовательности градиентов импульсного поля со стимулированным эхо - последовательности Карра-Парселла-Мейбума-Гилла, может быть получено тем же самым способом. Поэтому вычисления можно продемонстрировать применительно к следующему уравнению:
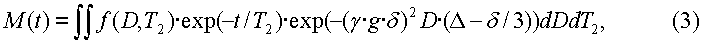
или к его дискретной версии, пригодной для численного решения:
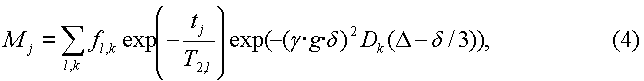
где индекс j=1,2,3,…,NE обозначает j-тое эхо, а NE суть суммарное число эхо-сигналов, зарегистрированных при использовании последовательности градиента импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла. Времена
T2,l релаксации, где l=1,2,3,…N, представляют собой набор из N фиксированных времен релаксации, которые перекрывают диапазон ожидаемых значений Т2. Удобно, но необязательно, выбирать фиксированные времена релаксации равномерно разнесенными по логарифмической шкале. Точно так же Dk является набором из N фиксированных коэффициентов диффузии, выбранных для перекрытия диапазона ожидаемых значений D. Матрица размера N×N, fl,k, представляет собой дискретное представление непрерывной двумерной функции распределения диффузии и времен релаксации. Эхо-сигналы наблюдаются в моменты времени:

где te1 - момент времени, в который наблюдается первое эхо, то есть te1=2τ, где τ - промежуток времени между 90° импульсом и первым 180° импульсом, показанными на фиг.4; и te - промежуток между вторым и последующими эхо-сигналами. Затем измеренные амплитуды эхо-сигналов соотносят с моделью прямой задачи в уравнении (4) с помощью уравнения:

где индекс р=1,2,3,…,Р использован для указания на конкретное измерение в наборе из Р измерений. Заметим, что индекс р также использован для обозначения параметров импульсов, используемых в конкретной последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла (например, параметрами являются δp, gp и Δp).
Из уравнения (6) следует, что измеренные амплитуды 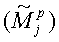 эхо-сигналов со скорректированными фазами включают в себя амплитуды
эхо-сигналов со скорректированными фазами включают в себя амплитуды 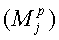 , определяемые моделью прямой задачи, и член
, определяемые моделью прямой задачи, и член 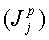 , посредством которого учитываются случайные тепловые шумы. Измеренные амплитуды эхо-сигналов обычно регистрируют, используя двухканальное квадратурное обнаружение. Корректируют фазы амплитуд, измеренных в двух каналах, после чего появляется возможность вычисления мощности (Ψp) шума для каждого измерения путем использования способов, раскрытых в патентах США №5291137 и №6229308 В1, оба выданы Freedman. Эти два патента полностью включены в настоящую заявку посредством ссылки. Инверсию уравнения (1) можно выполнить способами, раскрытыми в этих двух патентах. Например, можно вычислить набор оконных сумм
, посредством которого учитываются случайные тепловые шумы. Измеренные амплитуды эхо-сигналов обычно регистрируют, используя двухканальное квадратурное обнаружение. Корректируют фазы амплитуд, измеренных в двух каналах, после чего появляется возможность вычисления мощности (Ψp) шума для каждого измерения путем использования способов, раскрытых в патентах США №5291137 и №6229308 В1, оба выданы Freedman. Эти два патента полностью включены в настоящую заявку посредством ссылки. Инверсию уравнения (1) можно выполнить способами, раскрытыми в этих двух патентах. Например, можно вычислить набор оконных сумм 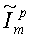 на основании скорректированных по фазе амплитуд спиновых эхо, то есть из уравнения
на основании скорректированных по фазе амплитуд спиновых эхо, то есть из уравнения
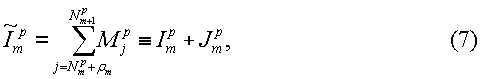
где 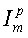 представляет собой сумму из модели прямой задачи (то есть теоретические, свободные от шума амплитуды эхо-сигналов) по набору заранее заданных окон и может быть записано в виде:
представляет собой сумму из модели прямой задачи (то есть теоретические, свободные от шума амплитуды эхо-сигналов) по набору заранее заданных окон и может быть записано в виде:
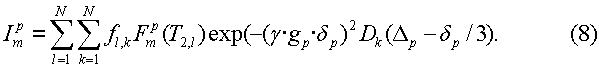
В приведенных выше уравнениях индекс 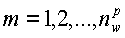 , где
, где 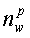 представляет собой число оконных сумм для измерения в наборе данных, имеющих индекс p=1,2,…,Nmeas, где Nmeas - число измерений в наборе данных. Величины
представляет собой число оконных сумм для измерения в наборе данных, имеющих индекс p=1,2,…,Nmeas, где Nmeas - число измерений в наборе данных. Величины 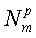 и
и 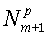 в уравнении (7) являются соответственно правыми и левыми крайними точками (номерами эхо-сигналов) m-го окна для p-го измерения; ρm находят с учетом следующего условия, введенного в патенте США №5291137, которое заключается в том, что только первое окно включает в себя его левую конечную точку, и оно определяется соотношением:
в уравнении (7) являются соответственно правыми и левыми крайними точками (номерами эхо-сигналов) m-го окна для p-го измерения; ρm находят с учетом следующего условия, введенного в патенте США №5291137, которое заключается в том, что только первое окно включает в себя его левую конечную точку, и оно определяется соотношением:

где δm,1 - хорошо известная дельта-функция Кронекера. Поэтому ρ1=0, а ρm=1, когда m не равно 1. Функции 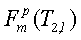 чувствительности в уравнении (8) задаются уравнением:
чувствительности в уравнении (8) задаются уравнением:
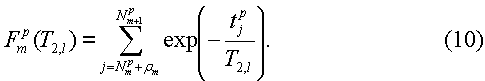
где 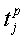 - момент времени, в который наблюдается j-тое эхо для измерения p в наборе данных.
- момент времени, в который наблюдается j-тое эхо для измерения p в наборе данных.
Как показано в патенте США №5291137, в случае некоррелированного шума дисперсия шума, просуммированная на протяжении m-го окна, определяется дисперсией шума на одно эхо, умноженной на число эхо-сигналов в окне. Это выражается уравнением:

где 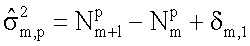 - число эхо-сигналов в m-том окне для p-го измерения в наборе данных.
- число эхо-сигналов в m-том окне для p-го измерения в наборе данных.
Матрица диффузии и времен релаксации может быть вычислена при соблюдении условия ограничения положительности путем минимизации относительно fl,k в уравнении (8) функции стоимости (или другой целевой функции) вида
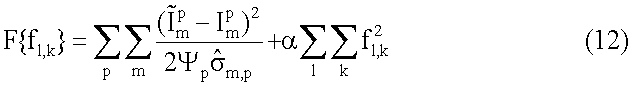
Минимизацией уравнения (12) относительно амплитуд в матрице распределения диффузии и времен релаксации обеспечивается решение обратной задачи путем согласования измеренных оконных сумм с теоретическими значениями. Член, включающий в себя параметр α, известен как регуляризация «квадратичной нормы» и добавляется с целью отбора физически осмысленных и устойчивых решений из бесконечного количества возможных решений. Параметр α может быть либо фиксированным, либо вычисленным на основании данных. Минимизация функций стоимости, имеющих вид, показанный на фиг.12, подробно описана в патенте США №6229308 В1, и ради краткости это описание здесь повторяться не будет.
Как показано на фиг.7, графическое построение матрицы fl,k, которая является следствием минимизации уравнения (12), дает двумерное распределение диффузии и времен релаксации. Набор данных, использованный для этой инверсии, представляет собой набор данных, полученных по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла, показанный на фиг.6 для пробы флюида, включающей в себя 70% сырой нефти со средней вязкостью и 30% воды. График двумерной функции распределения, показанный на фиг.7, может быть получен с помощью любого имеющегося в продаже программного обеспечения, такого как Matlab™, которое можно получить от Mathworks Corporation (Natick, MA). Как показано на фиг.7, по двумерной функции распределения, вычисленной согласно способу изобретения, точно предсказываются два компонента. Пик, центрированный относительно D=2,5×10-5 см2/с и Т2=5×103 мс, обусловлен водой, а пик, центрированный относительно D=1×10-6 см2/с и Т2=260 мс, обусловлен нефтью.
После того, как функция распределения вычислена, найденную функцию распределения (fl,k) из уравнения (1) можно использовать для вычисления теоретически предсказанных амплитуд спиновых эхо для каждого измерения в наборе данных. Затем набор вычисленных данных можно сравнить с данными, показанными на фиг.6. Любое отклонение теоретических амплитуд эхо-сигналов от измеренных значений может быть использовано для вычисления «хи-квадрата» или качества параметра соответствия, что является полезным для оценки качества решения. Специалистам в области техники, к которой относится изобретение, должно быть понятно, что анализ, представленный выше, может быть легко распространен на вычисление трехмерных функций распределения.
Одномерные распределения времен релаксации и коэффициентов диффузии
Одномерные времена релаксации и коэффициенты диффузии могут быть вычислены по двумерным или трехмерным распределениям путем интегрирования по другим переменным. Например, одномерная функция распределения времен релаксации может быть вычислена из интеграла:

Отметим, что в приведенных выше уравнениях использована понятная форма записи для функций распределения, в которой число и вид аргументов использованы для указания размерности и вида распределения. Используя дискретную форму двумерной функции распределения в уравнении (4), дискретную функцию распределения времен релаксации можно вычислить путем суммирования, то есть:

Одномерные функции распределения диффузии могут быть получены аналогичным образом путем интегрирования f(T2,D) по Т2 или путем суммирования fl,k по индексу l. Одномерная функция распределения диффузии, показанная на фиг.8, была вычислена по двумерной функции распределения (показанной на фиг.7) путем суммирования fl,k по индексу l. Это эквивалентно «проецированию» двумерной кривой на ось диффузии. На показанных на фиг.8 одномерных функциях распределения коэффициентов диффузии максимум А и максимум В отражают нефтяной пик и водный пик, соответственно, показанные на фиг.7.
Приведенным выше описанием проиллюстрирован способ изобретения, используемый при инверсии набора «закодированных диффузией» данных. Инверсия включает в себя модель прямой задачи и приводит к получению функции распределения, которая связывает коэффициенты диффузии флюидов с характеристиками ядерно-магнитного резонанса (например, с временами релаксации) флюидов. Затем из функции распределения могут быть извлечены индивидуальные характеристики флюидов. Например, на фиг.8 показаны коэффициенты диффузии компонентов флюида, полученные этим способом. Как показано в нижеследующих частях описания, функции распределения и полученные характеристики флюида (коэффициенты диффузии и времена релаксации) могут найти широкое применение при оценивании характеристик пластовых флюидов.
Свойства пластовых флюидов и насыщенность
Во многих ситуациях, представляющих практический интерес, коэффициенты диффузии различных компонентов в пластовом флюиде являются различимыми. В общем случае молекулы газа имеют самые большие коэффициенты диффузии, за которыми следуют коэффициенты диффузии воды, а затем нефти. По сравнению с нефтью со средней вязкостью (например, вязкость больше 5 сП и меньше 30 сП) молекулы воды диффундируют примерно в 10 раз быстрее. Это можно видеть на диаграмме, показанной на фиг.7 для пробы флюида, включающей в себя воду и нефть со средней вязкостью. На фиг.7 сигналы от нефти и воды хорошо разделены как в области коэффициентов диффузии, так в области времен релаксации. Выделение Т2 будет иным, если измерения ядерного магнитного резонанса выполнять относительно флюида в породе. Это происходит потому, что время релаксации для поверхности породы меньше времени Т2 релаксации для воды, что приводит к потенциальным перекрытиям распределений Т2 для воды и нефти. На фиг.7 наличие нефти и воды четко различимо, поскольку проба флюида не находится в породе. Горизонтальная линия на фиг.7 обозначает коэффициент диффузии воды, который в этом примере составляет около 2,5×10-5 см2/с, а наклонная линия отражает взаимосвязь между временами релаксации и коэффициентами диффузии для сырой нефти, предсказываемую конституэнтной моделью вязкости, раскрытой в патенте США №6229308 В1. В конституэнтной модели вязкости коэффициенты диффузии и времена релаксации компонентов флюида связаны в соответствии со следующим уравнением:

где f(GOR) - известная функция соотношения нефть/газ.
Для дегазированных нефтей (нефтей без газа) f(GOR) равна 1 и больше 1 для газированных нефтей. На фиг.7 значение λ для дегазированной нефти, составляющее 5,1×10-6 см2/с2, было использовано для построения наклонной линии. На графике D-Т2 амплитуда сигнала от нефти для большей части проб дегазированных сырых нефтей будет располагаться на или вблизи этой эталонной линии. Для газированных нефтей амплитуда сигнала может быть сдвинута к северо-западной части (вверх и влево) графика. В обоих случаях наклон линии, определяющий гребень максимума сигнала от сырых нефтей на графике D-Т2 в логарифмическом масштабе, должен быть близок к 1 (см., например, наклонную кривую на фиг.7).
Способ 1 для вычисления объемов флюидов
Двойной интеграл от f(D, T2) по D и T2 или двойная сумма fl,k по обоим индексам l и k равна суммарной амплитуде сигнала или суммарному исходному объему (VT) флюидов от всех флюидов в объеме измерения. Как рассмотрено ниже, в исходные объемы (то есть без введения поправок на влияние водородного показателя) флюидов могут быть введены поправки на влияние водородного показателя. В ситуациях, подобных показанной на фиг.7, где сигналы от воды и нефти хорошо разделены, несложно вычислить исходные объемы нефти, Vo, и воды, Vw. Как отмечалось выше, одномерное распределение (f(Dk)) диффузии, показанное на фиг.8, было вычислено на основании двумерного графика функции распределения диффузии и времен релаксации:

Поскольку на фиг.7 и 8 нефть и вода четко разделены, исходный объем (Vw) воды может быть вычислен путем суммирования f(Dk) по тем значениям Dk, которые находятся справа от вертикальной линии на графике на фиг.8. Затем исходный объем (Vo) нефти может быть найден из уравнения

или, что эквивалентно, путем суммирования показанной одномерной функции распределения диффузии по коэффициентам диффузии слева от вертикальной линии на фиг.8. Как показано в уравнении (20), водонасыщенность (Sw) может быть вычислена по этим исходным объемам после введения поправки на влияние водородного показателя. При приложении этого способа к одномерному распределению диффузии на фиг.8 была получена водонасыщенность 33,2%, которая хорошо выдерживает сравнение с истинной насыщенностью 30%.
Флюидонасыщенности могут быть вычислены путем введения поправки в исходные объемы флюидов на влияния водородного показателя. Эффективный водородный показатель (HIeff) может быть задан так, чтобы удовлетворялось

HIw и HIo представляют собой водородные показатели воды и нефти, соответственно. Водородный показатель (HIw) воды может быть вычислен на основании эмпирических соотношений, если соленость воды известна из результатов измерения удельного сопротивления или других измерений. Перестановкой членов в уравнении (18) эффективный водородный показатель (HIeff) может быть выражен через исходные объемы флюидов и водородные показатели воды и нефти:

Водонасыщенность (Sw) определяется отношением объема воды, скорректированного с учетом водородного показателя, к скорректированному суммарному объему флюида, например как:
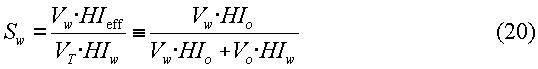
Следовательно, водонасыщенность может быть вычислена по исходным объемам, найденным на основании распределения диффузии и времен релаксации, если водородные показатели нефти и воды известны или могут быть оценены на основании других измерений. Водонасыщенность определяет «обводненность» пробы, извлеченной в пробоотборник флюидов. Нефтенасыщенность просто дается уравнением:
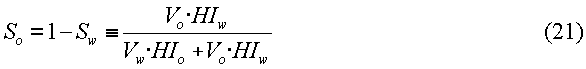
Способ 2 для вычисления объемов флюидов
Для способа вычисления исходных объемов флюидов по кривым распределений диффузии и времен релаксации, рассмотренного выше, необходимо, чтобы максимумы для компонентов флюидов были разделены. В случаях нефтей с низкой вязкостью и воды распределения диффузии и времен релаксации для нефтей и воды могут перекрываться друг с другом. В этом случае становится невозможным получение вертикальной линии, подобной линии, показанной на фиг.8. В таких случаях может быть использован способ, основанный на модели. Уравнением (15) распределения коэффициентов диффузии сырых нефтей связаны с распределениями времен релаксации для них. Рассмотрим дискретный набор амплитуд fl,k диффузии и времен релаксации. Имеются распределения N коэффициентов диффузии с логарифмическими средними, обозначенными как DLM(l), то есть по одному для каждого времени T2,l релаксации. Амплитуды в распределениях коэффициентов диффузии соответствуют различным значениям коэффициентов диффузии и являются строками в матрице fl,k. В случае пробы, включающей в себя воду и нефть, DLM(l) может быть связано с содержанием (Sw(l)) воды с временами релаксации T2,l уравнением:

Как показано ниже, DLM(l) можно вычислить по амплитудам fl,k, при этом коэффициент диффузии воды может быть определен по измеренной температуре пробы, а коэффициент диффузии нефти можно определить, используя уравнение (15). Для нахождения DLM(l) удобно сначала вычислить следующую величину:
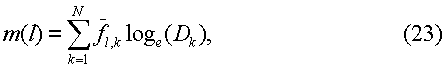
где Dk представляют собой коэффициенты диффузии в уравнении (4), и они равномерно разнесены по логарифмической шкале, например

где k=1,2,…,N; Dmin и Dmax задают минимальный и максимальный пределы значений коэффициентов диффузии, используемых при вычислении fl,k, и

Решая уравнение (22) относительно содержания воды со временем T2,l релаксации и используя уравнение (15), можно определить
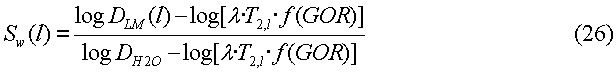
Суммарный (исходный) объем воды на основании всех значений T2,l дается суммой
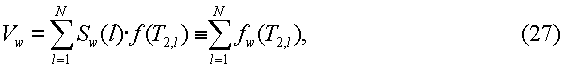
а суммарный объем нефти равен
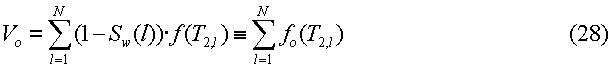
В приведенных выше уравнениях f(T2,l) представляет собой одномерную функцию распределения (как для нефти, так и для воды), вычисленную по двумерной функции распределения (показанной на фиг.7). Отметим, что функции fw(T2,l) и fo(T2,l) являются одномерными функциями распределения Т2 для воды и нефти, соответственно. Общая водонасыщенность (Sw) может быть вычислена на основании исходных объемов в уравнениях (27)-(28) при использовании уравнения (20). Частичные водонасыщенности в уравнении (26) иногда будут отрицательными или больше 1. Это может быть вызвано шумом или численными ошибками в распределении диффузии и времен релаксации. При использовании рассмотренного выше способа частичные значения, которые являются отрицательными, приравнивают к нулю, а значения, большие чем 1,0, приравнивают к 1,0. Вместе с двумерным распределением на фиг.7 уравнения (22)-(28) были использованы для вычисления общей водонасыщенности. Вычисленная водонасыщенность была 25,3%, и это значение достаточно хорошо совпадает с истинным значением 30%, которое было использовано при моделировании.
Способ 3 для вычисления объемов флюидов
Уравнения (22)-(28) для вычисления объемов флюидов отражают приближенную и упрощенную реализацию ядерно-магнитного резонансного способа оценивания характеристик флюидов, который разработал Freedman и описал в патенте США №6229308 В1 (в патенте '308). В этом патенте раскрыт основанный на диффузии способ отнесения флюида к определенному типу, предназначенный для ядерно-магнитных каротажных приборов, посредством которых измеряют характеристики флюидов в формациях, окружающих скважину. В способе из патента '308 используют набор кодированных диффузией данных, регистрируемых при статическом градиенте каротажного прибора. Как показано ниже, способ, который предложил Freedman, может быть применен для определения характеристик газированных пластовых флюидов, извлекаемых в модуль отбора проб, путем использования наборов данных, полученных по градиентам импульсного поля.
Рассмотрим пробу пластового флюида, который извлечен в отводную линию пробоотборника флюидов или отведен в специальную отборную камеру, в которой измерения по градиенту импульсного поля и другие ядерно-магнитные резонансные измерения могут быть выполнены при остановке потока (то есть на неподвижном флюиде). Пробы могут включать в себя нефть (o), воду (w) и/или газ (g). Многожидкостная модель прямой задачи для поперечной намагниченности, определяемой посредством выполнения набора измерений на такой пробе по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла, имеет следующий вид:
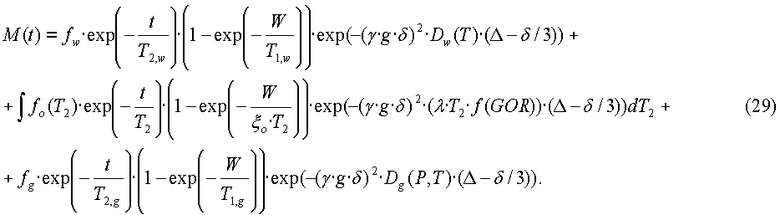 Должно быть понятно, что уравнения, подобные уравнению (29), могут быть применены к наборам данных, полученным по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла. Первый член в уравнении (29) представляет собой вклад в измеренную поперечную намагниченность от воды в пробе флюида. Амплитуда сигнала от воды составляет fw. Отметим, что спин-спиновый спад поперечной намагниченности на основании сигнала от воды в массе является простой экспоненциальной функцией со временем
Должно быть понятно, что уравнения, подобные уравнению (29), могут быть применены к наборам данных, полученным по последовательности градиентов импульсного поля - последовательности Карра-Парселла-Мейбума-Гилла. Первый член в уравнении (29) представляет собой вклад в измеренную поперечную намагниченность от воды в пробе флюида. Амплитуда сигнала от воды составляет fw. Отметим, что спин-спиновый спад поперечной намагниченности на основании сигнала от воды в массе является простой экспоненциальной функцией со временем
T2,w релаксации. Этим он сильно отличается от спин-спинового спада в случае воды, измеряемой в пористых породах, когда релаксация поверхности создает распределение времен релаксации. Аналогичным образом время продольной релаксации для воды в массе является простой экспоненциальной функцией со временем T1,w релаксации. Также отметим, что для воды в массе T2,w=T1,w. Однако это несправедливо для воды в пористых породах. Коэффициент Dw(T) диффузии воды является известной функцией температуры (Т) пробы, которая может быть измерена датчиком температуры.
Второй член в уравнении (29) представляет собой вклад в измеренную поперечную намагниченность от нефтей в пробе флюида. Сырые нефти имеют распределение времен спин-спиновой релаксации, и поэтому вклад нефтей включает в себя интеграл по распределению fo(T2) времен релаксации нефтей. Параметр ξo в поляризационной функции представляет собой отношение Т1/Т2 для сырой нефти. Отношение Т1/Т2 может существенно отличаться от 1, и установлено, что в общем случае оно возрастает с повышением частоты измерений и вязкости нефти. Способ оценивания характеристик флюида согласно патенту США №6229308 В1 был использован для учета распределения коэффициентов диффузии в сырых нефтях, то есть путем использования уравнения (15) величина Do(T) во втором члене уравнения (29) была заменена. Если отбор пробы флюида сделан из скважины, пробуренной с использованием бурового раствора на углеводородной основе, то в зависимости от степени загрязнения пробы относящийся к нефти член может описывать смесь природной сырой нефти и фильтрата бурового раствора на углеводородной основе.
Последний член в уравнении (29) представляет собой вклад в измеренную поперечную намагниченность от газа в пробе флюида. В случае пластов, содержащих газированные нефти, давление флюида во время отбора пробы обычно выше точки начала кипения, так что в пробоотборник закачивается одна фаза (нефть). Однако могут быть случаи, когда в пробе присутствуют обе фазы, газа и нефти. Амплитуда сигнала от газа равна fg. Сигнал от газа спадает с одним временем T2,g(P,T) спин-спиновой релаксации, которое может быть измеренной или вычисленной функцией температуры и давления. Точно так же релаксация газа происходит с одним временем T1,g(P,T)≈T2,g(P,T) продольной релаксации, и для газа имеется один коэффициент Dg(P,T), который может быть измеренной или вычисленной функцией температуры и давления.
Зависимая от модели поперечная намагниченность в уравнении (29) может быть инвертирована путем использования наборов данных, аналогичных использованным для инвертирования зависимой от модели поперечной намагниченности в уравнениях (1) и (3). Параметры модели, определенные посредством инверсии модели прямой задачи в уравнении (29), представляют собой амплитуды fw и fg для воды и газа, отношение Т1/Т2, ξо для нефти и распределение fo(T2) времен спин-спиновой релаксации сырой нефти. Далее амплитуды могут быть использованы для вычисления объемов флюидов и насыщенностей газа, воды и нефти. Параметрами модели, необходимыми для инверсии, являются T2,w, Dw(T), λ, соотношение газ/нефть и T2,g. За исключением соотношения газ/нефть эти параметры можно оценивать по эмпирическим соотношениям, если измерять посредством датчиков температуру и давление проб в пробоотборнике (Kleinberg and Vinegar, “NMR properties of reservoir fluids”, в: The Log Analyst, vol. 37, №6, p.20-32; Freedman et al., 2001, “A new NMR method of fluid characterization in reservoir rocks: Experimental confirmation and simulation results”, в: SPE Journal, vol. 6, №4, p.452-464). Соотношение нефть/газ может быть получено по результатам других измерений флюида в пробоотборнике, например по спектрам поглощения флюида в ближней инфракрасной области, которые могут быть измерены соответствующим прибором, таким как оптический анализатор флюидов, поставляемый Schlumberger Technology Corp. (см. патент США №6350986 В1, выданный Mullins et al.).
Точные значения для некоторых из этих параметров могут быть получены путем нахождения их из набора ядерно-магнитных резонансных измерений, например, путем инверсии независимых от модели уравнения для поперечной намагниченности (например, уравнений (1-3)) с целью вычисления двумерных или трехмерных функций распределения диффузии и времен релаксации, описанных выше. Кривая независимой от модели функции распределения, подобная кривой на фиг.7, включает в себя сигналы от всех имеющихся флюидов. Например, проба из фиг.7 включает в себя нефть и воду. Из графика видно, что максимум при T2,w≅5 с, Dw≅2,5×10-5 см2/с может быть приписан воде, и на основании функции распределения или ее графика можно определить, что λ≅5,1×10-6 см2/с2. Поэтому можно определить более точные значения объемов и насыщенностей флюидов, используя сначала уравнение (29) для нахождения зависимой от модели функции распределения диффузии и времен релаксации, чтобы получить более точные входные параметры для уравнения (29). Кроме того, поскольку независимая от модели функция распределения является полезной при идентификации имеющихся флюидов, то можно определить, какие члены должны быть включены в уравнение (29) и какие, если они имеются, могут быть отброшены.
Инверсию уравнения (29) можно выполнить, используя способ «оконной обработки», описанный выше, или используя любой другой подходящий способ, известный в области техники, для согласования набора измерений по градиентам импульсного поля с уравнением (29). Такие способы включают в себя, например, способы наименьших квадратов, максимальной энтропии или другие способы с минимальной ошибкой. После инверсии можно легко определить объемы и насыщенности флюидов. Например, насыщенности флюидов могут быть определены в соответствии со следующими уравнениями:
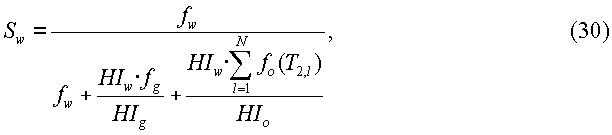
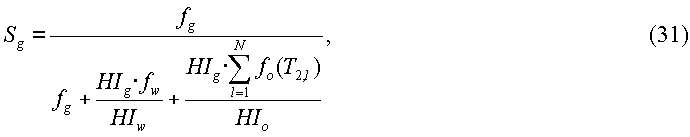
и So=1-Sw-Sg.
Вычисление вязкости, соотношения нефть/газ, состава нефти и температуры пласта
В приведенных выше частях описания описаны три способа для вычисления флюидонасыщенности и объемов флюидов и способ для определения отношения Т1/Т2 для нефти на основании измерений по градиентам импульсного поля. Вязкость нефти, соотношение газ/нефть, состав нефти и температуру пласта также можно вычислить на основании этих измерений. В следующих частях для примера описаны способы для вычисления этих параметров.
Вязкость
Вязкость нефти может быть вычислена на основании любых известных соотношений, которые связывают вязкость с временами релаксации. Например, логарифмическое среднее T2,LM одномерного распределения времен релаксации может быть связано с вязкостью (ηо) нефти и соотношением газ/нефть определенным эмпирически уравнением, раскрытым в: Freedman et. al., 2001, “A new NMR method of fluid characterization in reservoir rocks: Experimental confirmation and simulation results”, SPE Journal, vol. 6, №4, p.452-464):

где Т - температура в градусах Кельвина, f(GOR)≥1 - определяемая эмпирически функция (Lo et al., “Mixing rules and correlations of NMR relaxation time with viscosity, diffusivity, and gas/oil ratio of methane/hydrocarbon mixtures”, в: SPE Journal, vol. 7, №1, p.24-34, March 2002), а параметр a≅(0,004-0,009) с·сП·K-1 зависит от типа нефти (Freedman and Heaton, “Fluid characterization using nuclear magnetic resonance logging”, в: Petrophysics, vol. 45, №3, p.241-251, 2004). Это изменение параметра означает, что вязкость можно оценить только с точностью до множителя, имеющего значение около 2. В уравнении (32) вязкость выражена в единицах сантипуаз (сП), а логарифмическое среднее времени релаксации - в секундах.
Для вычисления вязкостей в дополнение к уравнению (32) также могут быть использованы другие функции, которыми T1,LM связано с вязкостью. Например, логарифмическое среднее DLM одномерного распределения диффузии также может быть использовано для вычисления вязкости нефти

В уравнении (33) параметр b=5,05×10-8 см2·сП·K-1 является эмпирически определяемой постоянной, которая справедлива для многих сырых нефтей. Должно быть понятно, что уравнения (32) и (33) основаны на соотношениях, определяемых посредством ядерно-магнитного резонанса в слабом поле (например, протонные частоты Лармора составляют от 1 до 4 МГц), и что параметры (например, a и b) в этих уравнениях может быть придется изменить при выполнении измерений на более высоких частотах.
Соотношение газ/нефть
После вычисления одномерных распределений для диффузии и времен релаксации функцию f(GOR) (и, следовательно, соотношение газ/нефть) можно оценить на основании уравнения:

где значение λ определяют из двумерного распределения диффузии и времен релаксации,
или можно использовать номинальное значение λ≈5,1×10-6 см2/с2, которое, как установлено, справедливо для многих нефтей.
Состав нефти
В публикации патентной заявки США №2003/0128032 А1, поданной Heaton et al. и переуступленной правопреемнику настоящей заявки, раскрыты пути вычисления молекулярного состава сырых нефтей по измеренным функциям распределения времен релаксации и диффузии. Эта заявка полностью включена в настоящую заявку посредством ссылки.
Температура пласта
Температура пробы флюида необходима для вычисления вязкости нефти на основании уравнений (32) и (33). Если проба флюида извлечена из пласта, содержащего воду, то зависимый от температуры коэффициент (Dw(T)) диффузии воды находят из двумерной функции, аналогичной показанной на фиг.7. Поскольку Dw(T) является монотонно возрастающей функцией температуры воды (см., например, Kleinberg and Vinegar, “NMR properties of reservoir fluids”, The Log Analyst, p.25, Nov. - Dec. 1996), то температура (Т) пробы может быть определена по измеренному коэффициенту диффузии воды. Поскольку вода находится в тепловом равновесии с любой нефтью или газом в пробе флюида, то температура воды также является температурой всей пробы флюида. Температуру воды можно рассматривать как нижнюю границу температуры пласта, поскольку может происходить некоторое охлаждение пробы флюида после ее отбора из пласта.
Вычисление распределений диффузии и времен релаксации в случае пространственно изменяющегося градиента
В предшествующем анализе предполагалось, что градиент g импульсного поля является постоянным в пределах объема пробы. На практике это условие не всегда просто соблюсти, и может иметься распределение градиентов, описываемое функцией F(g). В этом случае уравнения для поперечной намагниченности (см., например, уравнения (1-4)) могут быть видоизменены с целью включения вычисления интеграла от распределения градиентов. Например, уравнение (3) может быть перезаписано как
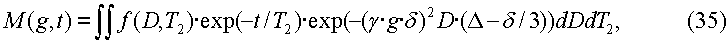
в котором в явном виде выражена зависимость намагниченности от градиента g. Затем, если имеется распределение градиентов, уравнение (3) может быть заменено следующим:
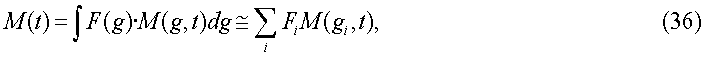 ,
,
в котором интеграл заменен дискретной суммой распределений. Как рассмотрено выше, в случае постоянного градиента можно выполнить инверсию уравнения (36).
К преимуществам изобретения можно отнести одно или несколько из следующих. Использование градиентов импульсного поля для кодирования информации о диффузии в отсутствие заметных статических градиентов может обеспечить достижение многих преимуществ по сравнению со способами каротажа скважин из предшествующего уровня техники, в которых используют градиент статического магнитного поля, создаваемого магнитом для ядерно-магнитного резонанса (см., например, “Experimental pulse NMR - A nuts and bolts approach”, Fukushima and Roeder, Perseus Publishing, Boulder, CO., 1986). Одно из преимуществ использования способов градиентов импульсного поля заключается в том, что во время регистрации эхо-сигналов градиент выключают. Это приводит к появлению более широких и более легко обнаруживаемых эхо-сигналов по сравнению со случаем статического градиента поля, когда наблюдается тенденция образования более узких эхо-сигналов. Кроме того, когда статический градиент создают во время действия радиочастотных импульсов, используемых для поворота намагниченности, резонируют только спины в оболочке толщиной порядка B1/G, где B1 - интенсивность радиочастотного поля и G - величина градиента статического поля. При небольшой радиочастотной мощности (то есть при небольших амплитудах B1) или в случае больших статических градиентов толщина оболочки и, следовательно, резонирующий объем пробы может быть меньше необходимого. Напротив, в случае способа градиентов импульсного поля может резонировать весь объем пробы, следствием чего являются лучшие отношения сигнала к шуму. Кроме того, градиентные импульсы могут быть использованы для кодирования информации о диффузии, а затем отключены с тем, чтобы данные о времени Т2 релаксации могли быть зарегистрированы в отсутствие градиента магнитного поля. Это обеспечивает преимущество, заключающееся в том, что характеристики флюидов с большими значениями Т2 могут быть измерены точно, поскольку отсутствуют потери амплитуды сигналов, обусловленные молекулярной диффузией при градиенте магнитного поля.
Хотя это изобретение было продемонстрировано при использовании ограниченного числа вариантов осуществления, должно быть понятно, что другие способы могут быть разработаны без отступления от объема изобретения, раскрытого в настоящей заявке. Поэтому объем изобретения должен ограничиваться только приложенной формулой изобретения.
Использование: для определения характеристик флюидов в скважинном каротажном приборе для отбора проб флюидов с помощью ядерного магнитного резонанса. Сущность: заключается в том, что используют пробоотборник проб пластового флюида в скважине, причем пробоотборник имеет постоянный магнит, создающий по существу однородное магнитное поле на отборной камере, и радиочастотную антенну, окружающую отборную камеру, экранируют радиочастотную антенну от постоянного магнита так, чтобы осциллирующее радиочастотное магнитное поле, создаваемое радиочастотной антенной, не взаимодействовало с постоянным магнитом, регистрируют набор ядерно-магнитных резонансных измерений пробы флюида путем использования последовательности импульсов, которая включает в себя градиентные импульсы импульсного поля для кодирования информации о диффузии, при этом каждое магнитно-ядерное резонансное измерение в наборе регистрируют при отличающемся значении параметра в градиентных импульсах импульсного поля для получения отличающегося диффузионного эффекта, обрабатывают набор ядерно-магнитных резонансных измерений и определяют характеристики пластового флюида на основании функции распределения. Технический результат: осуществление измерений в условиях, максимально приближенных к естественному залеганию флюидов, а также более достоверное определение характеристик пластовых флюидов. 2 н. и 10 з.п. ф-лы, 8 ил., 1 табл.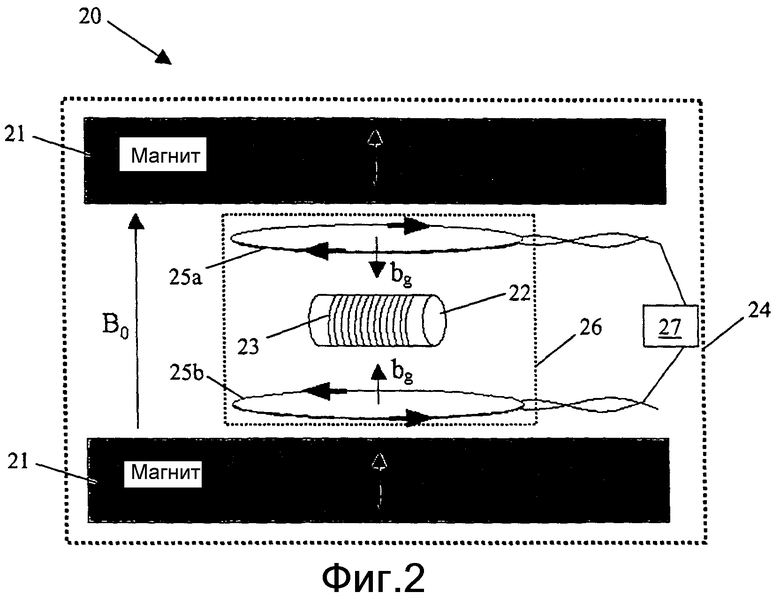
1. Способ для определения характеристики пластового флюида, включающий в себя
обеспечение пробоотборника проб пластового флюида в скважине, причем пробоотборник имеет постоянный магнит, создающий по существу однородное магнитное поле на отборной камере, и радиочастотную антенну, окружающую отборную камеру;
экранирование радиочастотной антенны от постоянного магнита так, чтобы осциллирующее радиочастотное магнитное поле, создаваемое радиочастотной антенной, не взаимодействовало с постоянным магнитом;
регистрацию пробы пластового флюида в отборной камере;
регистрацию набора ядерно-магнитных резонансных измерений пробы флюида путем использования последовательности импульсов, которая включает в себя градиентные импульсы импульсного поля для кодирования информации о диффузии, при этом каждое магнитно-ядерное резонансное измерение в наборе регистрируют при отличающемся значении параметра в градиентных импульсах импульсного поля для получения отличающегося диффузионного эффекта;
инвертирование набора ядерно-магнитных резонансных измерений для получения функции распределения, которая связывает диффузионные характеристики пробы флюида с характеристикой ядерного магнитного резонанса пробы флюида, и
определение характеристики пластового флюида на основании функции распределения.
2. Способ по п.1, в котором спиновое эхо, которое следует за градиентными импульсами импульсного поля, для каждого измерения в наборе повторно рефокусируют посредством 180-градусных импульсов, которые создают серию сигналов спинового эха, чтобы получить информацию о временах спин-спиновой релаксации пробы флюида.
3. Способ по п.1, в котором каждое ядерно-магнитное резонансное измерение регистрируют при отличающимся времени ожидания, чтобы получить информацию о временах продольной релаксации пробы флюида.
4. Способ по п.1, в котором градиентные импульсы импульсного поля содержат последовательность градиентных импульсов импульсного поля со стимулированным эхо.
5. Способ по п.1, в котором параметр в градиентных импульсах импульсного поля выбирают из величины градиента (g), длительности (δ) градиентных импульсов импульсного поля и временной задержки (А) между градиентными импульсами.
6. Способ по п.1, в котором регистрацию выполняют при наличии по существу однородного статического магнитного поля.
7. Способ по п.1, в котором при инвертировании используют модель, которая связывает релаксацию намагниченности с диффузией пробы флюида.
8. Способ по п.1, в котором функция распределения представляет собой двумерную функцию распределения или трехмерную функцию распределения.
9. Способ по п.1, в котором характеристика ядерного магнитного резонанса представляет собой время спин-спиновой релаксации.
10. Способ по п.1, в котором характеристики пластового флюида выбирают из коэффициента диффузии, вязкости, соотношения газ/нефть, молекулярного состава нефти, водонасыщенности и нефтенасыщенности.
11. Датчик (20) ядерного магнитного резонанса для скважинного прибора, содержащий
корпус, образующий часть скважинного прибора;
отборную камеру в корпусе;
постоянный магнит, расположенный в корпусе (21), создающий по существу однородное магнитное поле на отборной камере (22); радиочастотную антенну (23), расположенную в корпусе и окружающую отборную камеру (22), при этом радиочастотная антенна (23) выполнена с возможностью создания осциллирующих магнитных полей, которые имеют магнитные моменты, по существу ортогональные к направлению по существу однородного магнитного поля, создаваемого постоянным магнитом (21);
экран, расположенный внутри корпуса, причем экран разделяет радиочастотную антенну от постоянного магнита так, чтобы осциллирующее радиочастотное магнитное поле, создаваемое радиочастотной антенной, не взаимодействовало с постоянным магнитом; и
по меньшей мере, одну катушку (25), расположенную в корпусе и подключенную к блоку (27) управления, при этом по меньшей мере одна катушка (25) и блок (27) управления выполнены с возможностью создания градиента импульсного магнитного поля в отборной камере (22) управляемым образом, так что градиент импульсного магнитного поля имеет выбранную величину и заранее определенную длительность.
12. Датчик ядерного магнитного резонанса по п.11, в котором корпус (24) выполнен из материала с высокой магнитной проницаемостью.
| US 5796252 A, 18.08.1998 | |||
| US 6346813 B1, 12.02.2002 | |||
| US 6051973 A, 18.04.2000 | |||
| US 2003128032 A1, 10.07.2003 | |||
| СПОСОБЫ ИЗМЕРЕНИЯ ДИФФУЗИИ ПОСРЕДСТВОМ ЯДЕРНОГО МАГНИТНОГО РЕЗОНАНСА (ВАРИАНТЫ) | 1991 |
|
RU2104565C1 |
| US 5023531 A, 11.06.1991 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИКИ ПОРИСТОЙ ПОДЗЕМНОЙ ФОРМАЦИИ | 1995 |
|
RU2134894C1 |
| Способ измерения диффузии адсорбированных молекул жидкостей | 1976 |
|
SU649996A1 |
Авторы
Даты
2009-12-27—Публикация
2005-06-03—Подача