Область техники, к которой относится изобретение
В широком смысле это изобретение относится к статистическому анализу случайных переменных, посредством которого моделируют поле характеристик. Точнее, это изобретение относится к многоточечным геостатистическим способам и имитационным моделям.
Уровень техники
Геостатистика является дисциплиной, относящейся к пространственно распределенным случайным переменным (также называемым «регионализированными переменными»), обычно применяемой к задачам наук о Земле, таким как оценка запасов полезных ископаемых и выявление месторождений полезных ископаемых, углеводородных коллекторов и водоносных горизонтов. Многоточечная (или основанная на множестве точек) геостатистика отличается от остальной геостатистики в основном тем, что в ней пространственная изменчивость характеризуется с использованием образов (наборов из точек), которые содержат более двух точек.
Одна из задач многоточечной геостатистики заключается в моделировании, а именно, в образовании числовых значений вдоль линии, на поверхности или в объеме, так что посредством набора значений оценивают некоторые заданные характеристики пространственной корреляции (обычно получаемые на основании набора данных, называемых «аналогом» или «тренировочным образом»), тогда как при желании (в случае, называемом «условным моделированием») оценивают заранее заданные данные. На практике «аналогом» может быть, например, хорошо известный объем породы, который статистически аналогичен все еще малоизвестному оконтуренному нефтяному коллектору, а заранее заданные данные, подлежащие оцениванию, могут быть наблюдениями литологии в скважинах или вероятностями литологических показателей, полученных на основании сейсмических данных. Таким образом, с помощью имитационных моделей многоточечной геостатистики оценивают абсолютные или так называемые жесткие ограничения на основании данных, зарегистрированных в скважинах или на обнажениях горных пород, и условные или мягкие ограничения на основании сейсмических данных, полей вероятностей фаций и сеток ограничения поворота и аффинности (или масштаба). Такие данные используют в процессе стохастического моделирования для образования одномерных, двумерных и/или трехмерных карт геологических фаций или свойств породы. Поскольку имеется случайная компонента, включенная в имитационные модели многоточечной геостатистики, отдельные реализации полей характеристик, получаемые с помощью алгоритмов многоточечной геостатистики, различаются, но множество реализаций обеспечивает геофизикам и специалистам по разработке месторождений получение улучшенных количественных оценок пространственного распределения и неопределенности геологических фаций или свойств породы в полученном моделированием объеме коллектора.
Недавно было обнаружено, что многоточечные геостатистические способы являются целесообразными в вычислительном отношении, и они были проверены на реальных базах данных, что изложено в: i) Strebelle, “Conditional simulation of complex geological structures using multiple-point statistics”, Mathematical Geology, v.34, №1, 2002, p.1-22, ii) Strebelle et al., “Modeling of deepwater turbidite reservoir conditional to seismic data using principal component analysis and multiple-point geostatistics”, SPE Journal, vol.8, №3, 2003, p.227-235, и iiii) Liu et al., “Multiple-point simulation integrating wells, three-dimensional seismic data, and geology”, American Association of Petroleum Geologists Bulletin, v.88, №8, 2004, p.905-921.
Традиционные геостатистические способы основаны на вариограмме, предназначенной для описания геологической непрерывности. Однако вариограмма, которая является двухточечным показателем пространственной изменчивости, не может описать реальные криволинейные или геометрически сложные картины. В многоточечных геостатистических способах для получения геологической информации используют тренировочный образ (вместо вариограммы). Тренировочный образ обеспечивает концептуальное описание подземной геологической неоднородности, содержащей, возможно, сложные многоточечные картины геологической неоднородности. При многоточечном статистическом моделировании эти картины связывают со скважинными данными (и/или с данными обнажения горных пород) и с полученной сейсмическим способом информацией (и/или с информацией о поле вероятностей или с сеткой (сетками) ограничения).
Тренировочный образ часто, но необязательно, имеет низкое разрешение (а именно, обычно несколько сотен пикселов вдоль стороны). Каждый пиксел тренировочного образа имеет уровень (который может быть двоичным значением, значением серого или значением цвета), относящийся к нему. Уровень при каждом пикселе в настоящей заявке именуется категорией. Обычно имеются приблизительно от 5 до 10 возможных категорий при каждом пикселе тренировочного образа, но это число может быть больше или меньше. Формы геологических элементов (элемента), определяемые с помощью тренировочного образа, представляют модель реальных геологических элементов, при этом каждая категория обычно представляет особую геологическую фацию или геологическое тело особого вида.
Геостатистика основана на хорошо известной концепции случайных переменных. Говоря просто, свойства коллектора на различных местах сетки являются в основном неизвестными или неопределенными; поэтому каждое представляющее интерес свойство на каждом месте сетки преобразуют в переменную, изменчивость которой описывается функцией вероятности. Чтобы выполнить геостатистическое моделирование любого вида, необходимо иметь решение или предположение относительно стационарности. В многоточечных геостатистических способах использование тренировочных образов ограничивается принципом стационарности, что описано в: Caers et al., “Multiple-point geostatistics: a quantitative vehicle for integrating geologic analogs into multiple reservoir models”, AAPG Memoir, Integration of Outcrop and Modern Analogs in Reservoir Modeling, (eds.) Grammer, G.M, 2002. В случае двумерного или трехмерного моделирования коллектора считается, что случайная переменная случайного процесса является стационарной, если все ее статистические параметры не зависят от местоположения ее в пространстве (инвариантны к любому параллельному переносу). В случае тренировочных образов стационарность может состоять из, но без ограничения ими,
- стационарности ориентации, когда направленные элементы не поворачиваются в пределах тренировочного образа; и
- стационарности масштаба (когда размер элементов изображения не изменяется в пределах тренировочного образа).
Хотя концепцию стационарности привязывают к статье Caers и соавторов под названием “Multiple-point geostatistics: a quantitative vehicle for integrating geologic analogs into multiple reservoir models”, эта статья не оправдывает надежд в части раскрытия способа для автоматической оценки и проверки стационарности заданного тренировочного образа, необходимых для уверенности в том, что тренировочный образ является подходящим для многоточечных геостатистических способов.
Сущность изобретения
Поэтому задача изобретения заключается в создании способа для автоматической оценки и проверки стационарности заданного тренировочного образа для уверенности в том, что тренировочный образ является подходящим для многоточечных геостатистических способов.
Другая задача изобретения заключается в формировании структур данных, характеризующих свойства тренировочного образа, которое может быть использовано в многоточечных геостатистических способах.
В соответствии с этими задачами, которые будут рассмотрены подробно ниже, предложен реализуемый с использованием компьютера способ, который автоматически характеризует и проверяет стационарность тренировочного образа, предназначенного для использования при многоточечном геостатистическом анализе. Предпочтительно характеризовать тренировочный образ статистическими показателями стационарности ориентации, стационарности масштаба и стационарности распределения категорий.
Следует учесть, что реализуемые с использованием компьютера способы настоящего изобретения обеспечивают автоматическое и точное определение, является или не является отобранный тренировочный образ стационарным и, следовательно, пригодным для реализаций многоточечной геостатистики, для которых необходимы такие стационарные тренировочные образы. Вследствие этого геологи, использующие реализуемые с использованием компьютера способы настоящего изобретения, сберегут время и исключат прогон ненужных реализаций многоточечной геостатистики с использованием неподходящих тренировочных образов.
Согласно предпочтительному осуществлению изобретения статистические показатели, которые характеризуют стационарность ориентации тренировочного образа, включают в себя по меньшей мере один из следующих: (i) первый набор статистических показателей, которые характеризуют неравномерность поля ориентации и поэтому обеспечивают указание на то, что имеется одно или несколько предпочтительных направлений в сетке ориентации, (ii) второй набор статистических показателей, которые характеризуют нормальность распределения направлений в сетке ориентации и поэтому обеспечивают указание на то, что имеется главное направление в поле ориентации, и (iii) третий набор статистических показателей, которые характеризуют повторяемость поля ориентации, которые обеспечивают указание на то, что поле ориентации является аналогичным на протяжении различных зон изображения. Предпочтительно, чтобы статистические показатели, которые характеризуют стационарность масштаба тренировочного образа, включали в себя расстояния между первым набором векторов признаков и вторым набором векторов признаков. Первый набор векторов признаков получают на основании первого набора изображений смещения, который формируют, подвергая изображение воздействию множества операций зависящего от поворота взятия выборок. Второй набор векторов признаков получают на основании второго набора изображений смещений, который формируют, подвергая эталонный образ, выбранный из изображения, воздействию операций зависящего от поворота и масштаба взятия выборок.
Дополнительные задачи и преимущества изобретения станут понятными для специалистов в данной области техники при обращении к подробному описанию, предоставленному совместно с сопровождающими чертежами.
Краткое описание чертежей
На чертежах:
фиг.1(А) - структурная схема компьютерной системы обработки информации, посредством которой реализуется способ настоящего изобретения;
фиг.1(В) - блок-схема последовательности операций, иллюстрирующая последовательность действий реализуемого с использованием компьютера способа для автоматического формирования и проверки тренировочного образа и последующего, основанного на них многоточечного геостатистического анализа согласно настоящему изобретению;
фиг.2(А)-2(Е) - последовательность изображений, которыми иллюстрируются операции обработки изображения, выполняемые относительно отобранного изображения, в рамках последовательности действий из фиг.1(В); в этом примере отобранное изображение представляет собой цветной аэрофотоснимок дельты реки;
фиг.3(А)-3(D) - последовательность изображений, которыми иллюстрируются операции обработки изображения, посредством которых выделяют поле ориентации для категории тренировочного образа в рамках последовательности действий из фиг.1(В); при этом на фиг.3(А) представлен тренировочный образ; на фиг.3(В) представлено изображение, иллюстрирующее компоненту Y двумерного поля градиентов, которое формируют, применяя фильтр Gy Превитта в пределах категории тренировочного образа из фиг.3(А); на фиг.3(С) представлено изображение, иллюстрирующее компоненту X двумерного поля градиентов, которое формируют, применяя фильтр Gx Превитта в пределах типичной категории тренировочного образа из фиг.3(А); и на фиг.3(D) представлено изображение, иллюстрирующее поле ориентации категории тренировочного образа из фиг.3(А);
фиг.4 - блок-схема, иллюстрирующая операции, посредством которых формируют статистические показатели ориентации и количественный показатель, основанный на них, в рамках последовательности действий из фиг.1(В);
фиг.5(А) и 5(В) - графики, которыми иллюстрируется плотность распределения вероятностей для случая распределения фон Мизеса;
фиг.6(A)-6(I) - диаграммы, которыми иллюстрируется разделение категории тренировочного образа на перекрывающиеся зоны; эти перекрывающиеся зоны используют при вычислении статистических показателей стационарности ориентации (и количественного показателя, основанного на них), статистических показателей стационарности масштаба (и количественного показателя, основанного на них) и статистических показателей стационарности распределения категорий (и количественного показателя, основанного на них) в рамках последовательности действий из фиг.1(В);
фиг.7 - блок-схема, иллюстрирующая операции, посредством которых формируют статистические показатели стационарности масштаба и количественный показатель, основанный на них, в рамках последовательности действий из фиг.1(В);
фиг.8 - график, иллюстрирующий круговую систему 4-го порядка взятия выборок в окрестности;
фиг.9 - график, иллюстрирующий круговую систему 4-го порядка взятия выборок в окрестности, приспособленную для зависящего от поворота и масштаба взятия выборок; при этом зависящее от поворота взятие выборок используют для взятия выборок из тренировочного образа и выделения векторов признаков из тренировочного образа; зависящее от поворота и масштаба взятие выборок используют для взятия выборок из эталонного образа и выделения векторов признаков из эталонного образа; эти векторы признаков анализируют для формирования статистических показателей стационарности масштаба и количественного показателя, основанного на них, в рамках последовательности действий из фиг.1(В);
фиг.10(A)-10(Y) - диаграммы, иллюстрирующие набор из 25 пар множителей аффинности; эти пары множителей аффинности используют при вычислении статистических показателей стационарности масштаба и количественного показателя, основанного на них, в рамках последовательности действий из фиг.1(В);
фиг.11 - схематическая диаграмма, иллюстрирующая операции, посредством которых вычисляют статистические показатели стационарности масштаба и аффинную карту, основанную на них, в рамках последовательности действий из фиг.1(В);
фиг.12(А) - пример тренировочного образа, которое получают копируя/вставляя верхний левый угол (очерченный прямоугольником) в другие части изображения при различных аффинных преобразованиях, применяемых к ним;
фиг.12(В) - набор аффинных карт, которыми иллюстрируются расстояние между векторами признаков для соответствующих частей в тренировочном образе и различные пары множителей аффинности в пределах эталонного образа для тренировочного образа из фиг.12(А), при этом верхний левый угол выбран в качестве эталонного образа; пикселы каждого двумерного изображения являются полутоновыми, при этом расстояния представлены пикселами, квантованными в полутоновом диапазоне значений;
фиг.12(С) - набор аффинных карт, которыми иллюстрируются расстояние между векторами признаков для соответствующих частей в тренировочном образе и различные пары множителей аффинности в пределах эталонного образа для тренировочного образа из фиг.12(А), при этом верхний левый угол выбран в качестве эталонного образа; пикселы каждого двумерного изображения являются двоичными, при этом расстояния представлены пикселами, приписанными к двоичному диапазону значений; наиболее близкие расстояния поставлены в соответствии одному двоичному значению (то есть, черному цвету), тогда как другие расстояния поставлены в соответствии другому двоичному значению (то есть, белому цвету);
фиг.13 - график, которым иллюстрируется результат измерений разброса точек в двумерном пространстве; этот результат измерений используют для вычисления статистических показателей стационарности масштаба и количественного показателя, основанного на них, в рамках последовательности действий из фиг.1(В);
фиг.14 - диаграмма, иллюстрирующая трехмерный график количественных показателей стационарности для некоторого количества тренировочных образов; оси соответствуют трем различным показателям стационарности, при этом ось X соответствует показателю стационарности распределения категорий, ось Y соответствует показателю стационарности масштаба и ось Z соответствует показателю стационарности ориентации; области этого трехмерного пространства могут быть определены как ограничивающие качественные тренировочные образа, и их используют в качестве критерия принятия решений для автоматического установления, является ли конкретный тренировочный образ в достаточной степени стационарным для использования при многоточечном геостатистическом анализе, для которого необходима такая стационарность;
фиг.15 - схематическая диаграмма, иллюстрирующая способ геостатистического анализа и моделирования на основе одного нормального уравнения;
фиг.16(А) - схематическая диаграмма, иллюстрирующая способ геостатистического анализа и моделирования на основе образов; и
фиг.16(В) - схематическая диаграмма, иллюстрирующая расширение способа моделирования на основе образов, в котором использована основанная на признаках геостатистика.
Подробное описание предпочтительного осуществления
На фиг.1(А) представлена структурная схема вычислительной системы 10 общего назначения, которая реализует настоящее изобретение. Вычислительная система 10 может включать в себя рабочую станцию (или высококачественный персональный компьютер), которая выполняет надлежащие вычисления и решающие логические операции, рассмотренные ниже, например, обработку тренировочных образов, формирование и оценку статистических показателей стационарности тренировочных образов и многоточечный статистический анализ, основанный на них. Например, вычислительная система 10 может включать в себя дисплейное устройство 12 и устройства ввода пользователя, такие как клавиатура 14 и мышь 16. Вычислительная система 10 также включает запоминающее устройство 18 (например, запоминающее устройство для долговременного хранения, такое как магнитный жесткий диск, а также запоминающее устройство для недолговременного хранения, такое как один или несколько модулей динамической оперативной памяти), в котором хранятся прикладные программы (программа), исполняемые на процессоре 20 для осуществления надлежащих вычислений и выполнения решающих логических операций, рассмотренных ниже, например, обработки тренировочных образов, формирования и оценки статистических показателей стационарности тренировочных образов и многоточечного статистического анализа, основанного на них. Такие прикладные программы, которые содержат запрограммированную последовательность команд и данные, обычно хранятся на одном или нескольких оптических дисках и загружаются в запоминающее устройство 18 с помощью накопителя на оптических дисках (непоказанным) для долговременного хранения в нем. В качестве альтернативы такие прикладные программы могут быть загружены в запоминающее устройство 18 через сетевое соединение (например, сеть Интернет) или другим подходящим средством для долговременного хранения в нем. В приведенном ниже описании «изображение» неопределенно относится к любой линии или поверхности или объему и состоит из непрерывной матрицы одинаковых пикселов, каждый из которых может иметь значение (или номер).
На фиг.1(В) показана последовательность действий, посредством которых согласно настоящему изобретению с использованием компьютера реализуется принцип автоматического формирования и подтверждения правильности тренировочных образов и выполнения многоточечного геостатистического моделирования, основанного на них. Отобранные изображения, используемые для формирования тренировочных образов, сохраняют в базе 101 данных изображений, которая может быть реализована в виде электронного, оптического или магнитного запоминающего устройства любого вида. В блоке 103 отобранное изображение импортируют из базы 101 данных изображений. На этой стадии отобранное изображение может быть любого вида, черно-белым, полутоновым, цветным или мультиспектральным изображением, и может быть с любой четкостью (разрешением). Для простоты описания отобранное изображение в блоке 105 называется изображением высокого разрешения.
В блоке 107 отобранное изображение из блока 105 обрабатывают для корректировки количества категорий пикселов изображения, если это желательно, и для корректировки разрешения, если это желательно. Для типичных многоточечных геостатистических способов требуется тренировочный образ с небольшим количеством категорий, например с менее чем 11. Часто размеры тренировочного образа должны составлять несколько сотен пикселов вдоль стороны. Задача уменьшения числа уровней серого/цвета отобранного изображения при сохранении геологической значимости заданных категорий отобранного изображения является задачей переменной трудности и зависит от сложности и качества отобранного изображения, в том числе от наличия шума и эффектов засветки. Перечень операций по обработке изображения, которые могут быть использованы в рамках этого этапа, включает в себя, но без ограничения ими, математические операции морфологии над изображениями, пороговую обработку или группировку по общему признаку цветных или полутоновых гистограмм, фильтрацию нижних частот изображения или полосовую фильтрацию. Часто желаемый результат может быть получен только путем сочетания последовательных операций по обработке изображения для исходного изображения. Может быть предусмотрен графический интерфейс пользователя, который предоставляет пользователю возможность осуществлять взаимосвязь таких блоков, визуализировать такие взаимосвязи с помощью графика и затем сохранять последовательность взаимосвязанных операций по обработке изображения для последующего использования. Окончательное изображение, сформированное с помощью процесса обработки изображения в блоке 107, в блоке 109 именуется тренировочным образом низкого разрешения с небольшим количеством категорий. Размеры и категории тренировочного образа из блока 109 соответствуют размерам и категориям, необходимым для последующих многоточечных геостатистических способов (блок 119).
На фиг.2(А)-2(Е) показан пример последовательности действий из блока 107 по обработке отобранного изображения, которое представляет собой цветной аэрофотоснимок дельты реки. На фиг.2(А) представлена полутоновая копия цветного аэрофотоснимка. На фиг.2(В) представлен результат исключения влияния засветки на изображение из фиг.2(А) путем применения морфологической операции. На фиг.2(С) представлен результат цветовой сегментации изображения из фиг.2(В) и удаления больших связанных участков (в данном случае реки и моря) способом сплошной заливки. На фиг.2(D) сохранен только уровень серого, соответствующий реке, а два других уровня серого слиты вместе. На фиг.2(Е) представлен вырезанный яркий участок изображения из фиг.2(D) и показана картина речных каналов, которая сохранена с целью применения отобранного тренировочного образа в многоточечных геостатистических способах. Эта картина имеет 2 категории, реку и фон.
В блоке 111 оценивают стационарность тренировочного образа из блока 109. Из таких операций получают статистические показатели стационарности, которые характеризуют стационарность тренировочного образа. Предпочтительно, чтобы такие статистические показатели характеризовали стационарность поля ориентации (блок 111А), стационарность масштаба изображения (блок 111В) и стационарность распределения категорий (блок 111С) для тренировочного образа из блока 109.
В блоке 113 статистические показатели стационарности, полученные в блоке 111, анализируют для определения, удовлетворяет ли тренировочный образ из блока 109 системе заданных ограничений, которыми определяется, должен или не должен использоваться тренировочный образ при последующем многоточечном геостатистическом анализе (например, в блоке 119). Если статистические показатели стационарности удовлетворяют таким заданным ограничениям, тренировочный образ добавляют в базу 115 данных тренировочного образа, которая может быть реализована в виде электронного, оптического или магнитного запоминающего устройства любого вида. Этот тренировочный образ может быть вызван из базы 115 данных (или выведен непосредственно из блока 113) для использования (блок 119) при многоточечном геостатистическом анализе (МТГА). Такие операции могут включать в себя представление (блок 117) тренировочного образа в формате сетки тренировочного образа в соответствии с форматом, необходимым для многоточечного геостатистического анализа (блок 119).
Если в блоке 113 определяют, что статистические показатели стационарности не удовлетворяют заданным ограничениям, пользователь выбирает, должен или не должен нестационарный тренировочный образ добавляться (блок 121) в базу 115 данных тренировочных образов или отбрасываться (блок 123). Нестационарный тренировочный образ может быть вызван из базы 115 данных (или выведен непосредственно из блока 121) для использования при многоточечном геостатистическом анализе (блок 127). При таких операциях нестационарный тренировочный образ может использоваться в качестве основы для сетки нестационарного тренировочного образа (блоки 125А, 127А), сетки ограничения масштаба (блоки 125В, 127В) или сетки ограничения ориентации (блоки 125С, 127С).
Для нестационарных изображений (например, изображений, не отброшенных в блоке 123) операции могут быть рекурсивно переведены обратно к блоку 107, согласно которому различные способы обработки изображений могут быть применены для выделения других признаков из отобранного изображения из блока 105, чтобы получить тренировочный образ, который удовлетворяет критериям стационарности (блоки 109-113).
На фиг.4 показаны операции блока 111А, которые характеризуют стационарность поля ориентации тренировочного образа из блока 109. Предполагается, что для каждого тренировочного образа категории тренировочного образа соответствуют различным геологическим элементам. Чтобы разделить статистические показатели стационарности ориентации по категориям и видам геологических элементов, каждую категорию изолируют, и поле ориентации и статистические показатели, устанавливаемые на основании этого, получают для конкретной категории. Чтобы изолировать конкретную категорию, все пикселы из любой другой категории приписывают к одной и той же исходной категории. Затем статистические показатели стационарности при категории могут быть усреднены или снабжены весами в соответствии со значимостью, которую пользователь захочет приписать им.
Операции над тренировочным образом (обозначенным блоком 401) начинают путем установки отсчета (переменной “k”) в 1 (блок 403) и затем преобразования копии тренировочного образа так, чтобы категория, соответствующая отсчету k (то есть, k-ой категории), была изолирована (блок 405) от других категорий. Это изображение ниже именуется «категорией тренировочного образа».
В соответствии с блоками 407 и 409 получают поле ориентации для категории тренировочного образа. Согласно предпочтительному осуществлению поле ориентации определяют, первоначально вычисляя поле градиентов категории тренировочного образа путем использования двумерной конволюции, такой как «вертикальный» и «горизонтальный» фильтры Превитта, и затем вычитая первую главную компоненту поля градиентов в пределах скользящего окна фиксированного размера (которое называется «ядром») с использованием анализа главных компонент (АГК). Такой анализ подробно описан в источниках: Feng X., “Analysis and approaches to image local orientation estimation”, thesis submitted for an MSc in Computer Engineering at University of California at Santa Cruz, 2003, и Randen et al., “Three-dimensional texture attributes for seismic data analysis”, Schlumberger Stavanger Research, SEG 2000 Expanded Abstracts, 2000, которые полностью включены в настоящую заявку посредством ссылок. «Вертикальным» фильтром Превитта
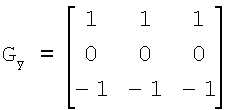
подчеркиваются «горизонтальные» края (то есть, края вдоль направления X). «Горизонтальным» фильтром Превитта
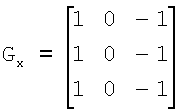
подчеркиваются «вертикальные» края (то есть, края вдоль направления Y).
Поле градиентов состоит из двумерного вектора для каждого пиксела категории тренировочного образа. Используя анализ главных компонентов, первую главную компоненту поля градиентов выделяют на протяжении круговой маски, сканируемой по изображению. Это аналогично вычислению собственных векторов и собственных значений матрицы
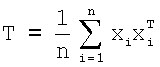 .
.
Круговую маску получают на основании квадратного окна (ядра) фиксированного размера N, где пикселы задаются весовой функцией W(x,y), как и в двумерном окне W(x,y) Гаусса, при этом:
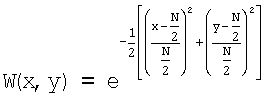 ,
,
где 0≤x<N и 0≤y<N.
При анализе главных компонент образуют два атрибута: (i) единичный корневой вектор V/|V| (как значение в радианах или как компоненты x и y); и (ii) соответствующее ему главное значение s1, которое также является модулем корневого вектора и которое подчеркивает сильные изотропные тренды. Следует отметить, что, поскольку векторы градиентов являются ортогональными к желаемой ориентации изображения, главное направление должно быть повернуто на π/2 радиан. Поле ориентации определяется единичным корневым вектором и соответствующим ему главным значением (или величиной) на фиксированных интервалах с типичными значениями, составляющими 64 пиксела для размера ядра или маски и 16 пикселов для разнесения двух последовательных выборок. Поле ориентации может быть представлено углом и величиной корневых единичных векторов (где все углы вычисляют по модулю 180°) или компонентами X и Y корневых единичных векторов и относящимися к ним главными значениями.
На фиг.3(A)-3(D) представлены последовательные изображения, которые иллюстрируют операции по обработке изображений, при которых поле ориентации для категории тренировочного образа выделяют в рамках последовательности действий из фиг.1(В). На фиг.3(А) представлен пример категории тренировочного образа. На фиг.3(В) представлено изображение, иллюстрирующее компоненту Y двумерного поля градиентов, которую образуют, применяя фильтр Gy Превитта в пределах категории тренировочного образа из фиг.3(А). На фиг.3(С) представлено изображение, иллюстрирующее компоненту X двумерного поля градиента, которую образуют, применяя фильтр Gx в пределах категории тренировочного образа из фиг.3(А). Главная компонента векторов ориентации может быть вычислена в скользящих, перекрывающихся, регулярно опрашиваемых окнах (также называемых ядрами ориентации). На фиг.3(D) представлено изображение, иллюстрирующее поле ориентации, где ядро ориентации имеет размер 64×64 пикселов и выбираются каждые 16 пикселов.
Вернемся к фиг.4, где в блоке 411 поле ориентации, образованное в блоке 409, используют для получения статистических показателей, которые характеризуют осевую ориентацию категории тренировочного образа и один или несколько количественных показателей, связанных с ними. Предпочтительно, чтобы такие статистические показатели были параметрами распределения, с помощью которых оценивают распределение фон Мизеса поля ориентации и количественные показатели (показатель), связанные с ним, которые характеризуют одно или несколько из следующих: (i) равномерность/неравномерность кругового распределения данных поля ориентации, которая обеспечивает указание на то, что имеется одно или несколько предпочтительных направлений на изображение, (ii) нормальность кругового распределения данных категории тренировочного образа, которая обеспечивает указание на то, что имеется доминирующее направление поля ориентации, и (iii) повторяемость поля ориентации, которая обеспечивает указание на то, что поле ориентации является подобным на протяжении различных зон на изображении.
В блоке 413 определяют, соответствует ли отсчет “k” последней категории (K) тренировочного образа. Если нет, осуществляют приращение отсчета “k” на единицу (то есть, k=k+1) в блоке 415 и возвращают процесс выполнения операций к блоку 405 для изоляции следующей категории тренировочного образа и вычисления статистических показателей стационарности ориентации для следующей категории (блоки 407-411). После того, как последняя категория обработана (k=K в блоке 413), выполнение операций продолжают в блоке 417 с целью визуального воспроизведения результатов обработки стационарности ориентации, полученных в блоках 407-411, для каждой категории тренировочного образа. Затем статистические показатели стационарности согласно категории могут быть усреднены или взвешены в соответствии со значимостью, которую пользователь захочет приписать им, для последующей обработки и принятия решения.
Согласно предпочтительному осуществлению предполагается, что поле ориентации подчиняется круговому нормальному распределению. В этом случае являются существенными углы ориентации векторов по модулю 180°, а величины таких векторов являются нерелевантными. Поэтому распределение должно иметь осевую симметрию. Конечно, гипотеза относительно нормальности является ограничивающей, но может быть оправдана тем, что поле ориентации вычисляют при больших ядрах. Этим обеспечивается гипотеза дважды свернутого распределения фон Мизеса, которое более подробно описано в источнике: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972, p.57-69, который полностью включен в настоящую заявку посредством ссылки. Распределение фон Мизеса задается двумя параметрами, масштабным параметром κ и параметром µ положения, и оно подчиняется функции плотности распределения вероятностей,
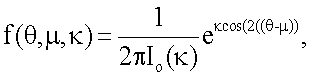
показанной на фиг.5(А) и 5(В). Переменная κ представляет собой концентрацию (обратную величину «разброса» угла θ ориентации), а переменная µ является средним направлением ее. Функция Io(κ) представляет собой функцию Бесселя нулевого порядка, определяемую через
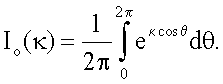
Распределение фон Мизеса является по характеру одновершинным до тех пор, пока концентрация κ не станет равной 0, тогда оно становится равномерным. Все статистические показатели и критерии относительно распределения фон Мизеса могут быть получены путем умножения углов на 2. Простое распределение фон Мизеса подчиняется функции плотности распределения вероятностей,
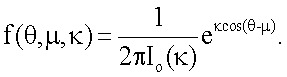
В предположении одновершинного, нормально распределенного поля ориентации предпочтительно использовать следующие формулы для получения оценки 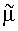 среднего µ по окружности:
среднего µ по окружности:
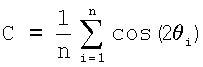 ,
,
 ,
,
 ,
,
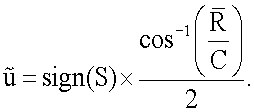
Здесь С и S являются направляющими косинусами и синусами, а величина 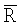 определена как средняя результирующая длина и непосредственно связана с концентрацией κ. Детально эти уравнения описаны в источнике: Rock, “Lecture Notes in Earth Science 18 - Numerical Geology”, Springer Verlag, 1988, полностью включенном в настоящую заявку посредством ссылки. Отметим, что углы являются предварительно удвоенными, и поэтому должны быть разделены на два на завершающей стадии. Оценка
определена как средняя результирующая длина и непосредственно связана с концентрацией κ. Детально эти уравнения описаны в источнике: Rock, “Lecture Notes in Earth Science 18 - Numerical Geology”, Springer Verlag, 1988, полностью включенном в настоящую заявку посредством ссылки. Отметим, что углы являются предварительно удвоенными, и поэтому должны быть разделены на два на завершающей стадии. Оценка 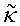 может быть получена на основании оценки максимального правдоподобия. В качестве альтернативы оценка
может быть получена на основании оценки максимального правдоподобия. В качестве альтернативы оценка 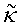 может быть получена путем использования следующего приближения:
может быть получена путем использования следующего приближения:
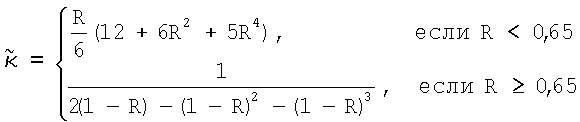
Для оценивания стационарности ориентации категории тренировочного образа требуется анализ, заключающийся в том, что определяют, является ли распределение векторов поля ориентации автомодельным в различных областях категории тренировочного образа. По этой причине проверки на неравномерность и нормальность осуществляют по всему изображению и в каждой одной из множества перекрывающихся зон. В примере, показанном на фиг. 6(A)-6(I), категория тренировочного образа подразделена на 9 перекрывающихся зон, которые обозначены как Z1, Z2, …Z9. При такой конфигурации имеются 1+9=10 различных критериев. Чтобы проверить изображение на стационарность ориентации, эмпирически находят три (3) показателя: (i) неравномерность поля ориентации, которая обеспечивает указание на то, что имеется одно или несколько предпочтительных направлений в поле ориентации, (ii) нормальность распределения направлений в поле ориентации, которая обеспечивает указание на то, что имеется доминирующее направление в поле ориентации, и (iii) повторяемость поля ориентации, которая обеспечивает указание на то, что поле ориентации является подобным на протяжении различных зон изображения. Проверка на повторяемость заключается в сравнении статистических показателей ориентации, взятых по всем парам зон. При использовании 9 зон, показанных на фиг.6(A)-6(I), имеются 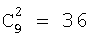 комбинаций этих пар.
комбинаций этих пар.
Неравномерность кругового распределения данных поля ориентации оценивают с помощью критерия Релея, основанного на значении средней результирующей длины 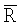 , рассмотренной выше, при двух следующих гипотезах: (i) HA0: нулевой гипотезе равномерности, то есть, когда поле ориентации не имеет предпочтительного направления и может выбираться из случайного распределения; и (ii) HA1: неравномерности кругового распределения данных поля ориентации. В случае небольших значений N≤100 критерием является просто
, рассмотренной выше, при двух следующих гипотезах: (i) HA0: нулевой гипотезе равномерности, то есть, когда поле ориентации не имеет предпочтительного направления и может выбираться из случайного распределения; и (ii) HA1: неравномерности кругового распределения данных поля ориентации. В случае небольших значений N≤100 критерием является просто 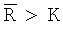 , а критические значения для
, а критические значения для 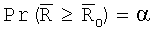 при следующих доверительных уровнях α∈{1%, 5%, 2,5%, 1%, 0,1%} основаны на таблице, и предпочтительно выбирать их из таблицы на странице 300 источника: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972. В случае N>100 критерий основан на
при следующих доверительных уровнях α∈{1%, 5%, 2,5%, 1%, 0,1%} основаны на таблице, и предпочтительно выбирать их из таблицы на странице 300 источника: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972. В случае N>100 критерий основан на 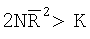 , где функция
, где функция 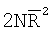 распределена как χ2 2. Критическими значениями для α∈{10%, 5%, 2,5%, 1%, 0,1%} являются χ2 2∈{4,605; 5,991; 7,378; 9,21; 13,816}. В результате этой проверки значение доверительного уровня α, которое дает критическое значение, наиболее близкое к проверяемому значение, изменяется в обратном направлении. В таком случае процент неопределенности для неравномерности имеет вид 1-α. Все 9 зон и все поле ориентации проверяют на равномерность. Конечный количественный показатель неравномерности для всего изображения при заданном масштабе (или размере ядра ориентации) имеет вид:
распределена как χ2 2. Критическими значениями для α∈{10%, 5%, 2,5%, 1%, 0,1%} являются χ2 2∈{4,605; 5,991; 7,378; 9,21; 13,816}. В результате этой проверки значение доверительного уровня α, которое дает критическое значение, наиболее близкое к проверяемому значение, изменяется в обратном направлении. В таком случае процент неопределенности для неравномерности имеет вид 1-α. Все 9 зон и все поле ориентации проверяют на равномерность. Конечный количественный показатель неравномерности для всего изображения при заданном масштабе (или размере ядра ориентации) имеет вид:
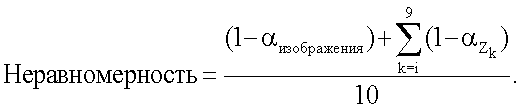
Основное ограничение этого критерия Релея заключается в его гипотезе нормальности кругового распределения, позволяющей вычислять величину 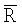 , которая является средней результирующей длиной, на которой основана проверочная статистика. Таким образом, если распределение имеет, например, две очевидные формы, которые отстоят друг от друга на 40-60°, проверка может дать высокую вероятность неравномерности вследствие относительно высокого значения
, которая является средней результирующей длиной, на которой основана проверочная статистика. Таким образом, если распределение имеет, например, две очевидные формы, которые отстоят друг от друга на 40-60°, проверка может дать высокую вероятность неравномерности вследствие относительно высокого значения 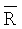 . Следовательно, критерий не может рассматриваться как критерий, позволяющий оценивать гипотезу равномерности в противовес одновершинности. Предпочтительный подход заключается в приравнивании количественного показателя неравномерности заданной зоны к 0, если проверка не может быть осуществлена вследствие отсутствия нормальности распределения относительно этой зоны.
. Следовательно, критерий не может рассматриваться как критерий, позволяющий оценивать гипотезу равномерности в противовес одновершинности. Предпочтительный подход заключается в приравнивании количественного показателя неравномерности заданной зоны к 0, если проверка не может быть осуществлена вследствие отсутствия нормальности распределения относительно этой зоны.
Нормальность кругового распределения данных поля ориентации оценивают по критерию согласия, в соответствии с которым определяют, является ли предположение относительно распределения фон Мизеса корректным, и тем самым подтверждают нормальное распределение, которое имеет предпочтительное направление (теоретически одновершинное в соответствии с его плотностью распределения вероятностей) или которое может стать равномерным при экстремальном значении 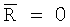 . Критерий имеет две гипотезы: (i) HB0: нулевую гипотезу хорошего соответствия дважды свернутому распределению фон Мизеса (то есть, нормальности распределения); и (ii) HB1: не распределения фон Мизеса (то есть, не нормального распределения). Классический критерий согласия, χ2, может быть использован путем сравнения круговой гистограммы {Oi}i∈[1, 18] измеренного поля ориентации с теоретической гистограммой {Ei}i∈[1, 18], которая задается дважды свернутым распределением фон Мизеса с теми же самыми оцененными средним направлением
. Критерий имеет две гипотезы: (i) HB0: нулевую гипотезу хорошего соответствия дважды свернутому распределению фон Мизеса (то есть, нормальности распределения); и (ii) HB1: не распределения фон Мизеса (то есть, не нормального распределения). Классический критерий согласия, χ2, может быть использован путем сравнения круговой гистограммы {Oi}i∈[1, 18] измеренного поля ориентации с теоретической гистограммой {Ei}i∈[1, 18], которая задается дважды свернутым распределением фон Мизеса с теми же самыми оцененными средним направлением 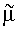 и параметром
и параметром 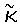 концентрации и вычисляется по тем же самым столбикам θi∈[1, 18] гистограммы. Измеренные осевые данные находятся между -90 и 90° и рассортированы по 18 столбикам {Oi}i∈[1, 18] гистограммы шириной 10°, которые имеют следующие центры столбиков:
концентрации и вычисляется по тем же самым столбикам θi∈[1, 18] гистограммы. Измеренные осевые данные находятся между -90 и 90° и рассортированы по 18 столбикам {Oi}i∈[1, 18] гистограммы шириной 10°, которые имеют следующие центры столбиков:
θi∈[1, 18]={-85; -75; -65; -55; -45; -35; -25; -15; -5; 5; 15; 25; 35; 45; 55; 65; 75; 85;},
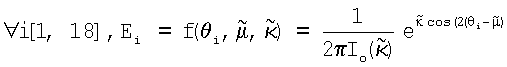
Критерием проверки является χ2>χα,ν 2, где 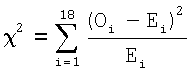 .
.
В случае критерия χ2 используют ν=18-2-1=15 степеней свободы (при сравнении гистограмм с 18 столбиками, и при этом распределения фон Мизеса имеет 2 параметра, положение и масштаб). Критическими значениями для:
α∈{99,5%, 99%, 97,5%, 95%, 90%, 75%, 50%, 25%, 10%, 5%, 2,5%, 1%, 0,5%}
являются:
χ15 2∈{4,60; 5,23; 6,26; 7,26; 8,55; 11,04; 14,34; 18,25; 22,31; 25,00; 27,49; 30,58; 32,80}.
В результате проверки осуществляется возврат к значению доверительного уровня α, который дает критическое значение, наиболее близкое к проверяемому значению. Все 9 зон и все поле ориентации проверяют на нормальность. Окончательный количественный показатель нормальности для всего изображения при заданном масштабе (или размере ядра ориентации) имеет вид:
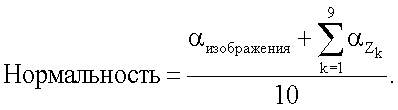
Критерий согласия, χ2, имеет ограничения вследствие сортировки круговых данных в гистограмму, ограничения, которые становятся более очевидными, когда значение оцениваемой концентрации становится очень высоким. В этом случае проверка может дать очень низкий или нулевой доверительный уровень при проверке на нормальность, тогда как данные несомненно являются унимодальными. Следовательно, могут быть заданы два условия, при соблюдении которых автоматически получается доверительный уровень α=100%: например, (i)  ; и (ii) card({Oi}i∈[1, 18]<3. Кроме того, предусматривают коррекцию числового артефакта, обусловленного сортировкой в столбики, который заключается в том, что для данного столбика i очень небольшое значение оцененного наблюдения 0<Ei<<1 и фактическое наблюдение Oi=1 (при относительно большом общем количестве наблюдений) будут вносить большое число в статистический показатель критерия χ2 и, следовательно, делать критерий недействительным. Поскольку неадекватная сортировка в столбики в основном вносит вклад в этот результат, вклад этого конкретного фактического наблюдения в статистический показатель критерия χ2 может быть приравнен к нулю.
; и (ii) card({Oi}i∈[1, 18]<3. Кроме того, предусматривают коррекцию числового артефакта, обусловленного сортировкой в столбики, который заключается в том, что для данного столбика i очень небольшое значение оцененного наблюдения 0<Ei<<1 и фактическое наблюдение Oi=1 (при относительно большом общем количестве наблюдений) будут вносить большое число в статистический показатель критерия χ2 и, следовательно, делать критерий недействительным. Поскольку неадекватная сортировка в столбики в основном вносит вклад в этот результат, вклад этого конкретного фактического наблюдения в статистический показатель критерия χ2 может быть приравнен к нулю.
Повторяемость распределения поля ориентации оценивают с помощью двух частичных критериев. Первый критерий представляет собой непараметрический критерий, при использовании которого сравнивают два распределения, взятых из двух зон изображения. В критерии используются две гипотезы: (i) HC0: нулевая гипотеза наличия двух выборок из одной и той же совокупности (распределения); и (ii) HC1: две выборки не из одного и того же распределения. В данном случае это две выборки, которые включают в себя n1 и n2 наблюдений, где N=n1+n2. Обе выборки объединяют и затем упорядочивают. Множества {ai}i∈[1,N] и {bj}j∈[1,N] задают следующим образом. Множество {ai}i∈[1,N] состоит из некоторого количества наблюдений из первой выборки наряду со статистическими показателями i первого порядка смешанной выборки. Множество {bj}j∈[1,N] состоит из некоторого количества наблюдений из второй выборки наряду со статистическими показателями j первого порядка смешанной выборки. Значение U2 вычисляют следующим образом:
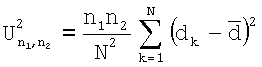 ,
,
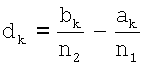 ,
,
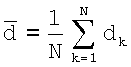 .
.
Критические значения 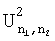 для доверительных уровней α∈{10%, 5%, 1%, 0,1%} приведены на странице 314 в: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972. Детали этого двухвыборочного критерия U2 Ватсона описаны в источнике: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972, p.201-203, который полностью включен в настоящую заявку посредством ссылки.
для доверительных уровней α∈{10%, 5%, 1%, 0,1%} приведены на странице 314 в: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972. Детали этого двухвыборочного критерия U2 Ватсона описаны в источнике: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972, p.201-203, который полностью включен в настоящую заявку посредством ссылки.
Двухвыборочный критерий U2 часто оказывается недействительным, когда разброс направлений является очень узким, вероятно, вследствие того, что направления не перемежаются регулярно. В качестве альтернативы может быть использован следующий критерий, который также является чувствительным к очень узким распределениям углов 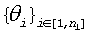 и
и 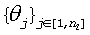 :
:
если 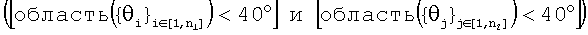 ,
,
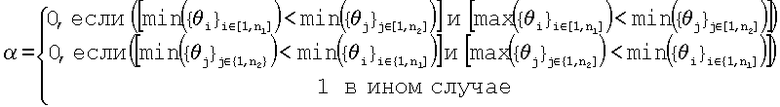 ,
,
else
выполнить проверку по непараметрическому критерию U2 Ватсона
endif.
После того, как проверка осуществлена для всех 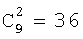 возможных пар зон, первую часть количественного показателя повторяемости вычисляют следующим образом:
возможных пар зон, первую часть количественного показателя повторяемости вычисляют следующим образом:
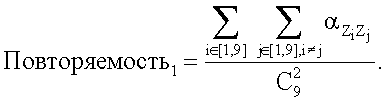
Вторым критерием для оценивания повторяемости распределения поля ориентации является параметрический критерий, согласно которому сравнивают два распределения, взятых из двух зон изображения в предположении, что оба распределения являются распределениями фон Мизеса. Первая часть этого параметрического критерия представляет собой критерий равных концентраций с доверительным уровнем ακ. В этой первой части для 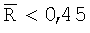 статистический показатель
статистический показатель
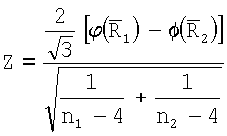
(где 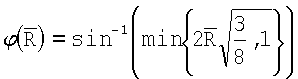 ) вычисляют и сравнивают со среднеквадратическим нормальным отклонением. Вместо поиска критических значений в таблицах вычисляют доверительный уровень по статистическому показателю Z, используя интегральную функцию
) вычисляют и сравнивают со среднеквадратическим нормальным отклонением. Вместо поиска критических значений в таблицах вычисляют доверительный уровень по статистическому показателю Z, используя интегральную функцию
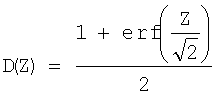 нормального распределения.
нормального распределения.
Поскольку критическая область состоит из одинаковых хвостов кривой распределения, доверительный уровень получают согласно записи 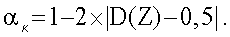 Для
Для 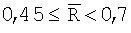 статистический показатель
статистический показатель
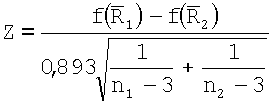
(где 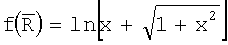 и где
и где 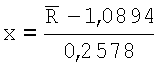 ) вычисляют и сравнивают со среднеквадратическим нормальным отклонением. Вместо поиска критических значений в таблицах вычисляют доверительный уровень по статистическому показателю Z, используя интегральную функцию
) вычисляют и сравнивают со среднеквадратическим нормальным отклонением. Вместо поиска критических значений в таблицах вычисляют доверительный уровень по статистическому показателю Z, используя интегральную функцию 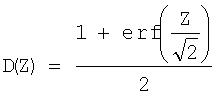 нормального распределения. Поскольку критическая область состоит из одинаковых хвостов кривой распределения, доверительный уровень получают согласно записи
нормального распределения. Поскольку критическая область состоит из одинаковых хвостов кривой распределения, доверительный уровень получают согласно записи 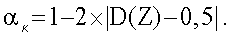 Для
Для 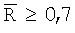 статистический показатель
статистический показатель 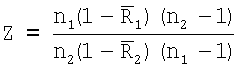 вычисляют и сравнивают с критическими значениями Фишера для распределения со степенями свободы n1-1 и n2-1. Критические значения Фишера можно отыскать в таблицах или найти, используя интегральную функцию распределения:
вычисляют и сравнивают с критическими значениями Фишера для распределения со степенями свободы n1-1 и n2-1. Критические значения Фишера можно отыскать в таблицах или найти, используя интегральную функцию распределения:

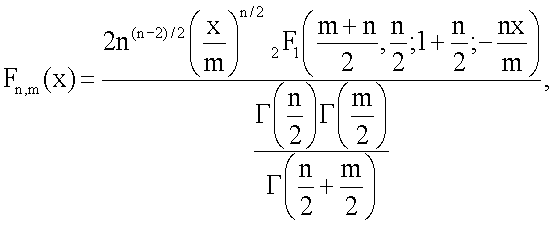
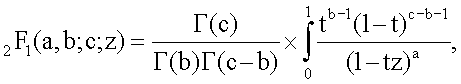
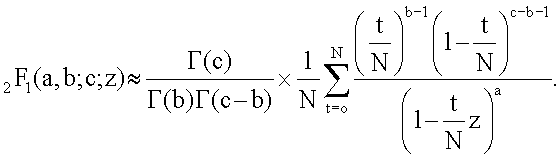
Поскольку критическая область состоит из одинаковых хвостов кривой распределения, доверительный уровень может быть получен согласно записи 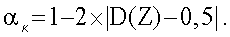
Вторая часть параметрического критерия для повторяемости распределения поля ориентации представляет собой критерий равных средних направлений с доверительным уровнем αµ. Статистический показатель
критерия согласно этому критерии вычисляют и сравнивают с критическими значениями Фишера для распределения с 1 и N-2 степенями свободы. Для этого конкретного критерия критические значения Фишера получают с помощью операции табличного поиска при следующем доверительном уровне α∈{10%, 5%, 2,5%, 1%}. Если данные не распределены нормально (сравните с критерием χ2 для нормальности) или если доверительный уровень для критерия равных концентраций составляет 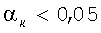 , то доверительный уровень для критерия повторяемости дается значением 0. В ином случае доверительный уровень критерия средних направлений равен доверительному уровню αµ критерия повторяемости.
, то доверительный уровень для критерия повторяемости дается значением 0. В ином случае доверительный уровень критерия средних направлений равен доверительному уровню αµ критерия повторяемости.
Часть равных концентраций или часть средних равных направлений второго критерия повторяемости может оказаться недействительной при очень узких распределениях углов и высоких значениях оцененных концентраций. Возможно, это происходит потому, что значения оценок концентраций становятся менее надежными, когда распределения являются узкими или критерий становится более чувствительным с приближением 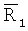 и
и 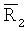 очень близко к 1 (для обоих критериев, основанных на концентрациях и средних ориентациях). Следовательно, при желании вторая проверка на повторяемость может быть пропущена, когда обе оценки
очень близко к 1 (для обоих критериев, основанных на концентрациях и средних ориентациях). Следовательно, при желании вторая проверка на повторяемость может быть пропущена, когда обе оценки 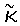 выше порогового значения 20, а разность средних направлений меньше 15°. Точнее,
выше порогового значения 20, а разность средних направлений меньше 15°. Точнее,
если 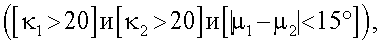
α=1
else
выполнить вторую проверку на повторяемость
endif.
После выполнения второй проверки на повторяемость для всех 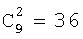 возможных пар зон количественный показатель для второй проверки на повторяемость вычисляют следующем образом:
возможных пар зон количественный показатель для второй проверки на повторяемость вычисляют следующем образом:
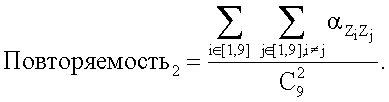
Подробности, относящиеся к первой и второй частям второго критерия повторяемости, изложены в источнике: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972, p.161-162 (относительно равных концентраций) and p.152-155 (относительно равных средних направлений), который полностью включен в настоящую заявку посредством ссылки.
Затем количественные показатели первой и второй проверок на повторяемость складывают для получения суммарного количественного показателя повторяемости (например, повторяемость = повторяемость1 + повторяемость2). В заключение, результаты проверок на нормальность, неравномерность и повторяемость при заданном масштабе (заданном размере ядра ориентации) группируют вместе. Например, они могут быть сгруппированы вместе в виде:
Стационарность ориентации = 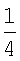 нормальность +
нормальность + 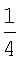 неравномерность +
неравномерность + 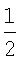 повторяемость.
повторяемость.
Предпочтительно приравнивать размер ядра к половине наименьшего размера изображения. Следует отметить, что количественные показатели стационарности ориентации выражаются в процентах.
На фиг.7 показаны операции из блока 111В (фиг.1(В)), которые характеризуют масштаб и стационарность аффинности тренировочного образа из блока 109. Масштаб и стационарность аффинности тренировочного образа зависят от поворота. Поэтому операции над тренировочным образом (охарактеризованным в блоке 701) начинают с вычисления (блок 703) поля ориентации тренировочного образа. Предпочтительно вычислять поле ориентации тренировочного образа, используя такие же способ и параметры, как и описанные выше применительно к блокам с 407 по 409 на фиг.4. Поле ориентации вычисляют для всех категорий тренировочного образа. Текстурные атрибуты, используемые для вычисления масштаба и статистических показателей аффинности, являются признаками, извлекаемыми из матриц смежности уровней серого (поясняемых ниже применительно к блокам 709 и 719). Для осуществления этого принципа требуется измерение различия в интенсивности уровней серого между соседними парами пикселов при заданных смещениях. Каждый пиксел изображения сравнивают с пикселами из того же самого изображения, но взятыми при некотором количестве различных смещений (в предпочтительном осуществлении используют 28 различных смещений). Для конкретного смещения смещенные пикселы группируют в изображение смещения. Таким образом, в соответствии с предпочтительным осуществлением имеются 28 изображений смещения. В блоках 705 и 707 берут выборки из тренировочного образа, используя поле ориентации в качестве направляющей для выделения некоторого количества различных изображений смещения (28 различных изображений смещения согласно иллюстративному осуществлению). Согласно предпочтительному осуществлению, описанному ниже, информацию об ориентации включают в состав изображений смещения, используя зависящее от поворота взятие выборок. Эти изображения смещения используют для вычисления матриц смежности уровней серого (МСУС) в небольших скользящих окнах, сканируемых по изображению (блок 709). Векторы текстурных признаков получают (блок 711) из этих матриц смежности уровней серого.
Параллельно выбирают (блок 713) область (или зону) тренировочного образа. Эта область или зона, которая ниже именуется эталонным образом, имеет такие же размеры, как и скользящие окна, используемые в блоке 709. Аналогично операциям блоков 705-711 из эталонного образа берут (блок 715) выборки, используя поле ориентации в качестве направляющей. Однако, когда берут выборки из небольшого изображения эталонного образа, то не только осуществляют коррекцию изображения на ориентацию, но и задают различные аффинные преобразования для круговой системы окрестностей, используемой при получении выборок. Путем модификации множителей аффинности получают различные масштабы и растяжения вдоль осей X и Y, в результате чего получают (блок 717) изображения смещения с различными аффинностями. Поэтому согласно предпочтительному осуществлению вместо того, чтобы иметь только 28 изображений смещения и 1 вектор текстурных атрибутов (как в случае тренировочного образа), операции осуществляют на основании 28×N изображений смещения эталонного образа и N векторов текстурных атрибутов для эталонного образа, где N - число пар (X-, Y-) аффинностей. Для каждого выбора X- и Y-аффинности из эталонного образа берут зависящие от поворота выборки. Согласно иллюстративному осуществлению, показанному на фиг.10, N выбирают равным 25 с 5 возможными значениями для аффинности вдоль оси X (например, x0,5; x0,667; x1; x1,5; x2) и 5 возможными значениями для аффинности вдоль оси Y (например, x0,5; x0,667; x1; x1,5; x2). Изображения, сформированные в блоке 719, используют для вычисления (блок 719) матриц смежности уровней серого из небольших скользящих окон, сканируемых по изображению. Векторы текстурных признаков получают (блок 721) из этих матриц смежности уровней серого. Векторы текстурных признаков, формируемые в блоке 721, получают в результате различных масштабных преобразований (которые в настоящей заявке иногда именуются «расширениями аффинности») одного и того же эталонного образа. В блоке 723 выполняют операции измерения подобия (например, евклидово расстояния) между векторами текстурных признаков, образованными в блоке 721, и векторами текстурных признаков, образованными в блоке 711. В блоке 725 для заданной зоны (скользящего окна) тренировочного образа выполняют операцию выбора аффинного преобразования, дающего расширенную версию эталонного образа, который минимизирует показатель подобия, вычисленный в блоке 723. Эти результаты могут быть интерпретированы как аффинная карта тренировочного образа в предположении, что один однозначно определенный эталонный образ воспроизводится на протяжении всего изображения в различных масштабах. В блоке 727 вычисляют статистические показатели и количественный показатель стационарности, используя аффинные преобразования, идентифицированные в блоке 725. В блоке 729 могут быть визуально воспроизведены аффинные карты (в настоящей заявке также именуемые картами подобия). Статистические показатели и количественный показатель, вычисленные в блоке 727, и аффинная карта, визуально воспроизведенная в блоке 729, относятся к конкретному эталонному образу, выбранному в блоке 713.
В блоке 731 определяют, должно ли выполнение операций возвратиться обратно к блоку 713. Такое решение может быть принято в соответствии с входным сигналом пользователя или автоматически с помощью скользящего окна. Если решением в блоке 731 является «да», в блоке 713 выбирают другой эталонный образ, а статистические показатели и количественный показатель стационарности, относящиеся к нему, образуют, как описано выше, в соответствии с блоками 715-729. Если решением в блоке 731 является «нет», среднее количественных показателей, образованных в блоке 727, может быть вычислено в блоке 733 по некоторому количеству эталонных образов, и/или составная аффинная карта, образованная на основании аффинных карт, полученных в блоке 725 по некоторому количеству эталонных образов, может быть визуально воспроизведена в блоке 735, и обработка заканчивается.
Согласно предпочтительному осуществлению для получения изображений смещения в блоках 705/707 и блоках 715/717 используют главный элемент круговой системы окрестности N-го порядка, которая подробно поясняется в: Deng et al., “Gaussian MRF rotation-invariant features for image classification”, IEEE Transaction on Pattern Analysis and Machine Intelligence, vol.26, №7, July 2004. Точнее, эту изотропную круговую систему окрестностей используют для взятия выборок пикселов, прилегающих к опорному центральному пикселу. Все окрестности, из которых берут выборки, расположены по концентрическим окружностям с радиусами пикселов, составляющими r=1, r=2, r=3, … r=N, где N - порядок окрестности. Билинейная интерполяция может быть использована для интерполяции значений интенсивности выборок, которые не попадают точно на центр пикселов.
На фиг.8 показана круговая система окрестностей 4-го порядка, используемая в предпочтительном осуществлении, с 4, 6, 8 и 10 выборками, взятыми на полуокружностях с радиусами соответственно r1=1, r2=2, r3=3 и r4=4. Эти выборки суммируют следующим образом для получения 4+6+8+10=28 точек смещения:
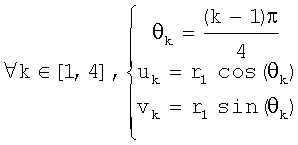
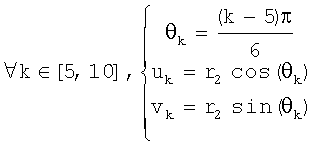
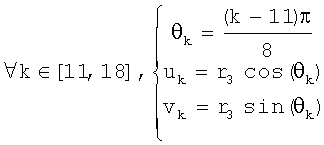
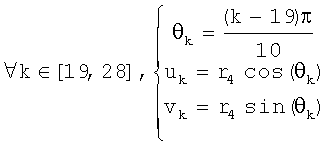
Такое взятие выборок обеспечивает преимущество, заключающееся в полном охвате каждого пиксела в круговой окрестности без попадания в ловушку выборок несколько раз одного и того же пиксела или пар пикселов.
Для операций из блоков 705 и 707, при выполнении которых формируют изображения смещения для тренировочного образа, круговую систему окрестностей приспосабливают для зависящего от поворота взятия выборок. Точнее, пусть u и v будут координатами векторов-столбцов выборочных точек в плоскости X-Y для угла поворота, равного 0, и пусть u' и v' будут результатами после поворота на угол φ при зависящем от поворота взятии выборок в окрестности. Тогда поворот на угол φ координат взятия выборок в окрестности имеет вид:
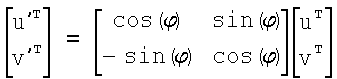 .
.
Примерное осуществление такого зависящего от поворота взятия выборок с использованием круговой системы 4-го порядка взятия выборок в окрестности показано на фиг.9 при повороте на φ=-60°. Кроме того, в осуществление на фиг.9 добавлено зависящее от масштаба взятие выборок, описанное выше, которое может быть проигнорировано для задач блоков 705 и 707. Аналогично взятию выборок в окрестности без поворота билинейная интерполяция может быть использована для интерполяции значений интенсивности выборок, которые не попадают точно на центр пикселов. Поскольку для представления изображения на экране используется косвенная система прямоугольных координат, в которой положение оси Y изменено на обратное, и она ориентирована «вниз», тогда как ось X по-прежнему ориентирована «вправо», поворот на угол -φ применяется к круговым координатам взятия выборок в окрестности. Параметры поворота системы взятия выборок в окрестности, описанной выше, получают на основании векторов поля ориентации, вычисленных в блоке 703. Точнее, для каждого пиксела тренировочного образа или каждого пиксела эталонного образа имеется одно значение направление φ вектора ориентации, дающего параметр φ поворота системы взятия выборок в окрестности. Согласно предпочтительному осуществлению круговым взятием выборок в окрестности с поворотом обеспечивается формирование 28 смещенных пикселов для каждого пиксела тренировочного образа. Таким образом, зависящее от поворота взятие выборок дает 28 изображений смещения тренировочного образа для последующего анализа в блоке 711.
Для операций из блоков 715 и 717, посредством которых формируют изображения смещения для конкретного эталонного образа, круговую систему окрестностей приспосабливают для зависящего от поворота и масштаба взятия выборок. Точнее, аффинное преобразование системы n-ого порядка взятия выборок в окрестности используют для получения текстурных признаков при заданном локальном масштабе по осям X и Y и заданной локальной ориентации. Этот подход является противоположным стохастическому формированию изображений с помощью многоточечной геостатистики. В действительности, как поясняется в: Caers, “Geostatistical history matching under training-image based geological model constraints”, SPE Journal, №74716, 2003, p.218-226, информация о локальном масштабе (аффинности) и ориентации может быть использована для управления реализацией стохастического процесса и обеспечивает возможность повторения образа с различными масштабами и ориентациями. Множители ax и ay аффинности описывают масштабное преобразование (растяжение) эталонного образа вдоль оси X и оси Y, соответственно. В иллюстративном осуществлении, показанном на фиг.10, имеются 5 возможных значений для множителя ax аффинности (например, x0,5; x0,667; x1; x1,5; x2) и 5 возможных значений для множителя ay аффинности (например, x0,5; x0,667; x1; x1,5; x2), в результате чего получаются в совокупности 25 различных пар (или попарно связанных) множителей аффинности. Когда отношение размеров ay/ax не равно 1, этот образ растягивается вдоль оси X или оси Y. Общее аффинное и вращательное преобразование круговых координат взятия выборок в окрестности может быть записано в следующем виде:
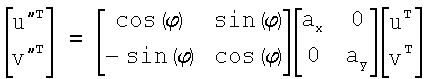 .
.
Иллюстрация повернутой и масштабированной круговой системы 4-го порядка взятия выборок в окрестности дана на фиг.9 при повороте на φ=-60° и паре (ax,ay)=(0,5; 1) множителей аффинности. Множитель ax аффинности, равный 0,5, указывает на то, что масштаб взятия выборок в окрестности увеличивается вдоль оси X, когда берут выборки из образа. Это эквивалентно растяжению эталонного образа в 2 раза вдоль оси X. Параметры поворота системы взятия выборок в окрестности, описанной выше, получают на основании векторов поля ориентации, вычисленных в блоке 703. Точнее, для каждого пиксела тренировочного образа или каждого пиксела эталонного образа имеется одно значение направления φ вектора ориентации, дающее параметр φ поворота системы взятия выборок в окрестности. Параметры (ax,ay) аффинности являются постоянными на всем изображении. Однако для каждого набора этих параметров аффинности вычисляют новый набор изображений смещения для последующего анализа в блоке 721. Согласно предпочтительному осуществлению при круговом, зависящем от поворота и масштаба взятия выборок в окрестности формируют 25 наборов из 28 смещенных пикселов для каждого пиксела эталонного образа, по одному набору для каждой совокупности показателей X- и Y-аффинности. Таким образом, при зависящем от поворота и масштаба взятии выборок получают 25 наборов из 28 изображений смещения эталонного образа для последующего анализа в блоке 721.
Как описывалось выше, при выполнении операций из блоков 709 и 711 получают текстурные признаки (ниже именуемые «текстурными атрибутами» или «элементами») из матриц смежности уровней серого, вычисленных по изображениям смещения тренировочного образа. Согласно предпочтительному осуществлению матрицы смежностей уровней серого вычисляют следующим образом. Сначала тренировочный образ и изображения смещения квантуют на G уровней серого (например, G=32). Следует отметить, что даже при выполнении анализа черно-белых образов с переменной разрешающей способностью используют более 2 уровней серого, поскольку во время кругового взятия выборок в окрестности с преобразованиями масштаба и ориентации большая часть выборок не попадает на центры пикселов, и осуществляют интерполяцию. В дополнение к этому, если в тренировочном образе категорий больше 2, но меньше G, то такое квантование на уровни серого позволяет выполнять операции для сохранения отличительной особенности каждой категории. Затем квантованные изображения обрабатывают для вычисления набора матриц смежности. Для каждой матрицы смежности, которая может быть обозначена Cd(k,l), оценивают вероятность уровней k и l серого, наблюдающихся на квантованном изображении l(x,y) при смещении d. Эту вероятность определяют путем подсчета числа пар (x,y) и (x',y'), где l(x,y)=k, l(x',y')=l и (x'-x, y'-y)=d и после этого деления этого числа пар на суммарное количество смежных пикселов в изображении. Набор матриц смежности формируют путем сравнения каждого одного из квантованных изображений смещения с квантованным тренировочным образом. Согласно предпочтительному осуществлению получают 28 матриц Cd(k,l) смежности. Для заданного смещения d или для заданной пары (тренировочных образов, изображений смещения) каждый элемент матрицы смежности подчиняется формуле, приведенной ниже:
Cd(k,l)=Pr[I(x',y')=l|I(x,y)|=k].
Как показано на фиг.11, каждую матрицу смежности вычисляют не по всему тренировочному образу, а по небольшим скользящим окнам, выделяемым из изображения, из которых регулярно берут выборки. На фиг.11 показано формирование матриц смежности (и векторов текстурных признаков, получаемых из них). На фиг.11 тремя областями a, b и с показаны возможные положения скользящего окна. Согласно предпочтительному осуществлению в положениях скользящего окна регулярно берут выборки на протяжении всего тренировочного образа. Для каждой одной из областей a, b, c из фиг.11 имеются 28 изображений смещения, которых интерполируют, и 28 последовательных матриц смежности и статистических показателей матриц смежности, которых вычисляют. Следует отметить, что, если размер скользящего окна увеличить, больше текстурных признаков будет захвачено; однако же разрешение аффинных карт, получаемых на основании их в блоке 725, уменьшается.
После вычисления набора матриц смежности вычисляют шесть текстурных признаков на основании каждой матрицы смежности, используя нижеследующие формулы (где p(k,l) представляет собой элемент заданной матрицы смежности):
i) Энергия (угловой второй момент): 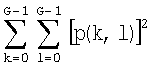 ;
;
ii) Контраст (инерция): 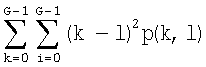 ;
;
iii) Не подобие (абсолютное значение): 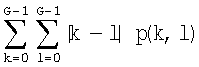 ;
;
iv) Обратная разность: 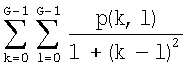 ;
;
v) Энтропия: 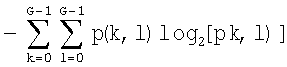 ;
;
vi) Максимальная вероятность: 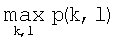 .
.
Более конкретные детали, касающиеся этих дескрипторов, могут быть обнаружены в: Haralick et al., “Texture features for image classification”, IEEE Transaction on Systems Man and Cybernetics, SMC-3, №6, 1973, p.610-621, и Materka et al., “Texture Analysis Methods - A Review”, Technical University of Lodz, Institute of Electronics, COST B11 report, Brussels, 1998, и эти источники полностью включены в настоящую заявку посредством ссылок. Таким образом, вектор из 6 элементов характеризует каждую матрицу смежности, которая уменьшает размерность текстурных показателей. Согласно предпочтительному осуществлению 6 текстурных признаков для каждой одной из 28 матриц смежности группируют вместе для образования вектора из 168 элементов, которые связаны с тренировочным образом.
Согласно предпочтительному осуществлению операции, аналогичные описанным выше применительно к блокам 709 и 711, выполняют для получения текстурных признаков на основании матриц смежности уровней серого (МСУС), вычисленных по изображениям смещения эталонного образа в блоках 719 и 721. При выполнении таких операций набор матриц смежности (предпочтительно 28) вычисляют для каждой назначенной пары множителей аффинности (например, для каждой одной из 25 пар множителей аффинности). Каждую матрицу смежности вычисляют по всему эталонному образу. Затем для каждой матрицы смежности формируют 6 текстурных признаков. Согласно предпочтительному осуществлению образуют 25 векторов текстурных признаков (при этом каждый вектор содержит 168 элементов). 25 векторов соответствуют 25 парам показателей аффинности, описанным выше применительно к фиг.10.
Как описывалось выше, при выполнении операций из блока 723 определяют подобие (например, евклидово расстояние) между векторами текстурных признаков, образованными в блоке 721, и векторами текстурных признаков, образованными в блоке 711. Согласно предпочтительному осуществлению это осуществляют путем формирования для каждой области r тренировочного образа расширения a (из 25 возможных расширений aff) эталонного образа, которое минимизирует евклидово расстояние между векторами VTi,r и VRP,aff текстурных признаков, что выражается математически в следующем виде:
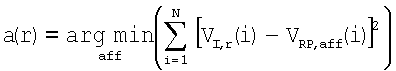 .
.
Растяжение a(r) вычисляют для каждой области r, указанной тонколинейными стрелками, которые на фиг.11 соединяют пары векторов признаков. На фиг.11 показаны для сравнения векторы текстурных признаков для трех различных областей a, b, c тренировочного образа и различные аффинные преобразования эталонного образа, обозначенные (x1,y1), (x2,y2), (x3,y3) … (xN,yN).
Минимальное евклидово расстояние между векторами признаков дает аффинную карту, отражающую наилучшие множители аффинности для областей тренировочного образа. На фиг.11 показан пример аффинной карты, иллюстрирующей наилучшие параметры аффинности (xa,ya), (xb,yb), (xc,yc) для областей a, b, c, соответственно. Как описывалось выше, аффинная карта может быть визуально воспроизведена в блоке 729.
На фиг.12(В) и 12(С) показана другая форма аффинной карты, где отдельные двумерные изображения предусмотрены для пар показателей аффинности. Каждое двумерное изображение характеризует расстояние между векторами признаков для соответствующих частей в тренировочном образе и эталонном образе. В аффинной карте из фиг.12(В) пикселы каждого двумерного изображения являются полутоновыми с расстояниями, представленными пикселами, квантованными в полутоновом диапазоне значений. На аффинной карте из фиг.12(С) пикселы каждого двумерного изображения являются двоичными с расстояниями, представленными пикселами, приписанными к двоичному диапазону значений. Наиболее близкие расстояния приписаны к одному двоичному значению (то есть, к черному цвету), тогда как другие расстояния приписаны к другому двоичному значению (то есть, к белому цвету). Что касается примера из фиг.12(А)-12(С), то изображение из фиг.12(А) получают путем копирования/вставления классического тренировочного образа (в верхний левый угол) при различных аффинных преобразованиях над остальной частью изображения: в верхнем левом углу образ имеет аффинное преобразование (ax=1, ay=1); в верхнем правом углу образ воспроизводится дважды при аффинном преобразовании (ax=1, ay=0,5); в средней левой части изображения образ воспроизводится дважды при аффинном преобразовании (ax=0,5, ay=1); в средней правой части изображения образ воспроизводится 4 раза при аффинном преобразовании (ax=0,5, ay=0,5); в нижней части изображения образ имеет аффинное преобразование (ax=2, ay=1). Полное изображение из фиг.12(А) представляет собой тренировочный образ. Выделенный прямоугольник в верхнем левом углу изображения из фиг.12(А) выбран в качестве эталонного образа. Аффинная карта из фиг.12(В) отражает расстояние по шкале уровней серого между векторами текстурных признаков, выделенных из тренировочного образа, и векторами текстурных признаков эталонного образа для 9 различных пар множителей аффинности. Аффинная карта из фиг.12(С) отражает расстояние в двоичном виде (то есть, ближайшие расстояния в черном цвете) между векторами текстурных признаков, выделенными из тренировочного образа, и векторами текстурных признаков эталонного образа для 9 различных пар показателей аффинности. Корреляция между видимой аффинностью тренировочного образа и результатами является очень хорошей, поскольку способом обнаруживается аффинность (ax=2, ay=1) для большинства пикселов в нижней части тренировочного образа, аффинность (ax=0,5, ay=1) для большинства пикселов в средней левой части тренировочного образа, аффинность (ax=0,5, ay=0,5) для большинства пикселов в средней правой части тренировочного образа и аффинность (ax=1, ay=0,5) для большинства пикселов в верхнем правом углу тренировочного образа. Алгоритмом также обнаруживается аффинность (ax=1, ay=1) в двух местах тренировочного образа: как и ожидалось, в верхнем левом углу тренировочного образа, который также был использован в качестве эталонного образа, и по направлению к нижней части тренировочного образа. Этот артефакт при аффинности (ax=1, ay=1) обусловлен краевым разрывом в двумерном изображении, который интерпретируется как изменение масштаба.
Согласно предпочтительному осуществлению при выполнении операций из блока 727 используют принципы построения аффинных карт, описанные выше, для формирования статистических показателей стационарности масштаба. Стационарность масштаба по отношению к эталонному образу может быть найдена путем определения того, сколько различных масштабов (и отношений размеров) охватывается этим изображением, или как изображение растягивается в масштабном пространстве в предположении, что изображение получают в результате повторения уникального образа при различных масштабах и ориентациях. Точнее, стационарность масштаба может быть определена как отклонение от единственного кластерного значения (X×1, Y×1) на аффинной карте; поэтому любое изменение вдоль оси X или Y аффинной карты указывает на нестационарное изображение. В предпочтительном осуществлении стационарность масштаба изображения находят путем вычисления разброса облака точек p1, p2, … pn, определяемых при наилучших соответствиях между изображением и растянутыми образами. В таком случае, как показано на фиг.13, показатель разброса может быть просто вычислен как показатель разброса точек в двумерном пространстве. Эти наилучшим образом согласованные точки расположены в масштабном пространстве, где ось X соответствует возможному растяжению вдоль оси X, а ось Y - возможным растяжениям вдоль оси Y. Каждая из этих точек, которые могут представлять особую небольшую зону на изображении, описывается местоположением в этом масштабном пространстве, при этом x и y являются показателями растяжения. Масштабное пространство является не непрерывным, а дискретным, поскольку вычисляют только небольшое количество растяжений эталонного образа. Показатели растяжения отображают в масштабное пространство с помощью биекции (то есть, взаимно однозначного отображения). Согласно предпочтительному осуществлению показателями x-растяжения являются 1/2, 2/3, 1, 3/2 и 2, и они соответствуют -1, -1/2, 0, 1/2 и 1 по оси абсцисс. Такое масштабное пространство представлено на фиг.13. В этом примере пространственно-масштабное представление разброса облака точек обозначено эллипсом. Показаны направления первой и второй главных компонент. Две главные компоненты точек p1, p2, … pn получают с помощью разложения 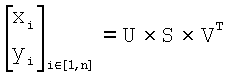 по особым значениям. Первая главная компонента задает направление самой сильной вариации точек, а вторая главная компонента ортогональна первой главной компоненте и задает направления самой слабой вариации точек. Отношение s2/s1 двух особых значений s1 и s2 (которые могут быть выбраны из диагонали матрицы S) дает значимость вариации точек p1, p2, … pn вдоль направления второго главного направления. Пусть u=(ux,uy) является единичным вектором, задающим направление первой главной компоненты и пусть v=(vx,vy) является единичным вектором, задающим направление второй главной компоненты (u и v являются ортогональными). Единичные векторы u и v можно получить путем нормирования первого и второго столбцов матрицы V. Координаты p1, p2, … pn в системе координат u, v можно получить из
по особым значениям. Первая главная компонента задает направление самой сильной вариации точек, а вторая главная компонента ортогональна первой главной компоненте и задает направления самой слабой вариации точек. Отношение s2/s1 двух особых значений s1 и s2 (которые могут быть выбраны из диагонали матрицы S) дает значимость вариации точек p1, p2, … pn вдоль направления второго главного направления. Пусть u=(ux,uy) является единичным вектором, задающим направление первой главной компоненты и пусть v=(vx,vy) является единичным вектором, задающим направление второй главной компоненты (u и v являются ортогональными). Единичные векторы u и v можно получить путем нормирования первого и второго столбцов матрицы V. Координаты p1, p2, … pn в системе координат u, v можно получить из 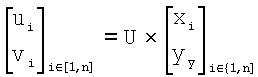 . «Разброс» облака точек находят в зависимости от дисперсии вдоль первого главного направления и эффекта дисперсии вдоль второго, ортогонального главного направления. Изменчивость вдоль первого главного направления вычисляют как:
. «Разброс» облака точек находят в зависимости от дисперсии вдоль первого главного направления и эффекта дисперсии вдоль второго, ортогонального главного направления. Изменчивость вдоль первого главного направления вычисляют как: 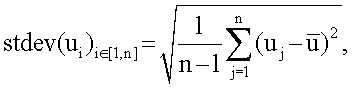 где
где 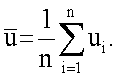
Суммарный разброс облака точек p1, p2, … pn находят следующим образом:
разброс = 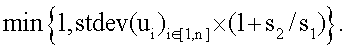
Эта формула составлена так, что задает более сильный разброс, когда облако точек имеет эллиптическую или круговую форму, чем в случае разброса с только постоянным отношением Y/X. Кроме того, она также ограничена между значениями 0 (все точки сконцентрированы в средней точке (0, 0), то есть все масштабы суть ×1, ×1) и 1. Количественным показателем стационарности масштаба является просто 1 - разброс (то есть, стационарность масштаба = 1-разброс), и он выражен в процентах. Согласно предпочтительному осуществлению полностью автоматизированное вычисление количественного показателя стационарности масштаба используется в блоке 727, согласно которому определяют минимальное значение 9 количественных показателей стационарности масштаба, вычисляемых с помощью эталонных образов, расположенных в верхней правой, верхней средней, верхней левой, средней правой, центральной, средней левой, нижней правой, нижней средней и нижней левой частях тренировочного образа, и это вычисление аналогично вычислению количественного показателя стационарности ориентации, описанному выше. Математически эти операции могут быть представлены как:
стационарность масштаба = 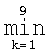 (стационарностьk масштаба).
(стационарностьk масштаба).
При выполнении операций из блока 111С (фиг.1(В)), которыми характеризуется стационарность распределений категорий тренировочного образа из блока 109, осуществляют проверку того, что распределение категорий не изменяется значительно от одной области изображения к другой. Согласно предпочтительному тренировочному образу изображения подразделяют на зоны таким образом, как это описано выше применительно к фиг.6(А)-6(I) при формировании статистических показателей ориентации. Гистограмму Hk распределения категорий вычисляют по каждой зоне k из 9 зон согласно предпочтительному осуществлению. Все гистограммы распределений категорий содержат G столбиков, где G - количество категорий. Подобие двух полутоновых гистограмм Hk и Hl определяют, используя евклидово расстояние между векторами Hk и Hl:
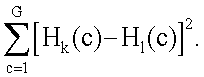
Количественный показатель стационарности распределений категорий для всех зон вычисляют из:
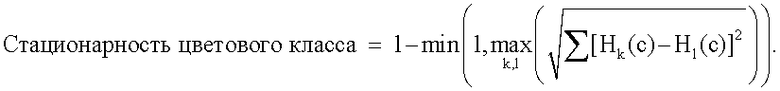
В блоке 113 количественные показатели стационарности, сформированные в блоке 111, анализируют для определения, удовлетворяет ли тренировочный образ набору заданных ограничений, которыми предписывается, должен или не должен тренировочный образ использоваться при последующем многоточечном геостатистическом анализе. Согласно предпочтительному осуществлению количественный показатель (111А) стационарности ориентации, количественный показатель (блок 111В) стационарности масштаба и количественный показатель (111С) стационарности распределений категорий наносят на трехмерный график, оси которого, как показано на фиг.14, соответствуют трем количественным показателям. Находят набор поверхностей, которые характеризуют одну или несколько областей в трехмерном пространстве, ограничивающих качественные тренировочные образа. Если три количественных показателя для конкретного тренировочного образа попадают в одну или более областей, ограничивающих качественный тренировочный образ, критерий стационарности из блока 113 удовлетворяется; в ином случае критерий стационарности из блока 113 не выполняется.
В случае, когда критерий стационарности из блока 113 удовлетворяется, тренировочный образ может быть экспортировано как сетка изображения для многоточечного геостатистического анализа (блок 119). Примеры такого многоточечного геостатистического анализа включают в себя реализацию с использованием компьютера алгоритма моделирования на основе одного нормального уравнения и/или реализацию с использованием компьютера алгоритма моделирования на основе образов.
В способе моделирования на основе одного нормального уравнения (SNESIM) условную функцию плотности вероятностей для всех категорий в одной точке вычисляют, используя информацию о значении в небольшом количестве ближайших точек и статистические показатели, обеспечиваемые тренировочным образом. Осуществление моделирования на основе одного нормального уравнения возможно только с дискретными значениями (то есть, с конечным и обычно небольшим количеством категорий, например, с пятью различными видами породы). Предположим, что должны моделироваться две категории: А (внутриканальная) и В (канальная). Тренировочный образ содержит полное представление (то есть, пример) пространственного распределения А и В. Предположим также, что категория, имеющаяся в 4 точках (u1, u2, u3, u4), которые могут представлять скважины, является известной. По существу, способом моделирования на основе одного нормального уравнения вычисляют вероятность нахождения категорий А или В в пятой точке (u?) путем принятия во внимание тренировочного образа для всех появлений «образа» (u1, u2, u3, u4) (то есть, всех появлений 4 точек с такими же относительными местоположениями и такими же значениями категорий тренировочного образа), показанных на фиг.15. Если обнаруживают 5 таких появлений (также называемых репликами), и 4 из 5 реплик свидетельствуют о категориях В в относительном положении неизвестной точки (u?), то в соответствии со способом делают вывод, что вероятность нахождения В в неизвестной точке составляет 80% (тогда как для А составляет 20%). Кроме того, в соответствии со способом можно присвоить категорию неизвестной точке путем случайного выбора значения из распределения с 80%-ной вероятностью В и 20%-ной вероятностью А. На практике способ моделирования на основе одного нормального уравнения начинают с пустого объема, подлежащего моделированию, или объема, который содержит лишь немного точек данных, подлежащих оцениванию, и сначала принимают решение о случайной траектории для посещения каждого из пустых пикселов один и только один раз. В первом пикселе способом вызывают для исследования ближайшие известные точки внутри эллипсоида поиска. При обнаружении одного или нескольких известных (или уже определенных) пикселов приступают, как описано выше, к нахождению вероятности обнаружения категорий А или В в неизвестной точке. После снабжения вероятностями каждой категории в неизвестной точке, используя способ, случайным образом извлекают значение (взвешенное известными вероятностями) и приписывают его к неизвестной точке. Процесс повторяют в следующем пикселе по первоначально определенной случайной траектории до тех пор, пока все пикселы не будут приписаны.
Такая методология была хорошо известна в начале 1990-х годов (до того, как она стала известной как способ моделирования на основе одного нормального уравнения). Однако одна из ее проблем заключалась в том, что она требовала очень большого объема вычислений для многократного просмотра тренировочного образа. В 2000 г. был открыт способ запоминания информации, содержащейся в тренировочном образе, в специальной древовидной структуре, что позволило значительно сократить вычисления. Методологию с таким усовершенствованием обычно называют способом моделирования на основе одного нормального уравнения. В сочетании с непрерывным увеличением мощности цифровых вычислительных средств это свело проблему просмотра изображений до приемлемой (хотя все еще имеющей значение).
Основа методологии моделирования на основе одного нормального уравнения имеет несколько вариантов и дополнений, которые делают ее в осуществлении более эффективной и полезной. Одним усовершенствованием добавляется способность к обработке на последовательных этапах с повышенным разрешением, что улучшает горизонтальную непрерывность признаков. Количество измельчений сетки называют кратностью. Другое усовершенствование обеспечивает способность к использованию мягких вероятностей (возможно, полученных на основании сейсмических данных) для дополнительного управления моделированием. Благодаря дальнейшим добавлениям способом моделирования на основе одного нормального уравнения можно осуществлять масштабные преобразования просто путем масштабирования расстояний до известных точек (u1, u2, u3, u4) в примере выше в соответствии с предоставляемой пользователем, зависящей от местоположения информации о масштабировании. Аналогично этому можно включать информацию относительно поворота геологических признаков (таких, как направления каналов) путем поворота набора точек в соответствии с локальным значением предоставляемого пользователем поля поворота.
В способе моделирования на основе образов (SIMPAT) вычисляют вероятность появления всех сочетаний значений в пределах небольшого набора смежных точек (таких, как прямоугольная матрица). В отличие от способа моделирования на основе одного нормального уравнения способ моделирования на основе образов может оперировать с дискретными (категориальными) значениями или с непрерывными числовыми значениями. Точнее, в способе моделирования на основе образов такие вероятности в тренировочном образе оценивают путем подсчета появлений этих образов с помощью скользящего прямоугольного шаблона, которым сканируют по всему изображению. Например, в случае применения к двоичному двумерному изображению шаблона из 2×2 пикселов способом задается вероятность появления каждого результата исхода от шаблона с пикселами 2×2 (а именно, 24 или 16 возможных результатов). Следствием является распределение вероятности, область которого содержит 24 сочетания пикселов, показанные на фиг.16(А). На практике, использование более крупных шаблонов (до приблизительно 8×8 пикселов) приводит к очень большому количеству возможных сочетаний, хотя многие могут иметь интервал появления или вероятность, равную нулю, если они отсутствуют в тренировочном образе. Моделирование достигается взятием выборки случайным образом из распределения для постепенного заполнения исходно пустого изображения. Необходимо соблюдать осторожность в отношении оценочных пикселов, уже учтенных, или пикселов, которые представляют точные кондиционирующие данные. Это может быть достигнуто путем взятия выборки из поднабора исходного распределения пиксельных групп, а именно, из поднабора тех пиксельных групп, которыми оценены уже существующие данные.
Необходимость согласования с уже существующими точками может приводить к увеличению времени вычислений при более крупных образах, поскольку необходимо одновременно согласовывать много точек вдоль границ более крупных образов. Это приводит к использованию до некоторой степени более уточненного способа, называемого «основанной на выделении признаков» геостатистикой, который основан на шаблоне, содержащем внутренний «признак» и наружный «скин-слой», показанные фиг.16(В). На практике, признак обычно крупнее, чем 2×2 пикселов, но скин-слой обычно имеет ширину в один пиксел. Такое разбиение облегчает классификацию шаблонов. Путем сканирования изображения способ позволяет получать набор признаков и вероятности появления их. Заданный признак (2×2 пикселов в этом примере) может встречаться несколько раз, но каждый раз с иным скин-слоем. Поэтому каждый признак имеет одну вероятность, но много возможных скин-слоев, при этом каждый, в свою очередь, имеет свою вероятность (относительно признака). Когда после этого признак необходимо поставить в соответствие существующему признаку, его извлекают из всех признаков вместе с соответствующим скин-слоем, взвешенным по вероятности каждого возможного скин-слоя в существующем признаке. Поэтому скин-слой ограничивает вероятность появления признаков в непосредственной близости и обеспечивает возможность согласования окрестных признаков.
Способ моделирования на основе образов может быть расширен путями, которые до некоторой степени являются аналогичными путям расширений способа моделирования на основе одного нормального уравнения. А именно, при выполнении моделирования последовательными отдельными этапами с переходом от грубой сетки (например, сетки, в которой используют только каждый пятый пиксель в каждом направлении) до мелкой сетки и использовании результатов каждого предшествующего (неточного) этапа, когда значения должны быть оценены на следующем (более точном) этапе, существенно повышается способность способа моделирования на основе образов оценивать непрерывность протяженных признаков (таких, как каналы). Кроме того, образы могут быть масштабированы и повернуты для оценивания предоставляемой пользователем информации о локальном масштабировании и повороте. В общем случае способом моделирования на основе образов получают более качественные результаты, чем способом моделирования на основе нормального уравнения (в том смысле, что статистические показатели исходного тренировочного образа оцениваются способом более точно), но при том, что в вычислительном отношении он является более медленным.
В случае, когда критерий стационарности из блока 113 не удовлетворяется, нестационарный тренировочный образ может быть экспортирован как сетка изображения для многоточечного геостатистического анализа (блок 127А). Аналогичным образом сетка ориентации и аффинные карты, получаемые в настоящей заявке в рамках вычисления статистических показателей стационарности, могут быть экспортированы в качестве сеток ограничений для многоточечного геостатистического анализа, для которого являются подходящими нестационарные тренировочные образа.
Основанный на использовании компьютера способ, описанный выше, может быть распространен на трехмерные тренировочные образа. Точнее, последовательность действий из фиг.1В должна быть модифицирована следующим образом. Во-первых, блоки 101-105 приспосабливают для запоминания и извлечения трехмерных изображений. Во-вторых, блок 107 приспосабливают для использования трехмерных версий операций по обработке двумерных изображений, описанных выше, чтобы предварительно обрабатывать трехмерные изображения и формировать качественные трехмерные тренировочные образы. Наконец, блок 111 приспосабливают, чтобы использовать трехмерные версии двумерных операций, описанных выше, для формирования статистических показателей стационарности. Точнее, вместо подразделения двумерного тренировочного образа на 9 перекрывающихся прямоугольников (фиг.6(А)-6(I)) трехмерный тренировочный образ может быть подразделен на 27 перекрывающихся кубов. Используют трехмерную версию операций, посредством которых выделяют поле ориентации тренировочного образа. В этом случае первые главные компоненты векторов трехмерной ориентации перпендикулярны к градиентным поверхностям. Эти векторы трехмерной ориентации представляют собой сферические данные, на основании которых получают статистические показатели стационарности. Трехмерные версии операций, описанных выше для определения стационарности поля ориентации, рассмотрены в следующих источниках: Mardia, “Statistics of Directional Data”, Academic Press, New York, 1972, и Rock, “Lecture Notes in Earth Sciences 18 - Numerical Geology”, Springer Verlag, 1988, полностью включенных в настоящую заявку посредством ссылок. Трехмерные версии операций, описанных выше для определения стационарности масштаба, также должны быть использованы. При выполнении таких операций для матриц смежности уровней серого, использованных в настоящей заявке, необходима сферическая система окрестностей вместо круговой системы. Сами статистические показатели стационарности масштаба должны быть нанесены на трехмерные масштабно-пространственные аффинные карты с использованием трехмерной версии разложения по особым значениям и среднеквадратического отклонения. Статистические показатели стационарности категорий могут быть легко получены по распределениям категорий на основании 27 перекрывающихся кубов трехмерного изображения (вместо 9 перекрывающихся прямоугольников двумерного изображения). Критерии стационарности из блока 113 должны применяться аналогичным образом для сохранения или отбрасывания трехмерных тренировочных образов. Точно так же сетки тренировочных образов, а также сетки ограничений масштаба и ориентации могут быть экспортированы как трехмерные сетки (вместо двумерных сеток).
Основанный на использовании компьютера способ настоящего изобретения может быть также легко распространен на выполнение действий над тренировочными образами, которые имеют непрерывные значения вместо небольшого количества категорий. Поэтому способ пригоден для многоточечных геостатистических методов, в которых допускаются сетки тренировочных образов, содержащие значения характеристик (вместо категорий).
Основанные на использовании компьютера способы настоящего изобретения были проверены на основании библиотеки из тридцати восьми тренировочных образов, и было показано, что вне зависимости от того, будет или не будет правильно осуществлена идентификация, стационарность отобранного тренировочного образа делает способы пригодными для реализаций многоточечной геостатистики. Вследствие этого геологи сберегут время и исключат необходимость выполнения реализаций многоточечной геостатистики с использованием непригодных тренировочных образов. Кроме того, основанные на использовании компьютера способы настоящего изобретения являются эффективными в вычислительном отношении и обычно могут быть выполнены на обычном носимом компактном персональном компьютере всего лишь за несколько секунд, тогда как приходится ожидать намного дольше результатов одной реализации алгоритмов многоточечной геостатистики. Наконец, результаты статистических показателей стационарности, полученные основанным на использовании компьютера способом настоящего изобретения, были тщательно проверены, и было обнаружено, что они аналогичны результату интерпретации человеком, основанной на визуальном исследовании тренировочных образов.
В настоящей заявке были описаны и пояснены основанные на использовании компьютера способы для автоматической оценки стационарности тренировочных образов, предназначенных для использования при многоточечном геостатистическом анализе. Хотя были описаны конкретные осуществления изобретения, не подразумевается, что изобретение ограничено ими, поскольку предполагается, что изобретение будет рассматриваться настолько широким в объеме, насколько дозволяется областью техники, к которой относится изобретение, и что описание будет толковаться таким же образом. Поэтому специалистам в данной области техники должно быть понятно, что тем не менее другие модификации могут быть сделаны к предложенному изобретению без отступления от заявленных сущности и его объема.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИК ГЕОЛОГИЧЕСКОЙ ФОРМАЦИИ, ПЕРЕСЕКАЕМОЙ СКВАЖИНОЙ | 2009 |
|
RU2440591C2 |
| СПОСОБ ГЕНЕРИРОВАНИЯ ЧИСЛЕННЫХ ПСЕВДОКЕРНОВ С ИСПОЛЬЗОВАНИЕМ ИЗОБРАЖЕНИЙ СКВАЖИНЫ, ЦИФРОВЫХ ОБРАЗОВ ПОРОДЫ И МНОГОТОЧЕЧНОЙ СТАТИСТИКИ | 2009 |
|
RU2444031C2 |
| СПОСОБ И УСТРОЙСТВО ДЕТЕКТИРОВАНИЯ ЛОКАЛЬНЫХ ОСОБЕННОСТЕЙ НА ИЗОБРАЖЕНИИ | 2013 |
|
RU2535184C2 |
| Способ распознавания структуры ядер бластов крови и костного мозга | 2021 |
|
RU2785607C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ИЗОБРАЖЕНИЯ ТЕКСТУРЫ КЛЕТОК | 2008 |
|
RU2385494C1 |
| СПОСОБ РАСПОЗНАВАНИЯ И КЛАССИФИКАЦИИ ФОРМЫ ОБЪЕКТОВ В ЛАБИРИНТНЫХ ДОМЕННЫХ СТРУКТУРАХ | 2012 |
|
RU2522869C2 |
| СПОСОБ МИКРОСКОПИЧЕСКОГО ИССЛЕДОВАНИЯ ОБРАЗЦА, СОДЕРЖАЩЕГО МИКРООБЪЕКТЫ С РАЗНОРОДНЫМИ ЗОНАМИ | 2006 |
|
RU2308745C1 |
| Способ распознавания структуры ядер бластов крови и костного мозга с применением световой микроскопии в сочетании с компьютерной обработкой данных для определения В- и Т-линейных острых лимфобластных лейкозов | 2017 |
|
RU2659217C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОМПЕНСАЦИИ ДВИЖЕНИЯ С ПРЕДСКАЗАНИЕМ | 2016 |
|
RU2634703C2 |
| ПРОЦЕСС ОБРАБОТКИ МЕДИЦИНСКИХ ИЗОБРАЖЕНИЙ | 2014 |
|
RU2681280C2 |
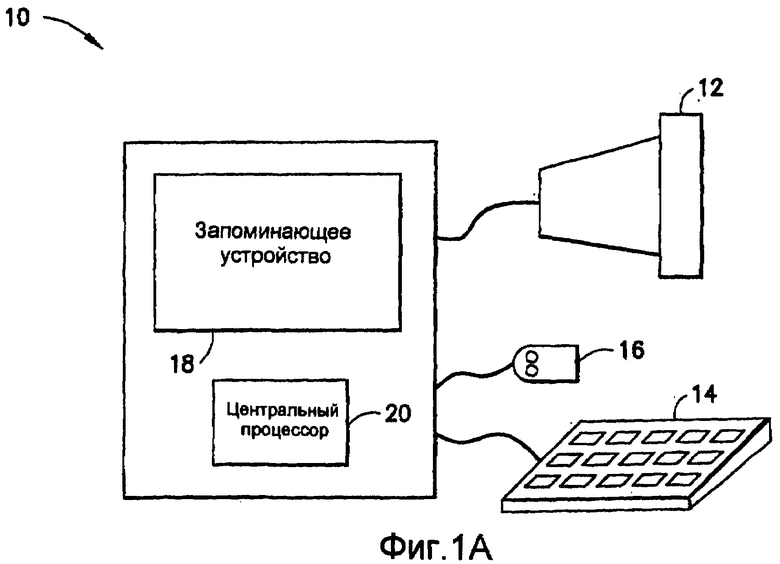
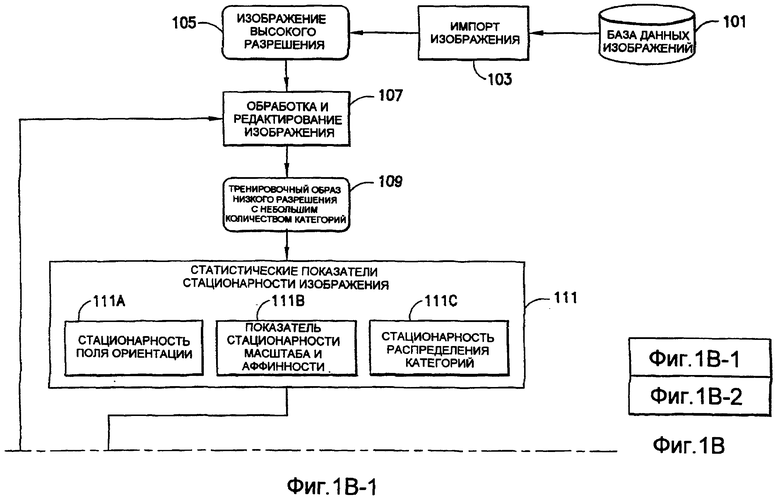


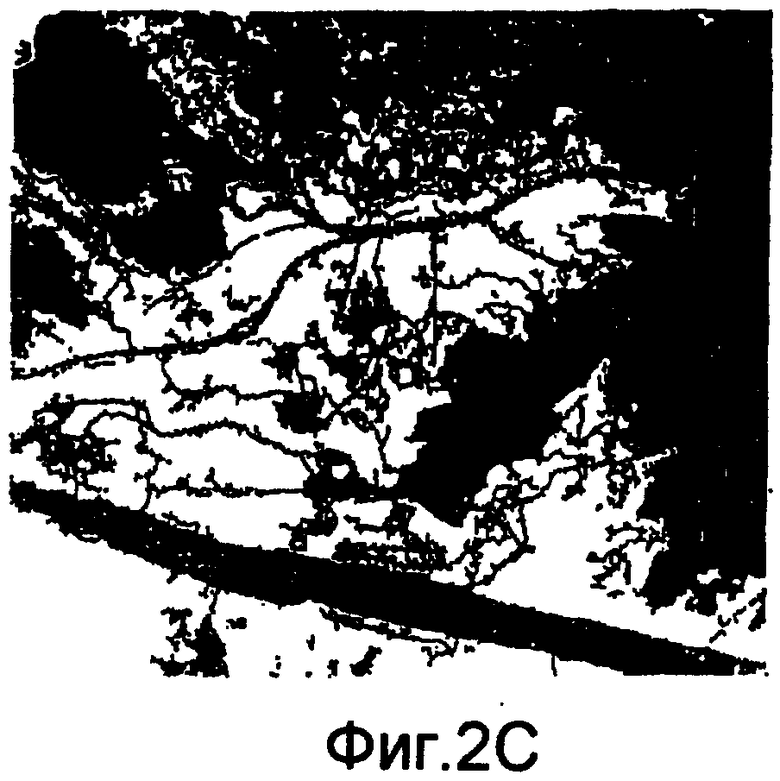
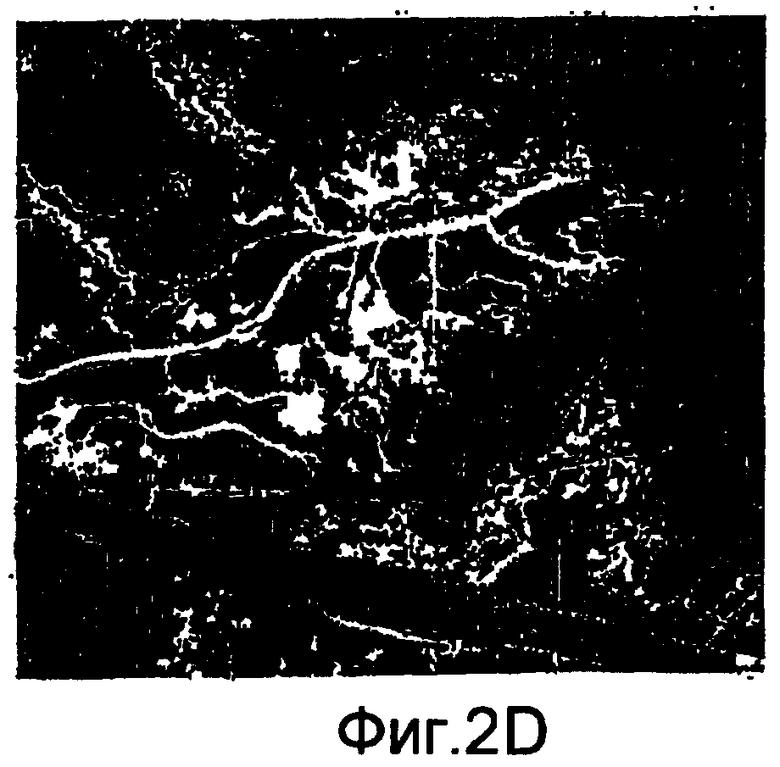



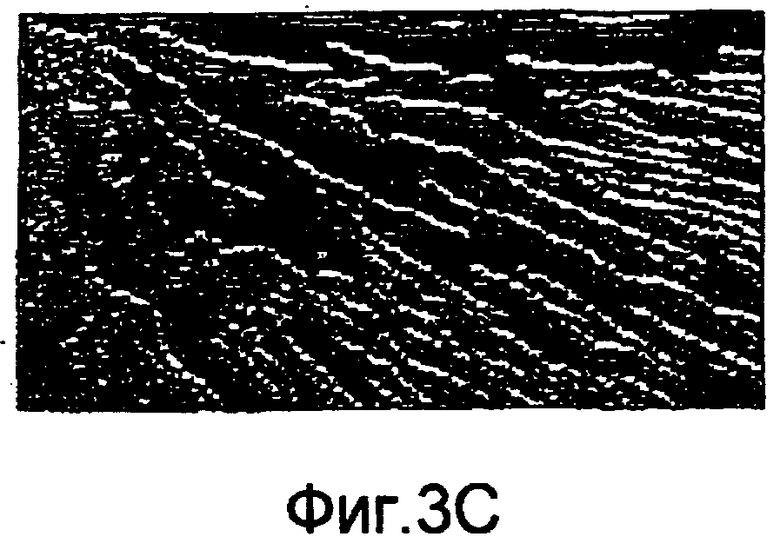
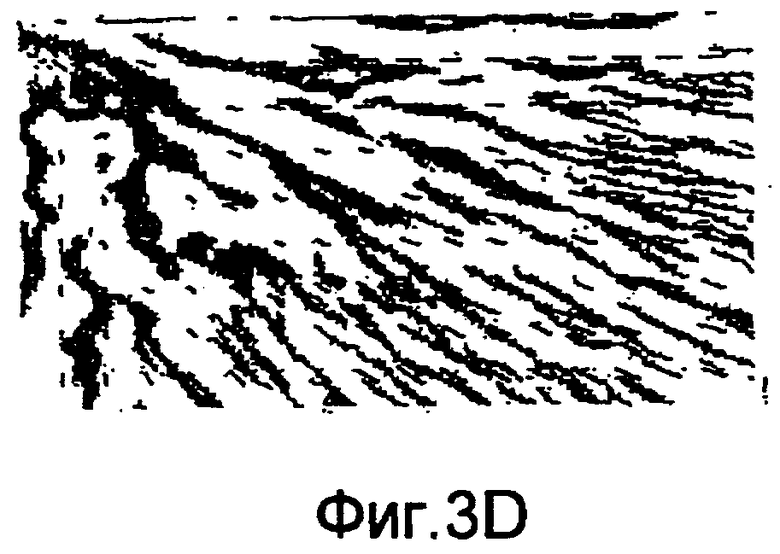
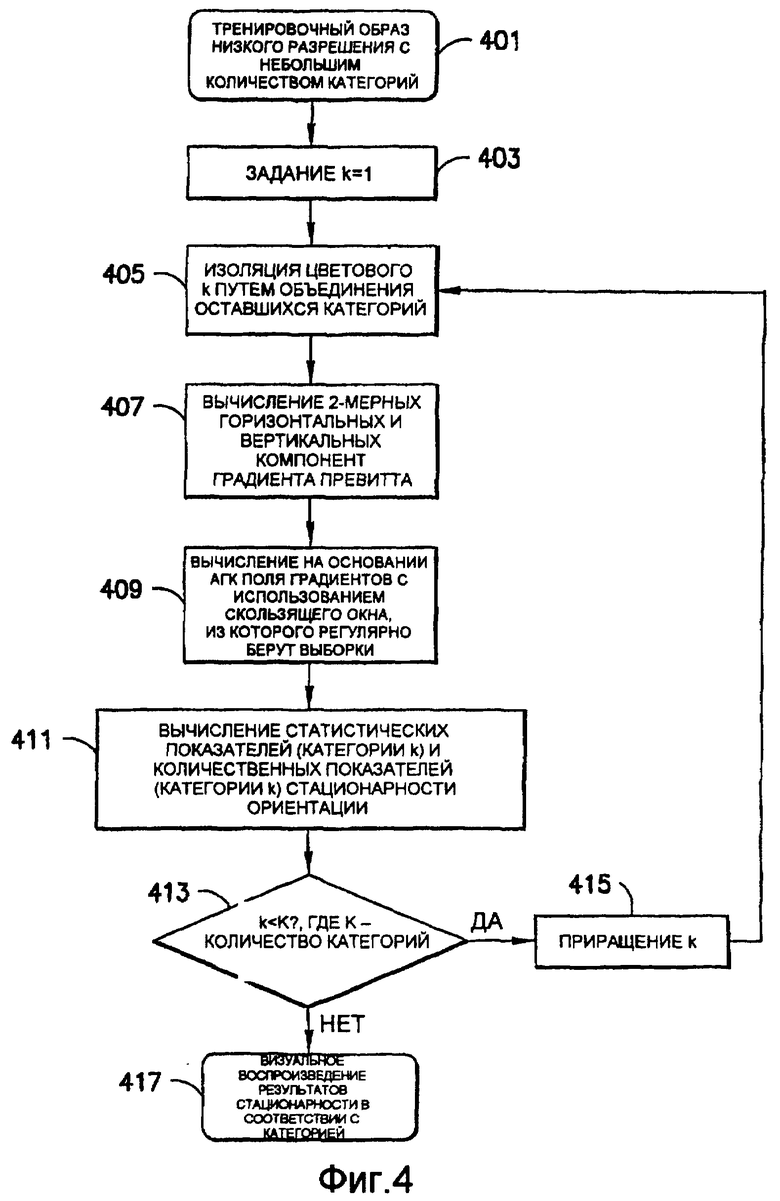
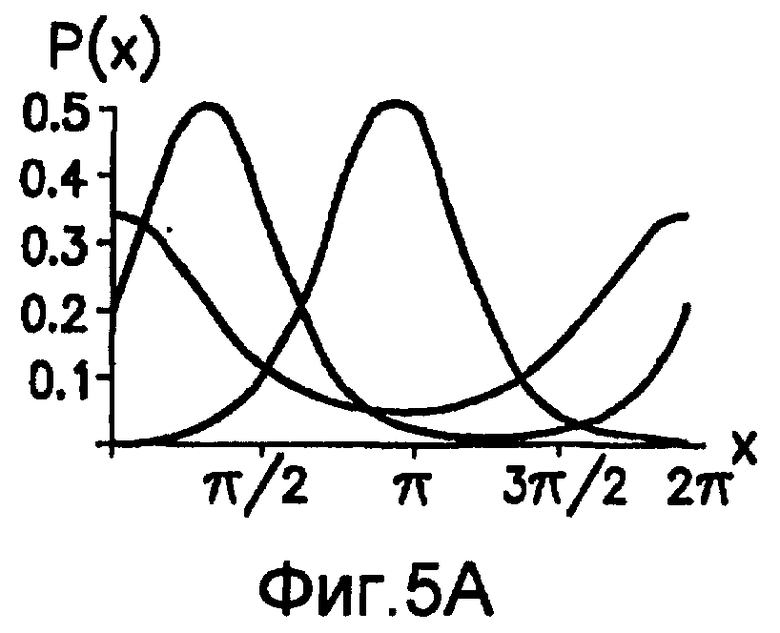
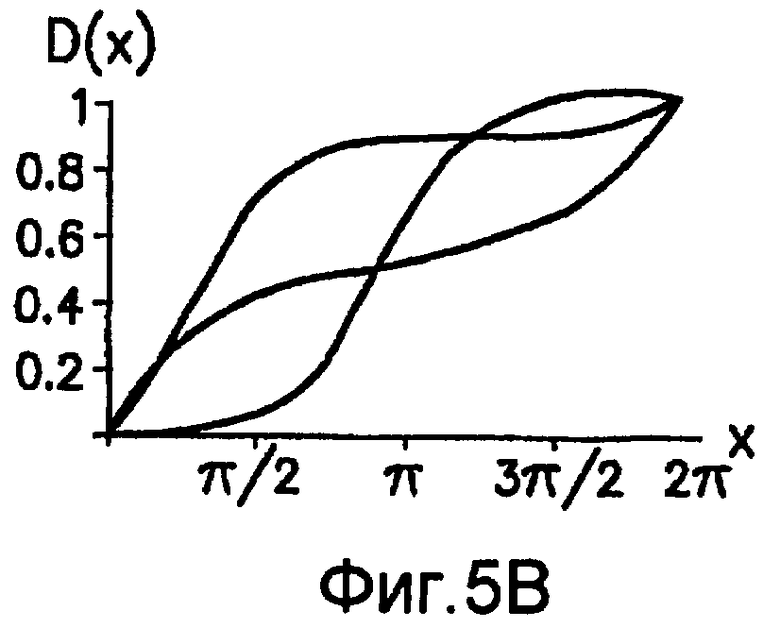
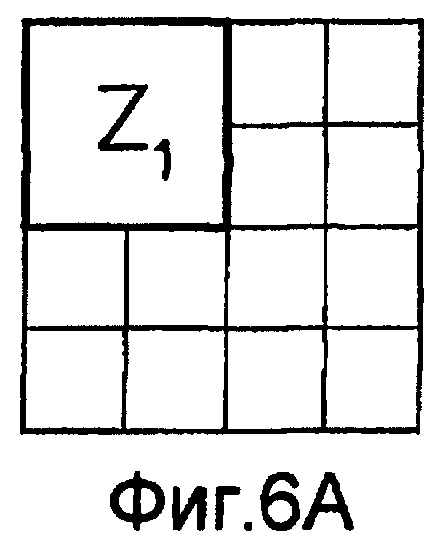
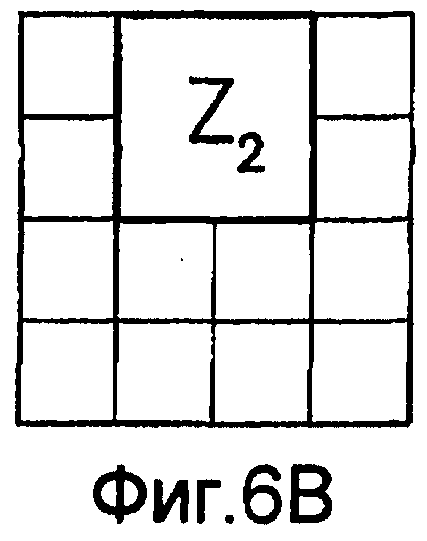
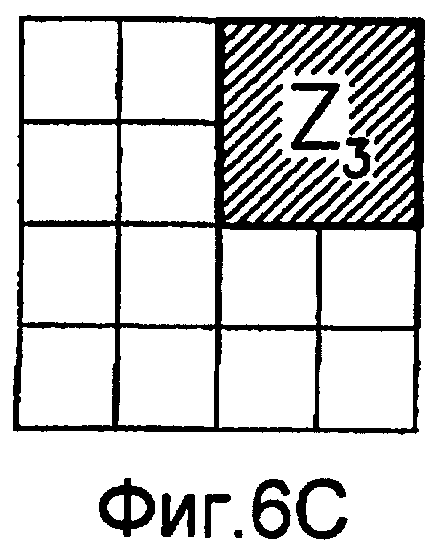
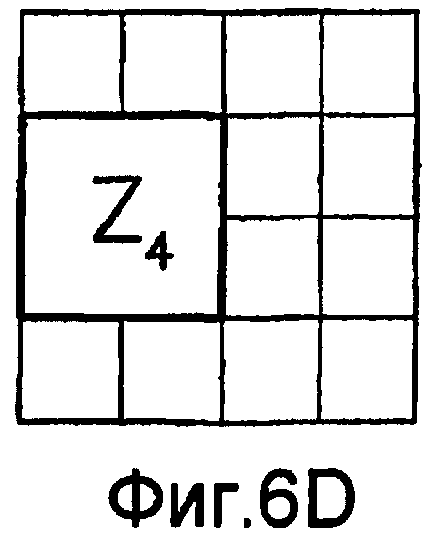
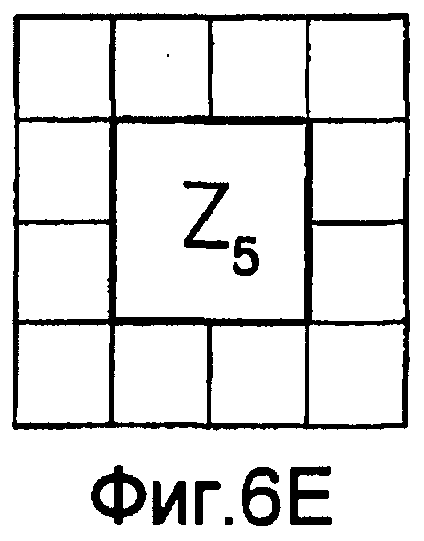
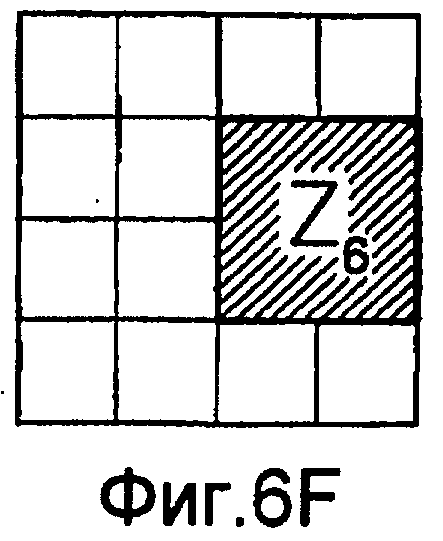
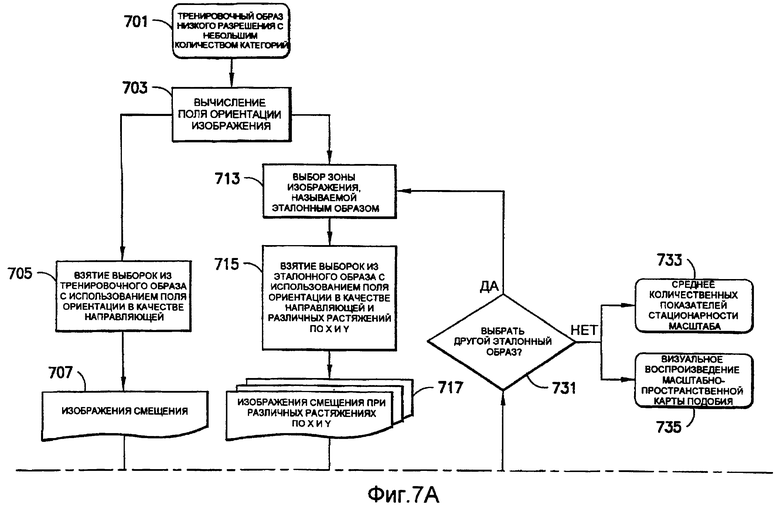
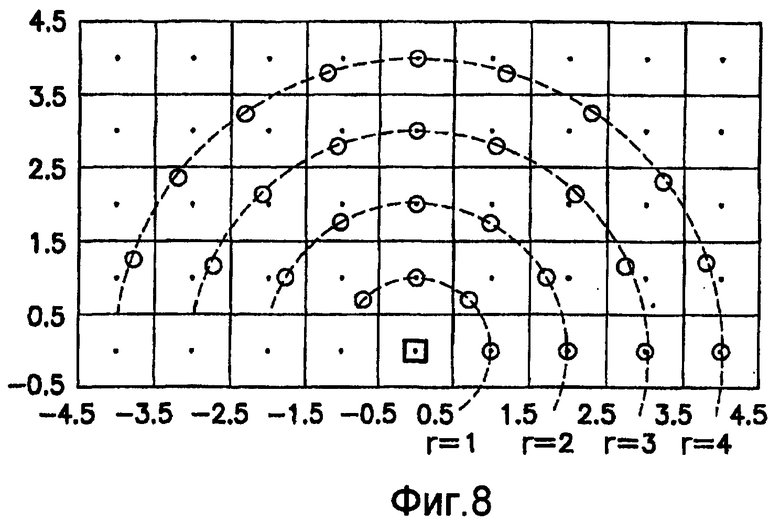
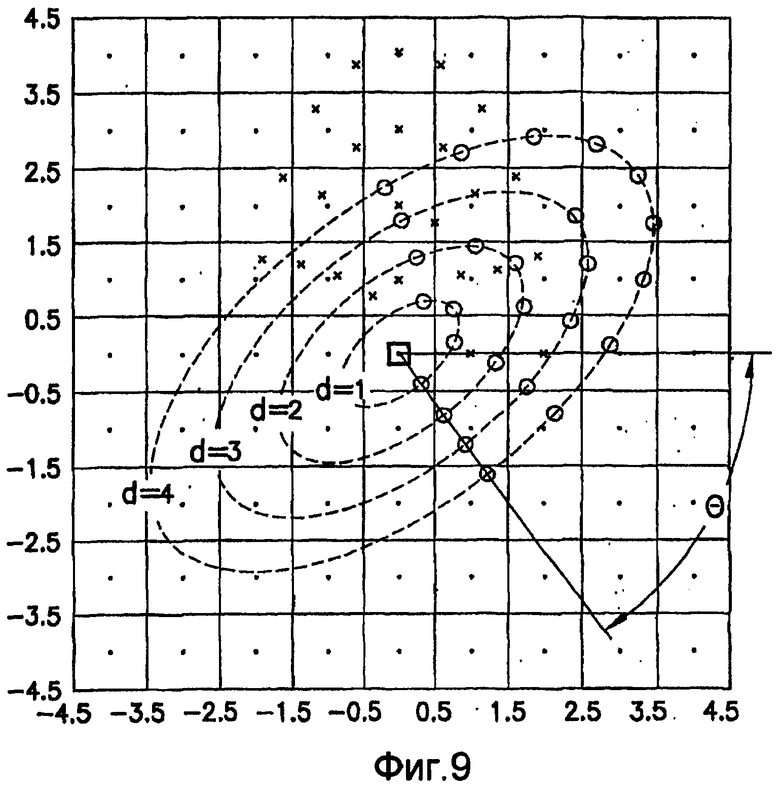
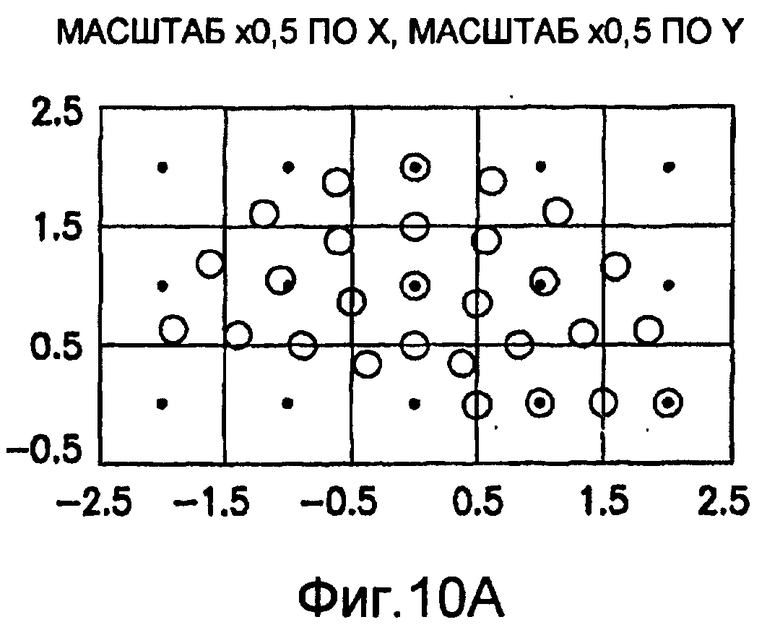
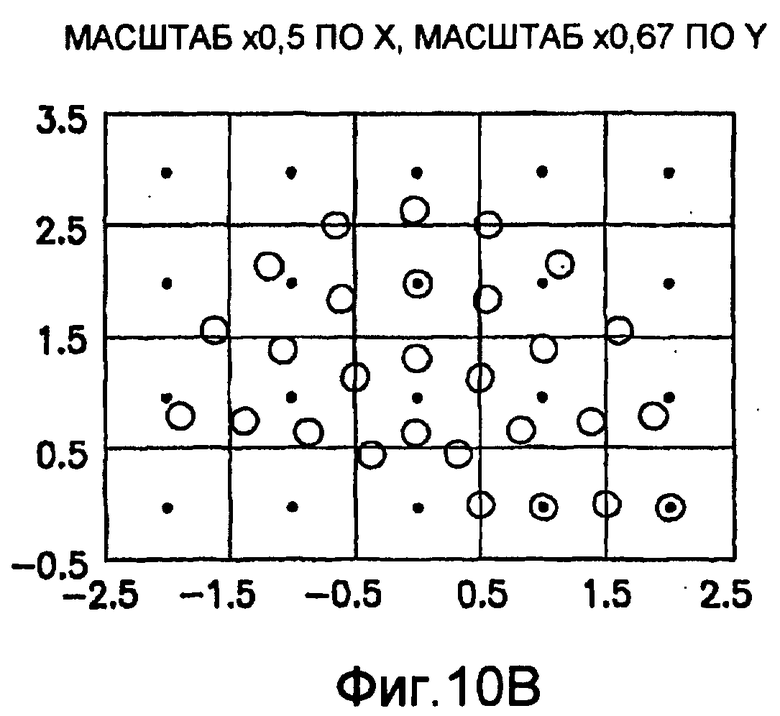
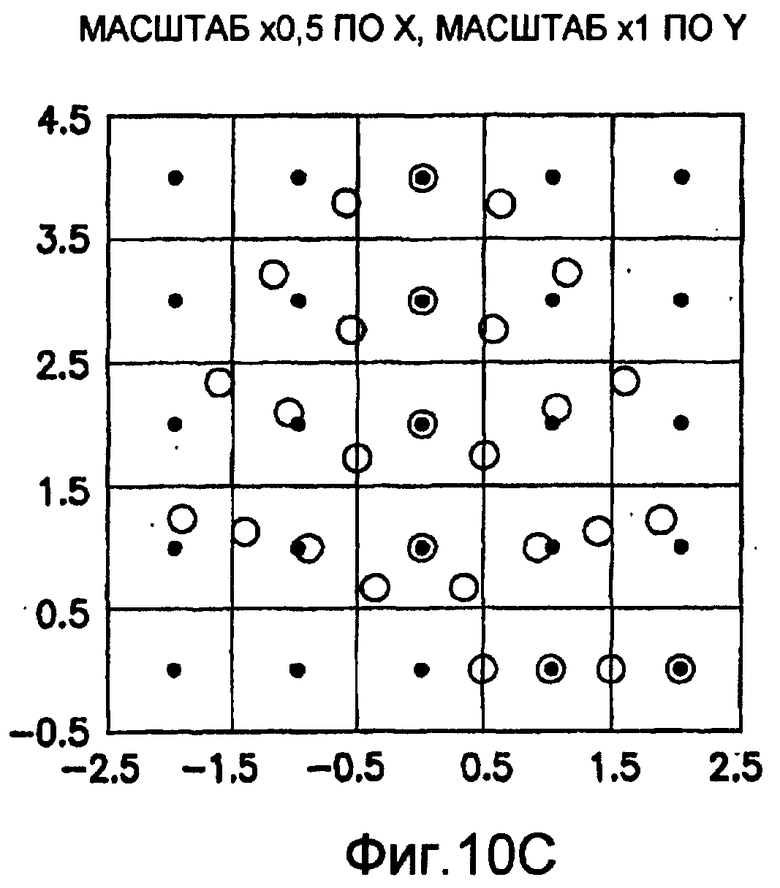

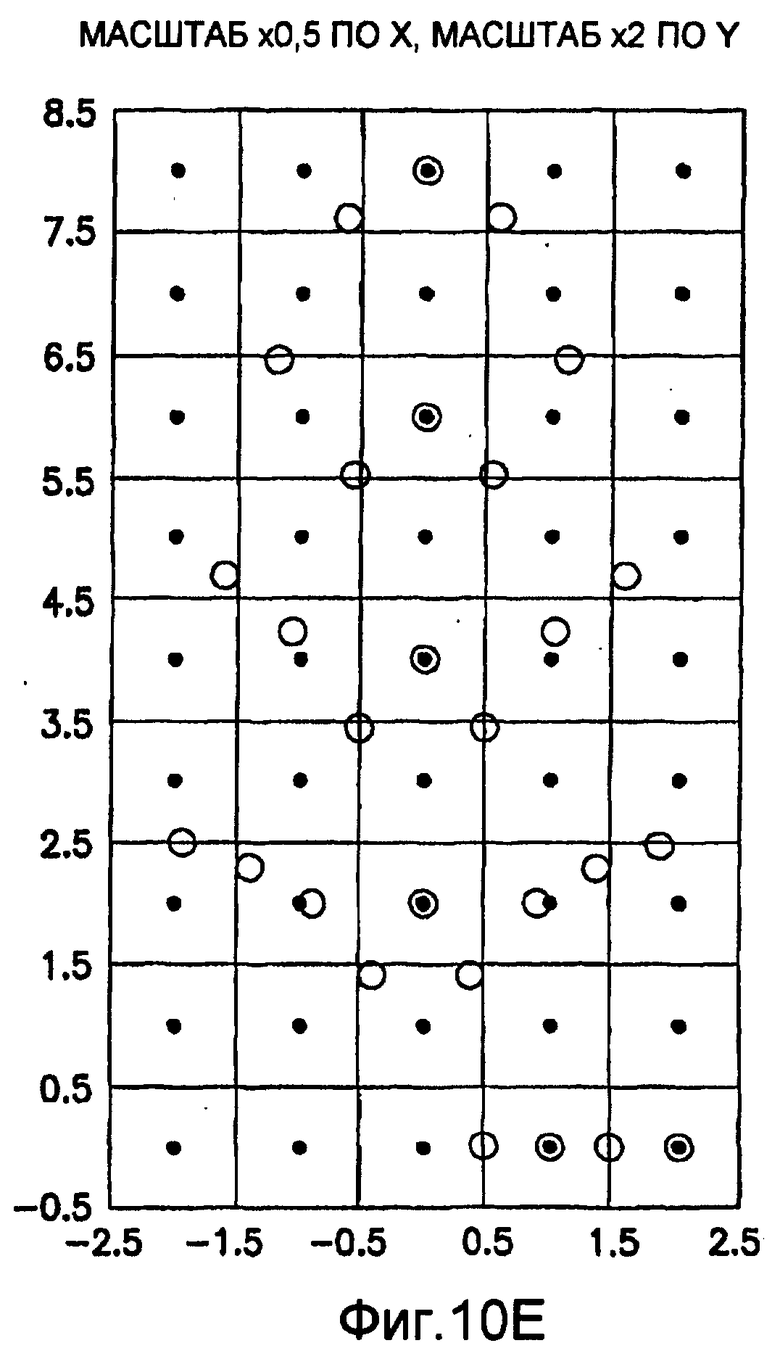
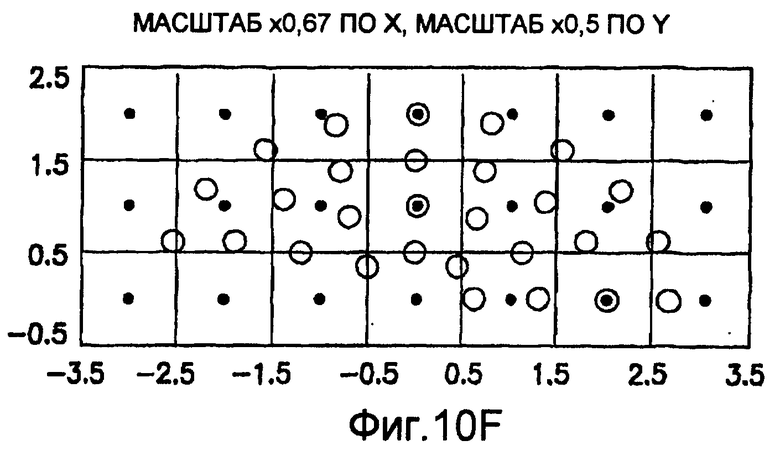
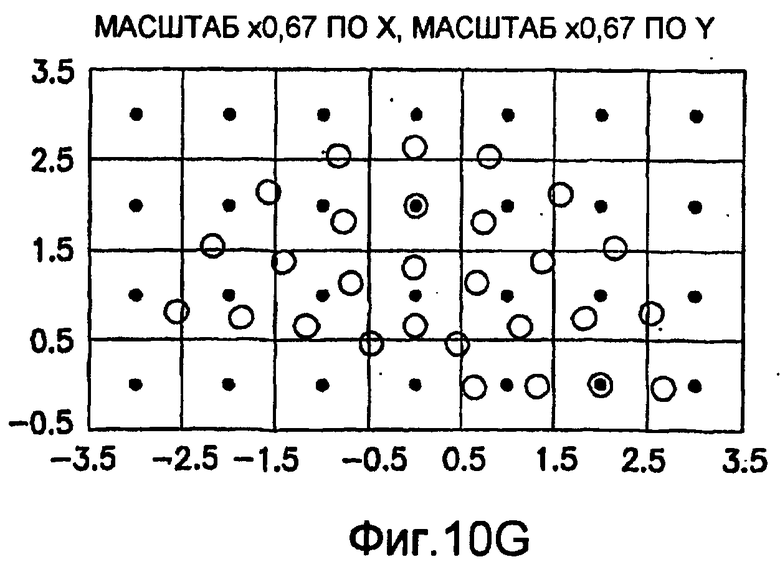
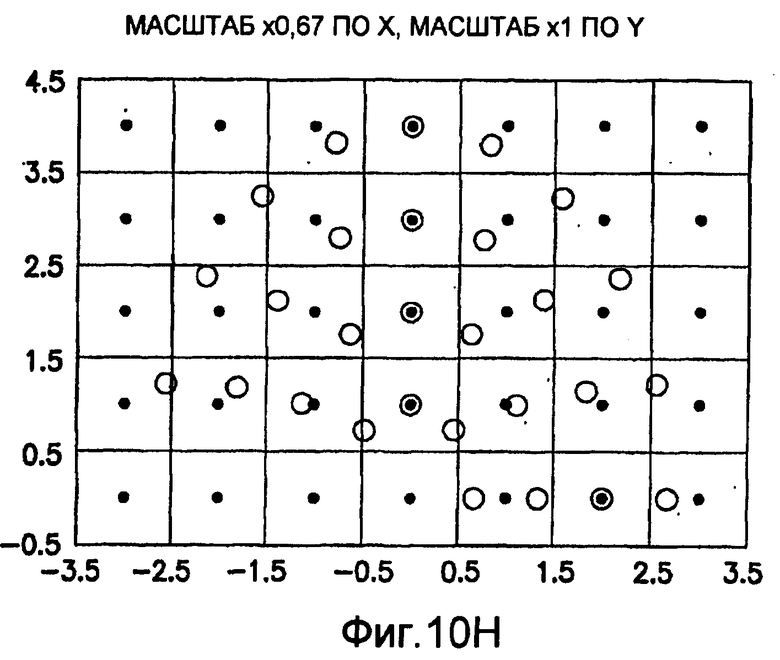
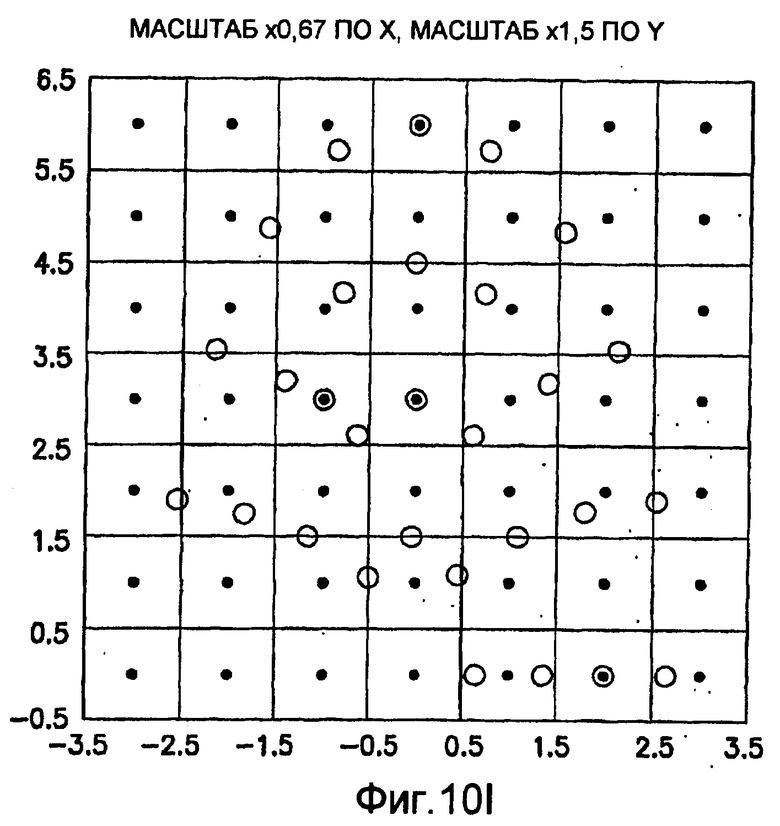
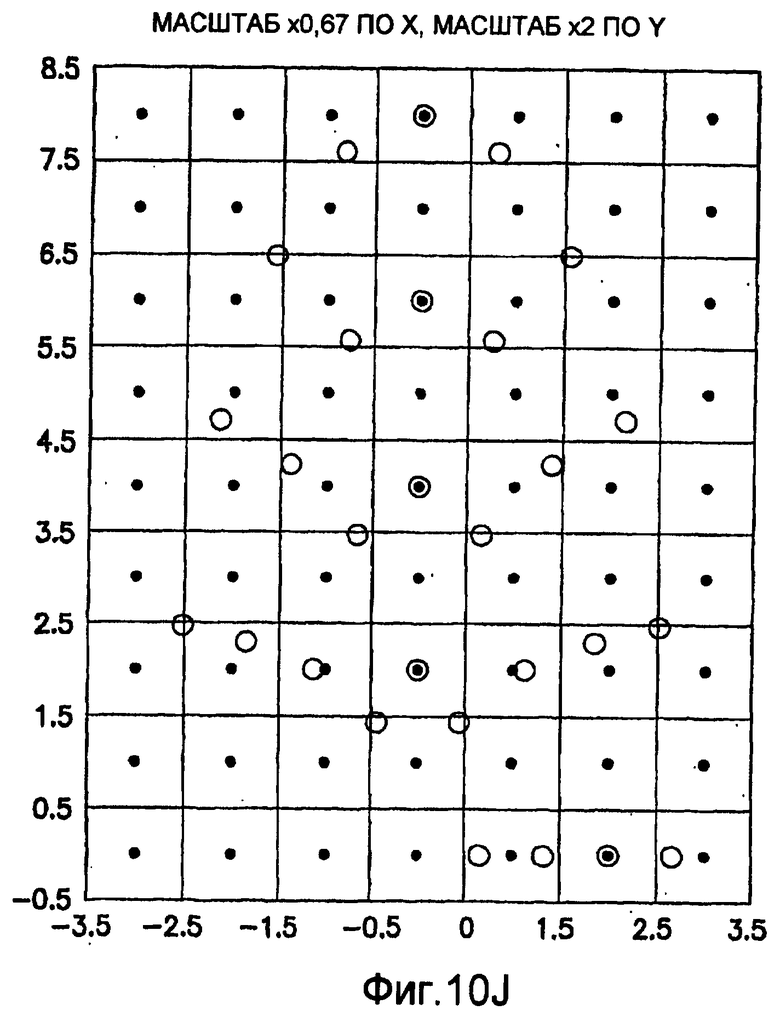
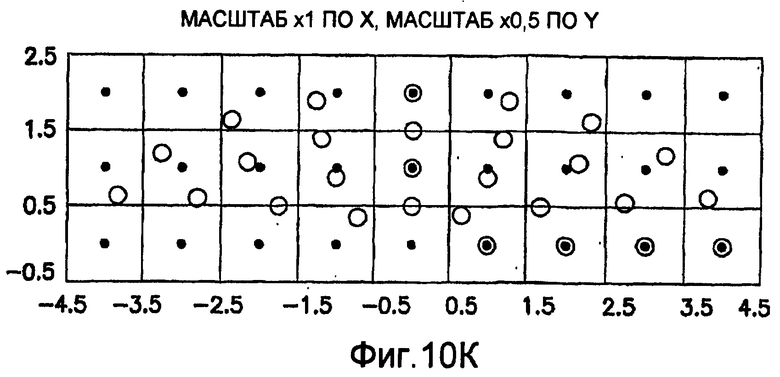
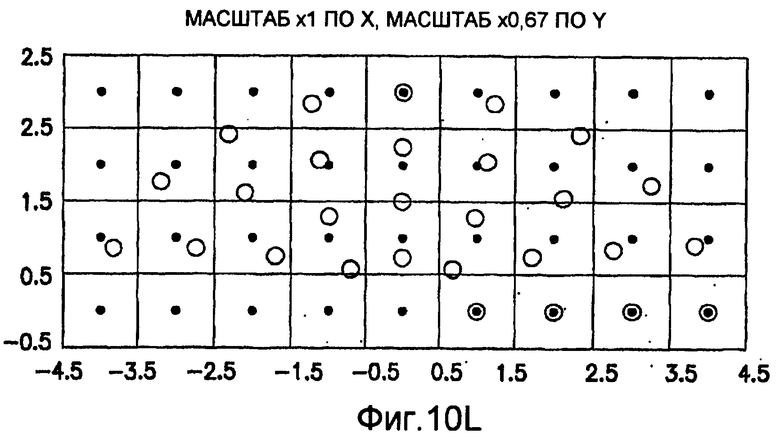
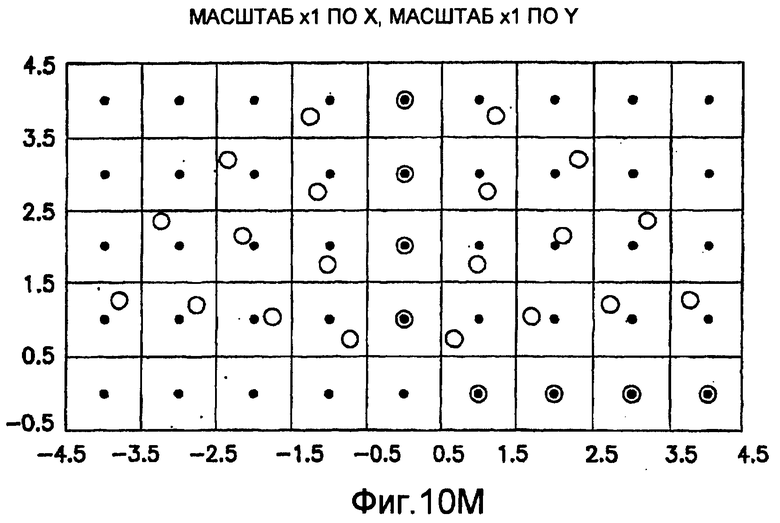
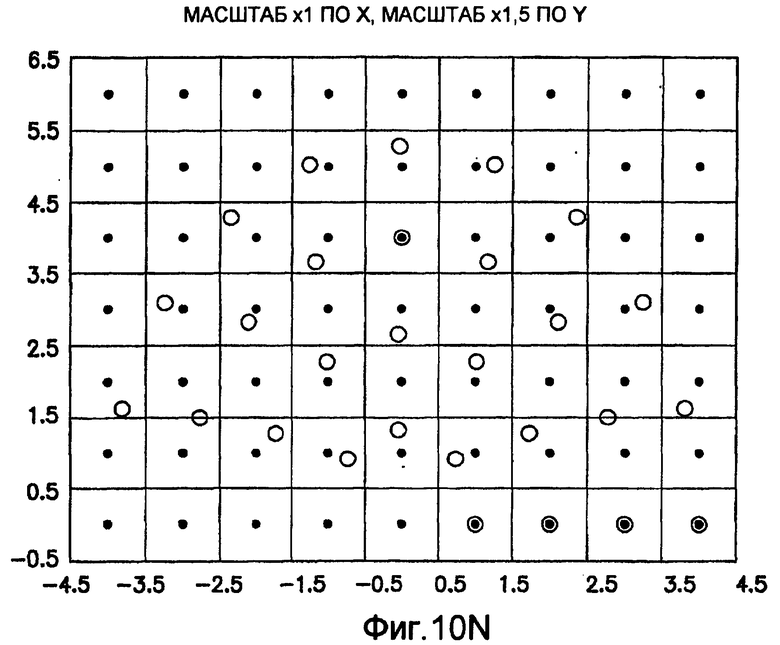
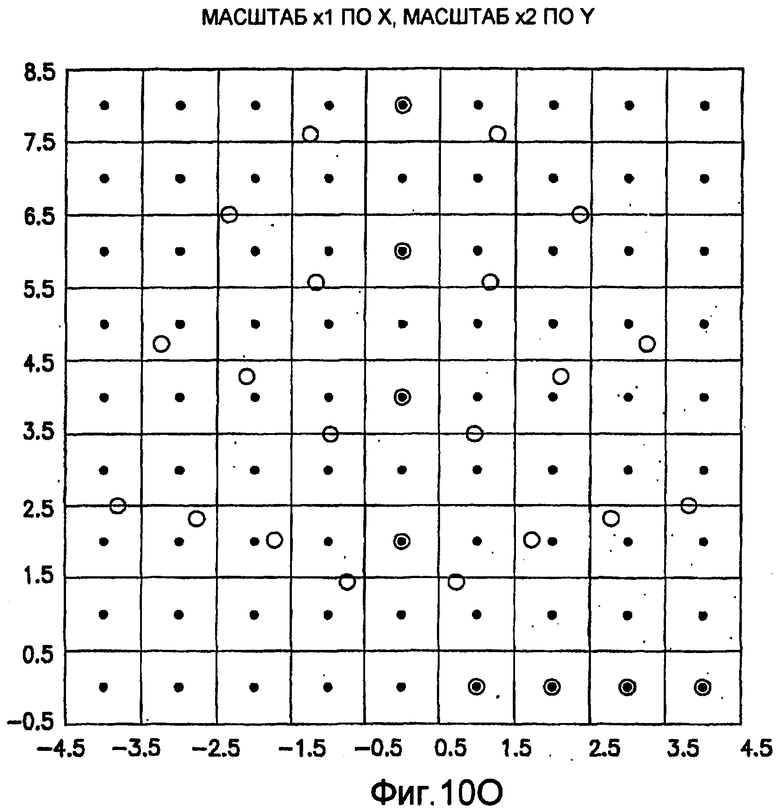
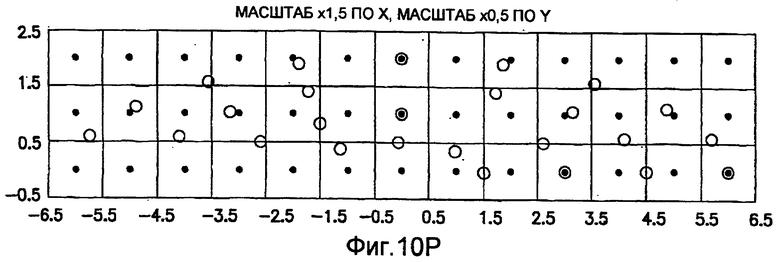
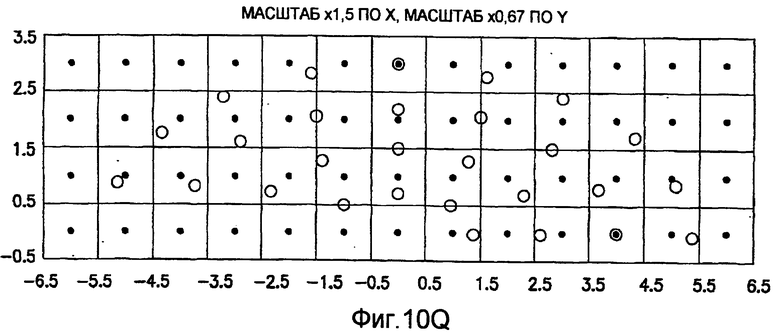
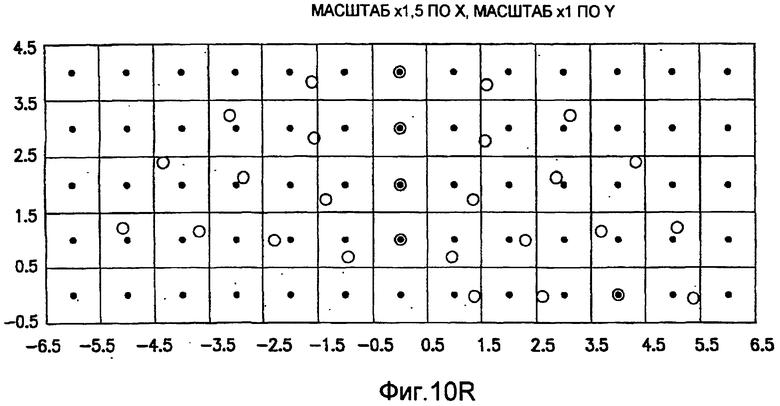
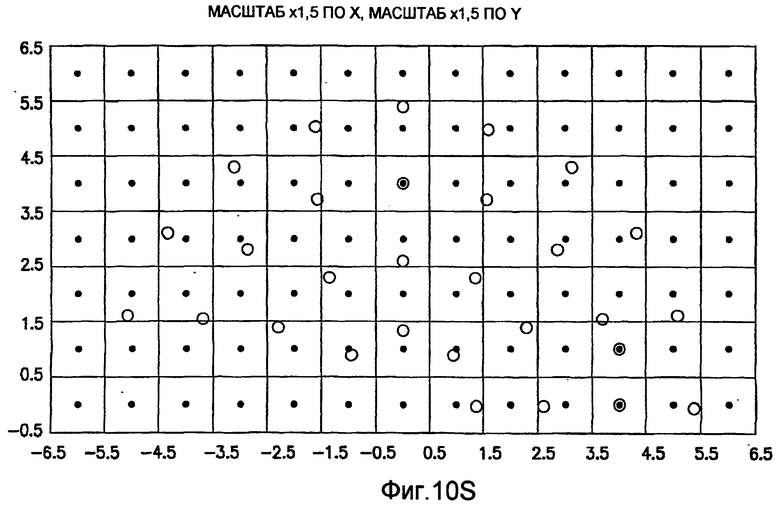
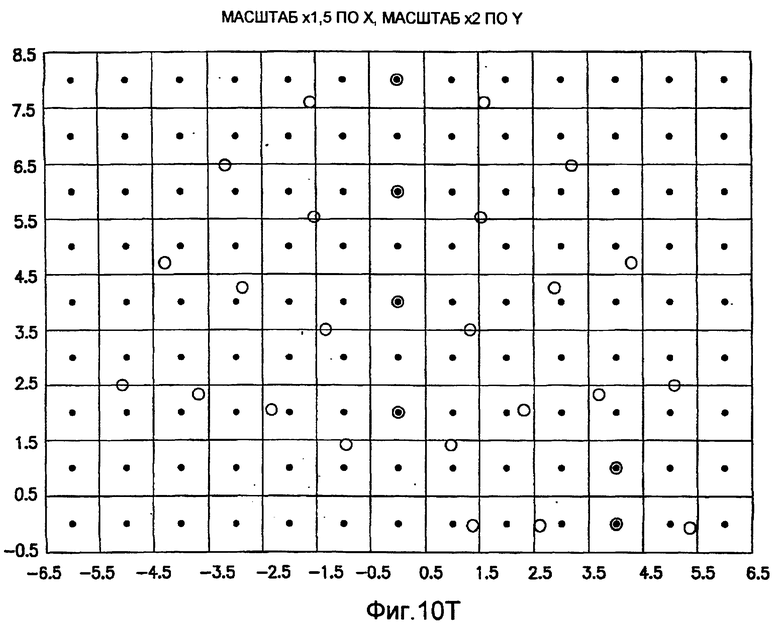
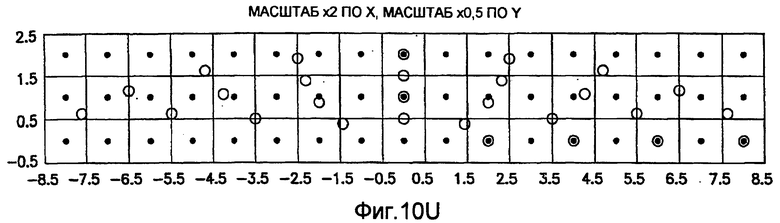
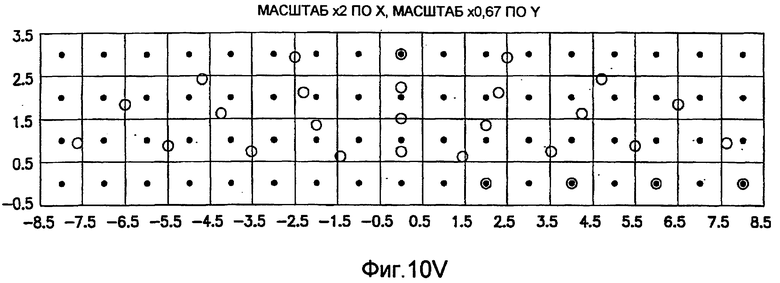
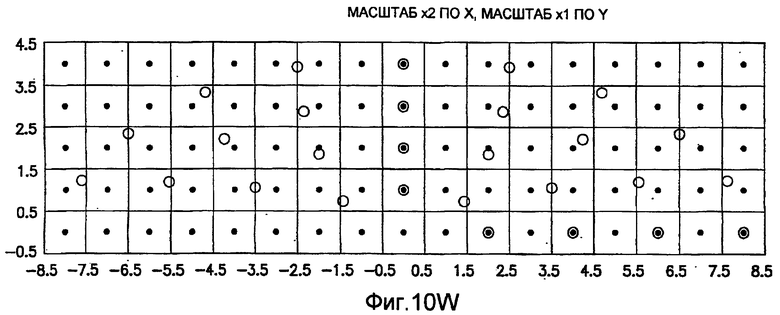
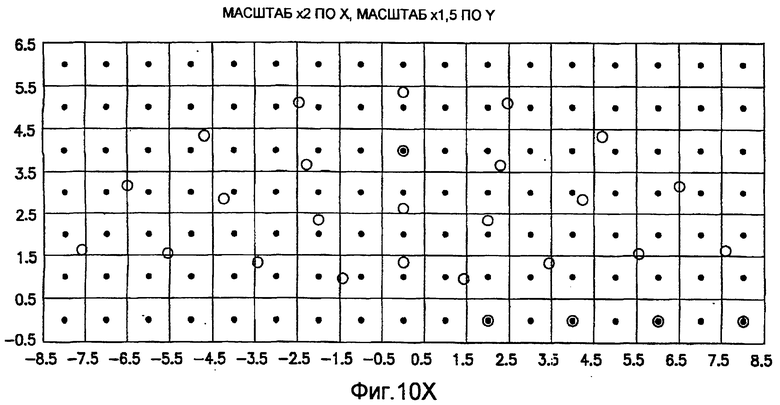
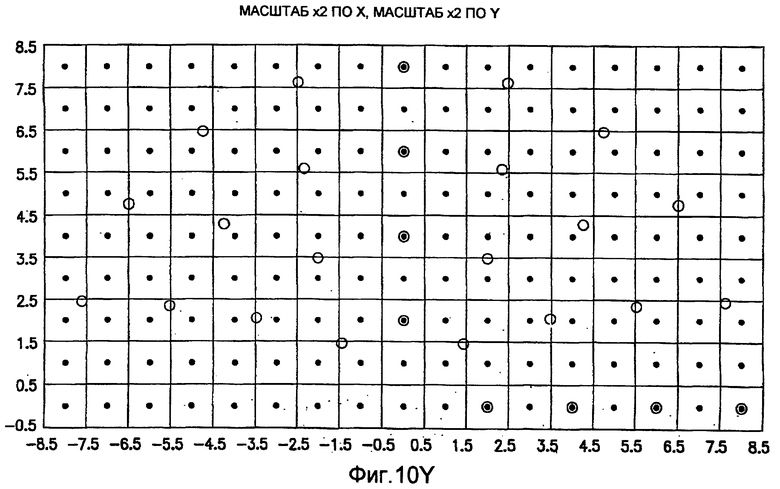
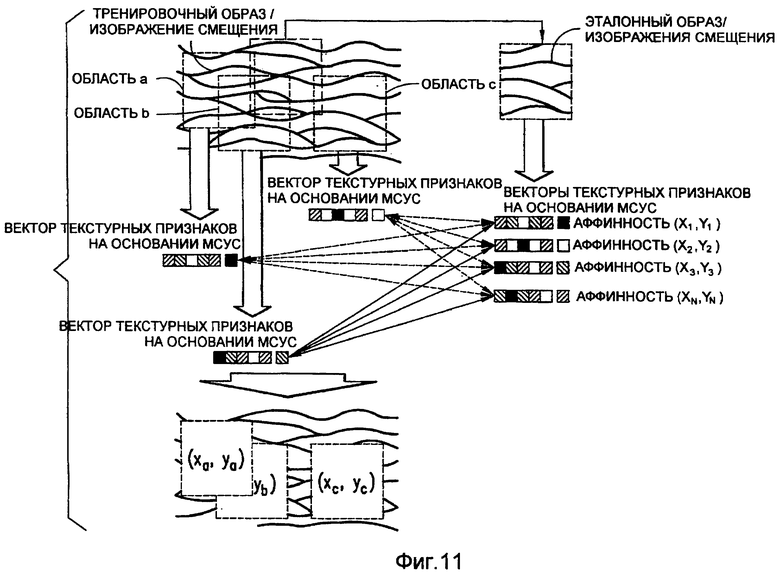

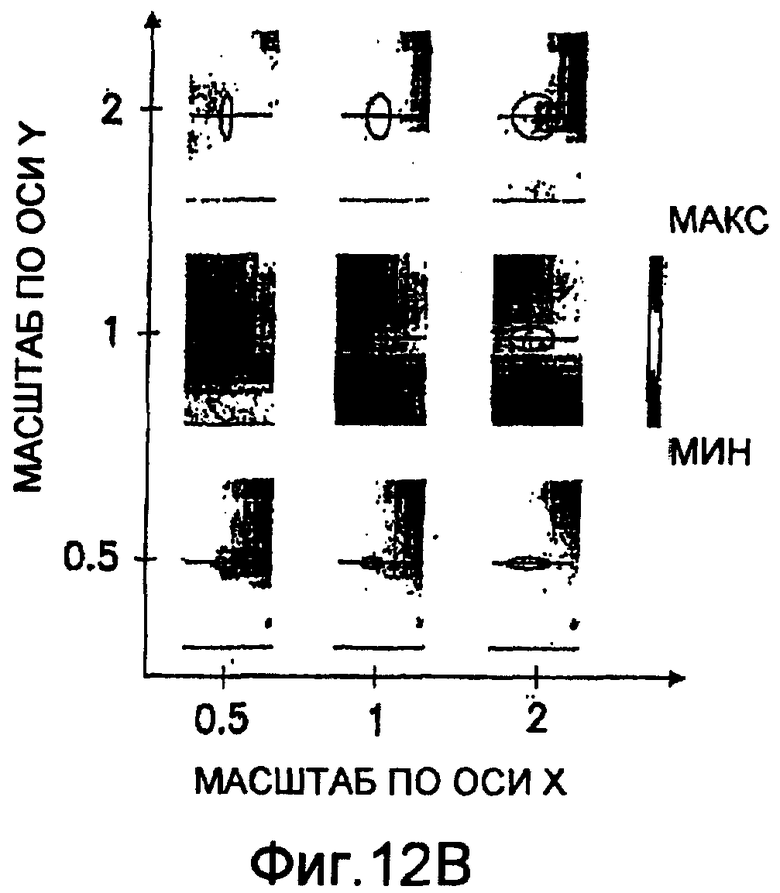
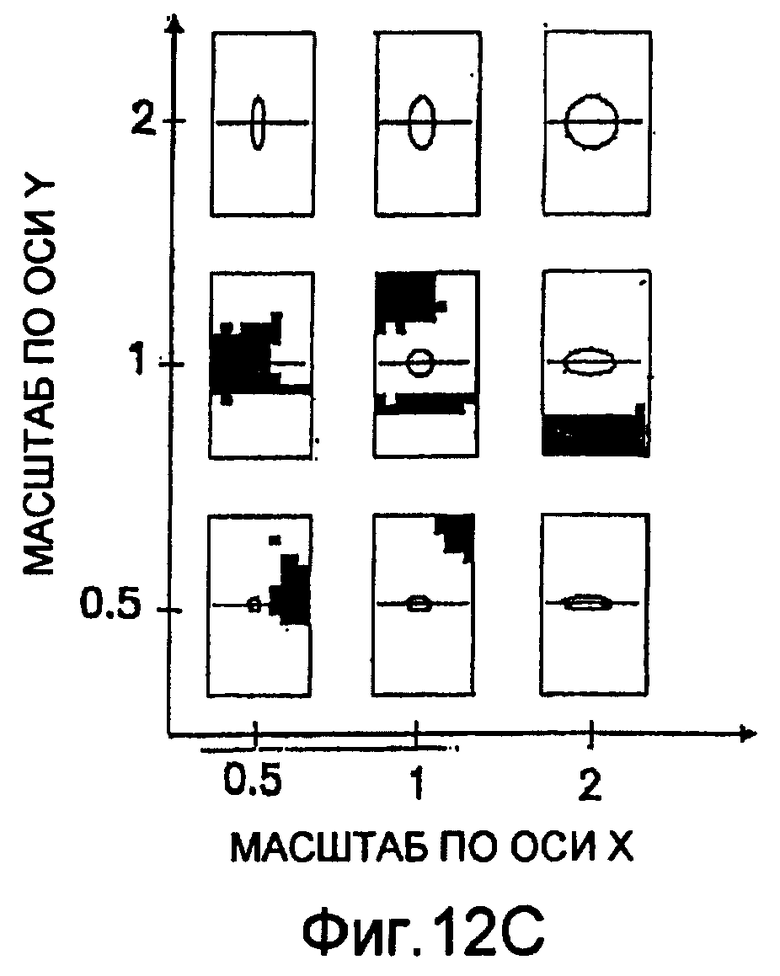
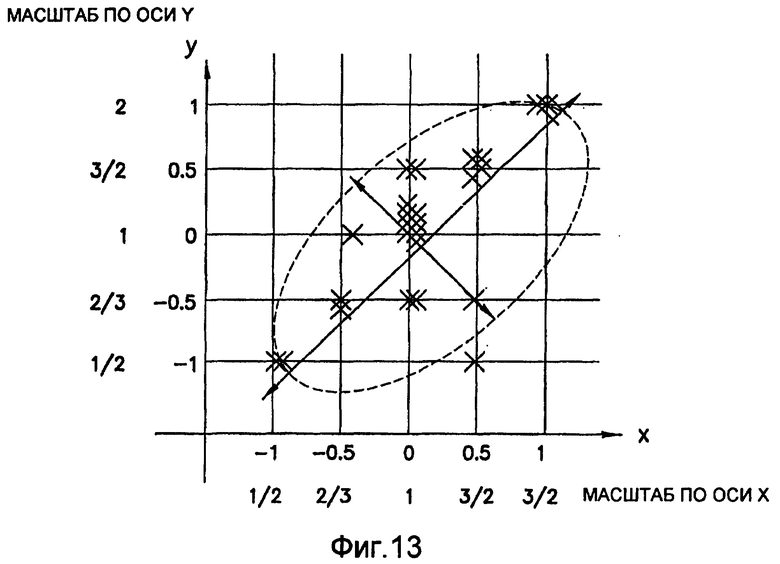
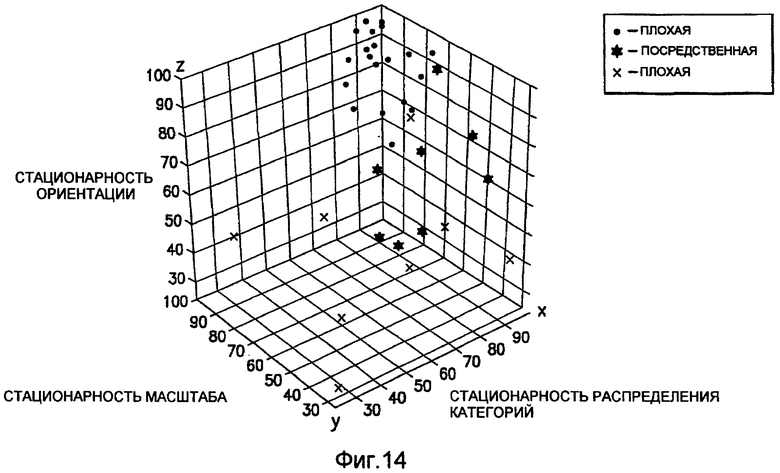
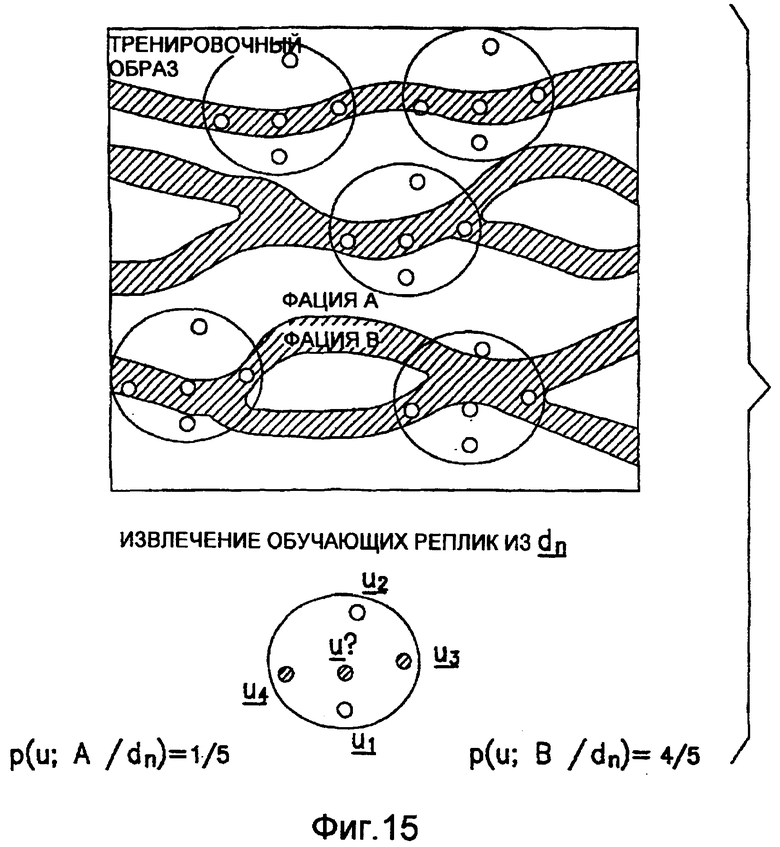
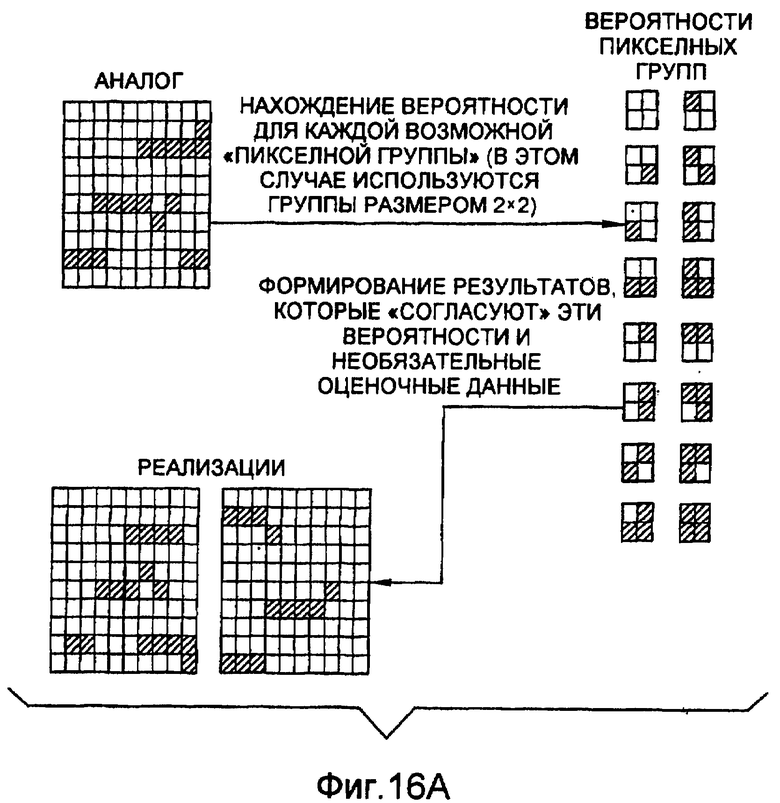
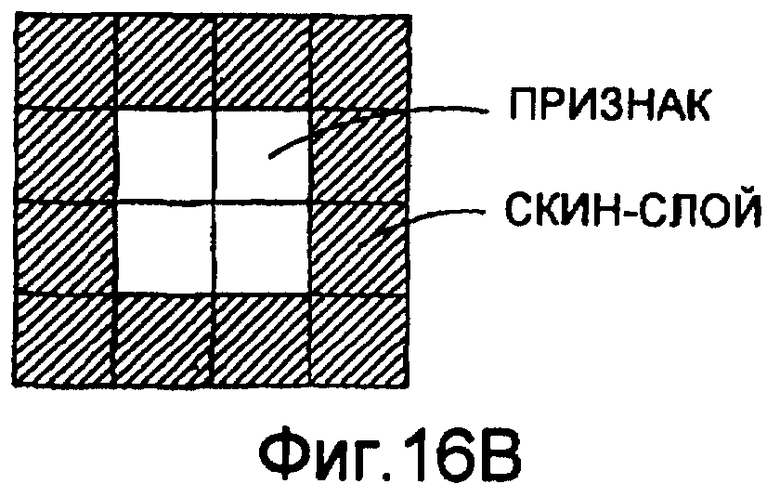
Использование: для моделирования поля характеристик посредством многоточечной геостатистики. Сущность: заключается в том, что оценка и анализ стационарности/нестационарности изображения содержит этапы на которых: с использованием компьютера анализируют цифровые данные, представляющие изображение, которое представляет собой одно из печатной копии изображения, цифрового изображения либо оба из них, чтобы сформировать по меньшей мере один статистический показатель, характеризующий стационарность изображения; получают по меньшей мере один количественный показатель на основании по меньшей мере одного статистического показателя; определяют, удовлетворяет ли или нет указанный, по меньшей мере, один количественный показатель критерию стационарности; и при установлении, что указанный по меньшей мере один количественный показатель удовлетворяет указанному критерию стационарности, сохраняют или выводят указанное изображение для использования в качестве сетки стационарного тренировочного образа при по меньшей мере одном многоточечном геостатистическом анализе, или при установлении того, что указанный по меньшей мере один количественный показатель не удовлетворяет указанному критерию стационарности, сохраняют или выводят указанное изображение для использования в качестве сетки нестационарного тренировочного образа при, по меньшей мере, одном многоточечном геостатистическом анализе. Технический результат: обеспечение возможности создания тренировочного образа, являющегося подходящим для многоточечных геостатистических способов, а также формирование структур данных, характеризующих свойства тренировочного образа, которое может быть использовано в многоточечных геостатистических способах. 22 з.п. ф-лы, 16 ил.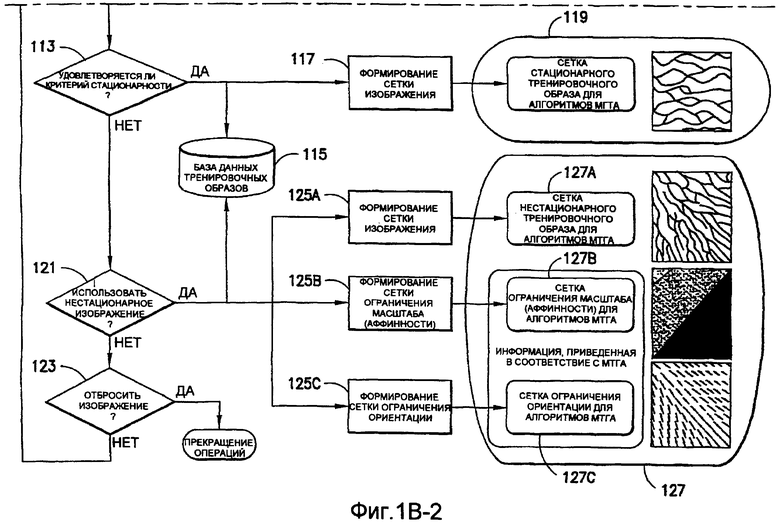
1. Способ оценки и анализа стационарности/нестационарности изображения, содержащий этапы, на которых:
с использованием компьютера анализируют цифровые данные, представляющие изображение, которое представляет собой одно из печатной копии изображения, цифрового изображения либо оба из них, чтобы сформировать по меньшей мере один статистический показатель, характеризующий стационарность изображения;
получают по меньшей мере один количественный показатель на основании по меньшей мере одного статистического показателя;
определяют, удовлетворяет ли или нет указанный, по меньшей мере, один количественный показатель критерию стационарности; и
при установлении, что указанный по меньшей мере один количественный показатель удовлетворяет указанному критерию стационарности, сохраняют или выводят указанное изображение для использования в качестве сетки стационарного тренировочного образа при по меньшей мере одном многоточечном геостатистическом анализе, или при установлении того, что указанный по меньшей мере один количественный показатель не удовлетворяет указанному критерию стационарности, сохраняют или выводят указанное изображение для использования в качестве сетки нестационарного тренировочного образа при, по меньшей мере, одном многоточечном геостатистическом анализе.
2. Способ по п.1, в котором:
указанный по меньшей мере один статистический показатель содержит множество статистических показателей, которые характеризуют стационарность поля ориентации, выделенного из указанного изображения.
3. Способ по п.2, в котором:
указанное поле ориентации вычисляют путем получения поля градиентов посредством двумерной конволюции над указанным изображением и затем выделения главной компоненты поля градиентов в пределах скользящего окна фиксированного размера путем использования анализа главных компонент.
4. Способ по п.3, в котором:
при двумерной конволюции используют фильтры Превитта.
5. Способ по п.2, в котором:
множество статистических показателей, которые характеризуют стационарность поля ориентации, включает в себя по меньшей мере один из следующих: (i) первый набор статистических показателей, которые характеризуют неравномерность поля ориентации и поэтому обеспечивают указание на то, что имеется одно или несколько предпочтительных направлений в сетке ориентации, (ii) второй набор статистических показателей, которые характеризуют нормальность распределения направлений в сетке ориентации и поэтому обеспечивают указание на то, что имеется главное направление в поле ориентации, и (iii) третий набор статистических показателей, которые характеризуют повторяемость поля ориентации, которые обеспечивают указание на то, что поле ориентации является аналогичным на протяжении различных зон изображения.
6. Способ по п.5, в котором:
множество статистических показателей вычисляют в пределах множества перекрывающихся зон в изображении.
7. Способ по п.5, в котором дополнительно:
получают первый количественный показатель на основании первого набора статистических показателей;
получают второй количественный показатель на основании второго набора статистических показателей;
получают третий количественный показатель на основании третьего набора статистических показателей; и
получают количественный показатель, который характеризует стационарность ориентации изображения, на основании первого, второго и третьего количественных показателей.
8. Способ по п.7, в котором:
количественный показатель, который характеризует стационарность ориентации изображения, вычисляют по взвешенному среднему первого, второго и третьего количественных показателей.
9. Способ по п.1, в котором:
указанный по меньшей мере один статистический показатель содержит множество статистических показателей, которые характеризуют стационарность масштаба указанного изображения.
10. Способ по п.9, в котором:
множество статистических показателей, которые характеризуют стационарность масштаба изображения, содержит расстояния между первым набором векторов признаков и вторым набором векторов признаков, при этом первый набор векторов признаков получают на основании первого набора изображений смещения, который формируют, подвергая изображение воздействию множества операций зависящего от поворота взятия выборок, а второй набор векторов признаков получают на основании второго набора изображений смещения, который формируют, подвергая эталонный образ, выбранный из изображения, воздействию операций зависящего от поворота и масштаба взятия выборок.
11. Способ по п.10, в котором:
при множестве операций зависящего от поворота взятия выборок используют взятие выборок в круговой окрестности вместе с преобразованиями ориентации; и
при множестве операций зависящего от поворота и масштаба взятия выборок используют взятие выборок в круговой окрестности вместе с преобразованиями как масштаба, так и ориентации.
12. Способ по п.11, в котором:
преобразования ориентации осуществляют в пределах заданного числа пар множителей аффинности.
13. Способ по п.10, в котором:
первый набор векторов признаков определяют, вычисляя матрицы смежности уровней серого по первому набору изображений смещения; и
второй набор векторов признаков определяют, вычисляя матрицы смежности уровней серого по второму набору изображений смещения.
14. Способ по п.10, в котором дополнительно:
образуют аффинную карту, которая характеризует расстояния между первым набором векторов признаков и вторым набором векторов признаков в пределах тренировочного образа.
15. Способ по п.14, в котором:
аффинная карта идентифицирует области изображения и конкретную пару множителей аффинности, связанных с каждой заданной областью, при этом образующие конкретную пару множители аффинности идентифицируют, уменьшая до минимума расстояние между векторами признаков первого набора, относящимися к заданной области и векторами признаков второго набора, относящимися к другим парам множителей аффинности.
16. Способ по п.14, в котором:
аффинная карта включает в себя подкарты, при этом каждая соответствует особой паре множителей аффинности, в котором заданная подкарта характеризует расстояния между векторами признаков первого набора и векторами признаков второго набора, относящимися к конкретной паре множителей аффинности заданной подкарты.
17. Способ по п.16, в котором:
каждая подкарта содержит множество полутоновых пикселов.
18. Способ по п.16, в котором:
каждая подкарта содержит множество двоичных пикселов.
19. Способ по п.14, в котором дополнительно:
визуально воспроизводят аффинную карту.
20. Способ по п.1, в котором:
указанный по меньшей мере один статистический показатель содержит множество статистических показателей, которые характеризуют стационарность распределения категорий указанного изображения.
21. Способ по п.2, в котором дополнительно:
сохраняют или выводят указанное поле ориентации для использования при по меньшей мере одном многоточечном геостатистическом анализе.
22. Способ по п.14, в котором дополнительно:
сохраняют или выводят указанную аффинную карту для использования при по меньшей одном многоточечном геостатистическом анализе.
23. Способ по п.1, в котором дополнительно:
применяют операции обработки изображения относительно отобранного изображения для формирования изображения, пригодного для анализа, при котором формируют по меньшей мере один статистический показатель, характеризующий стационарность изображения, при этом указанными операциями обработки изображения уменьшается число уровней серого/цвета отобранного изображения при сохранении геологической значимости присвоенных категорий отобранного изображения.
| БИОМАРКЕРЫ ДЛЯ ОЦЕНКИ ЭФФЕКТИВНОСТИ АЛИСКИРЕНА В КАЧЕСТВЕ ГИПЕРТЕНЗИВНОГО АГЕНТА | 2006 |
|
RU2408363C2 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Способ получения аллилбромида | 1987 |
|
SU1498748A1 |
| US 6813565 В1, 02.11.2004. | |||
Авторы
Даты
2010-06-10—Публикация
2006-07-10—Подача