Изобретение относится к области передачи информации и видеоинформационной техники и предназначено для преобразования, сжатия и восстановления одномерных и двумерных сигналов (изображений) в информационных системах.
Телекоммуникационные системы нового поколения ориентированы на передачу мультимедийной информации (речь, фото, видео). При этом весьма актуальным становится вопрос об устранении информационной избыточности из сигналов и разработке эффективных вычислительных процедур для реализации алгоритмов сжатия потоков информации и ее восстановления на приемном конце.
В настоящее время для целей информационного сжатия сигналов и изображений используются два принципиально разных подхода: 1) сжатие без потерь; 2) сжатие с регулируемыми потерями.
Первый подход не может дать существенного сжатия информационного потока.
Для сжатия информации, заключенной в аудио- и видеосигналах, целесообразен способ кодирования источника сигнала с регулируемыми потерями. В рамках этого подхода применяется линейное ортогональное преобразование: дискретное косинусное преобразование (ДКП) и его модификации.
Сжатие сигналов на основе ДКП реализовано в стандартах: JPEG - для статических изображений, Н.261-264, MPEG1-4 - для видео, звука - в стандарте МР3. Однако возможности данного преобразования в настоящее время исчерпаны.
Его недостатками являются: невысокий коэффициент сжатия сигнала, равный отношению количества информации в исходном сигнале к количеству информации в преобразованном сигнале, резкое ухудшение качества восстановленного сигнала с увеличением коэффициента сжатия. Матрица прямого и обратного преобразования ДКП является квадратной, что ограничивает возможность трансформации сигнала в потоке: исходный сигнал - спектр сигнала - восстановленный сигнал. Так масштабирование изображения можно осуществить только после его восстановления с помощью вспомогательных процедур интерполяции.
Таким образом, указанное линейное преобразование не может в полной мере удовлетворить всевозрастающие требования к системам передачи мультимедийной информации.
В аналоговой обработке сигналов предпринята попытка применения некоторых классических ортогональных полиномов (Лагерра, Лежандра) для преобразования одномерных сигналов как функции времени с помощью резистивно-реактивных RLC цепей. (Куля В.И. Ортогональные фильтры. - Киев: Техника, 1967, - 240 с., Горбацевич Е.Д. Коррелометры с аппроксимацией. - М.: Энергия, 1971. - 95 с.)
Однако в цифровых устройствах применение ортогональных полиномов приводит к трудно разрешимой проблеме бесконечных значений у весовой функции, сопутствующей ортогональному полиному и вычислению интегралов от быстро осциллирующих полиномов высокого порядка.
В работах (Радченко Ю.С. Оптимальные быстрые алгоритмы представления изображений в базисе ортогональных полиномов / Ю.С.Радченко, М.Ю.Радченко // Digital Signal Processing and its Applications: The 1 International Conference: DSPA'98, Moscow, Russia, 1998. - М., 1998. - Vol. IIIE. - P.104-107), (Радченко Ю.С. Алгоритм сжатия изображений на основе полиномиальных преобразований / Ю.С.Радченко // Цифровая обработка сигналов. - 2002. - №1. - С.2-6) теоретически показана возможность преобразования одномерных и двумерных сигналов с помощью особым образом дискретизированных ортогональных полиномов, обоснован способ неравномерной дискретизации сигналов, основанный на свойствах нулей ортогональных полиномов.
Наиболее близким по технической сущности к предлагаемому является способ, описанный в книге «Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео» / Д.Ватолин, А.Ратушняк, М.Смирнов, В.Юкин. - М.: Диалог-МИФИ, 2003. - 384 с., принятый за прототип.
Способ-прототип включает равномерную дискретизацию сигнала, разбиение отсчетов сигнала на блоки по N штук (N×N - для изображения), применение прямого дискретного косинусного преобразования для получения из N отсчетов сигнала N спектральных коэффициентов (N×N - для изображения), квантование спектральных коэффициентов, применение обратного косинусного преобразования для получения из N спектральных коэффициентов блока из N отсчетов восстановленного сигнала (N×N - для изображения).
Недостатками способа-прототипа являются:
- невысокий коэффициент сжатия сигнала;
- быстрая деградация восстановленного сигнала с увеличением сжатия;
- количество отсчетов неизменно в процессе преобразования «входной сигнал - спектр сигнала - восстановленный сигнал»;
- при масштабировании требуется использовать дополнительные алгоритмы интерполяции.
Задачей предлагаемого способа является повышение быстродействия вычисления компонент обобщенного спектра сигнала, уменьшение искажений восстановленного сигнала, обусловленных ошибками преобразования сигнала в спектр и спектра в сигнал, увеличение коэффициента сжатия сигнала и возможность осуществления масштабирования и сдвига восстановленного сигнала без дополнительной операции интерполяции над ним.
В заявляемом способе предлагается новый вид дискретных ортогональных преобразований для сжатия и восстановления сигнала изображения, основанный на применении произвольных ортогональных полиномов, неравномерной дискретизации по определенному закону сигналов и использовании квадратурных формул гауссовского типа.
Для решения поставленной задачи в способе дискретного преобразования сигналов на основе ортогональных полиномов, включающем равномерную дискретизацию сигнала, разбиение отсчетов сигнала на блоки, прямое преобразование сигнала в спектр, квантование спектральных коэффициентов, обратное преобразование спектральных коэффициентов в сигнал, согласно изобретению производят разбиение отсчетов сигнала на блоки по N1 штук, неравномерное прореживание блока из N1 до N отсчетов по закону расположения нулей ортогонального полинома pN(хi)=0, интерполяцию нулевого или первого порядка для получения N сэмплов s(xi), или неравномерную дискретизацию отрезка сигнала по закону, определяемому расположением нулей ортогонального полинома, для получения N сэмплов, N прямое полиномиальное преобразование 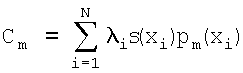 , m=0…(M-1), состоящее в умножении N сэмплов на матрицу преобразования с элементами pm(xi), m=0…(M-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М спектральных коэффициентов, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала
, m=0…(M-1), состоящее в умножении N сэмплов на матрицу преобразования с элементами pm(xi), m=0…(M-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М спектральных коэффициентов, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала 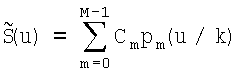 , где «u» переменная, которая используется как аргумент сдвинутого дискретного преобразования Фурье, при k=L/N1≠1 происходит эффект временного или пространственного масштабирования, а также любой заданный сдвиг восстановленного сигнала по времени или пространственной координате.
, где «u» переменная, которая используется как аргумент сдвинутого дискретного преобразования Фурье, при k=L/N1≠1 происходит эффект временного или пространственного масштабирования, а также любой заданный сдвиг восстановленного сигнала по времени или пространственной координате.
На фиг.1 представлена блок-схема устройства, реализующего предлагаемый способ при равномерной дискретизации; на фиг.2 - блок-схема устройства, реализующего предлагаемый способ при неравномерной дискретизации; на фиг.3 - образец расположения сэмплов; на фиг.4 приведены примеры преобразования на основе полиномов Чебышева с масштабированием k=0.5, 1, 2.
Из литературы известно, что сэмплы - значения сигналов в определенных точках, которые используются в дискретном преобразовании. Сэмплы могут формироваться путем неравномерной дискретизации сигнала либо на основе комбинации выборочных значений сигнала дискретизации с равномерным шагом (первичных отсчетов) (Ричардсон Я. «Видеокодирование. Н. 264 и MPEG-4 - стандарты нового поколения». - М.: Техносфера, 2005, с.29).
Предлагаемый способ заключается в следующем.
Производится равномерная дискретизация сигнала, разбиение отсчетов сигнала на блоки по N1 отсчетов (N1×N1 - для изображения), неравномерное прореживание блока из N1 отсчетов до N отсчетов по закону расположения нулей ортогонального полинома, интерполяция нулевого или первого порядка для получения N сэмплов или неравномерная дискретизация отрезка сигнала по закону, определяемому расположением нулей ортогонального полинома рN(хi)=0 с целью получения N сэмплов s(xi). Далее происходит прямое полиномиальное преобразование, состоящее в умножении N сэмплов на матрицу преобразования с элементами pm(xi), m=0..(M-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М коэффициентов разложения (обобщенного спектра).
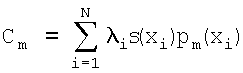 , m=0..(M-1),
, m=0..(M-1),
где xi - корни производящего полинома pN(xi)=0.
В общем случае M≤N. Следующими действиями будут: квантование коэффициентов разложения (обобщенного спектра) и обратное деквантование спектра при восстановлении сигнала, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала.
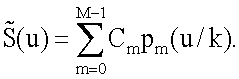
При k=L/N1≠1 возникает эффект временного или пространственного масштабирования. При восстановлении сигнала можно обеспечить заданный временной или пространственный, в том числе с субпиксельной точностью, сдвиг.
Предлагаемый способ может быть реализован, например, следующими техническими средствами.
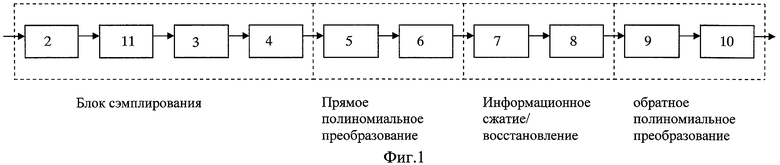
На фиг.1 представлена схема устройства, реализующего предлагаемый способ при равномерной дискретизации, где обозначено:
2 - аналого-цифровой преобразователь (АЦП);
3, 4 - процессоры, выполняющие функции прореживания, интерполяции и получения сэмплов;
5, 6 - процессоры, выполняющие функции умножения сэмплов на весовые коэффициенты и прямого полиномиального преобразования;
7, 8 - процессоры, выполняющие функции квантования и кодирования спектра сигнала, а также обратные операции декодирования и деквантования спектра;
9 - процессор, выполняющий обратное полиномиальное преобразование;
10 - сдвиговый регистр (буферная память), выполняющий вывод блока из L отсчетов сигнала (k=L/N1 - коэффициент масштабирования);
11 - запоминающее устройство (ЗУ) для блока отсчетов.
Устройство содержит блок сэмплирования, состоящий из последовательно соединенных АЦП 2, ЗУ для блока отсчетов 11, процессоров 3 и 4, выполняющих функции прореживания, интерполяции и получения сэмплов, а также процессоры 5 и 6, выполняющие функции умножения сэмплов на весовые коэффициенты и прямого полиномиального преобразования, процессоры 7 и 8, выполняющие функции квантования и кодирования спектра сигнала, а также обратные операции декодирования и деквантования спектра, процессор 9, выполняющий обратное полиномиальное преобразование и сдвиговый регистр (буферная память) 10, выполняющий вывод блока из L отсчетов сигнала (k=L/N1 - коэффициент масштабирования).
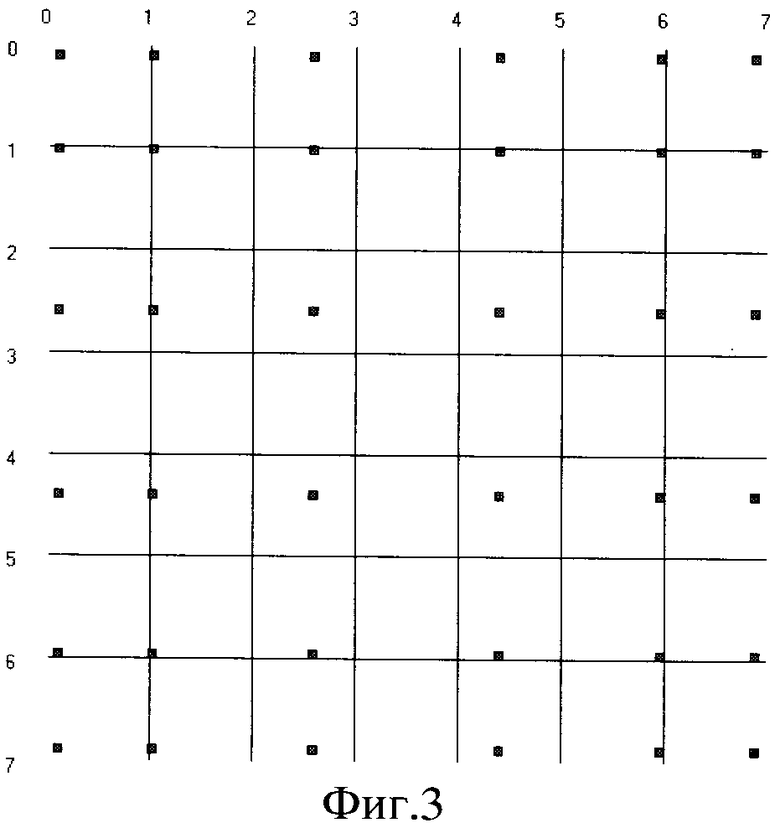
На фиг.2 представлена схема устройства, реализующего предлагаемый способ при неравномерной дискретизации, где обозначено:
1 - блок стробирования;
2 - управляемый аналого-цифровой преобразователь (АЦП);
5, 6 - процессоры, выполняющие умножение сэмплов на весовые коэффициенты и прямое полиномиальное преобразование;
7, 8 - процессоры, выполняющие квантование и кодирование спектра сигнала и обратные операции декодирования и деквантования спектра;
9 - процессор, выполняющий обратное полиномиальное преобразование,
10 - сдвиговый регистр (буферная память), выполняющий вывод блока из L отсчетов сигнала (k=L/N1 - коэффициент масштабирования).
Устройство содержит блок сэмплирования, состоящий из последовательно соединенных блока стробирования 1 и управляемого АЦП 2, а также процессоры 5 и 6, выполняющие функции умножения сэмплов на весовые коэффициенты и прямого полиномиального преобразования, процессоры 7 и 8, выполняющие функции квантования и кодирования спектра сигнала, а также обратные операции декодирования и деквантования спектра, процессор 9, выполняющий обратное полиномиальное преобразование и сдвиговый регистр (буферная память) 10, выполняющий вывод блока из L отсчетов сигнала (k=L/N1 - коэффициент масштабирования).
Приведем пример реализации способа-прототипа и предлагаемого способа.
Способ-прототип, рекомендуемый стандартами JPEG, MPEG2-4 обработки изображений, заключается в следующем. Предварительно оцифрованное изображение разбивается на блоки отсчетов N×N=8×8 пикселей. Матрица отсчетов умножается на квадратную матрицу размером 8×8 прямого косинусного преобразования, в результате чего получается матрица 8×8 спектральных коэффициентов. Далее элементы этой спектральной матрицы квантуются и кодируются, а результат этой операции запоминается либо передается по каналу связи.
При восстановлении сигнала после декодирования принятой информации спектральная матрица размером 8×8 умножается на матрицу обратного косинусного преобразования. Результатом является блок изображения N×N=8×8, подобный исходному.
Предлагаемый способ. Предварительно оцифрованное изображение разбивается на блоки отсчетов N1×N1=12×12 пикселей. Блок отсчетов N1×N1=12×12 преобразуется в матрицу сэмплов N×N=8×8 путем прореживания по закону расположения нулей ортогонального полинома 8 порядка. Такой ускоренный способ организации сэмплов представляет собой интерполяцию нулевого порядка для режима работы устройства с повышенным уровнем искажений сигнала. Для режима с минимальным уровнем искажений сигнала, требующего дополнительных операций, значения N×N=8×8 сэмплов уточняются путем интерполяции первого порядка. Образец расположения сэмплов приведен на фиг.3. Матрица сэмплов N×N=8×8 умножается на весовые коэффициенты, определяемые видом ортогонального полинома. Взвешенная матрица сэмплов умножается на прямоугольную матрицу размером 8×6 прямого полиномиального преобразования, в результате чего получается матрица М×М=6×6 коэффициентов обобщенного спектра. Далее элементы этой матрицы обобщенного спектра квантуются и кодируются, а результат этой операции запоминается либо передается по каналу связи.
При восстановлении сигнала после декодирования принятой информации обобщенная спектральная матрица размером М×М=6×6 умножается на прямоугольную матрицу M×L=6×24 обратного полиномиального преобразования. Результатом является блок изображения L×L=24×24 пикселей, который является масштабированным в k=L/N1=24/12=2 раза по размеру вариантом исходного блока. На фиг.4а, б, в, г приведены примеры такого преобразования на основе полиномов Чебышева с масштабированием k=0.5, 1, 2.
Таким образом, заявляемый способ использует меньшее количество отсчетов сигналов, обладает повышенной точностью вычисления обобщенного спектра и устойчивостью к искажениям при преобразовании и восстановлении сигнала. В процессе восстановления сигнала предлагаемый способ позволяет проводить его масштабирование и заданный сдвиг по времени или пространству.

Изобретение относится к области передачи информации и видеоинформационной технике и предназначено для преобразования, сжатия и восстановления одномерных и двумерных сигналов (изображений) в информационных системах. Техническим результатом изобретения является повышение быстродействия вычисления компонент обобщенного спектра сигнала, уменьшение искажений восстановленного сигнала, обусловленных ошибками преобразования сигнала в спектр и спектра в сигнал, увеличение коэффициента сжатия сигнала за счет дополнительного прореживания отсчетов по закону расположения нулей ортогонального полинома, возможность осуществлять масштабирование и сдвиг восстановленного сигнала без дополнительной операции интерполяции над ним. Производят разбиение отсчетов сигнала на блоки по N1 штук, неравномерное прореживание блока из N1 до N отсчетов по закону расположения нулей ортогонального полинома, интерполяцию нулевого или первого порядка для получения N сэмплов или неравномерную дискретизацию отрезка сигнала по закону, определяемому расположением нулей ортогонального полинома, для получения N сэмплов, прямое полиномиальное преобразование, состоящее в умножении N сэмплов на матрицу преобразования с элементами pm(xi), m=0…(M-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М спектральных коэффициентов, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала. 3 з.п. ф-лы, 4 ил.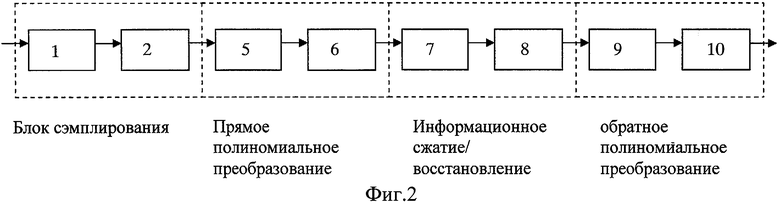
1. Способ дискретного преобразования сигналов на основе ортогональных полиномов, включающий равномерную дискретизацию сигнала, разбиение отсчетов сигнала на блоки, прямое преобразование сигнала в спектр, квантование спектральных коэффициентов, обратное преобразование спектральных коэффициентов в сигнал, отличающийся тем, что производят разбиение отсчетов сигнала на блоки по N1 штук, неравномерное прореживание блока из N1 до N отсчетов по закону расположения нулей ортогонального полинома pN(xi)=0, интерполяцию нулевого или первого порядка для получения N сэмплов s(xi) или неравномерную дискретизацию отрезка сигнала по закону, определяемому расположением нулей ортогонального полинома, для получения N сэмплов, прямое полиномиальное преобразование 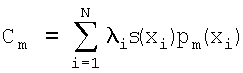 m=0…(M-1), состоящее в умножении N сэмплов на матрицу преобразования с элементами рm(хi), m=0…(М-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М спектральных коэффициентов, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала
m=0…(M-1), состоящее в умножении N сэмплов на матрицу преобразования с элементами рm(хi), m=0…(М-1) из отсчетов ортогональных полиномов и умножении на весовые коэффициенты λi, определяемые видом ортогонального полинома, для получения М спектральных коэффициентов, обратное полиномиальное преобразование М спектральных коэффициентов в L отсчетов сигнала 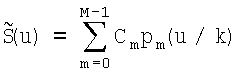 , при k=L/N1≠1 происходит эффект временного или пространственного масштабирования, а также любой заданный сдвиг восстановленного сигнала по времени или пространственной координате.
, при k=L/N1≠1 происходит эффект временного или пространственного масштабирования, а также любой заданный сдвиг восстановленного сигнала по времени или пространственной координате.
2. Способ по п.1, отличающийся тем, что матрица прямого полиномиального преобразования в общем случае прямоугольная, а векторы обобщенных спектральных коэффициентов Cm, m=0…(M-1) имеют размер М, не связанный с числом сэмплов N.
3. Способ по п.1, отличающийся тем, что восстановление сигнала производят с применением прямоугольной матрицы размером M×L обратного полиномиального преобразования по произвольной сетке отсчетов, позволяющий восстановить сигнал в любом масштабе и с заданным временным или пространственным, в том числе с субпиксельным, смещением.
4. Способ по п.1, отличающийся тем, что восстановленный сигнал является устойчивым к искажениям при преобразовании сигнала.
| ВАТОЛИН Д | |||
| Методы сжатия данных | |||
| Устройство архиваторов, сжатие изображений и видео | |||
| - М.: Диалог-МИФИ, 2003, с.384 | |||
| СПОСОБ ФИЛЬТРАЦИИ ПАРАМЕТРОВ ТРАЕКТОРИИ ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2307376C1 |
| JP 8275116 A, 18.10.1996 | |||
| Устройство для восстановления непрерывных функций по дискретным отсчетам | 1987 |
|
SU1495825A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
2010-11-27—Публикация
2008-11-05—Подача