Заявляемое изобретение относится к области ракетной техники и может быть использовано в системах наведения для формирования сигнала управления ракеты. Техническим результатом изобретения является повышение точности наведения ракеты на маневрирующую цель.
Известен способ формирования команд наведения управляемой ракеты с использованием пропорциональной навигации, в котором сигнал пропорциональный угловой скорости визирования цели несет информацию о мгновенном промахе, полученном в предположении, что начиная с данного момента времени движение ракеты и цели будет прямолинейным с постоянными скоростями (Крипецкий Е.И. Системы самонаведения. М.: Машиностроение 1970).
Недостатком известного способа является то, что с ростом ошибок определения оценки дальности «ракета-цель» точность наведения быстро снижается, особенно при перехвате маневрирующих целей.
Лучший результат можно получить в том случае, если задаться более правдоподобной гипотезой о будущем движении маневрирующей цели. Известен способ наведения, полученный в предположении, что начиная с данного момента времени, в которое выбирается управление, движение ракеты и маневрирующей цели будет происходить с постоянными осевой и нормальной перегрузками (Крипецкий Е.И. Системы самонаведения. М: Машиностроение 1970). Задаваясь различными критериями точности наведения, гипотезами о будущем движении маневрирующей цели и используя методы теории оптимального управления, можно получить различные методы наведения.
Основным недостатком известных способов является задание программы будущего движения маневрирующей цели, которая является неизвестной.
За наиболее близкий аналог (прототип) заявляемого изобретения принят способ наведения ракетой (патент №2148236 «Способ наведения ракеты на цель», 1999 г.). Он основан на определении параметров цели и ракеты: дальностей, скоростей, угла между их линиями визирования, угла между вектором скорости ракеты и линией визирования ракеты на цель, угловой скорости линии визирования. Управление ракетой производится с учетом текущего промаха. За счет определения угловой скорости линии визирования цели и текущего промаха, и использования их в управлении ракетой, увеличивается точность наведения ракеты на цель.
Основным недостатком известного способа является то, что отклонение реальной программы движения цели от расчетной приводит к увеличению промаха.
Перед заявляемым изобретением поставлена задача повысить точность наведения ракет при стрельбе по высокоскоростным и высокоманевренным целям.
Решение поставленной задачи достигается за счет прогнозирования гарантированного промаха, который не будет увеличиваться в процессе наведения при любом маневре цели.
В предлагаемом изобретении для вычисления сигнала наведения ракеты не требуется задания гипотезы о какой-либо программе движения маневрирующей цели, так как способ основан на информации о взаимном положении областей достижимости, которые строятся с учетом всевозможных программ движения, удовлетворяющих заданным ограничениям на управления.
Способ формирования сигнала управления ракеты при наведении на маневрирующую цель основан на расчете треугольных областей достижимости, учитывающих характерные точки областей достижимости ракеты и маневрирующей цели, и выборе управления ракеты на основе информации о положении наиболее удаленной вершины треугольной области достижимости маневрирующей цели относительно треугольной области достижимости ракеты для выбранного гипотетического момента встречи. Предлагаемый способ формирования управления базируется на решении антагонистической дифференциальной игры, в которой участвуют два игрока.
Заявляемый способ формирования управления ракеты при наведении на маневрирующую цель поясняется чертежами. На фиг.1 изображены области достижимости ракеты и маневрирующей цели. На фиг.2 изображены области достижимости ракеты и маневрирующей цели, аппроксимированные треугольниками в системе координат 01ξη.
Поставленная задача решается следующим образом. Пусть первый игрок действует в интересах ракеты и ищет минимум критерия
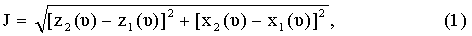
интересы второго игрока (маневрирующей цели) противоположны.
Здесь {zi, xi} при i=1 - координаты центра масс ракеты в горизонтальной плоскости, а при i=2 - маневрирующей цели. Момент ϑ определяется в процессе сближения, причем ϑ≤T, где T - заданное время.
Требуется найти управление ракеты, обеспечивающее минимум функционала (1) в момент времени ϑ в предположении, что интересы маневрирующей цели противоположны.
Для решения задачи используем геометрическую интерпретацию метода "экстремального прицеливания" (Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.). В данной игре оптимальными способами выбора управлений игроков являются позиционные стратегии. Однако решить конфликтную задачу сближения с использованием позиционных стратегий очень трудно. Для ее решения используем следующий подход.
Управление ракеты будем определять в дискретные моменты времени t0, t0+Δt, t0+2Δt и т.д., где Δt - шаг выбора управления.
Для выбора управления ракеты в позиции {t*, y1(t*)=y1*, y2(t*)=y2*} вместо решения позиционной задачи конфликтного управления перейдем к решению вспомогательной задачи программного управления и определим β1p(t*), а затем возьмем β1(t*)=β1p(t*) (Красовский H.H., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.). Здесь yi(t*) - фазовый вектор i-го игрока.
Сформулируем вспомогательную задачу программного оптимального управления.
Заданы начальные условия:
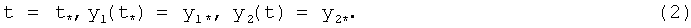
Требуется определить программу управления ракеты β1p(t), обеспечивающую минимум критерия (1) к гипотетическому моменту времени ϑ* в предположении, что интересы маневрирующей цели противоположны. Здесь t*≤ϑ*≤T. Управлениями являются углы скольжения, удовлетворяющие ограничениям
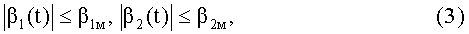
где βiм - максимально допустимый угол скольжения.
Вспомогательная задача программного управления может быть решена с использованием принципа максимума Л.С.Понтрягина (Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983. 392 с.), но это требует большого объема вычислений. Поэтому рассмотрим алгоритм для решения вспомогательной задачи оптимального управления, учитывающий особенности областей достижимости летательных аппаратов и особенности программ управлений, обеспечивающих попадание летательного аппарата на границу области достижимости.
Область достижимости летательного аппарата с аэродинамическим управлением в горизонтальной плоскости имеет вид, показанный на фиг.1. Границу Г1 области достижимости можно построить в результате многократного решения задачи о максимальном смещении летательного аппарата в направлении единичного вектора l (Толпегин О.А. Численные методы решения задач оптимального программного управления: Учеб. пособие / Ленингр. мех. ин-т. 1987. 88 с.). Границе Г2 соответствуют программы движения с максимальными углами скольжения и одним моментом переключения знака управления.
Оптимальные функции управления, обеспечивающие попадание летательного аппарата на границу Г1 можно аппроксимировать программами следующего вида:
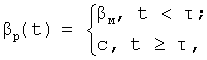
где C≤c≤βм, t*≤τ≤ϑ*.
Если экстремальная точка прицеливания ракеты находится на границе 1-3 области достижимости, то β1p(t*)=β1м, а если на границе 3-2, то β1p(t*)=-β1м. Если экстремальной точкой прицеливания ракеты является точка 3 области достижимости или область достижимости маневрирующей цели находится внутри области достижимости ракеты, то β1(t*)=0.
Таким образом, если оптимальная точка прицеливания находится на границе Г1, то требуется выбрать только знак оптимального управления ракеты в позиции {t*, y1(t*), y2(t*)}.
Знак оптимального управления ракеты будет выбран правильно, если область достижимости аппроксимировать треугольниками, проходящими через точки 1, 2 и 3 границы области достижимости, а гипотетический момент встречи ϑ* выбрать из условия наименьшего расстояния между треугольной области достижимости ракеты и наиболее удаленной вершиной треугольной области достижимости маневрирующей цели.
Граница 1-3 заменяется прямой 1-3, а граница 2-3 - прямой 2-3. Перемещение области достижимости при изменении гипотетического момента встречи ϑ* происходит по направлению вектора скорости для позиции, в которой выбирается управление. Поэтому экстремальная точка прицеливания ракеты всегда находится на выпуклой границе области достижимости ракеты.
В этом случае вогнутую часть границы области достижимости можно заменить прямой, проходящей через угловые точки области достижимости.
Аналогичные замены можно выполнить и для границы области достижимости маневрирующей цели.
Поэтому для решения вспомогательной задачи с переменным гипотетическим моментом встречи ϑ* области достижимости ракеты и маневрирующей цели заменяются треугольниками, две вершины которого совпадают с угловыми точками 1 и 2 области достижимости, а третьей вершиной является точка 3 на границе области достижимости.
При этом из геометрии области достижимости следует, что треугольные области достижимости гораздо точнее аппроксимируют области достижимости (например, по площади), чем эллипсоиды, целиком содержащие области достижимости, или расположенные внутри областей достижимости.
Вершины 1 соответствуют движению ракеты и цели по программе βi(t)=+βiм, вершины 2 - движению по программе βi(t)=-βiм, а вершины 3 - движению по программе βi(t)=0. Таким образом, для выбора управления ракеты в позиции {t*, y1(t*), y2(t*)} используется нижеприведенный алгоритм.
1. Одновременно интегрируются три системы дифференциальных уравнений для ракеты и три для маневрирующей цели на интервале времени от t=t* до t=T с начальными условиями (2). Первая система интегрируется с управлением βi(t)=βiм, вторая - с управлением βi(t)=-βiм, а третья - с βi(t)=0. Значения координат вершин (zi(t), xi(t)} запоминаются.
2. Задается начальное значение для гипотетического момента встречи ϑ*0=T.
3. Вводится вспомогательная прямоугольная система координат 01ξη (фиг.2). Ось 01η проходит через вершины 1 и 2 треугольной области достижимости ракеты, а ось 01ξ - через вершину 3. Координаты вершин треугольных областей достижимости ракеты и цели пересчитываются в новую систему координат.
4. Вычисляются расстояния от вершин треугольной области достижимости цели до треугольной области достижимости ракеты - r1(ϑ*0), r2(ϑ*0), r3(ϑ*0). Если какая-либо вершина треугольной области достижимости цели находится внутри или на границе треугольной области достижимости ракеты, то расстояние от этой вершины до треугольной области достижимости ракеты равно нулю.
5. Гипотетический момент встречи ϑ*0 уменьшается на величину Δϑ. Для нового гипотетического момента времени ϑ*1=ϑ*0-Δϑ выполняются п.3, 4 и находятся r1(ϑ*1), r2(ϑ*1), r3(ϑ*1) и т.д.
6. Гипотетический момент встречи уменьшается до момента ϑ*N, начиная с которого расстояния от всех вершин треугольной области достижимости цели до треугольной области достижимости ракеты возрастает.
Для каждого набора {(rj(ϑ*0), rj(ϑ*1), …, rj(ϑ*N) (j=1, 2, 3) находится наименьшее значение rjм и соответствующий гипотетический момент встречи 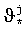 .
.
Определяется 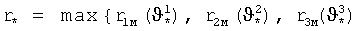 и гипотетический момент времени
и гипотетический момент времени 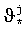 , соответствующий r*, принимается в качестве гипотетического момента времени встречи ϑ* для исходной позиции.
, соответствующий r*, принимается в качестве гипотетического момента времени встречи ϑ* для исходной позиции.
7. Управление ракеты в позиции (t*, y1(t*),y2(t*)} определяется соотношением
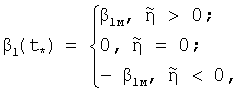
где 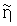 - координата наиболее удаленной вершины треугольной области достижимости цели от треугольной области достижимости ракеты, построенных для гипотетического момента встречи ϑ*. Например, на фиг.2 наиболее удаленной вершиной треугольной области достижимости цели от треугольной области достижимости ракеты является вершина 1.
- координата наиболее удаленной вершины треугольной области достижимости цели от треугольной области достижимости ракеты, построенных для гипотетического момента встречи ϑ*. Например, на фиг.2 наиболее удаленной вершиной треугольной области достижимости цели от треугольной области достижимости ракеты является вершина 1.
Управление ракеты выбирается в дискретные моменты времени t0, t0+Δt, t%+2Δt и т.д. С выбранным управлением ракета осуществляет движение в течение времени Δt. Одновременно маневрирующая цель совершает движение с некоторым управлением, неизвестным ракете. Для выбора управления маневрирующей цели можно использовать любую стратегию. Процесс сближения продолжается до минимального расстояния между ракетой и маневрирующей целью.
Таким образом изобретение позволило получить технический результат, а именно повысить точность наведения ракеты на цель, увеличить эффективность применения боевого снаряжения ракеты при стрельбе по высокоскоростным и высокоманевренным целям.
| название | год | авторы | номер документа |
|---|---|---|---|
| УЛУЧШЕННЫЙ СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ РАКЕТЫ ПРИ НАВЕДЕНИИ НА МАНЕВРИРУЮЩУЮ ЦЕЛЬ | 2017 |
|
RU2684432C2 |
| СПОСОБ ФОРМИРОВАНИЯ УПРАВЛЕНИЯ РАКЕТ ПРИ НАВЕДЕНИИ НА ГРУППУ МАНЕВРИРУЮЩИХ ЦЕЛЕЙ | 2010 |
|
RU2464520C2 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ СИСТЕМОЙ СТАБИЛИЗАЦИИ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2011 |
|
RU2487052C1 |
| СПОСОБ НАВЕДЕНИЯ РАКЕТЫ НА УЧАСТКЕ ВОЗРАСТАНИЯ СКОРОСТНОГО НАПОРА | 2006 |
|
RU2331839C1 |
| СПОСОБ КОМБИНИРОВАННОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2586399C2 |
| СПОСОБ НАВЕДЕНИЯ ТЕЛЕУПРАВЛЯЕМОЙ РАКЕТЫ | 2016 |
|
RU2645850C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ЛЕТАТЕЛЬНОГО АППАРАТА | 2012 |
|
RU2496081C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО НАВЕДЕНИЯ ОРУЖИЯ НА ПОДВИЖНУЮ ЦЕЛЬ | 2014 |
|
RU2555643C1 |
| СПОСОБ КОМАНДНОГО ТЕЛЕУПРАВЛЕНИЯ РАКЕТОЙ | 2000 |
|
RU2188381C2 |
| БОРТОВОЙ КОМПЛЕКС УПРАВЛЯЕМОГО СТАБИЛИЗИРОВАННОГО ПО КРЕНУ ЛЕТАТЕЛЬНОГО АППАРАТА С ТЕЛЕВИЗИОННОЙ ГОЛОВКОЙ САМОНАВЕДЕНИЯ | 2003 |
|
RU2239770C1 |

Способ включает измерение параметров движения маневрирующей цели и собственного движения ракеты и формирование сигналов управления ракеты. При осуществлении способа задают начальный гипотетический момент встречи, рассчитывают координаты вершин треугольных областей достижимости ракеты и цели в горизонтальной плоскости для этого момента встречи из позиции, соответствующей моменту выбора управления ракеты. Определяют расстояния от вершин треугольной области достижимости цели до области достижимости ракеты, которые совместно с гипотетическим моментом встречи запоминают. Варьируют гипотетический момент встречи в диапазоне от момента времени, в которое выбирают управление, до максимально допустимого момента окончания наведения. Для каждой вершины треугольной области достижимости цели находят свой оптимальный гипотетический момент встречи, соответствующий минимальному расстоянию между областью достижимости ракеты и этой вершиной. Запоминают оптимальные гипотетические моменты встречи для каждой вершины области достижимости цели и расстояние от этой вершины до области достижимости ракеты. Выбирают ту вершину области достижимости цели, которая при своем оптимальном гипотетическом моменте встречи имеет наибольшее удаление от области достижимости ракеты, и по взаимному расположению этой вершины и области достижимости ракеты, построенной для того же гипотетического момента встречи, выбирают управление ракеты. Технический результат заключается в повышении точности наведения ракеты, увеличении эффективности применения боевого снаряжения ракеты при стрельбе по высокоскоростным и высокоманевренным целям. 2 ил.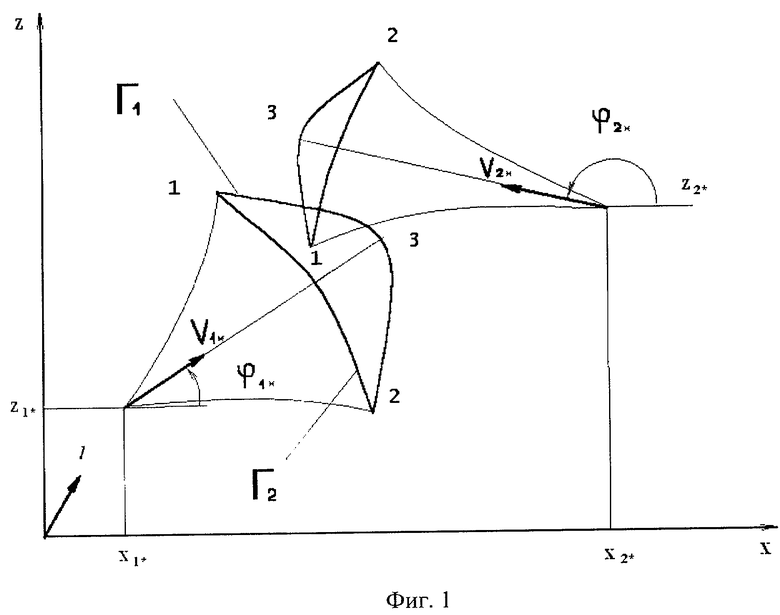
Способ формирования сигнала управления ракеты при наведении на маневрирующую цель, включающий измерение параметров движения маневрирующей цели и собственного движения ракеты, формирование сигналов управления ракеты, отличающийся тем, что задают начальный гипотетический момент встречи, который больше текущего момента времени и меньше максимально допустимого момента окончания наведения, рассчитывают координаты вершин треугольных областей достижимости ракеты и цели в горизонтальной плоскости для этого гипотетического момента встречи из позиции, соответствующей моменту выбора управления ракеты, при движении ракеты и цели с максимально допустимыми положительными углами скольжения, максимально допустимыми отрицательными углами скольжения и нулевыми углами скольжения, определяют расстояния от вершин треугольной области достижимости цели до области достижимости ракеты, которые совместно с гипотетическим моментом встречи запоминают, варьируют гипотетический момент встречи в диапазоне от момента времени, в которое выбирают управление, до максимально допустимого момента окончания наведения и для каждой вершины треугольной области достижимости цели находят свой оптимальный гипотетический момент встречи, соответствующий минимальному расстоянию между областью достижимости ракеты и этой вершиной, запоминают оптимальные гипотетические моменты встречи для каждой вершины области достижимости цели и расстояние от этой вершины до области достижимости ракеты, выбирают ту вершину области достижимости цели, которая при своем оптимальном гипотетическом моменте встречи имеет наибольшее удаление от области достижимости ракеты, и по взаимному расположению этой вершины области достижимости цели и области достижимости ракеты, построенной для того же гипотетического момента встречи, выбирают управление ракеты.
| СПОСОБ НАВЕДЕНИЯ РАКЕТЫ НА ЦЕЛЬ | 1999 |
|
RU2148236C1 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ РАКЕТОЙ | 2006 |
|
RU2335730C2 |
| KR 20060036439 A, 28.04.2006 | |||
| JP 5045094 A, 23.02.1993 | |||
| JP 10122795 A, 15.05.1998. | |||
Авторы
Даты
2011-05-20—Публикация
2009-07-20—Подача