Изобретение - цифровая вертушка для вычисления квадратов двузначных чисел - относится к учебным пособиям, помогающим устному счету.
Цифровая вертушка, формат которой задает телефонная Т-матрица, имеет две плоскости, поворачивающиеся вокруг общей оси. На основной и поворотной плоскостях изображены цифры. На основной плоскости нарисованы четные цифры 2, 4, 6 и 8 так, как они крестообразно изображены на телефонной Т-матрице: цифра 2 - сверху, 4 - слева, 6 - справа, 8 - снизу. Плоскость, называемая пропеллером, несет крестообразную фигуру из чисел 1, 4, 9, 16 (пифагоровы квадраты). Повороты пропеллера показывают соответствие цифр на подвижной и неподвижной плоскостях, позволяя прочитать цифры десятков и единиц ответов для разных диапазонов исходных данных.
Наиболее близким аналогом изобретения является вращающаяся таблица умножения, содержащая поворотную и неподвижную плоскости с изображениями цифр от 1 до 9, расположенными в виде Т-матрицы в три ряда и три столбца, и с прорезями в неподвижной плоскости, через которые видны цифры на подвижной плоскости, показывающие результат арифметического действия, причем цифры единиц результата умножения возникают как повороты матрицы единиц, размещенной на подвижной плоскости (см. патент RU N2139574, МПК 6 G09B 19/02, 1999).
Недостаток известного устройства заключается в том, что оно предназначено для умножения только однозначных чисел и не обеспечивает получение квадратов двузначных чисел.
Техническим результатом изобретения цифровых вертушек для вычисления квадратов двузначных чисел, использующих телефонную Т-матрицу, является непосредственное указание комбинаций цифр, помогающих запомнить полученные ответы. Технический результат достигается путем использования специальных свойств десятичных чисел на Т-матрице, показанных комбинациями цифр на двух плоскостях.
Цифра единиц E ответа задается лучом крестообразной фигуры пропеллера, цифра десятков D ответа указана тем же лучом среди четных цифр на основной плоскости. Цифры тысяч и сотен ответа вычисляются в уме исходя из известных квадратов полных десятков.
Указанный технический результат достигается тем, что в известной динамической модели, предназначенной для получения результатов умножения натуральных чисел A×B, содержащей поворачиваемые фигуры, соответствующие формату цифр телефонной Т-матрицы из трех строк и трех столбцов, расположенных в ячейках таблицы по правилам «плюс один» при шаге направо и «плюс три» при шаге вниз, согласно изобретению, содержит поворачиваемую крестообразную жесткую фигуру, лучам которой приписаны числа 1, 4, 9 и 16 в относительном порядке: 1 - сверху, 4 - слева, 9 - справа, 16 - снизу, позволяющую прочитать цифры квадратов двузначных чисел в сочетаниях цифр, возникающих при поворотах подвижной плоскости.
Изобретение поясняется следующими фигурами.
На фиг.1 показана поворотная плоскость цифровой вертушки, содержащая крестообразную фигуру, лучам которой приписаны числа 1, 4, 9 и 16 в порядке 1 - сверху, 4 - слева, 9 - справа, 16 - снизу.
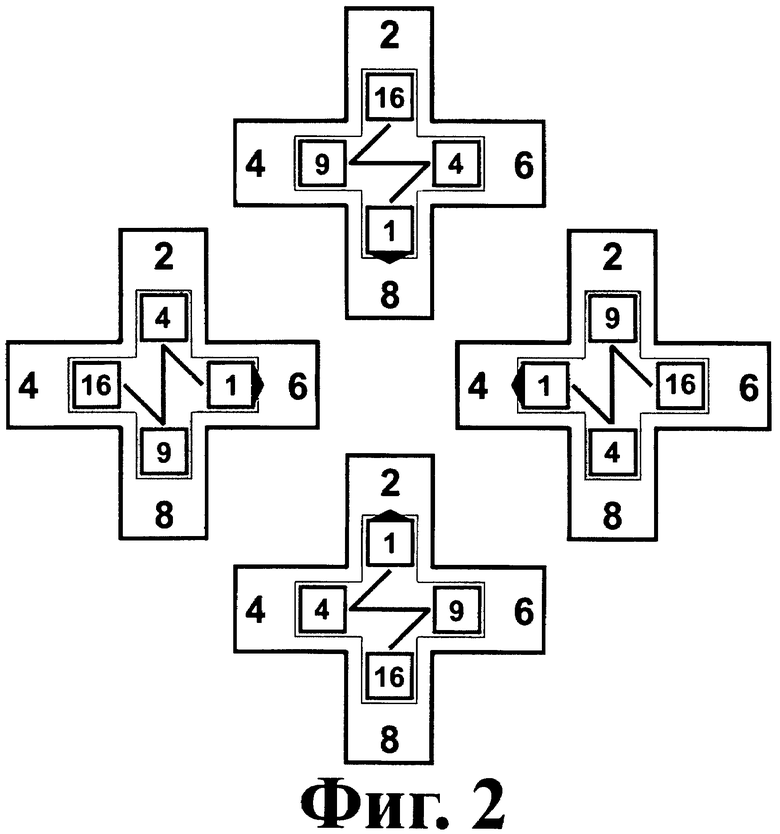
На фиг.2 изображены четыре положения поворота пропеллера по отношению к четным числам телефонной Т-матрицы, создающие на каждом луче комбинации цифр основной плоскости и пропеллера. Цифры десятков D ответов для квадратов двузначных чисел читаются на четном кресте. Цифры единиц Е ответов - на поворачивающемся пропеллере.
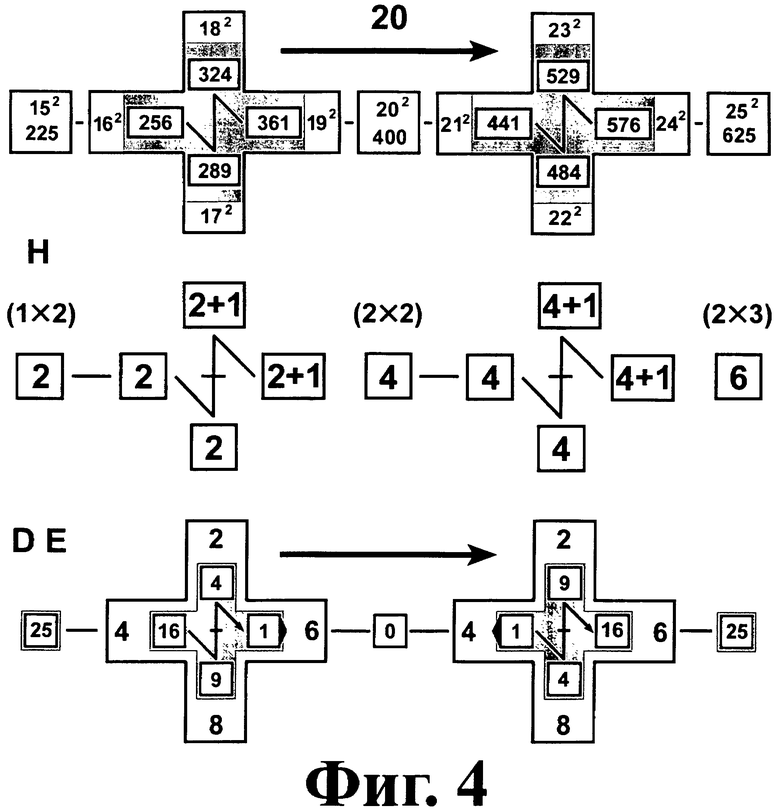
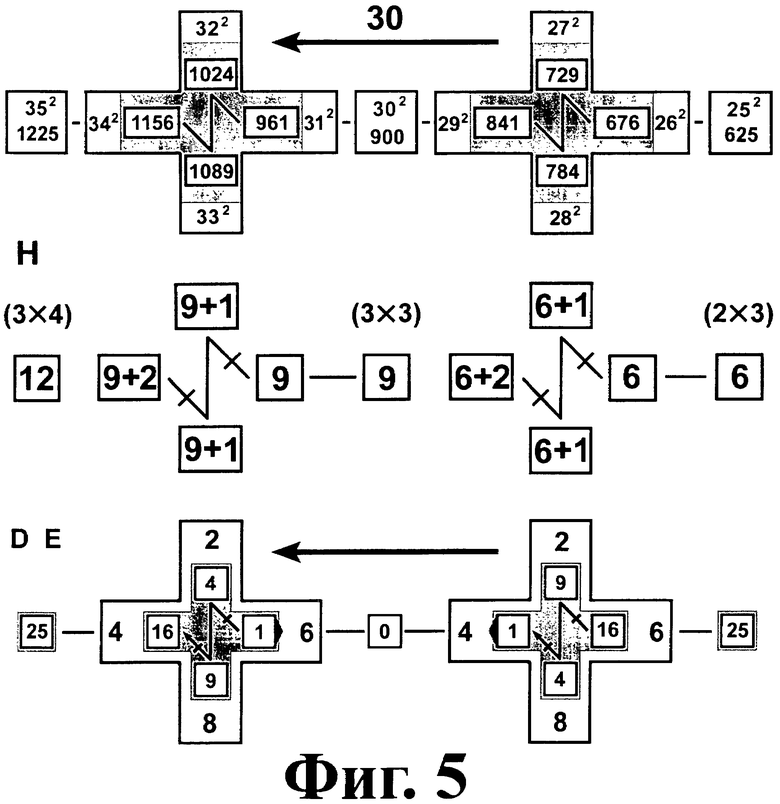
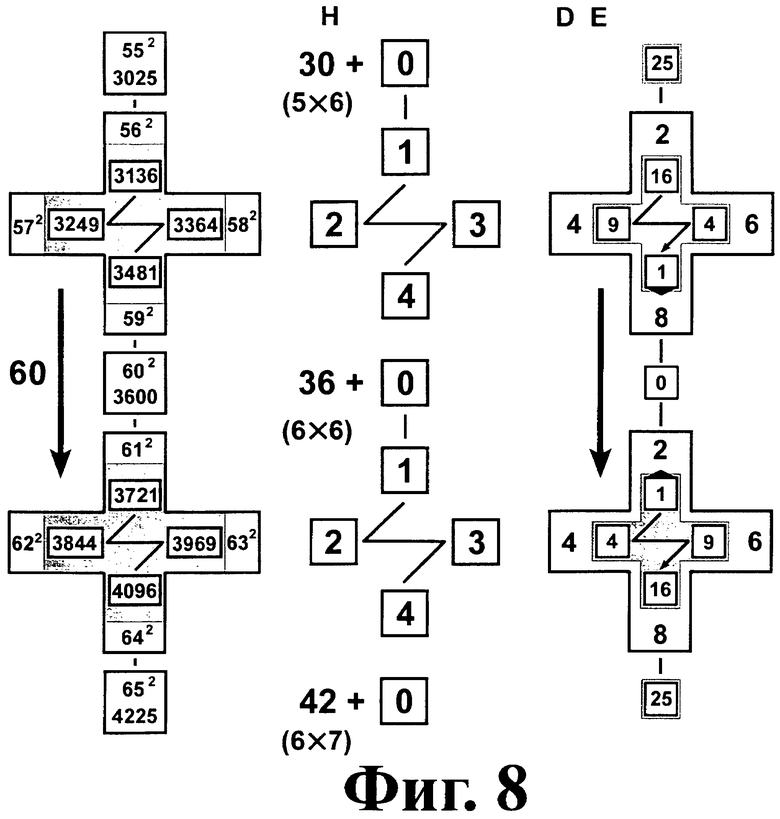
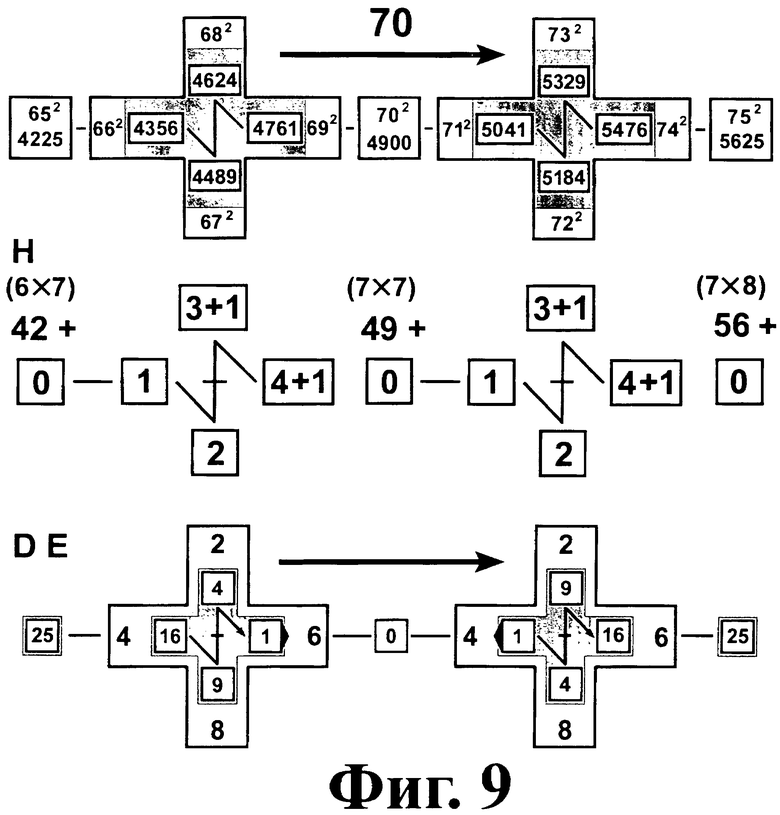
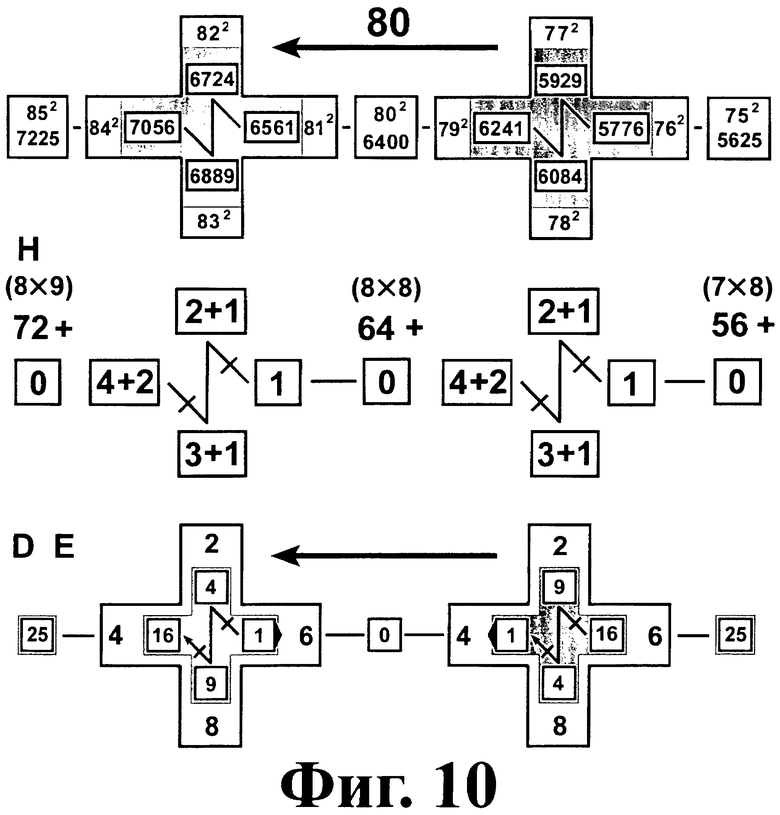
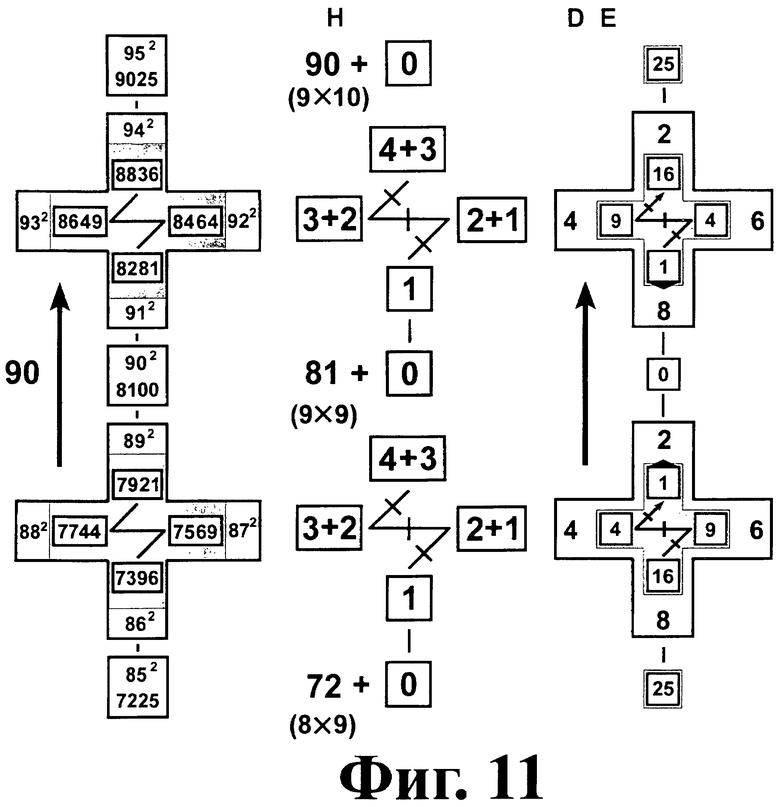
На фиг.3 - фиг.11 показаны схемы указания цифр десятков D и единиц E ответов, а также способы устного вычисления тысяч и сотен [Т, Н] для диапазонов множителей [5÷15], [15÷25], [25÷35], [35÷45], [45÷55], [55÷65], [65÷75], [75÷85], [85÷95].
Ситуация для диапазонов чисел, близких к 0, 50 и 100, является особой, так как нулевой цифры десятков D=0 нет на телефонной Т-матрице, поэтому цифра единиц Е должна быть прочитана с пропеллера без четных цифр телефонной Т-матрицы основной плоскости (фиг.7).
Конструкция цифровой вертушки для вычисления квадратов двузначных чисел состоит из неподвижной плоскости, на которой нарисованы четные числа {2, 4, 6, 8}, и поворотной плоскости - пропеллера.
На поворотной плоскости (пропеллере) крестообразно расположены числа 1, 4, 9 и 16 (пифагоровы квадраты): 1 - сверху, 4 - слева, 9 - справа, 16 - снизу (фиг.1). Лучи на пропеллере пронумерованы: номер A=1→1, A=2→4, A=3→9, A=4→16. Или же нумерация тех же лучей A=9→1, A=8→4, A=7→9, A=6→16. Цифра единиц для A×A равна цифре единиц 1, 4, 9 или 6 (для 16).
Поворот пропеллера на прямой угол совмещает крестообразные фигуры на пропеллере и основной плоскости (фиг.2).
Пропеллер цифровой вертушки, удобный для устного счета, содержит два жестко соединенных креста пифагоровых квадратов. Лучи одного креста пропеллера нумеруются числами 1, 2, 3, 4, другого креста - номерами 6, 7, 8, 9. Отдельные ячейки соответствуют номерам 0 и 5, в которых записаны числа 0 и 25. Нуль 0 размещен в этой конструкции пропеллера между двумя крестами. Луч пропеллера с номером 1 и луч с номером 9 показывают на ячейку 0. На основной плоскости изображаются кресты из четных цифр. Положение пропеллера для множителей диапазона [5÷15] показано на фиг.3.
Эта цифровая вертушка охватывает диапазоны по 11 множителей [5÷15], [15÷25], …, [85÷95] с центрами в полных десятках 10, 20, …, 90 (фиг.3-11).
Пусть [T, H, D, E] цифры ответа (10M+A)2, где разряды T - тысячи, H - сотни, D - десятки, E - единицы. При поворотах пропеллера из комбинаций цифр на подвижной и неподвижной плоскостях составляется две цифры ответа: D - десятки, читаемые на основе, и E - единицы на пропеллере.
Для полного десятка 10M число M называется базовым числом. Все множители, возводимые в квадрат, разделяем на отрезки {10M, 10M+1, …, 10M+5} и {10M-5, 10M-4, …, 10M}, близкие к полному десятку 10M. Числа меньше 10M представлены обычно как числа предыдущего десятка, например 40-2=38 или 30-4=26, в общем виде:
{10(M-1)+5, 10(M-1)+6, 10(M-1)+7, 10(M-1)+8, 10(M-1)+9, 10M}.
Случаи A=0 и A=5. Вычисление квадратов выполняется в уме (10M)2=100×M×M и (10M+5)2=100×M×(M+1)+25=[M×(M+1),2,5].
Случаи A≠0 и A≠5, тогда цифры ответа [D, E] для квадрата (10M+A)2 можно прочитать на цифровой вертушке, повернув пропеллер цифровой вертушки в определенное положение. Разряды тысяч и сотен [T, H] вычисляются устно по известным ответам.
Положение поворота пропеллера определяется следующим способом. Лучи 1 и 6 указывают одинаковую цифру на основе Z ∈ {2, 4, 6, 8}, которая определяет точку ориентации пропеллера. Для базового числа 1≤M≤4 начальное число Z=2M. Для базового числа 6≤M≤9 число Z=2M-10.
Для базовых чисел M=0, M=5 или M=10 точка ориентации Z=0. Цифры ответа E в этом случае читаются на пропеллере без четных цифр основной плоскости (фиг.7), так как здесь цифра десятков D=0.
Для квадратов двузначных чисел (10M+A)2 цифру единиц E указывает луч пропеллера с номером A. Этот же луч показывает цифру десятков D на четном кресте основной плоскости. Алгоритм применения цифровой вертушки для вычисления квадрата (10M+A)2 таков.
Шаг 1. Для множителя (10M+A) определяем ближайшее базовое число десятков M. Если 0≤A≤5, тогда базовое число равно M. Если 5<A≤9, тогда базовое число увеличиваем на единицу M+1.
Вычисляем начальное число Z=2M. Если Z≥10, тогда отбрасываем десятки в его записи. Поворачиваем пропеллер, имеющий две крестообразных фигуры так, что луч 1 и луч 6 указывают на точку ориентации Z на основной плоскости.
Шаг 2. Величина десятков D (до нормализации) указана лучом A на матрице из четных чисел.
Шаг 3. Величина единиц E указана лучом A на пропеллере. Составляем число 10D+E, дающее две последние младшие цифры в разряде десятков и единиц ответа.
Шаг 4. Число сотен и тысяч [T, H] определяется по базовому числу (10M)2 или (10M+5)2.
Способ устного вычисления цифр сотен и тысяч [T, H] следующий. Для пятерки чисел [10M, …, (10M+4)] начальное приближение [T0, H0]=M×M. Для пятерки чисел [10(M-1)+5, …, (10(M-1)+9)] меньше 10M начальное значение [T0, H0]=(M-1)×M.
Пусть базовое число M<5. Перемещаемся по лучам пропеллера в порядке возрастания номеров лучей 1, 2, 3, 4 либо 6, 7, 8, 9 до луча А. Сравниваем числа, указанные соседними лучами на четном кресте основной плоскости. Если на каком-то шаге перемещения четное число уменьшается (есть инверсия), тогда к сотням прибавляем единицу H0+1.
Пусть базовое число M≥5. Тогда к предыдущему промежуточному числу сотен [T, H] на каждом переходе к следующему лучу добавляем еще одну единицу [T, H]+1.
Источники информации
1. RU 2174713 С1 10.10.2001.
2. RU 2139575 С1 10.10.1999.
3. JP 2005148280 A, 09.06.2005.
4. US 3999310 A, 27.12.1976.
5. RU 2139574 С1 10.10.1999 /прототип/.
6. GB 2253507 А, 09.09.1992.
7. US 3787988 А, 29.01.1974.
8. GB 2066547 А, 08.07.1981.
9. US 3766667 А, 23.10.1973.
10. DE 2322005 А, 21.11.1974.



Изобретение относится к учебным пособиям, помогающим устному счету. Техническим результатом изобретения является непосредственное указание комбинаций цифр, помогающих запомнить полученные ответы. Динамическая модель, предназначенная для получения результатов умножения натуральных чисел А×В, содержащая поворачиваемые фигуры, соответствующие формату цифр телефонной Т-матрицы из трех строк и трех столбцов, расположенных в ячейках таблицы по правилам «плюс один» при шаге направо и «плюс три» при шаге вниз. Также содержит поворачиваемую крестообразную жесткую фигуру, лучам которой приписаны числа 1, 4, 9 и 16 в относительном порядке: 1 - сверху, 4 - слева, 9 - справа, 16 - снизу, позволяющую прочитать цифры квадратов двузначных чисел в сочетаниях цифр, возникающих при поворотах подвижной плоскости. 11 ил.
Динамическая модель, предназначенная для получения результатов умножения натуральных чисел А·В, содержащая поворачиваемые фигуры, соответствующие формату цифр телефонной Т-матрицы из трех строк и трех столбцов, расположенных в ячейках таблицы по правилам «плюс один» при шаге направо и «плюс три» при шаге вниз, отличающаяся тем, что содержит поворачиваемую крестообразную жесткую фигуру, лучам которой приписаны числа 1, 4, 9 и 16 в относительном порядке: 1 - сверху, 4 - слева, 9 - справа, 16 - снизу, позволяющую прочитать цифры квадратов двузначных чисел в сочетаниях цифр, возникающих при поворотах подвижной плоскости.
| ДИНАМИЧЕСКАЯ МОДЕЛЬ ТАБЛИЦЫ УМНОЖЕНИЯ, ИСПОЛЬЗУЮЩАЯ УКАЗАТЕЛИ ЦИФР, ПОНЯТНЫЕ ИНОПЛАНЕТЯНАМ | 2000 |
|
RU2174713C1 |
| СПОСОБ ОБУЧЕНИЯ И МОДЕЛЬ ТАБЛИЦЫ УМНОЖЕНИЯ/ДЕЛЕНИЯ НА ОСНОВЕ ДЕВЯТИ МАТРИЦ - ДЕВЯТИЛИСТНИКА, ОБЛАДАЮЩЕГО ДВУХУРОВНЕВЫМИ ЛОКАЛЬНЫМИ И ГЛОБАЛЬНЫМИ СИММЕТРИЯМИ | 1999 |
|
RU2139575C1 |
| JP 2005148280 A, 09.06.2005 | |||
| US 3999310 A, 27.12.1976. | |||
Авторы
Даты
2011-10-27—Публикация
2010-09-20—Подача